1 Introduction

Titanium alloy has become a preferable material for key parts in the aerospace industry due to its merits such as high strength, strong corrosion resistance, and low-temperature performance [1, 2]. Cutting tools meet new challenges as the manufacture of high-end equipment makes an increasing demand on the machining quality and efficiency of titanium alloy components. Nowadays, the frequently used ball-end milling cutters (BEMC) have large-curvature cutting edge and thus tend to shrink milling step to ensure good machined surface quality, but this decreases the efficiency of machining titanium alloy and meanwhile increases the manufacturing cost more or less [3, 4]. Therefore, it is essential and urgent to improve the efficiency of milling titanium alloy for its better application and promotion.

In designing processing tools for titanium alloy, Chen et al. [5] presented a new mathematical model for S-shaped edge curve. The model overcomes the complex computation and poor adaptability of the traditional modeling method and enhances the cutting efficiency and stability of BEMC. Masahiko et al. [6] developed successfully two types of BEMC with a unique cutting edge and verified experimentally that a high finishing accuracy and minor cutting forces were realized by the above-mentioned cutting tools. Engin et al. [7] established a generalized mathematical model of most helical end milling cutters and verified correctness of the model by the experiment on milling titanium alloy. Altinta et al. [8, 9] presented a generalized mathematical model for most helical end milling cutters and solved the problems of chatter vibrations, torque and power constraints, and dimensional form errors. Li et al. [10] presented a barrel-ball milling cutter for blisk machining, and proposed the selection of cutter parameter and calculation of cutter location.

Many scholars have researched the trajectory and posture of grinding wheel and novel methods for grinding. Ren et al. [11] proposed a novel method of five-axis flute grinding based on the theories of analytic geometry and envelope and verified the validity of the method by 3D simulations and machining experiments. The results show that this grinding method can effectively reduce the errors in grinding helical flutes. Pham et al. [12] proposed a manufacturing model of flat-end milling cutters using a five-axis computer numerical control grinding machine, based on the research into a given wheel profile and the relative movements between workpiece and grinding wheel. The model was practical and efficient for the manufacture of an end milling cutter. Wang et al. [13] generated a model of grinding wheel trajectory for machining helical grooves in terms of the grinding wheel’s position and orientation and provided a new approach for flute grinding of end milling cutters. Chen et al. [14] proposed new mathematical models and grinding methods of BEMC based on the orthogonal spiral cutting edge curve. It was found through the grinding experiments that both rake face with equal rake angle and flank face with equal clearance angle improved effectively chip removal conditions and machining performance of BEMC. Li et al. [15] reported a graphical analysis method to obtain the structural parameters and geometric shapes of helical grooves. Based on this, the influence of the geometry and grinding parameters of grinding wheels was discussed on radial rake angles, groove width, and core radius. Tang et al. [16] proposed three practical and reliable grinding methods based on the research into mathematical models of spiral grooves, conical flank, and cutter clearance and verified experimentally reliability of the proposed grinding methods. Chen et al. [17] presented a novel method to grind the rake face of a taper BEMC using a CBN spherical grinding wheel. This method used the self-adaptation characteristics of a sphere to decrease the number of simultaneous cooperative axes of the CNC tool grinder from 5 to 4. This boosted the grinding accuracy of rake faces. Chen et al. [18] carried out research on the design and manufacturing of new concave-arc ball-end milling cutters. By computing the radial and axial cutting speeds of the grinding wheel, an ideal geometric profile accuracy of milling cutters was obtained.

To sum up, the overall research into the milling cutters for machining titanium alloy mostly focuses on the designing, grinding and cutting performance of BEMC [19,20,21,22]. Nowadays, some companies such as Walter and Fraisa have proposed a few novel cutting tools for machining titanium alloy, such as NB-NVDS and MC230 Advance. The novel cutters partly increase the curvature of side cutting edge through reducing the edge radius of ball end and thus enhance side milling efficiency. Nonetheless, smaller radius of bottom edge increases grinding difficulty and decreases overall tool rigidity. Consequently, combined with the design idea for integration of tool design and manufacture [23], this paper employed the differential geometry method for designing a circular-arc milling cutter (CAMC) with large curvature, resolving the contradiction of the above novel cutters between edge radius of ball end and overall tool rigidity. This provides a new idea and method for the design and manufacture of milling cutters for machining titanium alloy.

2 Design of CAMC

2.1 Presentation of tool structure and establishment of geometric model

The CAMC designed in this paper is a rotary tool. The tool contour can be obtained by rotating the generatrix around the rotation axis. Figure 1 shows the generatrix of the CAMC in the X0OZ0 coordinates. The generatrix consists of end cutting edge AB, transitional arc BC, and circumferential cutting edge CD. The two parts of cutting edge are connected by the transitional arc. R1 stands for the arc radius of generatrix AB at the end cutting edge, and its circle center is expressed as O1. R2 stands for the arc radius of the generatrix at the circumferential cutting edge, and its circle center is expressed as O2. The radius of transitional cutting edge BC is expressed as r, and its circle center O3. In order to ensure that each section of the arc is tangent and the arc radius of the transitional cutting edge is reduced, the arc radius of circumferential cutting edge CD can be 4–12 times as long as that of the tool shank.

Figure 1.
figure 1

Generatrix of the CAMC

Full size image

Here, the equation for the generatrix of end cutting edge AB is expressed as follows:

$$ \left\{\begin{array}{l}x(u)={R}_1\sin \left(\frac{u}{R_1}\right)\\ {}z(u)=\sqrt{{R_2}^2-{\left[\left({R}_2-{d}_2\right)+{d}_1\right]}^2}-\sqrt{{R_1}^2-{d_1}^2}+{R}_1\cos \left(\frac{u}{R_1}\right)\\ {}\kern2em ={C}_2+{R}_1\cos \left(\frac{u}{R_1}\right)\end{array}\right.\kern0.5em 0\le u\le {k}_1 $$
(1)

In the above equation, u stands for the arc length from starting point A to any point on the generatrix AD and has a value range of 0 ≤ u ≤ k1.

Here are the equations for the generatrix of circumferential cutting edge CD:

$$ \left\{\begin{array}{l}x(u)={R}_2\sin \left(\frac{\left(u-{k}_1\right)+{k}_2}{R_2}\right)-\left({R}_2-{d}_2\right)\\ {}z(u)={R}_2-{R}_1\cos \left(\arcsin \frac{d_1}{R_1}\right)\\ {}\kern1.00em -{R}_2\cos \left(\frac{\left(u-{k}_1\right)+{k}_2}{R_2}\right)\end{array}\right.{k}_1\le u\le {k}_1+\left(0.5\pi {R}_2-{k}_2\right) $$
(2)

k1 and k2 are respectively expressed as follows:

$$ {\displaystyle \begin{array}{l}{k}_1={R}_1\arcsin \left(\frac{d_1}{R_1}\right)\\ {}{k}_2={R}_2\arcsin \left(\frac{\left({R}_2-{d}_2\right)+{d}_1}{R_2}\right)\end{array}} $$
(3)

Figure 2 displays the rotational contour of the CAMC in the coordinate system O(X0Y0Z0). Z0 stands for the rotational axis. The equation for the rotational contour surface of the CAMC is expressed as follows:

$$ {s}_m=\left[\begin{array}{c}x(u)\cos \left(\varphi \right)\\ {}x(u)\sin \left(\varphi \right)\\ {}z(u)\\ {}1\end{array}\right] $$
(4)
Figure 2.
figure 2

Rotational contour of the CAMC

Full size image

In the above equation, φ refers to the angle rotating around Z0 axis. The mathematical model for the structural contour surface of the CAMC is obtained by putting Eqs. (1) and (2) into Eq. (4). In order to facilitate the subsequent coordinate transformation of grinding wheel, the fourth row of the calculated pose matrix is set as 1. Here, the mathematical model for the generatrix of end cutting edge AB goes as follows:

$$ {s}_{mAC}={\left[{R}_1\sin \left(\frac{u}{R_1}\right)\cos \left(\varphi \right),\kern0.5em {R}_1\sin \left(\frac{u}{R_1}\right)\sin \left(\varphi \right),\kern0.5em {C}_2+{R}_1\cos \frac{u}{R_1},\kern0.5em 1\right]}^T $$
(5)

The mathematical model for the structural contour surface of circumferential cutting edge generatrix CD is expressed in the following:

$$ {s}_{mCD}=\left[\begin{array}{c}\left[{R}_2\sin \left(\frac{u-{k}_1+{k}_2}{R_2}\right)-\left({R}_2-{d}_2\right)\right]\cos \left(\varphi \right)\\ {}\left[{R}_2\sin \left(\frac{u-{k}_1+{k}_2}{R_2}\right)-\left({R}_2-{d}_2\right)\right]\sin \left(\varphi \right)\\ {}{R}_2-{R}_1\cos \left(\arcsin \frac{d_1}{R_1}\right)-{R}_2\cos \left(\frac{u-{k}_1+{k}_2}{R_2}\right)\\ {}1\end{array}\right] $$
(6)

The lead of the equal-lead edge curve of the CAMC is expressed in p. When a point on the edge line passes the rotational angle dφ of the tool shaft, the axial movement distance is equal to the product of the partial derivative of the edge line equation r to u and the generatrix distance differential variable du, expressed as follows:

$$ pd\varphi =\frac{\partial r}{\partial u} du $$
(7)

The expression of the equal-lead edge curve of the CAMC is obtained by integrating Eq. (7), as shown below:

$$ \varphi (u)=\int \frac{1}{p}\sqrt{{\left(x\hbox{'}\right)}^2+{\left(z\hbox{'}\right)}^2} du+\varphi c $$
(8)

c stands for the constant of integration, φc = 0. The equation for the edge curve of the CAMC is derived from simultaneous Eqs. (1), (2), (4), (5), and (8).

The equation for the end edge curve of the CAMC is expressed as follows:

$$ {r}_{AC}=\left[\begin{array}{c}{R}_1\sin \left(\frac{u}{R_1}\right)\cos \left(\frac{u}{p}\right)\\ {}{R}_1\sin \left(\frac{u}{R_1}\right)\sin \left(\frac{u}{p}\right)\\ {}{C}_2+{R}_1\cos \left(\frac{u}{p}\right)\\ {}1\end{array}\right] $$
(9)

The following is the equation for the circumferential edge curve of the CAMC:

$$ {r}_{CD}=\left[\begin{array}{c}\left[{R}_2\sin \left(\frac{u-{k}_1+{k}_2}{R_2}\right)-\left({R}_2-{d}_2\right)\right]\cos \left(\frac{u}{p}\right)\\ {}\left[{R}_2\sin \left(\frac{u-{k}_1+{k}_2}{R_2}\right)-\left({R}_2-{d}_2\right)\right]\sin \left(\frac{u}{p}\right)\\ {}{R}_2-{R}_1\cos \left(\arcsin \frac{d_1}{R_1}\right)-{R}_2\cos \left(\frac{u-{k}_1+{k}_2}{R_2}\right)\\ {}1\end{array}\right] $$
(10)

In selecting the parameters, it is necessary to ensure that the CAMC has a large circumferential cutting edge to improve cutting efficiency and avoid reducing the end cutting edge to improve the overall stiffness of the cutter. The common milling parameters are selected for numerical simulation. The arc radius R1 of the generatrix of end cutting edge AC was set as 6 mm and d1 4 mm; the arc radius R2 of the generatrix of circumferential cutting edge CD was set as 118 mm and d2 5 mm; lead p was respectively set as 8 mm, 12 mm, and 16 mm. The simulation results are shown in Figure 3.

Figure 3.
figure 3

Simulation of the equal-lead edge curve of the CAMC. a p = 8 mm. b p = 12 mm. c p = 16 mm

Full size image

2.2 Model for rake faces of the CAMC

Figure 4 shows rake and flank faces of the CAMC. In the figure, the base plane is set as Pr, the normal plane Pn, and the cutting plane Ps. The normal rake angle γn is defined as the angle between rake face Pf and base plane Pr, measured on the normal plane Pn. Nf (n1, n2, n3) stands for the unit normal vector of the rake face and Nb(n4, n5, n6) the one of the flank face.

Figure 4.
figure 4

Rake and flank faces of the CAMC

Full size image

The following equation is derived from the geometric angle relationship between the rake face and the base plane of the CAMC:

$$ {\displaystyle \begin{array}{l}\frac{1}{\sqrt{1+{\left(\frac{R_1}{p}\right)}^2\sin {\left(\frac{u}{R_1}\right)}^2}}\Big\{{n}_1\left[\cos \left(\frac{u}{R_1}\right)\cos \left(\frac{u}{p}\right)-\frac{R_1}{p}\sin \left(\frac{u}{R_1}\right)\sin \left(\frac{u}{p}\right)\right]\\ {}+{n}_2\left[\cos \left(\frac{u}{R_1}\right)\sin \left(\frac{u}{p}\right)+\frac{R_1}{p}\sin \left(\frac{u}{R_1}\right)\cos \left(\frac{u}{p}\right)\right]+{n}_3\sin \left(\frac{u}{R_1}\right)\Big\}=0\end{array}} $$
(11)
$$ {\displaystyle \begin{array}{l}\cos \left({\gamma}_n\right)=-{N}_f\cdotp {N}_r\\ {}=\frac{1}{\sqrt{1+{\left[\frac{R_1}{p}\sin \left(\frac{u}{R_1}\right)\right]}^2}}\Big\{-{n}_1\left[\sin \left(\frac{u}{p}\right)-\frac{R_1}{p}\sin \left(\frac{u}{R_1}\right)\cos \left(\frac{u}{R_1}\right)\cos \left(\frac{u}{p}\right)\right]\\ {}+{n}_2\left[\cos \left(\frac{u}{p}\right)-\left(\frac{R_1}{p}\right)\sin \left(\frac{u}{R_1}\right)\cos \left(\frac{u}{R_1}\right)\sin \left(\frac{u}{p}\right)\right]-{n}_3\frac{R_1}{p}{\sin}^2\left(\frac{u}{R_1}\right)\Big\}\end{array}} $$
(12)
$$ {n_1}^2+{n_2}^2+{n_3}^2=1 $$
(13)

The normal vector of the rake face Nf (n1, n2, n3) is obtained by solving simultaneous Eqs. (11), (12), and (13).

3 Manufacture and detection of the CAMC

3.1 Establishment of grinding model for the CAMC

For the establishment of the mathematical model for the grinding trajectory of the CAMC, the coordinates of any point in the grinding wheel coordinate system are needed to be converted to the workpiece coordinate system. Then the normal vector of the central point in grinding wheel was derived, based on the equations for edge curve as well as the relative position relationship between grinding wheel and workpiece. Furthermore, the mathematical model for grinding wheel position was deduced in milling. As is shown in Figure 5, in any position, the grinding wheel coordinate system Og—XgYgZg was first moved parallel along the Xg, Yg, and Zg axes and then rotated respectively around the Xg, Yg, and Zg axes. Here, the translational distance is respectively expressed as ax, ay, and az and the rotational angles φx, φy, and φz.

Figure 5.
figure 5

Conversion from grinding wheel to workpiece coordinate systems

Full size image

The conversion matrix from grinding wheel to workpiece coordinates is expressed as follows:

$$ {\displaystyle \begin{array}{l}o{A}_g= Rot\left({Z}_g,\varphi \right) Trans\left({a}_x,{a}_y,{a}_z\right) RPY\left({\varphi}_x,{\varphi}_y,{\varphi}_z\right)\\ {}\begin{array}{c}\begin{array}{c}\end{array}\end{array}\begin{array}{c}\end{array}=\left[\begin{array}{cccc}{\Delta}_1C{\varphi}_y& {\Delta}_1S{\varphi}_yS{\varphi}_x-{\Delta}_2C{\varphi}_x& {\Delta}_1S{\varphi}_yC{\varphi}_x+{\Delta}_2S{\varphi}_x& axC\varphi - ayS\varphi \\ {}{\Delta}_2C{\varphi}_y& {\Delta}_1S{\varphi}_yS{\varphi}_x+{\Delta}_1C{\varphi}_x& {\Delta}_2S{\varphi}_yC{\varphi}_x-{\Delta}_1S{\varphi}_x& axS\varphi + ayC\varphi \\ {}-S{\varphi}_y& C{\varphi}_zS{\varphi}_x& C{\varphi}_zC{\varphi}_x& az\\ {}0& 0& 0& 1\end{array}\right]\end{array}} $$
(14)

In the above equation, S, C, Δ1, and Δ2 are respectively abbreviations for sin(φ), cos(φ), cos(φ + φz), and sin(φ + φz).

The coordinates of the rotational contour surface of grinding wheel were put into the conversion matrix for calculation. For convenience of calculation, the fourth line of the position matrix is set as 1, and then the position matrix of the rotational contour surface of grinding wheel is derived in the workpiece coordinates, as shown below:

$$ {s}_{og}{=}^o{A}_g\cdot \left[\begin{array}{c}x(h)\cos (v)\\ {}x(h)\sin (v)\\ {}z(h)\\ {}1\end{array}\right]=\left[\begin{array}{l}{k}_3C{\varphi}_y C\varphi +{k}_4\left[S{\varphi}_yS{\varphi}_x C\varphi -C{\varphi}_x S\varphi \right]+\\ {}{k}_5\left[S{\varphi}_yC{\varphi}_x C\varphi +S{\varphi}_x S\varphi \right]+{a}_x C\varphi -{a}_y S\varphi, \\ {}{k}_3C{\varphi}_y S\varphi +{k}_4\left[S{\varphi}_yS{\varphi}_x S\varphi +C{\varphi}_x C\varphi \right]+\\ {}{k}_5\left[S{\varphi}_yC{\varphi}_x S\varphi -S{\varphi}_x C\varphi \right]+{a}_x S\varphi +{a}_y C\varphi, \\ {}-{k}_3C{\varphi}_y+{k}_4C{\varphi}_yS{\varphi}_x+{k}_5C{\varphi}_yC{\varphi}_x+{a}_z,\\ {}\begin{array}{ccc}& & \end{array}\kern1.50em 1\end{array}\right] $$
(15)

In the equation, h stands for the length of the grinding wheel generatrix and v the angle of the grinding wheel generatrix rotating around the Zg axis. k3, k4, and k5 are all relevant parameters of the rotational surface of grinding wheel. Their expressions are specifically as follows:

$$ {k}_3=x(h)\cos (v)\kern0.5em {k}_4=x(h)\sin (v){\displaystyle \begin{array}{cc}& \end{array}}{k}_5=z(h) $$

The unit normal vector nog of the central point Og in grinding wheel is expressed in the workpiece coordinates as follows:

$$ {\displaystyle \begin{array}{l}{n}_{og}{=}^o{A}_g\cdot \frac{1}{\sqrt{x\hbox{'}{(h)}^2+z\hbox{'}{(h)}^2}}\left[\begin{array}{c}z\hbox{'}(h)\cos (v)\\ {}z\hbox{'}(h)\sin (v)\\ {}-x\hbox{'}(h)\\ {}0\end{array}\right]\\ {}\kern0.5em =\left[\begin{array}{c}\begin{array}{l}-z\hbox{'}(h)C(v)C{\varphi}_y{\varDelta}_1-z\hbox{'}(h)S(v)\left[S{\varphi}_yS{\varphi}_x{\varDelta}_1-C{\varphi}_x{\varDelta}_2\right]\\ {}+x\hbox{'}(h)\left[S{\varphi}_yS{\varphi}_x{\varDelta}_1+S{\varphi}_x{\varDelta}_2\right],\end{array}\\ {}\begin{array}{l}-z\hbox{'}(h)C(v)C{\varphi}_y{\varDelta}_2-z\hbox{'}(h)S(v)\left[S{\varphi}_yS{\varphi}_x{\varDelta}_1-C{\varphi}_x{\varDelta}_2\right]\\ {}+x\hbox{'}(h)\left[S{\varphi}_yC{\varphi}_x{\varDelta}_2-S{\varphi}_x{\varDelta}_1\right],\end{array}\\ {}z\hbox{'}(h)C(v)S{\varphi}_y-z\hbox{'}(h)S(v)C{\varphi}_yS{\varphi}_x+x\hbox{'}(h)C{\varphi}_yC{\varphi}_x,\\ {}0\end{array}\right]\end{array}} $$
(16)

Based on the simultaneous solution for the rotational surface matrix of grinding wheel (Eq. (15)) and the structural contour surface equations of tools (Eqs. (5), (6)) in the workpiece coordinates, the grinding wheel position equation is derived during grinding the rake face of the CAMC, as shown in the following:

$$ {\displaystyle \begin{array}{l}{R}_1S\left(\frac{u}{R_1}\right)C\left(\frac{u}{R_1}\right)={k}_3C{\varphi}_y C\varphi +{k}_4\left[S{\varphi}_yS{\varphi}_x C\varphi -C{\varphi}_x S\varphi \right]\\ {}\begin{array}{cc}& \end{array}\kern1.50em +{k}_5\left[S{\varphi}_yC{\varphi}_x C\varphi +S{\varphi}_x S\varphi \right]+{a}_x C\varphi -{a}_y S\varphi \end{array}} $$
(17)
$$ {\displaystyle \begin{array}{l}{R}_1S\left(\frac{u}{R_1}\right)S\left(\frac{u}{R_1}\right)={k}_3C{\varphi}_y S\varphi +{k}_4\left[S{\varphi}_yS{\varphi}_x S\varphi +C{\varphi}_x C\varphi \right]\\ {}\begin{array}{cc}& \end{array}\kern1.50em +{k}_5\left[S{\varphi}_yC{\varphi}_x S\varphi -S{\varphi}_x C\varphi \right]+{a}_x S\varphi +{a}_y C\varphi \end{array}} $$
(18)
$$ {C}_2+{R}_1C\left(\frac{u}{R_1}\right)=-{k}_3C{\varphi}_y+{k}_4C{\varphi}_yS{\varphi}_x+{k}_5C{\varphi}_yC{\varphi}_x+{a}_z $$
(19)

The normal vector of the rotational surface of grinding wheel nog , the equation for the rotational contour surface of the tool generatrix, and the grinding wheel position equations (Eqs.(17), (18), (19)) are simultaneously solved, and thus the expressions for the normal vector of the rotational surface of grinding wheel is derived during grinding the rake face of the CAMC as follows:

$$ {n}_1(u)=\frac{-z\hbox{'}(h)C(v)C{\varphi}_y C\varphi -z\hbox{'}(h)S(v)\left[S{\varphi}_yS{\varphi}_x C\varphi -C{\varphi}_x S\varphi \right]+x\hbox{'}(h)\left[S{\varphi}_yS{\varphi}_x C\varphi +S{\varphi}_x S\varphi \right]}{\sqrt{x\hbox{'}{(h)}^2+z\hbox{'}{(h)}^2}} $$
(20)
$$ {n}_2(u)=\frac{-z\hbox{'}(h)C(v)C{\varphi}_y S\varphi -z\hbox{'}(h)S(v)\left[S{\varphi}_yS{\varphi}_x C\varphi -C{\varphi}_x S\varphi \right]+x\hbox{'}(h)\left[S{\varphi}_yC{\varphi}_x S\varphi -S{\varphi}_x C\varphi \right]}{\sqrt{x\hbox{'}{(h)}^2+z\hbox{'}{(h)}^2}} $$
(21)
$$ {n}_3(u)=\frac{z\hbox{'}(h)C(v)S{\varphi}_y-z\hbox{'}(h)S(v)C{\varphi}_yS{\varphi}_x+x\hbox{'}(h)C{\varphi}_yC{\varphi}_x}{\sqrt{x\hbox{'}{(h)}^2+z\hbox{'}{(h)}^2}} $$
(22)

In grinding the milling cutter, in order to ensure that the grinding wheel was in contact with the workpiece, the relative radial velocity at the contact point was kept 0. Thus, the equation for the relative velocity at the contact point was obtained by differentiating the t time on the position matrix of the rotational surface of the grinding wheel (Eq.(15)), as is shown in the following:

$$ \frac{ds_{og}}{dt}=\left[\begin{array}{l}\left(\begin{array}{l}{k}_3\left[-\varphi {\hbox{'}}_yS{\varphi}_y C\varphi -\varphi \hbox{'} S\varphi C{\varphi}_y\right]+{k}_4\Big[\varphi {\hbox{'}}_yC{\varphi}_yS{\varphi}_x C\varphi +\varphi {\hbox{'}}_xC{\varphi}_yS{\varphi}_x C\varphi \\ {}-\varphi \hbox{'}S{\varphi}_yS{\varphi}_x S\varphi +\varphi {\hbox{'}}_xS{\varphi}_x S\varphi -\varphi \hbox{'}C{\varphi}_x C\varphi \left]+{k}_5\right[\varphi {\hbox{'}}_yC{\varphi}_yC{\varphi}_x C\varphi -\varphi {\hbox{'}}_xS{\varphi}_yS{\varphi}_x C\varphi \\ {}-\varphi \hbox{'}S{\varphi}_yC{\varphi}_x S\varphi +\varphi {\hbox{'}}_xC{\varphi}_x S\varphi +\varphi \hbox{'}S{\varphi}_x C\varphi \Big]+a{\hbox{'}}_x C\varphi -{a}_x\varphi \hbox{'} S\varphi -{a}_y S\varphi -a{\hbox{'}}_y\varphi \hbox{'} C\varphi \end{array}\right.\\ {}\left(\begin{array}{l}{k}_3\left[-\varphi {\hbox{'}}_yS{\varphi}_y S\varphi +\varphi \hbox{'}C{\varphi}_y C\varphi \right]+{k}_4\Big[\varphi {\hbox{'}}_yC{\varphi}_yS{\varphi}_x\sin \varphi +\varphi {\hbox{'}}_xS{\varphi}_yC{\varphi}_x\sin \varphi \\ {}+\varphi \hbox{'}S{\varphi}_yS{\varphi}_x C\varphi -\varphi {\hbox{'}}_xS{\varphi}_x C\varphi -\varphi \hbox{'}C{\varphi}_x S\varphi \left]+{k}_5\right[\varphi {\hbox{'}}_yC{\varphi}_yC{\varphi}_x S\varphi -\varphi {\hbox{'}}_xS{\varphi}_yS{\varphi}_x S\varphi \\ {}+\varphi \hbox{'}S{\varphi}_yC{\varphi}_x C\varphi -\varphi {\hbox{'}}_xC{\varphi}_x C\varphi +\varphi \hbox{'}S{\varphi}_x S\varphi \Big]+a{\hbox{'}}_x S\varphi +{a}_x\varphi \hbox{'} C\varphi +a{\hbox{'}}_y C\varphi -{a}_y\varphi \hbox{'} S\varphi \end{array}\right.\\ {}\left(-{k}_3\varphi {\hbox{'}}_yC{\varphi}_y+{k}_4\left[-\varphi {\hbox{'}}_yS{\varphi}_yS{\varphi}_x+\varphi {\hbox{'}}_xC{\varphi}_yC{\varphi}_x\right]+{k}_5\left[-\varphi {\hbox{'}}_yS{\varphi}_yC{\varphi}_x-\varphi {\hbox{'}}_xC{\varphi}_yS{\varphi}_x\right]+a{\hbox{'}}_z\right.\\ {}0\end{array}\right] $$
(23)

The equations for the circumferential and end edge curves of the CAMC were put into the above equation set and solved, and thus the mathematical models for the grinding wheel position ax, ay, az, φx, φy, and φ were derived in grinding the rake face of the CAMC.

3.2 Manufacture and detection of the CAMC

The CAMC was ground on the SAACKE UWI five-axis grinding center, and the D64 flat grinding wheel and the 11V9 bowl-shape grinding wheel were used. The tool bar material is the K88UF carbide tungsten steel, its Rockwell hardness 91.7 HRA, and the particle size 0.8μm. The grinding site of the CAMC is shown in Figure 6.

Figure 6.
figure 6

Grinding site of the CAMC

Full size image

In order to ensure the cutting performance for the use requirements, the manufactured CAMC must be detected in the dimensional and angular accuracy. The Genius 3 tool test instrument made in ZOLLER company was used for measuring the accuracy, meeting the demand for the dimensional tolerance less than 0.01 mm and the angular tolerance less than 0.5°. The cutting parameters are detected as follows. For CAMC, the arc radius of end edge R1 is 6 mm, d1 4 mm, the arc radius of circumferential edge R2 118 mm, d2 5 mm, the arc radius of transitional cutting edge r 0.5 mm, and the lead parameter p 8 mm, while for BEMC, the arc radius of end edge is 5 mm and the helical angle of side edge 30°.

Figure 7 shows the site and results of detecting the contour accuracy of the machined CAMC by the tool test instrument. The red lines represent the theoretical contour and the blue ones the grinding tolerance zone in the figure. The test results of grinding accuracy show that the grinding accuracy of the circumferential edge contour of the CAMC met the requirements and there were minor errors in the upper end cutting edge and the transitional arc areas within the tolerance zone, so no impact was exerted on the normal use of the cutter. Furthermore, the derived equation for grinding the CAMC in this paper can meet the requirement for the accuracy range in practical machining, so the equation was proved correct and can be used for manufacturing cutting tools.

Figure 7.
figure 7

Site and results of detecting the contour accuracy of CAMC

Full size image

4 Comparative experiments on side milling of TC4

4.1 Experimental design

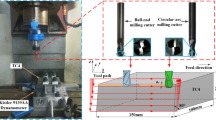
Aiming to evaluate the cutting performance of the CAMC, this paper designed comparative experiments on side milling of TC4 titanium alloy using the BEMC and CAMC, and the experimental site is shown in Figure 8a. The VDL-1000E three-axis milling center was selected as the machine tool. The two types of milling cutters for the experiments differed only in contour, while they were the same in other geometric parameters. Namely, the diameters were both 10 mm, the helical angles 30°, the rake angles 6°, the flank angles 12°, and the edge number 2. The tool material was cemented carbide tungsten steel, the coating material AlCrN, and the workpiece material TC4 titanium alloy with a dimension of 150 mm × 100 mm × 50 mm. In the cutting parameters, the milling velocity was 70 m/min, the feed per tooth 0.06 mm/z, the milling depth 0.2 mm, and the milling width 0.3 mm.

Figure 8.
figure 8

Experimental system and milling method. a Experimental system. b Milling method

Full size image

The CAMC and BEMC are mostly used for machining inclined end faces of titanium alloy components, and thus the workpiece surface to be machined was first made into an inclined plane at an angle of 80° to the horizontal plane before the experiment.

The CAMC and BEMC are mostly used for machining inclined end faces of titanium alloy components. In order to compare the side milling performance of BEMC and CAMC, the workpiece with 80° inclined surface is used for side milling. The specific milling method is shown in Figure 8b.

The Kistler 9139A three-component piezoelectric dynamometer was used in the experiments to collect milling forces. The milling cutter was removed after milling every 3 m, and then the VHX-1000 ultra-depth three-dimensional microscope and the SU3500 scanning electron microscope were used to observe and detect the tool wear morphology. Afterwards, the workpiece was removed, and then the Taylor Surface CCI white light interferometer was used for observing the surface morphology of the machined workpiece. Several standard CAMC and BEMC were ground and tested three times.

4.2 Analysis of cutting performance of the CAMC

Figure 9 shows the comparison of the unworn CAMC and BEMC in milling forces and chip morphology. It is observed from the figure that the tangential force generated by the BEMC was obviously more than that by the CAMC, while the peak values of radial forces were close to each other. This is because the CAMC has a cutting edge with larger curvature and this decomposed effectively the milling forces in the tangential and axial directions, naturally reducing the radial force. Based on the overall change tendency for the chip morphology and milling forces, the tangential and radial forces generated by the CAMC were more stable than the ones by the BEMC, and the chips coming from the former were less serrated. The reason for the above is that larger curvature of the CAMC cutting edge causes longer cutting edge involved in cutting, and chip thinning makes heat dissipation easier so that chips are easier to be removed, and thus milling forces are more stable.

Figure 9.
figure 9

Milling forces and chip morphology generated by the BEMC and CAMC. a BEMC. b CAMC

Full size image

Figure 10 shows the comparison of the two milling cutters in flank wear micromorphology and machined surface quality. At the milling length of 60 m, adhesion occurred on both flank faces, while a certain amount of coating peeling and tool tipping happened to the BEMC, causing poor surface quality of the machined workpiece. Compared with the BEMC, the CAMC showed no obvious tool tipping and realized relatively flat machined surface at the milling length of 120 m. Furthermore, the energy spectrum analysis was conducted of both milling cutters. Some elements such as O, W, Co, and Ti were found in Zone A of the BEMC, indicating that some diffusion wear occurred, while only the elements of Ti, Al, etc. from the workpiece were found on the flank face of the CAMC, showing that only coating peeling appeared. Here, it was found that the workpiece surface machined by the BEMC was characterized by a large fluctuation in peak and trough and the root mean square deviation of surface contour height arithmetic mean deviation of the surface contour height Sa was larger than that by the CAMC.

Figure 10
figure 10

Flank wear micromorphology and machined surface quality of BEMC and CAMC. a At the milling length of 60 m. b At the milling length of 120 m. c At the milling length of 60 m. d At the milling length of 120 m

Full size image

5 Conclusion

In this paper, the research was conducted on design, manufacture, and cutting performance of circular-arc milling cutters (CAMC) for machining titanium alloy. Based on the cutting experiments, a comparative analysis was made of milling forces, chip morphology, tool wear, and machined surface quality in milling titanium alloy with the CAMC and BEMC. The conclusions were drawn as follows:

  1. (1)

    The research on design of the CAMC was carried out. The contour equations for the end and circumferential cutting edges of the CAMC were derived by the differential geometry method, and on this basis, the mathematical model for the equal-lead helical edge line of the CAMC was established and verified by MATLAB.

  2. (2)

    The conversion matrix between grinding wheel and workpiece coordinates was derived, and the mathematical model for the rake face grinding trajectory of the CAMC was established. Grinding the CAMC and testing its geometric accuracy has realized evaluation for the grinding accuracy of developed cutting tools.

  3. (3)

    Compared with the BEMC, the CAMC shows greater curvature of cutting edge, making the tangential and radial forces more stable in machining. According to the chip morphology, the chips generated by the CAMC are less serrated than the ones by the BEMC, and the unit chip shows no large deformation so that the chip removal is easier.

  4. (4)

    By contrast with the BEMC, the CAMC is worn slower, shows no diffusion wear, and keeps better cutting performance. With increase of milling length, the residual height and roughness of the workpiece surface machined by the CAMC are still at a low level, and the surface contour changes slowly in shape and displays no obvious defects.