1 Introduction

The world market of micro-scale products grows with a speed of over 20% every year, a number of micro-components with a dimension ranging from 0.1 to 10 mm and feature dimension from 1 μm to 1 mm came into application [1], most notably in the industries of electronics and biomedical [2]. These micro-components are made of a variety of materials including metallic alloys, ceramics, and polymers. Among all the micro-fabrication methods, micro-milling is one of the most promising techniques for its outstanding machinability for a wide range of materials [3, 4]. Besides, compared to lithography, laser machining, and micro-electro-mechanical systems, micro-milling is capable of complex 3D structure fabrication [5].

In micro-milling process, the diameter of cutting tools varies from 0.05 to 1 mm [6]. With the decreasing of cutting tool’s diameter, the cutting tool rigidity reduces, and it is easier to break. Due to the limitations of cutting tool manufacturing technology, blunt radius cannot be reduced proportionally with the diameter decreasing, which makes micro-milling process different from macro-milling. Blunt radius of micro-milling tool usually ranges from 0.5 to 5 μm, which is similar to the range of feed per tooth. Therefore, cutting edge is not considered as absolutely sharp in micro end milling, and issues including minimum chip thickness, tool runout effect, and plowing effect occur [7]. As a manifestation of size effect, cutting force model is vital to optimize micro-milling process.

Tansel et al. found that the static force in the feed direction of micro end milling was a simple and reliable indicator of tool condition monitoring, including tool wear and cutting edge-damage, and thus proposed two methods for estimation of the static cutting force [8]. Bao and Tansel developed an analytical cutting force model to predict cutting force in micro end milling. The instant uncut chip thickness was calculated by considering cutting edge as a trochoidal trajectory [9]. However, tool runout was not considered in the proposed model. Further, the uncut chip thickness model was modified with consideration of tool runout. The tool runout can be estimated from experimental cutting force data [10]. Li et al. proposed a new model for determining the undeformed chip thickness in micro-milling [11]. The method was based on a true tooth path and using a Taylor’s series rather than numerical method for theoretical analysis. Dow et al. established a force model and calculated tool deflection [12]. The proposed model includes cutting force on rake face and friction on the flank face. Vogler et al. developed a cutting force model by considering the minimum chip thickness effect [13]. Cutting coefficients were obtained using finite element (FE) simulation. Bissacco et al. obtained the cutting coefficients by analytical expressions and proposed cutting force model [14]. Lai et al. modified a Johnson-Cook constitutive equation to model material strengthening behaviors [15]. An analytical model was developed based on FE simulation using slip-line theory. Malekian and Park identified cutting coefficients by a nonlinear curve fitting with minimized error through a steepest descent algorithm, and plastic recovery was included in the proposed model [16]. Jin et al. obtained the cutting coefficients based on FE simulation result [17]. In the proposed model, cutting coefficients were expressed as an exponential function of uncut chip thickness and cutting edge radius. Predicted cutting force well coincides with experimental data in the normal direction but less accurately in the feed direction. Jing et al. used a hybrid approach to develop a force model [18]. Cutting coefficients were obtained based on FE simulation. De oliveira et al. studies the size effect in different milling scales and found that size effect exists in both macro- and micro-milling [19]. The minimum uncut chip thickness varied approximately between 1/4 and 1/3 of tool edge radius. Grossi et al. studied cutting coefficient in milling operations and found it changes appreciably with spindle speed [20]. Mamedov et al. put forward a new model by considering tool deflection, but tool runout was not considered [21]. Thepsonthi et al. predicted cutting force totally based on FE simulation, but it is hard to set up a model of real tools due to different machining technology [22]. Zhang et al. established an accurate geometric model of instant uncut chip thickness for both plowing domain and shearing domain, and based on the geometric model, the error between predicted and experimental forces was below 16% [23]. Yuan et al. proposed a force model and discussed the influence of tool runout on cutting force. Single-edge-cutting phenomenon occurred when tool runout increases [24, 25]. Zhou et al. discussed tool runout effect in different situations and established an uncut chip thickness model and observed that elastic recovery has significant effect on cutting force at a low feed speed [26]. Zhang et al. modeled cutting force in micro flat end milling process and by considering tool runout and tilt deviation [27]. The influence of bottom edge effect can be significant when axial depth is small.

In most research, the cutting force model combined both analytical method and FE simulation. FE simulation was often used to obtain cutting force coefficients. Micro end milling is promising for its machinability of variety materials, but FE simulation is limited by its finite material library. Besides, a precise FE model of cutting tool is unreachable due to complex manufacturing technology of cutting tools. Blunt radius is discrepant even for the same series of cutting tools, and different coating layers behave differently in milling process. The minimum uncut chip thickness in above models was mainly estimated in an orthogonal FE simulation instead of experimental operation, which demands a higher accuracy of FE model. Some researchers calculate cutting coefficients with an analytic expression. However, tool geometric parameters still need to be measured with various instruments. There is also another way to obtain cutting coefficients by conducting orthogonal cutting experiments, which are costly and time-consuming for new combination of tools and materials.

In order to overcome limitation of current research, a new cutting force model is developed in micro end milling, which obtains cutting force coefficients using milling experiment instead of FE simulation and orthogonal cutting experiment. The proposed model is developed based on mechanistic model presented by Armarego, which is used to predict macro-milling force. The mechanistic model is adapted to micro end milling by taking tool runout and trochoid trajectory into account. A new method is proposed to measure tool runout precisely. The approach proposed in this paper can be easily extended to any milling process and estimate cutting force rapidly without huge amount of calculation.

This paper is organized as follows: Sect. 2 describes algorithm for calculating cutting coefficients and the mechanistic model of micro-milling force by consideration of tool runout. Section 3 shows the details of experiment setup and cutting parameters. Results are presented and discussed in Sect. 4 and followed by conclusions in Sect. 5.

2 Cutting force model

The cutting force model is based on the conventional generic mechanics of cutting approach theory proposed by Armarego [28]. The instantaneous tangential and radial components of cutting force are proportional to the cutting area. The cutting force model below takes the tool runout into consideration and utilizes a new way to predict cutting force coefficients based on experiment in specific cutting conditions.

2.1 Mechanical model of cutting force

During micro end milling, there exist two different material removal mechanisms, plowing effect and shear effect. Plowing effect is negligible when the feed per tooth is twice larger than minimum chip thickness. Thus, cutting force can be predicted in several specific cutting conditions without consideration of plowing effect. The general slot end milling process is shown in Fig. 1. The x axis and y axis are opposite to feed direction and cross the feed direction, respectively. To model cutting forces, the cutting tool is segmented into a number of elements along z axis with equal thickness dz; each element can be considered as an oblique cutting with an inclination angle equal to helix angle. Cutting force components of each element can be expressed by:

$$ \left\{\begin{array}{c}\mathrm{d}{Ft}_j\left(\theta \right)=\left[{K}_{te}+{K}_{tc}h\left(\theta \right)\right]\mathrm{d}z\\ {}\mathrm{d}{Fr}_j\left(\theta \right)=\left[{K}_{re}+{K}_{rc}h\left(\theta \right)\right]\mathrm{d}z\\ {}\mathrm{d}{Fa}_j\left(\theta \right)=\left[{K}_{ae}+{K}_{ac}h\left(\theta \right)\right]\mathrm{d}z\end{array}\right. $$
(1)

where dFtj(θ), dFrj(θ), dFaj(θ) represent the tangential, radial, and axial cutting force component at the rotation angle θ of jth cutting edge. Ktc, Krc, and Kac are the cutting force coefficients in tangential, radial, and axial directions, respectively. Kte, Kre, and Kae are the edge force coefficients in tangential, radial, and axial directions, respectively. h(θ) denotes the instantaneous uncut chip thickness at rotation angle θ. θ is measured clockwise from positive y axis relative to jth cutting edge. The rotation angle of element at axial location z of jth cutting edge can be expressed as θjz=θ+2jπ/N0-R·z·tanβ, where N0 is the number of cutting edges and β and R are helix angle and radius of cutting tool, respectively.

Fig. 1
figure 1

General slot milling process

Full size image

To transform cutting force components into milling coordinate, dFtj(θ,z) and dFrj(θ,z) are decomposed along x axis and y axis and added, which is shown as follows:

$$ \left\{\begin{array}{c}\mathrm{d}{F}_x=-\mathrm{d}{F}_t\cos \left(\theta \right)-\mathrm{d}{F}_r\sin \left(\theta \right)\\ {}\mathrm{d}{F}_y=\mathrm{d}{F}_t\sin \left(\theta \right)-\mathrm{d}{F}_r\cos \left(\theta \right)\end{array}\right. $$
(2)

As shown in Fig. 2, due to existence of helix angle, the height of element along axial direction can be expressed as:

$$ \mathrm{d}z=\frac{R\mathrm{d}\theta }{\tan \beta } $$
(3)

where R and dθ represent actual cutting radius and the radius of cutting edge’s projection on end face and β is helix angle of cutting tools.

Fig. 2.
figure 2

Relationship between dz and θ in cutting tool element

Full size image

Substituting Eqs. (3) and (2) into Eq. (1), the following equation can be obtained:

$$ \left\{\begin{array}{c}d{F}_x\left(\theta \right)=\left(-\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\cos \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{te}\right)\sin \left(\theta \right)\right)\frac{Rd\theta}{\tan \beta}\\ {}d{F}_y\left(\theta \right)=\left(\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\sin \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{te}\right)\cos \left(\theta \right)\right)\frac{Rd\theta}{\tan \beta}\\ {}d{F}_y\left(\theta \right)=\left({K}_{ae}+{K}_{ac}h\left(\theta \right)\right)\frac{Rd\theta}{\tan \beta}\end{array}\right. $$
(4)

By integrating the dFx, dFy, and dFa along the cutting edges, the resultant cutting forces in the x, y, and z directions can be obtained as follows:

$$ \left\{\begin{array}{c}{F}_x\left(\theta \right)={\int}_{\theta_l}^{\theta_u}\left(-\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\cos \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\sin \left(\theta \right)\right)\frac{R}{\tan \beta}\mathrm{d}\theta \\ {}{F}_y\left(\theta \right)={\int}_{\theta_l}^{\theta_u}\left(\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\sin \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\cos \left(\theta \right)\right)\frac{R}{\tan \beta}\mathrm{d}\theta \\ {}{F}_a\left(\theta \right)={\int}_{\theta_l}^{\theta_u}\left({K}_{ae}+{K}_{ac}h\left(\theta, z\right)\right)\frac{R}{\tan \beta}\mathrm{d}\theta \end{array}\right. $$
(5)

where θl and θu are the lower and upper integration limit angles. The relationship between θl and θu can be expressed by:

$$ {\theta}_u={\theta}_l+\frac{a_p\tan \beta }{R} $$
(6)

where ap and θl represent the cutting depth and rotation angle on the end face of cutting tool, respectively. R represents actual cutting radius.

Due to helix angle effect, cutting area is divided into three zones named as entry, intermediate, and exit zones, as shown in Fig. 3. Only in the intermediate zone is the cutting edge fully engaged into cutting. Integration limit in different cutting areas is shown in Table 1, where θs and θe represent start and exit angles, which will be discussed in the following sections.

Fig. 3
figure 3

Entry, intermediate, and exit zone

Full size image
Table 1 Integration limits in different cutting areas
Full size table

2.2 Tool runout effect

The ideal situation is that the geometry center of cutting tool should coincide with the spindle rotation center. However, due to manufacture tolerance and installation errors, the tool geometry center always deviates from the rotation center, which makes the effective radius of cutting tools different from nominal dimension, and tool runout phenomenon occurs [29]. In conventional milling, feed per tooth usually varies from dozens of microns to several millimeters. The tool runout is usually less than 1μm. Thus, the effect of tool runout is negligible in conventional milling process. However, in micro-milling process, the feed per tooth is usually just several microns or less, which is comparable to tool runout and will significantly influence the cutting force in micro end milling. Besides, due to lower strength and stiffness of micro-tools, runout will also cause much more vibration.

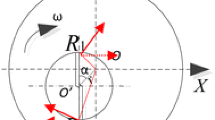
The cutting tool moves in a curve of uniparted hyperboloid due to tool runout and tilt. Since the cutting tool has two degrees of freedom including rotation about the z axis and transition along the z axis, four parameters need to be determined in order to describe the cutting tool spatial position and orientation, as shown in Fig. 4. Space angle of cutting tool and rotation axis is defined by γ. λ is measured when the cutting tool is paralleled with the yz plane. Axial offset and runout phase angle are defined by r and τ in end face of cutting tool. Cutting depth in micro end milling usually varies from several to dozens of micrometers, which is negligible compared to tool length. Hence, the tool runout r can be considered as a constant during milling process.

Fig. 4
figure 4

Model of tool runout: a axis offset and tilt, b tool runout in end face

Full size image

Cutting tool radii (NP and NQ) are the same in ideal situation. However, due to tool runout effects, actual cutting radii MP and MQ are different, which are hard to be measured directly. The difference between MP and MQ can be obtained directly by displacement sensor. ϕ and τ can be calculated from the result of displacement sensor, where ϕ represents the phase difference of two cutting radii. According to Fig. 4, Eqs. (7) and (8) can be obtained according to cosine formula:

$$ \cos \left(\varphi \right)=\frac{MQ^2+{MP}^2-{PQ}^2}{2\cdot MQ\cdot MP} $$
(7)
$$ \cos \left(\tau \right)=\frac{MN^2+{MP}^2-{PN}^2}{2\cdot MN\cdot MP} $$
(8)

where PN is ideal cutting tool’s radius R.

In order to obtain runout phase angle τ, two laser displacement sensors are fixed along the z axis at the height of rotational axis as shown in Fig. 5. Cutting tool rotates about point M. Laser sensor 1 returns two different minimum values when MP and MQ lie collinear with MB. Laser sensor 2 returns a maximum value when MN lies collinear with MB. By comparing the results of laser sensor 1 and 2, τ and ϕ can be calculated. The relationship between MQ and MP is given by:

$$ \Delta = MP- MQ $$
(9)

where Δ is peak difference of laser sensor 1 and it can be obtained in experiment.

Fig. 5
figure 5

Method of tool runout measurement

Full size image

Substituting Eq. (9) into Eq. (7), MP can be calculated by:

$$ MP=\frac{\sigma_1-\varDelta +\varDelta \cos \left(\varphi \right)}{2\left(\cos \left(\varphi \right)-1\right)} $$
(10)

where σ1 can be expressed as:

$$ {\sigma}_1=\sqrt{\left(\cos \left(\varphi \right)-1\right)\left({\varDelta}^2-8{R}^2+{\varDelta}^2\cos \left(\varphi \right)\right)} $$
(11)

Substituting Eq. (11) into Eq. (8), tool runout MN can be calculated as:

$$ MN=\cos \left(\tau \right) MP-\sqrt{\cos {\left(\tau \right)}^2{MP}^2+{R}^2-{MP}^2} $$
(12)

From Eq. (11), it is noted that actual cutting radius varies along the z axis due to tool runout and helix angle. As shown in Fig. 6, point N is geometry center of cutting tool. Rl and Rs represent the longer and shorter actual cutting radii in section △MPQ. Rl' and Rs' represent the longer and shorter actual cutting radii in section △MP'Q'. Ideal cutting radius PN rotates to line P'N in section M'P'Q. Rotation angle about point N can be expressed as follows:

$$ \angle {P}^{\hbox{'}} NP=\frac{z\tan \beta }{R} $$
(13)

where z is the distance from current section to end face along z axis.

Fig. 6
figure 6

Actual cutting radius of different z position, a section position, b cutting radius on different sections

Full size image

By solving above equations, Rl' and Rs' can be given as follows:

(14)

2.3 Algorithm for calculating instantaneous uncut chip thickness

The cutting force is determined by instantaneous uncut chip thickness. Thus, a precise algorithm for instantaneous uncut chip thickness is necessary for cutting force calculation. Conventional instantaneous uncut chip thickness can be approximately expressed as:

$$ h\left(\theta \right)={f}_z\sin \left(\theta \right) $$
(15)

where fz is feed per tooth.

Equation (15) is generally used to calculate the resultant cutting force in macro end milling for its conciseness. However, the tool runout and tool deflection are comparable to feed per tooth in micro end milling. These effects should be considered in instantaneous uncut chip thickness calculation.

Figure 6 demonstrates the cutting edge trajectory with consideration of tool runout. The position of cutting tool’s geometric center (green line) can be calculated by:

$$ \left\{\begin{array}{l}x= ft+{r}_0\sin \left(\omega t+\tau \right)\\ {}y={r}_0\cos \left(\omega t+\tau \right)\end{array}\right. $$
(16)

where r0 and ω denote the tool runout and angular velocity of cutting tool, respectively. t is the cutting time. The trajectory of cutting edges (blue and red lines) can be calculated by Eqs. (18) and (19).

$$ \left\{\begin{array}{l}{x}_s= ft+{R}_s\sin \left(\omega t+\varphi \right)\\ {}{y}_s={R}_s\cos \left(\omega t+\varphi \right)\end{array}\right. $$
(17)
$$ \left\{\begin{array}{l}{x}_l= ft+{R}_l\sin \left(\omega t\right)\\ {}{y}_l={R}_l\cos \left(\omega t\right)\end{array}\right. $$
(18)

where xs and ys represent coordinate of shorter cutting edge and xl and yl represent coordinate of longer cutting edge.

As shown in Fig. 7, cutting areas of first and second cutting edges are shown as blue and orange shadows, respectively. Under ideal condition, the blue line ABCD left by cutting edge 1 should be removed by cutting edge 2. However, due to tool runout, the actual cutting edge’s radius is different, and the blue line is removed from B to C; line segments AB and CD are formed and removed only by cutting edge 2, making two cutting edges’ instantaneous uncut chip thickness different.

Fig. 7
figure 7

Cutting edge trajectory

Full size image

One single turn is chosen to model the instantaneous uncut chip thickness, because the cutting process is endless repetitions. Blue line ABCD is assumed to be the start surface. At time tk, the cutting edge 1 is located at point P as shown in Fig. 9. Q represents the intersection point of Rs and start surface. PQ is considered to be the instantaneous uncut chip thickness. The coordinate of rotation center Otk is calculated as:

$$ \left\{\begin{array}{l}{x}_o={ft}_s\\ {}{y}_o=0\end{array}\right. $$
(19)

With coordinate of Otk and slope of line POtk, POtk can be given as:

$$ y=\left(x\hbox{-} {ft}_s\right)/\tan \left(\omega {t}_s+\varphi \right) $$
(20)

Substituting Eq. (18) into Eq. (20), a function about t can be calculated by:

$$ f(t)-{R}_l\cos \left(\omega t\right)-\left( ft+{R}_l\sin \left(\omega t\right)-{ft}_s\right)/\tan \left(\omega {t}_s+\varphi \right)=0 $$
(21)

Newton’s iteration method is utilized to solve the equation because f(t) is a nonlinear equation of t. The basic form of Newton’s iteration method is given as:

$$ {t}_{k+1}={t}_k-\frac{f\left({t}_k\right)}{f^{\hbox{'}}\left({t}_k\right)} $$
(22)

where tk is initial solution and f'(tk) is the derivative of f(t) at point tk, which can be expressed as:

$$ {f}^{\hbox{'}}(t)=-{R}_l\omega \sin \left(\omega t\right)-\left(f+{R}_l\omega \cos \left(\omega t\right){ft}_s\right)/\tan \left(\omega {t}_s+\varphi \right) $$
(23)

A proper initial value of tk is important for the Newton’s iteration method. Considering the phase difference of two cutting edges, t0 is chosen as the initial value of t and given by:

$$ {t}_0={t}_s-\frac{2\pi }{\omega {N}_0} $$
(24)

For any precision ϵ, the solution of tl can be solved according to Fig. 8.

Fig. 8
figure 8

Flowchart for calculating instantaneous uncut chip thickness

Full size image

When Rl is engaged in cutting, as drawn by ROtl in Fig. 9, the instant uncut chip thickness consists of two parts including curve AB and curve BF. At time tl, Rl is placed coincide with line ROtl, which can be expressed as:

$$ y=\left(x\hbox{-} {ft}_l\right)/\tan \left(\omega {t}_l\right) $$
(25)
Fig. 9
figure 9

Model of instantaneous uncut chip thickness calculation

Full size image

Substitute Eqs. (17) and (18) into Eq. (25), respectively, Eq. (27) can be obtained:

$$ \left\{\begin{array}{c}f\left({t}_{s1}\right)={R}_s\cos \left(\omega {t}_{s1}\right)-\left({ft}_{s1}+{R}_s\sin \left(\omega {t}_{s1}\right)\hbox{-} {ft}_l\right)/\tan \left(\omega {t}_l\right)=0\\ {}f\left({t}_{s2}\right)={R}_s\cos \left(\omega {t}_{s2}+\varphi \right)-\left({ft}_{s2}+{R}_s\sin \left(\omega {t}_{s2}+\varphi \right)\hbox{-} {ft}_l\right)/\tan \left(\omega {t}_l\right)=0\end{array}\right. $$
(26)

Finally, instantaneous uncut chip thickness can be calculated with ts1 in section AB and ts2 in section BF.

A series of tl can be calculated for a series of corresponding ts along curve ABCD. The instantaneous uncut chip thickness of Rs and Rl can be expressed as:

$$ {h}_{ts}=\left({x}_{ts}-{x}_{tl}\right)/\tan \left(\omega {t}_s+\varphi \right) $$
(27)
$$ {h}_{tl}=\min \left\{\left({x}_{tl}-{x}_{ts1}\right)/\tan \left(\omega {t}_l\right),\left({x}_{tl}-{x}_{ts2}\right)/\tan \left(\omega {t}_l\right)\right\} $$
(28)

A positive value of hts means cutting is in process, while a negative hts means not. The critical value between positive and negative value means start angle or end angle. Instantaneous uncut chip thickness of each element can be calculated in the same process.

2.4 Identification of cutting force coefficients

Cutting force coefficients will be estimated based on the cutting force model in this section. It should be noted that the cutting depth is constant during a slot milling process. The cutting force component is proportional to instantaneous uncut chip thickness. Thus, the resultant cutting force during the whole milling process is proportional to removal material volumes in a single turn of cutting tool. Without considering tool runout, removal material volumes are relative only to feed per tooth in case the cutting tool’s radius is determined. The proportion coefficients are relative only to the cutting force coefficients Ktc, Krc, and Kac. Thus, the helix angle can be no longer considered in the resultant force. To reduce the complexity of the formula, instantaneous uncut chip thickness can be approximately written as Eq. (15) because the removal material volume should be cared rather than the instantaneous value of uncut chip thickness.

Substituting Eq. (1) into Eq. (2), the component force dFxtj and dFyrj can be calculated as:

$$ \left\{\begin{array}{c}\mathrm{d}{F}_x=\left(-\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\cos \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\sin \left(\theta \right)\right)\mathrm{d}z\\ {}\mathrm{d}{F}_y=\left(\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\sin \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\cos \left(\theta \right)\right)\mathrm{d}z\end{array}\right. $$
(29)

Taking integration of Eq. (29) from z=0 to z=ap, instantaneous cutting force of a single cutting edge can be calculated as follows:

$$ \left\{\begin{array}{c}\mathrm{d}{F}_x=\left(-\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\cos \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\sin \left(\theta \right)\right){a}_p\\ {}\mathrm{d}{F}_y=\left(\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\sin \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\cos \left(\theta \right)\right){a}_p\end{array}\right. $$
(30)

where ap is the cutting depth.

Taking integration of instantaneous cutting force on θ, total force of a single cutting edge during one turn can be calculated by:

$$ \left\{\begin{array}{c}F{x}_{\mathrm{sum}}={\int}_0^{\uppi}\left(-\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\cos \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\sin \left(\theta \right)\right){a}_p\mathrm{d}\theta \\ {}F{y}_{\mathrm{sum}}={\int}_0^{\uppi}\left(\left({K}_{tc}h\left(\theta \right)+{K}_{te}\right)\sin \left(\theta \right)-\left({K}_{rc}h\left(\theta \right)+{K}_{re}\right)\cos \left(\theta \right)\right){a}_p\mathrm{d}\theta \\ {}F{z}_{\mathrm{sum}}={\int}_0^{\uppi}\left({K}_{ac}h\left(\theta \right)+{K}_{ae}\right){a}_p\mathrm{d}\theta \end{array}\right. $$
(31)

Integration limits of Eq. (31) vary from 0 to π, which are ideal entry and exit angles. Two cutting edges’ cutting conditions are all the same without considering tool runout effect. By simplifying Eq. (31), the following equation can be obtained:

$$ \left\{\begin{array}{c} Fx=-\frac{K_{rc}{a}_p\uppi}{2}{f}_z-2{a}_p{K}_{re}\\ {} Fy=\frac{K_{tc}{a}_p\uppi}{2}{f}_z+2{a}_p{K}_{te}\\ {} Fz=2{K}_{ac}{a}_p{f}_z+{a}_p\uppi {K}_{ae}\end{array}\right. $$
(32)

Equation (32) indicates that resultant force components are a linear function of fz, and the slopes are relative only to cutting force coefficients, and intercepts are relative only to cutting edge coefficients. The cutting force coefficients can be estimated with a linear fit of cutting force and feed per tooth.

3 Experimental setup

The validation of cutting force model is conducted by a series of micro slot end milling process. The details of experiment setup will be explained in this section. It should be pointed out in advance that due to size effect, the experiment is carried out in a small feed speed range to obtain cutting coefficients.

In order to verify the precision of cutting force model proposed above, a self-build machining system is used to conduct experiments. Two-edged solid carbide miniature end mills with radius of 0.2 mm and 0.4 mm (Karnasch Art. 3062020040010) are employed to perform end milling on copper alloy (T2Y). Helix angle of cutting tool is 30°. The workpiece is attached on a 3-component force sensor (Kistler 9317B), which has a sensitivity of −26pC/N in the x-y direction and −11pC/N in the z direction. Natural frequency of the force sensor is 5 kHz, and linearity error is less than 0.5% of full scale. Force sensor is mounted on a x-y linear stage with a high linearity of 3μm and a resolution of 1μm. In order to achieve a required cutting speed, an electric spindle (Nakanish BM 320) is used to perform milling process which has a max speed of 80,000 rpm and spindle runout less than 1μm. Schematic diagram of experiment is shown in Fig. 10.

Fig. 10
figure 10

Schematic diagram of experimental setup

Full size image

Force measurement system is made up of an 8-channel charge amplifier (Kistler type 5080A) and a DAQ system (Kistler type 5697A). The signal drift of charge amplifier under DC measuring mode is less than ±0.03mV/s. Thus, force acquisition is conducted separately in every feed procedure to avoid signal drift. DAQ system has a maximum sampling rate of 333kS/s with resolution of 16 bit for each channel. Two laser sensors with a repeatability of 0.025μm (Keyence LK-H050) are placed in a plane parallel with z axis to measure tool runout before cutting as shown in Fig. 11. In order to make sure laser sensors focus on the rotation axis, two y axis micro motion stages are used to mount laser sensors. Two laser sensors focus on the tool tip and tool shank, respectively, to obtain runout phase angle. Blunt radius of end mills is measured by Edge Master G4 Vc6 of Alicona. Cutting parameters are shown in Table 2.

Fig. 11
figure 11

Actual setup of experiment

Full size image
Table 2 Cutting parameters of experiment
Full size table

4 Results and discussions

4.1 Cutting force coefficients

Results of blunt radius measurement are shown in Fig. 12. Two different cutting radius end mills have similar blunt radii of 2.5μm and 2.8μm. The average cutting forces in different cutting parameters are shown in Fig. 13. Three linear models are used to analyze the influence of feed per tooth using Eq. (32). Three models’ coefficients are 0.9377, 0.9779, and 0.9792, respectively, which means force data has a good linear correlation. Cutting coefficients vary with tool’s diameter as shown in Table 3 even if they have similar blunt radii. A tool with a smaller blunt radius has larger cutting force coefficients. It can be explained with the fact that the contact length is larger at larger radius, which creates more friction. Besides, cutting coefficients may also be affected by manufacturing technique of cutting tools.

Fig. 12
figure 12

Measure result of blunt radius: a blunt radius of end mill R=0.2mm, b blunt radius of end mill R=0.4mm

Full size image
Fig. 13
figure 13

Average cutting force of 0.2-mm radius end mill at different feed speeds: a average cutting force in x direction, b average cutting force in y direction, c average cutting force in z direction

Full size image
Table 3 Cutting coefficients of different end mills
Full size table

4.2 Tool runout measurement

Figure 14 shows the result of tool runout measurement. Blue line has two peaks of different values during one revolution because of tool runout effect, corresponding to Rl and Rs in Fig. 6. Besides, phase difference of two peaks in the same line is not perfect 180°. τ is indicated by a difference of two different line peaks in Fig. 4. The difference of actual cutting radii MP and MQ can be measured directly in the diagram. Real cutting radii Rl and Rs are calculated to be 0.4003 mm and 0.3997 mm using Eqs.(7)–(14).

Fig. 14
figure 14

Experiment data of tool runout measurement (r=0.4mm)

Full size image

The influence of τ and r0 on actual cutting radius Rl is shown in Fig. 15. Tool runout r0 limits range of Rl and phase angle τ affects the value of cutting radius. When τ is about π/2, the tool runout has negligible effect on actual cutting radius. When phase angle equals to 0 or π, the change of actual cutting radius reaches to maximum value, and the difference between two cutting edge equals to twice of r0, which will increase the unevenness of tool wear. It is hard to fully eliminate the r0 in actual installation, but it can be reduced by adjusting phase angle τ. Besides, a cutting tool with more cutting edges can reduce the differences among cutting edges and has a better performance in cutting process.

Fig. 15
figure 15

Influence of τ and r0 on Rl

Full size image

The influence of τ and r0 on instantaneous uncut chip thickness in different situations is shown in Fig. 16. h(θ) represents instant uncut chip thickness. When cutting tool’s geometry center is placed perfectly at the rotation center, two cutting edges’ h(θ) is completely identical as shown in Fig. 16a. Figure 16b and c show the influence of tool runout and runout phase angle. The difference between two cutting edges rises with increasing of r0 and decreasing of τ, and τ has a more significant effect on h(θ). It can be inferred that h(θ) will reduce to zero with r0 increasing; then single-edge cutting occurs. Besides, the cutting edge which removes more material will have more severe wear.

Fig. 16
figure 16

h(θ) in different situations: a h(θ) of different feed per tooth fz (R=0.2mm), b h(θ) of different runout r0 (R=0.2mm, fz=3mm), c h(θ) of different runout phase angle τ (R=0.2mm, fz=3μm, r0=0.2μm)

Full size image

Tool runout has a significant impact on entrance angle and exit angle of Rs but has little effect on Rl. As shown in Fig. 17, where θls, θle, θss, and θse represent entrance angle of Rl, exit angle of Rl, entrance angle of Rs, and exit angle of Rs. The former surface is formed by Rl itself when Rl rotates into workpiece, which can be illustrated by point A in Fig. 9. Thus, the difference between two cutting radii has little effect on θls and θle, which is caused by tool runout. Entrance and exit angles of Rl are related only to feed speed, and they should be 180° and 360° when feed speed equals to zero. However, when Rs rotates into workpiece, the former surface is formed by Rl, which can be illustrated by point B in Fig. 9. Difference of Rs and Rl will rise with tool runout increasing, causing a larger entrance angle and smaller exit angle.

Fig. 17
figure 17

Cutting angle of Rs and Rl at different tool runouts

Full size image

4.3 Cutting force model validation

Figures 18 and 19 show the comparisons of predicted cutting forces and experimental results in different feed speeds. Fx and Fy are depicted with blue and red lines, respectively, and experimental force and predicted force are plotted by dotted lines and solid lines, respectively. There are two different peaks in one revolution because of tool runout effect; the longer cutting radius tends to have more uncut chip thickness and bear larger cutting force. The difference between the maximum value of predicted and experimental cutting forces in different feed speed is less than 8%, which is in good agreement with the research of Zhang et al. [7].

Fig. 18
figure 18

Comparison of predicted and experiment cutting forces (fz=2μm)

Full size image
Fig. 19
figure 19

Comparison of predicted and experiment cutting forces (fz=3 μm)

Full size image

Cutting force in z direction is not presented because it is negligible compared to x and y directions. It has been shown by Mittal et al. that axial cutting force has no significant effect to regenerative chatter [30].

Fig. 20 shows experimental cutting forces in x and y directions when fz is 0.5 μm. Theoretical cutting force should have only one peak in one revolution because the difference of Rl and Rs is larger than 0.5 μm. However, experimental result has a smaller peak because longer cutting edge will have more elastic deformation than the other, which makes actual difference between Rl and Rs slightly smaller than 0.6 μm. Besides, h(θ) is not only affected by the tool’s trochoidal trajectory, deflection, and tool runout, but also affected by the shape of previous formed surface including the chip thickness accumulation [31]. Hence, a smaller peak appears in Fig. 20.

Fig. 20
figure 20

Cutting force in the x and y directions (fz=0.5 μm)

Full size image

Fig. 21 shows cutting forces in x and y directions of different τ when fz is 2 μm and tool runout equals to 0.3 μm. With increasing of τ, the difference of two peaks during one revolution decreases, and two cutting edges have similar peak values until τ equals to π/2. It indicates that the effect of tool runout can be reduced by adjusting τ.

Fig. 21
figure 21

Predicted cutting forces with different τ when fz=2μm, r0=0.3μm. a τ=0. b τ=π/4. c τ=π/2

Full size image

5 Conclusion

In the paper, an accurate cutting force model in micro end milling has been developed based on a novel algorithm of instant uncut chip thickness. This model is fully based on experimental data and takes tool runout effect and minimum chip thickness into consideration. Based on the investigations conducted, the following conclusions can be obtained:

  • A new method is proposed to measure tool runout in micro end milling using laser displacement sensor. To avoid the effect of tool tilt, tool runout is measured at the end face instead of tool shank.

  • The tool is assumed to exist a parallel offset from rotation axis for calculating instant uncut chip thickness. The offset distance and phase angle are used to redefine cutting radii, which are used to calculate trajectory of cutting edge. Offset distance affects the actual instant uncut chip thickness, while runout phase angle determines the influence of offset distance. By adjusting runout phase angle, the influence of tool runout can be diminished.

  • Entry angle and exit angle are calculated according to instant uncut chip thickness. Tool runout affects only one cutting edge and has few influences on the other.

  • An experiment-based method is used to determine cutting coefficients. This method performs well in micro end milling though it was used in macro end milling. Maximum deviation between predictive and experimental cutting forces is less than 8%.

  • Cutting coefficients vary with blunt radius of tools, and larger blunt radius tends to have larger cutting coefficient. Even the same type of tools may have different cutting coefficients due to machining technology.