1 Introduction

With the development of overall design concept of aircraft, the demand for high-performance materials such as titanium alloys continues to increase. Especially for some new fighters, titanium alloys are used in large quantities as high as 41% [1]. In the field of advanced aviation manufacturing, the machining accuracy of titanium alloy thin-walled workpiece affects the service performance of aircrafts directly [2]. However, the processing chatter caused by its weak stiffness property damages the machined surface quality and results in poor geometrical accuracy inevitably [3]. Apart from this, the unstable milling environment is easy to bring about the machining deformation [4]. Therefore, the chatter problem of thin-walled parts has always been the focus of scholars. The existing research on vibration control of thin-walled workpiece milling involves two types mainly such as chatter avoidance and stability improvement [5].

In terms of the chatter avoidance, the stability lobe diagrams (SLDs) and online chatter detection are common methods. The former accomplishes offline predication while the latter could conduct online chatter recognition and machining parameters adjustment. For example, Altintas and Budak [6] presented a zero-order approximation way (ZOA) which was widely applied to obtain milling SLDs. Nevertheless, this method has difficulty to predict chatter stability boundary with little radial cutting depth accurately. The semi-discrete method (SDM) proposed by Insperger and Stepan [7] and second-order full-discretization method (FDM) presented by Ding et al. [8] solve this problem successfully. They have the advantage of high-precision simulation and serve the important avenues to obtain SLDs of thin-walled workpiece. In addition, Wan et al. [9] researched the SLDs construction mechanism of low stiffness machining system from the perspective of multiple modes and delays. Qu et al. [10] established a stability analysis model for thin-walled workpieces through assuming the tool as rigid body. According to tool position variation in the milling process, the three-dimensional SLDs were obtained. Yang et al. [11] found that the machining dynamic characteristic of thin-walled curved surface workpieces was related to tool length, machining position, and material removal which were important factors affecting the milling stability. Gao et al. [12] provided an online chatter detection approach based on continuous wavelet transform of acoustic signals in thin-walled component milling process. And the accuracy of this method was proved by the experimental results effectively. However, the above methods avoid milling chatter by reducing machining parameters and sacrificing processing efficiency.

Therefore, the stability improvement viewed as an alternative way is employed to solve the problem of milling chatter. For instance, Budak et al. [13] held view that the machining stability could be enhanced by optimizing system design parameters and operational parameters. Wan et al. [14] presented an idea that the dynamic characteristic of thin-walled workpiece could be strengthened by putting additional masses on it. As a result, the milling stability was improved apparently. A new type of vibration controller acted on workpieces was developed by Smis [15]. It could restrict machining vibration through adjusting its own stiffness and damping. Yang et al. [16] improved machining stability region through designing a device. It could generate forces to counteract processing vibration. Bolsunovsky et al. [17] presented a tuned mass damper to suppress milling chatter. These approaches mentioned above have achieved very good effect on chatter control of thin-walled workpiece. Nevertheless, most studies have failed to provide accurate SLDs for guiding actual production. And they have difficulty to improve the difficult-to-machine circumstance of titanium alloys thin-walled workpieces which is induced by its material property and structure feature. Titanium alloys milling is restricted to low spindle speed and little feed rate because of high cutting temperature and large cutting force.

Currently, ultrasonic vibration-cutting technology is widely applied for processing difficult-to-machine materials since it has the advantage of reducing milling force [18, 19], improving machined surface quality [20, 21] and strengthening structure stiffness [22]. Therefore, it is used to suppress milling chatter of titanium alloy thin-walled workpieces in this paper. Compared with the conventional milling, it achieves the pulsed intermittent cutting with tool-chip separation by adding an ultrasonic vibration signal to the cutter (or workpiece) [23, 24]. For the case of vibration acted on the tool (VAT), it is difficult to design an ultrasonic device since this equipment is mounted on the spindle rotating in processing [25]. Thereby, the majority of studies about ultrasonic milling are based on the vibration of workpiece (VOW) which is droved by the ultrasonic vibration workbench [26]. Nevertheless, the VOW restricts the size and weight of workpieces greatly. Especially for large aerospace parts, the working space of table and transducer load are hard to meet the processing requirements. Thus, its application is limited in the aviation industry. In this study, to avoid this problem, the ultrasonic vibration acts on the milling cutter called rotary ultrasonic milling (RUM). The published literatures [27,28,29] about the chatter stability focus on ultrasonic vibration milling with absolute separation of the tool and workpiece mainly. In this condition, the discontinuous feature of dynamic milling force contributes to the improvement of milling stability [30]. However, for the RUM with single axial ultrasonic vibration, it is difficult to make the cutter and workpiece separate completely during milling. As a result, the milling forces are continuous. Previous chatter stability models based on cutting separation effect are no longer suitable for RUM with non-separation characteristic. Therefore, in this paper, a novel stability analysis method is proposed for RUM thin-walled workpiece (RUM-tww). The effectiveness and accuracy of stability boundary obtained by SDM are proved by the experiments of RUM titanium alloy webs.

2 Motion characteristics of RUM-tww

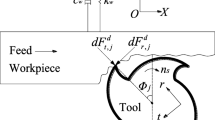
On the basis of common milling thin-walled workpiece (CM-tww), RUM-tww is added with a micron-level vibration effect along the axial direction of milling cutter. As shown in Fig. 1a, the high frequency ultrasonic vibration causes intermittent contact between the bottom of cutter and machined surface of workpiece. It affects the material removal inevitably with the changing of tool kinematic laws. Thus, the motion analysis is the basis and premise of constructing RUM-tww stability model.

Fig. 1
figure 1

A 3-DOF stability model of RUM-tww. a Front view of milling process. b Top view of milling process. c Velocity analysis. d Dynamic chip thickness. e Dynamic milling force

Full size image

2.1 Movement trajectory and velocity analysis

As presented in Fig. 1a, b, the point P is the any point on the cutting edge. H0 denotes the height of OP from the tool bottom (mm). Ot is coordinate origin. Z-axis represents positive direction of ultrasonic vibration. Y-axis is perpendicular to the X-axis while the X-axis along the feed direction. Without loss of generality, the point P is viewed as research object. The cutting movement is composed of axial ultrasonic vibration (Vv), circumferential rotation (Vc), and horizontal feed (Vf). Its motion trajectory can be expressed as follows:

$$ \left\{\begin{array}{c}{\zeta}_x(t)=R\ \mathit{\cos}\left(\omega t\right)+{V}_{\mathrm{f}}t\\ {}{\zeta}_y(t)=R\ \mathit{\sin}\left(\omega t\right)\\ {}{\zeta}_z(t)={H}_0+\left(S/1000\right)\mathit{\sin}\left(2\pi {f}_vt\right)\end{array}\right. $$
(1)

Where ζx(t), ζy(t), and ζz(t) are the track coordinates; R represents the tool radius (mm);ω is the angular velocity (rad/s); t is the time (s);S represents the ultrasonic amplitude (μm);fv is ultrasonic vibration frequency (Hz).

By differentiating the expression of ζz(t), the ultrasonic vibration velocity (Vv) can be written as follows:

$$ {V}_{\mathrm{v}}=2\pi {f}_v\cdotp \left(S/1000\right)\cdotp \mathit{\cos}\left(2\pi {f}_vt\right) $$
(2)

Figure 1 c describes the rate variation of RUM in single ultrasonic vibration period. Meantime, a new coordinate system is established based on the point P. The direction of ZA-axis is same as the Z-axis. The XR-axis indicates OP direction while the YC-axis represents the direction of cutting speed (Vc). The feed rate (Vf) is decomposed into XR and YC direction. They could be written as follows:

$$ {V}_{XR}={V}_f\cdotp \mathit{\sin}\left({\varphi}_j\right) $$
(3)
$$ {V}_{YC}={V}_f\cdotp \mathit{\cos}\left({\varphi}_j\right) $$
(4)

Among them, the VYC is much smaller than cutting speed (Vc). Thus, it could be ignored. In this study, φj denotes the radial immersion angle of tooth j. By considering the tool helix angle (λ), it can be expressed as follows:

$$ {\varphi}_j=\left(2\pi \mathrm{n}/60\right)\cdotp t+2\pi \left(j-1\right)/{N}_z-\left[{a}_p/(2R)\right]\cdotp \mathit{\tan}\ \lambda $$
(5)

where n denotes the spindle speed; Nz is the tooth number of milling cutter; ap represents the axial depth of cut.

2.2 RUM function angle definition

As illustrated in Fig. 1c, the addition of axial ultrasonic vibration makes the radial speed VXR of common milling move to VRv. And the VRv changes with the time t in single ultrasonic vibration period. In order to describe this variation clearly, an ultrasonic function angle (α) is defined according to the above motion analysis. The parameter α denotes the angle between VRv and the negative direction of ZA-axis. In the plane ZAPXR, it can be written as follows:

$$ \alpha =\left\{\begin{array}{c}\mathit{\arctan}\left|\frac{V_{XR}}{V_v}\right|,{V}_v\le 0\\ {}\pi -\mathit{\arctan}\left|\frac{V_{XR}}{V_v}\right|,{V}_v>0\end{array}\right. $$
(6)

It is worth noting that the ultrasonic vibration is along the negative direction of ZA-axis when Vv <0. At this time, α is an acute angle; when Vv >0, the tool vibrates along the positive direction of ZA-axis. Then, α is an obtuse angle; when Vv=0, α denotes right angle. As a result, the RUM turns into CM. The angle α varies with the time t in single ultrasonic vibration period. Thus, the axial ultrasonic vibration changes the direction of external excitation during RUM. It is very likely to affect the milling stability of thin-walled workpiece with low-stiffness.

3 Dynamic model of RUM-tww

During RUM-tww, the machine tool system could be assumed to be a rigid structure without occurring vibration. Generally, the stiffness of thin-walled workpiece is much smaller than machine tools. Modal property of the former occupies a dominant position on SLDs. In this study, the milling system of thin-walled workpiece is equivalent to a mass-spring-damping system as shown in Fig. 1a, b. Meantime, as presented in Fig. 1c, the high-frequency vibration of tool changes external excitation direction of thin-walled workpiece continuously in single ultrasonic vibration period. Thereby, the milling force of Z-direction should not be ignored. For RUM-tww, the dynamic differential equation with three degrees of freedom (3-DOF) can be defined as follows:

$$ \left[{M}_W\right]\ddot{\chi}+\left[{C}_W\right]\dot{\chi}+\left[{K}_W\right]\chi =\left[{dF}_W\right] $$
(7)

where MW, CW, and KW with dimensions being 3 × 3 are the physical mass, damping, and stiffness matrices of thin-walled workpiece. χ and dFW are the vectors of displacement and dynamic milling force, respectively.

3.1 Chip thickness model

For milling, the chip includes two parts such as the static thickness (hs) and dynamic thickness (dh). Among them, the static chip thickness (hs) can be defined as follows:

$$ {h}_s=\frac{2\pi R\cdotp {V}_f}{N_z\cdotp {V}_C}\cdotp \mathit{\sin}\left({\varphi}_j\right) $$
(8)

In CM, the dynamic thickness (dhc,j) of tooth j is usually measured along the tool radial direction (XR) as shown in Fig. 1d. It can be written as follows:

$$ \mathrm{d}{h}_{\mathrm{c},\mathrm{j}}=\left[{x}_j(t)-{x}_j\left(t-{T}_{j-1}\right)\right]\cdotp \mathit{\sin}\left({\varphi}_j\right)+\left[{y}_j(t)-{y}_j\left(t-{T}_{j-1}\right)\right]\cdotp \mathit{\cos}\left({\varphi}_j\right) $$
(9)

where xj(t)−xj(t−Tj−1) and yj(t) yj(t−Tj−1) represent the dynamic displacement vectors. However, this characterization method of dynamic chip thickness cannot be simply used for RUM-tww since the ultrasonic vibration effect changes the external excitation direction of thin-walled workpiece system. Thus, the dynamic chip thickness (dhv,j) under the effect of ultrasonic energy should be calculated along the radial velocity direction (VRv). By considering the vibration of Z-direction, it can be defined in three-dimensional space as follows:

$$ {dh}_{v,j}={\mathrm{dh}}_{\mathrm{c}}\cdotp \mathit{\sin}\left(\alpha \right)\hbox{-} \left[{z}_j(t)-{z}_j\left(t-{T}_{j-1}\right)\right]\cdotp \mathit{\cos}\left(\alpha \right) $$
(10)

It is worth noting that dhv,j is smaller than dhc,j when the ultrasonic function angle α is an acute angle. While α becomes right angle, the dhv,j is equal to the dhc,j. Otherwise, the dhv,j is larger than dhc,j if ultrasonic vibration is along the positive direction of ZA-axial. That is to say, the value of dhv,j varies within one ultrasonic vibration cycle continuously.

For RUM-tww, the total chip thickness (Thv,j) can be written as follows:

$$ T{\mathrm{h}}_{v,j}={h}_s+{dh}_{v,\mathrm{j}} $$
(11)

3.2 Dynamic milling force model

In RUM-tww, the cutting force on the tooth j could be denoted by the radial milling force (TFr,j), axial milling force (TFa,j), and the tangential milling force (TFt,j), which changes with the variety of ultrasonic vibration direction. Based on the exponential force model, they could be defined as follows:

$$ \left[\begin{array}{c}{TF}_{r,j}\\ {}{TF}_{t,j}\\ {}{TF}_{a,j}\end{array}\right]=\Psi \left({\varphi}_j\right)\cdotp \left\{\left[\begin{array}{c}{k}_r\\ {}{k}_t\\ {}{k}_a\end{array}\right]\cdotp {\left({Th}_{v,j}\right)}^{\gamma }+\left[\begin{array}{c}{k}_{re}\\ {}{k}_{te}\\ {}{k}_{ae}\end{array}\right]\right\}\cdotp \left[{a}_p+\left(S/1000\right)\cdotp {s}_v\right] $$
(12)

Among them, sv=sin(2πfvt); the parameters kr, kt, and ka are average shear force coefficients while the kre, kte, and kae represent average plowing force coefficients; γ is exponential constant; Ψ (φj) is a window function, and its value range is 0 or 1[6].

Based on the literature [31], total milling force with ultrasonic vibration (TFv,j) in the Eq. (12) could be linearized at χ=0 as follows:

$$ {TF}_{\mathrm{v},j}={TF}_{v,j}\left(\chi =0\right)+{dF}_{v,j} $$
(13)

Among them, TFv,j(χ=0) represents the static cutting force without chatter occurrence while the dFv, j is the dynamic milling force causing instability phenomenon. In this study, the dFv, j could be calculated by the Eq. (13) as follows:

$$ \left[\begin{array}{c}{dF}_{r,j}\\ {}{dF}_{t,j}\\ {}{dF}_{a,j}\end{array}\right]=\Psi \left({\varphi}_j\right)\left\{\left[\begin{array}{c}{k}_r\\ {}{k}_t\\ {}{k}_a\end{array}\right]\cdotp \left[{a}_p+\left(S/1000\right)\cdotp {s}_v\right]\cdotp \gamma \cdotp {\left({Th}_{\mathrm{v},j}\right)}^{\gamma -1}\cdotp \left({dh}_{v,j}\right)\right\} $$
(14)

Obviously, the plowing force coefficients (kre, kte, and kae) are eliminated after the formula transformation.

According to the geometric relationship of dynamic milling force presented in Fig. 1e, the dynamic milling force of tooth j (dFx,j, dFy,j and dFz,j) could be obtained by projecting the forces (dFr,j, dFt,j and dFa,j) to X, Y, and Z direction, respectively. They satisfy the following matrix transformation as follows:

$$ \left[\begin{array}{c}\mathrm{d}{F}_{x,j}\\ {}{dF}_{y,j}\\ {}{dF}_{z,j}\end{array}\right]=\left[\begin{array}{ccc}-\sin \left({\varphi}_j\right)\cdotp \sin \alpha & -\cos \left({\varphi}_j\right)& -\sin \left({\varphi}_j\right)\cdotp \cos \alpha \\ {}-\cos \left({\varphi}_j\right)\cdotp \sin \alpha & \sin \left({\varphi}_j\right)& -\cos \left({\varphi}_j\right)\cdotp \cos \alpha \\ {}-\cos \alpha & 0& \sin \alpha \end{array}\right]\cdotp \left[\begin{array}{c}{dF}_{r,j}\\ {}{dF}_{t,j}\\ {}{dF}_{a,j}\end{array}\right] $$
(15)

Then, by taking the Eq. (14) into Eq. (15) and summing the dynamic milling forces of all teeth continuously, the total dynamic milling forces under the X, Y, and Z direction could be written as follows:

$$ \left[\begin{array}{c}\mathrm{d}{F}_x\\ {}{dF}_y\\ {}{dF}_z\end{array}\right]={a}_p\cdotp {A}_1(t)\cdotp \left\{\chi \right\}+S\cdotp {A}_2(t)\cdotp \left\{\chi \right\} $$
(16)

Among them, the matrixes A1(t) and A2(t) satisfy the relationship as A2(t)=sv·A1(t). And A1(t)3×3 can be expressed as follows:

$$ {A}_1(t)=\left[\begin{array}{ccc}{\mathrm{a}}_{xx}& {a}_{xy}& {a}_{xz}\\ {}{a}_{yx}& {a}_{yy}& {a}_{yz}\\ {}{a}_{zx}& {a}_{zy}& {a}_{zz}\end{array}\right] $$
(17)

where

$$ {\displaystyle \begin{array}{l}{\mathrm{a}}_{xx}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp \left(-{s}^{\prime }{s}^{{\prime\prime}}\right)\cdotp \left({\mathrm{k}}_r\cdotp {s}^{\prime }{s}^{{\prime\prime} }+{K}_t\cdotp {c}^{\prime }+{k}_a\cdotp {s}^{\prime }{c}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{x\mathrm{y}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp \left(-{c}^{\prime }{s}^{{\prime\prime}}\right)\cdotp \left({\mathrm{k}}_r\cdotp {s}^{\prime }{s}^{{\prime\prime} }+{K}_t\cdotp {c}^{\prime }+{k}_a\cdotp {s}^{\prime }{c}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{x\mathrm{z}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp {c}^{{\prime\prime}}\cdotp \left({\mathrm{k}}_r\cdotp {s}^{\prime }{s}^{{\prime\prime} }+{K}_t\cdotp {c}^{\prime }+{k}_a\cdotp {s}^{\prime }{c}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{yx}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp \left(-{s}^{\prime }{s}^{{\prime\prime}}\right)\cdotp \left({\mathrm{k}}_r\cdotp {c}^{\prime }{s}^{{\prime\prime} }-{k}_t\cdotp {s}^{\prime }+{k}_a\cdotp {c}^{\prime }{c}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{y\mathrm{y}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp \left(-{c}^{\prime }{s}^{{\prime\prime}}\right)\cdotp \left({\mathrm{k}}_r\cdotp {c}^{\prime }{s}^{{\prime\prime} }-{k}_t\cdotp {s}^{\prime }+{k}_a\cdotp {c}^{\prime }{c}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{y\mathrm{z}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp {\mathrm{c}}^{{\prime\prime}}\cdotp \left({\mathrm{k}}_r\cdotp {c}^{\prime }{s}^{{\prime\prime} }-{k}_t\cdotp {s}^{\prime }+{k}_a\cdotp {c}^{\prime }{c}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{\mathrm{zx}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp \left(-{s}^{\prime }{s}^{{\prime\prime}}\right)\cdotp \left({k}_r\cdotp {c}^{{\prime\prime} }-{k}_a\cdotp {s}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{\mathrm{zy}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp \left(-{c}^{\prime }{s}^{{\prime\prime}}\right)\cdotp \left({k}_r\cdotp {c}^{{\prime\prime} }-{k}_a\cdotp {s}^{{\prime\prime}}\right)\\ {}{\mathrm{a}}_{\mathrm{zz}}=\sum \limits_{j=1}^{N_z}\Psi \left({\varphi}_j\right)\cdotp \gamma \cdotp {\left({h}_s\right)}^{\gamma -1}\cdotp {c}^{{\prime\prime}}\cdotp \left({k}_r\cdotp {c}^{{\prime\prime} }-{k}_a\cdotp {s}^{{\prime\prime}}\right)\end{array}} $$

4 Stability analysis by SDM

4.1 Dynamic expressions of RUM-tww system

During RUM-tww, the cutting chatter is usually caused by the displacement feedback. At present, the SDM [7] viewed as an effective means is widely applied for solving SLDs. Due to the effect of ultrasonic vibration, its dynamic expressions should be sorted into the delay differential equations with 3-DOF:

$$ \left[\begin{array}{c}\ddot{x}(t)\\ {}\ddot{y}(t)\\ {}\ddot{z}(t)\end{array}\right]+{H}_W\left[\begin{array}{c}\dot{x}(t)\\ {}\dot{y}(t)\\ {}\dot{z}(t)\end{array}\right]+{B}_W\left[\begin{array}{c}x(t)\\ {}y(t)\\ {}z(t)\end{array}\right]={E}_W\left[\begin{array}{c}x{\left(t-\tau \right)}_i\\ {}y{\left(t-\tau \right)}_i\\ {}z{\left(t-\tau \right)}_i\end{array}\right] $$
(18)

where i denotes the ith time interval; x(t-τ)i , y(t-τ), and z(t-τ)i represent the delay differential terms of X, Y, and Z directions, respectively; HW, BW, and EW are all three by three matrixes. By considering the modal property of thin-walled workpiece system such as relative damping (ξnx, ξny, and ξnz), the angular natural frequency (ωnx, ωny, and ωnz), and the modal mass (mtx, mty, and mtz), they could be expressed as follows:

$$ {H}_W=\left[\begin{array}{ccc}2{\xi}_{nx}{\omega}_{nx}& 0& 0\\ {}0& 2{\xi}_{ny}{\omega}_{ny}& 0\\ {}0& 0& 2{\xi}_{nz}{\omega}_{nz}\end{array}\right] $$
$$ {E}_W=\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp \left[\begin{array}{ccc}\frac{\alpha_{xx}}{m_{tx}}& \frac{\alpha_{xy}}{m_{tx}}& \frac{\alpha_{xz}}{m_{tx}}\\ {}\frac{\alpha_{yx}}{m_{ty}}& \frac{\alpha_{yy}}{m_{ty}}& \frac{\alpha_{yz}}{m_{ty}}\\ {}\frac{\alpha_{zx}}{m_{tz}}& \frac{\alpha_{zy}}{m_{tz}}& \frac{\alpha_{zz}}{m_{tz}}\end{array}\right] $$
$$ {B}_W=\left[\begin{array}{ccc}{\omega}_{nx}^2+\frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{xx}}{m_{tx}}& \frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{xy}}{m_{tx}}& \frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{xz}}{m_{tx}}\\ {}\frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{yx}}{m_{ty}}& {\omega}_{ny}^2+\frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{yy}}{m_{ty}}& \frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{yz}}{m_{ty}}\\ {}\frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{zx}}{m_{tz}}& \frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{zy}}{m_{tz}}& {\omega}_{nz}^2+\frac{\left({a}_p+S\cdotp {\mathrm{s}}_v\right)\cdotp {\alpha}_{zz}}{m_{tz}}\end{array}\right] $$

4.2 SDM and stability limit calculations

Firstly, Eq. (18) can be further expressed as first-order differential form by Cauchy transformation:

$$ {\dot{q}}_W(t)={U}_W(t)\cdotp {q}_W(t)+{V}_W(t)\cdotp {q}_W\left(t-\tau \right) $$
(19)

where qW denotes the coordinates x, y, and z; UW(t) and VW(t) are periodic matrices determined by the dynamic milling force. They can be displayed as follows:

$$ {U}_W(t)=\left[\begin{array}{cc}0& I\\ {}-{B}_W& -{H}_W\end{array}\right] $$
$$ {V}_W(t)=\left[\begin{array}{cc}0& 0\\ {}{E}_W& 0\end{array}\right] $$

Among them, I represents the unit matrix.

The delay time τ could be divided into k discrete time intervals Δt, and satisfyτ=kΔt. Based on the research of Insperger and Stepanas [7], a coefficient matrix Di is written as follows:

$$ {D}_i=\left[\begin{array}{cccc}{P}_D& 0& {R}_{Da}& {R}_{Db}\\ {}G& 0& 0& 0\\ {}0& I& 0& 0\\ {}0& 0& I& 0\end{array}\right] $$
(20)

Among them,

$$ {P}_D=\left[\begin{array}{cccccc}{P}_{i,11}& {P}_{i,12}& {P}_{i,13}& {P}_{i,14}& {P}_{i,15}& {P}_{i,16}\\ {}{P}_{i,21}& {P}_{i,22}& {P}_{i,23}& {P}_{i,24}& {P}_{i,25}& {P}_{i,26}\\ {}{P}_{31}& {P}_{i,32}& {P}_{i,33}& {P}_{i,34}& {P}_{i,35}& {P}_{i,36}\\ {}{P}_{i,41}& {P}_{i,42}& {P}_{i,43}& {P}_{i,44}& {P}_{i,45}& {P}_{i,46}\\ {}{P}_{i,51}& {P}_{i,52}& {P}_{i,53}& {P}_{i,54}& {P}_{i,55}& {P}_{i,56}\\ {}{P}_{i,61}& {P}_{i,62}& {P}_{i,63}& {P}_{i,64}& {P}_{i,65}& {P}_{i,66}\end{array}\right]\mathrm{and}\ {G}_{\left(3\times 6\right)}=\left[I\kern0.5em 0\right] $$
$$ {R}_{Da}=\left[\begin{array}{ccc}{R}_{i,11}& {R}_{i,12}& {R}_{i,13}\\ {}{R}_{i,21}& {R}_{i,22}& {R}_{i,23}\\ {}{R}_{i,31}& {R}_{i,32}& {R}_{i,33}\\ {}{R}_{i,41}& {R}_{i,42}& {R}_{i,43}\\ {}{R}_{i,51}& {R}_{i,52}& {R}_{i,53}\\ {}{R}_{i,61}& {R}_{i,62}& {R}_{i,63}\end{array}\right] and\;{R}_{Db}=\left[\begin{array}{ccc}{R}_{i,11}& {R}_{i,12}& {R}_{i,13}\\ {}{R}_{i,21}& {R}_{i,22}& {R}_{i,23}\\ {}{R}_{i,31}& {R}_{i,32}& {R}_{i,33}\\ {}{R}_{i,41}& {R}_{i,42}& {R}_{i,43}\\ {}{R}_{i,51}& {R}_{i,52}& {R}_{i,53}\\ {}{R}_{i,61}& {R}_{i,62}& {R}_{i,63}\end{array}\right] $$

In this study, the Pi =exp (UWΔt) and Ri = 0.5·[exp(UWΔt)-I]·(UW)−1VW.

By coupling Eq. (20) for i = 0,1,…,k-1, the transition matrix Φ which reflects the cutting state characteristic could be expressed as follows:

$$ \Phi ={D}_{k-1}{D}_{k-2}\cdots {D}_1{D}_0 $$
(21)

The RUM-tww system is stable when all the eigenvalues of matrix Φ in modulus are less than 1. Otherwise, the machining system will lose stability under this processing condition. Based on this, the law of RUM-tww stability boundary varying with spindle speed could be obtained by inputting modal parameters and cutting force coefficients.

5 Stability lobes simulation and experimental verification

5.1 Thin-walled workpiece modes and milling force coefficients

In this study, the milling experiments are conducted to verify the accurateness of SLDs achieved by Section 4. The thin-walled workpiece used for verification tests is titanium alloy web. As illustrated in Fig. 2, its geometric size is 215 mm × 145 mm × 3 mm. In terms of the difficult-to-machine material like titanium alloys, the processing parameters (feed rate and cutting depth) are usually very small. Meantime, the purpose of this paper is to clarify the inhibition mechanism of ultrasonic vibration energy on the milling chatter of titanium alloy thin-walled parts. Thereby, during RUM-tww titanium alloy webs, the influence of material removal and tool position variation on machining stability is ignored. By taking the workpiece clamping method into consideration, the modal parameters of titanium alloy web can be acquired by the finite element analysis. The simulation results are shown in Table 1.

Fig. 2
figure 2

Schematic diagram of titanium alloy web workpiece

Full size image
Table 1 Modal parameters of titanium alloy web
Full size table

The tool applied for RUM-tww is cemented carbide cutter with three teeth. Its parameters are presented in Table 2. The milling forces are measured by the Kistler 9257B 3-component dynamometer. Based on the cutting force data obtained by milling groove experiments of titanium alloy web, the average milling force coefficients with or without ultrasonic vibration could be calculated as shown in Table 3. In addition, Fig. 3 presents the processing site map. The RUM-tww system includes the machine center (MCV-L850), contactless rotary ultrasonic device and titanium alloy web. As shown in Fig. 3, the ultrasonic tool shank is mounted on the spindle of machining tool. Its working principle is that the electric signal generated by ultrasonic generator is transformed into ultrasonic tool shank by the contactless power transmission firstly. Then, regular mechanical vibration occurs under the effect of piezoelectric ceramic transducer. Furthermore, it can be enlarged by the amplitude transformer effectively. Finally, the stable and high-frequency vibration (20,000 Hz) with sine or cosine form appears at the end of the milling cutter. Meanwhile, the ultrasonic amplitude is controlled by ultrasonic current. The result measured by the Laser Vibrometer (Polytec, CLV2534) along three-coordinate direction shows that when the ultrasonic current is equal to 150 mA, the ultrasonic amplitude (S) reaches 10 μm at the tool tip. At this time, the ultrasonic device works at its best state with the largest amplitude. In addition, the RUM-tww is transformed into CM-tww when ultrasonic current is 0 mA.

Table 2 Cutting tool parameters
Full size table
Table 3 Values of milling force coefficients
Full size table
Fig. 3
figure 3

Experimental setup for stability verification

Full size image

5.2 Stability lobe simulation results

On the basis of modal parameters and milling force coefficients, the SLDs of RUM-tww (S=10 μm) and CM-tww (S=0 μm) could be obtained by the MATLAB software as shown in Fig. 4. The milling type is set as up-milling along the X direction (feed rate 40 mm/min and cutting width 4 mm). The envelope area of SLDs could be obtained by the area recognition function in Origin8 software. The result demonstrates that the SLDs areas of RUM-tww and CM-tww are 923.44 and 512.12, respectively. It means that compared with CM-tww, the RUM-tww stability is improved by 80.32% within the spindle speed range (1000 r/min to 5000 r/min). There are two main reasons for this situation. On the one hand, the impact effect of high-frequency vibration (or ultrasonic energy) makes the difficult-to-machining material around the cutting edge easier to be removed. On the other hand, the existence of ultrasonic function angle α may decrease dynamic milling force greatly by changing the external excitation direction of the workpiece. Therefore, the introduction of ultrasonic energy has good effect on the stability improvement of weak-stiffness thin-walled parts. It is worth noting that the RUM-tww stability lobe is shifted to the left compared with CM-tww in Fig. 4. As a result, the ultrasonic vibration machining occurs chatter while the common milling is at stable state under some processing parameters. The main reason lies in that the separation characteristic between the cutter and workpiece caused by high-frequency ultrasonic vibration changes the time delay presented in Eq. (18) dynamically. Hence, RUM-tww stability is worse than CM-tww in some machining parameters. And this offset phenomenon enables RUM-tww to obtain a greater depth of cut at a smaller spindle speed. The range of available processing parameters satisfying the stability demand becomes wider in the low-spindle speed stage. During titanium alloy milling, it has advantages of reducing the cutting force and cutting temperature significantly. As a result, the tool life and machining quality are improved. This is another advantage for RUM-tww besides improving milling stability.

Fig. 4
figure 4

Stability region comparison of RUM-tww and CM-tww (circles denote stable milling and crosses represent unstable milling. The black shape is CM-tww while the red denotes RUM-tww.)

Full size image

From the theoretical modeling of stability analysis, the ultrasonic function angle α reflects the effect of ultrasonic vibration. The smaller value α is, the better RUM-tww stability will be. Meantime, according to Eq. (6), the value of angle α decreases with the rise of ultrasonic vibration amplitude and frequency. As a result, the RUM-tww stability is effectively improved with the increasing of ultrasonic parameters (S and fv). As shown in Fig. 5, however, the SLDs has no obvious extension when ultrasonic vibration frequency increases from 10,000 to 30,000Hz. This is due to that the increase in fv is not enough to reduce the value of α significantly. Then, the effect of ultrasonic vibration frequency on RUM-tww stability has difficulty to be reflected in Fig. 5. For RRUM-tww with one-dimensional axial ultrasonic vibration, the S and fv determine the improvement extent of processing stability jointly. Only slightly increasing one of the factors has weaker suppression effect for the milling chatter of titanium alloy web.

Fig. 5
figure 5

RUM-tww SLDs under different ultrasonic vibration frequencies

Full size image

5.3 Experimental results for SLDs verification

In order to verify the accuracy and reasonableness of SLDs, five groups of parameters in Fig. 4 are selected to carry out comparative experiments of RUM-tww and CM-tww. For the purpose of making the experimental plan as reasonable as possible, there are four situations. As shown in Fig. 4, the RUM-tww stability of groups 1 and 3 is better than CM-tww, which is the opposite of group 4. The group 2 denotes that the processing methods with or without ultrasonic vibration are at loss of stability while the group 5 is stable milling. After milling experiments, the surface chatter mark, surface cutter mark, and surface flatness of the workpiece were investigated to prove the effectiveness and rationality of chatter stability boundary (Fig. 4). The final judgment results of chatter stability are also presented in Fig. 4.

5.3.1 Surface chatter mark

In this study, the machined surface morphology of titanium alloy webs is measured by KEYENCE laser microscope (KEYENCE, VK-X 100 series). The experimental results of five group parameters are presented in Fig. 6. Among them, RUM1 represents the RUM-tww of point 1 while the CM1 is CM-tww (point 1), and so on. The areas marked by the yellow line are the obvious chatter mark patterns. It can be observed from the group 1 that CM-tww surface has obvious vibration marks. They destroy the consistency of surface morphology and affect the quality of machined surface inevitably. On the contrast, the surface morphology produced by RUM-tww possesses very good consistency without chatter marks. It means that the high-frequency vibration and impact of tool could suppress milling chatter of titanium alloy thin-walled parts. It is consistent with the prediction results of point 1 in Fig. 4. In group 2, both RUM-tww and CM-tww show the apparent chatter marks under the experimental parameters (spindle speed 2000 r/min and cutting depth 0.3 mm). The experimental results are also same as the prediction results. In addition, the rest groups of verification experiments agree well with SLDs presented in Fig. 4. Therefore, the accuracy of stability boundary could be proved to some extent.

Fig. 6
figure 6

Surface morphology diagrams of RUM-tww and CM-tww

Full size image

5.3.2 Surface cutter mark

During milling, the cutter marks which may destroy machined surface consistency are usually formed by adjacent tool paths. Particularly, when machining chatter occurs, they are bound to be further deteriorated and result in the reduction of machined surface quality. Figure 7 presents the cutter mark diagrams of RUM-tww and CM-tww. As shown in groups 1 and 3, the addition of ultrasonic energy enhances the uniformity of surface morphology by making cutter marks unobvious. In group 2, the machined surfaces exist significant height differences on both sides of the cutter mark. For RUM-tww and CM-tww in group 3, the machined surfaces own good quality. It is worth noting that the cutter mark with ultrasonic vibration is more obvious than CM-tww since the RUM-tww occurs chatter. The specific measurement results of cutter mark height are illustrated in Fig. 8. It can be found that all the cutter mark heights are more than 8 μm on the groups with processing chatter. For groups 1 and group 3, the cutter mark heights formed by RUM-tww with stable machining are reduced by 43% compared with CM-tww. The above analysis about surface cutter mark verifies the effectiveness of stability region (in Fig. 4) further.

Fig. 7
figure 7

Cutter mark diagrams of milling titanium alloy web

Full size image
Fig. 8
figure 8

Cutter mark height of machined surface

Full size image

5.3.3 Machined surface flatness

Apart from chatter mark and cutter mark, the flatness is also an important index to evaluate the quality of milling surface. The milling force generated by severe chatter may cause machining deformation of thin-walled workpieces, which could lower the flatness of the machined surface. In this paper, the flatness of workpiece surface was obtained by the three-coordinate measuring instrument (RA-7525 SEI). And the measurement tests were carried out quickly after milling experiments in order to avoid the workpieces deformation caused by the residual stress release. As shown in Fig. 9, the workpiece was fixed on the table with double-sided tape. Two hundred points were uniformly measured on the machined surface, and the flatness was calculated by the corresponding supporting software. The measurement results are shown in Fig. 10. The smaller flatness value is, the better machined surface flatness will be. All the flatness data of experimental parameters with milling chatter are greater than 0.05, and the maximum value reaches 0.076. Meantime, the stable milling flatness is between 0.04 and 0.05. In addition, as presented in groups 1 and 3, the flatness of RUM-tww surface is significantly superior to CM-tww. This is due to that the ultrasonic vibration could reduce the deformation of titanium alloy web by restricting the milling vibration. The accuracy and effectiveness of SLDs presented in Fig. 4 are verified again.

Fig. 9
figure 9

Flatness measurement of titanium alloy web

Full size image
Fig. 10
figure 10

Flatness of titanium alloy web

Full size image

6 Conclusions

In this paper, the chatter stability of rotary ultrasonic milling titanium alloy web is investigated. Aiming at the weak stiffness characteristic of thin-walled workpiece, a novel stability analysis method is proposed for obtaining RUM-tww stability lobes. Meanwhile, the inhibition mechanism of ultrasonic vibration energy on milling chatter of thin-walled workpiece is clarified. Based on the stability simulation and experimental results, three conclusions can be summarized as follows:

  1. (1)

    The introduction of ultrasonic vibration energy has the advantage of lowering dynamic milling force by changing the external excitation direction of the workpiece. As a result, RUM-tww stability region is improved by 80.32% than CM-tww within the spindle speed from 1000 r/min to 5000 r/min.

  2. (2)

    Compared with CM-tww, RUM-tww can improve the surface morphology consistency of titanium alloy web by making surface chatter marks and cutter marks unobvious. In addition, the flatness of RUM-tww surface is also strengthened by ultrasonic vibration under stable milling condition.

  3. (3)

    The rationality and accuracy of SLDs are proved by the experimental results of RUM-tww and CM-tww effectively. They could be employed to guide the selection of suitable cutting parameters for thin-walled parts milling.