1 Introduction

Hydrostatic spindles have many good advantages such as high stiffness, the excellent absorption capacity of vibration, never wear, high accuracy, etc. and are widely used in precision turning, milling and grinding, and other processing occasions. Hydrostatic spindles are usually designed with the thrust bearing at the front end. However, because the journal bearing of such spindles is far from the spindle nose, the bearing capacity of the spindle is reduced. Therefore, some researchers have proposed hydrostatic spindles with a mid-thrust bearing structure, which can achieve higher radial stiffness under the same structural size [1,2,3].

For the rotor with mid-thrust bearing, it is necessary to machine the journals on both sides in two grinding processes, so the manufacturing errors of the journal and thrust bearings, such as coaxiality and perpendicularity, tend to increase. In the past few years, some scholars have studied the relationship between rotor manufacturing error and spindle performance. Xun et al. established the influence function of shape tolerance and dimensional tolerance of rotor on bearing oil film clearance and pointed out that the rotor form error related to rotation will lead to a periodic oscillation of spindle [4]. Peng et al. compared the number of oil recesses in journal bearing with the number of roundness waves of the journal and found that when the journal roundness is kept unchanged, the journal bearing with six oil recesses had the least influence on the spindle runout, which has been verified by experiment [5].

The rotor’s form error causes the running oil film thickness to deviate from the calculated oil film thickness and generates an additional disturbing force on the rotor so that the perturbing load pushes the rotor to produce rotational errors. For the coupled journal-thrust hydrostatic spindle, radial runout caused by the journal’s form error is usually taken as the principal object to analyses because the size of the journal bearing is much larger than that of the thrust bearing [6]. Also, classifying the spindle rotational accuracy into synchronous error and asynchronous error according to the relationship between the runout and the spindle speed, the rotor from error mainly produces the synchronous deviation at the same frequency as the spindle speed [7]. Therefore, when analyzing the influence of rotor’s form error on the spindle runout, the oil film can be equivalent to the multi-degree-of-freedom spring damping system. Then the dynamic response of the rotor, which is supported by the spring damping system under the disturbance force caused by the rotor form error, can be calculated from the rotor motion equation. Usually, the Euler method is employed to solve the above motion differential equation to obtain the acceleration, velocity, and displacement of the rotor so that the spindle runout can be evaluated by fitting the motion trajectory of the rotor [8, 9].

When the rotor speed is relatively low, the inertia force and damping force are negligible, and the spindle runout can be solved from the statics equilibrium equation of the rotor. Jun et al. have established a fluid control model for the low-speed hydrostatic rotary table with multi-recess and studied the influence of the tolerances such as coaxiality between the journal bearings, perpendicularity between journal bearing and thrust bearing, and journal roundness on spindle rotation accuracy and provided theoretical analysis basis for error design and assembly of hydrostatic spindle [10].

When the rotor speed is high, the dynamic analysis method is usually adopted to study the influence of dynamic characteristics of the spindle on the motion trajectory of the rotor. Chen et al. studied the stiffness and damping coefficients of the spindle under different eccentricity ratio of the rotor and used the rotor dynamic equation to calculate the transient response of the spindle in the time domain and frequency domain and to evaluate the rotor motion of the spindle under the excitation of unbalanced force and periodic load, etc. [11]. As the rotor with rotating herringbone grooves, the spindle stiffness and damping coefficient matrices are time-varying with the rotation of the rotor. Jang and Yoon developed the gas film clearance as a Fourier series and substituted it into the dynamic stiffness and damping matrix equation and then obtained the whirl trajectory of the rotor by using the rotor dynamics analysis method [12]. Zha et al. employ the rotor dynamics analysis method to study the effect of different filmland widths, oil film thickness, oil supply pressure, rotor speed, and external load on the spindle runout under an angle error between the thrust plate and the journal bearing. Furthermore, the difference between the calculated results based on the above method and the experimental results is less than 9.3% [13].

The nonlinear and linearization solution methods are usually adopted to solve the rotor motion equation. The nonlinear method is employed to solve the instantaneous oil film force in each time step according to real-time parameters such as rotor posture and velocity. This method requires the iterative and cyclic solution of the Reynolds equation, with low computational efficiency but high computational accuracy. When the rotor is oscillating in a quasi-static position, the linearized stiffness and damping coefficients can be obtained by retaining the lower order term of the Taylor expansion of the stiffness and damping coefficients [14]. Sinhasan and Goyal solved the rotor motion equation of hydrostatic bearing by using linearization and nonlinear methods, analyzed the trajectory and stability of the rotor under different operating parameters, and pointed out that the precision of nonlinear analysis was slightly higher than that of the linearization method [15]. Sharma and Kushare researched the symmetric two-lobe non-recessed journal bearing system with linearization and nonlinearization methods. They concluded that the journal center motion trajectories, critical journal mass, and threshold speed margin solved by the two methods are slightly different [16]. In summary, the above literature indicated that the linear analysis was an available solution to engineering design problems.

In addition, different working media have a great influence on the dynamic and static characteristics of the hydrostatic spindle. Urreta et al. compared the influence of regular and magnetic fluids on the spindle performance and pointed out that magnetic fluids could improve the hydrodynamic effect around 50% and achieve quasi-infinite static stiffness within a load range [17,18,19].

In the past, many researchers have carried out detailed analyses and experiments on the impact of bearing and rotor error on hydrostatic spindle runout, but fewer deeply analyze the effect of the coaxiality of rotor and spindle runout under different operating parameters. At first, this paper sets up the five degree-of-freedom (DOF) rotor motion equations of the high-precision hydrostatic spindle. Then the mathematical perturbation method is adopted to solve the fluid flow control model of the journal and thrust bearings to obtain the stiffness and damping coefficients of the spindle. Furthermore, the paper determines the amplitude amplification factor (AAF) and the rotor motion trajectory of the bearing support system, according to the rotor dynamics and Euler method. Finally, the effects of different coaxiality, rotating speed, oil film clearance, eccentricity, and oil supply pressure on the spindle runout are verified by computer simulation. Such simulation results would offer guidance for the design of the precision hydrostatic spindle.

2 Mathematical models

2.1 Spindle structure and rotor coaxiality error

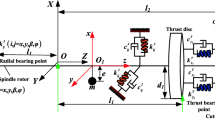
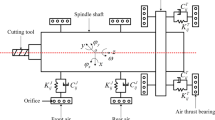
Figure 1(a) shows the schematic view of the hydrostatic spindle with mid-thrust bearing, which includes a pair of journal bearings, a pair of thrust bearings, the torque motor, encoder, etc. The external oil supply system injects pressure oil into the lubricating recesses of the journal bearings and thrust bearings through the orifice restrictors to form the bearing oil film. Besides, for small- and medium-sized specifications of the hydrostatic spindle, the bearings with four rectangular oil recesses of equal depth uniformly distributed along the circumference have less stiffness anisotropy [20]. Therefore, the paper adopts such layout shown in Fig. 1.

Fig. 1
figure 1

Hydrostatic spindle with mid-thrust bearing. a Structure diagram: 1, encoder; 2, rotor; 3, torque motor; 3, left journal bearing; 4, left thrust bearing; 5, right thrust bearing; 6, right journal bearing. b Coaxiality distribution

Full size image

Because the geometrical error and roughness of the rotor have a significant effect on the stiffness and runout of the spindle, Pang recommended the geometrical error of the rotor as (0.1–0.2)h0 and the surface roughness of the rotor as Ra0.16 μm [20]. Furthermore, the rotor coaxiality error can be defined as non-coaxiality of the axis of both sides of the journal, and such error is usually a spatial free curve. In the process of machining journals on both sides of the rotor, coaxiality error usually occurs due to the decomposition of the grinding process of two sides of the journals, which affects the precision of the spindle. Previous research shows, when the axis of both sides of the journals of the rotor was parallel offset, the spindle runout caused by the coaxiality of the rotor is the highest [6]. Without loss of generality, this paper assumes the coaxiality ee to uniformly distribute on both sides of the rotor, as shown in Fig. 1(b).

2.2 Rotor motion equation

For the rigid rotor, its five DOF motions consist of three linear movements along the x, y, and z directions and two tilt motions around the x and y directions, as shown in Fig. 2. The rotor usually bears loads such as oil film force, unbalanced force, cutting force, gravity, etc., which form a dynamic equilibrium system. Based on Newton’s laws and the principle of angular momentum, the rotor motion equation can be established by ignoring gyro force in coordinate o − xyz as follows [21, 22]:

$$ M\ddot{X}+{C}_R{\dot{X}}_R+{C}_L{\dot{X}}_L+{C}_T\dot{X}+{K}_R{X}_R+{K}_L{X}_L+{K}_TX={F}_e $$
(1)
Fig. 2
figure 2

The dynamic model of the rigid rotor system

Full size image
$$ {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} $$
$$ {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} $$
$$ {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} $$
$$ {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} $$

where X = [x y z θx θy]T are the five generalized coordinates to describe the position of the rotor; m is mass of rotor; Ix, Iy, and Iz are the mass moments of inertia of the rotor about x, y, and z axes, respectively; Lj is the axial length of the journal bearing; ee is the rotor coaxiality error; g is the acceleration of gravity; ω is the spindle angular velocity; \( {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} \) are the cutting forces and cutting moments; CL, CR, CT are the damping matrices of left journal bearing, right journal bearing, and thrust bearing; KL, KR, KT are the stiffness matrices of left journal bearing, right journal bearing, and thrust bearing; kij, cij(i, j = x, y, z, θx, θy) are the stiffness and damping coefficients; and L, R, and T represent the left journal bearing, right journal bearing, and thrust bearing, respectively.

As stated in the introduction, linearization and nonlinear methods are commonly used to solve Eq. (1). For the sake of simplicity and efficiency, this paper will adopt the linearization method, which is usually necessary to solve the spindle stiffness and damping coefficients as the rotor is at the quasi-static position. The following section introduces the solution procedure based on the mathematical perturbation method to obtain the spindle stiffness and damping coefficients in detail.

2.3 Determination of the dynamic coefficients

2.3.1 Governing equations

The following assumptions are made to establish the governing equations: (1) the liquid is laminar flow and incompressible; (2) the pressure difference in the direction of oil film thickness is negligible; (3) the oil flows at a constant temperature; and (4) the steady and transient pressures are the same in the recesses. Then the fluid governing equations of the journal and thrust bearings are written as [23]:

$$ \frac{\partial }{\partial \theta}\left({\overline{h}}^3\frac{\partial \overline{p}}{\partial \theta}\right)+\frac{\partial }{\partial \overline{z}}\left({\overline{h}}^3\frac{\partial \overline{p}}{\partial \overline{z}}\right)={S}_h\frac{\partial \overline{h}}{\partial \theta }+2{S}_h\frac{\partial \overline{h}}{\partial \overline{t}} $$
(2)
$$ \frac{\partial }{\partial \overline{R}}\left({\overline{R}\overline{h}}^3\frac{\partial \overline{\mathrm{p}}}{\partial \overline{R}}\right)+\frac{\partial }{\partial \theta}\left(\frac{{\overline{h}}^3}{\overline{R}}\frac{\partial \overline{p}}{\partial \theta}\right)={S}_t\overline{R}\frac{\partial \overline{h}}{\partial \theta }+2{S}_t\overline{R}\frac{\partial \overline{h}}{\partial \overline{t}} $$
(3)

The nondimensional parameters in Eqs. (2) and (3) are defined as:

$$ \theta =\frac{x}{D/2},\overline{\ z}=\frac{z}{D/2},\kern0.5em \overline{p}=\frac{p}{p_s},\overline{\ h}=\frac{h}{C_0},\kern0.5em \overline{t}=\omega t,U=\frac{D\omega}{2},{S}_h=\frac{6\eta \omega}{p_s}{\left(\frac{D}{2{C}_0}\right)}^2,\overline{R}=\frac{r_i}{R_4},{S}_t=\frac{6\eta \omega}{p_s}{\left(\frac{R_4}{C_0}\right)}^2 $$

where θ is angular coordinate; xyz is the local coordinate system;\( \overline{z} \) is the dimensionless axial coordinate; D is the diameter of the journal bearing; p, \( \overline{p} \) are the oil film pressure and its dimensionless form; ps is oil supply pressure; h, \( \overline{h} \) are the transient oil film thickness of the bearings and its dimensionless form; U C0 is the designed oil film thickness of all bearings; U is the velocity on the surface of journal bearing; Sh is the Sommerfeld number of journal bearing; St is the Sommerfeld number of thrust bearing; t, \( \overline{t} \) are the time and its dimensionless form; ω is the \( \upomega, \overline{\upomega} \) angular velocity of shaft; ri, \( \overline{R} \) are the radius of the thrust bearing and its dimensionless form; R4 is the outer radius of thrust bearing; and η is the coefficient of viscosity.

2.3.2 Oil film clearance

Figure 1(b) shows the initial position of the spindle rotor in coordinates o − xyz, indicating that the phase difference between the axis of the left and right journal is 180°. So, the coaxiality error of two journals with the ideal axis is ee/2. If the displacement increment of the rotor in coordinates o − xyz at time t is \( {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} \), the oil film clearance in the dimensionless form of the journal bearings and thrust bearings on the left and right sides of the rotor are:

$$ {\overline{h}}_j=1-\left(\Delta \overline{x}\pm {\overline{Z}}_i\Delta {\theta}_y-\frac{{\overline{e}}_e}{2}\mathit{\cos}\left(\varphi +\psi \pi \right)\right) cos\theta -\left(\Delta \overline{y}\mp {\overline{Z}}_i\Delta {\theta}_x-\frac{{\overline{e}}_e}{2}\mathit{\sin}\left(\varphi +\psi \pi \right)\right) sin\theta $$
(4)
$$ {\overline{h}}_t=1\mp \left(\Delta \overline{z}+\Delta {\theta}_x{\overline{r}}_i sin\theta +\Delta {\theta}_y{\overline{r}}_i cos\theta \right) $$
(5)

where \( {\overline{h}}_j \) and \( {\overline{h}}_t \) are the oil film thicknesses of the journal and thrust bearings, respectively.

The nondimensional parameters in Eqs. (4) and (5) are defined as:

$$ \Delta \overline{x}=\frac{\Delta x}{C_0},\Delta \overline{y}=\frac{\Delta y}{C_0},\Delta \overline{z}=\frac{\Delta z}{C_0},{\overline{Z}}_i=\frac{z_i}{C_0},{\overline{e}}_e=\frac{e_e}{2{C}_0},\kern0.5em {\overline{r}}_i=\frac{r_i}{C_0} $$

where \( {\overline{Z}}_i \) are the dimensionless displacement of the spindle rotor; zi, \( {\overline{Z}}_i \) are the axial position of the journal bearing and its dimensionless form; ee,\( {\overline{e}}_e \) are the rotor coaxiality error and its dimensionless form; and \( {\overline{r}}_i \) is the dimensionless oil film thickness of thrust bearing. In Eq. (4), “±” in the second item and “∓” in the third item represent right and left journal bearings, respectively; ψ is 0 for the right journal bearing, and ψ is 1 for the left journal bearing. In Eq. (5), “∓” represents right and left thrust bearings, respectively.

2.3.3 Boundary condition

Appropriate external and internal boundary conditions are applied to solve the Reynolds equations (2) and (3) as follows:

(a) The outlet pressure of oil film is zero, p = 0.

(b) The pressure and flowrate are both continuous along the circumferential direction.

(c) The pressure in each recess is assumed uniform.

(d) The perturbed outlet pressures of oil film are \( {\overline{p}}_{\zeta }=0 \),\( \left(\zeta =0,x,y,z,{\theta}_x,{\theta}_y,\dot{x},\dot{y},\dot{z},{\dot{\theta}}_x,{\dot{\theta}}_y\right){\overline{\mathrm{p}}}_{\upzeta}=0 \).

2.3.4 Perturbation equations

The first-order Taylor expansion of oil film thickness and pressure distribution function concerning small displacements and velocities are carried out at their static equilibrium position to obtain the perturbation form of the Reynolds equations as follows [24]:

$$ \overline{h}={\overline{h}}_0+\sum \frac{\partial \overline{h}}{\partial \xi}\Delta \overline{\xi}+\sum \frac{\partial \overline{h}}{\partial \dot{\xi}}\Delta \overline{\dot{\xi}} $$
(6)
$$ \overline{p}\left(\theta, z\right)={\overline{p}}_0+\sum \frac{\partial \overline{p}}{\partial \xi}\Delta \overline{\xi}+\sum \frac{\partial \overline{p}}{\partial \dot{\xi}}\Delta \overline{\dot{\xi}} $$
(7)

where ξ = x, y, z, θx, θy.

Substituting the Taylor expansion equations (6) and (7) into Reynolds equations (2) and (3), the perturbation equations of the journal and thrust bearings are obtained after arranging according to displacement and velocity terms, respectively:

$$ \left\{\begin{array}{c}R\left({\overline{p}}_0\right)={S}_h\frac{\partial {\overline{h}}_0}{\partial \theta}\kern24.25em \\ {}R\left({\overline{p}}_x\right)={S}_h sin\theta +\frac{\partial }{\partial \theta}\left(3{h}_0^2 cos\theta \frac{\partial {\overline{p}}_0}{\partial \theta}\right)+\frac{\partial }{\partial z}\left(3{h}_0^2 cos\theta \frac{\partial {\overline{p}}_0}{\partial \overline{z}}\right)\kern5em \\ {}R\left({\overline{p}}_y\right)=-{S}_h cos\theta +\frac{\partial }{\partial \theta}\left(3{h}_0^2 sin\theta \frac{\partial {p}_0}{\partial \theta}\right)+\frac{\partial }{\partial z}\left(3{h}_0^2 sin\theta \frac{\partial {p}_0}{\partial \overline{z}}\right)\kern4.25em \\ {}R\left({\overline{p}}_z\right)=0\kern26.5em \\ {}R\left({\overline{p}}_{\theta_x}\right)=\pm {S}_h{\overline{Z}}_i cos\theta \mp \frac{\partial }{\partial \theta}\left(3{h}_0^2{\overline{Z}}_i sin\theta \frac{\partial {p}_0}{\partial \theta}\right)\mp \frac{\partial }{\partial z}\left(3{h}_0^2{\overline{Z}}_i sin\theta \frac{\partial {p}_0}{\partial \overline{z}}\right)\kern0.75em \\ {}R\left({\overline{p}}_{\theta_y}\right)=\pm {S}_h{\overline{z}}_i sin\theta \pm \frac{\partial }{\mathrm{\partial \uptheta }}\left(3{\overline{h}}_0^2{\overline{Z}}_i cos\theta \frac{\partial {\overline{p}}_0}{\partial \theta}\right)\pm \frac{\partial }{\partial z}\left(3{h}_0^2{\overline{Z}}_i cos\theta \frac{\partial {p}_0}{\partial \overline{z}}\right)\kern0.5em \\ {}R\left({\overline{p}}_{\dot{x}}\right)=-2{S}_h cos\theta \kern22em \\ {}R\left({\overline{p}}_{\dot{y}}\right)=-2{S}_h sin\theta \kern22.25em \\ {}R\left({\overline{p}}_{\dot{z}}\right)=0\kern26.5em \\ {}R\left({\overline{p}}_{\theta_{\dot{x}}}\right)=\pm 2{S}_h{\overline{Z}}_i sin\theta \kern20.75em \\ {}R\left({\overline{p}}_{\theta_{\dot{y}}}\right)=\mp 2{S}_h{\overline{Z}}_i cos\theta \kern20.25em \end{array}\right. $$
(8)

where \( R\left({\overline{p}}_{\zeta}\right)=\frac{\partial }{\partial \theta}\left({\overline{h}}_0^3\frac{\partial {p}_{\zeta }}{\partial \theta}\right)+\frac{\partial }{\partial \overline{z}}\left({h}_0^3\frac{\partial {p}_{\zeta }}{\partial \overline{z}}\right) \),\( \zeta =0,x,y,z,{\theta}_x,{\theta}_y,\dot{x},\dot{y},\dot{z},{\dot{\theta}}_x,{\dot{\theta}}_y \).

$$ \left\{\begin{array}{c}R\left({\overline{p}}_0\right)={S}_t\overline{R}\frac{\partial {\overline{h}}_0}{\partial \theta}\kern24.25em \\ {}R\left({\overline{p}}_x\right)=0\kern27.25em \\ {}R\left({\overline{p}}_y\right)=0\kern27em \\ {}R\left({\overline{p}}_z\right)=\mp \frac{\partial }{\partial \overline{R}}\left(3\overline{R}{\overline{h}}_0^2\frac{\partial {\overline{p}}_0}{\partial \overline{R}}\right)\mp \frac{\partial }{\partial \theta}\left(\frac{3{\overline{h}}_0^2}{\overline{R}}\frac{\partial {\overline{p}}_0}{\partial \theta}\right)\kern13.5em \\ {}R\left({\overline{p}}_{\theta_x}\right)=\mp \frac{\partial }{\partial \overline{R}}\left(3{\overline{h}}_0^2\overline{R}\frac{\partial {\overline{p}}_0}{\partial \overline{R}}{\overline{r}}_i sin\theta \right)\mp \frac{\partial }{\partial \theta}\left(\frac{3{\overline{h}}_0^2}{\overline{R}}\frac{\partial {\overline{p}}_0}{\partial \theta }{\overline{r}}_i sin\theta \right)\pm {S}_t\overline{R}{\overline{r}}_i cos\theta \kern0.5em \\ {}R\left({\overline{p}}_{\theta_y}\right)=\mp \frac{\partial }{\partial \overline{R}}\left(3{\overline{h}}_0^2\overline{R}\frac{\partial {\overline{p}}_0}{\partial \overline{R}}{\overline{r}}_i cos\theta \right)\mp \frac{\partial }{\partial \theta}\left(\frac{3{\overline{h}}_0^2}{\overline{R}}\frac{\partial {\overline{p}}_0}{\partial \theta }{\overline{r}}_i cos\theta \right)\mp {S}_t\overline{R}{\overline{r}}_i sin\theta \\ {}R\left({\overline{p}}_{\dot{x}}\right)=0\kern27.25em \\ {}R\left({\overline{p}}_{\dot{y}}\right)=0\kern27.25em \\ {}R\left({\overline{p}}_{\dot{z}}\right)=\pm 2{S}_t\overline{R}\kern24.5em \\ {}R\left({\overline{p}}_{{\dot{\theta}}_x}\right)=\pm 2{S}_t\overline{R}{\overline{r}}_i sin\theta \kern21.25em \\ {}R\left({\overline{p}}_{{\dot{\theta}}_y}\right)=\pm 2{S}_t\overline{R}{\overline{r}}_i cos\theta \kern20.75em \end{array}\right. $$
(9)

where \( R\left({\overline{p}}_{\zeta}\right)=\frac{\partial }{\partial \theta}\left(\frac{h_0^3}{\overline{R}}\frac{\partial {p}_{\zeta }}{\partial \theta}\right)+\frac{\partial }{\partial \overline{R}}\left(\overline{R}{h}_0^3\frac{\partial {p}_{\zeta }}{\partial \overline{R}}\right) \),\( \zeta =0,x,y,z,{\theta}_x,{\theta}_y,\dot{x},\dot{y},\dot{z},{\dot{\theta}}_x,{\dot{\theta}}_y \).

2.3.5 Flow continuity equation

The journal and thrust hydrostatic bearings of the spindle adopt four rectangular oil recesses of equal depth uniformly distributed along the circumference, as shown in Fig. 3. An orifice restrictor to compensate for bearing stiffness is arranged in the middle of the oil recess. Given that the flowrate flowing into the oil recess through the orifice is Qin, the flowrate flowing out of the oil recess through the film land around the oil recess is Qout. For incompressible liquid, its flow continuity equation is:

$$ {Q}_{in}={Q}_{out} $$
(10)
$$ {Q}_{in}=\alpha \frac{\pi {d}_c^2}{4}\sqrt{\frac{2\Delta p}{\rho }} $$
(10-1)
$$ {Q}_{out}={\int}_{ae}\frac{h^3}{12\eta}\frac{dp}{dz} dx+{\int}_{ce}\left(\pm \frac{Uh}{2}+\frac{h^3}{12\eta}\frac{dp}{dx}\right) dz+{A}_r\frac{\partial h}{\partial t} $$
(10-2)

where α α is the flowrate coefficient (α = 0.6 − 0.7α = 0.6 − 0.7); dc dc is the diameter of the orifice restrictor;∆p Δp is the differential pressure flowing through the orifice restrictor; ρ ρ is the oil density; Ar Ar is the recess area; ae represents the axial edge of recess; ce represents the circumferential edge of recess; and “±” represents the right and left edge of the circumferential edge of the recess.

Fig. 3
figure 3

The unwrapped flow field of bearings

Full size image

Introducing dimensionless factor \( \frac{p_s{C}^3}{12\eta } \), Eqs. (10-1) and (10-2) can be rewritten in dimensionless form as:

$$ {\overline{Q}}_{in}=\delta \sqrt{1-\overline{p}} $$
(11)
$$ {\overline{Q}}_{out}={\int}_{ae}{\overline{h}}^3\frac{\partial \overline{p}}{\partial \overline{z}} d\theta +{\int}_{ce}\left(\pm {S}_h\overline{h}+{\overline{h}}^3\frac{\partial \overline{p}}{\partial \theta}\right)d\overline{z}+2{S}_h\frac{\partial \overline{h}}{\partial \overline{t}} d\theta d\overline{z} $$
(12)

where \( \delta =\frac{3\sqrt{2}\pi \alpha {d}_c^2\eta }{C_0^3\sqrt{\rho {p}_s}} \).

Expand the flow continuity Eqs. (11) and (12) as Taylor expansion to solve for steady and transient pressures, as follows [25]:

$$ {\overline{Q}}_{in}={\overline{Q}}_{in}^0+\frac{\partial {\overline{Q}}_{in}}{\partial \zeta}\Delta \xi +\frac{\partial {\overline{Q}}_{in}}{\partial \dot{\zeta}}\Delta \dot{\xi} $$
(13)
$$ {\overline{Q}}_{out}={\overline{Q}}_{out}^0+\frac{\partial {\overline{Q}}_{out}}{\partial \zeta}\Delta \xi +\frac{\partial {\overline{Q}}_{out}}{\partial \dot{\zeta}}\Delta \dot{\xi} $$
(14)

where ξ = x, y, z, θx, θy.

Steady-state and transient flowrate equilibrium equations can be obtained according to the flow continuity principle as follows:

$$ \left\{\begin{array}{c}{\overline{Q}}_{in}^0={\overline{Q}}_{out}^0\\ {}\frac{\partial {\overline{Q}}_{in}}{\partial \xi }=\frac{\partial {\overline{Q}}_{out}}{\partial \xi}\\ {}\frac{\partial {\overline{Q}}_{in}}{\partial \dot{\xi}}=\frac{\partial {\overline{Q}}_{out}}{\partial \dot{\xi}}\end{array}\right.,\xi =x,y,z,{\theta}_x,{\theta}_y $$
(15)

2.4 Dynamic characteristics of the spindle

Using the finite difference method (FDM) to solve the simultaneous Eqs. (8, 9, 10, 11, 12, 13, 14, and 15), the steady-state pressure and transient pressure of journal bearings are p0j(θ, z), pξj(θ, z), and \( {p}_{\dot{\xi}j}\left(\theta, z\right) \), respectively, and that of the thrust bearings are p0t(θ, r), pξt(θ, r), and \( {p}_{\dot{\xi}t}\left(\theta, r\right) \), respectively.

2.4.1 Stiffness and damping coefficients

By integrating the transient pressure pξj(θ, z) and \( {p}_{\dot{\xi}j}\left(\theta, z\right) \) along the radial and axial directions of the journal bearing, the stiffness and damping coefficient matrices of the journal bearing are obtained. Furthermore, the solution methods of the left and right journal bearings are the same as follows [26, 27]:

$$ {\overline{k}}_{ij}\left(i,j=x,y,{\theta}_x,{\theta}_y\right) $$
(16)
$$ {\overline{k}}_{ij}\left(i,j=x,y,{\theta}_x,{\theta}_y\right) $$
(17)

where \( {\overline{k}}_{ij}\left(i,j=x,y,{\theta}_x,{\theta}_y\right) \) are the stiffness coefficients of the journal bearing and \( {\overline{c}}_{ij}\left(i,j=x,y,{\theta}_x,{\theta}_y\right) \) are the damping coefficients of the journal bearing.

Similarly, the stiffness and damping coefficient matrices of the thrust bearings in the dimensionless form are calculated as:

$$ {\overline{k}}_{ij}\left(i,j=x,y,{\theta}_x,{\theta}_y\right) $$
(18)
$$ {\overline{k}}_{ij}\left(i,j=x,y,{\theta}_x,{\theta}_y\right) $$
(19)

where \( {\overline{k}}_{ij}\left(i,j=z,{\theta}_x,{\theta}_y\right) \) are the stiffness coefficients of the thrust bearing and \( {\overline{c}}_{ij}\left(i,j=z,{\theta}_x,{\theta}_y\right) \) are the damping coefficients of the thrust bearing.

2.4.2 Amplitude amplification factor

Without loss of generality, this paper assumes that the coaxiality error of the left and right journal bearings of the rotor is symmetric along the axis, as shown in Fig. 1(b). Hence, the rotor motion trajectory is mainly represented as the rotation motions around the x/y direction. For rigid rotors, the dynamic characteristics and motion errors of the spindle can be effectively evaluated by using the frequency-amplitude response diagram. When the rotor is in the center position, the equivalent spring and damping coefficients of oil film satisfy the following relations:

$$ {k}_{\theta_x{\theta}_x}={k}_{\theta_y{\theta}_y},{k}_{\theta_x{\theta}_y}=-{k}_{\theta_y{\theta}_x},{c}_{\theta_x{\theta}_x}={c}_{\theta_y{\theta}_y},{k}_{\theta_x{\theta}_y}={k}_{\theta_y{\theta}_x}=0 $$
(20)

AAF is introduced to represent the ratio of the amplitude of forced vibration to the static deformation of the rotor, and this index can easily characterize the amplitude amplification characteristics of the rotor at different speeds. According to Rowe’s algorithm to calculate the AAF of two DOF rigid rotors, the rotor dynamics equations can be simplified as follows [28]:

(21)

where \( {M}_x^f \) and \( {M}_y^f \) are the transient moments of oil film along the x/y axis, respectively; ξ = x, y, z, θx, θy.

Then, the amplitude-frequency characteristic was obtained as follows:

$$ {k}_{\theta_x{\theta}_x}\frac{\theta_x}{M_x^f}=\sqrt{\frac{A^2+{B}^2}{C^2+{D}^2}} $$
(22)
$$ {k}_{\theta_y{\theta}_y}\frac{\theta_y}{M_y^f}=\frac{k_{\theta_x{\theta}_y}}{k_{\theta_x{\theta}_x}}\frac{1}{\sqrt{C^2+{D}^2}} $$
(23)

where ωn is the natural frequency, \( {\omega}_n=\sqrt{\frac{k_{\theta_x{\theta}_x}}{I_x}} \); λ is the frequency ratio, \( \lambda =\frac{\omega }{\omega_n} \); χ is the damping coefficient, \( \chi =\frac{c_{\theta_x{\theta}_x}}{2\sqrt{k_{\theta_x{\theta}_x}{I}_x}} \); and define other parameters as A = 1 − λ2, B = 2χλ, \( C={\left(1-{\lambda}^2\right)}^2-{\left(2\chi \lambda \right)}^2+{\left(\frac{k_{\theta_x{\theta}_y}}{k_{\theta_x{\theta}_x}}\right)}^2 \), D = 4χλ(1 − λ2).

2.4.3 Motion trajectory of the rotor

Rewrite Eq. (1) to obtain the rotor motion trajectory as:

$$ \ddot{X}=\frac{1}{M}\left({F}_e-\left({C}_R{\dot{X}}_R+{C}_L{\dot{X}}_L+{C}_T\dot{X}+{K}_R{X}_R+{K}_L{X}_L+{K}_TX\right)\right) $$
(24)

The stiffness matrix, damping matrix, and external load solved in the previous sections are substituted into Eq. (24) to obtain the instantaneous acceleration of the rotor; then, the velocity and displacement of the rotor are calculated by integrating the acceleration. Furthermore, draw the displacement diagram of the rotor axis, and use the envelope method to work out the runout of the spindle. The general algorithms for solving the above differential equations are the fourth-order Runge-Kutta method or the Euler method. Since the solution process of the Runge-Kutta method is complex and has low efficiency, the Euler method with better convergence and higher computational efficiency is adopted in this paper, as follows [29, 30]:

$$ \left\{\begin{array}{c}\dot{X}\left(t+\Delta t\right)=\dot{X}(t)+\ddot{X}(t)\Delta t\kern2.5em \\ {}X\left(t+\Delta t\right)=X(t)+\dot{X}\left(t+\Delta t\right)\Delta t\end{array}\right. $$
(25)

where ∆t is the simulation time step, which is usually 10−7 s.

3 Results and discussion

3.1 The simulation parameters

This section develops the simulation program with MATLAB based on the preceding theory to verify the influence of rotor coaxiality on the spindle runout and to study the variation rule of rotor coaxiality, rotation speed, external load, oil film clearance, and oil supply pressure on the spindle runout. The parameters of the journal and thrust bearings of the spindle are summarized in Tables 1, 2, and 3, respectively.

Table 1 The specifications of the spindle
Full size table
Table 2 Parameters of the journal bearing
Full size table
Table 3 Parameters of the thrust bearing
Full size table

3.2 Linearization verification

While the linearization method is employed to solve Eq. (24), substitute the spindle stiffness coefficients and damping coefficients acquired when the rotor is at the quasi-static position into the above equation to solve the rotor acceleration. When the rotor has a small oscillation around the equilibrium position, the stiffness and damping coefficients of the spindle will change with the shift of the rotor position. In this section, the influence of the rotor displacement on the stiffness and damping coefficients of the spindle is validated by computer simulation.

Figure 4 shows that when the rotor eccentricity ratio is less than 0.1, the stiffness coefficient and damping coefficient change very little and have a linear relationship with the eccentricity ratio. Specifically, when the eccentricity ratio varies from 0 to 0.1, the variation of damping coefficients is less than 2%, and the maximum change of stiffness coefficients is less than 5%. The above simulation results indicate that when the eccentricity ratio of the rotor is less than 0.1, the errors of the stiffness and damping coefficient dealt with by linearization are small, which can fully meet the requirements of engineering calculation [22].

Fig. 4
figure 4

Stiffness and damping coefficients versus the rotor’s displacement (n = 0rpm, F = 0N, h = 0.016mm, ps = 4MPa). (a) Force stiffness coefficients due to translation, (b) moment stiffness coefficients due to tilt motion, (c) force damping coefficients due to translation, and (d) moment damping coefficients due to tilt motion

Full size image

3.3 Coaxiality error versus runout

Dynamic oil film loads caused by rotor coaxiality error include the force along the x/y/z axis and the moment around the x/y axis. If the rotor coaxiality error is symmetrical, the force and torque variation trend along each axis is basically the same. Without loss of generality, cutting torque Mx and angular displacement θx around the x-axis are selected as examples to study the relationship between spindle runout and oil film dynamic force and frequency-amplitude characteristics.

According to the above simulation conditions, the moment stiffness coefficients due to tilt motion and the moment damping coefficients due to tilt motion are calculated as follows: \( {k}_{\theta_x{\theta}_x}={k}_{\theta_y{\theta}_y}=1.37\times {10}^7 \)(Nm/rad), \( {k}_{\theta_x{\theta}_y}=-{k}_{\theta_y{\theta}_x}=1.33\times {10}^6\left( Nm/ rad\right) \), \( {c}_{\theta_x{\theta}_x}={c}_{\theta_y{\theta}_y}=-9.04\times {10}^4\left( Nms/ rad\right) \), \( {k}_{\theta_x{\theta}_y}={k}_{\theta_y{\theta}_x}=0 \). Substituting the above coefficients into Eq. (24), the natural frequency and damping coefficients of the spindle are calculated as 2038 Hz and 45, respectively, and the corresponding frequency-amplitude diagram of the spindle is obtained from Eq. (24), as shown in Fig. 5(a). The figure shows that the AAF of the system decreases rapidly with the increase of spindle speed, which is determined by the large damping characteristic of the system.

Fig. 5
figure 5

Coaxiality error versus runout (n = 3000rpm, F = 0N, h = 0.016mm, ps = 4MPa). a Frequency-amplitude diagram, b moment caused by oil film, c 3D rotor trajectory diagram, d rotor trajectory on the measured plane, e relationship between the coaxiality and the runout

Full size image

Figure 5(b) shows that the torque Mx formed by the oil film force presents periodic changes, and its change frequency is the same as that of the spindle rotation; i.e., a simple harmonic excitation force caused by rotor coaxiality exerts on the rotor. The simulation results show that |Mx|max increases linearly with the rise of coaxiality because the stiffness and damping coefficients of the spindle are approximately constant while the rotor movement is near the quasi-static position.

Figure 5(c) shows the three-dimensional motion trajectory diagram of the rotor and also depicts that the principal movement of the rotor is the rotation motion around the x/y axis, while the displacement of the center point of the rotor along the x/y/z axis is 0. Because the coaxiality error of the rotor is assumed to be distributed symmetrically along the rotor axis, the resultant oil film force acting on the rotor is 0 along the x/y/z axis, and the torque around the x/y axis causes the rotor to wobble. A section perpendicular to the rotor axis at z equals 100 mm is taken as the measured plane to evaluate the radial runout of the spindle, as shown in Fig. 5(d). The figure shows that the rotor trajectories corresponding to different coaxiality errors are perfect circles, and the radius of the rotor motion orbit increases with the rise of coaxiality. Further, in Fig. 5(e), the relationship between spindle runout and coaxiality is drawn directly with eccentricity ee as the abscisic and spindle runout as the ordinate, and the results show that the relationship between the two is linear amplification. The reason for the above phenomenon is that when the spindle speed is constant, its AAF remains unchanged, while the dynamic force of the oil film increases linearly with the growth of coaxiality.

3.4 Rotational speed versus runout

Figure 6(a) and 6(b) show that with the increase of the spindle speed, the stiffness coefficients \( {k}_{\theta_x{\theta}_y} \), \( {k}_{\theta_y{\theta}_x} \) rise due to the enhanced wedging effect of the oil film in the filmland; however, the other stiffness and damping coefficients basically remain constant. Meanwhile, Fig. 6(a) and (b) show that \( {k}_{\theta_x{\theta}_y} \), \( {k}_{\theta_y{\theta}_x} \) increase in proportion to the spindle speed and meet the following condition: \( {k}_{\theta_x{\theta}_y}=-{k}_{\theta_y{\theta}_x} \). According to the stiffness and damping coefficients shown in Fig. 6(a) and 6(b), the natural frequency and the damping coefficient are, respectively, 2038 Hz and 45 solved from Eq. (23). Besides, as the stiffness coefficients \( {k}_{\theta_x{\theta}_y} \), \( {k}_{\theta_y{\theta}_x} \) vary with the spindle speed, the frequency-amplitude characteristics at different spindle speeds can be calculated by Eq. (23), as shown in Fig. 6(c). The above figure shows that the amplitudes of the system generally decrease with the increase of the frequency ratio λ. Furthermore, when λ is near 0, the AAF declines with the growth of spindle speed; when λ is higher than 0.01, the AAF is little affected by the spindle speed.

Fig. 6
figure 6

Rotational speed versus runout (ee = 0.3μm, F = 0N, h = 0.016mm, ps = 4MPa). a Moment stiffness coefficients due to tilt motion, b moment damping coefficients due to tilt motion, c frequency-amplitude diagram, d moment around x-axis caused by oil film, e rotor trajectory on the measured plane, and f relationship between the rotary speed and the runout

Full size image

Figure 6(f) shows the dynamic oil film torque |Mx|max corresponding to different spindle speeds, which changes periodically at the same frequency with the spindle speed and increases significantly with the growth of the spindle speed. Figure 6(g) represents the rotor’s operation trajectory diagram on the measured plane at different spindle speeds, and the motion trajectories are all approximately perfectly circular because the coaxiality distribution of the rotor is assumed to be symmetric. Assuming that the spindle speed is the abscissa and the runout is the ordinate, draw the relationship between the spindle speed and the runout in Fig. 6(h). The figure shows that when the spindle speed is low, the runout rises faster with the increase of the spindle speed, but when the spindle speed is higher than 3000 rpm [32], the increase rate of the runout slows down. Further, across the operating speed range, the runout change is less than 0.01 μm. Combined with Fig. 6(e) and 6(f), it can be found that the dynamic force of the oil film acting on the rotor increases significantly with the increase of spindle speed, but the AAF of the system decreases with the growth of spindle speed. Therefore, the spindle runout is less affected by the change of spindle speed on the whole.

3.5 Cutting force versus runout

Figure 7(a, b, c, d, e, f, g, and h) show the relationship between the dynamic characteristics of the spindle and the cutting load. Among them, force stiffness coefficients due to translation, moment stiffness coefficients due to tilt motion, force damping coefficients due to translation, and moment damping coefficients due to tilt motion shown in Fig. 7(a), 7(d), 7(e), and 7(h) vary slightly with the change of cutting load. Therefore, the natural frequency and damping ratio of the spindle change little with the cutting load, and the spindle still has a large damping property. On the other hand, Fig. 7(b), 7(c), 7(f), and 7(g) illustrates that force stiffness coefficients due to tilt motion, moment stiffness coefficients due to translation, force damping coefficients due to tilt motion, and moment damping coefficients due to translation increase significantly with the growth of cutting load due to the rise of the rotor’s eccentricity. According to the spindle dynamic characteristic parameters shown in Fig. 7(a, b, c, d, e, f, g, and h), calculate the frequency-amplitude diagram of the spindle under different cutting loads shown in Fig. 7(i). Due to the large damping characteristic of the system, the AAF in the above figure decreases rapidly with the increase of frequency ratio λ, and different cutting loads have little influence on the AAF of the system.

Fig. 7
figure 7figure 7

Cutting force versus runout (ee = 0.3μm, n = 3000rpm, h = 0.016mm, ps = 4MPa). a Force stiffness coefficients due to translation, b force stiffness coefficients due to tilt motion, c moment stiffness coefficients due to translation, d moment stiffness coefficients due to tilt motion, e force damping coefficients due to translation, f force damping coefficients due to tilt motion, g moment damping coefficients due to translation, h moment damping coefficients due to tilt motion, i frequency-amplitude diagram, j moment around x-axis caused by oil film, k rotor trajectory on the measured plane, and l relationship between the cutting force and the runout

Full size image

In Fig. 7(j), the dynamic oil film torque |Mx|max under different loads presents periodic changes and is at the same frequency as the spindle speed. Also, force stiffness coefficients due to tilt motion, moment stiffness coefficients due to translation, force damping coefficients due to tilt motion, and moment damping coefficients due to translation increase by skew-symmetric tendency with the rise of the cutting load. Hence, the cutting load only changes the quasi-static working position of the rotor, and it has little influence on the amplitude of |Mx|max, as shown in the local magnification image of Fig. 7(j).

The above simulation results show that the dynamic force of oil film and the AAF are little affected by the cutting load, so the spindle runout is almost not affected by the change of cutting load. Figure 7(k) shows that as the cutting load increases, the quasi-static equilibrium position of the rotor gradually shifts away from the center of the spindle, and the trajectory of the rotor under different loads is a perfect circle. Further, assuming that the cutting force is the abscissa and the runout is the ordinate, the relationship between the cutting load and the spindle runout is shown in Fig. 7(l). The curve indicates that the spindle runout caused by the change of cutting load is less than 0.001 μm.

3.6 Oil supply pressure versus runout

In the hydrostatic bearing compensated by the orifice restrictor, changing the oil supply pressure can obtain the different spindle dynamic characteristics, as shown in Fig. 8(a, b, c, and d). When the oil supply pressure increases from 2MPa to 4MPa, the principal stiffness coefficients kxx, kyy, \( {k}_{\theta_x{\theta}_x} \), and \( {k}_{\theta_y{\theta}_y} \) decrease by about 10%, while the principal damping coefficients cxx, cyy, \( {c}_{\theta_x{\theta}_x} \), and \( {c}_{\theta_y{\theta}_y} \) decrease by about 60%. According to the stiffness and damping coefficients determined in Fig. 8(b) and 8(d), the frequency-amplitude diagram of the spindle under different oil supply pressures can be obtained from Eq. (23), as shown in Fig. 8(e). This figure shows that due to the high damping characteristics of the spindle, the overall AAF decreases rapidly with the growth of frequency ratio. On the other hand, increasing the oil supply pressure will cause the damping of the system to drop, so the AAF corresponding to high oil supply pressure at the same frequency ratio will increase slightly.

Fig. 8
figure 8

Oil supply pressure versus runout (ee = 0.3μm, n = 3000rpm, F = 0N, h = 0.016mm). a Force stiffness coefficients due to translation, b force stiffness coefficients due to tilt motion, c moment stiffness coefficients due to translation, d moment stiffness coefficients due to tilt motion, e frequency-amplitude diagram, f moment around x-axis caused by oil film, g rotor trajectory on the measured plane, and h relationship between the oil supply pressure and the runout

Full size image

Figure 8(f) and its partial enlarged detail show that the dynamic oil film torque |Mx|max is less affected by the changes of oil supply pressure because the stiffness and damping coefficients of the spindle change in the opposite direction with the increase of oil supply pressure. Hence, the resultant torque acting on the rotor decreases slightly with the increase of oil supply pressure.

Since the oil supply pressure has little influence on the AAF and the dynamic torque of oil film, it has little effect on the spindle runout. The simulation results in Fig. 8(g) and 8(h) illustrate that when the oil supply pressure varies between 2 MPa and 4MPa, the spindle runout trajectories are close to a perfect circle, and the variation of the spindle runout is only 0.001 μm.

3.7 Oil film clearance versus runout

Figure 9(a, b, c, and d) shows the relationship between the oil film clearance and the dynamic performance of the spindle. Figure 9(b) explains that the moment stiffness coefficients \( {k}_{\theta_x{\theta}_x} \) and \( {k}_{\theta_y{\theta}_y} \) start to increase as the oil film clearance increases at the beginning; when h increases to 0.015 mm,\( {k}_{\theta_x{\theta}_x} \) and \( {k}_{\theta_y{\theta}_y} \) start to decrease after they cross the inflection point. Besides, moment damping coefficients \( {c}_{\theta_x{\theta}_x} \) and \( {c}_{\theta_y{\theta}_y} \) are on a sustained downward trend as the oil film clearance is increasing, and \( {c}_{\theta_x{\theta}_x} \) and \( {c}_{\theta_y{\theta}_y} \) decrease by about 50% when the oil film clearance increased from 0.012 to 0.02 mm. Combined with the cross stiffness coefficients ratio \( {k}_{\theta_x{\theta}_y}/{k}_{\theta_x{\theta}_x} \) of the system, the relationship between the AAF and the oil film clearance can be solved from Eq. (23), as shown in Fig. 9(e). The above figure shows that with the increase of the oil film clearance, the damping coefficients of the system decreases gradually, which makes the AAF corresponding to the high oil film clearance slightly increase at the same frequency ratio.

Fig. 9
figure 9

Oil film clearance versus runout (ee = 0.3μm, n = 3000rpm, F = 0N, ps = 4MPa). a Force stiffness coefficients due to translation, b moment stiffness coefficients due to tilt motion, c force damping coefficients due to translation, d moment damping coefficients due to tilt motion, e frequency-amplitude diagram, f moment around x-axis caused by oil film, g rotor trajectory on the measured plane, and h relationship between the oil film clearance and the runout

Full size image

Figure 9(f) shows that as the oil film clearance increases from 0.012 to 0.02 mm, the dynamic oil film torque |Mx|max also rises from 0.01 to 0.014 Nm. The comparison between Fig. 9(e) and Fig. 9(f) shows that the dynamic oil film torque and the AAF both increase with the rise of the oil film clearance and implies that the runout of the spindle will increase with the growth of the oil film clearance. The simulation results in Fig. 9(g) verify the above inference and show that the rotor running trajectory corresponding to different oil film thicknesses is approximately perfectly circular. Figure 9(h) shows that when the oil film clearance increases from 0.012 to 0.02 mm, the runout of the spindle rises from 0.21 m to 0.275 μm linearly.

4 Conclusions

The results show that when the rotor coaxiality error is coupled with the operating parameters of the spindle, the spindle speed, cutting force, and oil supply pressure are non-sensitive factors, while the oil film clearance is a sensitive factor in the hydrostatic spindle with mid-thrust bearing layout. The conclusion not only provides a guidance for the selection of operating parameters for the spindle accuracy design but also puts forward the corresponding manufacturing requirements for the geometric tolerances of the key components of the spindle. The main conclusions obtained are listed below:

  1. (1)

    When the rotor oscillates slightly near the quasi-static position, the variation range of stiffness and damping coefficients are less than 5%, which means that the linearization can meet the requirements of engineering accuracy of rotor dynamics and trajectory analysis.

  2. (2)

    When the rotor speed is far below the critical stability speed, the five degree-of-freedom hydrostatic spindle has the characteristics of large damping, and the amplitude amplification factor of the spindle rapidly decreases with the increase of the spindle speed.

  3. (3)

    When the ratio of coaxiality to oil film thickness is less than 0.1, the dynamic oil film force and spindle runout caused by coaxiality are proportional to coaxiality error.

  4. (4)

    The amplitude amplification factor is slightly affected by the variation of the oil film clearance; on the other hand, the dynamic force of the oil film increases significantly with the growth of the oil film clearance. Thus, the spindle runout develops obviously with the increase of the oil film clearance.

  5. (5)

    Although the changes of rotor speed, external load, and oil supply pressure have distinct influences on the spindle’s stiffness and damping coefficients, these factors have little effect on the spindle runout taking the variation trend of stiffness and damping into account comprehensively.