1 Introduction

Chip gullet is a basic structure of the broaching tools for chip curling and evacuating during the broaching process. Particularly, against the traditional ring type gullets, the helical gullet provides excellent working performance, i.e., smooth the fluctuation of broaching force, promote the chip curling, and improve the quality of machined surfaces, with the help of semi-continuous cutting of oblique cutting teeth along the helical gullets instead the periodic engaging-exiting of cutting teeth. Besides, chip break grooves are eliminated when helical chip gullets are adopted; it benefits to the economics of broaching tools. In practical, commonly, the helical rake flank is periodically sharped to ensure the sharpness of cutting teeth for material cutting, and it is crucial to prolong the life of broaching tool and reduce the tool cost. In the rake flank sharpening process, the parameters of broaching tools like rake angle, core radius, and smoothness of the helical chip gullet, which directly determine the cutting performance of the broaching tool, are the vital factors to be ensured. However, it is a challenge that to find appropriate wheel orientation and position to meet these parameters.

As the basis to identify the orientation and position of wheel for helical rake flank sharpening, predicting the accurate machined profile is the premise to evaluate the interest parameters. It is generally carried out by analytical, graphical, and Boolean-based methods. Commonly, the analytical methods identify the instant contact line enveloping theory via envelop theory and differential geometry [1,2,3,4,5]. The points on the wheel surface that satisfy the cutting speed is perpendicular to the normal vector consistent of the instant contact line; then, all of them are translated to the cross-section to obtain the machined transversal profile. Analytical method is easy to implement with implicit or explicit formulations; however, singular points are likely appeared when adopting complex wheels. Consequently, dedicate processes are required to deal with singular points; e.g., Nguyen et al [6] constructed the contact line via insert effective cutting edge curves between singular points, while Xiao et al [7] figured out the contact line of grinding wheel as segment curves. The graphic methods focus on finding the machined transversal profile of the blank with discrete ideology [8,9,10,11,12,13,14]. In detail, the wheel is expressed as a serial of thin disks, and/or the motion of each of them is approximate to discrete solids according to the helical feeding trajectory. Then, by figuring out the intersection curves between each wheel disk solid and the cross-section of blank, the external enveloping profile of these intersection curves is distinguished numerically. Graphic methods are capable to avoid the singular point conditions rather than analytical methods. Nevertheless, density discretization is required to reach high level of precision for machined profile, which leads to huge computational loads. Boolean method performs the cutting of blank by moving the wheel discretely along its helical feeding motion. The main calculations are finished by the core of CAD engine [15,16,17,18]. In fact, auxiliary programming frame or SDK are required, which increase the cost. Most of the transversal profiles of helical gullets can be figured out by these methods, in practical, aim to satisfy the profile calculation with diverse wheel; the one with strong robustness is appreciated even pay higher computation load.

Aiming to obtain desired transversal profile of helical gullet, two kinds of methods are applied in common: (i) design the specific profile for a cutter with given orientation and position and (ii) find proper orientation and position for cutter with given profile. For helical rake flank sharpening, the second method shows advantages like reduce the cost and easy the sharpening management, rather than the first method which provides excellent capability to manufacture complex geometries. Therefore, identifying the proper wheel orientation and position is addressed as minimize the difference between the desired transversal profile and machined profile, and plenty of strategies have been discussed. Rabahah et al [19] identified the orientation of the grinding wheel in several stages, first to match the normal of wheel with the normal rake angle of the helical rake flank, and then to fix the wheel position by ensuring the core radius equals to the minimum distance from the effective grinding edge to the rotation axis of blank. Instead, Xiao et al [7] and Tang et al [20] identified the core radius at first, and then figured out the wheel orientation and positon by satisfying rake angle. Alternatively, the wheel orientation is performed as an iterative searching problem. Wang et al [21] addressed this optimization with explicit objects for rake angle, core radius, and groove width, and with considering the geometric constraints like interference-free and feasible flute profile. Ren et al [22] formulated the wheel orientation as a nonlinear equation group, and solved by numerical searching. Karpuschewski et al [23] proposed a particle swarm searching method to identify the reasonable setup of the grinding wheel, in which both the wheel orientation and position were adjusted to approximate the desired sectional profile. Li et al [24] developed an intelligent wheel position searching method with adopted NPSO to satisfy different precision requirement for grooves, in which the influences of configuration parameters were investigated and the profile identification method with strong robustness was employed. Jia et al [5] involved the distribution of instant contact line for wheel orientation searching; however, it was only discussed the ring type wheel and confusion of dual instant contact lines were exited. To summarize, one can see that these methods were effective to obtain proper wheel orientation and positon, and the analytical ones show short compute time while the numerical ones provided better generality for diverse tasks. All these methods mainly focus on producing the precise transversal profile; however, little attention has been paid on the specific grinding processes for rake flanks with respect to the generality, which are significant to ensure the quality broaching tool after sharpening.

In this study, a wheel orientation and position identification method with considering specific process constraints for helical broach tools sharpening is provided, and the graphic-based transversal profile calculation method is adopted to enhance its robustness. The rest of this work is arranged as follows: Section 2 presents the basic mathematical models include wheel geometry, wheel setup model, graphic transversal profile distinguishing, and deriving of instant contact line. Section 3 models the specific grinding process constraints for rake flank sharpen and builds the wheel orientation identification model. At last, experiments and simulations are carried out to verify this method and investigates the solution space of wheel orientation.

2 Section profile calculation in helical flank sharpening

The axial-section profile of the helical gullet is determined by the wheel profile, the wheel orientation, and the grinding trajectory. Therefore, accurate axial-section profile calculation is the basis to figure out proper wheel orientation for desired helical gullet obtaining.

2.1 Mathematical modeling for grinding wheel

2.1.1 Wheel profile definition

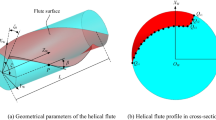
The coordinate system Og-XgYgZg for the grinding wheel is provided as shown in Fig. 1, where the origin Og locates on the external end face of the grinding wheel, Zg-axis coincides with its rotation axis, Xg–axis and Yg-axis are perpendicular to each other and are fixed by right hand law. The axial-section profile of the grinding wheel is described in plane XgOgZg. Aiming to maintain the generality, the profile is decomposed into a serial of curve segments; each of the ith segment is expressed as function Rg = fi(z). Therefore, the external surface Sg(θ,z) of the grinding wheel can be given by rotating the axial-section profile f(z) along Zg-axis as follow:

$$ {\mathbf{S}}_g\left(\theta, z\right)=\left[\begin{array}{c}{f}_i(z)\cos \left(\theta \right)\\ {}{f}_i(z)\sin \left(\theta \right)\\ {}z\\ {}1\end{array}\right] $$
(1)

where θ ∈ [0,2π), i = 1,2,…, Nf, and Nf is the number of curve segments of wheel axial-section profile.

Fig. 1
figure 1

Definition of the grinding wheel

Full size image

Furthermore, the normal vector Ng(θp,zp) of point Sg(θp,zp) on the external surface of wheel can be determined by differential geometry as follow:

$$ {\mathbf{N}}_g\left(\theta, z\right)={\left.\frac{\frac{\partial {\mathbf{S}}_g\left(\theta, z\right)}{\partial z}\times \frac{\partial {\mathbf{S}}_g\left(\theta, z\right)}{\partial \theta }}{\left|\frac{\partial {\mathbf{S}}_g\left(\theta, z\right)}{\partial z}\times \frac{\partial {\mathbf{S}}_g\left(\theta, z\right)}{\partial \theta}\right|}\right|}_{\theta ={\theta}_p,z={z}_p} $$
(2)

2.1.2 Grinding wheel installation

Proper expression for the position and orientation of the grinding wheel relative to the broach tool are the fundament to calculate the axial-section profile of machined helical gullet. As shown in Fig. 2, the broach coordinate system Ob-XbYbZb is fixed to the broach, and Zb-axis is coincided with the rotation axis of broach tool; Xb-axis and Yb-axis are perpendiculars to each other according to the right hand law. Then the grind wheel is installed relative to the broach tool with a five-axis machining configuration, i.e., the swivel angle Σ around Xg-axis, the tilt angle λ around Yg-axis, and the center distance Ex and Ey that from Og to Xb-axis and Yb-axis, respectively.

Fig. 2
figure 2

Configuration of the grinding wheel in helical rake flank grinding

Full size image

Thus, the homogeneous coordinate transformation matrix Mbg from the grinding wheel system to the broach system is given as follow:

$$ {{\mathbf{M}}_b}^g=\left[\begin{array}{cccc}\cos \left(\lambda \right)& 0& \sin \left(\lambda \right)& {E}_x\\ {}\sin \left(\Sigma \right)\sin \left(\lambda \right)& \cos \left(\Sigma \right)& -\sin \left(\Sigma \right)\cos \left(\lambda \right)& {E}_y\\ {}-\cos \left(\Sigma \right)\sin \left(\lambda \right)& \sin \left(\Sigma \right)& \cos \left(\Sigma \right)\cos \left(\lambda \right)& 0\\ {}0& 0& 0& 1\end{array}\right] $$
(3)

Then the grinding wheel surface Sgb(θ,z) and its normal vector Ngb(θ,z) can be given in broach system as follows:

$$ {{\mathbf{S}}_g}^b\left(\theta, z\right)={{\mathbf{M}}_b}^g\cdot {\mathbf{S}}_g\left(\theta, z\right) $$
(4)
$$ {{\mathbf{N}}_g}^b\left(\theta, z\right)={{\mathbf{M}}_b}^g\cdot {\mathbf{N}}_g\left(\theta, z\right) $$
(5)

In practical, the dimension of the bottom part of the helical gullet requires exactly manufacturing. Since it is swept by the external surface of the grind wheel, we can assume the wheel surface tangents with the bottom of the helical gullet at point P = [Rb,0,0,1]T, where the external vector parallels to Xb-axis. Herein, contact point K on the wheel surface can be determined by solving the following equation with numerical methods.

$$ g\left(\theta, z\right)={{\mathbf{N}}_g}^b\left(\theta, z\right)\cdot {\left[-1,0,0,0\right]}^T=1 $$
(6)

Then, by translating contact point K into broach system, Ex and Ey can be given with associating point P = [Rb,0,0,1]T as follows:

$$ \left\{\begin{array}{l}{E}_x={R}_b-{x}_K\cos \left(\lambda \right)-{z}_K\sin \left(\lambda \right)\\ {}{E}_y={z}_K\sin \left(\Sigma \right)\cos \left(\lambda \right)-{x}_K\sin \left(\Sigma \right)\sin \left(\lambda \right)-{y}_K\cos \left(\Sigma \right)\end{array}\right. $$
(7)

2.1.3 Wheel grinding motion

During the helical gullet grinding, the high speed rotation of grinding performs the main cutting motion, while the spiral feeding motion relative to the broaching tool generates the desired helical rake flank according to its geometric parameters, i.e., hand of rotation and lead of gullet Lb. The feeding motion is formulated as a time-varying homogeneous coordinate transformation matrix Ms(t) from grinding wheel system to broach tool system.

$$ {\mathbf{M}}_s(t)=\left[\begin{array}{cccc}\cos \left(\omega (t)\right)& -\sin \left(\omega (t)\right)& 0& 0\\ {}\sin \left(\omega (t)\right)& \cos \left(\omega (t)\right)& 0& 0\\ {}0& 0& 1& \omega (t){L}_b/2\pi \\ {}0& 0& 0& 1\end{array}\right] $$
(8)

where ω(t) is the angular speed of the feeding motion.

2.2 Axial-section profile calculation

Due to the grinding wheel performs forming manufacturing to the helical rake flank, for each axial-section, the machined profile is generated once the grinding wheel goes through it thoroughly. Looking for stronger robustness of axial-section profile calculation for diverse tasks, discrete ideology is adopted instead of the analytical ones to avoid the singular points. Then, the establishing of wheel swept volume, machined profile distinguishing, and the instant contact curve deriving are studied in detail.

2.2.1 Wheel swept volume establishing

For a given axial-section of broach tool Sb: y = 0, as shown in Fig. 3, it is contacted to the grinding wheel at time moment ts and te, respectively. This indicates the swept volume of grinding wheel during time interval [ts,te] produced the axial-section profile on Sb. Then, the time interval can be determined according to the tangent contact condition between the wheel surface and the axial-section Sb; i.e., the normal vector of the contact point on the wheel surface is vertical to the axial-section plane. Consequently, following equation group for variable t can be given.

$$ \left\{\begin{array}{l}{\mathbf{M}}_s(t)\cdot {{\mathbf{M}}_b}^g\cdot {\mathbf{N}}_g\left(\theta, z\right)={\left[0,\pm 1,0,1\right]}^T\\ {}{\mathbf{M}}_s(t)\cdot {{\mathbf{M}}_b}^g\cdot {\mathbf{S}}_g\left(\theta, z\right)\cdot {\left[0,1,0,1\right]}^T=0\end{array}\right. $$
(9)

where the positive and negative sign denotes the grinding wheel engaging and exiting, respectively. The corresponding time ts and te can be obtained by numerical searching method.

Fig. 3
figure 3

Discrete wheel swept volume and section intersect curves

Full size image

Instead of the analytical swept volume of grinding wheel, we can approximate the axial-section profile cutting by grinding wheels with Nt time moments that sampling during [ts,te] evenly according to the feeding motion Ms(t). Then the approximate swept volume of the grinding wheel Vg can be expressed as follow:

$$ {\mathbf{V}}_g=\sum \limits_{k=1}^{N_t}{\mathbf{M}}_s\left({t}_k\right)\cdot {{\mathbf{M}}_b}^g\cdot {\mathbf{S}}_g $$
(10)

where each tk is given as tk = ts + k(te − ts)/(Nt − 1).

2.2.2 Axial-section profile distinguishing

According to the discrete manner, for each grinding wheel instance of Vg, it performs cutting with Sb as an intersection curve. Therefore, after the grinding wheel goes through Sb thoroughly, the external envelop profile of all these intersection curves is the machined axial-section profile of the broach tool in final. Then, identifying the intersection curve between the grinding wheel and Sb, and distinguishing the external enveloping profile are two basic questions for axial-section profile calculation.

In the basis of the definition of grinding wheel, its surface can be composed by a serial of spatial circles that are rotating by the points on the wheel transverse profile around the wheel axis. Consequently, the intersection curve between the grinding wheel Sg and the axial-section Sb of broach tool can be determined by the points between the spatial circles of wheel surface Sg and axial-section Sb one by one. For each ti grinding wheel in the approximate swept volume Vg, the intersection point Ei,j that corresponding to the jth point Qi,j = [fi(zj),0,zj,1]T of wheel transverse profile can be determined by the function of rotation angle θ as follow:

$$ {\mathbf{M}}_s\left({t}_k\right)\cdot {{\mathbf{M}}_g}^b\cdot {\mathbf{M}}_z\left(\theta \right)\cdot {\mathbf{Q}}_{i,j}\cdot {\left[0,1,0,0\right]}^T=0 $$
(11)

where

$$ {\mathbf{M}}_z\left(\theta \right)=\left[\begin{array}{cccc}\cos \left(\theta \right)& -\mathrm{s} in\left(\theta \right)& 0& 0\\ {}\mathrm{s} in\left(\theta \right)& \cos \left(\theta \right)& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right] $$
(12)

Actually, there are two intersection points; the one close to the axis of the broach tool is ascertained as the truth.

Similarly, as shown in Fig. 3, the external envelop profile of all these intersection curves on the axial-section of broach tool is distinguished as discrete points. By dividing the specified radial range [Rb,Rt] into NR segments uniformly, each one determines a line that parallel to the broach axis. Then by identifying the intersection points between all these intersection curves and the line, the ones with the maximum and minimum z-component are specified as envelop profile points. The procedure of envelop profile calculation is illustrated as in Fig. 4.

Fig. 4
figure 4

Flowchart for axial-section profile calculation

Full size image

2.2.3 Grinding contact line identification

During the form grinding process, the wheel contacts the helical rake flank with a spatial curve that is termed as instant contact line, which generates the rake flank according to the helical feeding motion. Naturally, each point of the axial-section profile of the broach tool must coincide with one point of the instant contact line for cutting. The envelop profile distinguishing principle indicates that for each intersection point Ek, it is produced by one spatial circle of the wheel surface at specified time tk; concurrently, Ek is just coincided with one instant contact point of the wheel at tk in broach coordinate system. Therefore, by transforming each envelop point Eb into wheel coordinate system after aligning all of them to the same time reference according to the feeding motion, the point Eg of instant contact line on the wheel surface can be ascertained as follow:

$$ {\mathbf{E}}_g={\mathbf{M}}_s\left(-{t}_k\right)\cdot {\left({{\mathbf{M}}_b}^g\right)}^{-1}\cdot {\mathbf{E}}_b $$
(13)

3 Determination of wheel orientation

In order to obtain excellent working performance of the broach tool, the orientation of grinding wheel for helical rake flank sharpening not only ensure the precise geometry of rake flank but also meet the grinding process constraints.

3.1 Geometry of helical gullet

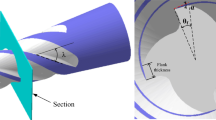
During the helical rake flank sharpening process, the grinding wheel penetrates the rake flank and sweeps a new one. Looking for easy the lateral calculation, the axial-section profile as drawn in Fig. 5 is divided by 4 points as P1-P2-P3-P4, where point P1 and P4 locate on the outer diameter of the broach tool, P3 locates on the bottom of the gullet, and P2 is determined by the specified radius Rd. Clearly, the segment P1-P2-P is corresponding to the rake flank, while P3-P4 belongs to the back of the front cutting teeth.

Fig. 5
figure 5

Geometry of the helical gullet

Full size image

In this basis, the distance between P1 and P4 is defined as the width of machined gullet. Meanwhile, the intersection angle from vector P1P2 to [− 1,0,0,0]T is defined as the rake angle γ in the axial-section plane. It is given as follow:

$$ \gamma =\frac{{\mathbf{P}}_1{\mathbf{P}}_2\times {\left[1,0,0\right]}^T}{\mid {\mathbf{P}}_1{\mathbf{P}}_2\mid } $$
(14)

3.2 Constraints for helical rake flank sharpening

In order to improve the quality of ground rake flank, the wheel orientation must satisfy the following process constraints.

  1. (i)

    The rake angle of the ground rake flank by given wheel orientation ought to equivalently to the desired rake angle γ0.

$$ \gamma ={\gamma}_0 $$
(15)
  1. (ii)

    The grind wheel should depart from the back of the front cutting teeth, to avoid the interference which will reduce the strength of the cutting teeth. For simplicity, the width of machined gullet |P1P4| must less than the designed gullet width Wb of the broach tool.

$$ \left|{\mathbf{P}}_1{\mathbf{P}}_4\right|<{W}_b $$
(16)
  1. (iii)

    During the grinding process, the elimination of the burrs on the top cutting edge and the sharpness of the cutting edge can be guaranteed once the grinding wheel cutting the rake flank from cutting edge to the bottom of the gullet as illustrated in Fig. 6. This indicates the instant contact line should distribute on the wheel surface that z-component of cutting speed is negative. For convenience, each instant contact point E is subjected to one side of the wheel surface that divided by Xb-Ob-Zb plane as following inequality.

Fig. 6
figure 6

Geometries of the instant contact line of helical rake flank sharpening

Full size image
$$ \mathbf{E}\cdot {\left[0,\pm 1,0,0\right]}^T\ge 0 $$
(17)

where plus sign denotes the wheel takes anti-clockwise rotation, while minus sign denotes the wheel takes clockwise rotation.

  1. (iv)

    Each point of the instant contact line performs different cutting speed since different rotation radius. In practical, consistent cutting speeds are helpful to gain better surface finish. To this purpose, we restrict the instant contact line into a small radius range, i.e., all the contact points are outside the specified radius Rs on the wheel surface as shown in Fig. 6. Each of the contact point should meet the following inequality:

$$ \left|{\mathbf{O}}_g\mathbf{E}\right|\ge {R}_s $$
(18)

3.3 Wheel orientation calculation

The rake angle of helical gullet is a function of the wheel orientation, γ = G(Σ, λ), due to each given wheel orientation produces an axial-section profile of the broach tool and determines the rake angle. As a result, which combine the constraints of rake flank sharpening, the wheel orientation for desired rake flank figured out as a nonlinear inequality constrained optimization question.

$$ {\displaystyle \begin{array}{ll}\mathbf{\min}& {\left(G\left(\Sigma, \lambda \right)-{\gamma}_0\right)}^2\\ {}\mathbf{s}.\mathbf{t}.& \begin{array}{l}\left|{\mathbf{P}}_1{\mathbf{P}}_4\right|<{W}_b\\ {}\mathbf{E}\cdot {\left[0,\pm 1,0\right]}^T\ge 0\\ {}\left|{\mathbf{O}}_g\mathbf{E}\right|\ge {R}_s\end{array}\end{array}} $$
(19)

In fact, there are abundant wheel orientations (Σ, λ) since this question takes two variables. Generally, we setup a swivel angle Σ like the helical angle of broach tool gullet at first, then identify the proper tilt angle λ. Thus, the calculation procedure is designed as shown in Fig. 7 to reduce the computational loading. In practical application, once there is no feasible solution, we can enlarge the radius constrain of the instant contact line at first to gain feasible solutions, and use a thinner wheel as standby strategy.

Fig. 7
figure 7

Flowchart of the wheel orientation calculation

Full size image

4 Validations

In order to verify the effectiveness of this method, the wheel orientation calculations for broach tools are carried out by experiments and simulations, and the feasible solutions are investigated.

4.1 Verification

Firstly, as shown in Fig. 8a, a helical rake flank sharpen experiment was performed for by a CBN wheel on a rough bar with a left-hand rotated chip gullet. The detailed parameters on geometry and wheel position/orientation calculation are listed in Table 1. Rake flank ground were implemented twice on universal numeric broaching grinding machine tool (QMK008/simense 840D) with take swivel angle Σ as 4.0° and 4.5°, respectively. The detailed setup parameters were solved by proposed method as in Table 2, and the contact curve in Fig. 8a satisfies the grinding process requirement. At last, on-site measurements were implemented by a Renishaw probe, in which 14 points on the axial-section of the broach bar were sampled to estimate the machined rake angle. The results demonstrated in Fig. 8b show the machined errors of rake angle are no more than 2%, which proof the effectiveness of proposed method.

Fig. 8
figure 8

Rake flank sharpening on a raw bar and on-site measurement

Full size image
Table 1 Parameters for the helical rake flank sharpening task
Full size table
Table 2 Grinding wheel orientations and corresponded machined errors
Full size table

Furthermore, simulation on wheel orientation calculation is performed for a helical broaching tool with right-hand rotation chip gullets by a wheel that takes clockwise rotation as drawn in Fig. 9. Related parameters for these simulations are listed in Table 1.

Fig. 9
figure 9

The profile of the grinding wheel

Full size image

The wheel orientation calculations were simulated for 3 tasks, of which the rake angle of the broaching are specified as 10°, 12°, and 15°, respectively. In further, the swivel angle Σ is specified as 13.5° and 14.5° for each task to identify the tilt angle λ and the width of machined gullet W. The results are listed as in Table 2. Then, by calculating rake angles via analytical method [5] with corresponded wheel orientations, we can figure out that all the deviations of rake angles are less than 2%, which proofs the practicality of this method. Meanwhile, the working conditions between the wheel and the rake flank of these tasks are demonstrated from Fig. 10a to f in sequence. Except the task as shown in Fig. 10a, in which the instant contact line escapes the specified radius Rs, other ones satisfy the constraint (iv). Besides, the grinding wheels are interferences-free, but the one as shown in Fig. 10f which the machined gullet width is larger than the standard width 8 mm. These verify this method is effect to consider the process constraints of rake flank sharpening.

Fig. 10
figure 10

Grinding conditions for helical rake flank

Full size image

4.2 Investigation of feasible solutions

Aiming to investigate the influence of the constraints on the feasible wheel orientations, we construct the solution space for rake flank sharpening tasks that take rake angles 10°, 12°, 15°, and 18°, with utilize the parameters in Table 1. At first, the tilt angles are calculated for given swivel angle from 6.5 to 16.5° to establish the solution space as shown in Fig. 11a without considering the process constraints. Then by identifying the process constraints conditions of each wheel orientation, the solution space is described by the contour map with the machined gullet width, and we can obtain the solutions with feasible machined gullet width as denoted by circles in Fig. 11b, while the solutions satisfy the instant contact location condition as denoted by circles in Fig. 11c. Without considering the radial distribution of instant contact line, the feasible solutions are denoted by circles as in Fig. 11d, where the ineffective solutions are denoted by triangles.

Fig. 11
figure 11

Solution space of the wheel orientations

Full size image

The solution space indicates that for each grinding task, the tilt angle λ of the wheel is increasing when the swivel angle Σ is departing to the helix angle of the chip gullet; consistently, the width of the machined gullet is enlarging. Besides, for a given wheel, enlarging the swivel angle Σ is the basis to ensure the instant contact line places on the engage side of the grinding wheel; nevertheless, the maximum one has been determined by the interference-free constraint. In summary, the feasible wheel orientations are limited in a regional area where the interference-free and instant contact line location condition is met.

5 Conclusions

This paper proposed an orientation calculation method for helical rake flank sharpening by a wheel with general profile. The main contributions are concluded as follows:

  1. (i)

    The wheel orientation model for helical rake flank sharpening was established for wheels with general profiles. Firstly, the wheel orientation was described by swivel and tilt angle, and then the spatial positioning parameters was given by the contact condition between the wheel and gullet bottom surface.

  2. (ii)

    The distinguishing algorithm for wheel machined axial-section profile was introduced based on approximate swept volume of the grinding wheel. The detail mathematic models, like identification of the effective motion interval of the wheel, the intersection points calculation, and the external enveloping profile distinguishing, were provided. Besides, the derivation of the instant contact line was given based on the discrete motion sequence and proper matrix transformation.

  3. (iii)

    The wheel orientation calculation for rake flank sharpening was not only looking for the precise rake angle but also with respect to the practical grinding process constraints; i.e., the location of instant contact line must ensure the cutting speeds are pointing to the bottom of the cutting teeth for burr avoidance and cutting edge sharpness, the instant contact line is distributed in a smaller radial range to achieve consistent cutting speeds for high surface finish, and the width of machined gullet must less than the standard gullet width for interference avoidance.

  4. (iv)

    The calculation procedure for wheel orientation was given according to the relationship between the constraints and orientation angles. Both the simulations and experiments show that the deviations of machined rake angle were less than 2%; it proofed this method was applicable in practical productions. Moreover, the solution space of wheel orientation has indicated the tilt angle is increasing with the enlarging of swivel angle, and the width of machined gullet is increasing at the same time.