1 Introduction

Machining of exotic metals such as Titanium, Aluminum T6061, and metal-matrix carbide (MMC) have enormously increased the demand of carbide tools in aerospace industry. Due to long life and adaptive characteristics with coatings, solid carbide end-mill cutters have become essential and high-demand cutting tools in the machining industry. These end-mill cutters are well-designed cutting tools which include all the parameters of the functional features such as number of flutes, primary and secondary relief faces, end-cutting edges with the defined rake and relief faces, and the gash [1] (see Fig. 1).

Fig. 1
figure 1

Main features of an end-mill cutter

Full size image

In end-mills cutters, geometry of a helical flute is bounded between the rake face of cutting edge and the secondary relief surface that does not include the primary and the secondary relief surfaces [1]. The rake face is inclined with a rake angle which has a direct influence over the cutting forces generated during the machining process. Whereas, the flute geometry provides the chip removal ability and rigidity to the cutter. Hence the geometry of the flutes eventually influences the end-mill cutting life and performance. To grind a prescribed flute accurately, the inverse method is often adopted. In this method, a grinding-wheel of a free-form profile is specially made and used to grind the flute in a two-axis grinding process. This is achieved by the meshing condition that is the normal vector at each point of the contact curve between the grinding wheel and the cutter flute must pass through the rotation axis of the wheel (see Fig. 2). A comprehensive literature review has been reviewed and an optimal and practical method is proposed to grind the flutes with the simplified and easy to manufacture grinding wheels accurately. The new approach is confirmed using two virtually ground end-mill cutters, which are presented as examples in Section 6 of this article.

Fig. 2
figure 2

Inverse grinding of an end-mill using grinding wheel of a free-form profile

Full size image

In past decades, many researches were conducted to model the ground solid carbide end-mills. The researches on the direct method of end-mill cutter grinding are focused on building accurate computer-based models of the end-mill cutter. These researches presented the geometries of the ground flutes related to the selected wheel and the relative motion during the grinding process.

Kim et al. presented accurate CAD models of the end-mill cutter defining the auxiliary angles of the cutter necessary to provide efficient cutting. Authors described the geometry of the end-mill cutter using standard CAD elements and constructed the geometry using the surface modeling [2, 3]. Ko et al. proposed a method for constructing the machined flute profile; in this method, the grinding wheel is represented by discretization of wheel into thin circular disks. The shape cut by each disk into a cross-section of the tool is determined and then as result of all the cuts, the profile of flute on the cross-section is developed [4]. Ren et al. presented design of constant pitch helical end-mill with machined using a two-axis NC milling machine. The design of the flute profile is based on straight lines and circular arc. Whereas, the profile wheel of the grinding wheel was generated using the inverse method applied on the two-axis machining of the mill-cutter [5]. Wu et al. established a manufacturing process model, to determine the NC tools path and process parameters for the grinding of end-mill cutter flutes. In this model, the geometry of the grinding wheel is developed using the inverse method. Compensation in grinding is also incorporated to finish the end-mill cutter [6]. Chen et al. also used inverse method to develop the grinding wheel profile for the grinding of concave cone-end mill cutters. Compensation for the machining errors is also incorporated in the process parameters to increase the accuracy of the model [7, 8]. Another group of researchers (Chen et al.) proposed an integrated approach for the designing of grinding wheel and process parameter. Inverse method has been adopted by the author to develop the grinding wheel profile. Post-processing and simulations are also presented in the work to confirm the design approach [9, 10]. Kim constructed virtual solid models of the ground end-mill cutter, which were able to retrieve some geometric information from these models that were difficult to measure in earlier researchers [11]. Puig et al. presented a virtual grinding system in which a wheel motion is represented by several Boolean operations. Solid model of the end-mill cutter is generated through applying several Boolean operations at the discrete cross-sections of the cutter billet with the wheel. Finally rendering the multiple cross-section into the three-dimensions [12]. Feng et al. worked on a torus-shaped grinding wheel to machine the taper-ball end mill cutter with the constant helical angle. In this research, the normal rake angle of the end-mill cutter is precisely grinded using a moving coordinate system [13]. Chen et al. proposed an analytical model to derive the helical groove and cutting-edge profile of the circular-arc ball-end mill cutter developed during the grinding process. In this model, the process parameters are controlled to precisely develop the end-mill cutter [14]. Hsieh et al. presented a simulation model, to design and manufacture the geometry of helical end-mill cutter using a toroid-cone shaped revolving cutters. The main feature of the model is to optimize the process parameters to grind the end-mill cutter accurately. Experimental validation is also conducted to check the robustness of the model [15, 16]. Kim et al. proposed a simulation-based model to investigate the cutter geometry, grinding wheel geometry, and cutter location for the multi-axis grinding of end-mill cutters. In this method, an analytical approach has been adopted to develop the grinding wheel geometry for the given cutter geometry using the Boolean operations [17]. F. Chen et al. proposed a novel approach to grind the accurate normal angle and cutting edge of the CBN end-mill cutter using the CNC tool grinder and a moving coordinate system. Simulation is also performed to validate the accuracy of the model [18]. Lei et al. presented two models to accurately grind the end-mill cutter by optimizing the five-axis grinding parameter using the standard 1V1/1A1 wheels. In this research, the major geometric parameters of the end-mill cutters are controlled by the taking the advantage of five-axis machine. Simulations are also performed to study the accuracy and precision of the proposed model [19, 20]. Similar work was also developed by Hein et al.; three setting parameters were considered for the flute grinding (flute width, rake angle, and core radius) with no control over the complete flute shape [21]. Xin et al. proposed an optimization model for the evaluation of grinding wheel geometry and tool path for the grinding of end-mill cutter using a multi-axis grinding machine. VERICUT is used to simulate the results for the validations [22]. Han et al. presented a parametric model of the end-mill cutter using straight lines and arc and defined the rake and relief angles on the cutter. Grinding wheel geometry is determined for the cutter and process parameters are determined for the grinding [23].

Tool manufacturers have designed few accurately ground, new end-mill cutters with tight tolerances of the important functional features. To grind a prescribed flute, the inverse method is vastly adopted. In this method, a profile of the grinding wheel is determined using the machine configuration, where a two-axis machine is normally used, in which the tool grinding configuration is defined by moving the wheel and rotating the cutter simultaneously. Most of the research articles cited above proposed accurate grinding using the inverse method. The researches in cited articles mainly applied the inverse method to the end-mill cutters with the helices of constant pitches, concave-cone end-mills, end-mills with circular arc, ball end-mills with constant pitch helical flutes, toroidal end-mills with concave-arc generators, concave arcs ball end-mill cutters, circular arc ball end-mill cutters, toroidal cone end-mills, and truncated-cone ball end-mills. The core activities of these research works include (1) determination of grinding-wheel profile for the two-axis grinding, and (2) calculating the end-mill rotation speed and the feed rate of grinding-wheel. To grind the rake face with the defined normal rake angle accurately, two group of researchers used special grinding wheels to generate the rake faces of tapered ball end-mill cutters [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23].

Unfortunately, all the methods discussed in the literature require a grinding wheel designed using free-form profiles which are difficult and expensive to produce. The side-cutting edges of the ground end-mills are inaccurate, and the helical angles are smaller than the designs, leading to inaccurate normal rake angle. The issue of the free-form grinding wheels and the inaccuracy occurred in the cutting edges and in the prescribed rake angles is critically discussed in the literature [24, 25].

The objective of this research is to achieve precise flute grinding of the end-mill cutter through the five-axis grinding machine. The novelty in this work is the optimization of the grinding wheel path and profile based on simple geometric features to provide end-mill flutes with exact geometries. Also, the grinding wheel is not complex to manufacture as compared to the grinding wheel formed by the free-form curves. CNC programming is presented to determine the machine settings for the generation of the end-mill cutters. The same approach can be extended to other end-mills with minor differences. In this work, the parametric models of the end-mill flute and the grinding wheel profile are developed. The generic mathematical model for the relative location and orientation of the grinding wheel and the end-mill cutter, during the five-axis grinding process are derived, the wheel path to grind the accurate flute on the end-mill cutters are also derived considering the normal rake angle of the cutter. Finally, the accurate end-mill ground model is compared with the flute design model.

The cutting force models for grinding operations can also be incorporated, to optimize the cutting parameters and to predict the tool’s deflections, and to predict the shapes of the actual end-mills produced from the grinding operations. However, this is beyond the focus of this research work, and hence generating the end-mill shapes is limited to the geometric interaction with the grinding wheel.

This research article consists of seven sections, among which the first section has already introduced the research work. In the next two sections, parametric models of a generic end-mill cutter and a grinding wheel profile are defined, while in the fourth section, the mathematical relationship of the end-mill cutter geometry with the wheel geometry is developed. In the fifth section, the five-axis CNC programming is presented, whereas the sixth section addresses the application of this mathematical model with two numerical examples. Finally, the last section concludes the research work.

2 Flute design of cylindrical end-mill cutter

To model a flute of a cylindrical end-mill cutter, parametric model of a cylindrical blank is developed. Analytical model of a side-cutting edge on the cutter billed is also developed. Following sections defined these two steps to define the flute design of the cutter.

2.1 Flute profile of end-mill cutter

Flute geometry is especially important to the cutting function of the end-mills, since each cross-sectional of a flute includes the rake face related with the rake angle which directly affects the cutting forces and temperature. Also, it is tangent to the core of the tool thus it determines the core size, which is a key factor of the tool rigidity [2,3,4]. Moreover, proper geometry of the flute profile can easily break and efficiently evacuate chips during the milling process. To generalize the end-mill cutter, a four-flute tool is considered in this research, for which a tool blank is first considered to define the reference system of the tool. A tool blank is first considered to define the reference system in the tool. A tool coordinate system \( {\mathfrak{R}}^{\mathrm{T}}=\left({\mathbf{o}}^{\mathrm{T}}{\mathbf{x}}^{\mathrm{T}}{\mathbf{y}}^{\mathrm{T}}{\mathbf{z}}^{\mathrm{T}}\right) \) is considered such that the origin oT is rigidly attached at one of the tool end, secondly the zT-axis coincide with the tool axis directing toward the tool length and finally the plane xTyT is perpendicular to the zT-axis, where the xT-axis passes through the side-cutting edge. Figure 3 illustrates the blank of an end-mill cutter with its tool coordinate system.

Fig. 3
figure 3

A blank of end-mill cutter with tool coordinate system

Full size image

Figure 4 illustrates a profile of a four-flutes end-mill cutter in a plane parallel to the xTyT plane. A flute profile in the defined plane is bounded between the two circles of radius rT and rC, which are tool circle radius and core radius, respectively. The profile is defined using three segments: (1) line segment f0f1, making radial rake angle αR with the xT-axis, it forms the rake face of the side-cutting edge of the end-mill; (2) circular arc f1f2 of radius r1, tangent to both f0f1 and the core circle; and (3) circular arc f2f3 of radius r2, tangent to the arc f1f2, and the line segment f3f4. As shown in Fig. 4, line segment f3f4 is tangent to the arc f2f3, makes a secondary relief angle γs with the xT-axis and generates the secondary relief surface of the side-cutting edge in 3D model. Another line segment f4f5 in inclined with an angle of primary relief angle γp which generates the primary relief surface of the side-cutting edge. In the conventional manufacturing processes, the flute between f0 and f3 is often ground in one path with a special grinding wheel where the primary and the secondary relief surfaces are then produced with a standard grinding wheel in two separate paths.

Fig. 4
figure 4

Cross-section of a four-flutes end-mill cutter

Full size image

Flute profile length is defined by a parameter l. The parametric equation of segment f0f1 is given by

$$ \mathbf{F}(l)=\left[\begin{array}{c}{r}_{\mathrm{T}}\\ {}0\end{array}\right]-l\cdotp \left[\begin{array}{c}\cos {\alpha}_{\mathrm{R}}\\ {}\sin {\alpha}_{\mathrm{R}}\end{array}\right] $$
(1)

where\( l\in \left[0,{l}_{f_1}\right] \) and \( {l}_{f_1} \) be the length of line f0f1.

The parametric equation of f1f2 is described as

$$ \mathbf{F}(l)={\mathrm{o}}_1+\left[\begin{array}{c}{r}_1\cdotp \sin \left({\alpha}_{\mathrm{R}}-\frac{l-{l}_{{\mathbf{f}}_1}}{r_1}\right)\\ {}-{r}_1\cdotp \cos \left({\alpha}_{\mathrm{R}}-\frac{l-{l}_{{\mathbf{f}}_1}}{r_1}\right)\end{array}\right] $$
(2)

where \( l\in \left[{l}_{f_1},{l}_{f_2}\right] \) and \( {l}_{f_2} \) be the length of curve f1f2 bounded between the angles subtended by radius r1 from point f1 to f2 on the curve.

Equation of the third circular arc segment f2f3 of radius r2 is given by

$$ \mathbf{F}(l)={\mathrm{o}}_2+\left[\begin{array}{c}-{r}_2\cdotp \sin \left({\alpha}_{\mathrm{R}}-\frac{l_{{\mathbf{f}}_2}-{l}_{{\mathbf{f}}_1}}{r_1}+\frac{l-{l}_{{\mathbf{f}}_2}}{r_2}\right)\\ {}{r}_2\cdotp \cos \left({\alpha}_{\mathrm{R}}-\frac{l_{{\mathbf{f}}_2}-{l}_{{\mathbf{f}}_1}}{r_1}+\frac{l-{l}_{{\mathbf{f}}_2}}{r_2}\right)\end{array}\right] $$
(3)

where \( l\in \left[{l}_{f_2},{l}_{f_3}\right] \) and \( {l}_{f_3} \) be the length of curve bounded between the angles subtended by radius r2 from the point f2 to f3 on the curve.

For a given length of line segment f4f5, \( {l}_{f_4{f}_5} \) the parametric equation of the arc segment, f3f4 can be represented as

$$ \mathbf{F}(l)=\left[\begin{array}{c}{l}_{{\mathbf{f}}_4{\mathbf{f}}_5}\cdotp \cos {\gamma}_{\mathrm{P}}\\ {}{r}_{\mathrm{T}}-{l}_{{\mathbf{f}}_4{\mathbf{f}}_5}\cdotp \sin {\gamma}_{\mathrm{P}}\end{array}\right]+\left({l}_{{\mathbf{f}}_4}-l\right)\cdotp \left[\begin{array}{c}\cos {\gamma}_{\mathrm{S}}\\ {}-\sin {\gamma}_{\mathrm{S}}\end{array}\right] $$
(4)

where \( l\in \left[{l}_{f_3},{l}_{f_4}\right] \) and \( {l}_{f_4} \) be the length of segment f3f4.

Similarly, the parametric equation of the last line segment, f4f5, can be expressed as

$$ \mathbf{F}(l)=\left[\begin{array}{c}0\\ {}{r}_{\mathrm{T}}\end{array}\right]+\left({l}_{{\mathbf{f}}_5}-l\right)\cdotp \left[\begin{array}{c}\cos {\gamma}_{\mathrm{P}}\\ {}-\sin {\gamma}_{\mathrm{P}}\end{array}\right] $$
(5)

where \( l\in \left[{l}_{f_4},{l}_{f_5}\right] \) and \( {l}_{f_5} \) be the length of segment f4f5.

Hence generally, \( {l}_{f_1} \)can be the length of the flute profile at point f1 starting from point f0 where i ∈ {0, 1, …, 5}, and can be obtained together with o1 and o2 using the geometric relations.

2.2 Helical side-cutting edge

Each side-cutting edge can be defined by a helix having a helical angle ψ on the blank of the tool [2,3,4]. The parameter of the side-cutting edge can be defined by rotation angle θ about the zT-axis. Its parametric equation C(θ) is expressed in \( {\mathfrak{R}}^{\mathrm{T}} \) as

$$ \mathbf{C}\left(\theta \right)=\left[\begin{array}{c}{r}_{\mathrm{T}}\cdotp \cos \theta \\ {}{r}_{\mathrm{T}}\cdotp \sin \theta \\ {}\frac{r_{\mathrm{T}}}{\tan \psi}\cdotp \theta \end{array}\right] $$
(6)

where angle θ is measured in radians.

3 Geometry of grinding wheels

Grinding wheels are the abrasive tools used to grind the solid carbide end-mill cutters where standard wheels are largely used in manufacturing due to the cost effectiveness. However, to machine some special shapes, non-standard grinding wheels with complex profiles are proposed in earlier research [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. These grinding wheels are more expensive to manufacture, especially the wheels constructed with free-form profiles. Therefore, in this work, a grinder wheel profile consists of line-line-circle-circle-line is adopted (shown in Fig. 5). Since the profile includes some simple geometric features, the cost of making such grinding wheels is expected to be lower than grinding wheels having free-form curves which need non-traditional ways of contouring, especially in case of splines. The parameters of these geometric features are optimized to accurately grind the end-mill flutes with tight tolerances of its designs.

Fig. 5
figure 5

Proposed grinding wheel profile

Full size image

Consider a coordinate system \( {\mathfrak{R}}^{\mathrm{G}}=\left({\mathbf{o}}^{\mathrm{G}}{\mathbf{x}}^{\mathrm{G}}{\mathbf{y}}^{\mathrm{G}}{\mathbf{z}}^{\mathrm{G}}\right) \), which is defined in following way: first the origin oG is rigidly attached at the center-face of the wheel, secondly the xG-axis is directed along the radial direction of the wheel, and finally the zG-axis is directed along the width of the grinding wheel, where the yG-axis is defined by the right-hand rule.

The grinding-wheel profile is described using five segments: (1) line segment oGP1 aligned horizontally, emerging from point oG and having a length of T1; (2) another line segment P1P2 making an angle β1 with the xG-axis and having a length of T2; (3) circular arc P2P3 of radius R1 with center O1, tangent to the line segment P1P2; (4) another circular arc segment P3P4 having radius R2 with center O2, tangent to the arc P2P3 as shown in Fig. 5; and (5) a line segment P4P5 along the xG-axis and having a length of T3. The profile is closed using line oGP5 along the wheel axis.

The parametric equation of the profile can be given by

$$ R(u)=\left\{\begin{array}{l}{T}_1+\frac{u}{\tan {\beta}_1}\kern7.5em 0\le u\le {T}_2\cdotp \sin {\beta}_1\\ {}{\mathrm{O}}_1^x+\sqrt{{R_1}^2-{\left(u-{\mathrm{O}}_1^z\right)}^2}\kern2.25em {T}_2\cdotp \sin {\beta}_1\le u\le {\mathrm{P}}_3^z\\ {}{\mathrm{O}}_2^x-\sqrt{{R_2}^2-{\left(u-{\mathrm{O}}_2^z\right)}^2}\kern2em {\mathrm{P}}_3^z\le u\le T\end{array}\right. $$
(7)

where u be the parameter of grinding-wheel along its width.

Therefore, the solid model of the grinding wheel can be generated by revolving the profile of the grinding wheel about the zG-axis or rotation axis of the wheel. Considering v as the angular parameter of the wheel, where the angular displacement is measured in radian, the parametric 3D model of the wheel can be given by

$$ \mathbf{W}\left(u,v\right)=\left[\begin{array}{c}R(u)\cdotp \cos v\\ {}R(u)\cdotp \sin v\\ {}u\end{array}\right] $$
(8)

In the preceding equations, the circular arcs origins \( {\mathbf{O}}_i=\left[\begin{array}{c}{\mathrm{O}}_i^x\\ {}{\mathrm{O}}_i^y\\ {}{\mathrm{O}}_i^z\end{array}\right] \), where i = {1, 2}, were calculated as

$$ {\mathrm{O}}_1={\mathrm{P}}_2+\left[\begin{array}{c}-{R}_1\cdotp \sin {\beta}_1\\ {}0\\ {}{R}_1\cdotp \cos {\beta}_1\end{array}\right] $$
(9)
$$ {\mathrm{O}}_2={\mathrm{O}}_1+\left[\begin{array}{c}\left({R}_1+{R}_2\right)\cdotp \sin {\beta}_2\\ {}0\\ {}\left({R}_1+{R}_2\right)\cdotp \cos {\beta}_2\end{array}\right] $$
(10)

Similarly, the profile points \( {\mathbf{P}}_i=\left[\begin{array}{c}{\mathrm{P}}_i^x\\ {}{\mathrm{P}}_i^y\\ {}{\mathrm{P}}_i^z\end{array}\right] \), where i = {1, 2, …, 5}, were calculated in terms of the geometric parameters as \( {\mathbf{P}}_1=\left[\begin{array}{c}{T}_1\\ {}0\\ {}0\end{array}\right] \), \( {\mathbf{P}}_1=\left[\begin{array}{c}{T}_1+{T}_2\cdotp \cos {\beta}_1\\ {}0\\ {}{T}_2\cdotp \sin {\beta}_1\end{array}\right] \),\( {\mathbf{P}}_3={\mathrm{O}}_1+\left[\begin{array}{c}{R}_1\cdotp \sin {\beta}_2\\ {}0\\ {}{R}_1\cdotp \cos {\beta}_2\end{array}\right] \), \( {\mathbf{P}}_4={\mathrm{O}}_2+\left[\begin{array}{c}{R}_2\cdotp \sin \left({\beta}_2+\beta \right)\\ {}0\\ {}{R}_2\cdotp \cos \left({\beta}_2+\beta \right)\end{array}\right] \), and \( {\mathbf{P}}_5=\left[\begin{array}{c}{T}_3\\ {}0\\ {}T\end{array}\right] \)

4 Relationship between end mill cutter flute and grinding wheel

In the earlier two sections, parametric models of end-mill cutter and profile of the grinding wheel have been developed. In this section, the two profiles are mathematically related with each other. So that these are inside the five-axis flute grinding CNC machine such that the two profiles are engaged together and follow the meshing condition, which is later described in Section 4.2. Therefore, the structure of five-axis flute grinding machine has been defined, and the relation between the cutter and the grinding wheel with reference to the CNC machine are developed.

4.1 Structure of tool grinding machine

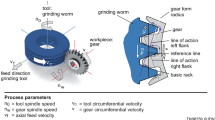
The simple geometry of cylindrical end-mills makes it possible to be ground using two-axis grinding machines. However, the later processes for the further detailing of rake angles along the side cutting edge are also employed. To avoid the subsequent processes on the end-mill cutters, five-axis grinding of the tool using a CNC grinding machine is employed. A five-axis tool grinding CNC machine is shown in Fig. 6. The machine contains five axes, in which three primary axes are XM, YM, and ZM, among which XM axis is used to denote the displacement of the end-mill carriage assembly along the longitudinal direction of the bed and YM and ZM axes represent the linear displacement of the grinding wheel along the height-wise direction and the lateral direction of the machine bed, respectively. The two secondary axes, AM, and BM, represent the angular displacements of the mill-cutter about its axis and about the carriage assembly rotation axis, respectively. This CNC machine can simultaneously perform the linear motion along XM, YM, and ZM axes and the rotation about AM and BM axes. In the proposed method of five-axis grinding of tool, location and orientation of a grinding wheel should be determined first, and then its profile can be optimized. This will ensure that the cutting edge of the cutter and the normal rake angle of its rake face are accurate and are not altered by the wheel geometric parameters.

Fig. 6
figure 6

Five-axis CNC grinding machine

Full size image

4.2 Relative location and orientation of grinding wheel

The core objective of the five-axis tool grinding is to generate the helical side-cutting edge and the rake face with an exact normal rake angle. To achieve this objective, tangency between the grinding wheel and the rake face of the cutter at a point during the grinding is maintained. Hence, the flute machining can be represented by a mathematical model that is the normal vector of the rake face, derived at the side-cutting edge, and the unit normal of the grinding-wheel, both be aligned together at the contact point but with opposite directions. This mathematical model is the principle core of determining the grinding-wheel position and orientation in five-axis tool grinding [24, 25].

Grinding wheel position and orientation can be evaluated using a unit normal vector at the rake face. The process of finding the normal is illustrated here. A point PC is considered on the helical cutting edge C(θ) on the cutter in the \( {\mathfrak{R}}^{\mathrm{T}} \) coordinate system shown in Fig. 7. The first step is to construct a plane Γ passing through the point PC and perpendicular to the cutting edge. The tangent vector I of the side-cutting edge at point PC can be easily obtained, and the plane Γ is perpendicular to I. The second step is to establish a plane Π, normal to the cutting velocity, where direction of the cutting velocity can be imagined by a tangent on the cross section (circular) of the tool blank at the point PC. Hence, the plane Π passes through the zT-axis and point PC. The third step is to construct the rake face. The intersection between planes Γ and Π forms line S. The given normal rake angle αn of the end-mill cutter can be measured on plane Π, which is the angle between line S and vector J along the rake face. Thus, the vector J is determined for a given normal rake angle αn. The Rake face is defined by vectors I and J, hence its unit normal K can be determined by the cross product of I and J. The equation of the unit normal of the rake face and its derivation are rendered in another research article [24].

Fig. 7
figure 7

Rake face and its unit normal vector

Full size image

It is necessary to relate the two-surface tangent to each other in a single reference system and for the condition of tangency between the end-mill cutter flute and the grinding-wheel surface. The two conditions must be met: (1) the alignment of the unit vectors on the two surfaces at that contact point, and (2) the contact between a point on the end-mill cutter flute and the grinding wheel. Based on the unit normal K, the relative orientation of the wheel in \( {\mathfrak{R}}^{\mathrm{T}} \) coordinate system is determined.

It can be seen in Fig. 8 that the normal N on the grinding wheel surface is of opposite direction to that of unit normal K on the rake face. Therefore, for the first condition, that is to properly orient the grinding wheel, the two vectors must be aligned together, hence the grinding wheel is rotated about xG-axis with an angle μ and about zG-axis with an angle η. Thus, the orientation of the grinding wheel includes the two angles, μ and η. By solving the vector relationship presented in Fig. 7, the orientation of grinding-wheel in term of angles μ and η are given by

$$ \mu =\left\{\begin{array}{c}{\sin}^{-1}\left(\frac{c}{\sqrt{a^2+{b}^2}}\right)-\phi \\ {}\pi -{\sin}^{-1}\left(\frac{c}{\sqrt{a^2+{b}^2}}\right)-\phi \end{array}\right. $$
(11)

where \( \sin \phi =\frac{a}{\sqrt{a^2+{b}^2}} \), \( \sin \phi =\frac{b}{\sqrt{a^2+{b}^2}} \), a = cos β1, b =  − sin v · sin β1, and c = cos αn · sin ψ.

$$ \eta =\left\{\begin{array}{c}{\eta}_1\ \mathrm{if}\kern0.75em {\eta}_1={\eta}_{3,4}\\ {}{\eta}_2\ \mathrm{if}\kern0.75em {\eta}_2={\eta}_{3,4}\end{array}\right. $$
(12)

where

$$ {\eta}_{1,2}=\left\{\begin{array}{c}{\sin}^{-1}\left(\frac{c_1}{\sqrt{{a_1}^2+{b_1}^2}}\right)-{\phi}_1\\ {}\pi -{\sin}^{-1}\left(\frac{c_1}{\sqrt{{a_1}^2+{b_1}^2}}\right)-{\phi}_1\end{array}\right. $$
(13)

and,

Fig. 8
figure 8

CNC programming principles for the end-mill flute grinding

Full size image

\( \sin {\phi}_1=\frac{a_1}{\sqrt{{\left({a}_1\right)}^2+{\left({b}_1\right)}^2}} \), \( \cos {\phi}_1=\frac{b_1}{\sqrt{{\left({a}_1\right)}^2+{\left({b}_1\right)}^2}} \), a1 =  sin β1 ∙ cos v, b1 =  − cos β1 · sin μ − cos μ ∙ sin β1 ∙ sin v, and c1 =  − cos ψ ∙ cos αn ∙ sin θ + cos θ ∙ sin αn, and

$$ {\eta}_{3,4}=\left\{\begin{array}{c}{\sin}^{-1}\left(\frac{c_2}{\sqrt{{a_2}^2+{b_2}^2}}\right)-{\phi}_2\\ {}\pi -{\sin}^{-1}\left(\frac{c_2}{\sqrt{{a_2}^2+{b_2}^2}}\right)-{\phi}_2\end{array}\right. $$
(14)

where

\( \sin {\phi}_2=\frac{a_2}{\sqrt{{\left({a}_2\right)}^2+{\left({b}_2\right)}^2}} \), \( \cos {\phi}_2=\frac{b_2}{\sqrt{{\left({a}_2\right)}^2+{\left({b}_2\right)}^2}} \), a2 =  cos β1 ∙ sin μ + sin μ ∙ sin β1 ∙ sin v , b2 = sin β1 ∙ cos v and c2 =  cos ψ ∙ cos αn ∙ cos θ + sin θ ∙ sin αn .

From Figs. 6 and 8, it can be noted that the angles μ and η in the machine can be adjusted by rotating BM and AM axes, respectively.

For the second condition, consider a point Pw on a surface of grinding wheel which coincides with point PC on the side-cutting edge C(θ). Since the surface parameters of the grinding wheel are defined by u and v, the point Pw with its parameters can be expressed by \( {\mathbf{P}}_w\left({u}_{P_W},{v}_{P_W}\right) \) in \( {\mathfrak{R}}^{\mathrm{G}} \) coordinate system. To find the grinding wheel location, adopting the proper transformations from \( {\mathfrak{R}}^{\mathrm{G}} \) to \( {\mathfrak{R}}^{\mathrm{T}} \) coordinate system using the values of μ and η found, the point Pw can be presented in \( {\mathfrak{R}}^{\mathrm{T}} \) coordinate system as

$$ {\mathbf{P}}_W^T\left({u}_{P_W},{v}_{P_W}\right)={\mathbf{Rot}}_{\boldsymbol{x}}\left(\eta \right).\mathbf{Tran}\left({x}_{WL},{y}_{WL},{z}_{WL}\right).{\mathbf{Rot}}_{\boldsymbol{z}}\left(\mu \right).\left[\begin{array}{c}{\mathbf{P}}_W^G\left({u}_{P_W},{v}_{P_W}\right)\\ {}\mathbf{1}\end{array}\right] $$
(15)

where

\( {\mathbf{Rot}}_{\boldsymbol{z}}\left(\eta \right)=\left[\begin{array}{ccc}\cos \eta & -\sin \eta & 0\kern0.5em 0\\ {}\sin \eta & \cos \eta & 0\kern0.5em 0\\ {}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& 0\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right],\mathbf{Tran}\left({x}_{WL},{y}_{WL},{z}_{WL}\right)=\left[\begin{array}{ccc}1& 0& \begin{array}{cc}0& {x}_{WL}\end{array}\\ {}0& 1& \begin{array}{cc}0& {y}_{WL}\end{array}\\ {}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}1& {z}_{WL}\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right] \) and \( {\mathbf{Rot}}_{\boldsymbol{x}}\left(\mu \right)=\left[\begin{array}{ccc}1& 0& 0\kern0.5em 0\\ {}0& \cos \mu & \begin{array}{cc}-\sin \mu & 0\end{array}\\ {}\begin{array}{c}0\\ {}0\end{array}& \begin{array}{c}\sin \mu \\ {}0\end{array}& \begin{array}{c}\begin{array}{cc}\cos \mu & 0\end{array}\\ {}\begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right] \)

By coinciding both points (\( {\mathbf{P}}_w\left({u}_{P_W},{v}_{P_W}\right) \) andPC(θ)), the grinding wheel location, WL(xWL, yWL, zWL), can be derived as

$$ {\displaystyle \begin{array}{l}\left[\begin{array}{c}{x}_{\mathbf{WL}}\\ {}{y}_{\mathbf{WL}}\end{array}\right]=\left[\begin{array}{cc}\cos \eta & \sin \eta \\ {}-\sin \eta & \cos \eta \end{array}\right]\left[\begin{array}{c}{c}_1\\ {}{c}_2\end{array}\right]\\ {}{z}_{\mathbf{WL}}=\frac{r_{\mathrm{T}}}{\tan \psi}\cdotp \theta -{u}_{{\mathrm{P}}_{\mathrm{W}}}\cdotp \cos \mu -\sin \mu \cdotp \sin {v}_{{\mathrm{P}}_{\mathrm{W}}}\cdotp \left({T}_1+\frac{u_{{\mathrm{P}}_{\mathrm{W}}}}{\tan {\beta}_1}\right)\end{array}} $$
(16)

where

$$ {\displaystyle \begin{array}{l}{c}_1={r}_{\mathrm{T}}\cos \theta -{u}_{{\mathrm{P}}_{\mathrm{W}}}\cdotp \sin \mu \cdotp \sin \eta -\left({T}_1+\frac{u_{{\mathrm{P}}_{\mathrm{W}}}}{\tan {\beta}_1}\right)\cdotp \left(\cos \eta \cdotp \cos {v}_{{\mathrm{P}}_{\mathrm{W}}}-\cos \mu \cdotp \sin \eta \cdotp \sin {v}_{{\mathrm{P}}_{\mathrm{W}}}\right)\\ {}{c}_2={r}_{\mathrm{T}}\sin \theta +{u}_{{\mathrm{P}}_{\mathrm{W}}}\cdotp \sin \mu \cdotp \cos \eta -\left({T}_1+\frac{u_{{\mathrm{P}}_{\mathrm{W}}}}{\tan {\beta}_1}\right)\cdotp \left(\sin \eta \cdotp \cos {v}_{{\mathrm{P}}_{\mathrm{W}}}+\cos \mu \cdotp \cos \eta \cdotp \sin {v}_{{\mathrm{P}}_{\mathrm{W}}}\right)\end{array}} $$

The relative location of the grinding wheel WL(xWL, yWL, zWL) with the end-mill cutter in the \( {\mathfrak{R}}^{\mathrm{M}} \) (machine coordinate system) can be determined with the given machine specifications. Adopting the transformation between the wheel and the end-mill cutter in such way (i.e., Eq. 15) to describe the grinding wheel location WL(xWL, yWL, zWL) in terms of a stationary coordinate system coinciding with the end-mill coordinate system at η = 0. In other words, the end-mill is rotated about its axis by angle η when describing the grinding wheel location. For cylindrical end-mills, the variables xWL, yWL, and μ defines the initial position of the end-mill cutter in the machine and remains constants during the grinding process. These can be used as setting parameters in the two-axis grinding machines. Whereas, rotation of tool about the AM axis and the displacement of the wheel along the tool axis form the helical path of the contact to grind the end-mill cutter.

5 Optimization of grinding wheel and CNC programming

The parametric optimization of the grinding wheel profile is performed, to minimize the largest deviation between the cross-section of the ground flute profile and the given flute profile. With the optimal grinding wheel, its WLs along the side-cutting edge are calculated such that the normal rake angle is the same as specified. The specified value is obtained from a relation derived between the normal and the radial rake angles. Finally, the flute of the end-mill can be precisely ground with the optimal grinding-wheel in a five-axis grinding process.

5.1 Relationship between normal and radial rake angles

At any cross-section perpendicular to the end-mill axis, the side-cutting edge intersects the cross-section at point Pc. A unit vector vc defines the location of the point Pc in the OT coordinate system, where angle θ is the parameter of the side cutting edge which is shown in Fig. 9. Another unit vector vR passing through the point Pc makes the radial rake angle αR (shown in Fig. 9). These two vectors can be given by

$$ {\mathbf{v}}_{\mathbf{C}}=\left[\begin{array}{c}\cos \theta \\ {}\sin \theta \\ {}0\end{array}\right] $$
(17)
$$ {\mathbf{v}}_{\mathbf{R}}=\left[\begin{array}{c}\cos \left(\theta -{\alpha}_{\mathrm{R}}\right)\\ {}\sin \left(\theta -{\alpha}_{\mathrm{R}}\right)\\ {}0\end{array}\right] $$
(18)
Fig. 9
figure 9

Span of radial rake angle

Full size image

Since the unit vector vR is formed on the rake face, therefore, following relation for the cross product of vector vR and the unit normal K on the rake face can be considered.

$$ {\mathbf{v}}_{\mathbf{R}}\cdotp \mathbf{K}=0 $$
(19)

Simplifying Eq. (19), the mathematical relationship within the normal and the radial rake angles of the end-mill cutter can be represented as

$$ {\alpha}_{\mathrm{n}}={\tan}^{-1}\left(\tan {\alpha}_{\mathrm{R}}\cos \psi \right) $$
(20)

Similar relations can be used to relate the normal relief angles with the radial relief angles.

5.2 Determination of the ground flute profile

To optimize the grinding wheel profile for the minimum deviation of the ground flute profile with the pre-defined flute, it is critical to establish an analytical model of the ground flute profile. In general, moving the grinding wheel with the wheel path t forms a swept-volume and can be represented as

$$ \mathbf{SV}\left(u,v,t\right)=\mathbf{RO}{\mathbf{T}}_z\left(\eta (t)\right)\cdotp \mathbf{Tran}\left({x}_{\mathbf{WL}}(t),{y}_{\mathbf{WL}}(t),{z}_{\mathbf{WL}}(t)\right)\cdotp \mathbf{RO}{\mathbf{T}}_x\left(\mu (t)\right)\cdotp \left[\begin{array}{c}\mathbf{W}\left(u,v\right)\\ {}1\end{array}\right] $$
(21)

where the wheel path ‘t’ is the trajectory followed by the effective grinding edge W(u,v) and generated by the transformation above with the parameters η, xWL, yWL,zWL, and μ. Here, SV(u,v,t) describes the swept envelope (ground flute) formed by the transforming the effective grinding edge W(u,v). The parameters η, xWL, yWL,zWL, and μ can be determined using the condition of meshing as described in the Section 4.2 and applying the envelope theory, that is

$$ \left\Vert \frac{\partial \mathbf{SV}}{\partial u}\kern0.5em \frac{\partial \mathbf{SV}}{\partial v}\kern0.5em \frac{\partial \mathbf{SV}}{\partial t}\right\Vert =0 $$
(22)

Using the Eq. 22, parameters η, xWL, yWL,zWL, and μ and now known, using that, set of trajectories of effective grinding edge W(u,v) are known, which forms the swept envelope or machined flute surface. The ground flute profile, Fm, is the intersection of the ground flute with a plane M perpendicular to the end-mill axis (Fig. 10). However, it is too complicated to find a closed-form equation of ground flute profile. Therefore, a numerical method is employed to generate a group of points representing the profile.

Fig. 10
figure 10

Ground flute profile generated by a grinding wheel moving along path t

Full size image

5.3 Optimization of the grinding wheel profile

Flute profile F(l) is designed as a reference of the flute shape, and the ground flute profile Fm is eventually determined by the grinding wheel and its five-axis grinding path. Thus, the geometric parameters of grinding wheel profile is to be optimized in order to ensure that the actual flute profile is in good agreement with the designed flute profile. After specifying the geometry of the wheel profile and the point Pw, the ground flute profile Fm can be determined, which is then compared with the design flute profile F(l). Thus, an optimization process is employed for the wheel geometric parameters and the location of point Pw in order to minimize the deviation between the two profiles. Hence, the special grinding wheel with simple geometries can be made economically and can be used in the grinding of the cutter flute.

According to the profile of the grinding wheel rendered in Section 3, the geometric parameters are T1, T2, β1, β2, R1, and R2 (see Fig. 5). For the contact point Pw, the parameters are \( {u}_{P_w} \) and \( {v}_{P_w} \). The objective function of the deviation between the flute profiles and the designed flute can be constructed as

$$ \operatorname{Minimize}\ d\left({T}_1,{T}_2,{\beta}_1,{\beta}_2,{R}_1,{R}_2,{u}_{{\mathrm{P}}_{\mathrm{W}}},{v}_{{\mathrm{P}}_{\mathrm{W}}}\right)=\max \left\Vert {\mathbf{F}}_m-\mathbf{F}(l)\right\Vert $$
(23)

To elaborate more on this equation, for certain path and geometry of the grinding wheel, the machined flute profile Fm is obtained and compared with the designed flute profile F(l). The maximum deviation between both profiles along the three segments (f0f1, f1f2, and f2f3) is obtained as distance d. Minimizing the maximum deviation between both profiles (distance d) will lead to optimal values of the grinding wheel path and geometry that will produce end-mills with exact flute profiles.

Since this model is a complicated global optimization model, the differential evolution method is adopted in this work. The result of the optimization includes a set of values of the grinding wheel geometric parameters and the parameters of point \( {P}_w\left({u}_{P_w},{v}_{P_w}\right) \).

5.4 Applying differential evolution

To solve the optimization problem efficiently, a global optimization solver, differential evolution (DE), is employed. The main procedure of the DE method is explained here. First, the method randomly selects three elements from the main population (pop) of size m at a time say 7, 8, and 23. Then, element 7 will form the base vector and both 8 and 23 will form the differentiation vector. The ith element is now created according to the rule

figure a

where rnd is a random number, Cr is the crossover probability, and D is the constant of differentiation. This procedure will form P new elements that are evaluated and will become part of the new population if they have better function values than the original elements in the population; otherwise, these elements will be discarded.

Taking the difference between two elements is much similar to taking the derivative. However, as the two elements are quite apart, this difference is more a global measure of the objective function changes. As only the new elements with better objective functions are adopted for the new generation, the solution will approach to the global minimum. The output results are quite satisfactory as briefly discussed in the next section with practical examples.

6 Applications

To validate the current research and to demonstrate the advantages of this method over the inverse method, two examples of grinding flutes of end-mills are conducted. For the given end-mill flute profile, the grinding wheel profile is optimized. Five-axis CNC grinding programming for the cutter flute is computed, and the results are illustrated. Two end-mill cutters with different flute profiles are ground and presented as examples in comparison with the flutes ground through the inverse method.

6.1 Example 1

In example 1, the first end-mill cutter is ground using the optimized grinding wheel. The given values of flute profile geometry of the end-mill cutter are presented in Table 1, whereas the flute profile geometry is plotted in Fig. 11.

Table 1 Parameters of end-mill cutter—example 1
Full size table
Fig. 11
figure 11

Flute profile of the end-mill cutter—example 1

Full size image

For the given geometry of flute profile, the new approach has been applied to the CNC grinding programming for the five-axis grinding. The grinding wheel location (xWL, yWL, zWL) and orientation (μ and η) are presented in Table 2.

Table 2 Location and orientation of grinding wheel—example 1
Full size table

To optimize the grinding wheel profile, populations of 50 elements were used, and 52063 function evaluations were required to minimize the smallest deviation of the ground flute with the designed flute profiles below 0.324 mm. To show the advantage of current method over the conventional inverse method. The wheel profile generated through the inverse method is a free-form curve plotted in Fig. 12a. So, it is difficult to dress and make the grinding wheel. However, using the approach introduced here, the grinding wheel cross-section is optimized using simple geometric features as demonstrated in Fig. 12b. The values of the profile parameters of the grinding wheel are represented in Table 3, where T2 is pre-set to 15 mm prior the optimization, and the location of point Pw was determined from optimization as \( {u}_{P_w} \)=3.89 mm and \( {v}_{P_w} \)=153.59°.

Fig. 12
figure 12

Profile of the grinding wheel generated through the inverse and current methods—example 1. a Profile generated through the inverse method. b Profile generated through the current method

Full size image
Table 3 Parameters of grinding wheel profile—example 1
Full size table

Performing the five-axis grinding simulation using the grinding wheel obtained from the optimization process, the ground flute profile can be easily computed. To compare the two approaches, the ground and designed profile of the cutter are plotted together in Fig. 13, whereas the error curve is plotted in Fig. 14.

Fig. 13
figure 13

Ground verses designed flute profiles of the end-mill cutter—example 1

Full size image
Fig. 14
figure 14

Error curve of the ground flute profile—example 1

Full size image

Moreover, the end-mill cutter ground with the optimized grinding wheel (example 1) is generated using the Boolean operations as shown in Fig. 15. The side-cutting edge of the end-mill cutter generated from simulation is perfectly coincident with the designed cutting edge (Fig. 15a), and the normal rake angle measured on the end-mill at a plane normal to the cutting edge is found accurate (Fig. 15b).

Fig. 15
figure 15

End-mill cutter generated with the optimized grinding-wheel—example 1. a End-mill cutter generated with an exact side-cutting edge. b End-mill cutter generated with an accurate normal rake angle

Full size image

6.2 Example 2

In example 1, another end-mill cutter of radius 15 mm is ground. The values of the parameter of the flute profile are shown in Table 4, whereas the profile geometry is shown in Fig. 16.

Table 4 Parameters of end-mill cutter—example 2
Full size table
Fig. 16
figure 16

Flute profile of the end-mill cutter—example 2

Full size image

For the given flute profile, the new approach has been applied to develop the cutter location and orientation for the five-axis grinding of the cutter flute. Table 5 presents the location and orientation of the grinding wheel (example 2).

Table 5 Location and orientation of grinding-wheel—example 2
Full size table

The same population size is used as in the first example; the optimal solution is reached after 7682 function evaluations. The maximum deviation between the designed and the ground flute profile is 0.139 mm.

The values of the grinding wheel profile parameters are listed in Table 6, where T2 is pre-set to 9 mm prior the optimization, and the location of point Pw was determined from optimization as \( {u}_{P_w} \)=1.68 mm and \( {v}_{P_w} \)=165.48°.

Table 6 Parameters of grinding-wheel profile—example 2
Full size table

Same as presented in the example 1, a free-form curve; for the given flute profile is plotted in Fig. 17a. To compare with the current approach, the optimal grinding wheel profile is plotted in Fig. 17b.

Fig. 17
figure 17

Profile of the grinding wheel generated through the inverse and current methods—example 2. a Profile generated through the inverse method. b Profile generated through the current method

Full size image

Using the optimized grinding wheel, the ground flute profile is computed and compared with the designed profile in Fig. 18, whereas the profile error curve is plotted in Fig. 19.

Fig. 18
figure 18

Ground verses designed flute profiles of the end-mill cutter—example 2

Full size image
Fig. 19
figure 19

Error curve of the ground flute profile—example 2

Full size image

The end-mill ground with the optimized grinding wheel for the cylindrical end-mill of example 2 is also simulated using the Boolean operations and shown in Fig. 20. The side-cutting edge obtained is accurate within the tolerance, and the normal rake angle is accurate.

Fig. 20
figure 20

End-mill cutter generated with the optimized grinding-wheel—example 2. a End-mill cutter generated with an exact side-cutting edge. b End-mill cutter generated with an accurate normal rake angle

Full size image

7 Conclusions

For the given parametric models of end-mill cutter, the grinding wheel profile using the analytical geometries has been developed. Rather than using the free-form geometries and impractical grinding-wheels (such as B-spline curves or NURBS) which are impractical to machine, simple geometric features (such as lines and circular arc) of the grinding wheel profile are used, which are easier to manufacture. Using the direct method and the differential evolution technique, the grinding wheel profile geometry is optimized for the given geometry of the end-mill. This grinding wheel replaces the expensive free-form grinding wheels commonly used in the inverse method. To grind the flute of an end-mill with the accurate flute geometry and the defined rake and relief angles, the grinding wheel location and orientation are determined so that the rake face is ground with the defined normal rake angle, and the maximum deviation error between the ground flute and its designs is minimized. Finally, the end-mill cutter is virtually produced in the CAD/CAM software and the parameters of the end-mill cutter are evaluated. The produced side-cutting edge of the end-mill are found to be accurate as defined in the given designed. Overall, this work significantly contributes to the research of the flute grinding of the end-mill cutters and provides an accurate geometrical model for the ground flutes. This work does not only provide the accuracy in the manufacturing of end-mill cutters but also reduces the need of specialized grinding wheels with complicated profile and hence reduce the cost of the production as well.