A two-step feedrate planning of polygonal path for micro laser-cutting machines

Abstract

The sample machined with the polygonal path is a common feature in a micro laser-cutting machine. It brings a difficult problem in feedrate planning when the machining accuracy is limited to the scale of sub-micrometer. In this paper, the transition feedrate at the node point is determined by the dynamic capacity of a machine. Then, the jerk-limited feedrate planning is introduced to adjust the feedrate in a smooth manner. The feedrate profile is transferred into the discrete shape for the sampling mechanism of the interpolator in a CNC controller. Moreover, a two-step feedrate planning is proposed to handle the problem that, there exists a distance error, as the line segment is not divisible by the step calculated by feedrate and sample cycle. Firstly, the control parameters, namely, the command feedrate, acceleration and jerk in different stage of the feedrate profile, are estimated by the jerk-limited feedrate planning. Then, a correction scheme is developed to slightly regulate the control parameters. It aims to compensate the distance error caused by the discretization in the process of interpolation. Meanwhile, the proposed method is discussed in two cases according to the length of the line segment. The method of direct adjustment is applied to handle the situation where a line segment is long enough; otherwise, the method of numerical estimation will take the place. Finally, a simulation analysis is presented to demonstrate the performance of the proposed method in feedrate planning. Then, machining experiments are conducted on the self-developed micro laser-cutting machine to verify the effeteness of proposed method.

1 Introduction

The micro laser-cutting machine is one of the critical equipment in modern industry, especially in the area of electronics manufacturing, i.e., wafer dicing [1, 2], glass cutting [3, 4], and circuit repairing [5]. At present, with the increasing demand of high quality components, how to further improve the machining accuracy and increase the machining efficiency become key issues for the development of controllers for a laser micro-machining tool. Generally, the parts with polygonal shape have possessed a great proportion in a laser micro-machining tool, which are commonly machined by multiple line segments. It means that only the geometric continuity could be guaranteed at the node points of adjacent lines. Hence, it determines that a laser-cutting machine has to face with the frequent acceleration and deceleration, and to ensure that the positioning error is limited to a predefined tolerance. A proper feedrate planning should be developed to adjust the feedrate; otherwise, it would lead to the excessive vibration of the machine tool and thus affect the machining quality and efficiency.

Unfortunately, it is quite difficult to find the research approaches focused on the feedrate planning for the laser micro-machining tools. Basically, this kind of machines still belongs to a typical CNC machine tool, so the fundamentals and methods could be borrowed from the existing approaches. In a modern CNC system, a look-ahead module is usually applied to monitor the variation of feedrate and then a proper feedrate planning should be taken to adjust the feedrate under the constraints of machining accuracy, dynamics, etc., especially in the critical areas of the sculpture surface where the curvature is larger than the confined one [6, 7]. A smooth profile, including the position and feedrate for each line segment, could be achieved after feedrate planning. It will be transferred to the interpolation module and then processed by the corresponding interpolator. Subsequently, the interpolation is performed in every sample period, and then the increment motion for each axis is served as discrete position commands for a servo loop.

In a common machining process, the jumps of acceleration and jerk will appear at the node points when the tool is moved along the polygonal path [8]. Usually, it is referred as a sharp corner as there is just first order continuity at the node point. In this case, the feedrate is decelerated to zero at the end of the line segment, and then accelerated to the command one again. It is a simple solution, but a low machining efficiency that has to be embraced is its drawback. In fact, the transfer feedrate at the node point is determined by the dynamic capacity of a machine tool. It is presented to enhance the average feedrate of the machining process. Then, for a single line segment, the feedrate should be speeded up from the transfer feedrate to the command one from the start point, and be slowed down to the next transfer feedrate just when the tool reaches the end point.

Furthermore, a proper feedrate planning should be taken to regulate the feedrate, in order to meet the requirement of machining dynamics. The jerk-limited feedrate planning is developed to generate a smooth feedrate profile with S-shape, which integrates machining dynamics in the interpolation stage [9, 10]. It consists of several linear acceleration or deceleration stages in the acceleration profile which keeps the jerk constant. In addition, some feedrate planning with high order continuity, such as the jounce-limited method [11] and the sinusoid method [12], are applied to further reduce the fluctuation of feedrate and acceleration, while a longer sample period is required to conduct the heavy computation. Actually, due to the limited response time of a mechanical system, which is composed of ball screw, servo motor and the other components, the jerk-limited planning is still a cost-effective solution to regulate the feedrate profile.

In addition, a higher order continuity of the machining path could be achieved by integrating a transition profile into the polygonal path through the node points [13,14,15]. It aims to eliminate the feedrate fluctuation at the node points of adjacent line segments. A curve, i.e., arc is inserted into two adjacent line segments, in order to get a smooth feedrate transition. However, it brings a new error from the transition curve for the predefined position as the node point cannot be reached, and the error turns to be larger when the feedrate at the node point is increasing. Furthermore, the curve fitting method is another feasible solution to smooth the feedrate when machining with tiny line segments. A free-form curve, i.e., spline, B-spline, is applied to fit the node points of each line segment. Then, an adaptive feedrate profile could be achieved according to the curvature of the curve [16,17,18]. However, the overfitting problem, resulted from the new tool path generated by this method, is coming to the surface when machining with long segments. A heavy computation is also needed for the interpolation of a parametric curve, which leads to a longer sample cycle and thus makes it difficult to achieve real-time interpolation with high-feedrate.

Moreover, the interpolator in CNC systems is mainly based on the principle of data sampling method. The moving distance of the cutting tool is accumulated by the movement of discrete feedrate in each sample cycle, rather than the theoretical result calculated by the integration of continuous feedrate and time. Hence, the predetermined feedrate profile with acceleration-deceleration planning for the line segment is quite difficult to meet the time division conditions at various motion stages, which leads to an inevitable position error. In other words, a line segment might not be divisible by the step calculated by feedrate and sample cycle. A feedrate equipartition method is put forward to allocate the remaining distance to each sample period equally at the acceleration or deceleration stage, when regulating the feedrate to the next line segment [19]. It ensures that the cutting tool could be exactly driven to the given position defined by the tool path, and thus the deviation of distance after feedrate planning could be eliminated. However, the abrupt jumps could be found at the feedrate profile generated by this method. The machining dynamics of the machine tool might exceed the threshold value and thus excessive vibration will appear. Meanwhile, an additional feedrate profile with a symmetrical shape and its start and end point are set to zero, is developed to compensate the error caused by interpolation [20]. This is a guarantee that the starting and terminal feedrate are the same with the predefined ones, and the remaining distance could be compensated as well. However, the new feedrate profile is higher than the original one produced by look-ahead module, which means that the machining accuracy might not be achieved, especially for the high-speed machining.

Presently, the accuracy of the micro machine tool has been extended to the scale of sub-micrometer or even to nanometer. The profile accuracy is an important index to evaluate the machining accuracy of a micro laser-cutting tool. The controller should exactly position the laser beam to the node points within the scale of sub-micrometer, when machining with a polygonal path. Meanwhile, a smooth feedrate profile should be achieved to meet the requirement of high-speed cutting. It presents a big challenge to the development of a controller for micro laser-cutting tool with high accuracy and efficiency.

In this paper, a two-step feedrate planning is proposed to regulate the feedrate between two adjacent line segments, aiming to accurately position the laser beam to the node points with a smooth feedrate transition. Firstly, the limited feedrate at the node point is determined by the dynamic capacity of machine tools. Hence, the feedrate could be adjusted to the limited one, and accelerated back to command one with an S-shape feedrate profile. Then, a method of control parameter adjustment is applied to slightly regulate the feedrate profile with a two-step method, and to compensate the error caused by the discretization process. It ensures that the laser beam could be exactly driven to the node point, and the feedrate is slowed down to the limited feedrate at the same time. Hence, a high-precision position control and a smooth feedrate transition could be achieved between line segments. Finally, a verification experiment is conducted on a self-developed laser-cutting machine to test and validate the proposed method.

2 Feedrate profile for polygonal path

2.1 Transfer feedrate at the node points

In a typical laser-cutting machine, the laser beam focused by the objector, is driven by the motion system with high speed. Generally, the component with polygonal shape is a fairly common pattern in the laser-cutting process. As shown in Fig. 1, it is machined by a path with multiple line segments. The machined profile should be accurate and clear, while the corner at the node point of two adjacent lines should be sharp enough, especially in the scientific applications.

Fig. 1

The machining path with polygonal shape

As shown in Fig. 2, the feedrate of the line paths are v_i and v_i + 1 respectively when taking two adjacent segments P_iP_i + 1 and P_i + 1P_i + 2 as an example. Due to the dynamic capacity of a machine tool, the feedrate should be decelerated to ${v}_i^e$ when the laser beam reaches P_i + 1, and then it will be accelerated to v_i + 1.

Fig. 2

Limited feedrate at node point

Then, the machine tool has to experience an abrupt change of feedrate, Δv shown in Fig. 2, for the direction of path turns with an angle α_i at the node point P_i. Since it happens in a single sampling period, a considerable acceleration happens in this moment. The change of feedrate Δv could be defined by Eq. (1) as the terminal feedrate ${v}_{i-1}^e$ of former line and the starting feedrate ${v}_i^s$ are the same [21].

$$ \Big\{{\displaystyle \begin{array}{l}\varDelta v=2\left({v}_i^s\right)\sin \left(\frac{\alpha_i}{2}\right)\\ {}\frac{\varDelta v}{T}\le {A}_{\mathrm{max}}\end{array}} $$

(1)

where T and A_max refer to sampling cycle and the maximum acceleration respectively. The feedrate ${v}_i^e$ at the node point P_i + 1 should satisfy the condition that ${v}_i^s\le \left({A}_{\mathrm{max}}T\right)/\left(2\sin \left({\alpha}_i/2\right)\right)$, in order to meet the requirement of machining dynamics.

2.2 The discretization of feedrate profile

Furthermore, a proper planning is needed to regulate the feedrate between two adjacent node points. Taking the line segment P_iP_i + 1 as an example, the feedrate is set at ${v}_i^s$ at first, and it is accelerated to v_i when the laser beam is moved along the line path. Then, it is decelerated to ${v}_i^e$ when reaching the end point P_i + 1. If the feedrate profile is preset to be v(t) when adjusting the feedrate from ${v}_i^s$ to ${v}_i^e$ at the start and end points respectively, then, the theoretical distance of the line segment P_iP_i + 1 could be calculated by the following Eq. (2).

$$ \mid {P}_i{P}_{i+1}\mid =\int v(t) dt $$

(2)

However, the feedrate control in practice is a discrete process, since a line segment is further divided into many tiny line segments by the interpolator with a given step in each sampling cycle. As shown in Fig. 3, if the sampling cycle for each interpolation process is set to T, the actual distance of the line segment P_iP_i + 1 should be accumulated by the discrete movement v_jT according to the feedrate profile v(t). Thus, it should be corrected to the accumulation of ∑v_jT, rather than the integration of the feedrate profile ∫v(t)dt.

Fig. 3

Discrete feedrate profile for the line segment

According to Fig. 3, the distance of line P_iP_i + 1 should be transferred to Eq. (3).

$$ \mid {P}_i{P}_{i+1}\mid =\int v(t) dt=\sum {v}_jT+{S}_{\mathrm{err}} $$

(3)

In Eq. (3), the error term S_err refers to the distance error after the interpolation process. Obviously, the discrete feedrate sequence cannot drive the laser beam reaching the position of the end point P_i + 1 accurately. As shown in Fig. 4, the positioning error of the node point among line segments will be transferred and accumulated. If the error S_err has not been compensated in advance, it will result in the offset of the machining path and thus affect the machining quality.

Fig. 4

The error distance at the node point

The distance error S_err is determined by the limited feedrate ${v}_i^e$ at the node point P_i + 1, and it is less than the distance ${v}_i^e\ T$ moved by ${v}_i^e$ in a single sampling cycle. The distance error should not be ignored for the effect of accumulation when the machining path is constructed by thousands of line segments. Generally, an additional path, i.e., line or arc, is added into the original paths around the node point, in order to improve the machine accuracy.

It is an effective solution for the ordinary machine tools since the profile accuracy within several micrometers is still acceptable in the most cases. However, the position error cannot be ignored due to the requirement of machining accuracy in a micro-machine tool, which usually reaches to the scale of sub-micrometer or even to nanometer. The distance error S_err, which will result in the machining error δ shown in Fig. 5, should not be ignored during the feedrate planning in the case of micro-machining. Therefore, as shown in Fig. 6, the original feedrate profile after planning should be properly corrected, during the process of regulating the feedrate from v_i to v_i + 1. Then, the feedrate profile could be applied to drive the laser beam moving along the line segment P_iP_i + 1, and finally reaching P_i + 1 exactly.

Fig. 5

Additional segment integrated into original path

Fig. 6

Feedrate profiles before and after adjustment

In fact, a new feedrate profile v^'(t) after correction could be achieved by adjusting the control parameters at the preset feedrate profile v(t). By this way, the distance of P_iP_i + 1 could be expressed by the following equation Eq. (4).

$$ \mid {P}_i{P}_{i+1}\mid =\int v(t) dt=\sum v{\hbox{'}}_jT $$

(4)

The equation shows that the actual distance of the line segment P_iP_i + 1 could be obtained by the discrete interpolation points according to the new feedrate profile v^'(t). It is equal to the theoretical distance planned by the predetermined v(t), so as to eliminate the distance error S_err caused by the interpolation process. Therefore, a high precision positioning control and a smooth feedrate transition could be realized by the adjustment of the feedrate profile.

2.3 Discrete feedrate profile with S-shape

In the practical application of modern CNC system, the jerk-limited feedrate planning is a well-developed method to generate a smooth feedrate profile with S-shape, with the advantages of uniformity, smooth motion, and impact free. It could improve the machining quality and is especially suitable for the high speed and high precision machining.

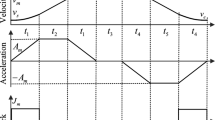
As shown in Fig. 7, a normal S-shape profile is usually divided into an acceleration stage, a constant feedrate stage, and a deceleration stage, while a typical acceleration or deceleration stage mainly composes of three regions, the regions one, two, and three for acceleration, and the regions five, six, and seven for declaration. To simplify the calculation, the feedrate profile is even assumed to be symmetric [22].

Fig. 7

S-shape feedrate planning

The control parameters of the feedrate profile with S-shape could be defined as follows: the sampling cycle of the interpolator is v_m, the command feedrate of the machine tool is v_m, the jerk is J, and the maximum acceleration is a_m, while the actual distance of the line segment is S_r, the starting feedrate is v_s, and the terminal feedrate is v_e. According to the S-shape acceleration and deceleration profile, the acceleration a_i and feedrate v_i of the interpolation point in the ith sampling cycle in the acceleration process, could be described by Eq. (5) as referred in [23].

(5)

where m_a refers to the number of cycles in the region two, while n_a represents the number of cycles in the region one and three at the acceleration stage. According to Eq. (4), the maximum acceleration a_m can be achieved by Eq. (6) when accelerating to the n_ath cycle.

$$ {a}_m=J{n}_aT $$

(6)

Meanwhile, according to Eq. (5), the feedrate v_m can be obtained by Eq. (7) when accelerating to the (2n_a + m_a)th cycle.

$$ {v}_m={v}_{2{n}_a+{m}_a}={v}_s+{a}_m\left({m}_a+{n}_a\right)T $$

(7)

The numbers of the cycles in the regions one and two at the acceleration stage can be calculated by Eq. (7).

$$ \Big\{{\displaystyle \begin{array}{l}{n}_a=\frac{a_m}{JT}\\ {}{m}_a=\frac{v_m-{v}_s}{a_mT}-{n}_a\end{array}} $$

(8)

In fact, the acceleration and deceleration stages could have a symmetrical shape. Similarly, the numbers of the cycles in the region five and seven at the deceleration stage can be deduced according to the intermediate acceleration a_i and the feedrate v_i at the ith interpolation point. The cycles n_d of the region five and m_d of the region seven could be defined by Eq. (9).

$$ \Big\{{\displaystyle \begin{array}{l}{n}_d=\frac{a_m}{JT}\\ {}{m}_d=\frac{v_m-{v}_e}{a_mT}-{n}_d\end{array}} $$

(9)

The number of sampling cycles, N_a, M_a, N_d, and M_d are taken as the upper integers of n_a, m_a, n_d, and m_d, respectively, to satisfy the time division condition during the interpolation process. The theoretical acceleration and deceleration distances should be corrected by Eq. (10) according to the feedrate v_i in the acceleration and deceleration stages.

$$ \Big\{{\displaystyle \begin{array}{l}{S}_a=\left({N}_a+\frac{M_a}{2}\right){v}_sT+\left({N}_a+\frac{M_a}{2}+1\right){v}_mT\\ {}{S}_d=\left({N}_d+\frac{M_d}{2}-1\right){v}_mT+\left({N}_d+\frac{M_d}{2}+1\right){v}_eT\end{array}} $$

(10)

The rest distance at the constant feedrate stage can be obtained by the theoretical distance S_a at the acceleration stage and the theoretical distance S_d at the deceleration stage, which could be calculated by the actual distance S_ru defined in Eq. (7).

$$ {S}_{ru}={S}_r-{S}_a-{S}_d $$

(11)

Then, the number of cycles in the region four can be calculated by Eq. (12).

$$ {n}_u=\frac{S_{ru}}{v_mT} $$

(12)

If n_u is not an integer, it should be corrected to the upper integer of N_u. After that, the theoretical distance S_u in the region four could be defined by Eq. (13).

$$ {S}_u={N}_uT{v}_m $$

(13)

Finally, the total distance of theoretical distance can be obtained by Eq. (14).

$$ {\displaystyle \begin{array}{c}{S}_t={S}_a+{S}_u+{S}_d\\ {}=\left({N}_a+\frac{M_a}{2}\right){v}_sT+\left({N}_a+\frac{M_a}{2}+1\right){v}_mT+{N}_u{v}_mT\\ {}+\left({N}_d+\frac{M_d}{2}-1\right){v}_mT+\left({N}_d+\frac{M_d}{2}+1\right){v}_eT\end{array}} $$

(14)

Thus, the numbers of cycles in the different feedrate stages could be determined byN_a, M_a, N_u, N_d, and M_d according to the S-shape feedrate planning. Then, they should be substituted into the expressions of the feedrate profile to get the intermediate feedrate in the different stages, and then a discrete feedrate profile could be achieved with the S-shape feedrate planning for the line segment.

3 Parameter adjustment method for feedrate planning

In a micro laser-cutting machine, the laser beam is driven by the discrete feedrate profile mentioned above. Hence, two critical conditions should be satisfied during the process of feedrate planning. Firstly, the feedrate should be smoothly adjusted when the laser beam moves along the path, to avoid the jumps of the feedrate. Then, the laser beam should be positioned to the node point within the preset tolerance δ, to satisfy the requirement of machining accuracy.

3.1 Distance error compensation

As mentioned above, it mainly concerns on calculating the accurate time at different motion stages. The time spent on the different stages of jerk-limited feedrate planning could be achieved by rounding the number of sampling cycles to integers at the acceleration and deceleration stages. Then, it will be applied to complete the whole feedrate profile in the discrete form. If the length, starting feedrate, and terminal feedrate in the current path section are given, then the numbers of cycles of acceleration and deceleration and the theoretical distances in different sections can be calculated by the proposed discrete feedrate planning. However, according to Eq. (12), it could not be guaranteed that the number of cycles n_u is an integer. Then, as shown in Fig. 8, there is a rounding error problem, leading to a distance error S_err between the theoretical and actual distances in the stage four, when the upper integer of N_u is substituted to n_u.

Fig. 8

Distance error at stage four

The distance error S_err could be expressed by Eq. (15).

$$ {S}_{\mathrm{err}}={S}_u-{S}_{ru} $$

(15)

The error fluctuates within the range of (0, v_mT). Therefore, the error variation turns to be larger in the high-speed machining. It will lead to the difficulty in positioning control and the fluctuation of feedrate at the node point, when the distance error is larger than the confined position error at the node points. As a result, it brings an adverse impact on the smoothness of feedrate profile and the quality of the cutting profile.

Hence, how to compensate the distance error S_err becomes an obstacle on the way to get a discrete feedrate profile. In this paper, a new method of parameter adjustment is proposed to slightly regulate the feedrate, acceleration, and jerk, in order to compensate the distance error. It ensures that the accumulation of the distance calculated by discrete feedrate could equal to the theoretical distance. Subsequently, the distance error S_err at the current segment could be judged by the confined tolerance δ to determine whether it could meet the requirement of machining accuracy.

Furthermore, there exists a probability that the distance is not long enough to implement all the sections of the feedrate profile, due to the limited distance of line segment. It means that the feedrate could not be accelerated to the command one for the length of line segment is fairly short. Thus, this paper will discuss the adjustment strategies in two cases according to the condition that whether the laser beam can reach to the command feedrate at each line segment. If the actual length of line segment is long enough, the distance error compensation could be implemented by just adjusting the original parameter slightly. However, if not, it determines that, the laser beam cannot be speeded up to the command one v_m for there is no enough space to complete all sections defined in Fig. 7. A significant adjustment is needed to complete the task of error compensation. These two conditions are discussed in detail in the following two sections according to S_u in Eq. (11).

3.2 Case 1: S _ru > 0

It means that there is enough space to complete the whole jerk-limited feedrate planning with seven stages, when the distance error is larger than the machining accuracy δ. Then, the feedrate in the stage four should be corrected at first. It aims to ensure that the theoretical distance S_u could equal to the actual distance S_ru. According to the starting and terminal feedrate, and the distance of the current line segment, if the federate can be accelerated to the command one, then the motion control scheme should consist of three processes, including acceleration, constant feedrate, and deceleration. When the error distance S_err caused by the discrete calculation process is greater than the position accuracy δ, the actual moving distance S_r should be applied to replace the theoretical distance S_t defined by Eq. (11), to re-calculate the command feedrate v_m at the constant feedrate stage. Then, the corrected feedrate v_m could be represented by Eq. (16).

$$ {v}_m^{\hbox{'}}=\frac{2{S}_r-\left(2{N}_a+{M}_a\right){v}_sT-\left(2{N}_d+{M}_d+2\right){v}_eT}{\left(2{N}_a+{M}_a+2{N}_u+2{N}_d+{M}_d\right)T} $$

(16)

The value of ${v}_m^{\hbox{'}}$ after re-calculating is smaller than the preset operation feedrate v_m, since the condition of S_r < S should be satisfied. Then, ${v}_m^{\hbox{'}}$ should be substituted into Eqs. (5) and (6) to re-calculate the acceleration a_am and jerk J_a at the acceleration stage, and the deceleration a_dm and jerk J_d at the deceleration stage, respectively. It ensures that the feedrate could be speeded up from v_s to ${v}_m^{\prime }$, and then slowed down from ${v}_m^{\prime }$ to v_e exactly. Hence, the corrected acceleration and jerk at the acceleration and deceleration parts, could be expressed by Eq. (17).

$$ \Big\{{\displaystyle \begin{array}{l}{a}_{am}=\frac{v_m^{\hbox{'}}-{v}_s}{\left({M}_a+{N}_a\right)T}\\ {}{J}_a=\frac{a_{am}}{N_aT}\\ {}{a}_{dm}=\frac{v_m^{\hbox{'}}-{v}_e}{\left({M}_d+{N}_d\right)T}\\ {}{J}_d=\frac{a_{dm}}{N_dT}\end{array}} $$

(17)

According to Eq. (17), the parameters at the acceleration and deceleration stages after re-calculating [a_am, J_a, a_dm, J_d] are all smaller than the predetermined control parameters (a_m,J). It happens to guarantee that the machining dynamics could always be within the capacity of a machine tool. Then, all the intermediate feedrate of the line segment can be calculated directly by Eq. (2). The results of feedrate are then multiplied by the interpolation cycle T to get the corresponding interpolation increment value. By this way, the laser beam could be accurately positioned to the destination with a smooth feedrate profile. It ensures that the transition speed at the node point is smooth enough.

3.3 Case 2: S _ru < 0

In addition, if the total distance needed to adjust the feedrate is shorter than the actual length of current line segment, then the feedrate will not be accelerated to the command one v_m. The command feedrate should be significantly reduced to shorten the travel distance according to Eq. (16). However, there is no analytical expression which could describe the relationship between the command feedrate and travel distance. A numerical solution is thus needed to estimate such feedrate, in order to complete the whole feedrate profile.

Meanwhile, the number of cycles [N_a, M_a, N_a, N_d, M_d, N_d] at the different stages could remain the same to simplify the estimation process. In this case, the command feedrate v_m has to experience a significant reduction to shorten the travel distance. Then, the profile will consist of the acceleration and deceleration parts, and the command feedrate ${v}_m^{\prime }$ after adjustment will only be implemented for one cycle. Hence, the estimation process of command feedrate ${v}_m^{\prime }$ is demonstrated in Fig. 9 using the dichotomy method.

Fig. 9

The estimation method for command feedrate

The new command feedrate ${v}_m^{\prime }$ could be obtained after the process of estimation shown in Fig. 7. Its value should satisfy the condition that the absolute distance error is smaller than the machining accuracy δ. After that, the travel distance is defined by the cycle number [N_a, M_a, N_a, N_d, M_d, N_d] and the feedrate of v_s, ${v}_m^{\prime }$, and v_e. Let S_t equal to the actual length of line segment S_r, then the feedrate ${v}_m^{\prime }$ needs to be corrected, and it could be solved according to Eq. (17). Eventually, the solution of ${v}_m^{\prime }$ is expressed by Eq. (18).

$$ {v}_m^{\hbox{'}}=\frac{2{S}_r-\left(2{N}_a+{M}_a\right){v}_sT-\left(2{N}_d+{M}_d+2\right){v}_eT}{\left(2{N}_a+{M}_a+2{N}_d+{M}_d\right)T} $$

(18)

The corrected feedrate ${v}_m^{\hbox{'}}$ is smaller than the command feedrate v_m. Then, the control parameters [a_am, J_a, a_dm, J_d] at the acceleration and deceleration stages should be corrected by Eq. (18). By this way, the laser beam is able to be positioned to the node point under the constraint of machining accuracy after the process of feedrate correction. In these two cases mentioned above, the adjustment and correction of the control parameters are implemented under the constraint of machining dynamics and accuracy. The parameters [a_am, J_a, a_dm, J_d], corrected by the proposed re-planning method, could eliminate the error distance S_err caused by discrete feedrate profile, which is generated during the interpolation process. Therefore, the proposed algorithm does not need to identify the deceleration point and the end point in advance as the current approaches do. After that, the interpolation points in the line segment could be achieved according to the discrete feedrate profile at different stages, in a quick and convenient manner.

4 Experiments

A self-developed micro laser-cutting machine is applied to conduct the experiments in this paper. As shown in Fig. 10, the platform is constructed by three linear axes, including X-axis, Y-axis, and Z-axis. Among them, X-axis and Y-axis shift the worktable, while Z-axis controls the focal position of the laser.

Fig. 10

Self-developed 4-axis micro-machining center

The power source is the femtosecond laser, with 100 fs pulse duration at 1 KHz repetition rate, and the 800 ± 10 nm wavelength. The objective lens used to deliver and focus laser beam is Mitutoyo Ltd’s Apo NiR Series (NA = 0.1, 5X). Before the actual cutting experiment, a simulation test is carried out to verify the proposed motion control for the polygonal path with multiple line segments. The cutting path has a shape of fish bone as shown in Fig. 11.

Fig. 11

The test sample with fish-bone shape

4.1 Simulation results and discussion

The software of Matlab is applied to implement the programming and simulation in this paper. The control parameters of the S-shape feedrate profile are set as follows: the maximum feeding feedrate is set to 15 mm/min, the allowable maximum acceleration is 800 mm/min², the jerk is set at 200000 mm/min³, while the sampling cycle of the interpolator is 2 ms. Then, the tolerance of the machining error is set to 0.1 μm, and the test examples are 32 continuous line segments whose starting and ending points are located at the same point (0, 0, 0). The simulation results of feedrate, acceleration, and jerk using the proposed method are demonstrated in Fig. 12 in detail.

Fig. 12

The simulation results after feedrate planning

A comprehensive solution is proposed to smoothly adjust the feedrate and exactly drive the laser beam to the node points when machining with the polygonal path. Obviously, the feedrate profile obtained by the proposed method is continuous without any acceleration or feedrate jumps. The transition feedrate at the node point is determined by the dynamic capacity of a machine, in order to meet the requirement of high-speed cutting. It could be found that the feedrate in the most area of the profile, cannot reach to the command one (the red line shown in Fig. 12), for the length of line segment is not long enough. Hence, a smooth machining process could be achieved when a high-speed machining is required. Actually, more attention should be paid on the cutting accuracy at the node point. According to the machining error defined in Fig. 5, two ordinary methods, inserting lines and arcs, are taken as the control groups to be compared with the proposed method. The simulation results are shown in Fig. 13.

Fig. 13

Machining errors of different methods

It could be found that the machining error using the method of inserting lines exceeds the predefined tolerance. A better performance could be achieved by the method of inserting arcs; however, with the exception of a few node points, most of the machining errors at the node points are out of the tolerance. Evidently, the ordinary solutions for the machining process with the polygonal path are not suitable when the machining accuracy is limited to the scale of sub-micrometer. In contrast, the proposed two-step feedrate planning could probably compensate the distance error caused by the line interpolator. It ensures that the laser beam could be driven to the node points exactly with the discrete feedrate profile. According to the results shown in Fig. 13, the maximum machining error at node point 10 is 8.3e-9 μm, which is far less than the predefined one. It can be attributed to the rounding error although it is the maximum one among all the node points at machining path. Meanwhile, its value is much less than the resolution of moving stages equipped in the machining center, and it can be ignored to some extent during the cutting process. Therefore, the method prosed in this paper could satisfy the requirement of high accuracy in the area of micro laser-cutting. It is a preferred solution for feedrate planning when machining with the polygonal path.

4.2 Machining results and discussion

Subsequently, three samples are machined in the micro laser-cutting machine center. The profile accuracy, especially at the node points is taken as the index, to compare the proposed method with the ordinary approach by inserting arc between two adjacent lines. A pure cooper with 10-mm width, 10-mm height is placed on the worktable as the test workpiece. It has been polished before the experiment. The path shown in Fig. 11 is applied to cut the sample when the laser is set at 19.20 J/cm². The cutting path is carried out only once to reduce the effect from the other factors using the laser beam with 15-μm spot after focusing. The first sample is cut by the proposed method with the adjustment of control parameters, aiming to drive the laser beam to the node points exactly. The other two samples are machined by the common methods, which insert lines and arcs respectively, to substitute the node points among the paths. The machined samples are shown in Fig. 14.

Fig. 14

Cutting samples with different path

According to the samples, there exist transition lines and arcs between two adjacent line segments as shown in Fig. 14b and c. The original sharp edge at the node point turns to be blunted as the distance error reaches to several micrometers. It is in accordance with the simulation results demonstrated in Fig. 13. Especially, in the sample achieved by inserting lines, a long line is needed to connect two adjacent lines, in order to smooth the polygonal path. However, it reduces the machining accuracy of the sample profile. In addition, the sample shown in Fig. 14c has a better performance, where an arc with small radius is added to the machining path, and the laser beam can be driven along the path with a high speed. However, the cost has to be paid for the original sharp edges are replaced by arcs. It is not acceptable in the application of micro-machining when a sample with high accuracy in the scale of sub-micrometers is required.

As shown in Fig. 14a, a clearer and sharper edge could be found from the profile machined by the proposed method, when compared with the ordinary approaches. The profile reproduces the predefined polygonal path accurately. The laser beam is driven to the node points exactly with the proposed two-step feedrate planning. Consequently, the proposed feedrate planning method makes it possible to further improve the machining accuracy of micro laser-cutting machine when processing with the polygonal path.

5 Conclusion

In this paper, a comprehensive solution is proposed to smoothly adjust the feedrate and exactly drive the laser beam to the node points when machining with the polygonal path. It is specially focused on the positioning accuracy for the application of micro laser-cutting machine when the machining error is limited to the scale of sub-micrometer. A two-step feedrate planning is proposed to compensate the distance error caused by the line interpolator. Firstly, the numbers of the cycles in different stages in the feedrate profile are estimated by the jerk-limited feedrate planning. The command feedrate, acceleration, and jerk, referred as control parameters, determine the shape of the feedrate profile. Then, a correction scheme is developed to slightly regulate the control parameters. It ensures that the laser beam could be driven to the node points exactly with the discrete feedrate profile. Finally, a simulation analysis is presented to evaluate the performance of the proposed method in feedrate planning. According to the results, the feedrate profile is smooth enough, and the profiles of acceleration and jerk are jump free. Subsequently, machining experiments are conducted on the self-developed micro laser-cutting machine to verify the effect of proposed method in position accuracy. A clearer and sharper edge could be found from the profile machined by the proposed method, when compared with the ordinary approaches.

Nowadays, the micromachining tools which employ ultra-fast laser beam as cutting tool are becoming more and more popular in research laboratories and commercial applications. The proposed feedrate planning method can be used to position the laser beam to the designed polygonal path with a smooth feedrate profile. As we expected, the proposed method can be extended to the applications of laser-based micromachining technology. It makes it possible to further enhance the machining quality and accuracy.