Vortex interactions of two burst-and-coast swimmers in a side-by-side arrangement

Abstract

Both schooling behavior and burst-and-coast gait could improve fish swimming performance. The extent to which fish can improve their swimming performance by combining these two strategies is still unknown. By examining two self-propelled pitching foils positioned side-by-side at different duty cycles (DC), we examine swimming speed and cost of transport efficiency (CoT) using the open-source immersed boundary software IBAMR. We find that a stable schooling formation can only be maintained if both foils employ similar and moderate DC values. In these cases, vortex interactions increase foils’ lateral movements, but not their swimming speed or efficiency. Additionally, we examine vortex interactions in both “schooling" and “fission" scenarios (which are determined by DC). The research provides useful insights into fish behavior and valuable information for designing bio-inspired underwater robots.

Graphic abstract

1 Introduction

The remarkable ability of aquatic animals to survive in complex environments with dramatic swimming performance can be attributed to long terms of evolutionary development [1]. The swimming organisms have evolved a variety of mechanisms to gain high thrust in viscous flows, including burst-and-coast locomotion [2,3,4] and swimming as a group [5,6,7,8,9,10]. With the burst-and-coast strategy, fish alternate between a continuous flapping (burst phase) and a non-flapping/gliding gait (coast phase) [11] (see Fig. 1c for an illustration). The hypothesis of fish gaining a higher swimming efficiency with the burst-and-coast strategy has been tested through biological observations, mathematical modeling, numerical simulations, and physical experiments [2,3,4, 12]. Muller et al. [12] compared energy costs of larval and adult zebrafish (zebra danios) swimming with burst-and-cost gaits and found that larval fish save less energy than adult ones due to the greater influence of viscosity. Subsequently, Wu et al. [13] quantified the kinematics and wake structures produced by koi (disambiguation) swimming with burst-and-coast gait, and reported an energy saving of 45 % compared to continuous swimming. In a recent study, Li et al. [14] reported that a rotkopfsalmler (hemigrammus bleheri) repeats an intrinsic basic movement and spends more time in the burst phase to maintain swimming efficiency and speed.

Based on the Bone-Lighthill boundary-layer thinning hypothesis [15], numerous studies have been conducted to estimate the energy savings of burst-and-coast strategies. A fish locomoting a specific distance and maintaining a constant depth was theoretically analyzed by Weihs [2]. Weihs’ results show that burst-and-coast swimmers are more efficient than continuous swimmers at the same speed, saving over 50% in the cost of transport. In a study that combined Weihs’s model [2] with kinematic data of real fish, Videler and Weihs [16] found that the energy savings from the burst-and-coast strategy are determined by the beginning and ending velocities of the burst phase. Blake [17] examined the effects of fish thickness on energy savings during burst-and-coast swimming, and Das et al. [18] provided universal scaling laws for both continuous and burst-and-coast swimmers using linearized potential theory and low-amplitude assumptions.

With the advancement of computer hardware and computational techniques, numerical simulations are providing vital insights into the hydrodynamics and benefits (if there are any) of burst-and-coast locomotion. Chung [19] conducted a numerical investigation on the impact of the duty cycle (DC), defined as the ratio of the burst period to the total swimming period (burst plus coast), Reynolds number (Re), and swimmer thickness on the swimming efficiency of a self-propelled NACA foil during burst-and-coast locomotion. They found that the optimal fineness ratio (= foil length/foil thickness) for maximum energy savings is 8.33 instead of 5, which is reported in [17]. Through CFD flow visualization, Chung also found that three vortex structures are shed during burst-and-coast swimming, while only two appear during continuous swimming. With inviscid numerical simulations, Akoz and Moored [3] discovered that an additional inviscid Garrick mechanism could save energy up to 60% for swimming using burst-and-coast compared to the continuous one. Additionally, they found inviscid energy savings positively correlated with the swimming amplitude but negatively correlated with the Lighthill number. Visualizing the flow field of numerical simulations, the authors [3] found that four vortex structures are shed after the burst-and-coast locomotion, which is contrary to Chung’s simulations [19]. Following [3], Akoz et al. [20] investigated how large-amplitude motion affects burst-and-coast swimmer performance in viscous and inviscid flows. In a recent research, Gupta et al. [4] found that burst-and-coast locomotion is advantageous to carangiform and thunniform swimmers but proves disadvantageous to anguilliform swimmers.

Besides the burst-and-coast strategy, swimming in a group is also believed to improve swimming efficiency [5,6,7,8,9,10, 21, 22]. Without losing generality, it is possible to reveal the hydrodynamic interactions between two individuals, since the flow around the two closest swimmers involves the most generic flow characteristics in a fish school, such as, separation and reattachment of the shear layer, vortex impingement, vortex-structure interactions, and vortex reorganization [23]. For example, in tandem swimming, the global phase difference between two foils, which combines the spacing and tailbeat phase lag, is considered a key parameter for estimating the downstream swimmer’s/follower’s performance. Based on numerical and experimental studies, researchers also found that the optimal improvement in thrust generation and efficiency of the follower is achieved at the anti-phase of tailbeats (known as the destructive mode), whereas the worst performance occurs in the constructive mode with an in-phase tailbeat [24,25,26,27,28,29,30,31]. In destructive mode, swimmers shed vortices with the same rotation direction that merge downstream of the follower. This results in a powerful vortex structure behind the follower, which provides a high-speed jet flow. Conversely, in the constructive mode, vortices cancel behind the downstream swimmer because two swimmers create vortices with opposite rotational directions. In a recent study, Lagopoulos et al. [32] reported that tandem configurations suppress the symmetry-breaking of reverse Kármán vortex street, which shows that the downstream flow field affects the leader swimmer significantly.

Schooling swimmers might benefit more from the side-by-side configuration than the tandem configuration [33]. As with tandem swimming, researchers have also studied how the gap between two swimmers and the tailbeat phase difference affect the hydrodynamic performance of side-by-side swimmers. According to Dong and Lu [34], at moderate gaps, thrust improvement occurs in the anti-phase mode, and energy saving occurs in the in-phase mode. The vortex interactions between two swimmers, when organized in-phase, results in three different flow patterns, namely vortex-pair row, single vortex row, and in-phase synchronized vortex street, depending on the gap between two swimmers. In contrast, the anti-phase mode provides only one typical wake structure—the synchronized vortex street. Similar conclusions have also been drawn in the numerical and experimental literature [35,36,37,38,39,40]. Some studies have also been conducted on a more general staggered configuration observed in nature [10, 41,42,43]. For example, Li et al. [10] found that the follower could alter the relative tailbeat phase difference linearly as a function of the front-back distance using a ‘vortex phase matching’ strategy, which is beneficial for energy conservation. For leaders, such a simple rule does not exist.

In light of the fact that both burst-and-coast locomotion and schooling behavior can improve swimmer hydrodynamic performance, it is worthwhile to investigate whether multiple burst-and-coast swimmers in the same group can improve that performance further. Fish et al. [44] found that golden shiners (notemigonus crysoleucas) employ a burst-and-coast strategy while swimming in a school. However, no hydrodynamic and cost of transport analyses were conducted on the collective burst-and-coast swimmers in [44]. As part of this study, we perform numerical simulations to investigate the swimming performance and vortex formation of two burst-and-coast swimmers evolving side-by-side at various DC values. Our current study investigates the following unexplored questions: (i) Can burst-and-coast swimmers keep schooling based solely on hydrodynamic interactions, i.e., without any active feedback control? (ii) What is the hydrodynamic performance of burst-and-coast swimmers, such as speed and CoT efficiency? (iii) What types of vortex formations could be expected?

2 Problem description and methodology

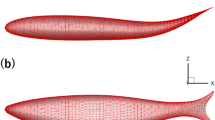
The problem setup consists of two foils (foil A and foil B) with the same tear-like geometry that self-propel from right to left in a rectangular domain (Fig. 1a). The foils can freely move in both horizontal (x) and vertical (y) directions. They are of length L and have head thickness of $D = 0.217 L$, as illustrated in Fig. 1b. At the beginning of the simulation ($t = 0$), the lateral distance between the two foils is set to $\Delta y = 0.5L$, while the horizontal distance is $\Delta x = 0$; thus the two foils are initially positioned in a side-by-side arrangement.

Fig. 1

a Sketch of the computational domain; b foil geometry and parameters; c normalized pitching angle versus normalized time for a continuous ($DC = 1.0$) and a burst-and-coast swimmer ($DC = 0.5$); and d an example of adaptive mesh refinement that tags the swimmer and regions of high vorticity magnitude during the simulation

Each foil oscillates around its head with a combined burst and coast pitching motion, that can be prescribed by the function:

$$\begin{aligned} \theta _i(t) = {\left\{ \begin{array}{ll} &{}S_i(t)\theta _m\sin (2\pi ft), \quad \ \ \ \ \ \, \, 0 \le t \le T_b,\\ &{}0, \qquad \qquad \qquad \qquad \qquad \qquad T_b \le t \le T_i. \end{array}\right. } \end{aligned}$$

(1)

Here,

$$\begin{aligned} S_i(t) = {\left\{ \begin{array}{ll} &{}-\tanh (9t)\tanh \left[ 9(t-1)\right] , \quad \ \ \ \ \, DC_i \le 1,\\ &{}{1}, \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad DC_i = 1 \end{array}\right. } \end{aligned}$$

(2)

is a smoothing function that is used to remove discontinuous angular rates and accelerations at the junction of the burst and coast phase (Fig. 1c) [25]. The subscript i denotes the $i^\textrm{th}$ foil ($i = 1$ denotes the upper foil A, $i=2$ denotes the lower foil B), $\theta _m = 15^{\circ }$ is the maximal angular displacement, $f = 1$Hz is the pitching frequency of the burst phase, t denotes the time, $T_b$ is the time period of the burst phase ($T_b = 1/f$), $T_i$ is the total swimming period (which includes both burst and coast phase of the foil), and $DC_i = T_b/T_i$ is the duty cycle of the $i^\textrm{th}$ foil. In our model, we keep $T_b$ the same and vary the total swimming period $T_i$ to change the duty cycle value $DC_i$. This is consistent with the previous burst-and-coast models used in the literature [3, 20]. In the remainder of the paper, all lengths and velocities are normalized by the foil length L and traveling wave velocity Lf, respectively. This includes the coordinates (x and y) and the swimming velocities ($u_{i}$ is the instantaneous swimming velocity, $v_{i}$ is the instantaneous lateral velocity, $\bar{U}_{i}$ is the time-averaged swimming velocity and $\bar{V}_{i}$ is the time-averaged lateral velocity).

Numerical investigations are conducted using the open-source IBAMR software, a distributed-memory parallel implementation of the immersed boundary (IB) method incorporating Cartesian grid adaptive mesh refinement (AMR) framework [45, 46]. Specifically, we employ a fully-Eulerian implementation of the IB method for simulating the fluid–structure interaction in this work. The details of the method are presented in our prior works [47,48,49,50]. IBAMR has been extensively used for studying fish-like swimming behavior [51,52,53]. The computational domain is a rectangular box of size $200\,L \times 20\,L$ with periodic boundary conditions along the axial direction and no-slip boundary conditions in the lateral direction (Fig. 1a) We employ a four-level Cartesian grid in this study for all numerical simulations. On levels 0, 1, 2, 3, the magnitude of vorticity $\Vert \omega \Vert \ge 0.25, 0.5, 1, 2$ is tagged for refinement, respectively. Figure 1d shows an example of AMR mesh. The kinematic viscosity of the fluid $\nu$ is set to 0.001. Following Lin et al. [43], we scale the velocity in the burst phase as $U_b = 10^{2}\nu /(0.5L)$. The burst-phase Reynolds number ${\text {Re}}_b$ is defined here as ${\text {Re}}_b = U_bL/\nu$, and it is fixed at 200. Consequently, the burst-phase-based swimming number is $Sw_b = 2\pi LAT_b/\nu \approx 1500$ [54]. Natural swimmers operate at ${\text {Re}}_b$ and $Sw_b$ of the order of $10 - 10^9$ [54], while we consider the hydrodynamics of two burst-and-coast swimming larvae at a low Reynolds number. Our burst-and-coast motion consists of a burst phase at a constant flapping frequency ($f = 1/T_b$), and a non-flapping coast phase following the burst phase, as described in previous works (e.g., [18,19,20]). This simple model reveals essential characteristics of burst-and-coast swimming. Natural swimmers, however, may adopt different swimming frequencies during two neighboring burst-and-coast periods. Moreover, swimmers may also exhibit two burst phases and one coast phase in a single burst-and-coast cycle [14]. These kinds of kinematics shall be considered in our future stuides.

The grid and time-step size convergence tests are conducted with a single self-propelled foil at $DC = 0.2$, and with two foils at $(DC_1, DC_2) = (0.2, 1.0)$. Grid size independence tests are done using three grid sets. For all three grids, the computational domain is progressively discretized using the AMR framework. Mesh resolution at the finest level on the three grids is: 0.016L (M1), 0.010L (M2), and 0.008L (M3). Keeping the time-step size $\Delta t = 0.001T_b$ fixed, time-histories of the swimming velocity (u, $u_{1}$ and $u_{2}$) for the three grids are presented in Fig. 2a, c, and d, while the steady time-averaged swimming velocity after 150 $T_b$ ($\bar{U}$, $\bar{U}_{1}$, and $\bar{U}_{2}$) are provided in Table 1. Here, $\bar{U}$ is the time-averaged swimming velocity of the single isolated foil in the domain. The differences in $\bar{U}$, $\bar{U}_{1}$, and $\bar{U}_{2}$ between M2 and M3 are quite small (0.41%, 0.46%, 0.02%, respectively). Thus, grid M2 is chosen for the time-step size convergence study.

Fig. 2

Left column: a grid-size convergence and b time-step size convergence study for an isolated foil in the domain. Middle column: grid-size convergence study for swimming velocities of c upper foil A d lower foil B. Right column: time-step size convergence study for swimming velocities of e upper foil A and f lower foil B

With M2, three values of time step size $\Delta t/T_b$ = 0.005, 0.001, and 0.0005 are considered. The corresponding time-histories of u, $u_{1}$ and $u_{2}$ are presented in Fig. 2b, e, and f, while the steady-swimming velocities are provided in Table 2. $\bar{U}$, $\bar{U}_1$, and $\bar{U}_2$ differ by 0.52%, 1.31%, and 0.99%, respectively, between $\Delta t2$ and $\Delta t3$. Considering accuracy and computational resources, M2 and $\Delta t2$ are chosen for the remaining simulations. Further convergence studies related to the immersed boundary method have been published in our previous works [47,48,49,50].

Table 1 Grid size convergence study using $\Delta t = 0.001T_b$

Table 2 Time-step size convergence study with M2

3 Hydrodynamic analyses of an isolated foil

A baseline study on a single foil in the domain is conducted before investigating the swimming performance and vortex formation of two burst-and-coast swimmers. We first show how DC affects horizontal and lateral swimming distances, i.e., $D_{x}^\textrm{max}$ and $D_{y}^\textrm{max}$ in Fig. 3a, where $D_{x}^\textrm{max}$ increases monotonically with DC. On the other hand, $D_{y}^\textrm{max}$ varies non-monotonically with DC, where $D_{y}^\textrm{max} < 0$ and $D_{y}^\textrm{max} > 0$ emerges at $DC \le 0.6$ and $DC \ge 0.8$, respectively; see Fig. 3b. We measure $D_{x}^\textrm{max}$ and $D_{y}^\textrm{max}$ at the end of the simulation at $t = 80\, T_b$. Previous studies have shown that the foil moves upward when $D_{y}^\textrm{max} > 0$; see for example [51]. The current study reveals that lateral movement is significantly affected by DC. A lower DC value even causes the swimmer to move downward. The swimming velocity improves with an increase in DC because a larger DC implies a longer time in the burst phase (thus a larger inertial force). This trend is captured by the relative swimming velocity $\bar{U}_\textrm{rel} = \frac{\bar{U}}{\bar{U}(DC = 1)}$ in Fig.  3c. A relationship of the form $\bar{U}_\textrm{rel} \sim \sqrt{DC}$ emerges, which was also obtained by Das et al. [18] previously. For estimating swimming efficiency, we use the mechanical CoT, which is defined as the ratio between time-averaged total power and time-averaged swimming speed. Swimming efficiency is higher when CoT is smaller [55]. According to Fig. 3c and d a smaller DC value leads to smaller $CoT_\textrm{rel} = \frac{CoT}{CoT(DC = 1)}$. The relationship $CoT_\textrm{rel} \sim DC$ emerges from the plotted data. Therefore, a higher DC value would result in inefficient swimming, but a faster swim. The time histories of horizontal and lateral swimming velocities are plotted in Fig. 3e and f. In contrast to continuous swimming, burst-and-coast swimming ($DC < 1$) results in significant fluctuations in u and v, and smaller instantaneous velocity.

Fig. 3

Maximum swimming distance measured at the end of the simulation ($t = 80\, T_b$) for various DC values: a axial distance $D_{x}^\textrm{max}$ b and lateral distance $D_{y}^\textrm{max}$. Variation of the relative c time-averaged swimming speed $\bar{U}_\textrm{rel}$ and d efficiency $CoT_\textrm{rel}$ with DC. $CoT_\textrm{rel}$ is normalized by the CoT value of the continuous swimmer ($DC = 1$). Time histories of swimming velocities: e axial $u_{x}$ and f lateral v. g–l Flow patterns produced by the burst-and-coast and continuous swimmers

Figure 3g–l illustrate the vortex structures produced by an isolated foil undergoing burst-and-coast and continuous swimming motions. The burst-and-coast locomotion produces the 2P wake [56] at all examined DC values, where a bifurcation occurs at the trailing edge of the foil. A vortex pair moves downward during the burst phase due to foil oscillation. A second vortex pair is then generated by the shear layer shedding at the foil trailing edge during the coast phase. The two vortex pairs can be viewed as two dipoles. As shown in Fig. 3h, the upper dipole causes an induced velocity with a positive component in the y-direction ($v^\textrm{up}$), whereas the lower dipole causes an induced velocity with a negative component in the y-direction ($v^\textrm{down}$). Thus, the non-monotonic dependence of lateral movement on DC (Fig. 3b) can be explained by the sum of the $y-$components of the induced velocity: $v^\textrm{up} + v^\textrm{down}$. In the case of continuous oscillation, the 2 S wake [56] forms as reverse Kármán vortex street.

4 Hydrodynamics of two burst-and-coast swimmers

Fig. 4

a Phase diagram in the $DC_1$ - $DC_2$ plane. The term “schooling" refers to two swimmers swimming together; the term “fission" refers to two swimmers that initially swam together but separated after some time; and the term “fusion” refers to the two swimmers colliding with each other. b–f Evolution of the horizontal and lateral distance between the two foils, $\Delta x$ and $\Delta y$, respectively

To investigate the swimming performance and vortex formation of two burst-and-coast foils, we systematically investigate the swimming speed and power expenditure of two foils at various values of duty cycle: $DC_i = 0.2, 0.4, 0.5, 0.6, 0.8$ and 1.0. Recall that $DC_i = 1.0$ describes the continuous swimming motion of foil i. The simulation time is up to $t = 200\, T_b$. The classification results are presented first, followed by detailed analysis results.

On the basis of horizontal distance $\Delta x = D_{x,1}^\textrm{max} - D_{x,2}^\textrm{max}$ and lateral distance $\Delta y = D_{y,1}^\textrm{max} - D_{y,2}^\textrm{max}$ between foils A and B, six conditions have been identified: (i) schooling; (ii) fission I (F-I); (iii) fission II (F-II); (iv) fission III (F-III); (v) fission IV (F-IV); and (vi) fusion (Fig. 4a). The schooling condition describes that $\Delta x$ and $\Delta y$ gradually approach quasi-steady (Fig. 4b), which is obtained at $DC_1 = DC_2 = 0.4, 0.5, 0.6$, and 0.8. This result suggests that two burst-and-coast swimmers can self-organize with hydrodynamic interactions only (without feedback control) when they employ the same and moderate values of DC. At smaller DC ($DC_1 = DC_2 = 0.2$), they would swim as two isolated foils, and at $DC_1 = DC_2 = 1.0$, they would fuse/collide. Two-foil fusion occurs when pressures on outer sides are greater than those on inner sides. The horizontal and lateral gaps of two foils at the beginning of the simulation affect the fusion of two continuous swimmers. This is reported in Lin et al. [43]. From our simulations, we find that a small DC difference between two foils would also induce the fusion condition when $DC_i$ is large enough (Fig. 4a).

Fig. 4a shows that F-I and F-II modes occur when $DC_1 > DC_2$. In these conditions, the upper foil A generates a faster swimming speed than the lower foil B (Fig. 3a). The horizontal distance between the two foils gradually increases as the simulation progresses; see Fig. 4c1 and d1. Therefore, a larger difference between $DC_1$ and $DC_2$ results in a higher $\Delta x$. The difference in $\Delta x$ between the two foils is large enough that there are no significant hydrodynamic interactions. Consequently, $\Delta y$ is mainly affected by $v_1$ and $v_2$: $\Delta y < 0$ at $(DC_1, DC_2) = (0.5, 0.2)$ and $\Delta y > 0$ at $(DC_1, DC_2) = (0.5, 0.4)$. The opposite is true for the F-III and F-IV modes, in which $DC_1 < DC_2$ and $\Delta x < 0$, as observed in Fig. 4a. Because the lower foil B has a higher value of DC, it has a faster swimming speed than the upper foil A.

Fig. 5

Vortex patterns corresponding to a an F-I formation at $(DC_1, DC_2) = (0.5, 0.2)$; b an F-II formation at $(DC_1, DC_2) = (0.5, 0.4)$; c an F-III formation at $(DC_1, DC_2) = (0.5, 0.6)$; and d an F-IV formation at $(DC_1, DC_2) = (0.5, 0.8)$. Three time instances $t/T_b = 50$, 100, and 200 are considered

We illustrate the vortex formation at fission conditions at $t/T_b = 50, 100$, and 200 in Fig. 5. In an F-I formation at $(DC_1, DC_2) = (0.5, 0.2)$, the follower foil B (green foil in Fig. 5a) approaches the lower edge of the upper vortex pairs produced by the leader foil A (black foil). As shown in Fig. 5a1, foil A and foil B produce vortex pairs that merge. At $t/T_b = 100$, foil B alternately swims through the positive and negative vortices of the upper vortex pairs generated by the leading foil A; see Fig. 5a2. However, at $t/T_b = 200$ the two-foil system separates out completely as seen in Fig. 5a3. In the F-II condition where $(DC_1, DC_2) = (0.5, 0.4)$, foil B swims at the lower side of the lower vortex pairs generated by the leading foil A, where the vortex pair generated by foil A in the burst phase merges with the vortex pair created by foil B in the coast phase to form a complex wake structure (Fig. 5b). At $(DC_1, DC_2) = (0.5, 0.6)$, two foils are in an F-III formation, where they are close to one another at $t/T_b = 50$ and $t/T_b = 100$. Upper vortex pairs generated by foil B merge with lower vortex pairs generated by foil A (Fig. 5c1 and c2). By the end of the simulation ($t/T_b = 200$), the vortex pairs generated by foil B merge with the vortex pair generated by foil A, forming a stronger flow structure than an isolated foil (Fig. 5c3). When foil B employs a larger $DC_2 = 0.8$ and foil A swims with a smaller $DC_1 = 0.5$, the follower foil A gradually crosses the upper and lower vortex pair created by the leading foil B (Fig. 5d). As a result, the follower foil with a smaller DC travels in the leader’s vortex wake (or in between the two rows of vortices). Eventually, the two foils swim in isolation with increasing time. We do not show the flow patterns generated by the fusion condition since it describes two foils colliding with each other.

Fig. 6

Relative a horizontal swimming speed, b CoT efficiency, and c lateral swimming speed of the group. Schooling condition of two in-phase foils

At $DC_1 = DC_2 =$ 0.4, 0.5, 0.6, and 0.8, two foils swim as a quasi-steady group, so it is worthwhile to find out if the combined effects of burst-and-coast locomotion and hydrodynamic interactions from the partner in the group can improve swimming performance. Figure 6a illustrates the relative time-averaged horizontal swimming speed of the group $\bar{U}_\textrm{grp} = \frac{\bar{U}_1 + \bar{U}_2}{2\bar{U}}$. It can be seen that $\bar{U}_\textrm{grp} < 1$ for all schooling cases. When the two foils keep schooling on the basis of hydrodynamic interactions only, the normalized swimming speed of the two-foil system is less than that of an isolated foil swimming at the same DC value. In terms of swimming efficiency, $CoT_\textrm{grp} = \frac{CoT_1 + CoT_2}{2CoT}$ gradually decreases with increasing DC; see Fig. 6b. The two-foil group spends more energy at $DC_1 = DC_2 = 0.4$ and 0.5, compared to the isolated foil case, while it decreases slightly at $DC_1 = DC_2 = 0.6$ and 0.8. We further analyze the lateral movement of foils in school. Figure 6c shows an increase in the lateral velocity of the two-foil system $\mid \bar{V}_\textrm{grp} \mid = \mid \frac{\bar{V}_1 + \bar{V}_2}{2\bar{V}} \mid$. The peak value of $\mid \bar{V}_\textrm{grp}\mid = 9.87$ is obtained at $DC_1 = DC_2 = 0.6$. In the schooling condition, the two foils move upward, whereas an isolated foil moves downward at $DC = 0.6$. The burst phase of the two-foil system generates a powerful downward-moving vortex pair. As a result, two foils are pushed upward by a strong jet flow (Fig. 7).

Fig. 7

Flow structures of two in-phase foils. The direction of the jet is indicated by arrows. Here, $\phi = 0$ indicates that the two foils have an identical tailbeat pattern

Additionally, we examine how the phase difference $\phi$ between the tailbeat of two foils affects their schooling. Here, we consider the case of $DC_1 = DC_2$ and $\phi = \pi$ (out-of-phase tailbeat). Figure 8 shows the variation in horizontal distance $\Delta x$ and lateral distance $\Delta y$ over time of two out-of-phase foils initially positioned in a side-by-side arrangement. As shown in Fig. 8a1, b1, c1 and d1, $\Delta x < 0.05$ during the simulation and it oscillates about the zero value. The two foils maintain a roughly side-by-side configuration with an out-of-phase tailbeat, while they form a staggered arrangement with an in-phase tailbeat ($\Delta x \approx 0.4$ in Fig. 4b). $\Delta y$ oscillates harmonically around a mean value in the lateral direction (Fig.  8a2, b2, c2 and d2). Accordingly, two foils with an out-of-phase motion can swim together in a side-by-side arrangement.

Fig. 8

Time evolution of the horizontal distance $\Delta x$ and lateral distance $\Delta y$ between the two out-of-phase foils

Fig. 9

a Horizontal swimming speed, b CoT efficiency, and c lateral swimming speed of the two-foil schooling system relative to a single foil swimming at the same DC value. Here, the two foils swim in an out-of-phase manner ($\phi = \pi$)

Fig. 10

Flow structures of two foils swimming in an out-of-phase manner. The direction of the jet is marked by arrows

Figure 9 illustrates how $\bar{U}_\textrm{grp}$, $CoT_\textrm{grp}$, and $\mid \bar{V}_\textrm{grp} \mid$ are affected by DC when two out-of-phase foils maintain a collective swimming motion at the same DC (i.e., $DC_1 = DC_2$). As shown in Fig  9a, $\bar{U}_\textrm{grp} < 1$ emerges at all examined DC values, suggesting that fish schooling decreases the swimming speed of two out-of-phase foils. However, $CoT_\textrm{grp} > 1$ is observed in Fig. 9b. Based on this evidence, schooling foils with out-of-phase gaits do not improve swimming performance. It can be seen, however, that $\mid \bar{V}_\textrm{grp} \mid \approx 0$ when the phase difference between two foils is $\phi = \pi$ (Fig. 9c). In contrast, two foils swimming in phase move upward (Fig. 6c). A visual representation of the wake (in Fig. 10) produced by the two foils can explain this phenomenon. For the out-of-phase case, the resulting jet flow is horizontal and it remains symmetric about the centerline of the two-foil system. We find that the initial configuration, $\Delta x$ and $\Delta y$, the tailbeat phase difference $\phi$, and the duty cycle values $DC_1$ and $DC_2$ all affect the schooling behavior of two burst-and-coast foils. In order to fully understand the swimming performance of the two-foil system, further research is needed to explore this large parameteric space.

We next explain the vortex interactions that occur during an in-phase burst-and-coast motion at $(DC_1, DC_2, \phi ) = (0.5, 0.5, 0)$ in detail. Here, $t*$ describes the starting time of the burst phase after two foils school. At $t = t^*$, two foils are just finishing their coast phase and pitching to the positive extreme ($\theta _i(t) = \theta _{m}$) from their mean position. There is a negative (blue) leading edge vortex (LEV) generated by foil A, marked as N1 (N refers to negative), while the negative and positive LEVs, N2 and P1 (P refers to positive, red color), are generated by foil B (Fig. 11a). The last burst phase generated a negative N3, which is behind foil B. When two foils pitch at the positive extreme $\theta _i(t) = \theta _{m}$ at $t = t^* + T_b/4$ (Fig. 11b), the upper shear layer at foils’ trailing edge rolls up and sheds downstream, forming the trailing edge vortex (TEV). N4 and N5 are the negative TEVs produced by foil B and foil A, respectively. In the meantime, the powerful N3 moves to the trailing edge of foil B. This happens at the same time when P1 moves to the trailing edge of foil B. When the foil swims in isolation, the LEV will reattach at the trailing edge, merge with the TEV, and finally form a powerful vortex. However, when the LEV is located on the inner side of two foils, this type of vortex evolution is broken. The LEV on the outer side has not been affected. N1 does not merge with N5 as a result. As two foils pitch back to the mean position at $t = t^* + T_b/2$, N3 merges with N4, forming a powerful negative vortex N6, as shown in Fig. 11c. Meanwhile, P1 moves to foil B’s trailing edge. The negative extreme $\theta _i(t) = -\theta _{m}$ is achieved at $t = t^* + 3T_b/4$ (Fig. 11d), where P1 merges with the TEV generated by foil B, resulting in a powerful P2. When foil A produces the TEV P3, N2 approaches the trailing edge of foil B. N2 is shed downstream at the end of the burst phase (also at the beginning of the coast phase). During this process, the shear layer N1 produced by the upper side of foil A (outer side of two foils) is attached to the upper side of foil B (inner side of two foils). Between N2 and N5, P3 provides a barricade, and between N2 and N6, P2 provides an obstruction. The dipole A is formed when N2 and P2 rotate together (Fig. 11a). In the next burst phase, N1 becomes N3, and P4 becomes P1 (Fig. 11a and f).

Fig. 11

Vortex interactions during in-phase burst-and-coast schooling. Here, $t^*$ refers to the starting time of the burst phase. The schooling condition corresponds to $(DC_1, DC_2, \phi ) = (0.5, 0.5, 0)$ in the simulation

The flow evolution of two out-of-phase foils at $(DC_1, DC_2, \phi ) = (0.5, 0.5, \pi )$ is depicted in Fig. 12. At $t = t^* + T_b/4$, the upper foil A produces a negative vortex N1, while the lower foil B produces a positive vortex P1. Following this, the shear layer on the inner side of the two foils moves to the trailing edge, producing P2 for upper foil A and N2 for lower foil B (Fig. 12c). P2 and N2 merge with the TEV generated at $t = t^* + T_b/4$ to form P3 and N3, respectively. As the burst phase ends, the shear layer at the outer edge of the two foils moves to the trailing edge. Vortex N4 and P4 are formed behind upper foil A and lower foil B, respectively. In the coast phase, the vortex structures N1, P1, P3, N3, N4, and P4 organize into a massive structure A (Fig. 12f and a), which finally becomes a 2P wake. This is shown by the dashed circle B in Fig. 12a. With respect to their centerline, two out-of-phase foils exhibit symmetric flow patterns. As a result of this symmetric wake, two foils that are out of phase swim side-by-side (Fig. 8).

Fig. 12

Vortex interactions during out-of-phase burst-and-coast schooling. Here, $t^*$ refers to the starting time of the burst phase. The schooling condition corresponds to $(DC_1, DC_2, \phi ) = (0.5, 0.5, \pi )$ in the simulation

5 Conclusions

Using IBAMR, two burst-and-coast self-propelled foils are numerically investigated for their swimming performance and vortex formation. Foils are initially arranged side-by-side and are free to move both horizontally and laterally. The benchmarking work is conducted on an isolated burst-and-coast foil with differing DC values, revealing a decline in swimming speed and CoT efficiency as DC increases. Further, the 2P wake downstream of the burst-and-coast foil causes upward or downward (depending upon DC) movement in the lateral direction.

By varying the duty cycle of two burst-and-coast foils, the swimming performance of the foils is systematically studied. Based on the horizontal and vertical distance between two foils, six different conditions are observed. Two foils can school at $DC_1 = DC_2 =$ 0.4, 0.5, 0.6, and 0.8, but not at other combinations of duty cycles. When two in-phase/out-of-phase foils were schooled, neither swimming speed nor efficiency increased significantly compared to individual swimming. During the schooling condition, two in-phase foils have increased lateral movement, while two out-of-phase foils can remain side-by-side without deviating laterally. Our simulations suggest that burst-and-coast swimmers do not gain a significant hydrodynamic advantage (in terms of swimming speed or reduction in the cost of transport) due to schooling. The in-phase gait produces a significant lateral deviation, which can only be circumvented through a well-coordinated out-of-phase gait between schooling swimmers.