1 Introduction

The dam-break flow has been a topic of significant research interest due to its practicality in many fields, such as in hydraulic [8, 38], coastal [31], and ocean engineering [28] for dam-break type problems. The sudden release of the water reservoir results in violent impact forces, unsteady problems involving wave motion, and complex interaction with structures or static fluid downstream. In addition to its direct application to dams, the study of dam-break flow has essential applications in the polymer industry [43]. The drag reduction by linear viscosity model in turbulent channel flow has been the object of numerous studies. The viscous flows down an inclined plane from point and line sources contribute to geological engineering [1] and a range of industrial processes, as is evident from the examples of warm-water discharge from power plants, spreading of oil on the sea surface [2, 14, 23].

Experiments on a smaller scale are required due to the difficulties in obtaining data in situ of dam-break flows. Bell et al. [4] studied the effects of upstream reservoir depth, channel depth, and channel roughness on two-dimensional dam-break flows. Lauber and Hager [20] experimented with a sloping dry-rectangular channel to investigate the positive and negative wavefronts and the effect of viscosity. The authors have established a time criterion for which the gate removal can be considered instantaneous. For a dry bed downstream, Leal et al. [21] indicated that the friction coefficient is the critical factor that dictates the amplitude of the wavefront celerity. An investigation of dam-break flow in a smooth rectangular channel with lateral contraction over a horizontal dry bed was carried out by Kocaman and Ozmen-Cagatay [19]. The formation (due to reflection against contraction) and propagation of negative-waves over time were also examined. Lobovský et al. [24] studied the pressure loads at the downstream vertical wall over a dry horizontal bed and investigated the decay time and the pressure impulse.

Few experimental studies have addressed the effect of viscosity on dam-break flow properties. Jánosi et al. [17] added a dilute solution of a polymer (polyethylene-oxide) in water to increase the viscosity from 5 to 10% compared to that of water. The authors showed that, for the dry-bed case, the front propagates faster in the presence of polymer than in the case of clean water. The polymer effect is almost negligible whenever a thin ambient layer is present in downstream. The authors affirmed that the turbulent drag reduction varies as a threshold function of polymer concentration. Pronounced drag reduction has been found at low polymer concentration resulting in faster flow; however, the reducing effect of polymer disappears when the concentration increases. Ancey et al. [2] investigated the dam-break flow behavior of highly concentrated glucose–water solutions. The dynamic viscosity ranged from 345 to 352 Pa.s, and the glucose–water solutions were Newtonian fluids. The authors focused on flow regimes in the large-capillary-number and low-Reynolds-number to limit the effects of inertia and surface tension. Didden and Maxworthy [10] studied the viscous spreading of plane current experimentally. The authors determined the proportional factors between the dimensionless length and thickness of surface gravity currents versus time.

In the past, dam-break over a dry bed was the object of an analytical pioneer study by Ritter [32] based on an idealized wave structure. Stoker [37] extended Ritter’s solution for dam-break with nonzero tailwater depth. More recently, Castro-Orgaz and Chanson [5], Stansby et al. [36] used Ritter’s solution with the assumption of hydrostatic pressure and uniform velocity over depth to plot the profiles of surface elevation. Huppert [16] studied the viscous gravity currents propagating over rigid horizontal surfaces using a lubrication-theory approximation. The authors established a correlation of spreading front for saltwater by comparing the experimental data of Didden and Maxworthy [10] to the theoretical results. Ancey et al. [2] extended the model proposed by Huppert for determining the short- and long-time behavior of a highly viscous dam-break flow on a horizontal or inclined flume. The numerical solution for the horizontal flume converged better than that of nonzero flume inclination. The front evolution and the flow-depth profiles with time were established. One of the few authors who studied the upward mushroom-like jet was Peregrine [30]. The Cauchy’s integral theorem and the discretization of the integral kernels were used to get quadrature formulae suitable for velocity and surface motion. However, the method requires a smooth surface and breaks down if the curvature at any point becomes too high for accurate numerical resolution [36].

With the increase in computer processing power in recent years, numerical simulations of dam-break flow constitute an interesting topic in the literature. Aguirre-Pe et al. [1] simplified full two-dimensional Navier–Stokes equations to develop a one-dimensional numerical model for a high-viscosity fluid dam-break wave on a dry and inclined bottom. The simulations were conducted using the MacCormack explicit scheme (predictor-corrector method). Otherwise, numerous studies have been conducted with the shallow water equations (SWEs, also known as “depth-averaged approximations”) based on the vertical integration of the Navier–Stokes equations over the water depth or with the nonlinear SWE [12]. The vertical velocities, as well as accelerations, are negligible [3]. Hui Pu et al. [15] considered that the “SWE model has proven to be less effective to reproduce the highly distorted free surface in dam-break flows due to its meshing features that prohibit any wave-breaking or violent flow simulations.” Effectively, the SWEs are well known for their efficiency for the depth ratio (downstream depth versus upstream depth) under 0.55. Above this value, Castro-Orgaz and Chanson [6] used Serre–Green–Naghdi (SGN) equations to describe the undular surge. SWE equations fail to predict the effects of varying topography like contraction-expansion [19], triangular channel [42], presence of hump [29], of the box [18] in downstream.

In order to overcome these problems, the volume of the fluid (VOF) method has been used by Kleefsman et al. [18] to study the wave impact on a box that represents a container on the deck of an offshore floater. The numerical simulation of the dynamic loads generated during a dry dam-break flow impact on a wall was investigated by Mokrani and Abadie [26]. The investigation of dam-break flood waves in a dry channel with a hump undertaken by Ozmen–Cagatay et al. [29] showed that the VOF method associated with a \(k-\varepsilon \) turbulence model is better than using simple SWE. Ye and Zhao [44] investigated the downstream water–upstream water interface and free surface in dam-break flow with a wet bed by coupling a VOF method with an immersed boundary method. The effects of gate thickness, gate removal velocity, and ambient water depth were established. Recently, Li and Zhao [22] proposed a coupled VOF and discrete element method (DEM) to model the fluid and particle phases in the mixture. Hui Pu et al. [15] demonstrated that the incompressible smoothed particle hydrodynamics (ISPH) modeling technique has a better prediction of the dam-break peak wave building-up time compared to the SWE method.

For a curved channel, Shaheed et al. [34] showed that the VOF method associated with a standard \(k-\varepsilon \) turbulence model performs better than the realizable \(k-\varepsilon \). However, for a confluent channel, the realizable \(k-\varepsilon \) model is better. The simulations of dam-break flow are frequently constrained by the comparatively small spatial scales in laboratories. The effects of fluid–wall interaction should be taken into account by the \(k-\omega \) model [25] associated with the VOF method. This coupling is more accurate concerning the near-wall treatment with an automatic switch from wall function to a low-Reynolds-number formulation based on grid spacing. By comparing the performance of eight Reynolds-averaged Navier–Stokes (RANS) models, two sub-grid scales (SGS), large eddy simulation (LES) models in the scenario of unsteady flow around a finite circular cylinder at a Reynolds number of Re\(=\)20000, Zhang [45] found that the \(k-\omega \) shear-stress transport turbulence (SST) model possesses the best overall performance in terms of the mean surface pressure coefficient distribution, the mean drag coefficient, and the distribution of mean bed-shear-stress amplification on the bottom wall. By subtracting the asymptotically known singular behavior of \(\omega \) at wall, the regularized approach proposed by Tomboulides [40] aimed to lead to grid-independent solutions. The performance of the proposed method was examined on an infinite channel and a backward-facing step.

Despite numerous studies of dam-break flow previously cited, the effects of viscosity are still not sufficiently understood. The air bubble characteristics under the effects of surface tension and viscosity could be better experimentally and numerically explored. As such, the authors propose in this research an experimental study conducted in a rectangular smooth open flume. First, the dam-break flow on a dry bed and the effects of a shallow ambient layer on the propagation velocity will be examined. Then, the flocculant AN910 (polymer) allows for varying the solution viscosity as well as the surface tension to investigate their influences on the flow. After that, an analytical approach based on the research of [5, 16, 36, 37] will be detailed. Finally, considering the recommendations of previous studies [40, 45], and anticipation for future work, the numerical simulations by the VOF method coupled with the \(k-\omega \) SST were chosen despite its computational cost (8.24 Cores.Hours). This model aim at predicting the instantaneous elevation of free surfaces and the dynamic behavior of flows under the effects of viscosity. 

2 Experimental investigations

2.1 Experimental setup

The experiment was conducted in a rectangular smooth open channel (flume) with a closed end and with a removable metal gate at the other end (both ends of the channel could be closed). The walls were made of Plexiglas to observe the flow.

Fig. 1
figure 1

Schematic illustrating experiment of dam-break flow

Full size image

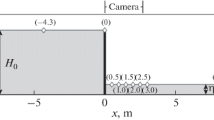
The flume width was 0.055 m, depth 0.120 m,  and length 2.000 m (Fig. 1). It was divided into two volumes by a vertical gate placed at 0.280 m from the closed end, and this volume was used as a reservoir of the dam. The reservoir’s initial water level was maintained at \(d_{\mathrm {0}} \quad =\) 11 cm, while the shallow ambient layer with depth d (cm) was varied from 0 to 6.6 cm. A hydraulic piston allowed the gate to be removed suddenly in a time shorter than \(1.25\sqrt{d_{0}/g}\) [20].

2.2 Measuring technique

A CMOS Basler camera with an acquisition rate of 203 frames per second and a resolution of 1280 \(\times \) 1024 pixels was installed perpendicularly to the channel side to record videos. The flume has contained methylene blue dye to enhance the recorded images, and the background of the opposite side was covered with white paper. The front propagation and free-surface profiles were observed using software for image analysis, which from the raw image allowed the extraction of the free water surface (Fig. 2) and the output of white pixel coordinates. A limitation of this technique is the capture of the side water surface profile. Careful preparation was required to limit wall effect, and when there was the appearance of close lines near the free surface, the mean water profile is manually checked.

Fig. 2
figure 2

Extracting free surface from raw images

Full size image

2.3 Dam-break experiment cases with variations of viscosity

To highlight the effect of viscosity and surface tension variations on the behavior of dam-break flow, flocculant AN910 (polymer) was added to the water, and its concentration was varied from zero to 2.1 g/L (Table 1, Fig. 3). All solutions were prepared using distilled water treated in a Millipore Milli-Q Plus system \((> 18.2\hbox { M}\Omega )\). The Brookfield DV III-Ultra Viscosymeter was used to measure the viscosity of the solution and to ensure that the fluid comportment was Newtonian. The surface tension decreases from 0.078 (water) to 0.043 N/m (solution at 2.1 g/L of flocculant), while the solution density remained constant at \(1000\, {\hbox {kg/m}}^{3}\).

A set of experiments (Table 2) were conducted using the setup described in Sect. 2.1, varying both the water depth in downstream and the solution viscosity.

Table 1 Viscosities of the solutions as a function of the concentration of AN910 flocculant
Full size table
Fig. 3
figure 3

Calibration curve of viscosity as a function of solution concentration

Full size image
Table 2 Dam-break experiment cases
Full size table

3 Numerical simulations by the volume of fluid method

The study used the volume of fluid method [13] to simulate the flow of a two-phase fluid (liquid-gas). Accordingly, the density \(\rho \) and the viscosity \(\mu \) of the mixture were averaged with the liquid volume fraction \(\alpha \) (Fig. 4) as

$$\begin{aligned} \rho= & {} \alpha .\rho _{l} +(1-\alpha ).\rho _{g} \end{aligned}$$
(1)
$$\begin{aligned} \mu= & {} \alpha .\mu _{l} +(1-\alpha ).\mu _{g} \end{aligned}$$
(2)
Fig. 4
figure 4

Sketch of liquid volume fraction \(\alpha \). The color blue represents volume of liquid, and the color white illustrates gas volume

Full size image

Transport equation for the liquid volume fraction can be expressed as

$$\begin{aligned} \frac{\partial \alpha }{\partial t}+\nabla .\left( {\alpha U} \right) =0 \end{aligned}$$
(3)

where U denotes the velocity field.

Mass and momentum equations take the form

$$\begin{aligned}&\nabla .U=0 \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial \rho U}{\partial t}+\nabla .\left( {\rho U\otimes U} \right) =-\nabla P+\nabla .\left( {\mu \left( {\nabla U+\nabla ^{T}U} \right) } \right) +\rho g-S_{st} \end{aligned}$$
(5)

where P is the pressure, \(S_{st}\) is the surface tension force which can be calculated by

$$\begin{aligned} S_{st} =\sigma .\kappa .\nabla \alpha =\sigma .\left( {-\nabla .\left( {\frac{\nabla \alpha }{\left| {\left. {\nabla \alpha } \right| } \right. }} \right) } \right) .\nabla \alpha \end{aligned}$$
(6)

where \(\sigma \) denotes the constant surface tension and \(\kappa \) the curvature of the interface.

Given the dimensions of the flume, the shear-stress transport turbulence model (\(k-\omega {SST}\)) proposed by Menter et al. [25] has been used to model the average flow characteristics for turbulent flow conditions in a Cartesian coordinate system \(O(x_{i}, x_{j}, x_{k})\). The \(k-\omega {SST}\) model is substantially accurate in the near-wall layers and has therefore been successful for flows with moderate adverse pressure gradients. The k-transport equation and the transport equation for \(\omega \) can be written as

$$\begin{aligned}&\frac{\partial \left( {\rho k} \right) }{\partial t}+\nabla .\left( {\rho kU} \right) ={\tilde{P}_{k}} -\beta ^{*}\rho k\omega +\nabla .\left( {\left( {\mu +\sigma _{k} \mu _{t} } \right) \nabla k} \right) \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\partial \left( {\rho \omega } \right) }{\partial t}+\nabla .\left( {\rho \omega U} \right) =\alpha \rho S^{2}-\beta \rho \omega ^{2}+\nabla .\left( {\left( {\mu +\sigma _{\omega 1} \mu _{t} } \right) \nabla \omega } \right) +2\left( {1-F_{1} } \right) \left( {\rho \frac{\sigma _{\omega 2} }{\omega }} \right) \nabla k\nabla \omega \end{aligned}$$
(8)

where,

  • \(F_{1}\) denotes the blending function depending on \(k, \omega ,\) and \(y^{+}\) (the distance to the nearest wall). \(F_{1}\) is equal to zero away from the wall and switches over to one inside the boundary layer.

  • The turbulent eddy viscosity \(\mu _{t}\) is defined as follows:

    $$\begin{aligned} \mu _{t} =\frac{\rho a_{1} k}{\max \left( {a_{1} \omega ,SF_{2} } \right) } \end{aligned}$$
    (9)

    where S represents the invariant measure of the strain rate \(S=\sqrt{2S_{ij} S_{ij} } \) and \(F_{2} \)is a second blending function.

    $$\begin{aligned} S_{ij} =\frac{1}{2}\left( {\frac{\partial U_{i} }{\partial x_{j} }+\frac{\partial U_{j} }{\partial x_{i} }} \right) \end{aligned}$$
    (10)

  • The production limiter \({\tilde{P}_{k}}\)is used to prevent the build-up of turbulence in stagnation regions

    $$\begin{aligned} \begin{array}{l} {\tilde{P}_{k}} =\min \left( {P_{k} ,10\beta ^{*}\rho k\omega } \right) \\ P_{k} =\mu _{t} \frac{\partial U_{i} }{\partial x_{j} }\left( {\frac{\partial U_{i} }{\partial x_{j} }+\frac{\partial U_{j} }{\partial x_{i} }} \right) \\ \end{array} \end{aligned}$$
    (11)

  • and the model constants are given by

    $$\begin{aligned} \beta ^{*}=0.09,\beta =3/40,a_{1} =0.3,\sigma _{k} =0.85,\sigma _{\omega 1} =0.5,\sigma _{\omega 2} =0.856, \quad \alpha ={5}/{9}F_{1} +0.44\left( {1-F_{1} } \right) . \end{aligned}$$

    The recommended boundary conditions [33] are

    $$\begin{aligned} \begin{array}{l} k_{wall} =0.0031 \\ \omega _{wall} =10\frac{6\mu }{\beta \rho \left( {y^{+}} \right) ^{2}} \\ \end{array} \end{aligned}$$
    (12)

    The open-source CFD code OpenFOAM®(solver InterFoam) was used to carry out numerical simulations. The calculation cycle is a time-stepping algorithm (Fig. 5), which requires the repetition of the following resolution scheme. The relative tolerance was 10\(^{\mathrm {-6}}\), whereas the absolute was \(10^{\mathrm {-8}}\). The time step and maximum mesh size in this study were \(1.0{\times }10^{\mathrm {-4}} s\) and 2  mm, respectively.

Fig. 5
figure 5

Algorithm of two-liquid VOF method in InterFoam solver

Full size image

4 Analytical methods

For the validation of experimental and numerical results (the freshwater case in which the effects of viscosity were negligible), the analytical model proposed by Stoker [37] and cited by Stansby et al. [36] was used. The authors considered the release of a constant fluid of depth \({\times }\) with as \(d_{0}\times L\) (Fig. 6) in a dry flume. With the assumption of hydrostatic pressure and ignoring the surface’s friction, the velocity is uniform over depth. The profile of surface elevation at time t can be expressed as [5, 36]

$$\begin{aligned} \left\{ {\begin{array}{l} for\,\,\,x\leqslant L-t:\,\,\,\,\,d(x,t)=d_{0} \\ for\,\,\,x>L-t:\,\,\,\,\,x(t)=\left[ {2\left( {g.d_{0} } \right) ^{1/2}-3\left( {g.d\left( {x,t} \right) } \right) ^{1/2}} \right] .t \\ \end{array}} \right. \end{aligned}$$
(13)

where d(x, t) is water surface elevation at flume length x(t).

Fig. 6
figure 6

Sketch of the two-dimensional current

Full size image

In terms of viscous fluid flows along a rigid horizontal surface, Huppert [16] used a lubrication-theory approximation to study a current of density \(\rho _{water}\) intruding into a fluid of lesser density \(\rho _{air}\) (Fig. 6). The comparison between the theoretical results and experimental data of Didden and Maxworthy [10] gives the spreading relationship

$$\begin{aligned} x_{front} (t)=0.804\left[ {\frac{g^{*}.\left( {L.d_{0} } \right) ^{3}}{\nu }} \right] ^{1/5}.t^{4/5} \end{aligned}$$
(14)

where \(g^{*}=\frac{\rho _{water} -\rho _{air} }{\rho _{water} }g;g=9.81m.s^{-2}.\)

For the case of the presence of shallow ambient water downstream, after the release of volume 1 (Fig. 7a), Stoker [37] extended the Ritter solution [32] and proposed an analytical solution to produce a wave that moves through the backwater, causing a recession of backwater height (point A, Fig. 7b) and a wave that moves through and over the downstream causing an increase in flow depth (point B).

Fig. 7
figure 7

The analytical model of Stoker’s study: two-dimensional stationary volumes a and free-surface profile after the release of volume 1 b

Full size image

Stoker’s solution predicts that the flow depth at the dam site attains a constant value \(d_{B}\) that depends on upstream height and ratio \(d/d_{0}\) (Fig. 8a). The velocity of this plateau varies depending on the depth ratio \(d/d_{0}\) and the initial velocity \(U_{0}\) (\(U_{0} =\sqrt{g.d_{0} } )\), as shown in Fig. 8b.

Fig. 8
figure 8

Flow depth in downstream and plateau velocity of Stoker’s solution

Full size image

The shock (front) velocity and the plateau’s front position can be determined using the Rankine–Hugoniot jump conditions as

$$\begin{aligned} \left\{ {\begin{array}{l} U_{front} =\frac{d_{B} .U_{B} }{d_{B} -d } \\ x_{front} =U_{front} .t \\ \end{array}} \right. \end{aligned}$$
(15)

At the same time, the backwater has a moving point \(x_{A}\) spreading back at velocity \(U_{A}\)

$$\begin{aligned} \left\{ {\begin{array}{l} U_{A} =-\sqrt{g.d_{0} } \\ x_{A} =U_{A} .t=-\sqrt{g.d_{0} } .t \\ \end{array}} \right. \end{aligned}$$
(16)

The profile of the free surface between the negative front and the flow depth at downstream (A and C in Fig. 7b) can be expressed as [5, 8]

$$\begin{aligned} d\left( {x,t} \right) =\frac{1}{9.g}\left( {-\frac{x}{t}+2\sqrt{g.d_{0} } } \right) ^{2} \end{aligned}$$
(17)

Despite the model’s ability of Peregrine [30, 36] to predict the mushroom-like jet, its limits in a rough surface and high curvature do not allow to capture the free surface of viscous dam-break flows in this study.

5 Results and discussion

5.1 Case of the dry channel

Figure 9 shows the experimental and numerical snapshots for the dry-bed case. Note that the color red represents volume fractions equal to 1 (water) numerically and the color blue illustrates volume fractions equal to zero (air). The numerical location of the air–water interface was chosen at a liquid volume fraction \(\alpha \) of 0.6. The numerical shape of the free surface is quite similar when compared to that of experiments. However, the numerical images show linear (oblique) free surfaces, while a short staircase cascade (plateau) has been observed on the experimental flows.

Fig. 9
figure 9

Experimental (upper) and numerical (bottom) snapshots at the times of 0.156 s and 0.468 s, respectively

Full size image

Figure 10 illustrates the analytical, experimental, and numerical surface profiles at 0.156 s, 0.281s, and 0.468 s. It can be observed that the analytical elevation is in line with the numerical curve. The difference from the experimental results is mostly at the early stage. At 0.156 s (Fig. 10a), the vertical removal of the gate allows partial water to escape and forms a jet-like flow at the bottom of the water column (at \(x=\)0.40 m). This flow grows and spreads over the channel bed, as shown by the profile drawn at 0.281s(Fig. 10b). A good agreement is observed between the analytical, experimental, and numerical results at 0.468 s(Fig. 10c). The free surface is more spread out (oblique or slightly parabolic convex) than it was in the early stages. However, the experimental curve still has a short “staircase” (plateau, flume lengths ranging from 0.4 to 0.6 m) in the middle, and its front lags behind the other fronts. A possible explanation for this phenomenon is the effect of bed friction that brakes the flow resulting in lower velocity. In contrast, it can be seen that these effects have not yet been well taken into account in the simulations. It can be seen that the numerical and experimental profiles are lower than the analytical free surface of flume length ranging from zero to 0.15 m, resulting in a faster negative wave velocity. Dressler [11], Lauber and Hager [20] linked this speeding to the existence of severe vertical accelerations.

Fig. 10
figure 10

Water profiles at the times of 0.156 s, 0.281 s, and 0.468 s, respectively

Full size image

5.2 Case of ambient water in downstream

Figure 11 shows a sequence of experimental and numerical snapshots for an ambient water layer depth of 1.32 cm at various points in time. At 0.156 s, the static layer in downstream resists a quick-release in upstream, forming a “mushroom-like jet”; its breaking results in the trapping of air bubbles lasting experimentally and numerically from 0.281 to 0.343 s. At later stages, the air bubble diameter decreases on the experimental snapshots, whereas it persists in the simulation figures.

Fig. 11
figure 11

Experimental (left) and numerical (right) snapshots of dam-break with shallow water at different times

Full size image

Figures 12, 13, and 14 illustrate the analytical, experimental, and numerical surface profiles for three ambient water depths (\(d=0.70\), 1.32, and 2.79 cm). For the results of the analytical model, these curves predict acceptably the free surface after releasing the reservoir as well as the plateaux, which represents well the crest height. However, the front wave is further advanced compared to the experimental and numerical developments. A possible explanation for this front-wave trend is that the front velocity was overestimated by Stoker’s solution (Fig. 8) and by the Rankine–Hugoniot jump conditions (Eq. 15).

At the early stage, an experimental and numerical upward “mushroom-like jet” is observed, as reported by Stansby et al. [36] and Jánosi et al. [17]. Under the energy of reservoir release, the crest of the mushroom-like jet curls over and drops onto the ambient water, releasing most of its energy at once in a relatively violent impact and forming some surface irregularities and small air bubbles. In general, the numerical results show a trend that matches the experimental data. At times of 0.281s and 0.468 s, the “water tongue” (plunging breaker) due to a flattening of mushroom-like jet curves appears in the simulation (Figs. 12b, 13b, 14b). Similar behavior is exhibited in the study of Peregrine [30, 36] based on boundary-integral methods. However, the plunging breaker happened quicker in the experiment; the air is entrained in the water column as a result of breakers in the form of bubbles. At 0.468 s, spilling breakers occur at the ambient water depth of 0.70 cm (Fig. 12c), while the experimental wave becomes steeper at 1.32, and 2.79 cm and generates plunging crests (Figs. 13c, 14c).

Fig. 12
figure 12

Water profiles for ambient water layer of 0.70 cm at times of 0.156 s, 0.281 s, and 0.468 s, respectively

Full size image
Fig. 13
figure 13

Water profiles for ambient water layer of 1.32 cm at times of 0.156 s, 0.281 s, and 0.468 s, respectively

Full size image
Fig. 14
figure 14

Water profiles for ambient water layer of 2.79 cm at times of 0.156 s, 0.281 s, and 0.468 s, respectively

Full size image

5.3 Variation of the average velocity of the dam-break front as a function of ambient water depth

The velocity fields for the dry channel and the case of ambient water (\(d=1.32\) cm) are plotted in Fig. 15 at times of 0.090 s (Fig. 15a–c) and 0.156 s (Fig. 15b–d), respectively. For each image, the length of the arrow is proportional to the velocity magnitude. It is observed that the numerical velocity field has a non-uniform distribution, with the high velocity at the wavefront for the dry channel (Fig. 15a, b) and in the “mushroom-like jet” when the ambient water is present (Fig. 15c, d). For the first case, the maximum velocity depends on the surface tension of the fluid and the wettability (friction) of the channel bed. For the latter case, with the presence of water downstream, the maximum velocity depends on the depth of the ambient layer (which means the energy of reservoir release due to the gradient of hydrostatic pressures between upstream and downstream).

Fig. 15
figure 15

Velocity fields at times of 0.090 s a, c and 0.156 s b, d, respectively, for dry channel a, b and ambient water layer of 1.32 cm c, d

Full size image

Figure 16a illustrates the variation of the average velocity U(m/s) of the dam-break front normalized by the initial velocity (\(U_{0} =\sqrt{g.d_{0} } )\) as a function of the depth ratio between the upstream water level and downstream water level, \(d/d_{0}\). It can be seen that the shock wavefront propagates slower with the increase of depth ratio. When the downstream water level is low \((d/d_{0}<0.15)\), the flow velocity exceeds \(U_{0}\). The fluid is “pulled” by the forces that move it (gravity mostly), without the fluid mass downstream being an impediment. When the level of the downstream water column becomes higher \((0.15< d/d_{0}< 0.40)\), the velocity decreases and becomes smaller than \(U_{0}\). It remains constant when the ratio \(d/d_{0}\) is more than 0.4. The results are in agreement with those of Jánosi et al. [17] (Fig. 16b). However, the average velocity decreases slightly below \(U_{0}\) in our study, whereas Jánosi et al. found that it stabilizes at \(U_{0}\) when \(d/d_{0}\) exceeds 0.2.

Fig. 16
figure 16

a Variation of normalized flow velocity versus downstream water level. b Variation of normalized flow velocity versus downstream water level by (Jánosi et al. [17])

Full size image

5.4 Influence of viscosity

5.4.1 Comparison of analytical/numerical/experimental results for the dry channel (d=0)

For comparative purposes, Figs. 17 and  18 show experimental and numerical free-surface profiles for two representative viscous fluids. As a reminder, \(0.2\,g/L\) and \(0.7\,g/L\) of flocculant concentrations lead to viscosity of 0.007 and \(0.03 \textit{Pa.s}\). It has been seen that when the viscosity is low \((0.007 \textit{Pa.s}\) and 0.001 Pa.s previously), the front wave in the simulation propagates faster than that of the experiment. At high viscosity (0.03 Pa.s), a close trend was observed but with a less significant gap. The shapes of the water surface are similar to those in the low-viscosity cases.

Fig. 17
figure 17

Fluid profiles at \(\mu =\textit{0.007 Pa.s}\); \(t=0.156\,s\,0.281{s}\), and 0.468s, respectively

Full size image
Fig. 18
figure 18

Fluid profiles at \(\mu =\textit{0.03 Pa.s}\); \(t=0.156\,s 0.281s\), and \(0.468\,s\), respectively

Full size image

Table 3 summarizes dam-break fronts (\(x_{front})\) from the analytical model of Huppert [16], the simulation, and the experiments at different stages. The experimental values are in line with the numerical ones, and the difference from the analytical results is most for viscous solutions (\(\mu =\)0.030, and 0.103 Pa.s). The Huppert’s correlation seems to be valid only for diluted fluids. As expected for the dry flume under the effects of fluid adherence to the bottom wall, it can be observed that the dam-break front propagates more slowly when the flocculant concentration increases.

Table 3 Comparison of dam-break fronts
Full size table

5.5 Comparison of free-surface profiles with the presence of shallow ambient water in downstream

At a flocculant concentration of \(0.7\, g/L (\mu =0.03 Pa.s)\), measured free-surface profiles have been compared against numerical curves for the ambient water depths of 0.70, 1.32 and 2.79 cm in Figs. 19, 20, and 21, respectively. At 0.156 s (Figs. 19a, 20a, 21a), the model predictions fit well with the experimental data; a mushroom-like jet is observed on simulations while a vertical jet appears on experiments. As previously observed for depths of 1.32 and 2.79 cm from 0.281 s to 0.468 s, the numerical jets grow and spread along with the shallow ambient layer (Figs. 19c, 20c, 21c). In experiments, the formation of air bubbles induced by the mushroom-like jet’s implosion appears in later stages. It can be observed that the numerical front propagates slightly faster compared to the experimental one and that the forming of some irregularities and small air bubbles appears on free surfaces of flume lengths ranging from 0.5 to 0.8 m.

Fig. 19
figure 19

Fluid profiles at \(\mu =\)0.03 Pa.s; \(d=\)0.7 cm; \(t=\)0.156 s, 0.281 s, and 0.468 s, respectively

Full size image
Fig. 20
figure 20

Fluid profiles at \(\mu =\)0.03 Pa.s; \(d=\)132 cm; \(t=\)0.156 s, 0.281 s, and 0.468 s, respectively

Full size image
Fig. 21
figure 21

Fluid profiles at \(\mu =\)0.03 Pa.s; \(d=\)2.79 cm; \(t=\)0.156 s, 0.281 s, and 0.468 s, respectively

Full size image

Figures 22, 23, 24 show the comparison of experimental free-surface profiles of freshwater (without additive) and water with flocculant at 0.7 \(g/L~(\mu =\textit{0.03 Pa.s})\) versus time. At 0.156 s (Figs. 22a, 23a, 24a), these profiles present a trough (flume length ranging from 0.3 to 0.4 m) that formed due to removing the dam that separated the reservoir from the ambient water. This trough is where the gradient of hydrostatic pressure between upstream and downstream reaches its maximum value.

While the free-surface profiles are similar at initial stages, there are differences seen between the formation of air bubbles for freshwater at the ambient water depth of 0.70 cm and the flume length of 0.4m to the right of the mushroom-like jet. At the ambient solution depth of 2.79 cm, the air bubble appears to the left of the mushroom-like jet.

At a time of 0.281 s (Figs. 22b, 23b, 24b) and over a distance of 0.4 m, the viscosity has not shown its influence on the propagation velocity. However, the freshwater front tends to move faster than that of viscous fluid. Air entrainment appears faster in freshwater. Soon, there is observed a significant advance (9%) of the freshwater wavefront compared to that of viscous fluid at 0.468 s (Figs. 22c, 23c, 24c), especially when the ambient solution depth is low (d= 0.7 cm). The results show similar behavior to those of Motozawa et al. [27] as expected for slightly smaller dimensions of the flume. The authors demonstrated that the wall shear stress of freshwater is lower than that of a viscous solution in the region upstream, and it gets higher in the far downstream. As a result, the front velocity decreases by dosing a viscous solution. For ambient solution depth of 0.7 cm, the free-water profiles are oblique because of the dissipation of release energy. However, for deeper ambient layer water, the kinetic energy continues to create local crests on the plateau (flume length ranging from 0.4 to 0.8 m).

Fig. 22
figure 22

Comparisons of free-surface profiles (experimental data) at C = 0 and C = 0.7 g/L (\(\mu \) = 0.03 Pa.s) for different ambient fluid depths d = 0.7 cmd = 1.32 cm, and d = 2.79 cm, respectively, at t = 0.156 s

Full size image
Fig. 23
figure 23

Comparisons of free-surface profiles (experimental data) at C = 0 and C = 0.7 g/L (\(\mu \) = 0.03 Pa.s) for different ambient fluid depths d = 0.7 cm d = 1.32 cm, and d = 2.79 cm, respectively, at t = 0.281 s

Full size image
Fig. 24
figure 24

Comparisons of free-surface profiles (experimental data) at C = 0 and C = 0.7 g/L (\(\mu \) = 0.03 Pa.s) for different ambient fluid depths d = 0.7 cm d = 1.32 cm and d = 2.79 cm, respectively, at \(t=\)0.468 s

Full size image

5.5.1 Numerical study of high-viscous fluids

 Following the \(k-\omega \) SST model validation, a numerical simulation of high-viscous fluids (10 and 50 Pa.s) was performed (Figs. 25, 26) to emphasize the effects of viscosity on flow dynamics. It can be observed that, as seen previously, the fluid moves more slowly when the viscosity increases. Figures 25a, 26a show that the free-surface profile of 50 Pa.s still looks like its original shape at 0.156 s,  whereas the fluid having a viscosity of 10 Pa.s has started to spread. At later stages of the dry case (Figs. 25b, c), the effects of fluid adherence to walls due to high viscosity can be seen on the left end of the flume (heights ranging from 9 to 11 cm) and on the flume bottom. When the fluid is present in downstream (Figs. 26a–c), the mushroom-like jet did not form like the low viscosity cases. The “water tongue” due to a flattening of the upstream reservoir appears above the interaction point between upstream and downstream

It is noteworthy that the time evolution of negative wavefront velocities (negative surge) is the important parameter in assessing the flood risk and planning for an eventual evacuation of the population from the tailwater of a river [5]. Some previous studies [11, 20] have hypothesized this wavefront evolution to the existence of severe vertical accelerations. As shown in Figures 25, 26, the negative wavefront velocity is higher at a low viscosity. The last one can play a significant role and must be taken into account in analytical models. (Until now, this velocity depends only on the upstream depth.)

Fig. 25
figure 25

Free-surface profiles at \(\mu =\)10    and    50 Pa.s; d\(=\) cm; \(t=\)0.156 s, 0.281 s, and 0.468 s, respectively

Full size image
Fig. 26
figure 26

Free-surface profiles at \(\mu =\)10    and    50 Pa.s; d =1.32 cm; \(t=0.156 s\), 0.281 s, and 0.468 s, respectively

Full size image

5.6 Characteristics of air bubbles

In the literature, Chanson [7] linked the presence of air bubbles to the drag reduction process. Stagonas et al. [35] summarized previous research examining the breaker type (spilling, plunging) as a function of surface tension and energy dissipation. Deike et al. [9] used the direct numerical simulation (DNS) to investigate the time dependence of the air entrainment, the void fraction and the bubble size distribution on the initial wave slope and the turbulent dissipation rate The last one is related to the fluid density and the characteristic phase speed of the breaking front. Inspired by experimental studies of [35, 39], we try to experimentally demonstrate in this section the role of the fluid viscosity and surface tension on the air entrainment properties.

Take a glance at a sequence of air bubbles snapshots (Fig. 27) of the 2.79 cm ambient fluid depth, the creation of an air bubble entrainment has been observed. As previously discussed, the kinetic energy of reservoir release reaches its maximum value near the interaction point between upstream and downstream (Fig. 27a), where it formed a mass of water riding in front of the wave crest. The air bubble formed between the jet and the fluid surface in downstream is compressed and rotated by the drop motion of the reservoir (Fig. 27b–d). Bubble breaks up (Fig. 27e) when the pressure forces due to the external mass exceed the restoring force of surface tension [35, 39]

Fig. 27
figure 27

Creation of an air bubble in viscous solutions at \(\mu =\textit{0.03 Pa.s}\)

Full size image

Figure 28 shows the air bubbles snapshots of three solution viscosities at the same time. It could be observed that the air bubble of fresh water is at the beginning of its creation while a second has been created on the left (Fig. 28a) by the micro-jet motion on the plateau. For viscous solution (Fig. 28b–c), the area of the air bubble is larger and no secondary bubble exists on the left

Fig. 28
figure 28

Air bubbles formed by plunging breakers in freshwater a, and in viscous solutions at \(\mu =\textit{0.007 Pa.s}\) b and \(\mu =\textit{0.03 Pa.s}\) c

Full size image

The dimensionless parameters called Weber (\(W_{e})\) and Bond (\(B_{o})\) numbers are used to characterize the fluid’s inertia compared to its surface tension for the first and the bubble shape for the second number, respectively.

$$\begin{aligned} \left\{ {\begin{array}{l} W_{e} =\frac{\rho .U_{front} .L_{c} }{\sigma } \\ B_{o} =\frac{\Delta \rho .g.L_{C}^{2} }{\sigma } \\ \end{array}} \right. \end{aligned}$$
(18)

where \(\rho , \Delta \rho \) are the liquid density and the difference in density of two phases (air, water), respectively, g the gravitational acceleration, \(L_{c}\) the characteristic length (Fig. 28b), \(U_{front} \)the velocity of the crest, and \(\sigma \)the surface tension.

Table 4 gives some experimental selected characteristics of air bubbles for three viscosities at the ambient fluid depth of 2.79 cm. The area of an elliptic air bubble was estimated from the measured length of the major axis \(L_{c} \)and the measured length of the minor axis \(H_{c}\) (Fig. 28b). The air bubble lasts from the moment of crest plunging (Fig. 27d) up to the air bubble breaking (Fig. 27e).

The area of the air bubbles and the velocity of the crest were found to increase with increasing viscosity, corresponding to the rise of kinetic energy. The shorter lifetime of the air bubble was observed in viscous fluids. Note that these evolutions are in agreement with the result given by Deike et al. [9], who fitted the energy decay by an exponential function of time. As the viscosity increases, the surface tension decreases, while the fluid’s inertia augments, which leads to a more significant Weber number. The intermediate bond number indicates that the air bubble shape ranges from the elliptic cap to the spherical cap.

Table 4 Comparison of characteristics of air bubbles at different viscosities and surface tensions at ambient fluid depth d of 2.79
Full size table

6 Conclusions

The present work has focused on experimental and numerical methods for studying viscous dam-break flows, conducted in a horizontal rectangular section channel, to fill the gaps of viscosity and surface tension effects in the literature. In the case of a dry channel, despite the satisfactory agreement between experimental/numerical and analytical free-surface profiles at a later stage of flow, the authors suspect that the gate’s vertical removal had a slight effect on the jet-like flow formation at an early stage. This initial disturbance plays a more limited role in the presence of ambient water downstream. When water is present downstream, the formation of a “mushroom-like” jet was observed experimentally and numerically. The water profiles and propagation fronts predicted by the numerical model are in line with experimental data and analytical estimations. The obtained results have shown that, under the conditions used in this work, the maximum velocity decreases when the water depth downstream increases. Concerning the increase of viscosity, experimental data, numerical predictions, and analytical estimations have shown slowing down of the front propagation. The air bubble characteristics, such as shape, area, and lifetime, were studied as a function of viscosity and surface tension.

Further refinement of the present research is in prospect; a rotary removal of the dam gate in a dry channel and its modeling by an immersed boundary will be investigated. Then, the high-speed particle image velocimetry (PIV) and the pressure measurement are being considered. Also, the numerical benchmark tests would be of value for validation of the \(k-\omega \) SST model extended to an erodible bed around a finite circular cylinder and its morpho-dynamic evolution. The study in perspective will focus on the simulation of scour using the coupled VOF-LPT (Lagrangian particle tracking) method [41].