Investigation of pressure and the Lewis number effects in the context of algebraic flame surface density closure for LES of premixed turbulent combustion

Abstract

Large scale industrial combustion devices, for example, internal combustion engines, gas turbine combustors, etc., operate under high-pressure conditions and utilize a variety of fuels. Unfortunately, the majority of the current numerical combustion modelling approaches are not fully validated for high-pressure and the non-unity Lewis number ($\hbox {Le} =$ thermal diffusivity/mass diffusivity) effects in premixed turbulent combustion. In any case, a numerical model needs to be checked for the effects of these parameters to guarantee generality of the model. In the present study, these two critical features of the models are numerically explored utilizing fundamental elements of several algebraic flame surface density reaction rate closure models accessible in the open literature. The Lewis number impact is likewise examined utilizing LES of recently published subgrid scale fractal flame surface density model, which indicated acceptable results for high and low-pressure methane fuelled applications. The computed numerical results are compared with an extensive experimental dataset for lean methane and propane fuels featuring various flow and turbulence conditions at operating pressures in the range of 1–10 bar. The quantitative results from most of the selected models do not show the experimentally observed trends at high-pressures and for non-unity Le number fuels. Modifications to the models are incorporated to reflect effects of these two important parameters utilizing a broad parametric investigation resulting in a satisfactory agreement with the experimental data.

1 Introduction

Large Eddy Simulation (LES) has shown potential to improve upon conventional Reynolds-averaged Navier Stokes (RANS) simulations for the predictions of turbulent reactive flows. However, the turbulent premixed combustion modelling faces the problem that the flame thickness is smaller than the typical LES filter sizes. Thus, a model is required to describe the extent of subgrid scale flame wrinkling. A few modelling approaches have been proposed by various scientists to overcome this issue, for example, the flame front tracking strategy (level-set of G-equation) [1, 2], the Artificially Thickened Flame (ATF) procedure [3, 4] and the idea of Flame Surface Density (FSD) [5, 6]. The well-established FSD based reaction rate closure approach exists with two principle variations. In one methodology, the closure is achieved through mathematical expressions [5], while the other one includes solving an additional FSD transport equation [6]. Various Algebraic Flame Surface Density (AFSD) models have been created and applied for premixed flame burners [7, 8]. They can be simpler, less expensive in terms of computational time and numerically more robust than models featuring a FSD transport equation, which however might be able to incorporate some non-equilibrium effects between production and destruction of FSD. The AFSD models are the focal point of the present work. Many practical industrial devices using premixed combustion operate under high-pressure conditions with a variety of fuels. So, a numerical model should account for the influence of pressure p and fuel effects on reaction closure to claim any generality. However, the greater part of the current AFSD models have been validated just for atmospheric methane flames and frequently using relatively fine LES computational grids, where the subgrid wrinkling factor $\varXi$ approaches one.

Pressure is known to influence both the turbulent flow field through variation of viscosity and laminar premixed flame structure by decreasing the flame thickness and flame speed. It has been observed experimentally by different researchers [9,10,11] that the flame wrinkling increases, the smaller turbulence scales (Taylor scales, Kolmogorov scales) shrink while the turbulent integral length scale remains nearly unchanged with increase of pressure if inlet velocity is left constant. The kinematic viscosity $\nu$ $=$ absolute viscosity/density $= \quad \mu /\rho$ is proportional to 1/p, so increased pressure results in higher turbulent Reynolds number ${\hbox {Re}}_\mathrm{t}=u^{'}l/\nu$, if the mean bulk velocity is kept constant, typically the turbulence intensity is also weakly influenced by pressure. Here l and $u^{'}$ refer to integral length scale and root mean square (RMS) turbulent velocity. The smallest turbulence scales shrink with increasing ${\hbox {Re}}_\mathrm{t}$, so estimated turbulence energy spectra are moved to higher wavenumbers [9]. The un-stretched laminar flame speed $s_\mathrm{L}^{0}$ and Zeldovich flame thickness $l_{F}$ also vary with pressure. The pressure scaling for methane and propane air mixtures are $s_\mathrm{L}^{0}\propto p^{-0.5}$, $l_{F}\propto p^{-0.5}$ and $s_\mathrm{L}^{0}\propto p^{-0.26}$, $l_{F}\propto p^{-0.74}$, respectively [1, 12, 13].

Experimental investigation of turbulent reacting flows under high-pressure conditions is very difficult and costly. With the recent advances in computational technology and availability of super powered computational clusters, Direct Numerical Simulation (DNS) is increasingly used to study turbulent reacting flows under high-pressure conditions [14,15,16,17,18]. These DNS based studies help the development and validation of numerical models applicable to conditions typical in the industry devices. The complexity of the high-pressure combustion puts tough requirements on the numerical models. Only a few numerical models in the open literature, mainly in the RANS context, are dealing specifically with the pressure dependence of turbulent premixed combustion [19]. Authors Dinkelacker, Muppala, Aluri et al. have contributed to turbulent premixed combustion modelling at high-pressures [20,21,22,23,24]. Muppala et al. [20] developed an algebraic turbulent premixed combustion model to correctly predict the turbulent flame speed $s_\mathrm{T}$ for different fuels under high-pressure conditions in the RANS context. The model showed satisfactory performance for methane, propane and ethylene fuels for pressures up to 10 bar. An explicit pressure correction term $\left( p/p_{0} \right) ^{n}$ , where $p_{0} =$ atmospheric pressure $=1$ bar, p is the operating pressure in bar and exponent n is a constant, was incorporated in the algebraic wrinkling factor expression to correctly predict the experimentally observed pressure dependency of turbulent flame speeds. Aluri et al. [21] investigated the performance of two algebraic flame surface density models including the FSD model of Muppala et al. [20] for high-pressure methane flames. They found a very good performance of the models (with explicit pressure correction term) for different turbulence conditions under high-pressures. Aluri et al. [22] also investigated the performance of Lindstedt and Váos model [25] with explicit pressure and Lewis number correction terms. They reported very good performance of the tuned model in terms of showing the effects of high-pressure and non-unity Le number fuels on the reaction source term. Keppeler et al. [26] presented a FSD premixed combustion model based on the fractal approach in the LES context. The model showed excellent performance for high-pressure flames at conditions typical for spark ignition engines, gas turbines, etc. Allauddin et al. [27] investigated the performance of a simplified version of the model presented by Keppeler et al. [26]. The simplifications to the original model were discussed and the performance of the new model was compared with the original model and experimental data. The original and simplified models were found suitable for predicting the performance of turbulent premixed flames under high-pressure conditions. Recently, Allauddin et al. [28] extended the Keppeler model [26] to the RANS context. The performance of the new RANS model was compared with the original LES model and experimental data. The RANS model showed similarly satisfactory performance in terms of predicting the turbulent flame speeds and flame structures of turbulent premixed flames at high-pressure conditions.

The influence of Le number on the turbulent reaction rate is explained elaborately in the work of Lipatnikov and Chomiak [29]. Le >1 represents a faster heat diffusion compared to diffusion of species, which may result in reduced turbulent flame propagation. So, the numerical models without explicit Le number dependency might predict higher values of turbulent flame speed especially at moderate to high turbulence. High Le number fuels have applications in spark ignition engines, gas turbines, etc., therefore, examination of the fuel effects on flame characteristics at high-pressures is crucial. Le number effects in highly turbulent premixed flames have been investigated in [30] and particularly for high-pressure conditions in [11]. In the RANS context, a 1/Le dependence of the algebraic FSD reaction rate closure was discovered effective for $\hbox {Le}\ge$ 1 fuels for pressures up to 10 bar [26]. The model was also extended to the LES context and checked for its relevance for a Bunsen-like burner, a sudden expansion dump combustor and a typical swirl-stabilised gas turbine combustor [8] indicating good agreement with the experiments. In [24], the RANS model is utilized to simulate lean premixed turbulent methane/hydrogen/air flames ($\hbox {Le} \le$ 1). The reaction rate closure approach with $1/\hbox {Le}$ prefactor was found to give a generally good agreement for all the flames with hydrogen content up to 20% and a reasonable agreement for 30% and 40% hydrogen. Chakraborty and Cant [31] also reported that the estimate $\overline{\left( \rho S_{d} \right) }_{S}\approx \rho _\mathrm{u}s_\mathrm{L}$ is not valid for non-unity Le number fuels and recommended

$$\begin{aligned} \overline{\left( \rho S_{d} \right) }_{S}\approx \rho _\mathrm{u}s_\mathrm{L}/\hbox {Le}, \end{aligned}$$

(1)

where $\rho$, $\rho _\mathrm{u}$, $S_{d}$ and $s_\mathrm{L}$ represent the density, density of unburnt reactants, flame displacement speed and stretched laminar flame speed, respectively, while the subscript S outside the parenthesis on left hand side of Eq. (1) refers to the surface filtering. In a recent study [32], based on a-priori analysis of DNS data for a range of different Le numbers, the performance of several subgrid scalar flux (SGSF) models and algebraic FSD models in the context of turbulent premixed combustion is investigated on an individual basis and in terms of their combined interactions. It is reported that the Le number correction given by Eq. (1) essentially improves the prediction of the surface-weighted filtered values of density-weighted displacement speed. The Le number expression (1/Le) is utilized in the present investigation to incorporate the fuel effects.

The focal point of the present study is to investigate some of the well-known AFSD models under high-pressure and non-unity Le number conditions. The chosen models are proposed by Angelberger et al. [33], Fureby [34] and Zimont [35]. The central elements of these models as utilized in the LES simulations are presented in Table 1. The resulting models are named Model-A, Model-F and Model-Z in the rest of the paper. An already developed LES subgrid combustion model [26], which indicated a good performance for turbulent Bunsen flames over a wide range of turbulence and pressures in the range of 1–20 bar, is additionally investigated for non-unity Le number fuel. This model is referred to Model-K in the rest of the paper.

Table 1 The main expressions of the AFSD models used in the current study

In the current work, the Model-K is adapted only for Le variation as its performance for high-pressure conditions is already investigated in the previous study [26]. The model-F is found to be extensively used by different researchers in the open literature. Therefore, the performance of this model is investigated for both high-pressure conditions and non-unity Le number fuel (Sect. 6.3). The expression 1/Le used in the Model-K is also used in the Model-F to bring the Le number dependency in the model. The results show that the adapted Model-K and Model-F give a quite good performance for non-unity Le number fuels and a reasonable agreement with the experiments. For the sake of brevity, the Model-A and Model-Z are only adapted for pressure variation. The authors expect that 1/Le prefactor would have a similar effect in these models to correctly repesent the Le number dependency of turbulent flame speed. The numerical predictions from the current study are compared with the experimental data of Kobayashi et al. [9, 12, 36].

The paper is organized as follows. First, a short description of the chosen AFSD models is presented. Second, the sections describing the experimental data utilized for the validation of the computed results and numerical setup are presented. Results are discussed in Sect. 6. The conclusions of the work are presented in the last section.

2 Mathematical background and description of numerical models

The reaction progress variable c for turbulent premixed combustion at constant pressure can be expressed in terms of temperature T as $c=\left( T-T_\mathrm{u} \right) /\left( T_\mathrm{b}-T_\mathrm{u} \right)$ which changes monotonically from 0 in reactants to 1 in totally burned products. Here subscripts u and b indicate unburnt and burnt states, respectively. Following [13] and assuming unity Le number, adiabaticity and low Mach number, the Favre-filtered transport equation for c becomes

$$\begin{aligned} \frac{\partial {\bar{\rho }}{\tilde{c}}}{\partial t}\mathrm {+}\frac{\partial \bar{\rho }{\tilde{c}}\tilde{u_\mathrm{i}}}{\partial x_\mathrm{i}}\mathrm {+}\frac{\partial }{\partial x_\mathrm{i}}\left( {\bar{\rho }}\tilde{u_\mathrm{i}c}\mathrm {-}\bar{\rho }\tilde{u_\mathrm{i}}{\tilde{c}} \right) \mathrm {=}\frac{\partial }{\partial x_{\mathrm {i}}}\left( \overline{\rho \alpha \frac{\partial c}{\partial x_\mathrm{i}}} \right) \mathrm {+}{\bar{\dot{{\omega }}}}, \end{aligned}$$

(2)

where $u_\mathrm{i}$, $\alpha$, ${\dot{\omega }}$ represent the $i^{th}$ component of flow velocity vector, progress variable diffusivity, progress variable chemical reaction rate, respectively. The overbar indicates a LES filtering operation and tilde represents Favre filtering. Utilizing the FSD method, the sum of the molecular diffusion of the reaction progress variable and the LES filtered reaction rate can be written as

$$\begin{aligned} \frac{\partial }{\partial x_{\mathrm{i}}}\left( \overline{\rho \alpha \frac{\partial c}{\partial x_{\mathrm{i}}}} \right) +\bar{{\dot{\omega }}}= \overline{\rho S_{d}\vert \nabla c\vert }\approx \rho _\mathrm{u}s_\mathrm{L}\varSigma _\mathrm{gen}, \end{aligned}$$

(3)

where $\varSigma _\mathrm{gen}=\bar{\vert \nabla c\vert }$ is the total subgrid FSD and the surface-filtered value of the density weighted displacement speed $\overline{\left( \rho S_{d} \right) }_{S}$ is approximated as${\rho }_\mathrm{u}s_\mathrm{L}$. The FSD can be expressed in terms of the subgrid scale wrinkling factor $\varXi =\bar{\vert \nabla c\vert }/\left| \nabla {\bar{c}} \right|$ yielding

$$\begin{aligned} \frac{\partial }{\partial x_{\mathrm{i}}}\left( \overline{\rho \alpha \frac{\partial c}{\partial x_{\mathrm{i}}}} \right) +\bar{\dot{\omega }}=\rho _\mathrm{u}s_\mathrm{L}\varSigma _\mathrm{gen}=\rho _\mathrm{u}s_\mathrm{L}\varXi \left| \nabla {\bar{c}} \right| . \end{aligned}$$

(4)

The fractal characteristic of premixed flames is notable and has been well demonstrated experimentally. The wrinkling factor $\varXi$ can be expressed in the form proposed by Gouldin [37]

$$\begin{aligned} {\Xi =}\left( \frac{\varepsilon _\mathrm{o}}{\varepsilon _\mathrm{i}} \right) ^{D\mathrm {-2}}\mathrm {,} \end{aligned}$$

(5)

where $\varepsilon _\mathrm{i}$, $\varepsilon _\mathrm{o}$ and D indicate inner and outer cut-off scales and a fractal dimension, respectively. Fractal based models obviously need accurate models for the fractal dimension and cut-off scales.

The other term, which should be modelled in Eq. (2), is the subgrid scalar transport $\left( {\bar{\rho }}\tilde{u_{\mathrm{i}}c}-\overline{\rho }\tilde{u_{\mathrm{i}}}{\tilde{c}} \right)$ In the current work, it is modelled utilizing the gradient hypothesis

$$\begin{aligned} {\bar{\rho }}\tilde{u_{\mathrm{i}}c}\mathrm {-}\bar{\rho }\widetilde{u_{\mathrm{i}}}{\tilde{c}}\mathrm {=-}\frac{\mu _\mathrm{sgs}}{{Sc}_\mathrm{t}}\mathrm {}\frac{{\partial }{\tilde{c}}}{{\partial }x_\mathrm{i}}, \end{aligned}$$

(6)

where ${Sc}_\mathrm{t}$ and $\mu _\mathrm{sgs}$ indicate the turbulent Schmidt number and subgrid scale dynamic viscosity. When utilizing the gradient hypothesis based model, counter gradient subgrid scalar fluxes are ignored. According to Boger et al. [5] in LES the unresolved contribution of the turbulent fluxes is considered to be small; the major contributions of the gradient and counter gradient scalar fluxes are expected to be captured at the resolved scales. Also, the use of $\left| \nabla {\tilde{c}} \right|$ rather than $\left| \nabla {\bar{c}} \right|$ in the LES expression of $\varSigma _\mathrm{gen}$ (as used in the present investigation) comprises a certain implicit counter gradient subgrid scalar flux model as reported in the work of Klein et al. [32] and Allauddin et al. [38]. In the LES, we solve the following transport equation for the Favre filtered reaction progress variable ${\tilde{c}}$

$$\begin{aligned} \frac{\partial {\bar{\rho }}{\tilde{c}}}{\partial t}+\frac{\partial {\bar{\rho }}{\tilde{c}}\tilde{u_{\mathrm{i}}}}{\partial x_\mathrm{i}}=\rho _\mathrm{u}s_\mathrm{L}\varXi \left| \nabla {\tilde{c}} \right| +\frac{\partial }{\partial x_\mathrm{i}}\left( \frac{\mu _\mathrm{sgs}}{{Sc}_\mathrm{t}}\frac{\partial {\tilde{c}}}{\partial x_\mathrm{i}} \right) . \end{aligned}$$

(7a)

Comparison to Eq. (4) shows explicitly the implicit counter-gradient model (last term on RHS)

$$\begin{aligned} \frac{\partial {\bar{\rho }}{\tilde{c}}}{\partial t}+\frac{\partial {\bar{\rho }}{\tilde{c}}\tilde{u_{\mathrm{i}}}}{\partial x_\mathrm{i}}=\rho _\mathrm{u}s_\mathrm{L}\varXi \left| \nabla {\bar{c}} \right| +\frac{\partial }{\partial x_\mathrm{i}}\left( \frac{\mu _\mathrm{sgs}}{{Sc}_\mathrm{t}}\frac{\partial {\tilde{c}}}{\partial x_\mathrm{i}} \right) -\rho _\mathrm{u}s_\mathrm{L}\varXi \left( \left| \nabla {\bar{c}} \right| -\left| \nabla {\tilde{c}} \right| \right) . \end{aligned}$$

(7b)

Recent studies [32, 38] show that LES results obtained with the FSD model using $\left| \nabla {\tilde{c}} \right|$ in the reaction rate modelling will not improve when more advanced subgrid scalar flux closures explicitly representing the effect of counter-gradient diffusion are used.

The subgrid scale velocity fluctuations ${u}_{\Delta }^{'}$ are determined as ${u}_{\Delta }^{'}=\sqrt{2k_\mathrm{sgs}/3}$. The subgrid turbulent kinetic energy $k_\mathrm{sgs}$ and subgrid scale viscosity are determined by utilizing the one equation eddy viscosity model proposed by Schumann [39] and further improved by Fureby et al. [40] with a transport equation for $k_\mathrm{sgs}$

$$\begin{aligned}&\frac{{\partial }{\bar{\rho }}k_\mathrm{sgs}}{{\partial }t}\mathrm {+}\frac{{\partial }\left( \bar{\rho }\tilde{u_\mathrm{i}}k_\mathrm{sgs} \right) }{{\partial }x_\mathrm{i}}\mathrm {-}\frac{\partial }{{\partial }x_\mathrm{i}}\left( \mu _{eff}\frac{{\partial }k_\mathrm{sgs}}{{\partial }x_\mathrm{i}} \right) \mathrm {=-}{\bar{\rho }}S_{ij}B_{ij}\mathrm {-}C_{e}\bar{\rho }\frac{k_\mathrm{sgs}^{\frac{\mathrm {3}}{\mathrm {2}}}}{{\Delta }}, \end{aligned}$$

(8)

$$\begin{aligned}&B_{ij}\mathrm {=}\frac{\mathrm {2}}{\mathrm {3}}k_\mathrm{sgs}\delta _{i\mathrm {j}}\mathrm {-2}\nu _{{\Delta }}\left\{ S_{ij}\mathrm {-}\frac{\mathrm {1}}{\mathrm {3}}\mathrm {tr}\left( S_{ij\mathrm {}} \right) \delta _{i\mathrm {j}}\right\} , \mu _\mathrm{sgs}\mathrm {=}C_\mathrm{K}{\bar{\rho }}\sqrt{k}_\mathrm{sgs} {\Delta ,}\nu _{{\Delta }}\mathrm {=}C_\mathrm{K}\sqrt{k}_\mathrm{sgs} \Delta , \end{aligned}$$

(9)

where $S_{ij}=\mathrm {0.5}\left( {\partial {\tilde{u}}_\mathrm{i}} \big / {\partial x_{j}}+{\partial {\tilde{u}}_{j}} \big / {\partial x_\mathrm{i}} \right)$ is the resolved strain rate, $\mu _{eff}=\mu +\mu _\mathrm{sgs}$ is the effective viscosity with $\nu _{\Delta }$ being eddy kinematic subgrid viscosity and ${\Delta }$ is the filter size. In the present study, the model coefficients $C_{e}$ and $C_\mathrm{K}$ are taken as 1.05 and 0.095, respectively. Model-A and Model-F additionally require the estimation of an efficiency function, which represents the net straining effect of all the vortices smaller than the LES filter width $\Delta$. The efficiency function $\varGamma$ utilized in Model-A and Model-F is modelled as

$$\begin{aligned} \varGamma = A {*} exp\left[ \frac{\mathrm {-}B}{\left( u_{{\Delta }}^{\mathrm {'}}\mathrm {/}s_\mathrm{L} \right) ^{\mathrm {0.3}}} \right] {*}\left( \frac{{\Delta }}{l_{F}} \right) ^{\mathrm {2/3}}, \end{aligned}$$

(10)

where $A =$ 0.75 and $B =$ 1.2.

Table 2 The un-stretched laminar flame speed, Zeldovich flame thickness and Markstein number values used in the current study

The stretched laminar flame speed $s_\mathrm{L}$ is modelled using the linear theory of instabilities [41]

$$\begin{aligned} s_\mathrm{L} = s_\mathrm{L}^{\mathrm {0}}\mathrm {-}\hbox {Ma}\ \mathrm {}\kappa l_{F}, \end{aligned}$$

(11)

where $s_\mathrm{L}^{\mathrm {0}}$ and $\hbox {Ma}$ represent the un-stretched laminar flame speed and Markstein number, respectively. The experimental values of these parameters [12, 42] are used in the current study and are summarized in Table 2. The effective stretch $\kappa$ is determined considering just strain effects, modelled by Hawkes and Cant [43]

$$\begin{aligned} \kappa {\approx }\kappa _\mathrm{s}\mathrm {=}\left( \delta _{i\mathrm {j}}\mathrm {-}n_{i\mathrm {j}} \right) \frac{{\partial }\tilde{u_{\mathrm{i}}}}{{\partial }x_{\mathrm {i}}}\mathrm {+}\varGamma _\mathrm{s}\frac{\sqrt{k}_\mathrm{sgs} }{{\Delta }}, \end{aligned}$$

(12a)

utilizing a second efficiency function $\varGamma _\mathrm{s}$ as proposed by [44]. Here $\delta _{ij}$ is the Kronecker delta, $n_{\mathrm{ij}}=\bar{\left( N_{\mathrm{i}} \right) }_\mathrm{s}\bar{\left( N_{\mathrm{i}} \right) }_\mathrm{s}+\left( \delta _{ij} \big / 3 \right) [1-\bar{\left( N_\mathrm{K} \right) }_\mathrm{s}\bar{\left( N_\mathrm{K} \right) }_\mathrm{s}]$ is the flame orientation factor with $\bar{\left( N_{\mathrm{i}} \right) }_\mathrm{s}=-(\partial {\bar{c}}/\partial x_\mathrm{i})/\varSigma _\mathrm{gen}$ being the $i^{\mathrm {th}}$ component of flame surface-weighted normal vector. The first and second terms in the RHS of Eq. (12a) represent strain rates resulting from resolved and unresolved scales, respectively. The second efficiency function $\varGamma _\mathrm{s}$ is determined as

$$\begin{aligned}&\log _{10}{(\mathrm {}\varGamma _\mathrm{s})}=\frac{-1}{s+\mathrm {0.4}}\exp \left\{ -\left( \mathrm {s+0.4} \right) \right\} +\left[ 1-\exp \left\{ -\left( s+\mathrm {0.4} \right) \right\} \right] \left\{ \sigma \left( \frac{u_{\Delta }^{'}}{s_\mathrm{L}^{0}} \right) s-\mathrm {0.11} \right\} , \end{aligned}$$

(12b)

$$\begin{aligned}&s\mathrm {=}\log _{10}\left( \frac{{\Delta }}{l_{F}} \right) \mathrm {,}\sigma \left( \frac{u_{{\Delta }}^{\mathrm {'}}}{s_\mathrm{L}^{\mathrm {0}}} \right) \mathrm {=}\frac{\mathrm {2}}{\mathrm {3}}\left[ \mathrm {1-0.5}exp\left\{ {\mathrm {-}\left( \frac{u_{{\Delta }}^{\mathrm {'}}}{s_\mathrm{L}^{\mathrm {0}}} \right) }^{\mathrm {1/3}} \right\} \right] \mathrm {,}u_{{\Delta }}^{\mathrm {'}}\mathrm {=}\left( \frac{\mathrm {2}}{\mathrm {3}}k_\mathrm{sgs} \right) ^{\mathrm {0.5}}. \end{aligned}$$

(12c)

In the following subsections a short description of the FSD models used in the present study will be presented for completeness.

2.1 Brief description of Model-A and Model-F

Angelberger et al. [33] based their model on DNS data of flame stretch and vortex pair interaction [41] and expressed $\varXi$ as

$$\begin{aligned} \varXi \mathrm {=}\left[ \mathrm {1+}C_\mathrm{A}\mathrm {}\varGamma \mathrm {}\frac{u_{{\Delta }}^{\mathrm {'}}}{s_\mathrm{L}} \right] , \end{aligned}$$

(13)

where $C_\mathrm{A}=1$ is a model constant.

Fureby [34] built his model on a fractal approach of $\varXi ,$ which is given by Eq. (5). In this model the inner and outer cut-off scales, fractal dimension and wrinkling factor are given by

$$\begin{aligned}&\displaystyle \varepsilon _\mathrm{i}\mathrm {=}\frac{s_\mathrm{L}{\Delta }}{u_{{\Delta }}^{\mathrm {'}}\mathrm {}\varGamma }, \end{aligned}$$

(14a)

$$\begin{aligned}&\displaystyle \varepsilon _\mathrm{o}=\Delta , \end{aligned}$$

(14b)

$$\begin{aligned}&\displaystyle D\mathrm {=}\frac{\mathrm {2.05}s_\mathrm{L}}{u_{{\Delta }}^{\mathrm {'}}\mathrm {+}s_\mathrm{L}}\mathrm {+}\frac{\mathrm {2.35}u_{{\Delta }}^{\mathrm {'}}}{u_{{\Delta }}^{\mathrm {'}}\mathrm {+}s_\mathrm{L}}, \end{aligned}$$

(14c)

$$\begin{aligned}&\displaystyle \varXi \mathrm {=}\left( \frac{\varepsilon _\mathrm{o}}{\varepsilon _\mathrm{i}} \right) ^{D\mathrm {-2}}. \end{aligned}$$

(14d)

2.2 Brief description of Model-K

Keppeler et al. [26] also used the fractal approach, using ideas from the RANS model of Lindstedt and Váos [25] in his extension to LES. In this model the inner and outer cut-off scales, fractal dimension, generalised FSD and wrinkling factor terms are defined as

$$\begin{aligned}&\displaystyle \varepsilon _\mathrm{i}\mathrm {=max}\left( l_{F}{\hbox {Ka}}_{{\Delta }}^{\mathrm {-1/2}}\mathrm {,}{\mathrm {2}l}_{F} \right) , \end{aligned}$$

(15a)

$$\begin{aligned}&\displaystyle \varepsilon _\mathrm{o}= 2.2 \Delta , \end{aligned}$$

(15b)

$$\begin{aligned}&\displaystyle D=\frac{8/3{\hbox {Ka}}_{\Delta }+2C_\mathrm{D}}{{\hbox {Ka}}_{\Delta }+C_\mathrm{D}},{\hbox {Ka}}_{\Delta }=\left( \frac{u_{\Delta }^{'}}{s_\mathrm{L}^{0}} \right) ^{\frac{3}{2}}\left( \frac{\Delta }{l_{F}} \right) ^{-\frac{1}{2}}, \end{aligned}$$

(15c)

$$\begin{aligned}&\displaystyle \varSigma _\mathrm{gen}=C_\mathrm{K}\left( \frac{\varepsilon _\mathrm{o}}{\varepsilon _\mathrm{i}} \right) ^{D-2}{\tilde{c}}\left( 1-{\tilde{c}} \right) \left| \nabla {\tilde{c}} \right| F\left( {\tilde{c}} \right) ^{-1}, \end{aligned}$$

(15d)

$$\begin{aligned}&\displaystyle \varXi =\left( \frac{\varepsilon _\mathrm{o}}{\varepsilon _\mathrm{i}} \right) ^{D-2}, \end{aligned}$$

(15e)

where $C_\mathrm{K}=4.5$ and $C_\mathrm{D}=0.03$ are model constants while ${\hbox {Ka}}_{\Delta }$ represents the subgrid Karlovitz number. In the CFD implementation, $F\left( {\tilde{c}} \right)$ is approximated by a simple polynomial fit: $F\left( {\tilde{c}} \right) =a_{1}-a_{2}\left( {\tilde{c}}-0.5 \right) ^{2}-a_{3}\left( {\tilde{c}}-0.5 \right) ^{4}$ with $a_{1}=1.00$, $a_{2}=2.82$ and $a_{3}=4.31$. The Model-K [26] demonstrates a very good agreement with the experimental data for turbulent methane Bunsen flames over a wide range of turbulence and pressures in the range of 1 and 20 bar, the conditions typical for industrial gas turbines, spark ignition engines, etc. A Kolmogorov-Petrovski-Piskunov (KPP) analysis demonstrated analytically that at high turbulence, D needs to go to 8/3 in this model to yield the experimentally observed pressure behaviour of the turbulent flame speed $s_\mathrm{T}$ for methane flames [45]. In addition, the time-averaged value of $s_\mathrm{T}$ predicted by the model are very robust to changes in LES grid resolution [26]. The model was derived with unity Le number assumption. In the present examination, Model-K will be also used for propane fuel which has Le >1.

2.3 Brief description of Model-Z

Zimont and Lipatnikov [35] utilized the expression for $\varSigma _\mathrm{gen}$ as function of $u_{\varDelta }^{'}$ and the Damköhler number Da

$$\begin{aligned} \varXi =\left[ 1+C_\mathrm{Z}\left( \frac{u_{\varDelta }^{'}}{s_\mathrm{L}} \right) ^{3/4}\left( \frac{\Delta }{l_{F}} \right) ^{1/4} \right] , \end{aligned}$$

(16)

where $C_\mathrm{Z}=0.51$ is a model constant. The model was at first developed for RANS simulations and for high turbulence cases. For more details regarding the models and their derivations, the reader is referred to the original papers where these models have been presented. The models utilized in the present investigations are summarized in Table 1.

3 Experimental data considered for validation

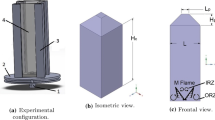
The numerical results of the current study are validated with an extensive experimental dataset presented by Kobayashi et al. [9, 12, 36]. In the experimental work, the influence of pressure on cone shaped turbulent premixed Bunsen flames issuing from a 20 mm diameter tube was examined in a high-pressure chamber (width 498 mm and length 600 mm). Four different types of perforated plates, installed 40 mm upstream of the chamber, were utilized as turbulence generators to create different turbulence levels and length scales. The temperature hot-wire anemometry technique was utilized to measure velocity and turbulence intensity at the centre of the burner exit. Data from lean methane/air mixtures at 1, 5, 10, 20 and 30 bar and propane/air mixtures at 1 and 5 bar at an equivalence ratio $\Phi =$ 0.9 and ethylene/air mixtures at $\Phi =$0.5, 0.7 and 0.9 for 1, 5 and 10 bar were investigated. The nozzle exit velocity U varied between 0.86 and 8.86 m/s, the maximum Reynolds number Re (based on burner exit diameter), the turbulence rms velocity $u^{'}$and the transverse integral length scalel took values up to 115,000, 2.06 m/s and 1.9 mm, respectively. Flames were visualised utilizing instantaneous Schlieren photos and rapid laser tomography. A typical Schlieren picture of an instantaneous turbulent flame is shown in Fig. 1a. The averaged flame front in the experiments, defined as ${\bar{c}}=0.5$ iso-contour, was obtained utilizing 50 instantaneous pictures of each flame and assuming rotational symmetry. The turbulent flame speed was then evaluated from

$$\begin{aligned} s_\mathrm{T}=Usin(\varphi /2), \end{aligned}$$

(17)

where $\varphi$ is the flame angle. It is reported that the averaged flame front exhibits a constant slope apart from the regions close to the flame tip and base. The experimental method used to calculate the turbulent flame speed is illustrated in Fig. 1b. The same method is used in the current study to evaluate the turbulent flame speed from the averaged LES ${\bar{c}}$-field. Figure 2 shows the experimentally observed flames in the Borghi-Peters diagram. It can be seen that the majority of the cases fall within the corrugated and wrinkled flamelet regime while few high-pressure cases fall within the thin reaction zone regime. The inlet and operating conditions of the validation cases are summarised in Table 3.

Fig. 1

a Instantaneous Schlieren image of a typical lean premixed turbulent flame from Kobayashi et al. [36] b method used in the experiment to determine turbulent flame speed

Fig. 2

Borghi-Peters diagram of the experimental data for methane and propane flames

Table 3 Characteristics of the experimental cases used for the validation of the numerical predictions made in the current study

4 Numerical setup

The combustion models used in the present study are implemented in OpenFOAM. The cylindrical computational domain of diameter of 80 mm and length 120 mm is discretised using a structured mesh, refined in the flame region, hence avoiding any issue related to anisotropic, inhomogeneous grids and to limit numerical diffusion. Typical filter sizes $\Delta$ in the flame region are 0.4 mm and 0.2 mm for coarse and fine meshes, respectively. The mesh resolution is decreased (increases the cell size) in the region away from the flame region with a ratio of 1.8. The computational domain is chosen large enough so that the results are not influenced by boundaries. The convective Courant–Friedrichs–Lewy (CFL) number is set to 0.3. A first order backward Euler scheme is utilized for time discretisation. The time-steps were used in the range of 1e−6 to 4e−6 for time integration. The convective term of the momentum equation is discretized utilizing an unlimited second order linear scheme while a Total Variable Diminishing (TVD) scheme with a flux limiter (limitedLinear) is utilized to discretize the convective term in the scalar transport equation. A second order linear scheme is utilized to discretize the diffusive terms. Dirichlet boundary conditions are utilized at the inlet for all parameters, with the exception of the pressure where Neumann boundary condition (zero gradient) is used. The experimentally measured turbulence intensity and integral length scale are specified at the inlet using the turbulence generator proposed by Kempf et al. [46] and implemented by Tangermann et al. [47] in OpenFOAM. In the current study, the combination of the “Total Pressure” boundary condition for pressure and “Pressure Inlet Outlet Velocity” for velocity is used at the exit to allow the backflow at the ambient conditions. This combination of boundary conditions is commonly used where inflow may take place into the domain, but the inflow velocity is not known [48]. For other variables, a mixed boundary condition is used at the exit. It switches between Neumann boundary condition (zero gradient) for flow out of the domain and Dirichlet boundary condition (fixed value) for flow into the domain [48]. For the inflow $T=$ 300 K, $k_\mathrm{sgs}=$ 1e−5 m$^{\mathrm {2}}$/s$^{\mathrm {2}}$ and $b=1-c=$ 0 are used at the exit.

Following the experimental method used to calculate the turbulent flame speed, the filtered reaction progress variable ${\bar{c}}$ contours are used to estimate the turbulent flame speeds from the numerical results. The ${\bar{c}}$ contours are determined from time and circumferentially-averaged ${\tilde{c}}$ contours, using the Bray Moss Libby relation [49]

$$\begin{aligned} {\bar{c}}=\frac{\left( 1+\tau \right) {\tilde{c}}}{1+\tau {\tilde{c}}}, \end{aligned}$$

(18)

where $\tau =\rho _\mathrm{u}/\rho _\mathrm{b}-\mathrm {1}$ represents a temperature rise parameter. A least squares fit method is used to get the slope of the isoline ${\bar{c}}=\mathrm {0.5}$ (which is the correct quantity to be compared to the experimental data), neglecting the curved portion of the flame front at the flame tip and base, assessing just the linear segment of the flame. It is found that ignoring around 10% of the flame front at the flame tip and base gives a linear portion of the flame for the cases investigated in the present work. With this slope, the calculation of flame angle $\varphi$ is made. The flow velocity U is known, so the flame speed can be evaluated using Eq. (17).

5 LES quality assessment

A detailed assessment of the quality of the present LES grids was done on three methodically refined grids in previous work [26]. The key features and findings of the study are described here for completeness. Table 4 demonstrates the key attributes of the grids, where $\Delta$ represents the averaged filter size in flame area. The proportion of the resolved turbulent kinetic energy $k_\mathrm{res}$ to the total turbulent kinetic energy $k_{tot}=k_\mathrm{sgs}{+k}_\mathrm{res}$ was found in the range of 85–90% and 90–95% with mesh resolutions A and C, respectively. In spite of the fact that the LES on the fine mesh resolves the turbulent kinetic energy sensibly well, a large fraction of the flame wrinkling is unresolved at high-pressures causing the subgrid combustion model to be very important at high-pressures [26]. For 10 bar case, the resolved flame wrinkling is about 20% and 12% on the fine and coarse mesh, respectively. For 5 bar case, it is about 37% and 20% on the fine and coarse mesh, respectively. On the contrary for 1 bar case, about 83% and 63% of the flame wrinkling is resolved on the fine and coarse mesh, respectively [26]. In addition, the time-averaged turbulent flame speeds predicted by the subgrid combustion model were also compared with the experimental data using three different mesh sizes in [26]. It is found that the results regarding the time-averaged ${\bar{c}}$ field and the derived turbulent flame speed are quite robust with respect to changes in mesh resolution. In the present work, grids with resolution A ($\Delta =$ 0.4 mm) and C ($\Delta =$ 0.2 mm) are utilized.

6 Results and discussion

In this section, the performance of the original and adapted versions of Model-K for non-unity Le number fuel and the performance of the original and adapted versions of Model-F under high-pressure conditions and non-unity Le number fuel will be discussed. Finally, the performance of the original and adapted versions of Model-A and Model-Z under high-pressure conditions will also be analysed.

Table 4 Summary of the grid characteristics used in the current study

6.1 Model-K with the Lewis number correction

Keppeler et al. [26] developed Model-K with unity Le number assumption. The model showed a very good agreement with the methane Kobayashi experimental data over a wide range of turbulence and pressure conditions in the range of 1–20 bar [26]. Thus, in the current work Model-K is adapted only for Le number variation. The performance of the adapted Model-K with explicit incorporation of a term representing fuel effects is investigated in this section. Despite the very good agreement of Model-K results with the experimental data for methane flames ($\hbox {Le} =1$) under atmospheric and elevated pressure conditions, when using propane fuel ($\hbox {Le} =1.62$) it was observed that the turbulent flame speed values overestimate the experimental findings, particularly at high turbulence intensity [26]. Following the discussion in Sect. 1, the modification given by Eq. (1) was incorporated in the FSD expression of the Model-K. Apart from that all the other expressions and constants are kept same in the adapted model. The performance of the tuned and original versions of the model is investigated and compared to the experimental data of turbulent flame speeds for propane fuel at 1 and 5 bar. The normalised flame speeds $s_\mathrm{T}/s_\mathrm{L}^{0}$ are plotted versus $u^{'}/s_\mathrm{L}^{0}$ in Fig. 3a, b at 1 and 5 bar, respectively. The Model-K without Le number correction shows deviations with increasing turbulence level and the turbulent flame speed is increasingly over-predicted. However, the model scales well with the pressure. With the adapted Model-K, the predicted propane turbulent flame speed values match the experimental data very well at 1 and 5 bar, (Fig. 3). Thus Eq. (18) is proven to be a suitable way of incorporating explicit fuel effects in the Model-K. The explicit Le number term is likewise incorporated into the Model-F and the results are presented and discussed in the next section.

Fig. 3

Comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values evaluated with the original and adapted Model-K on mesh A with experimental data for propane fuel at a 1 bar and b 5 bar

6.2 Investigation of the Model-F with the pressure and Lewis number corrections

Model-F is extensively used by different researchers in the open literature. Therefore, the performance of this model is investigated for both high-pressure conditions and non-unity Le numbers. In this section, the Model-F is examined by performing LES simulations with the original and adapted parameters. Earlier investigations [50,51,52,53,54] showed the Fureby model to be a promising representative of algebraic FSD closure technique. But it is worth noting that the most of these investigations focused a high Karlovitz number $\hbox {Ka}$ cases and atmospheric methane flames. Thus, the functionality of the model at high-pressures and low $\hbox {Ka}$ numbers needs to be checked. In the work by Chakraborty and Klein [50], a new power law based FSD model was proposed. The performance of the new model was compared with DNS data and thirteen other existing algebraic FSD models including the Fureby model [34]. At high $\hbox {Ka}$ number cases, Model-F gives satisfactory agreement while for low $\hbox {Ka}$ number cases the model under-predicts the FSD values as compared to the DNS results [50, pp. 8-11]. The authors discussed that the difference may be caused by inaccurate estimation of inner cut-off scale $\varepsilon _\mathrm{i}$, the fractal dimension D and the efficiency function $\varGamma$ values at these conditions. In the paper presenting the Fureby model [34], it was reported that Eq. (14c) was the only available empirical expression for D at that time. Moreover, a parameterization constant A is used to calculate $\varepsilon _\mathrm{i}$. It is reported that the adopted parameterization is probably not optimal and is likely to be improved and optimized when the performance of the model is evaluated with suitable DNS and experimental data. Another problem in the Model-F is that at zero/weak subgrid turbulence level, the model wrinkling factor $\varXi {=\left( \varepsilon _\mathrm{o}\mathrm {/}\varepsilon _\mathrm{i} \right) }^{D\mathrm {-2}}$ approaches zero. For high turbulence cases $\varXi \gg$ 1 anyway, but in the case of completely resolved flame wrinkling the wrinkling factor needs to go to one. Consequently, the original Fureby model can clearly be accurate only for cases with strong subgrid flame wrinkling. Ma et al. [51] analysed different algebraic FSD models, including Model-F, by performing LES of the ORACLES burner and Volvo Rig. In [51], Eq. (14d) of the Fureby model was used in the form $\varXi =\left( 1+\varepsilon _\mathrm{o}/\varepsilon _\mathrm{i} \right) ^{D-2}$ so that the wrinkling factor goes to 1 in case of completely resolved flame wrinkling. It is reported that the Fureby model gives wrinkling factor values close to one in this study. The studies of [52,53,54] showed similar findings. The present LES study (Fig. 4) likewise demonstrates that at ambient pressure, the Model-F predicts $\varXi$ near one for low $\hbox {Ka}$ number cases. In the present work, the stretched laminar flame speed $s_\mathrm{L}$ is utilized in the numerical simulations performed with the Model-F as in the original model proposed by Fureby [34]. Most other researchers have utilized the un-stretched laminar flame speed ${s}_\mathrm{L}^{0}$, rather than stretched laminar flame speed ${s}_\mathrm{L}$. The impact of strain effects on the performance of the original Model-F is investigated by performing LES simulations for the 10 bar cases with and without strain effects on mesh A. The normalised turbulent flame speed results are shown in Table 5. It can be seen that the turbulent flame speed is changed slightly by utilization of un-stretched laminar flame speed ${s}_\mathrm{L}^{0}$, but the calculated $s_\mathrm{T}$ values are still under-predicted as compared to the experiment data. Thus, the Model-F does not under-predict $s_\mathrm{T}$ due to incorporation of strain effects on $s_\mathrm{L}$.

Fig. 4

Comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values evaluated with the original and adapted Model-F on mesh A with experimental data and original Model-K for methane fuel at a 1 bar, b 5 bar and c 10 bar

The pressure dependence of the $s_\mathrm{T}$ expression of the Model-F is compared to the experimental ones for methane and propane flames using a straightforward theoretical investigation used by Muppala et al. [20] to develop a correct pressure dependence of the reaction rate closure in their combustion model. The pressure dependence of the wrinkling factor expression (Eq. (14d)) with the original and adapted parameters is determined by utilizing the pressure scaling of $s_\mathrm{L}^{0}\mathrm {,}l_{F}$ and $\alpha$ for methane and propane fuels. The pressure dependence of the turbulent flame speed $s_\mathrm{T}$ is determined by $\varXi *s_\mathrm{L}^{0}$. The key discoveries are summarised in Table 6. It can be seen that the model does not reproduce the experimentally observed dependence of $s_\mathrm{T}{\propto }p^{\mathrm {0.07}}$ for methane and ${\mathrm {}s}_\mathrm{T}{\propto }p^{\mathrm {0.24}}$ for propane [12]. This is in agreement with the numerical results shown in Fig. 4, where a large gap is observed between the numerically predicted and experimental values obtained with original Model-F and the difference becomes larger with pressure rise. Thus, both numerical and analytical investigations argue for an adaption in the pressure dependency of $s_\mathrm{T}$ expression of Model-F. This is achieved by using a modified estimation of D and $\varepsilon _\mathrm{i}$. In Model-F, D (Eq. 14c) achieves a limiting upper value of 2.35 and results in a negative power exponent of ${s}_\mathrm{T}$ as reported in Table 6. However, if D reaches to a constant upper value of 8/3 as used in Model-K, the constant experimentally observed pressure scaling for ${s}_\mathrm{T}$ is achieved as shown in Table 6.

The model constant A in Eq. (10) also needs to be changed from 0.75 to 9.5. The readers are referred to [55] for a detailed discussion on the tuning of model constantA. In [55, pp. 104-105], a parametric investigation of wrinkling factor $\varXi$ expressions of Model-F and Model-K (Eq. (14d) and Eq. (15e)) was done for a system that is representative of the current LES setup. It was shown that the original version of Model-F increasingly under-predicts the wrinkling factor values with increasing turbulence level as compared to the wrinkling factor values obtained with Model-K at 1 bar. The model constant A was tuned to get the right agreement between wrinkling factor values obtained with Model-K and Model-F. The model constant $A =$ 9.5 gave the correct agreement.

The inner cut-off scale can get smaller than the laminar flame thickness in the original Model-F, in contrast to findings of Driscoll [56], which states that the smallest wrinkling scale is always bigger than $C*l_{F}$ where C is a constant of the order of unity. In addition, the work of Kobayashi et al. [57] indicates that $\varepsilon _\mathrm{i}/l_{F}$ approaches a constant value for high-pressure turbulent flames. Therefore, $\varepsilon _\mathrm{i}$ is restricted to a value corresponding to $l_{F}$. The adapted Model-F is also examined on mesh A with value of ${D}_{\max } =$ 2.667 instead of ${D}_{\max } = 2.35$ in Eq. (14c)

$$\begin{aligned} D\mathrm {=}\frac{\mathrm {2.05}s_\mathrm{L}}{u_{{\varDelta }}^{\mathrm {'}}\mathrm {+}s_\mathrm{L}}\mathrm {+}\frac{\mathrm {2.667}u_{{\varDelta }}^{\mathrm {'}}}{u_{{\varDelta }}^{\mathrm {'}}\mathrm {+}s_\mathrm{L}}. \end{aligned}$$

(19)

The normalised turbulent flame speed values for cases 2, 4, 9 and 12 are compared to the experimental data and shown in Table 7. The adapted Model-F with Eq. (19) for D still under-predicts $s_\mathrm{T}$, while the model with Eq. (15c) for D gives turbulent flame speed values and pressure scaling in agreement with the experimental data. So, Eq. (15c) is utilized in the adapted Model-F in the rest of the calculations. The modifications made to the Model-F are outlined in Table 1. For a clear picture for the reader, the key modification made to the original version of the Model-F are summarised here:

• Eq. (15c) is used for D instead of Eq. (14c)

• Model constant $A =$ 9.5 is used instead of 0.75

• Eq. (1) is used to bring the Le number dependency

• Eq. (14a) is restricted to a value corresponding to $l_{F}$

• One is added inside the parenthesis of Eq. (15e)

The impact of the filter width on the time-averaged progress variable $\langle \bar{c}\rangle$, the instantaneous Favre filtered progress variable ${\tilde{c}}$, FSD ${\Sigma }_\mathrm{gen}$ and $\left| {\nabla }{\tilde{c}} \right|$ for case 4 and case 12 utilizing mesh A and C (hereafter signified as case-4A, case-4C, case-12A and case-12C where case-4A means case 4 from Table 4 with mesh A) are presented in Fig. 5 for the adapted Model-F. Other cases from Table 4 show similar outcomes. Figure 5a, c show the results with mesh A for pressures of 1 and 10 bar, respectively, while the results with mesh C are shown in Fig. 4b, d for 1 and 10 bar. It can be observed that $\left| {\nabla }{\tilde{c}} \right|$ contours (indicating the resolved flame surface) are more wrinkled for the finest mesh and smoother for the coarsest mesh. The instantaneous turbulent flame fronts get thinner on the fine grid, but the time-averaged turbulent flame fronts are not affected much when the mesh resolution is increased. This demonstrates the adapted Model-F is also robust to moderate changes of grid spacing.

Table 5 The comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values predicted by the original Model-F with and without strain effects on mesh A

Table 6 Comparison of pressure exponent x for different variables $f\sim p^{\wedge } x$ for the original and adapted Model-F

Table 7 The comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values predicted by the adapted Model-F utilising Eq. (19) and Eq. (15c) on mesh A

Fig. 5

Influence of filter width on the time-averaged $\langle \bar{c}\rangle$, instantaneous flame surface ${\tilde{c}}$, FSD $\varSigma _\mathrm{gen}$ and $\left| \nabla {\tilde{c}} \right|$ contours with the adapted Model-F for a case-4A, b case-4C, c case-12A and d case-12C

Fig. 6

Comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values evaluated with the adapted Model-F on mesh A with experimental data for propane fuel at a 1 bar and b 5 bar

Fig. 7

Comparison of time-averaged and instantaneous progress variable contours for case-4A with original versions of a Model-K, b Model-A and c Model-Z

The LES results when using the original and adapted Model-F for methane and propane fuels are compared with the experimental data and the Model-K. For methane, Fig. 4a–c show normalized flame speeds $s_\mathrm{T}/s_\mathrm{L}^{0}$ plotted versus $u^{'}/s_\mathrm{L}^{0}$ for 1, 5 and 10 bar, respectively. In contrast to original Fureby model, the adapted Model-F now gives excellent quantitative agreement with the experimental data and yields the right pressure scaling. Figure 6a, b show similar plots for propane fuel utilizing the adapted Model-F with and without the Le number correction given by Eq. (1). The adapted Model-F with the Le number correction also shows excellent performance compared to the experimental data over a wide range of turbulence and pressures in the range of 1–5 bar.

6.3 Numerical examination of the models concerning pressure dependency

The Le number dependency in the Model-F is brought by using the expression 1/Le as used in the Model-K. The results show that the adapted Model-K and Model-F give quite a good performance for non-unity Le number fuel and a reasonable agreement with the experiments. Model-A and Model-Z are only adapted for pressure variation for the sake of brevity. The authors believe that the expression 1/Le can also be used in these models to introduce the Le number dependency. Model-A and Model-Z LES simulations are performed for methane fuel at 1, 5 and 10 bar. Figure 7 shows the instantaneous and time-averaged progress variable contours from the original Model-A and Model-Z compared to Model-K for case-4A. It can be observed that longer flames are predicted with the original Model-A and Model-Z. Table 8 gives a comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values predicted by the original Model-A and Model-Z on mesh A with the experimental data and Model-K. For the 1 bar cases the turbulent flame speed values are under-predicted. The experimentally observed normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ for case 4 is 3.55 while $s_\mathrm{T}/s_\mathrm{L}^{0}$ from Model-K, Model-A and Model-Z are 3.60, 2.60 and 2.89, respectively. The lower flame speeds from Model-A and Model-Z suggest a tuning of model constants to reach the right quantitative agreement with the experimental data at 1, 5 and 10 bar. Good agreement for the Model-A and Model-Z could be achieved by changing the model constants and by incorporating an explicit pressure correction term $\left( p/p_{0} \right) ^{n}$ where exponent n is a constant similar to Muppala et al. [20] used in their algebraic reaction rate closure model. Obviously, from a theoretical point of view an explicit empirical pressure correction term is undesirable because of the absence of physical reasoning.

The turbulent flame speeds from LES results utilizing the Model-A and Model-Z with adapted model constants and with pressure correction term are noted in Table 8. The adaptations made to the models are presented in Table 1. The models with empirical pressure scaling reflect the experimental pressure dependence and turbulent flame speed values exhibit fairly good agreement with the experimental data. The method to calculate the exponent n for Model-A and Model-Z is shown in Appendix-1.

Table 8 The comparison of normalised turbulent flame speed $s_\mathrm{T}/s_\mathrm{L}^{0}$ values predicted by Model-A and Model-Z with and without explicit pressure correction term on mesh A with the experimental data and Model-K

7 Conclusion

A subgrid LES combustion model should include the effects of pressure and fuel type in the reaction rate closure to claim its generality. An extensive numerical investigation is performed in the present study to determine these two significant effects utilizing main elements of some well-known algebraic FSD models accessible in the open literature. The numerical results are compared with experimental data for lean turbulent Bunsen flames utilizing methane and propane fuels for various flow conditions at pressures in the range of 1–10 bar. With the original versions of the selected models, the turbulent flame speed is under-predicted with discrepancy increasing for high-pressures. The model constants were tuned and suitable pressure corrections were used to achieve correct quantitative agreement and pressure dependency of the turbulent flame speed with the experimental data. A new term (1/Le) was also incorporated introducing the fuel effects in the reaction rate closure of the Model-K and Model-F. With these adaptations the models predict the turbulent flame speed values in an excellent agreement with the experimental data of the turbulent flames.

Appendix 1

This section shows the calculation of pressure exponent n of the explicit pressure correction term for adapted Model-A and Model-Z.

Model-A

For $\varXi \gg 1$, Eq. (13) for Model-A without an explicit pressure correction term can be written as:

$$\begin{aligned} \varXi = \left[ C_\mathrm{A} \varGamma \frac{u_{{\varDelta }}^{\mathrm {'}}}{s_\mathrm{L}^{0}} \right] =\frac{s_\mathrm{T}}{s_\mathrm{L}^{0}}, \end{aligned}$$

(A1)

$$\begin{aligned} \varXi *s_\mathrm{L}^{0} =\left[ C_\mathrm{A} \varGamma \frac{u_{{\varDelta }}^{\mathrm {'}}}{s_\mathrm{L}^{0}} \right] s_\mathrm{L}^{0} = s_\mathrm{T}. \end{aligned}$$

(A2)

From Eq. (A2), the pressure dependence of the predicted turbulent flame speed $s_\mathrm{T}$ from the Model-A is calculated and compared with the experimentally observed pressure dependence of turbulent flame speed, which is $s_\mathrm{T}\propto p^{0.07}$ for methane [29]. For methane using $s_\mathrm{L}^{0}\propto p^{-0.5}$ and $l_{F}\propto p^{-0.5}$, the pressure dependence of the efficiency function from Eq. (10) is found to be $\varGamma \propto p^{1/3}$. Putting the pressure dependence values of $s_\mathrm{L}^{0}$ and $\varGamma$ in Eq. (A2) and we get $\varXi *s_\mathrm{L}^{0}\propto p^{1/3}/p^{-0.5}{*p}^{-0.5}=p^{1/3}$. The pressure exponent of 0.33 is larger than the experimental one 0.07. Now an explicit pressure correction term $\left( p/p_{0} \right) ^{n}$ is introduced in Eq. (A1) with a value of n giving the correct pressure dependence of $s_\mathrm{T}$:

$$\begin{aligned} \left( \frac{p}{p_{0}} \right) ^{n}*\varXi *s_\mathrm{L}^{0}\mathrm {=}\left( \frac{p}{p_{0}} \right) ^{n}\left[ C_\mathrm{A} \varGamma \mathrm {}\frac{u_{{\varDelta }}^{\mathrm {'}}}{s_\mathrm{L}} \right] s_\mathrm{L}^{0}. \end{aligned}$$

(A3)

For Model-A, n is found to be -0.25 which is giving the experimental dependence of $s_\mathrm{T}$close to zero for methane i.e. $\left( p/p_{0} \right) ^{n}*\varXi *s_\mathrm{L}^{0}\propto p^{-0.25}*p^{1/3}/p^{-0.5}{*p}^{-0.5}=p^{0.08}$. It is noted that in above calculations $u_{{\varDelta }}^{\mathrm {'}}$ is taken to be independent of pressure. At high Reynolds number and constant inlet velocity, $u^{'}$ will be approximately constant. However, with increasing pressure and thus increasing Reynolds number the Kolmogorov length decreases. At constant filter width the total subgrid turbulent energy and therefore $u_{{\varDelta }}^{'}$ may increase slightly. However, as discussed in Sect. 6.3, LES simulation using the adapted Model-A with $n=-0.25$ gives very good agreement of the predicted turbulent flame speed with the experimental data, justifying the assumption of a small effect of a pressure variation of $u_{{\varDelta }}^{\mathrm {'}}$ on the turbulent flame speed.

Model-Z

A similar analysis is performed for the Model-Z with Eq. (16) and n is found to be 0.15.