A truly meshless approach to structural topology optimization based on the Direct Meshless Local Petrov–Galerkin (DMLPG) method

Abstract

With a wide applicability in several types of engineering problems, topology optimization is one of the most interesting fields of structural optimization. Many meshless methods have been developed, however, they were less explored in topology optimization compared to other methods, as the Finite Element Method (FEM). The Direct Meshless Local Petrov–Galerkin (DMLPG) is characterized as a truly meshless method since it does not use a mesh at any stage of its development. It has been applied to solve many boundary value problems, achieving results with good precision and computational efficiency. Instead of performing the numerical integral of complicated shape functions, the DMLPG considers low-degree polynomials. The new topology optimization approach proposed in this work couples the DMLPG method with a Bi-Directional Evolutionary Structural Optimization (BESO) method. DMLPG is used to obtain smooth nodal displacements, strains, and stresses, and BESO updates the structural geometry based on design sensitivity values. Numerical examples performed were compared with the results obtained with FEM and with other works in the literature, showing the applicability and validity of the technique.

1 Introduction

In the last 30 years, the topology optimization of structures has attracted the attention of several researchers, and it was successfully applied in many fields of engineering (Sigmund and Maute 2013; Zhu et al. 2020; Stoiber and Kromoser 2021). Topology optimization aims to find the optimal distribution of material within a fixed design domain, minimizing or maximizing an objective function subject to appropriate constraints. Several approaches have already been proposed: the homogenization method (Bendsøe and Kikuchi 1988) and its variant, the Solid Isotropic Microstructure with Penalization (SIMP) method (Bendsøe 1989; Zhou and Rozvany 1991; Sigmund 2001; Bruns and Tortorelli 2001); the Evolutionary Structural Optimization (ESO) method (Xie and Steven 1992, 1993; Chu et al. 1996) and its variant, the Bi-Directional Evolutionary Structural Optimization (BESO) method (Querin et al. 1998); the Level-Set method (Sethian and Wiegmann 2000; Wang et al. 2004, 2007; Ullah and Trevelyan 2016); Topological Derivative (Eschenauer et al. 1994; Norato et al. 2007); among others (Wang and Zhou 2004; Sigmund and Maute 2013).

Traditionally, most approaches proposed in topology optimization are based on the Finite Element Method (FEM) (Bendsøe and Kikuchi 1988; Bendsøe 1989; Eschenauer et al. 1994; Querin et al. 1998; Sethian and Wiegmann 2000), owing to its efficiency and accuracy (Li et al. 2020). However, they are accompanied by the difficulties inherent in ensuring good quality meshes, particularly when remeshing becomes necessary. (Zheng et al. 2012; Juan et al. 2010; Li et al. 2020; Sohouli et al. 2020). Thus, in an endeavor to address some challenges linked with mesh-based approaches, several meshless methods have been proposed (Gingold and Monaghan 1977; Belytschko et al. 1994; Liu et al. 1995; Oñate et al. 1996; Babuska and Melenk 1997; Sukumar et al. 1998; Mirzaei 2013). Some of those meshless methods also have been applied to topology optimization of structures: Element-Free Galerkin (EFG) (Juan et al. 2010; Zhao 2014; He et al. 2014; Cui et al. 2017; Khan et al. 2019; Li et al. 2022; Zhang et al. 2022b; Ullah et al. 2022a); Meshless Local Petrov–Galerkin (MLPG) Mixed Collocation (Li and Atluri 2008a, b); Smoothed Particle Hydrodynamics (SPH) (Lin et al. 2017; Li et al. 2020); Finite Volume Meshless Local Petrov–Galerkin (FVMLPG) (Zheng et al. 2009); Meshless Galerkin (Luo et al. 2012a, b); Radial Point Interpolation Method (RPIM) (Zheng et al. 2010; Ai and Gao 2019); Natural Neighbour Radial Point Interpolation Method (NNRPIM) (Gonçalves et al. 2022c); Reproducing Kernel (RK) (Cho and Kwak 2006).

In meshless methods, the domain is discretized into a set of nodes, without any explicit connectivity between them. The high-order continuity of the trial functions leads to good precision and better adaptability, making meshless approaches very attractive (Li and Atluri 2008b; Zhang et al. 2022a; Nguyen and Bui 2022). However, most meshless approaches used in topology optimization cited previously, make use of a background grid during the integration process.

Mirzaei (2011) proposed the Direct Meshless Local Petrov–Galerkin (DMLPG) method, which is considered a truly meshless approach since it does not use mesh in any stage of the development. Based on a generalized form of Moving Least Squares (MLS), it completely ignores complicated shape functions and numerical integration is performed on low-degree polynomials, as in FEM (Mirzaei 2013), thus achieving results with accuracy equivalent to the original MLPG method, but with greater computational efficiency (Mirzaei 2011, 2013, 2014; Mirzaei and Schaback 2014; Ilati and Dehghan 2016). The DMLPG method can achieve an equivalent precision to finite element-based methods (Abbaszadeh et al. 2022), and it can also consume less computational time since it does not require the mesh generation step (Dehghan et al. 2022). Despite being a relatively recent method, DMLPG has already been used in several applications (Mazzia et al. 2012; Mirzaei 2014; Taleei and Dehghan 2014; Mirzaei and Schaback 2014; Mirzaei and Hasanpour 2015; Darani 2017; Hasanpour and Mirzaei 2018; Abbaszadeh and Dehghan 2020; Shokri and Bahmani 2021), but, to our knowledge, it has not yet been used in the field of topology optimization of structures.

Evolutionary approaches, in particular, have become quite popular among topology optimization methods due to their conceptual simplicity and ease of implementation (Ansola et al. 2007; Huang and Xie 2009; Koke et al. 2015; Teimouri and Asgari 2019; Jiang et al. 2023). In the ESO method, the structure evolves towards an optimum by slowly removing material from regions considered inefficient. A criterion associated with the level of stress or strain energy is used to assess inefficiency. Material is removed from regions with low stress or strain energy. The BESO method is an extension of the ESO method since, in addition to allowing the removal of material, it also allows the addition of material in regions considered efficient. Material is added in locations close to regions with high stress or strain energy. Although these methods have been coupled with meshless approaches, this field is still relatively less explored. For instance, Lee et al. (2009) combined ESO with RPIM to evolve two-dimensional truss structures, while Juan et al. (2010) integrated ESO with EFG to optimize continuum structures, aiming to minimize the weight as the objective function. Another study by Zhao (2014) coupled a modified BESO with EFG, employing the Shepard function to create a dual-level density approximation. Similarly, Shobeiri (2015) applied EFG with BESO to minimize mean compliance while constraining material weight. Recently, Gonçalves et al. (2022a) proposed a new approach using a BESO algorithm with RPIM, reinforcing important parts of the structure to prevent the material domain from becoming too thin, based on a methodology utilizing the cubic average of the Von Mises stress. Additionally, in subsequent works by Gonçalves et al. (2022b, 2022c), the RPIM was replaced with the NNRPIM.

Mesh-based methods have a rich history and are extensively utilized across various scientific and engineering disciplines. In contrast, meshless methods are relatively recent but are emerging as a significant alternative, offering complementary advantages to mesh-based approaches. Researchers in the meshless methods domain are thus tasked with following the trajectory of mesh-based methods to identify potential advantages and applications. In this paper, we explore the utilization of a true meshless method—the DMLPG method—in conjunction with the BESO optimization method to demonstrate their viability in topology optimization. As a result, adjustments have been made to the FEM-based BESO algorithm to facilitate its integration with a meshless framework. Tests performed on problems involving the minimization of the compliance of elastic structures demonstrate good convergence and feasibility of the method.

The article is organized as follows. In Sect. 2, we explain the DMLPG formulation based on the Generalized Moving Least Squares (GMLS) approximations, showing the elasticity problem to be addressed. In Sect. 3, we define the structural optimization problem and describe the process steps of the BESO method. In Sect. 4, we present the tests performed and discuss the obtained results. Finally, in Sect. 5, we present our conclusions.

2 Direct Meshless Local Petrov–Galerkin Method

In this section, the DMLPG formulation is presented, using an elastostatic problem. The section is organized in seven subsections: in Sect. 2.1, the elastostatic boundary value problem is defined; in Sect. 2.2, the local weak form is established and described in matrix form; in Sects. 2.3 and 2.4, the trial and test functions are given; in Sect. 2.5, the linear system to be solved is formalized; in Sect. 2.6, the enforcement of the essential boundary conditions is considered; and, in Sect. 2.7, an algorithm is presented.

2.1 Boundary value problem

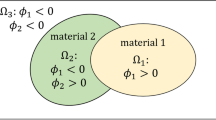
Consider the following linear elastic problem on a body with domain $\Omega \subset {\mathbb {R}}^d$ and boundary $\Gamma$, where d is the dimension of the problem. The solid is assumed to undergo infinitesimal deformations (Fig. 1), and the equation of equilibrium is given by (Mirzaei 2014)

$$\begin{aligned} \sigma _{ij,j} + b_i=0, \text { in } \Omega , \end{aligned}$$

(1)

where $\sigma _{ij}$ are the components of the Cauchy stress tensor, $b_i$ are the components of the body force, $1 \le i,j \le d$ and $(\cdot )_{,j}$ denotes $\partial (\cdot )/\partial x_j$.

Fig. 1

The global domain $\Omega$ and the global boundary $\Gamma$ of an arbitrary two-dimensional body. The boundaries $\Gamma _u$ and $\Gamma _t$ are, in that order, the parts of $\Gamma$ in which the essential and natural boundary conditions are specified. $\bar{{\textbf{u}}}$ and $\bar{{\textbf{t}}}$ are the prescribed displacement and traction, respectively, and ${\textbf{n}}$ is the unit outward normal vector at $\Gamma$

Two types of boundary conditions are established on $\Gamma$: the essential boundary condition at $\Gamma _u \subset \Gamma$ and the natural boundary condition at $\Gamma _t \subset \Gamma$ (Fig. 1), i.e.,

$$\begin{aligned}&u_i ({\textbf{x}}) = \bar{u}_i, \text { on } \Gamma _u, \end{aligned}$$

(2a)

$$\begin{aligned}&\sigma _{ij}n_j=\bar{t}_i, \text { on } \Gamma _t, \end{aligned}$$

(2b)

where $\bar{u}_i$ denotes the prescribed displacement components at $\Gamma _u$, $\bar{t}_i$ denotes the prescribed traction components at $\Gamma _t$ and $n_j$ denotes the component of the unit outward normal vector at $\Gamma$ (Mirzaei 2014). The displacement field ${\textbf{u}}({\textbf{x}})$ in the domain and on the domain’s boundary must be the solution of Eq. (1), and must satisfy Eqs. (2a) and (2b).

2.2 Local weak form

Consider that the domain of the body and its boundary are covered by arbitrarily scattered nodes, and that each node I has a local subdomain $\Omega _I$ with a local boundary $\Gamma _I$. The subdomains can have arbitrary shapes, such as squares, circles etc., as illustrated in Fig. 2 (Atluri and Shen 2002). Mirzaei (2014) observed that both circular and rectangular shapes yield satisfactory results in meshless methods. Hence, the selection between these shapes primarily depends on convenience (Liu 2009). In this work, we use only circular subdomains.

Fig. 2

Nodes distributions for the DMLPG approach. A local subdomain, with its local boundary, is assigned to each node, which can have an arbitrary shape as illustrated by the nodes $I=K$ (inner circle), $I = L$ (circle cutting the boundary) and $I = J$ (inner rectangle). $\Omega _J$, $\Omega _K$ and $\Omega _L$, represent, in this order, the local subdomains of the nodes J, K and L and their respective borders are $\Gamma _J$, $\Gamma _K$ and $\Gamma _L$. The boundary $\Gamma _L = \Gamma _{L0} \cup \Gamma _{Lu} \cup \Gamma _{Lt}$, where $\Gamma _{L0}$ is a part of $\Gamma _L$ in which no boundary condition is established and $\Gamma _{Lu}$ and $\Gamma _{Lt}$, respectively, are parts of $\Gamma _L$ in which the essential boundary condition and the natural boundary condition are specified. If a node is completely inside the domain, as nodes J and K, then $\Gamma _J=\Gamma _{J0}$ and $\Gamma _K=\Gamma _{K0}$

The boundary $\Gamma _I$ of node I’s subdomain $\Omega _I$ can be decomposed as (Liu 2009)

$$\begin{aligned} \Gamma _I=\Gamma _{I0} \cup \Gamma _{Iu} \cup \Gamma _{It}, \end{aligned}$$

(3)

where $\Gamma _{Iu}$ and $\Gamma _{It}$ are, respectively, the parts of $\Gamma _I$ where the essential boundary condition and the natural boundary condition are specified and $\Gamma _{I0}$ is the part of $\Gamma _I$ where no boundary condition is established, as illustrated in Fig. 2.

The local Petrov–Galerkin approach is based on a local weak form developed over the local subdomains. The differential equation can be rewritten as a generalized local weak form over the local subdomain $\Omega _{I}$ as (Liu 2009)

$$\begin{aligned} \int _{\Omega _I} \left[ \sigma _{ij,j}+b_i\right] v_{Ii}({\textbf{x}})\mathrm{{d}}\Omega =0, \end{aligned}$$

(4)

where $v_{Ii}({\textbf{x}})$ is the component of the test function associated with node I.

Applying the divergence theorem, decomposing boundary $\Gamma _{I}$ into its constituent parts [Eq. (3)] and imposing the natural boundary condition [Eq. (2b)] (Mirzaei 2014), Eq. (4) can be written in matrix form as

$$\begin{aligned} \begin{aligned}&\int _{\Omega _I} \varvec{\Psi }_{I}^{T} \varvec{\sigma } \mathrm{{d}}\Omega \\&-\int _{\Gamma _{I0}} {\textbf{V}}_{I} {\textbf{N}}\varvec{\sigma }\mathrm{{d}}\Gamma - \int _{\Gamma _{Iu}} {\textbf{V}}_{I} {\textbf{N}}\varvec{\sigma }\mathrm{{d}}\Gamma \\ {}&= \int _{\Gamma _{It}} {\textbf{V}}_{I} \mathbf {\bar{t}}\mathrm{{d}}\Gamma + \int _{\Omega _I} {\textbf{V}}_{I} {\textbf{b}} \mathrm{{d}}\Omega , \end{aligned} \end{aligned}$$

(5)

where $\varvec{\sigma }$ is the vector representation of the stress tensor, ${\textbf{V}}_{I}$ is the test function matrix, ${\textbf{N}}$ is the matrix of the components of the unit outward normal at the boundary $\Gamma$, $\mathbf {\bar{t}}$ is the prescribed traction vector at $\Gamma _{It}$, ${\textbf{b}}$ is the body force vector and ${\textbf{L}}_d$ is the matrix of differential operators used in $\varvec{\Psi }_{I} = {\textbf{L}}_d{\textbf{V}}_{I}$.

The stress is related to the displacement through (Liu 2009)

$$\begin{aligned}&\varvec{\sigma } = {\textbf{D}}\varvec{\varepsilon }, \end{aligned}$$

(6a)

$$\begin{aligned}&\varvec{\varepsilon }= {\textbf{L}}_d{\textbf{u}}, \end{aligned}$$

(6b)

where $\varvec{\varepsilon }$ is the vector representation of the strain tensor, ${\textbf{u}}$ is the displacement vector and ${\textbf{D}}$, in this work, is the elastic stiffness matrix of an isotropic material.

Substituting Eqs. (6a) and (6b) into Eq. (5), the local weak form is written as

$$\begin{aligned} \begin{aligned}&\int _{\Omega _I} \varvec{\Psi }_{I}^{T} {\textbf{D}} {\textbf{L}}_d {\textbf{u}} \mathrm{{d}}\Omega \\&-\int _{\Gamma _{I0}} {\textbf{V}}_{I}{\textbf{N}}{\textbf{D}} {\textbf{L}}_d {\textbf{u}} \mathrm{{d}}\Gamma -\int _{\Gamma _{Iu}} {\textbf{V}}_{I}{\textbf{N}}{\textbf{D}} {\textbf{L}}_d {\textbf{u}}\mathrm{{d}}\Gamma \\&=\int _{\Gamma _{It}} {\textbf{V}}_{I} \bar{{\textbf{t}}}\mathrm{{d}}\Gamma +\int _{\Omega _I} {\textbf{V}}_{I} {\textbf{b}} \mathrm{{d}}\Omega . \end{aligned} \end{aligned}$$

(7)

2.3 Trial functions

The DMLPG method uses the Generalized Moving Least Squares (GMLS) to approximate the displacement in the problem. In this section, we introduce GMLS and its weight function, based on Mirzaei (2013), Abbaszadeh and Dehghan (2020).

2.3.1 Generalized moving least squares

Consider the linear equation

$$\begin{aligned} \lambda ({\textbf{u}}) = \beta , \end{aligned}$$

(8)

where $\lambda$ and $\beta$ are linear functionals and the components of the unknown function ${\textbf{u}}$, e.g. displacement, $u_i \in C^m (\Omega )$ (the space of m times differentiable continuous functions).

Let ${\textbf{X}} = \{ {\textbf{x}}_1, \ldots , {\textbf{x}}_N \}$ be a set of nodes scattered in the domain $\Omega$. The GMLS approximation ${\hat{\lambda }}({\textbf{u}})$ of $\lambda ({\textbf{u}})$ is the linear combination

$$\begin{aligned} \lambda ({\textbf{u}}) \approx {\hat{\lambda }}({\textbf{u}}) = \sum _{J=1}^N a_{J}(\lambda ) \mu _{J} ({\textbf{u}}), \end{aligned}$$

(9)

of the functionals $\mu _{J} ({\textbf{u}})$ with coefficients $a_{J}$. The functionals $\lambda$ and $\mu _{J}$ can represent, for example: point evaluations of ${\textbf{u}}$ or any of its derivatives up to order m; a local integral that contains ${\textbf{u}}$ or any of its derivatives in the integrand etc. (Mirzaei 2013).

Consider ${\mathcal {P}} = \text {span} \{ {\textbf{p}}_1, \ldots , {\textbf{p}}_G \}$ a finite dimensional subspace, where the components,  $p_{ki},~i = 1,\dots , d$, of a basis vector ${\textbf{p}}_k$, for $k=1,\dots ,G$, have continuity $C^m(\Omega )$, with $G = \frac{(m+d)!}{m! d!}$. For all functions ${\textbf{p}} \in {\mathcal {P}}$, the equality

$$\begin{aligned} \lambda ({\textbf{p}})=\sum _{J=1}^N a_{J}(\lambda ) \mu _{J} ({\textbf{p}}) \end{aligned}$$

(10)

holds. Thus, we seek an approximation ${\textbf{p}}^*$ of ${\textbf{u}}$ that minimizes

$$\begin{aligned} \left\{ \sum _{J=1}^N (\mu _{J} ({\textbf{u}}) - \mu _{J} ({\textbf{p}}))^2 w_{J} \right\} , \end{aligned}$$

(11)

where $w_{J}$ is value of a weight function that measures the importance of node J on the minimization process.

Rewriting ${\textbf{p}}$ as a linear combination of the basis vectors of ${\mathcal {P}}$ and taking into account the linearity of the functionals $\mu _{J}$, then

$$\begin{aligned} \begin{aligned} \mu _{J}( {\textbf{p}}({\textbf{x}}) )&= \mu _{J} \left( \sum _{k=1}^G b_{k} {\textbf{p}}_k({\textbf{x}}) \right) \\ {}&= \sum _{k=1}^G b_{k} \mu _{J} ({\textbf{p}}_k({\textbf{x}}) ) = {\textbf{p}}_{\mu _{J}}^\mathrm{{T}}{\textbf{b}}, \end{aligned} \end{aligned}$$

(12)

where ${\textbf{p}}^\mathrm{{T}}_{\mu _{J}} = [ \mu _{J}({\textbf{p}}_1({\textbf{x}})) \; \cdots \; \mu _{J}({\textbf{p}}_G({\textbf{x}}))]$ and ${\textbf{b}}^\mathrm{{T}} = [ b_{1} \; \cdots \; b_{G}].$

Substituting Eq. (12) into Eq. (11) yields

$$\begin{aligned} J({\textbf{b}}) = \sum _{J=1}^N (\mu _{J} ({\textbf{u}}) - {\textbf{p}}_{\mu _{J}}^\mathrm{{T}}{\textbf{b}})^2 w_{J}. \end{aligned}$$

(13)

The coefficients ${\textbf{b}}^*$ from the optimal polynomial, ${\textbf{p}}^*~\in ~{\mathcal {P}}$ are obtained by minimizing $J({\textbf{b}})$, whose solution can be written as

$$\begin{aligned} {\textbf{b}}^* = {\textbf{A}}^{-1} {\textbf{B}} { { \varvec{\mu }}({\textbf{u}})}, \end{aligned}$$

(14)

where ${\textbf{A}}={\textbf{P}}^\mathrm{{T}}{\textbf{W}}{\textbf{P}}$ and ${\textbf{B}} = {\textbf{P}}^\mathrm{{T}}{\textbf{W}}$, with

$$\begin{aligned} {\textbf{P}} = \begin{bmatrix} {\textbf{p}}^\mathrm{{T}}_{{\mu }_1} \\ \vdots \\ {\textbf{p}}^\mathrm{{T}}_{{\mu }_N} \end{bmatrix}, ~ {\textbf{W}} = \begin{bmatrix} w_1&{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0&{} \cdots &{} w_N\\ \end{bmatrix} \end{aligned}$$

and ${\varvec{\mu }}{({\textbf{u}})} =[ {\mu }_1{({\textbf{u}})} \; \cdots \; {\mu }_N{({\textbf{u}})} ]^{\mathrm{{T}}}.$

In the GMLS approximation, the optimal solution is ${\hat{\lambda }}({\textbf{u}}) = \lambda ({\textbf{p}}^*)$ (Mirzaei 2013). Considering Eqs. (12) and (14), we have

$$\begin{aligned} {\hat{\lambda }}({\textbf{u}}) = {\lambda }({\textbf{p}}^*) = {\textbf{p}}^\mathrm{{T}}_\lambda {\textbf{b}}^* = {\textbf{p}}^\mathrm{{T}}_\lambda {\textbf{A}}^{-1} {\textbf{B}} { { \varvec{\mu }}({\textbf{u}})}. \end{aligned}$$

(15)

2.3.2 Weight function

Several weight functions can be used with the GMLS approximation, for instance: Gaussian function and spline function, both with circular compact support domain. In this work, we use the Gaussian function (Mirzaei 2014)

$$\begin{aligned} w_J=w(r_J) = \frac{\exp (-(\epsilon r_J)^2) - \exp (-\epsilon ^2)}{ 1 -\exp (-\epsilon ^2)}, \end{aligned}$$

(16)

for $0 \le r_J \le 1$, where $r_J = \Vert {\textbf{x}} - {\textbf{x}}_J\Vert / r_w$, with $r_w$ as the radius of the compact support of the weight function centered in ${\textbf{x}}$, and $\epsilon$ is a shape parameter of the function’s surface. As illustrated in Fig. 3, the nodes closer to ${\textbf{x}}$ give more contribution and the nodes outside the support region, i.e., $r_J\ge r_w$, do not give any contribution ($w(r_J)=0$). To ensure the invertibility of matrix ${\textbf{A}}$ [Eq. (14)], the number of nodes adjacent to ${\textbf{x}}$ with non-null contribution, N, must be greater or equal to the number of basis vectors, G, i.e. $N \ge G$ (Atluri and Zhu 1998; Liu 2009).

Fig. 3

A model illustrating radius $r_w$ that defines the compact support of the weight function centered at point ${\textbf{x}}$. Since node J is close to ${\textbf{x}}$, its associated weight is strong. On the other hand, since node K is located at the border of the support region, its associated weight is equal to zero

2.4 Test functions

The test functions are centered at the nodes, and their support regions are defined by the radius $r_e$. In this work, we use the DMLPG5 approach (Mirzaei 2014), which defines the test function as a Heaviside step function (Fig. 4). For a node I, the test function used in Eqs. (4)–(5) and (7) is defined as (Li et al. 2003)

$$\begin{aligned} v_{Ii}({\textbf{x}})=\Bigg \{\begin{array}{cl} 1, &{} {\textbf{x}}\in \Omega _I,\\ 0, &{} \text {otherwise}, \end{array} \end{aligned}$$

(17)

for $i = 1, \dots , d$.

Fig. 4

Heaviside step function in a two-dimensional case centered at node I of compact support with radius $r_e$

2.5 Discretization

Since the Heaviside step function is used as test function, the first integral from Eq. (7) vanishes. Based on Eq. (8), we can define the discretized problem as

$$\begin{aligned} \varvec{\lambda }_I ({\textbf{u}}) = \varvec{\beta }_{I}, \end{aligned}$$

(18)

where

$$\begin{aligned}&\varvec{\lambda }_I ({\textbf{u}}) = \begin{pmatrix} \lambda _{1}({\textbf{u}}) \\ \vdots \\ \lambda _{d}({\textbf{u}}) \end{pmatrix} := -\int _{\Gamma _{I0} \cup \Gamma _{Iu}} {\textbf{N}}{\textbf{D}} {\textbf{L}}_d {\textbf{u}} \mathrm{{d}}\Gamma , \end{aligned}$$

(19a)

$$\begin{aligned}&\varvec{\beta }_{I} = \begin{pmatrix} \beta _{1} \\ \vdots \\ \beta _{d} \end{pmatrix}:= \int _{\Gamma _{It}} \mathbf {\bar{t}}\mathrm{{d}}\Gamma +\int _{\Omega _I} {\textbf{b}} \mathrm{{d}}\Omega , \end{aligned}$$

(19b)

for $I = 1,\ldots M$. Considering ${\tilde{N}}$ as the total number of nodes that discretize the domain $\Omega$, then $M \ge {\tilde{N}}$ (Mirzaei 2013). In this work, for simplicity, $M={\tilde{N}}$. Note that the functionals $\lambda ({\textbf{u}})$ and $\beta$ [Eq. (8)] are also defined for each dimension $i = 1,\dots ,d$.

Considering Eqs. (9) and (15), in which the components of ${\varvec{\mu }}$ were taken as the evaluation of the displacement in direction i at the sample point ${\textbf{x}}_J$, we can approximate $\varvec{\lambda }_I({\textbf{u}})$ as

$$\begin{aligned} \hat{\varvec{\lambda }}_I({\textbf{u}}) = \sum _{J=1}^{N} a_{J}(\varvec{\lambda }_I) {\textbf{u}}({\textbf{x}}_J) = {\textbf{p}}_{\varvec{\lambda }_I}^\mathrm{{T}} \varvec{\Phi } {\textbf{u}}, \end{aligned}$$

(20)

where N is the number of nodes, adjacent to node I, at which the weight function centered at ${\textbf{x}}_I$ does not vanish, i.e. $w_J > 0$; and ${\textbf{p}}_{\varvec{\lambda }_I}^\mathrm{{T}} \in {\mathbb {R}}^{d\times dG}$ is defined as

$$\begin{aligned} {\textbf{p}}_{\varvec{\lambda }_I}^\mathrm{{T}} =[ \varvec{\lambda }_I({\textbf{p}}_1) \; \cdots \; \varvec{\lambda }_I({\textbf{p}}_G) ], \end{aligned}$$

(21)

with

$$\begin{aligned} \varvec{\lambda }_I({\textbf{p}}_k) = -\int _{\Gamma _{I0} \cup \Gamma _{Iu}} {\textbf{N}}{\textbf{D}} {\textbf{P}}_k \mathrm{{d}}\Gamma \end{aligned}$$

(22)

for $k = 1, \ldots , G$ and ${\textbf{P}}_k = {\textbf{L}}_d \begin{bmatrix} \text {diag}\{{\textbf{p}}_k\} \end{bmatrix}$. The notation $\text {diag}\{{\textbf{p}}_k\}$ represents a diagonal matrix whose diagonal elements are the basis vectors ${\textbf{p}}_k$ applied to ${\textbf{x}}$. $\varvec{\Phi } \in {\mathbb {R}}^{dG\times dN}$ is the block matrix

$$\begin{aligned} \varvec{\Phi } = \begin{bmatrix} \varvec{\Phi }_{11} &{} \cdots &{} \varvec{\Phi }_{1N}\\ \vdots &{} \ddots &{} \vdots \\ \varvec{\Phi }_{G1} &{} \cdots &{} \varvec{\Phi }_{GN} \end{bmatrix}, \end{aligned}$$

(23)

with each $d\times d$ block

$$\begin{aligned} \varvec{\Phi }_{kJ} = \begin{bmatrix} \varvec{\phi }_{kJ} &{} \cdots &{} 0\\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \varvec{\phi }_{kJ} \end{bmatrix}. \end{aligned}$$

(24)

In Eq. (24), $\varvec{\phi }_{kJ}$ is the element $[{\textbf{A}}^{-1}{\textbf{B}}]_{kJ}$ [Eq. (14)].

The linear system

$$\begin{aligned} {\textbf{K}}_{(dM\times dM)} {\textbf{u}}_{(dM\times 1)} = {\textbf{f}}_{(dM\times 1)} \end{aligned}$$

(25)

is assembled from each block ${\textbf{K}}_{IJ} \in {\mathbb {R}}^{d\times d}$ and ${\textbf{f}}_{I} \in {\mathbb {R}}^{d\times 1}$ where

$$\begin{aligned} {\textbf{K}}_{IJ} = {\textbf{p}}_{\varvec{\lambda }_I}^\mathrm{{T}} \varvec{\Phi }_{:,J} \end{aligned}$$

(26)

and

$$\begin{aligned} {\textbf{f}}_{I} = \varvec{\beta }_I. \end{aligned}$$

(27)

Here, $\varvec{\Phi }_{:,J}$ represents the J-th column of $\varvec{\Phi }$.

2.6 Enforcement of the essential boundary conditions

In this work, since the Kronecker Delta property cannot be guaranteed at the nodes, the essential boundary conditions are imposed using the MLS collocation method (Liu 2009; Mirzaei 2014). For a node I on the $\Gamma _u$ boundary, the corresponding row of the global linear system [Eq. (25)], where the condition is established for direction i, is zeroed. Then, based on Eq. (9), the following equation is applied,

$$\begin{aligned} { \bar{u}_{i}({\textbf{x}}_{I}) = \sum _{J=1}^{N} a_{J}(\delta _{{\textbf{x}}_{I}}){u}_{i}({\textbf{x}}_{J}) = {\textbf{p}}^\mathrm{{T}}_{\delta _{{\textbf{x}}_{I}}} \varvec{\phi } {\textbf{u}}_i,} \end{aligned}$$

(28)

where $\bar{u}_{i}({\textbf{x}}_I)$ is the prescribed essential boundary condition at node I with $i = 1, \dots , d$, the functional $\delta _{{\textbf{x}}_{I}}$ is the point evaluation at ${\textbf{x}}_I$, $\varvec{\phi }=~{\textbf{A}}^{-1}{\textbf{B}}$, ${\textbf{p}}_{\delta _{{\textbf{x}}_{I}}}^\mathrm{{T}} =[ p_{1i}({\textbf{x}}_{I}) \; \cdots \; p_{Gi}({\textbf{x}}_{I}) ]$ and ${\textbf{u}}_i^\mathrm{{T}} =[ u_{1i} \; \cdots \; u_{Ni} ]$.

After solving the linear system, a good approximation of the displacements are obtained (Mirzaei et al. 2012). However, to find the actual displacement at any point ${\textbf{x}}$, we can modify Eq. (20) as

$$\begin{aligned} {\textbf{u}}({\textbf{x}}) = \sum _{J=1}^{N} a_{J}(\varvec{\delta }_{\textbf{x}}){{\textbf{u}}}({\textbf{x}}_{J}) = {\textbf{p}}^\mathrm{{T}}_{\varvec{\delta }_{{\textbf{x}}}} \varvec{\Phi } {\textbf{u}}, \end{aligned}$$

(29)

where the components of $\varvec{\delta }_{\textbf{x}}$ are taken as the functionals $\delta _{{\textbf{x}}_i}$, then ${\textbf{p}}_{\varvec{\delta }_{{\textbf{x}}}}^\mathrm{{T}} =[ {\textbf{p}}_{1}({\textbf{x}}) \; \cdots \; {\textbf{p}}_{G}({\textbf{x}}) ].$

2.7 Algorithm

The steps of DMLPG method are presented in Algorithm 1. The input model is discretized (Line 2). Then, the adjacent nodes from a node I are found (Line 4) and the ${\textbf{A}}^{-1}{\textbf{B}}$ matrix is computed (Line 5). If ${\textbf{x}}_I \notin \Gamma _u$, the integration points are created, the local stiffness matrix and the local force vector are determinate and assembled in the global system (Lines 6 to 13). Otherwise, the essential boundary condition is enforced in the global system (Lines 14 to 19). The linear system is solved and the nodal displacements are obtained.

Algorithm 1

DMLPG method returning the approximated displacements ${\textbf{u}}$ at the nodes.

3 Topology optimization

The Topology Optimization is performed with a modified BESO method, which is based in the method presented by Huang and Xie (2010). Figure 5 illustrates the flowchart of the proposed technique. The structural optimization problem is defined as

$$\begin{aligned} \text {minimize }~~~~&C \approx \frac{1}{2} \sum _{I=1}^M \varvec{\varepsilon }_I^T \varvec{\sigma }_I V_I , \end{aligned}$$

(30a)

$$\begin{aligned} \text {subject to }~~~~&\textbf{Ku} = {\textbf{f}}, \end{aligned}$$

(30b)

$$\begin{aligned}&V^* - \displaystyle \sum _{I = 1}^M V_I ~ {\mathcal {X}}_I = 0, \end{aligned}$$

(30c)

$$\begin{aligned}&{\mathcal {X}}_I = {\mathcal {X}}_{\mathrm{{min}}} \quad \text {or} \quad 1, \end{aligned}$$

(30d)

where C is the approximation of the mean compliance (Lin et al. 2017), ${\mathcal {X}}_I$ is the binary design variable at node I, with ${\mathcal {X}}_I=1$ representing solid material and ${\mathcal {X}}_I= {\mathcal {X}}_{\mathrm{{min}}}$ denoting the void, $V^*$ is the prescribed volume and $V_I$ is the overestimated nodal volume. A small value, ${\mathcal {X}}_{\mathrm{{min}}}$, is used to represent the void material and to avoid the singularity of the stiffness matrix (Huang and Xie 2009).

Fig. 5

Overview of the proposed technique

The initial model is entered with its boundary conditions. Then, the nodes and the associated integration points are created. To reduce the computational costs, the matrix ${\textbf{A}}^{-1}{\textbf{B}}$ (14) is precomputed for each node.

The iterative procedure begins with the DMLPG analysis where a linear system is constructed and solved to find the displacements, strains and stress at each node. The nodal design sensitivity is calculated (Sect. 3.2) and some post processing is applied (Sect. 3.3). Next, the design variables are updated (Sect. 3.4) by the algorithm, which decides whether material will be added or removed at a node. If the optimization process converges (Sect. 3.5), the optimal design is achieved, otherwise the elastic stiffness matrix is updated at each integration point (Sect. 3.1) and the iterative process continues.

3.1 Elastic stiffness matrix

At each step of the iterative process, the elastic stiffness matrix must be updated at each integration point. For this purpose, an estimated design variable, ${\mathcal {X}}_q$, is defined for each integration point, at position ${\textbf{x}}_q$, as a weighted mean value based on the design variables at the adjacent nodes,

$$\begin{aligned} {\mathcal {X}}_q = \frac{\displaystyle \sum _{J=1}^{N} w(r_{J}){\mathcal {X}}_J}{\displaystyle \sum _{J=1}^{N} w(r_{J})}, \end{aligned}$$

(31)

where w is the weight function centered in ${\textbf{x}}_q$ [Eq. (16)] and N is the number of nodes inside the influence radius $r_w$.

The elastic stiffness matrix is calculated at each integration point in the numerical analysis, and also at each node in the sensitivity analysis. The matrix is modified as (Huang and Xie 2010)

$$\begin{aligned} {\textbf{D}} ({\mathcal {X}}) = {\mathcal {X}}^p {\textbf{D}}_0, \end{aligned}$$

(32)

where ${\mathcal {X}}$ is the design variable at an integration point (${\mathcal {X}} = {\mathcal {X}}_q$) or at a node (${\mathcal {X}} = {\mathcal {X}}_I$), p is the penalty exponent and ${\textbf{D}}_0$ is the initial elastic stiffness matrix [Eq. (6a)].

3.2 Sensitivity analysis

The sensitivity analysis is calculated as the design derivative of the compliance at a node. First, we substitute Eq. (32) into the definition of the stress tensor in Eq. (6a) to yield

$$\begin{aligned} \varvec{\sigma } = {\textbf{D}}({\mathcal {X}}_I) \varvec{\varepsilon }. \end{aligned}$$

(33)

Next, considering Eq. (33), the compliance [Eq. (30a)] is rewritten as

$$\begin{aligned} C \approx \frac{1}{2} \sum _{I=1}^M \varvec{\varepsilon }_I^T {\textbf{D}}({\mathcal {X}}_I) \varvec{\varepsilon }_I V_I. \end{aligned}$$

(34)

Finally, the design derivative is calculated as

$$\begin{aligned} \begin{aligned} \frac{\partial C}{\partial {\mathcal {X}}_I}&\approx \frac{1}{2} \sum _{I=1}^M \varvec{\varepsilon }_I^T \frac{\partial {\textbf{D}}({\mathcal {X}}_I)}{\partial {\mathcal {X}}_I} \varvec{\varepsilon }_I V_I\\&= \frac{p {\mathcal {X}}_I^{p-1} }{2} \varvec{\varepsilon }_I^T {\textbf{D}}_0 \varvec{\varepsilon }_I V_I. \end{aligned} \end{aligned}$$

(35)

Based on Eq. (35), the design sensitivity value at node I is defined as

$$\begin{aligned} \begin{aligned} \alpha _I = \frac{1}{p} \frac{\partial C}{\partial {\mathcal {X}}_I} = \frac{{\mathcal {X}}_I^{p-1}}{2} \varvec{\varepsilon }_I^T {\textbf{D}}_0 \varvec{\varepsilon }_I V_I. \end{aligned} \end{aligned}$$

(36)

3.3 Filter and stabilization processes

The use of filtering techniques is a common practice to avoid the numerical instabilities that usually occurs in topology optimization, e.g. checkerboard pattern. The filter used is based on a radius, $r_{\min }$, that helps to find the adjacent nodes that influence the sensitivity of a node I (Xia et al. 2018)

$$\begin{aligned} {\hat{\alpha }}_I = \frac{\displaystyle \sum _{J=1}^{{\bar{N}}} \omega (r_{IJ})\alpha _J}{\displaystyle \sum _{J=1}^{{\bar{N}}} \omega (r_{IJ})}, \end{aligned}$$

(37)

with

$$\begin{aligned} \omega (r)=\Bigg \{\begin{array}{cl} r_{\mathrm{{min}}} - r, &{} r < r_{\mathrm{{\min }}},\\ 0, &{} \text {otherwise}, \end{array} \end{aligned}$$

(38)

where ${\bar{N}}$ is the number of nodes that are inside the influence radius $r_{\mathrm{{\min }}}$ and $r = r_{IJ}$ is the Euclidean distance between nodes I and J.

To guarantee a better convergence of the BESO method, the average of design sensitivity values at the current and previous steps is used as a stabilization procedure (Huang and Xie 2010)

$$\begin{aligned} {\tilde{\alpha }}_I = \frac{{\hat{\alpha }}_{I,k} + {\tilde{\alpha }}_{I,k-1}}{2}, \end{aligned}$$

(39)

where k is the current iteration of the method.

3.4 Design update

The update of the design variables begins with the computation of the volume fraction at the current iteration (Huang and Xie 2009)

$$\begin{aligned} V_k = V_{k-1} (1 - ER), \end{aligned}$$

(40)

where ER is the evolutionary ratio, which represents a gradual decrease in the target volume until it archives the prescribed volume fraction, $V^*$.

The BESO method tries to balance the Strain Energy Density (SED) between all the nodes. The design variable of a node, ${\mathcal {X}}_I$, should be increased when the SED is high, and decreased when it is low (Huang and Xie 2010). The optimality criteria is defined as: strain energy densities of solid materials are always higher than those of soft materials (Zhao 2014). Therefore, if the design sensitivity at a node is high, the design variable ${\mathcal {X}}_I$ is updated to value 1, otherwise it is updated to ${\mathcal {X}}_{\mathrm{{min}}}$. The threshold used to rank the sensitivity value starts with the mean value of the maximum and minimum sensitivity values, and it is updated based on how much the structure must change to reach the target volume $V_k$.

3.5 Convergence criteria

The algorithm converges when the objective function stabilizes and the volume fraction is achieved. The first convergence criterion, based on the variation of the objective function, is defined as (Huang and Xie 2009)

$$\begin{aligned} \text {error} = \frac{ \Bigg | \displaystyle \sum _{i=1}^\eta ( C_{k-i+1} - C_{k-\eta -i+1} ) \Bigg |}{\displaystyle \sum _{i=1}^\eta C_{k-i+1}} \le \tau , \end{aligned}$$

(41)

where k is the current iteration number, $\tau$ is the defined threshold, $\eta$ is the number of iterations in which the compliance is analyzed. The convergence is achieved when the compliance stabilizes for at least $2\eta$ iterations.

4 Results

The tests presented in this section demonstrate the effectiveness of the DMLPG method combined with the BESO method applied to Topology Optimization problems of elastic structures. The implementation used C++ and the Eigen Library (Guennebaud et al. 2019). Eigen was used to handle matrix operations and to solve the linear system of algebraic equations. The tests were performed with an 11th Gen Intel®Core$^{\hbox {TM}}$ i7-11800 H @ 2.30 GHz $\times$ 16, 16.0 GB RAM running on Ubuntu 21.10.

The examples presented in this section are two-dimensional ($d=2$). Thus, the matrices in Eqs. (5) to (7) can be written as:

$$\begin{aligned} \begin{aligned}&\varvec{\sigma }=\Bigg (\begin{array}{c} \sigma _{11} \\ \sigma _{22}\\ \sigma _{12} \end{array}\Bigg ), \text { } \varvec{\varepsilon }= \Bigg (\begin{array}{c} \varepsilon _{11} \\ \varepsilon _{22}\\ \gamma _{12} \end{array}\Bigg ), \text { } {\textbf{u}} = \Bigg (\begin{array}{c} u_1\\ u_2\\ \end{array}\Bigg ),\\&\mathbf {\bar{t}}=\Bigg (\begin{array}{c} \bar{t}_1 \\ \bar{t}_2 \end{array}\Bigg ), \text { } {\textbf{b}}=\Bigg (\begin{array}{c} b_1 \\ b_2 \end{array}\Bigg ), \text { } {\textbf{V}}_{I} = \begin{bmatrix} v_{I1} &{} 0 \\ 0 &{} v_{I2} \end{bmatrix}, \\&{\textbf{N}} = \begin{bmatrix} n_1 &{} 0 &{} n_2 \\ 0 &{} n_2 &{} n_1 \end{bmatrix}, {\textbf{L}}_d^T= \begin{bmatrix} \dfrac{\partial }{\partial x_1} &{} 0 &{} \dfrac{\partial }{\partial x_2}\\ 0 &{} \dfrac{\partial }{\partial x_2} &{} \dfrac{\partial }{\partial x_1} \end{bmatrix} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} {\textbf{D}}= \dfrac{\bar{E}}{1-\bar{\nu }^2}\begin{bmatrix} 1 &{} \bar{\nu } &{} 0 \\ \bar{\nu } &{} 1 &{} 0\\ 0 &{} 0 &{} \dfrac{1-\bar{\nu }}{2} \end{bmatrix},\end{aligned}$$

with

$$\begin{aligned} \bar{E}= {\left\{ \begin{array}{ll} E &{}\text {for plane stress}, \\ \dfrac{E}{1-{\nu }^2} &{}\text {for plane strain}, \end{array}\right. } \\ \bar{\nu }= {\left\{ \begin{array}{ll} \nu &{} \text {for plane stress}, \\ \dfrac{\nu }{1-{\nu }} &{} \text {for plane strain}, \end{array}\right. } \end{aligned}$$

where E is the Young’s modulus and $\nu$ is the Poisson’s ratio of the material.

The integrations in Eq. (19) use Gauss–Legendre quadrature. Since the body force is not used, only the integrals over the boundary of the domain and subdomains are considered. Then the integration points are defined in the one-dimensional parametric space, $\xi$, of the curve (Fig. 6). For integration purposes, the circular domain is divided into four circular sectors of $90^{\circ }$ with four integration points each.

Fig. 6

The intersection line between the subdomain ($\Omega _I$) and the body’s boundary ($\Gamma$) can be used to create the integration points (${\textbf{x}}_q$) at the border. Each subdomain is divided into circular sector of angle $90^{\circ }$, where the integration points can be created on the boundary of the subdomain. Each circular arc is parametrized as a line domain with $-1\le \xi \le 1$

In all tests, the following parameters are used for the numerical analysis with the DMLPG method: Polynomial order, $m = 2$, leading to $G = 6$; Shape parameter of the Gaussian function, $\epsilon = 4$; Radii, $r_w = 4 d_{\mathrm{{min}}}$ and $r_e = 0.7 d_{\mathrm{{min}}}$, where $d_{\mathrm{{min}}}$ is the minimum Euclidean distance between two nodes. The radius $r_w$ is increased by $10\%$ if the matrix ${\textbf{A}}$ [Eq. (14)] is singular (Taleei and Dehghan 2014). The Elasticity modulus and Poisson’s coefficient of the material under plane stress are $E = 200$ GPa and $\nu = 0.3$, respectively.

For the structural topology optimization method the following parameters are defined: ${\mathcal {X}}_{\mathrm{{min}}} = 10^{-3}$, $r_{\mathrm{{min}}} = 3 d_{\mathrm{{min}}}$, $p = 3$, $ER=2\%$, $\eta = 5$ and $\tau = 10^{-3}$.

Since there is no analytical solution for topology optimization problems, the results are considered plausible when they are similar to the results in the literature (Eschenauer and Olhoff 2001; Li and Atluri 2008b). In order to validate our results, some tests were compared with a FEM-based BESO.

4.1 Cantilever beam

The cantilever beam problem uses the model illustrated in Fig. 7, where $L=0.08$ m, $D=0.05$ m, $P = 4500$ N is distributed over a region of $h = 0.004$ m times the thickness of ${0.001} {\text{m}}$ and $V^* = 40\%$. First, a test with a discretization of $81\times 51$ nodes was used to compare with a FEM solution of similar discretization. Since, in the FEM test, the mesh has $80\times 50$ elements, the number of nodes in both tests are the same. Despite small differences in the obtained designs, it can be seen that both methods yield similar results (Fig. 8).

Fig. 7

Cantilever beam problem definition

Fig. 8

Cantilever beam results. a Optimal design with $81 \times 51$ nodes. b Optimal design of a FEM based on Huang and Xie (2010) with $80 \times 50$ elements

To analyze the behavior of the technique with different discretizations, two tests with grid sizes of $65\times 41$ and $97\times 61$ nodes were conducted (Fig. 9). All optimal structures obtained have equivalent designs with the same number of holes, but the design with fewer nodes exhibits a different boundary shape. While some parameters and methods used may vary, our results align with others found in the literature (Huang and Xie 2007; Li and Atluri 2008b; Gonçalves et al. 2022c; Ullah et al. 2022a).

Fig. 9

Optimal design of the cantilever beam with a $65 \times 41$ nodes and b $97 \times 61$ nodes

The evolution history of the objective function for all discretizations is shown in Fig. 10. While the mean compliances increased, the volume fractions decreased. The abrupt jumps in the objective function are due to sudden design changes. In approximately 45 iterations, the volume fractions reached the volume target of $40\%$. The mean compliances stabilized until they satisfied the convergence criterion. It can be noted that the finer discretization yields a topology design with lower compliance, indicating higher structural stiffness. However, it required more iteration steps. Since there are more nodes, it also has an increased computational cost. Therefore, there is a trade-off between computational cost and achieving better compliance.

Fig. 10

Evolution history of the compliance and the volume fraction for the cantilever beam problem

4.2 Simply supported beam

A simply supported beam, as shown in Fig. 11a, is considered. To save computational effort, only the symmetrical part of the beam is analyzed (Fig. 11b), where $L=1.2$ m, $D=0.6$ m, $P = 200000$ N is distributed over a region of $l = 0.004$ m times the thickness of ${0.01} {\text{m}}$, and $V^* = 60\%$. The problem was initially analyzed with a discretization of $61 \times 61$ nodes to allow a fair comparison with the BESO based on FEM using $60\times 60$ elements (Fig. 12). Additionally, two more discretizations were tested with $56\times 56$ and $66\times 66$ nodes and are shown in Fig. 13. All results are plausible, as similar results have been archived in other works in the literature (Lee et al. 2009; Challis 2010; Zuo 2010). It is noteworthy that the final design with fewer nodes has a simpler design compared to the others. This indicates that a finer discretization can lead to designs with different topologies. A finer set of nodes is more capable of describing local substructures during the design, which is equivalent to the mesh dependency phenomenon in finite element-based topology optimization of structures (Luo et al. 2013).

Fig. 11

Simply supported beam problem definition. a Full model. b Symmetric part

Fig. 12

Simply supported beam results. a Optimal design with $61 \times 61$ nodes. b Optimal design of a FEM based on Huang and Xie (2010) with $60 \times 60$ elements

Fig. 13

Optimal design of the simply supported beam with a $56 \times 56$ nodes and b $66 \times 66$ nodes

Figure 14 presents the designs obtained with a discretization of $61\times 61$ nodes, both with and without the sensitivity filter process. It is evident that the DMLPG method, when combined with the BESO method, fails to eliminate the numerical instability of the checkerboard pattern unless additional schemes are included.

Fig. 14

Optimal design of the simply supported beam a with filter and b without filter

4.3 Beam with fixed supports

A beam with fixed supports, as depicted in Fig. 15a, is considered. To reduce computational effort, only half of the design domain is analyzed, as illustrated in Fig. 15b, due to symmetry. The parameters were set as $L=1.0$ m, $D=0.5$ m, $P = 200000$ N distributed over a region of $l = 0.004$ m times the thickness of ${0.01} {\text{m}}$, with a target volume fraction of $V^* = 40\%$. A discretization of $51\times 51$ nodes was utilized for comparison with a test using $50\times 50$ elements of the FEM based on (Huang and Xie 2010). Similar results were obtained (Fig. 16), reinforcing the plausibility of the proposed technique.

Fig. 15

Beam with fixed supports problem definition. a Full model. b Symmetric part

Fig. 16

Beam with fixed supports. a Optimal design with $51 \times 51$ nodes. b Optimal design of a FEM based on Huang and Xie (2010) with $50 \times 50$ elements

Figure 17 illustrates the iterative process of the previous result, showing the gradual addition/removal of material as the design evolves towards optimality. The evolution history of the objective function is presented in Fig. 18. The mean compliance begins to stabilize when the volume fraction reaches its target value around iteration 45. Around iteration 20, holes start to appear, leading to oscillations in the objective function, as depicted in Fig. 18. At iteration 40, an abrupt change in compliance occurs due to a structural connection break. Design and objective function stabilization is observed from around iteration 50, with the optimal design achieved at iteration 56.

Fig. 17

Initial design and a sequence of iterations

Fig. 18

Evolution histories of the compliance and the volume fraction for the beam with fixed supports problem

4.4 L-shaped beam

The L-shaped beam problem utilizes the model depicted in Fig. 19, where $L=0.1$ m, $P = 35000$ N distributed over a region of $l = 0.002$ m times the thickness of ${0.01} {\text{m}}$, and $V^* = 40\%$. The problem was analyzed with two different numbers of nodes: 2821 and 4033 (Fig. 20). This analysis aimed to investigate the influence of the number of nodes on the final design. As observed in Sect. 4.2, different discretizations can yield distinct designs. However, the obtained results are consistent with those found in the literature (Gonçalves et al. 2022c; Zhao 2014; Ullah et al. 2022b; Picelli et al. 2018). With an increase in the number of nodes, more holes appeared in the topology. Across all tests shown in previous sections, distinct material interfaces were observed in the designs, which would facilitate the manufacturing stage.

Fig. 19

L-shaped beam problem definition

Fig. 20

Optimal design of the L-shaped beam with a 2821 nodes and b 4033 nodes

The effectiveness of the filtering process is also examined, as depicted in Fig. 21. It is evident that without the filter, the checkerboard pattern instability becomes prominent, emphasizing the necessity of its application. However, the primary structural features are discernible in both cases.

Fig. 21

Optimal design of the L-shaped beam a with filter and b without filter

5 Conclusions

We have presented a novel approach to Topology Optimization, which combines the truly meshless method, DMLPG, with the well-known BESO method. The DMLPG approach has been applied to various engineering problems, demonstrating its efficiency and yielding accurate results.

Our examples focused on minimizing the compliance of two-dimensional elasticity problems. The optimal designs obtained were consistent with FEM results and findings from existing literature, thereby highlighting the feasibility of our proposed method. Notably, our technique distinguishes itself from other meshless methods in its integration procedure, as it operates without the need for a background mesh.

By incorporating a sensitivity filter, we ensured that our method remained robust against the occurrence of the checkerboard pattern, a common challenge in topology optimization. However, the phenomenon of discretization dependency persists. As part of future work, we aim to extend our method to handle multiple material problems and three-dimensional structures.