1 Introduction

The United States inland waterway system contributed $33.8 billion to GDP in 2014 (PricewaterhouseCoopers 2017). Locks and navigation dams play an important role in inland waterway systems by providing a consistent navigable channel in a series of pools along the entire waterway. Locks open a gate to give boats entry and allow boats to travel between pools. If a lock gate cannot perform this function, barge traffic shuts down in that portion of the waterway. The most common type of lock gate within the United States is the miter gate, more than half of which have exceeded their economic design life of 50 years (Foltz 2017), increasing the risk of major impacts to barge traffic.

The long life of many miter gates presents difficult life-cycle management decisions. To proactively schedule the maintenance of structures and thus reduce the overall life-cycle costs, numerous structural health monitoring (SHM) and damage prognosis (DP) strategies have been developed (Leser et al. 2017; Sabatino and Frangopol 2017; Su et al. 2021; Vega and Todd 2020; Yang et al. 2020). In SHM, damage diagnosis aims to detect and quantify the potential damage, which provides essential information about the current health state. Failure prognosis, in the meanwhile, uses the gathered damage information to simulate the evolution of the damage, and further predicts the remaining useful life (RUL) of the structures. In recent years, the “digital twin” concept has drawn intensive attention because of its ability to inform damage diagnostic and failure prognostic strategies by simulating life-cycle scenarios (Li et al. 2017; Tuegel et al. 2011; Ye et al. 2019).

For the digital twin concept, one of the most commonly used physics-based approaches in digital twin execution is high-fidelity finite element (FE) analysis, which computationally reflects the evolving physical system. For instance, Zhang et al. (2019) presented a reliability estimation procedure for RC structures at different corrosion levels which used X-ray and digital image processing technique to infer the spatial variability of steel corrosion. With a focus on the seismic cracking identification, Pirboudaghi et al. (2018) developed a damage detection procedure for concrete gravity dam by integrating the FE numerical model with the wavelet transform system identification. Jiang et al. (2022) proposed a model correction and updating scheme to improve the accuracy of failure prognostics by recovering the missing physics in the boundary condition degradation of miter gates. Eick et al. (2021) suggested a fatigue life updating method for embedded miter gate anchorages. Commonly, in a digital twin framework as shown in Fig. 1, a physical asset (i.e. the miter gate) is connected to its digital counterpart core (i.e., the FE model) through Bayesian updating methods and real-time SHM monitoring data. Bayesian updating methods infer the damage state based on monitoring data and thereby allow the digital twin to not only estimate the current damage level but also to forecast potential failure before it happens.

Fig. 1
figure 1

Digital twin concept of miter gates

Full size image

Even though current efforts have shown the promising potential of the digital twin in optimizing the maintenance activity of large-scale assets, they mainly focus on a single-mode failure scenario (e.g., boundary condition degradation of miter gates). For steel structures such as miter gates, fatigue cracks are another very common structural deterioration mechanism. As fatigue cracks propagate, they may interact with other failure modes. Cracks may be computationally modeled using extended/generalized finite element methods (XFEM/GFEM) (Duarte et al. 2001; Moës et al. 1999), which is much more mesh independent than quarter node element crack representation (Barsoum 1976; Henshell and Shaw 1975). Therefore, practitioners widely use XFEM/GFEM for crack modeling/analysis. Although FE analysis offers high interpretability (Gravouil et al. 2002; Moës et al. 2002; Shi et al. 2010; Xie et al. 2018), the separation in length scales between structural scale (e.g., at the scale of miter gates) and damage scale (e.g. at the scale of cracks) may increase numerical model discretization and add computational cost. Moreover, the existing methods rely upon strain measurements for model updating (Hoskere et al. 2020; Parno et al. 2018). With novel measurement techniques, such as cameras, and drones, developed for the monitoring of miter gates in recent years, there is an urgent need to develop an integrated diagnostic/prognostic capability that uses multiple data sources (including strain gages) to simultaneously account for multiple failure modes.

In this paper, we focus on two failure scenarios at different scales, including the boundary condition degradation at a global-scale and the crack growth of a cruciform at a very localized scale. Two types of measurements are considered: strain measurement data from strain gages and displacement observations extracted from digital images. In order to develop the framework for multiple failure modes and data sources, two main challenges need to be addressed, namely: (1) how to properly model different failure modes of miter gates; and (2) how to fuse multiple data sources for the model updating of the digital model.

The iterative global-local (IGL) method is employed to address the first challenge. Dealing with separation of scales is a broad field of research in crack modeling. Of particular interest are methods bridging scales non-intrusively with XFEM cracking represented in the local domain (Fillmore and Duarte 2018; Gupta et al. 2012). The IGL method offers particularly good non-intrusive characteristics (Allix and Gosselet 2020), requiring only the exchange of reaction and displacement related quantities along the local boundary. Despite the relatively simple coupling of global and local models, the IGL method can simulate nonlinearities in the local model with a linear global model (Gendre et al. 2009). Within the context of large structures modeled as shells, such as a miter gate, the IGL method has been successfully used to connect shell global domains to solid local domains with welds (Li et al. 2021).

To address the second challenge of fusing multiple data and uncertainty sources for model updating of miter gates with multiple failure modes, a dynamic Bayesian network (DBN) model is developed in this paper. DBNs have been widely used for studies where the topology structure represents causal relationships, and for building digital twins of complex engineering systems such as aircraft structures (Li et al. 2017) and nuclear power plants (Agarwal et al. 2017). For example, Li et al. (2017) suggested a digital twin framework for diagnosis and prognosis of an aircraft wing using a DBN as a versatile probabilistic model. A detailed discussion on using DBN as a unifying mathematical tool for digital twins at scale is available in Kapteyn et al. (2021). As a probabilistic graphic model, DBN allows for information fusion of various data and uncertainty sources (both aleatory and epistemic uncertainty sources) using Bayesian inference and conditional probabilistic models. The recursive updating scheme supports the digital twin’s need for real-time updating and prediction over time, which plays an essential role in fully realizing the promising potential of digital twin of miter gates.

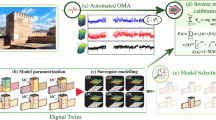
The main objective of this paper is to develop a framework that utilizes image-based observations and strain sensor data to diagnose and predict failure features in large-scale structures. The physics of two types of failure modes is represented in an FE model of the miter gate: the boundary condition loss represents the large-scale damage; the fatigue crack growth represents the small-scale local damage. For illustration purposes, this paper takes the crack growth on the bottom flange edge of a horizontal girder on a miter gate as an example. The underlying concepts, however, can be extended and applied to other locations and different types of structures. The proposed framework includes two main steps, as shown in Fig. 2: (1) effective simulation of failure modes in different length scales using a global-local modeling method with surrogate modeling to increase computational efficiency, and (2) online diagnostics and prognostics based on the two types of observations.

Fig. 2
figure 2

Overview of the proposed framework

Full size image

The rest of the paper is arranged as follows. Section 2 presents the modeling of miter gate failure scenarios based on an FE model. The proposed diagnostic and prognostic framework using multiple data sources and a DBN is described in Sect. 3. Sect. 4 gives the key results and discussion, followed by Sect. 5 which draws the conclusions.

2 Modeling of miter gate failures

2.1 Boundary condition degradation

Figure 3 shows the downstream side view of a miter gate in a dewatered state. The gudgeon and pintle function as pivots for the miter gate’s rotation. Normally, the bottom of the miter gates are submerged below water, resulting in hydrostatic pressure pushing the two leaves of the gate together. Hydrostatic pressures are applied on the upstream plate of the gate as shown in Fig. 4, where the upstream water level is denoted \(h_{up}\) and the downstream water level is denoted \(h_{down}\). Since the hydrostatic pressures is considered to be fully described by the water levels, the loading condition resulted by hydrostatic pressure will be symbolized by parameter \({\mathbf{h}}=[h_{up}, h_{down}]\) for the rest of the paper. When the gate holds enough water in the lock chamber, the miter contact block of both gate leaves come into contact and a symmetric pin is assumed preventing translational movement. The two gate leaves act as an arch, experiencing more axial compression under more hydraulic head. This compression causes the miter gate’s quoin contact block to thrust into the lock wall contact block. The quoin often experiences damage so that only part of it comes into contact with the lock wall. When the miter gate is open, boats can enter or leave the lock chamber. When the miter gate is closed, the lock chamber can be filled or emptied while the miter gate acts as a damming surface. More detailed information about miter gates may be found in (Daniel and Paulus 2019; Eick et al. 2019; Fillmore and Smith 2021).

Fig. 3
figure 3

Miter gate downstream side view. Photograph courtesy of John Cheek, USACE

Full size image
Fig. 4
figure 4

Miter gate hydrostatic pressure from upstream and downstream water levels

Full size image

The aging of the gate is manifested by multiple forms of damage. Often, the bottom portion of the quoin becomes damaged so that it cannot properly contact the wall. To account for the effects of quoin block damage, a simplified gap degradation model (Vega et al. 2021) is generalized below,

$$\begin{aligned} {\frac{\mathrm{{d}}l}{\mathrm{{d}}t}} = \exp (\sigma U(t))Q(l(t))^{w}, \end{aligned}$$
(1)

where U(t) is a random variable with a standard normal distribution; \(\sigma\), Q, and w are empirical parameters based on previous research (Jiang et al. 2022; Yang and Manning 1996).

The discrete-time form of Eq. (1) can be written as

$$\begin{aligned} l_i = l_{i-1} + \exp (\sigma U_i)Q(l_{i-1})^{w}, \end{aligned}$$
(2)

where \(l_i\) and \(l_{i-1}\) are the state variable (gap length) at time steps \(t_{i}\) and \(t_{i-1}\) respectively, and \(U_{i}\) is a standard normal random variable at \(t_{i}\).

An FE model was generated using Abaqus 2021 as shown in Fig. 5. The model represents the Greenup downstream miter gate, which has been previously validated with the field data to provide accurate physics (Eick et al. 2018). This model is employed in this paper in order to capture the global behavior and predict the strain responses of the gate. The quoin block contact loss is modeled by not applying the pinned boundary conditions along a certain length. For a more detailed description on the quoin block mechanism, refer to Fig. 8.37b in Daniel and Paulus (2019). For the rest of the paper, the length of the contact loss interface is referred to as the gap length denoted \(l_{i}\). The lengthening of this gap leads to a global re-distribution of the stress, which escalates crack evolution of the miter gates at different local regions. The gap damage state is connected with the strain responses as follows

$$\begin{aligned} \begin{aligned} {\mathrm{State}}:\;{l_i}&= {l_{i - 1}} + \exp (\sigma {U_i})Q{({l_{i - 1}})^w}, \\ {\mathrm{Measurement}}:\;{{\mathbf{s}}_i}&= g({l_i},\;{\mathbf{h}_i}) + {{{{\varepsilon }}}_i}, \\\end{aligned} \end{aligned}$$
(3)

where \(\mathbf{h}\) is the loading condition at a given time step \(t_i\), \(g({l_i},\;{\mathbf{h}_i})\) is the response of the FE model, \({{{\varepsilon }}_i} \sim N({\mathbf{0}},\;{\varvec{\sigma }}_{\mathbf{obs}}^\mathbf{2} \mathbf {I})\;\) are the uncorrelated measurement noise contributions characterized by standard deviation \({\varvec{\sigma }}_{\mathbf{obs}}^\mathbf{2}\), and \(\mathbf{I}\) is an identity matrix.

Fig. 5
figure 5

Finite element model of Greenup miter gate, showing global strain distribution

Full size image

2.2 Crack growth modeling using an iterative global-local algorithm

Besides the quoin block damage discussed above, fatigue cracks are a common form of miter gate damage due to the cyclic loads when the lock chambers are filled and emptied. Since the sparsely distributed strain gage sensor network is fairly insensitive to crack presence at an initial stage, conventional crack detection methods are mostly operated by in-situ inspectors, which makes the inspection somewhat subjective and labor-dependent. Besides, much of the gate is always submerged under water which increases the difficulty and accessibility of in-situ inspections. Thus, an accurate crack analysis using the miter gate FE model is necessary to understand the behavior of such localized effect. First, Paris’ law–one of the most commonly used crack growth models–is adopted to generate the physics of the model, or

$$\begin{aligned} \frac{\mathrm{{d}}a}{\mathrm{{d}}N}=c(\Delta K)^m \end{aligned}$$
(4)

where a is the crack length and \(\mathrm{{d}}a/\mathrm{{d}}N\) is the fatigue crack growth for a load cycle N, c and m are the empirical parameters of Paris’ law, and \(\Delta K\) is maximum stress intensity factor (SIF) difference in a loading cycle at the crack front, as shown in Fig. 6. The discrete-time form of Eq. (4) can be written as

$$\begin{aligned} a_i = a_{i-1} + c(\Delta K_i)^m, \end{aligned}$$
(5)

in which \(\Delta K_i\) stands for the SIF range at time step \(t_i\).

Fig. 6
figure 6

FE representation of the simulated crack front: a cruciform where crack initiates, and b a close view of crack front

Full size image

Three main assumptions are made here to the FE model simplify the problem:

  1. 1.

    The crack can only propagate in one direction with a fixed crack front shape;

  2. 2.

    The 13 nodes (12 elements) through the 0.625 in. thickness of the cracked plate (solid geometry with linear hexahedral elements with XFEM enrichment functions shown in Fig. 6b) are sufficient to represent the crack physics, where only the first cracking mode of the middle node, \(K_1\), is considered;

  3. 3.

    The geometry, boundary conditions, and discretization represent the Greenup gate leaf well enough for the diagnosis and prognosis in this research;

With all the above assumptions, the crack geometry can be described by one single parameter, a. This paper aims to provide a general framework for multi-mode failures of large-scale structures, the explicit form of crack representation is beyond scope of this paper. Thus, the crack problem is simplified in this study.

The maximum SIF difference in a loading cycle, \(\Delta K\), is a variable that is affected by gap length, crack length, and load conditions, where gap length is a global-scale damage and crack is a local-scale damage. The fatigue crack modeling requires the calculation of accurate SIF values at each time step to indicate the crack growth pattern. The SIF at \(t_i\) is a function of multiple factors,

$$\begin{aligned} \Delta K_i = {g_{\Delta K}}({l_i},\;{a_i},\;\Delta {s_i}), \end{aligned}$$
(6)

in which \(\Delta {s_i}\) is the loading condition caused by the cyclic fluctuation of the hydrostatic pressure \(\mathbf{h}\), and \(g_{\Delta K}({l_i},\;{a_i},\;\Delta {s_i})\) is an FE model to predict the SIF range \(\Delta K_i\) for given gap length, crack length, and loading cycle. Although the built-in Abaqus technology calculates SIF values through the contour integral method, crack analysis for the complicated and large-scale miter gate model is computationally expensive due to the fact that the crack can only be simulated with finely discretized solid elements in Abaqus. Given that, a coupled global-local FE model was generated using Abaqus 2021 as shown in Fig. 7. The IGL-based model is developed in order to address the challenge in estimating SIF caused by the two damage features in different length scales.

Fig. 7
figure 7

Illustrated IGL algorithm for miter gate with global, and local mesh discretizations. The global domain has parameters as l and \(\mathbf{h}\), with boundary condition described by parameter \({\varvec{f}}^G\). The local domain has parameter a

Full size image

All the elements of the global model are 3D linear reduced-integration shell elements which lowers the computational cost. The local model is defined as a cruciform whose local boundary is shared with the global model. The local model takes the displacements from the global model as its boundary condition. The local model is divided into two parts: One is the crack affected zone with Abaqus XFEM 3D solid geometry which allows for crack analysis; the second part of the local model is the rest of the cruciform which uses the 3D linear reduced-integration shell elements. The feature of interest is the crack, which is only explicitly represented in the solid area of the local model. More detailed IGL implementation information may be found in Fillmore et al. (2022). For any given \(l_{i}\), \(\Delta {s_i}\), and \(a_{i}\), the SIF value may be obtained. It is assumed that since a surrogate model trained on an identical FE model showed acceptable error (less than \(10\%\)), the surrogate model in this research also has acceptable accuracy.

3 Diagnosis and prognosis of miter gates using multiple data sources and DBN

3.1 Structural health monitoring (SHM) data sources

The physics of the miter gate in this study is parameterized by three factors: the loading condition \(\mathbf{h}\), the quoin block damage \(l_{i}\) that is imposed on the global domain, and the crack length \(a_{i}\) that is assigned to the local domain. Different combinations of such parameters induce different physical behaviors that are reflected in different observations. Image-based observations enable computer vision techniques to capture the cracks in the early stage while the strain sensor network detects the quoin block damage, resulting in load re-distribution within the whole structure. In this paper, two types of surrogate models are built-in order to efficiently perform probabilistic analysis based on the different measurements.

3.1.1 Strain sensor network data

To generate synthetic strain measurements, four sensor locations are selected in this paper, which are close to the location that quoin block damage most likely will happen, as shown in Fig. 8. The sensors are located in compression regions, and thus negative strain values are recorded.

Fig. 8
figure 8

Sensor locations: a Individual sensor location and corresponding value, and b locations of the selected four sensors

Full size image

At any time step \(t_i\), the strain measurements from the four strain gage sensors are related to the FE model shown in Sect. 2.1 as follows

$$\begin{aligned}{}[{s_{i1}},\;{s_{i2}},\; {s_{i3}} ,\;{s_{i4}}] = g({l_i},\;{{\mathbf{h}}_i}) + {{{\varepsilon }}_i}, \end{aligned}$$
(7)

where \(s_{i1}\) represents the response of the first selected strain gage at time step \(t_i\), and \(g({l_i},\;{{\mathbf{h}}_i})\) is the strain output of the FE model for a given gap length and loading cycle. The measurement noise \(\varepsilon _i\) is considered statistically independent and identical distributed Gaussian random variables.

Since the original FE model \(g({l_i},\;{{\mathbf{h}}_i})\) is computationally expensive for damage diagnostics and failure prognostics, Gaussian process regression (GPR)-based surrogate models are constructed to replace the original model. Considering that there are only four strain gages, we construct a GPR model for each sensor response separately. After that, Eq. (7) is rewritten as

$$\begin{aligned} {s_{ij}} = {{\hat{G}}_j}({l_i},\;{{\mathbf{h}}_i}) + {{{\varepsilon }}_i},\;\forall j = 1,\; \cdots ,\;4, \end{aligned}$$
(8)

where \({{\hat{G}}_j}({l_i},\;{{\mathbf{h}}_i})\) is the GPR model for the FEA response of the i-th strain gage and is given by

$$\begin{aligned} {{\hat{G}}_j}({l_i},\;{{\mathbf{h}}_i})\sim N({\mu _{ij}},\;\sigma _{ij}^2), \end{aligned}$$
(9)

in which \(N(\cdot , \cdot )\) is Gaussian distribution, \({\mu _{{ij}}}\) and \(\sigma _{{ij}}\) are respectively the mean and standard deviation of the prediction of the j-th surrogate model at time step \(t_{i}\).

Based on Eq. (8), the likelihood of observing \({\mathbf{s}}_i=[{s_{i1}},\;{s_{i2}},\;{s_{i3}},\;{s_{i4}}]\) at \(t_i\) for given \(l_i\) and \({{\mathbf{h}}_i}\) is then given by

$$\begin{aligned} f({{\mathbf{s}}_i} \vert {l_i},\;{{\mathbf{h}}_i}) = \prod \limits _{j = 1}^4 {\phi \left( \frac{{{s_{ij}} - {\mu _{ij}}}}{{\sqrt{\sigma _{ij}^2 + \sigma _{\varepsilon i}^2}}} \right) ,} \end{aligned}$$
(10)

where \(\phi \left( \cdot \right)\) is the PDF of a standard normal random variable.

3.1.2 Image monitoring data

The digital image is the key data source for crack detection. The evolution of the crack results in a displacement re-distribution of the surface which may be captured by cameras or drones. Note that the cruciform on which the crack initiates is located at the center of the second-from-bottom horizontal girder, which is always underwater during lock chamber filling and emptying. In reality, photos obtained underwater usually have lower contrast and may be blurred out by the water reflection. The optical flow method (Alvarez et al. 2000) and digital image correlation (DIC) (Pan 2011) methods can obtain the measured dense displacement field assumed in this research. Correspondingly, a simplified digital image model is developed to represent the process of obtaining the displacement measurements from images (a “measurement model”) using the optical flow method. Given the fact that Drews et al. (2014) found turbidity increases the error of optical flow fields and Madjidi and Negahdaripour (2006) proved that the low-contrast photo underestimates the magnitude of the optical flow field, the model down-sizes the displacement measurements and assigns a noise that represents the noise level of photos taken underwater. This noise also accounts for environmental factors such as camera vibration and light source movement over a lock filling event. The process of getting the displacement field can be expressed as follows

$$\begin{aligned}{}[\varvec{u_x}, \varvec{u_z}] = G_{OP}(l_i, a_i, {\mathbf{h}}_i), \end{aligned}$$
(11)

where \(\varvec{u_x}\) and \(\varvec{u_z}\) are the localized displacements related to \(\mathbf{h}\), \(l_i\), and \(a_i\), and \(G_{OP}(l_i, a_i, {\mathbf{h}}_i)\) is the displacement field prediction from optical flow model. The transformation \(G_{OP}\) depends on camera location, focal length, and other camera parameters. For simplicity here, the camera angle is normal to the crack location on the gate and the transformation from 3D to pixel coordinates is a linear scaling. Since the IGL algorithm developed in Sect. 2.2 offers an accurate way of measuring loading condition and the two different-scale damage states, the process of using optical flow model to generate synthetic displacements is represented by IGL model developed in Sect. 2.2.

$$\begin{aligned}{}[\varvec{u_x}, \varvec{u_z}] = G_{IGL}(l_i, a_i, {\mathbf{h}}_i)+{{ \epsilon }_i}, \end{aligned}$$
(12)

in which \(G_{IGL}(l_i, a_i, {\mathbf{h}}_i)\) is the IGL algorithm.

First, a surface of interest around the crack in the cruciform Abaqus model is determined with a dimension of \(10 \times 12\) inches. The built-in Abaqus post-processing provides the nodal displacements of all the nodes within the area, shown in Fig. 9. The irregular quadrilateral meshing elements generate nodal displacements at scattered locations. To simulate the uniformly distributed displacement field obtained from camera images, the scattered nodal displacements are interpolated onto a uniformly gridded surface as vectors (x, z, v) using the “nearest” method, where the point of interpolation specified by location (x, z) is assigned by the value of closest nodal displacement v.

Fig. 9
figure 9

Area of Interest: a Cruciform where the crack is evolving, and b the area in which all the nodal displacements are extracted

Full size image

Figure 10 shows an example of the displacements in two directions obtained from IGL and linear interpolation with a pixel length of 0.1 inches when \({\mathbf{h}}=[h_{up}, h_{down}] = [506.8, 339.8]\), \(l=27.2\), and \(a=2.16\).

Fig. 10
figure 10

Displacement-based observation: a displacement in x-direction, and b displacement in z-direction

Full size image

Since the IGL algorithm requires global-local model analysis, which is computationally expensive, we construct surrogate models for the localized displacements, similar to the surrogate models for the strain response. Since the high-dimensional displacement field is computationally impractical for surrogate modeling, singular value decomposition (SVD) is employed to construct the GPR models by following the procedure suggested in Vega et al. (2020). The surrogate modeling gives \(\varvec{u_x}\) and \(\varvec{u_z}\) as

$$\begin{aligned} \begin{aligned} {{\mathbf{u}}_x}&= \sum \limits _{j = 1}^{{N_x}} {{{{\hat{G}}}_{x,j}}({l_i},\;{a_i},\;{{\mathbf{h}}_i}){{\eta }_j}} + {{{\varepsilon }}_{x,i}}, \\ {{\mathbf{u}}_z}&= \sum \limits _{k = 1}^{{N_z}} {{{{\hat{G}}}_{z,k}}({l_i},\;{a_i},\;{{\mathbf{h}}_i}){{\eta }_k}} + {{{\varepsilon }}_{z,i}}, \end{aligned} \end{aligned}$$
(13)

where \({{\hat{G}}_{x,j}}({l_i},\;{a_i},\;{{\mathbf{h}}_i}) \sim N({\mu _{x,j}},\sigma _{x,j}^2)\) is the j-th GPR surrogate model in the latent space, \({\eta }\) is the vector that transforms the latent space prediction back into full-dimensional displacement, and \({\varepsilon }_{\mathbf{x,i}}\) is the corresponding noise assigned to the observation model.

Based on the surrogate modeling and following the derivations given in Eq. (13), the likelihood of observing \(\varvec{u_x}\) is computed by

$$\begin{aligned} \begin{aligned}&f({{\mathbf{u}}_x} \vert {l_i},\;{a_i},\;{{\mathbf{h}}_i}) \\&\quad = \frac{{\exp \left( { - 0.5{{\left( {{{\mathbf{u}}_x} - {{\mu }_x}} \right) }^\mathrm {T}}{\varvec{\Sigma }}_x^{ - 1}\left( {{{\mathbf{u}}_x} - {{\mu }_x}} \right) } \right) }}{{\sqrt{{{(2\pi )}^{{N_P}}} \vert {{\varvec{\Sigma }}_{x}} \vert } },} \end{aligned} \end{aligned}$$
(14)

where \({\mu }_x\) and \({\varvec{\Sigma }}_x\) are given by

$$\begin{aligned} {{\mu }_x} = \sum \limits _{j = 1}^{{N_x}} {{\mu _{x,j}}({l_i},\;{a_i},\;{{\mathbf{h}}_i}){{{\eta }}_j}} , \end{aligned}$$
(15)

and \({\varvec{\Sigma }}_x\) is a co-variance matrix with the (i, j)-th, \(\forall i,\;j = 1,\; \cdots ,\;{N_P}\) element given by

$$\begin{aligned} {\Sigma _{q,r}} = \sum \limits _{j = 1}^{{N_x}} {\sigma _{j,x}^2({l_i},\;{a_i},\;{{\mathbf{h}}_i}){{{\eta }}_{jq}}{{{\eta }}_{jr}}}, \end{aligned}$$
(16)

in which \({{\eta }}_{jq}\) and \({{\eta }}_{jr}\) are respectively the q-th and r-th element of the j-th basis \({{\eta }}_{j}\). The likelihood function \(f({{\mathbf{u}}_z} \vert {l_i},\;{a_i},\;{{\mathbf{h}}_i})\) of observing \(\varvec{u_z}\) is computed similarly to \(\varvec{u_x}\),

$$\begin{aligned} \begin{aligned}&f({{\mathbf{u}}_z} \vert {l_i},\;{a_i},\;{{\mathbf{h}}_i})\\&\quad = \frac{{\exp \left( { - 0.5{{\left( {{{\mathbf{u}}_z} - {{\mu }_z}} \right) }^\mathrm {T}}{\varvec{\Sigma }}_z^{ - 1}\left( {{{\mathbf{u}}_z} - {{\mu }_z}} \right) } \right) }}{{\sqrt{{{(2\pi )}^{{N_P}}} \vert {{{\varvec{\Sigma }}_z}} \vert } }}. \end{aligned} \end{aligned}$$
(17)

The focus of this research with regard to image monitoring data is its utilization for diagnosis and prognosis. Therefore, a simplified transformation from 3D to image coordinates is presented and synthetic camera measurements are generated. The accurate collection of camera displacement measurements to achieve the research’s diagnosis and prognosis results is left to future work. In particular, future work would define the correct transformation from the FE displacement results into image displacements. Then, a fatigue experiment on a cruciform similar to Fig. 9 here could be observed using high resolution cameras. The diagnosis and prognosis proposed in this research could be applied to estimate the crack length and parameters. Then this research could be validated against other experimental techniques.

The two types of the observations based on the miter gate physics are now fully described. We next consider the integration of multi-mode damage diagnosis and failure prognosis using a DBN framework.

3.2 SHM using DBN

3.2.1 DBN for miter gates with multiple failure modes

We assume that there is uncertainty from noise in the two data sources, i.e., sensor noise and camera image quality; thus, a DBN is constructed which accommodates measurement uncertainty of observations along with probabilistic transitions of damage modes over time. Figure 11 shows the feature of interest represented by different types of DBN nodes and their connections at two consecutive time steps (\(t_{i-1}\) and \(t_i\)). The continuous nodes represents the two state variables that quantify the two failure modes of miter gate at time step \(t_i\), referred to as \(l_i\) and \(a_i\). The observed nodes described the measurements associated with the unknown nodes. Besides the strain reading \(S^\mathrm{{obs}}\) and digital images \(I^{obs}\), the upstream and downstream water levels can be also measured at any time step. Thus, the hydrostatic pressure condition \(\mathbf{h}\) is assumed to be observable and static at each time step without measuring error (The staff gage measurement error is so low that it is ignored in this study). The arrows, meanwhile, indicate the probabilistic connection and interaction between different variables, i.e., the dashed lines represent the connection between continuous nodes in two consecutive time steps and the solid lines represent the interaction between nodes in individual time step. For example, the crack length \(a_i\) is dependent on not only the crack length at previous time step, i.e., \(a_{i-1}\), but also the crack increment that dominated by Paris’ law, i.e., c, m, \(\Delta K_i\). Table 1 summarizes the variables of the DBN.

Fig. 11
figure 11

Dynamic Bayesian network for miter gate with multi-failure modes

Full size image
Table 1 Nomenclature for the DBN
Full size table

3.2.2 Surrogate-based IGL in DBN

As mentioned above, the physics of the crack is simulated by the IGL algorithm, which provides the SIF value at any time step for the Paris’ law. However, a single run of getting the SIF result from the IGL global and local analysis takes up to 10 min due to the complex local XFEM model. Generally, probabilistic analysis for damage diagnostics and failure prognostics, such as Bayesian updating and uncertainty propagation, requires the model to be executed thousands of times. Thus, for a fast yet accurate calculation of SIF given the parameters \(\mathbf{h}\), \(l_{i}\) and \(a_i\), a surrogate-based IGL (SIGL) algorithm is used for the purpose of computational efficiency. Algorithm 1 presents a pseudocode of surrogate-based IGL method. Details of the SIGL method are available in Fillmore et al. (2022).

figure a

As shown in Fig. 12, the global FE analysis is accelerated by using static condensation (denote FastGlobal Algorithm 1) where the global displacement along global-local boundary is obtained directly from a static-condensed matrix; while the local FE analysis is replaced by GP-based surrogate model (denote SurrogateLocal in Algorithm 1). Such setup shortens the computational time for one global-local simulation from 10 min to less than 0.1 s, enabling damage diagnostics and failure prognostics.

$$\begin{aligned} \Delta K_i = {G_{SIGL}}({l_i},\;{a_i},\;\Delta {s_i}), \end{aligned}$$
(18)

where \({G_{SIGL}}({l_i},\;{a_i},\;\Delta {s_i})\) is the SIGL algorithm that enables a fast calculation of SIF range \(\Delta K_i\).

Fig. 12
figure 12

Surrogate-based IGL with global static condensation

Full size image

With the capability of acquiring SIFs via SIGL model in affordable amounts of time, the process of using a dynamic Bayesian network (DBN) with two synthetic observations is represented in the following section.

3.2.3 Diagnostics and prognostics of multiple failure modes with DBN and maintenance optimization

Based on the surrogate modeling, functional representation, and probabilistic modeling of different nodes in the DBN, we now present the diagnostics and prognostics of miter gates with multiple failure modes using the DBN and multiple data sources (i.e. strain measurements and image monitoring data).

3.2.3.1 Damage diagnostics with DBN

Under the Bayesian updating framework, the damage states including gap degradation \(l_i\) and crack length \(a_i\) at \(t_i\) are estimated along with the uncertain crack growth model parameters as follows

$$\begin{aligned} \begin{aligned}&f({c_i},\;{m_i},\;{l_i},\;{a_i}\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}) \\&\quad = { \frac{{f({\mathbf{y}}_i^{obs}\vert {\mathbf{h}}_i^{obs},\;{{\theta }_i})f'({{\theta }_i})}}{{\int { \cdots \int \!\!\!\int {f({\mathbf{y}}_i^{obs}\vert {\mathbf{h}}_i^{obs},\;{{\theta }_i})f'({{\theta }_i}){\mathbf{d}}{{\theta }_i}} } }}} \\&\quad \propto f({\mathbf{y}}_i^{obs}\vert {\mathbf{h}}_i^{obs},\;{{\theta }_i})f'({{\theta }_i}), \end{aligned} \end{aligned}$$
(19)

where

$$\begin{aligned} \begin{aligned}&{{\theta }_i} \buildrel \textstyle .\over = [{c_i},\;{m_i},\;{l_i},\;{a_i}] \\&{\mathbf{y}}_{1:i}^{obs} \buildrel \textstyle .\over = [\;{\mathbf{s}}_{1:i}^{obs},\;{\mathbf{u}}_{x,1:i}^{obs},\;{\mathbf{u}}_{z,1:i}^{obs}] \\&{\mathbf{y}}_i^{obs} \buildrel \textstyle .\over = [\;{\mathbf{s}}_i^{obs},\;{\mathbf{u}}_{x,i}^{obs},\;{\mathbf{u}}_{z,i}^{obs}] \end{aligned} \end{aligned}$$
(20)

\(f({\mathbf{y}}_i^{obs}\vert {\mathbf{h}}_{i}^{obs},\;{{\theta }_i})\) is the likelihood function of observing the two types of data sources (i.e. strain measurements and displacement images), and \(f'({{\theta }_i})\) is the prior distribution at time \(t_i\) given by

$$\begin{aligned} \begin{aligned} f'({{\theta }_i})&= f({c_i},\;{m_i},\;{l_i},\;{a_i}\vert {\mathbf{y}}_{1:i - 1}^{obs},\; {\mathbf{h}}_{1:i-1}^{obs}), \\&= \int { \cdots \int \!\!\!\int {f({{\theta }_i}\vert {{\theta }_{i - 1}})f({{\theta }_{i - 1}}\vert {\mathbf{y}}_{1:i - 1}^{obs},\; {\mathbf{h}}_{1:i-1}^{obs}){\mathbf{d}}{{\theta }_{i - 1}}} ,} \end{aligned} \end{aligned}$$
(21)

in which \({f({{\theta }_i}\vert {{\theta }_{i - 1}})}\) represents the state transition between two time steps.

Considering the two different types of data sources and according to the graphic model given in Fig. 11, the likelihood function \(f({\mathbf{y}}_i^{obs}\vert {\mathbf{h}}_{i}^{obs},\;{{\theta }_i})\) is computed based on the chain rule of Bayesian networks as follows

$$\begin{aligned} \begin{aligned}&L({\mathbf{s}}_i^{obs},\;{\mathbf{u}}_{x,i}^{obs},\;{\mathbf{u}}_{z,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{c_i},\;{m_i},\;{l_i},\;{a_i}) \\&\quad = f({\mathbf{s}}_i^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_i})f({a_i}\vert {\mathbf{h}}_i^{obs},\;{l_i},\;{c_i},\;{m_i}) \\&\qquad \times f({\mathbf{u}}_{x,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_i},\;{a_i})f({\mathbf{u}}_{z,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_i},\;{a_i}), \end{aligned} \end{aligned}$$
(22)

where \(f({\mathbf{s}}_i^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_i})\) is given in Eq. (10), \(f({\mathbf{u}}_{x,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_i},\;{a_i})\) and \(f({\mathbf{u}}_{z,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_i},\;{a_i})\) are given in Eq. (14), and \(f({a_i}\vert {\mathbf{h}}_i^{obs},\;{l_i})\) is obtained through uncertainty propagation using the surrogate-based IGL method, which first propagates the uncertainty of \({l_i}\) to the uncertainty of SIF range \(\Delta K_i\) using Eq. (18) and then to crack length \({a_i}\) using Eq. (5).

In this paper, the particle filter (PF) is used as the Bayesian inference algorithm which enables a quantitative way to track and evaluate the evolution of the state variables in the DBN. The PF is designed to achieve an optimum estimate of the posterior probability density functions \(f(l_i \vert S^{obs}_{1:i},\;{\mathbf{h}}^{obs}_{1:i})\) and \(f(a_i \vert S^{obs}_{1:i},\;I^{obs}_{1:i},\;{\mathbf{h}}^{obs}_{1:i})\) based on observations \(S^{obs}_{1:i}\), \(I^{obs}_{1:i}\), and \({\mathbf{h}}^{obs}_{1:i}\). It starts with prior samples of state variables in the network. For the first time step, the prior samples are generated according to empirical research and prior knowledge of the physics. For the other time steps, the prior samples are obtained through uncertainty propagation from the previous time step (i.e. Eq. (21)).

Assuming that \(N_p\) particles are generated at each time step, we have the particles of the state variables at \(t_{i}\) as

$$\begin{aligned} \begin{aligned}&{\theta }_i^p \buildrel \textstyle .\over = [{\mathbf{l}}_i^p,\;{\mathbf{a}}_i^p,\;{\mathbf{c}}_i^p,\;{\mathbf{m}}_i^p], \\&{\mathbf{l}}_i^p \buildrel \textstyle .\over = [l_{i1}^p,\; \cdots ,\;l_{i{N_p}}^p];\;{\mathbf{a}}_i^p \buildrel \textstyle .\over = [a_{i1}^p,\; \cdots ,\;a_{i{N_p}}^p]; \\&{\mathbf{c}}_i^p \buildrel \textstyle .\over = [c_{i1}^p,\; \cdots ,\;c_{i{N_p}}^p];\;{\mathbf{m}}_i^p \buildrel \textstyle .\over = [m_{i1}^p,\; \cdots ,\;m_{i{N_p}}^p]; \end{aligned} \end{aligned}$$
(23)

in which \(a_{ij}^p, a_{ij}^p, c_{ij}^p, \text {and} \, m_{ij}^p, \forall j=1, \cdots , N_p\) is the j-th particle at \(t_i\).

The likelihood function of each particle is then computed using Eq. (22) as

$$\begin{aligned} \begin{aligned}&\log {L({\mathbf{s}}_i^{obs},\;{\mathbf{u}}_{x,i}^{obs},\;{\mathbf{u}}_{z,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{\theta _{ij}})}\\&\quad = \alpha \cdot \log ({f({\mathbf{s}}_i^{obs}\vert {\mathbf{h}}_i^{obs},\;{l_{ij}})})\\&\qquad + \beta \cdot [\log ({f({\mathbf{u}}_{x,i}^{obs}\;\vert {\mathbf{h}}_i^{obs},\;{\theta _{ij}})})\\&\qquad +\log ({f({\mathbf{u}}_{z,i}^{obs}\;\vert {\mathbf{h}}_i^{obs},\;{\theta _{ij}})})], \end{aligned} \end{aligned}$$
(24)

where \(\alpha\) and \(\beta\) are the coefficients for two likelihood functions. When the importance of two measurements are equally considered, \(\alpha = 1\) and \(\beta = 1\), respectively. When only image data is considered, \(\alpha = 0\) and \(\beta = 1\).

Based on the above likelihood function, the weight of each particle is computed by

$$\begin{aligned} \begin{aligned} {w_j}&= {\frac{{L({\mathbf{s}}_i^{obs},\;{\mathbf{u}}_{x,i}^{obs},\;{\mathbf{u}}_{z,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{{\theta }_{ij}})}}{{\sum \nolimits _{j = 1}^{{N_p}} {L({\mathbf{s}}_i^{obs},\;{\mathbf{u}}_{x,i}^{obs},\;{\mathbf{u}}_{z,i}^{obs}\vert {\mathbf{h}}_i^{obs},\;{{\theta }_{ij}})} }}}, \\ \forall j&= 1,\; \cdots ,\,{N_p}. \end{aligned} \end{aligned}$$
(25)

The joint posterior distribution given in Eq. (19) is then approximated based on the particles based on re-sampling using the weights given in Eq. (25) as

$$\begin{aligned} \begin{aligned} f({c_i},\,{m_i},\;{l_i},\;{a_i}\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}) \approx \sum \limits _{j = 1}^{{N_p}} {{w_j}{\delta _{{{\theta }_i}}}}, \end{aligned} \end{aligned}$$
(26)

where \({\delta _{{{\theta }_i}}}\) is a delta function at \({\theta }_i=[c_i, m_i, l_i, a_i]\).

Let the posterior particles of l, a, c, and m at \(t_i\) after re-sampling be \({{\mathbf{l}''}_i} = [{l''_{i1}},\; \cdots ,\;{l''_{i{N_p}}}]\), \({{\mathbf{a}''}_i} = [{a''_{i1}},\; \cdots ,\;{a''_{i{N_p}}}]\), \({{\mathbf{c}''}_i} = [{c''_{i1}},\; \cdots ,\;{c''_{i{N_p}}}]\), and \({{\mathbf{m}''}_i} = [{m''_{i1}},\; \cdots ,\;{m''_{i{N_p}}}]\). These particles are then used to obtain the prior samples for \(t_{i+1}\) based on state transition probability \({f({{\theta }_i}\vert {{\theta }_{i - 1}})}\). For unknown constant parameter such as c and m, a very small noise amount is added to prevent particle degeneration during PF implementation. The transition equations are defined as below:

$$\begin{aligned} \begin{aligned} {c_{(i+1)j}^p}&= {c''_{ij}} + {\varepsilon _{c,i+1}}, \\ {m_{(i+1)j}^p}&= {m''_{ij}} + {\varepsilon _{m,i+1}}, \end{aligned} \end{aligned}$$
(27)

in which \({c_{(i+1)j}}\) and \({m_{(i+1)j}}\) are respectively the j-th prior sample of c and m at \(t_{i+1}\), \({\varepsilon _{c,i+1}}\) and \({\varepsilon _{m,i+1}}\) are very small noises to avoid sample degeneration as mentioned above.

For the gap length state variable, the posterior samples of \(l_i\) is used to obtain the prior samples at \(t_{i+1}\) as

$$\begin{aligned} \begin{aligned} l_{(i+1)j}^p&= l''_{ij} + exp(\sigma u_j)Q(l''_{ij})^{w}, \\ \forall j&=1, \cdots , N_p \end{aligned} \end{aligned}$$
(28)

where \(u_j\) is a random sample of a standard normal random variable.

For state variable \(a_i\), as shown in Fig. 11, the posterior samples are first passed through Eq. (18) (i.e. a functional node) to obtain samples of \(\Delta K_i\). The prior samples \(a_{(i+1)j}^p\) are then obtained through Eq. (5) given in Sect. 2. The above process (i.e. Eqs. (19) through (28)) is implemented recursively over time to perform damage diagnostics of miter gate with multiple failure modes.

3.2.3.2 Failure prognostics with DBN

Failure prognostics is a process of predicting the remaining useful life (RUL) of structural assets based on all the information available at the current time step. The RUL information gives the engineers insight into life-cycle maintenance. Figure 13 shows an illustration of how to perform RUL prediction based on failure prognostics.

Fig. 13
figure 13

Illustration of EOL to obtain RUL prediction based on failure prognostics

Full size image

Based on the state estimation from failure diagnostics at time step \(t_{i}\), the end of life (EOL) can be determined which is defined as the intersection point between feature limit state and predicted curve of damage growth path.

Through particles obtained at time step \(t_i\), a family of degradation curves can be obtained as illustrated in Fig. 13. Based on that, a distribution of EOL of the structures can be approximated by collecting all the intersection points. The RUL is determined as the difference between EOL and the current time step. The probability that the RUL at \(t_i\) is less than p conditioned on current observations is given by

$$\begin{aligned} \begin{aligned} \Pr \{ RUL_{l,i}&\le p\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}\} \\&= \int {\Pr \{ {l_{i + p}} \ge {l_e}\vert {l_i}\} f({l_i}\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs})} d{l_i}, \end{aligned} \end{aligned}$$
(29)

where \(RUL{_{l,i}}\) is the RUL at time step \(t_i\) for failure mode of gap degradation, \({l_e}\) is the failure threshold of gap length and \({f({l_i}\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs})}\) is the posterior distribution of gap length at time step \(t_{i}\).

Equation (29) is approximated using the Monte Carlo simulation method based on the posterior particles from DBN as follows

$$\begin{aligned} \begin{aligned} \Pr \{ RUL{_{l,i}}&\le p\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}\} \\&\approx {\frac{1}{{N_p}}}\sum \limits _{k = 1}^{{N_p}} {\Lambda ({l_{(i + p)k}} \ge {l_e}\vert l''_{ik})} , \end{aligned} \end{aligned}$$
(30)

in which \(N_p\) is the number of particles in the inference using DBN, \(l''_{ik}\) is the k-th posterior particle of gap length at \(t_i\), and \({\Lambda ({l_{(i + p)k}} \ge {l_e} \vert l''_{ik})}=1\) if \({{l_{(i + p)k}} \ge {l_e} \vert l''_{ik}}\) is true, otherwise \({\Lambda ({l_{(i + p)k}} \ge {l_e} \vert l''_{ik})}=0\), and \({{l_{(i + p)k}} \ge {l_e} \vert l''_{ik}}\) stands for a trajectory of random gap growth curve conditioned on initial state \(l''_{ik}\) as indicated in Fig. 13.

Similarly, the RUL at \(t_i\) corresponding to failure mode of fatigue crack is estimated by

$$\begin{aligned} \begin{aligned} \Pr \{ RUL{_{a,i}}&\le p\vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}\} \\&\approx {\frac{1}{{N_p}}}\sum \limits _{k = 1}^{{N_p}} {\Lambda ({a_{(i + p)k}} \ge {a_e} \vert l''_{ik},\;a''_{ik},\;c''_{ik},\;m''_{ik})} , \end{aligned} \end{aligned}$$
(31)

where \(RUL_{a,i}\) is the RUL corresponding to crack at \(t_i\), \(a_e\) is the failure threshold for fatigue crack, and \(a''_{ik},\;c''_{ik},\;m''_{ik}\) are the k-th posterior particle.

The overall system RUL is then obtained based on Eq. (29) through (31) as

$$\begin{aligned} \begin{aligned} \Pr \{ RUL&\le p \vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}\} \\&= \int F_{i \vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}}(p)] \\&\approx {\frac{1}{{N_p}}}\sum \limits _{k = 1}^{{N_p}} {\Lambda ({l_{(i + p)k}} \ge {l_e} \vert l''_{ik}\;} \\&\qquad \cup \;{a_{(i + p)k}} \ge {a_e} \vert l''_{ik},\;a''_{ik},\;c''_{ik},\;m''_{ik}), \\ \end{aligned} \end{aligned}$$
(32)

where \(F_{i \vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}}(p)]\) is the failure probability in the future p time steps conditioned on observations \(\mathbf{y}_{\mathbf{1:i}}^\mathbf{obs}\) and \(\mathbf{h}_{\mathbf{1:i}}^\mathbf{obs}\), and “\(\cup\)” indicates “union” of two events which means that the gate fails if either one of the two failure modes occurs.

3.2.3.3 Optimal maintenance planning based on failure prognostics

The RUL estimation in failure prognostics provides an informative way of understanding how damage progresses in time. Consequently, maintenance decisions may be optimized and updated based on the structural condition assessment. In this paper, the cost per unit of time (CPUT) is employed for maintenance optimization based on failure prognostics. CPUT is a cost function proposed by Barlow and Hunter (1960), which defines the cost of performing preventive maintenance at time t as

$$\begin{aligned} \begin{aligned} CPUT(t) = \frac{C_p[1-F_i(t)]+C_u[F_i(t)]}{[\int _{0}^{t} [1-F_i(\tau )] \,d\tau ]}, \end{aligned} \end{aligned}$$
(33)

where \(C_p\) is the preventative action cost, \(C_u\) is the unplanned action cost, and \(F_i(t)\) is the failure probability given in Eq. (32) (i.e., \(F_{i \vert {\mathbf{y}}_{1:i}^{obs},\;{\mathbf{h}}_{1:i}^{obs}}(p)\)). Note that Eq. (33) is meaningful only if the cost ratio, \(C_u/C_p\), is greater than 1, otherwise no maintenance operation is needed. It is suggested in Vega et al. (2020) that the corresponding cost ratio for some miter gates is close to 5. A larger cost ratio would represent the case that unplanned failure may have a much more severe consequence cost compared to preventative action. The optimal time for maintenance planning is then defined as the time when CPUT is minimized, given the different values of \(C_p\) and \(C_u\). In addition, the optimal maintenance time is decreasing over time as suggested in Vega et al. (2020).

Next, we will use a case study to illustrate the proposed framework for damage diagnostics and failure prognostics of multi-mode failure using multiple data sources.

4 Case study

4.1 Prior information and measurements

With the above formulated training process, the test case is carried below. In this paper, the physical value of one time step is set to be one month. The true values of parameters c and m are set as \(c=3 \times 10^{-4}\) and \(m=2.2\), respectively. The number of particles in the PF is set as \(N_p = 50,000\). Based on our best engineering assumptions, the truncated uniform prior distributions of c and m are set as \(c \sim U[1 \times 10^{-4},1 \times 10^{-3}]\) and \(m \sim U[1,3]\), where U[lb, ub] represents uniform distribution with lower bound lb and upper bound ub. The initial gap length and crack length are set as \(l_0=50 \; \text {inches}\) and \(a_0=1 \; \text {inch}\), respectively. Figure 14 shows the gap and crack growth curves used to generate synthetic data. The failure thresholds of gap length and crack length are set to \(l_{e}=100 \; \text {inches}\) and \(a_{e}=3 \; \text {inches}\). Correspondingly, the true EOLs are determined as 82.7 months and 87.7 months, respectively. Note that the true EOLs for the two damage features are selected on purpose to have similar values, in order to show the performance of damage prognostics using jointed observations.

Fig. 14
figure 14

True gap and crack growth curves for synthetic data generation

Full size image

The true states of the two failure modes are assumed to be unknown during the diagnosis and prognosis. To validate the proposed DBN framework, two sets of synthetic measurements are firstly generated based on the structure under crack and quoin block degradation. Figure 15 presents 1000 readings of the four strain gages obtained based on the synthetic gap data given in Fig. 14 and water level data where \(h_{up} \sim N(550,20)\), \(h_{down} \sim N(150,20)\). Figure 16 depicts the displacement measurements at each time step with a pixel size of 0.5 inches where the crack grows from 0.5 inches to 4 inches. As indicated in this figure, the displacement in the z direction increases with the growth of crack length, which is manifested in the displacement images as more red colors in the upper part and more blue colors in the lower part (surface fractures into opposite directions).

Fig. 15
figure 15

Synthetic strain measurements from the four sensor locations

Full size image
Fig. 16
figure 16

Displacement measurement with pixel size 0.5 in. and Gaussian noise

Full size image

4.2 Results and discussion

Based on the synthetic data presented in Sect. 4.1, the DBN model takes in the two measurements to calculate corresponding likelihood functions base on their weights of importance. By setting the coefficients for the two likelihood functions, \(\alpha\) and \(\beta\), the distributions of the state variables are updated at each time step. Figure 17 presents the diagnostic result of the two damage features, crack length a and quoin damage length l, when different measurement inputs of DBN are defined. In Fig. 17a and b, two types of observations are used, i.e., \(\alpha = 1\) and \(\beta = 1\). The mean prediction and the \(95\%\) confidence intervals suggest that both two variables a and l are estimated with high accuracy. For the case when only displacement data are available ( \(\alpha = 1\) and \(\beta = 1\)) as shown in Fig. 17c and d, the proposed damage estimation method is still able to accurately estimate the crack length length. However, the accuracy of the gap length estimation significantly drops, reflected by the error of mean prediction and increased confidence intervals. While the images taken far from the bottom quoin are not sensitive enough to detect the quoin block deterioration compared to the strain measurements, incorporating multiple data sources with different sensitivities to damages features are essentially required to obtain accurate prediction.

Fig. 17
figure 17

Diagnostic results when using different measurement inputs: a Posterior distribution of crack length a using both \(S^{obs}\) and \(I^{obs}\), b posterior distribution of quoin block damage length l using both \(S^{obs}\) and \(I^{obs}\), c posterior distribution of crack length a using \(I^{obs}\) only, and d posterior distribution of quoin block damage length l using \(I^{obs}\) only

Full size image

The failure prognosis depends upon the target damage feature and the definition of failure. The following prognostic results are carried out based on considering crack and quoin block damage individually and considering two damage features jointly. Figure 18 shows the prognostic result when considering the crack only. The true RUL of the structure is 82.7 months. Four cases are shown here which represent the four stages of the structural life-cycle: Fig. 18a is an early stage of the crack initiation, where the prognostic result overestimates the RUL of the structures by 10 months. The error between mean prediction and true value is improved to around 1 month after 20 months, shown in Fig. 18b. At the 60th month and 80th month, the prediction becomes more and more accurate.

Fig. 18
figure 18

RUL results based on crack prognostics only

Full size image

The prognostic result when considering gap length only is shown in Fig. 19. The true RUL of the structure is 87.5 months based on quoin block damage. In this case, the prediction is consistently accurate, as the prediction of the gap length follows the true RUL in all life stages.

Fig. 19
figure 19

RUL results based on gap prognostics only

Full size image

Figure 20 shows the prognostic result when the joint failure threshold is determined as the smaller of the crack and gap length damage limits. The predicted RUL outperformed both results of using single failure threshold. In the first stage (before 35 months), the prediction slightly overestimates the RUL of the structure; in the second state (after 35 months), the model tends to be more conservative about the prediction as the predicted RULs are smaller than the true values. Such pattern will lead to different risk-based life-cycle managements during the optimal maintenance planning process, considering the different combination of preventative action cost and unplanned action cost.

Fig. 20
figure 20

RUL results based on jointed failure threshold

Full size image

Figure 21 shows the overall RUL estimation at each time step and its confidence limits when considering the crack as the only damage feature. Although the prediction of the crack is very inaccurate in the early months, the model manages to converge the prediction to the true value after around 30 months with a high confidence level.

Fig. 21
figure 21

RUL estimation at all time steps based on crack prognostics only

Full size image

Figure 22 shows the RUL estimation at each time step and its confidence limits when considering gap as the only damage feature. The gap prediction fluctuates around the true gap RUL, and both prediction error and confidence limit converge to at the final time step.

Fig. 22
figure 22

RUL estimation at all time steps based on gap prognostics only

Full size image

Considering both the crack and the gap as damage features, Fig. 23 shows the RUL estimation at each time step and its confidence limits. Similarly, the prediction outperformed both results of using single failure threshold when the EOL is jointly determined from the two damage features.

Fig. 23
figure 23

RUL estimation at all time steps based on jointed failure threshold

Full size image

The RUL prediction from failure prognostics is actually related to the reliability. Based on the reliability function obtained from predicted RULs at each time step, the CPUT can be calculated and updated as time evolves. Figure 24 shows CPUT at time step 50th month with different cost ratios. It can be seen that as the unplanned action cost grows, i.e., \(C_u\) increases, the optimal maintenance time decreases, and the corresponding CPUT becomes stable at a large value.

Fig. 24
figure 24

CPUT at 50 months corresponding to different values of \(C_u\) and \(C_p\)

Full size image

To understand the impact of different monitoring techniques (e.g., strain gages and camera images) on decisions related to maintenance planning, the optimal maintenance time and minimum CPUT are calculated based on the prognostics results using measurements from both monitoring techniques and from camera images only. Figure 25 shows how the optimal maintenance time (i.e., the time when CPUT is minimized) are updated from the measurements over time, when \(C_u = 1\) and \(C_p = 50\). The vertical line in the figure represents the true end of life, which is the time that one of the two competing damage features first reaches its failure threshold. As noted, the two curves of optimal maintenance time are very similar, which is due to the high accuracy of the failure prognostics results. Figure 26a shows the minimum CPUT when \(C_u = 1\) and \(C_p = 50\). By zooming into the curve after 65 months, the result clearly proves that the uncertainty in Fig. 17d consequently leads to a higher minimum CPUT compared to that of Fig. 17b. It implies that including multiple monitoring techniques can help reduce the minimum CPUT, which will result in a minimized overall maintenance cost. This demonstrates the value of adopting an additional monitoring technique. It is worth noting that the amount of cost savings by adding an additional monitoring technique should be compared against the cost of installing the system to justify the adoption of the technique. It is an interesting topic that worth investigating in future work, using a value-of-information analysis.

Fig. 25
figure 25

Optimal maintenance time corresponding to \(C_u = 1\) and \(C_p = 50\)

Full size image
Fig. 26
figure 26

a Minimum CPUT corresponding to \(C_u = 1\) and \(C_p = 50\), b minimum CPUT approaching end of life

Full size image

5 Conclusions

In this paper, an online diagnostic and prognostic framework that efficiently used multi-source data was proposed for structures with multiple failure modes. A high-fidelity FE model was used as a physics-based emulator of two different kinds of deterioration mechanisms, the loss of contact “gap” and fatigue crack growth. The separation of damage scales has been carefully studied through global-local analysis. Two surrogate models were created and trained to generate synthetic observations (digital images and sensor data), which replaced the time-consuming FE model and enables the extensive model-based analysis of miter gates. The multi-source observations were passed through a dynamic Bayesian network for online diagnostics and prognostics. In diagnostics, the framework successfully determined the damage-related parameters as well as estimated damage conditions. In prognostics, the RUL of both failure modes were accurately predicted as time evolved. Based on the RUL results, the impact of the optimal maintenance planning of the miter gate was studied. It is found that including multiple monitoring techniques can help reduce the maintenance cost. The contributions of this paper can be summarized as: (1) Implementation of a digital twin concept for a practical engineering problem with complicated degradation behaviors, which requires extensive model-based analysis to capture the interactions between multiple damages; (2) The extension of the widely DBN framework to fuse information from strain gages and camera for damage diagnostics and failure prognostics of miter gates; and (3) The investigation of the impact of using multiple structural health monitoring data sources (i.e. strain sensor and camera) on the final maintenance decision making process.

To conclude, the proposed framework provides a new approach of using DBN to incorporate multiple data sources for structures under different scales of failure modes. Although the synthetic failure mechanisms and measurement data were simplified for illustration purposes, such DBN framework can be extended to more complicated structures for more informative life-cycle management and risk-based decision analysis. Future research will look at a more thorough study at the impact of digital image quality and more accurate failure representation.