1 Introduction

At the end of the twentieth century, Bendsøe and Kikuchi (1988) proposed the homogenization method and applied it to the field of structural topology optimization. Topology optimization shows the capability of providing more novel and highly efficient designs, which is far superior to traditional size and shape optimization. Since then, topology optimization has been widely used in many research fields and industrial production fields. Different topology optimization approaches have been developed, such as solid isotropic material with penalization (SIMP) approach (Sigmund 2001), the level-set method (LSM) (Allaire et al. 2004), and evolutionary structural optimization (Xie and Steven 1993) (ESO)/bi-evolutionary structural optimization (BESO) method (Querin et al. 1998). Sigmund and Maute (2013), Xia et al. (2018), and van Dijk et al. (2013) provide good overview of these works.

Most of the existing works carried out based on linear elastic materials in the case of small deformations and many meaningful research results are obtained. In most practical engineering problems, the linear assumption can be used to obtain a good design result. However, when large displacements or large strains occur in the structure, the linear assumption cannot reflect the real response of the structure, resulting in failure to obtain reasonable optimization results. For some problems, the linear assumption will no longer be valid, such as compliant mechanism design (Bendsøe and Sigmund 2004). Therefore, the nonlinear effects must be considered.

Research on nonlinear topology optimization can be traced back to the late 1990s. Bendsøe (1995), Jog (1996), and Bruns and Tortorelli (1998) made some upfront jobs. However, in their papers, the examples did not show the significant differences between optimized structures under the linear assumption and nonlinear assumption. Buhl et al. (2000) gave a very detailed description of the optimization formula after considering the geometric nonlinearity and sensitivity derivation process. The optimization framework he proposed has also become a standard framework for subsequent researchers to conduct research on nonlinear topology optimization.

In recent years, the job that focuses on topology optimization considering nonlinearity has been rapidly developed; much valuable work emerged. After Buhl (Buhl et al. 2000) proposed the SIMP-based nonlinear topology optimization framework, Kwak and Cho (2005) developed an analysis framework based on LSM in 2005, and Huang and Xie (2007, 2008) used the BESO method to solve nonlinear topology optimization in 2007. When conducting the nonlinear topology optimization, no matter what method used, it is inevitable that the “numerical instability” phenomenon occurs in the low stiffness regions during the optimization. The methods to solve numerical instability have become an essential part of studying nonlinear topology optimization. In this regard, many researchers have carried out very valuable work; e.g., Bruns and Tortorelli (2003) proposed the low-density element eliminated method, Yoon and Kim (2005) proposed the “element connection parameterization (ECP)” method, Wang et al. (2014) proposed the energy interpolation scheme, and Luo et al. (2015) proposed the “additive hyperelasticity technique.” The emergence of these numerical methods has dramatically improved the effect of nonlinear topology optimization and reduced the difficulty of problem-solving. In addition, there are also many researchers who studied the specific issues with nonlinear topology optimization, such as Pedersen et al. (2001), Bruns and Tortorelli (2001, 2003), and Luo and Tong (2008) who investigated the nonlinear topology optimization of compliant mechanisms from different aspects. Kang and Luo (2009) considered geometric nonlinearity in reliability-based topology optimization design. Li et al. (2019) developed a shape-preserving design using topology optimization based on geometric nonlinearity.

For most of the works relate to nonlinear topology optimization, it is based on the St. Venant Kirchhoff model. Nevertheless, the St. Venant Kirchhoff model is an extension of the linear model and does not provide a physically correct response under large loads. Especially for designing compliant mechanisms made from soft rubber materials, where choosing a constitutive that can describe the material response more accurately is essential. Recently, more realistic hyperelastic material models have employed in structural topology optimization. Such materials usually exhibit a strong nonlinear stress-strain relationship and can recover even after huge strains. At the same time, research shows that the use of hyperelastic material models in topology optimization can alleviate the numerical instability of low stiffness regions to a certain extent. Using hyperelastic material models in nonlinear topology optimization is a desirable option. In this regard, Ha and Cho (2008), Klarbring and Strömberg (2013), Wallin and Ristinmaa (2015), Luo et al. (2016), Chen et al. (2017), Chen et al. (2018), Chi et al. (2019), and Deng et al. (2019) have done a lot of valuable works that incorporate hyperelastic material models into nonlinear topology optimization.

Although research on nonlinear topology optimization has made great progress, there are still some problems that need further research. Firstly, most of the work mentioned above is based on the SIMP method or the level-set method. As an essential branch of the topology optimization method, research on nonlinear topology optimization based on ESO/BESO and its extension method is minimal. As far as the author knows, Besides Huang and Xie (2007, 2008) did groundbreaking work using the BESO method to deal with nonlinear topology optimization problems, only Abdi (Abdi et al. 2018) proposed to replace traditional FEA by XFEM under the framework of BESO, Xu (Xu et al. 2020) explored problems with stress constraints, and Shobeiri (2020) explored nonlinear topology optimization under dynamic loads using the BESO method. Obviously, research on nonlinear topology optimization based on this kind of evolutionary method is very lacking, especially in the case of large deformations. Secondly, the research for exploring nonlinear topology optimization methods that can achieve a smooth structural boundary representation without initial layout dependency is still limited. Thirdly, as we all know, fine branches inside the structure are likely to buckle under large loads, which will affect the structural performance. How to reduce the possibility of fine branches buckling in a simple way still needs to be further explored.

Motivated by the above considerations, this paper proposes a new framework aiming to solve the problem of designing hyperelastic structures that undergo large deformations. The new framework is based on the modified evolutionary topology optimization (M-ETO) method, which introduces the projection scheme into the evolutionary topology optimization (ETO) method (Da et al. 2018). The original ETO method is an extension of BESO. In M-ETO, just like the traditional BESO, the elemental sensitivity numbers are first calculated and then convert them into nodal sensitivity numbers. The nodal sensitivity numbers are used to construct the level-set function, which aims to achieve smooth structural boundary representation. To enhance robustness and manufacturability, the projection scheme is introduced. A combination strategy is introduced to handle the numerical instability, which contains an energy interpolation scheme and an adaptive step-size method.

Under the new framework, this work has made the following contributions. Firstly, the M-ETO method, as an extension method of BESO/ETO, it is proven that M-ETO can effectively solve nonlinear topology optimization problems under large loads. With end-compliance as the optimization goal, the M-ETO method can obtain highly similar results to the SIMP method under large load conditions. Prior to this work, when using the kind of evolutionary methods, no paper has given similar results under the same load. Secondly, we explore the optimization problems under a large evolution rate. In nonlinear topology optimization, the number of iteration steps directly reflects the total optimization time. It is proven that the M-ETO method can obtain optimized structures with a large evolution rate, which significantly reduces the time required for optimization. Thirdly, this work achieves the goal of smooth structural boundary representation without initial layout dependency. A reasonable initial layout can significantly speed up the optimization process without affecting the structural performance. Fourth, due to the introduction of projection, the M-ETO method achieves the minimal length scale, which significantly enhances the manufacturability of the structure and the robustness of the optimization process. Meanwhile, due to the reduction of fine branches inside the structure, the failure of buckling for fine branches is greatly postponed.

The remainder of this paper is organized as follows. In Section 2, the nonlinear modeling of the hyperelastic material model is illustrated, which includes defining the strain energy function and introducing the finite element analysis process. In Section 3, an effective modified evolutionary topology optimization method is proposed. The optimization formulation is given, and the sensitivity analysis is derived. In Section 4, we introduce the method to mitigate the numerical distortion of low stiffness regions. In Section 5, numerical examples are presented for illustrating the validity of the present framework, and finally, it is summarized and prospected in Section 6.

2 Constitutive model and finite element analysis procedures

The stress-strain behavior of the material can be modeled in many ways. The most common model used in topology optimization to represent the material behavior is the St. Venant Kirchoff model. This model describes a linear response of the stress-strain relation, and it is a valid approach when the material is under small strains. However, this model will lose ellipticity at moderate strains, and so it can make the problem ill-conditioned (Lahuerta et al. 2013). The St. Venant Kirchoff model can only be expected to be useful in a narrow range of small strains. One alternative approach is using a polyconvex constitutive model (Ball 1976). According to the research made by Ball, the hyperelastic constitutive models are polyconvex. They have better performance under large deformation and large strain conditions. Hence, it is more suitable to use the hyperelastic constitutive models in nonlinear topology optimization.

In this section, we will briefly introduce the used hyperelastic constitutive model and finite element analysis procedures.

2.1 The equilibrium equation and constitutive model

When a hyperelastic body undergoes a large deformation, as shown in Fig. 1, the configuration transits from the original undeformed state to a deformed state. The symbol Ω denotes the material region and the subscripts 0 and x represent the original state and the deformed state, respectively. In this paper, we use the total Lagrangian method, which uses the undeformed configuration as the reference configuration. In the following expressions, the bold black symbols represent vectors or tensors.

Fig. 1
figure 1

Deformation of a body from its undeformed configuration to a deformed configuration

Full size image

As shown in Fig. 1, a point X = [X1, X2, X3] in the reference configuration Ω0, through a mapping Φ(X, t), transfers to x = [x1, x2, x3] in the deformed configuration Ωx, i.e.,

$$ \mathbf{x}=\Phi \left(\mathbf{X},t\right)=\mathbf{X}+\mathbf{u}\left(\mathbf{X},t\right), $$
(1)
$$ d\mathbf{x}=\frac{\partial \mathbf{x}}{\partial \mathbf{X}}d\mathbf{X}\kern0.5em \Rightarrow \kern0.5em d\mathbf{x}=\mathbf{F}d\mathbf{X}, $$
(2)

where u represents displacement. The deformation gradient F is defined as

$$ \mathbf{F}=\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{X}}=\mathbf{I}+{\nabla}_0\mathbf{u}, $$
(3)

where I represents the second-order identity tensor. The deformation gradient is used to measure the volume change of the hyperelastic body before and after deformation. According to dx = FdX,

$$ {\displaystyle \begin{array}{l}{dV}_x={JdV}_0\kern0.5em \\ {}\frac{dV_x-{dV}_0}{dV_0}=J-1,\end{array}} $$
(4)

where J represents the determinant of the deformation gradient, i.e., J = det(F). When the used hyperelastic material is incompressible, J = 1. Because the deformed configuration is unknown, the physical quantity that needs to calculate in the deformed configuration can convert to calculate in the undeformed configuration by using J. The right Green-Cauchy deformation tensor can be defined as

$$ \mathbf{C}={\mathbf{F}}^T\mathbf{F}, $$
(5)

then we can derive the Green-Lagrangian strain E as

$$ \mathbf{E}=\frac{1}{2}\left({\mathbf{F}}^T\mathbf{F}-\mathbf{I}\right)=\frac{1}{2}\left(\mathbf{C}-\mathbf{I}\right)=\frac{1}{2}\left({\nabla}_0\mathbf{u}+{\nabla}_0{\mathbf{u}}^T+{\nabla}_0{\mathbf{u}}^T{\nabla}_0\mathbf{u}\right), $$
(6)

Subsequently, stress tensor can be defined. In total Lagrangian method, the second Piola-Kirchhoff stress tensor S, which defined in the undeformed configuration, is introduced as

$$ \mathbf{S}=J{\mathbf{F}}^{-1}{\boldsymbol{\upsigma} \mathbf{F}}^{-T}, $$
(7)

where σ is the Cauchy stress tensor. According to the principle of virtual work, the equilibrium equation is shown as follows:

$$ a\left(\mathbf{u},\overline{\mathbf{u}}\right)\equiv \underset{\Omega_0}{\int}\mathbf{S}\left(\mathbf{u}\right):\overline{\mathbf{E}}\left(\mathbf{u},\overline{\mathbf{u}}\right)d\Omega =\underset{\Omega_0}{\int }{\overline{\mathbf{u}}}^T{\mathbf{f}}^Bd\Omega +\underset{\Gamma_0^s}{\int }{\overline{\mathbf{u}}}^T\mathbf{t}d\Gamma \equiv l\left(\overline{\mathbf{u}}\right), $$
(8)

here,

$$ {\displaystyle \begin{array}{l}\overline{\mathbf{E}}\left(\mathbf{u},\overline{\mathbf{u}}\right)=\frac{1}{2}\left({\nabla}_0\overline{\mathbf{u}}+{\nabla}_0{\overline{\mathbf{u}}}^T+{\nabla}_0{\overline{\mathbf{u}}}^T{\nabla}_0\mathbf{u}+{\nabla}_0{\mathbf{u}}^T{\nabla}_0\overline{\mathbf{u}}\right)\\ {}\kern3.25em =\mathit{\operatorname{sym}}\left({\nabla}_0{\overline{\mathbf{u}}}^T+{\nabla}_0{\overline{\mathbf{u}}}^T{\nabla}_0\mathbf{u}\right)=\mathit{\operatorname{sym}}\left({\nabla}_0{\overline{\mathbf{u}}}^T\mathbf{F}\right),\end{array}} $$
(9)

where \( \overline{\mathbf{u}} \) is the virtual displacement, fB is the body force, and t is the surface traction on the boundary \( {\Gamma}_0^S \).

In this paper, in order to describe the response of the material more accurately, and make the optimization process more stable, we use the hyperelastic material model. The properties of hyperelastic material are expressed by the strain energy function, which is a function of the strain invariants. In the field of mechanical engineering, several hyperelastic models which including the Mooney-Rivlin model, Neo-Hookean model, and Yeoh model have been widely used. In this paper, the isotropic compressible Neo-Hookean model (Klarbring and Strömberg 2013) is used, which only depends on the first strain invariant. The strain energy function is described as

$$ {\omega}_{neo}=\frac{\mu }{2}\left({I}_1-3\right)+\frac{1}{2}\lambda {\left(J-1\right)}^2-\mu \ln J, $$
(10)

where I1 is the first strain invariant, and it can be defined as I1 = tr(C). μ and λ are Lame’s material parameters which are defined as

$$ \mu =\frac{E}{2\left(1+\nu \right)}\kern1em \lambda =\frac{\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}, $$
(11)

E represents Young’s modulus and ν represents Poisson’s ratio. Note the difference in the representation of Young’s modulus E and Green-Lagrangian strain tensor E. The second Piola-Kirchhoff stress tensor is defined by the derivative of the strain energy with respect to the deformation tensor, i.e.,

$$ \mathbf{S}=\frac{\partial {\omega}_{neo}}{\partial \mathbf{E}}=2\frac{\partial {\omega}_{neo}}{\partial \mathbf{C}}=2\left(\frac{\mu }{2}\frac{\partial {I}_1}{\partial \mathbf{C}}+\lambda \left(J-1\right)\frac{\partial J}{\partial \mathbf{C}}-\mu \frac{\partial \left(\ln (J)\right)}{\partial \mathbf{C}}\right), $$
(12)

According to

$$ {\displaystyle \begin{array}{l}\frac{\partial {I}_1}{\partial {C}_{ij}}={\delta}_{ij}\\ {}\frac{\partial J}{\partial {C}_{ij}}=\frac{1}{2}{JC}_{ij}^{-1}\\ {}\frac{\partial \left(\ln (J)\right)}{\partial {C}_{ij}}=\frac{1}{2}{C}_{ij}^{-1},\end{array}} $$
(13)

the second Piola-Kirchhoff stress tensor can be defined as

$$ {S}_{ij}=\lambda \left(J-1\right){JC}_{ij}^{-1}+\mu \left({\delta}_{ij}-{C}_{ij}^{-1}\right), $$
(14)

The material elasticity tensor is defined by the derivative of the second Piola-Kirchhoff stress tensor with respect to the deformation tensor, i.e.,

$$ \mathbf{D}=\frac{\partial \mathbf{S}}{\partial \mathbf{E}}=2\frac{\partial \mathbf{S}}{\partial \mathbf{C}}=4\frac{\partial^2{\omega}_{neo}}{\partial {C}_{ij}\partial {C}_{kl}}. $$
(15)

According to

$$ {\displaystyle \begin{array}{l}\frac{\partial {\delta}_{ij}}{\partial {C}_{ij}}=0\\ {}\frac{\partial {C}_{ij}^{-1}}{\partial {C}_{kl}}=-\frac{1}{2}{c}_{ij kl}=-\frac{1}{2}\left({C}_{ik}^{-1}{C}_{jl}^{-1}+{C}_{il}^{-1}{C}_{jk}^{-1}\right),\end{array}} $$
(16)

the material elasticity tensor can be defined as

$$ {D}_{ij kl}=\lambda \left(2J-1\right){JC}_{ij}^{-1}{C}_{kl}^{-1}-\lambda \left(J-1\right){Jc}_{ij kl}+\mu {c}_{ij kl}. $$
(17)

2.2 Finite element formulation

The necessary finite element formulas are briefly explained here, and many books give detailed derivation processes (Crisfield et al. 1991; Zienkiewicz and Taylor 2005). In the following expressions, the tensor is expressed as a matrix in Voigt notation, and bold black italics indicate matrices.

In the displacement-based implementation of finite elements, the displacement vector is defined at the node of each element. Here, we use \( {\boldsymbol{d}}_I \) which represents the displacement vector at node I and the subscript I represents the node. The displacement within the element can be obtained according to the following interpolation scheme:

$$ \boldsymbol{u}=\sum \limits_{I=1}^N{\boldsymbol{N}}_I\left(\boldsymbol{\xi} \right){\boldsymbol{d}}_I, $$
(18)

where N is the number of nodes of the element. Then the displacement gradient can be expressed as

$$ {\nabla}_0\boldsymbol{u}=\sum \limits_{I=1}^N\frac{\partial {\boldsymbol{N}}_I\left(\boldsymbol{\xi} \right)}{\partial \boldsymbol{X}}{\boldsymbol{d}}_I. $$
(19)

The relationship between the variation of Lagrangian strain \( \overline{\boldsymbol{E}} \) and the variation of nodal displacements \( \overline{\boldsymbol{d}} \) can be expressed as

$$ \overline{\boldsymbol{E}}={\boldsymbol{B}}_N\overline{\boldsymbol{d}}, $$
(20)

in the nonlinear finite element analysis, BN is no longer a constant matrix, and it can be decomposed and expressed as

$$ {\boldsymbol{B}}_N={\boldsymbol{B}}_L+{\boldsymbol{B}}_{NL}\left(\boldsymbol{u}\right), $$
(21)

the explicit formats of BN BL BNL are provided in the Appendix. When Lagrangian strain E is expressed in Voigt notation, it is needed to pay attention to the difference between the following two formulas:

$$ \boldsymbol{E}=\left({\boldsymbol{B}}_L+\frac{1}{2}{\boldsymbol{B}}_{NL}\right)\boldsymbol{d}\kern1em \overline{\boldsymbol{E}}=\left({\boldsymbol{B}}_L+{\boldsymbol{B}}_{NL}\right)\overline{\boldsymbol{d}}. $$
(22)

Define residual force R and external loads fext, and the equilibrium equation is rewritten as

$$ \boldsymbol{R}=0={\int}_{V_0}{\boldsymbol{B}}_N^T\boldsymbol{S} dV-{\boldsymbol{f}}^{ext}={\boldsymbol{F}}^{\mathrm{int}}-{\boldsymbol{f}}^{ext}. $$
(23)

The equilibrium equation needs to be solved iteratively using the Newton-Raphson method. Assumes that external loads are independent of nodal displacements, according to the definition of the tangent stiffness matrix, differentiate (23):

$$ \delta \boldsymbol{R}={\int}_{V_0}\delta {\boldsymbol{B}}_N^T\boldsymbol{S} dV+{\int}_{V_0}{\boldsymbol{B}}_N^T\delta \boldsymbol{S} dV=\left({\boldsymbol{K}}_{\sigma }+{\boldsymbol{K}}_0+{\boldsymbol{K}}_L\right)\delta \boldsymbol{d}={\boldsymbol{K}}_T\delta \boldsymbol{d}, $$
(24)

specifically,

$$ {\displaystyle \begin{array}{l}{\boldsymbol{K}}_0+{\boldsymbol{K}}_L={\int}_{V_0}{\boldsymbol{B}}_N^T{\boldsymbol{DB}}_N dV\\ {}{\boldsymbol{K}}_{\sigma }={\int}_{V_0}{\boldsymbol{G}}^T\boldsymbol{YG} dV,\end{array}} $$
(25)

where the explicit format of G is provided in the Appendix. Here (for 2D problems),

$$ \boldsymbol{Y}=\left[\begin{array}{cc}{\boldsymbol{S}}_{2\times 2}& 0\\ {}0& {\boldsymbol{S}}_{2\times 2}\end{array}\right]. $$
(26)

In order to make it easier for understanding, a flowchart is also added to explain the process of calculating the element stiffness matrices and second Piola-Kirchhoff stress tensor as shown in Fig. 2.

Fig. 2
figure 2

The flowchart of calculating element stiffness matrices and PK2 stress

Full size image

3 The modified evolutionary topology optimization method

In this section, the framework of the modified evolutionary topology optimization method is introduced in detail. The optimization formulation and sensitivity analysis will be discussed later.

3.1 The framework of modified evolutionary topology optimization

3.1.1 The design model and FEA model

The original evolutionary topology optimization (ETO) method was proposed by Da et al. (2018) in 2018. Through introducing a nodal sensitivity-based level-set function, this method succeeds in obtaining optimized structures with smooth boundary representation.

In general, the implementation of the kind of density-varied method is based on FEA, where the design domain is discretized into a series of finite elements. These elements are design variables and involve in the analysis. Nevertheless, in the ETO/M-ETO method, the design model is separated from the FEA model, the relationship between the two models, as shown in Fig. 3. To generate optimized structures with smooth boundary representation, each element is further discretized into Ng grid points (40 × 40 in 2D cases in this paper) in the design model. These grid points are classified as “solid” and “void,” and the guideline of classification will be described later. Herein, the volume fraction of each element \( {V}_i^f \) can be introduced. When \( {V}_i^f=1 \), it means all corresponding grid points in this element are solid, and the element would be a solid element. Similarly, if \( {V}_i^f=0 \), it means all corresponding grid points in this element are void, and the element would be a void element. The third case is \( 0<{V}_i^f<1 \), which element contains both solid and void grid points. Thus, this element would be a boundary element, and the value of \( {V}_i^f \) in this case will be discussed later. The three kinds of element are shown in Fig. 3. The mechanical properties of each element in the FEA model can be given according to \( {V}_i^f \):

$$ {E}_e=\left(1-{V}_i^f\right){E}_{min}+{V}_i^f{E}_0. $$
(27)
Fig. 3
figure 3

The design model and FEA model

Full size image

The subscripts 0 and min represent the solid and void material, respectively. Emin is a small value in order to avoid the singularity of the stiffness matrix. The total volume of the structure can be expressed as

$$ V=\sum \limits_{i=1}^{N_e}{V}_i^f{V}_i, $$
(28)

where Vi represents the volume of the ith element and Ne is the total element number.

3.1.2 The update scheme of topology layout

In order to achieve smooth structural boundary representation, the nodal sensitivity-based level-set function (LSF) ϕ is introduced. For each node, the value of LSF is equal to the nodal sensitivity number, i.e.,

$$ {\phi}_j={\alpha}_j^n, $$
(29)

where \( {\alpha}_j^n \) represents the sensitivity number at the jth node, and the superscript n means the physical quantity is calculated based on node. ϕj means the LSF value at the jth node. Furthermore, the LSF value at an arbitrary point o in elements can be obtained by interpolation (2D problem):

$$ \phi (o)=\sum \limits_{j=1}^4{N}_j(o){\phi}_i^j, $$
(30)

where \( {\phi}_i^j \) means the LSF value at jth node of ith element, and Nj is the widely used shape function in FEA:

$$ {N}_j(o)=\frac{1}{4}\left(\left(1+{\xi}_o{\xi}_j\right)+\left(1+{\eta}_o{\eta}_j\right)\right). $$
(31)

As mentioned, each element is discretized into Ng grid points, and the LSF value at grid points is calculated by (30). Therefore, the standard form of the LSF can be expressed as

$$ \left.\begin{array}{l}\phi (o)> LSV\kern0.5em \mathrm{o}\in {D}^{+}\\ {}\phi (o)= LSV\kern0.5em \mathrm{o}\in \Gamma \\ {}\phi (o)< LSV\kern0.5em \mathrm{o}\in {D}^{-}\end{array}\right\}, $$
(32)

where LSV is the level-set value, which is calculated iteratively. Different from the traditional level-set method, which uses the normal velocity to drive the boundary evolution. Herein, updating the topology layout is realized by setting the level-set value in each iteration, which is born from BESO. In each iteration, the value of LSV is defined as

$$ LSV=\frac{LS{V}_{upper}+ LS{V}_{lower}}{2}, $$
(33)

where the LSVupper and LSVlower represent the upper and lower bound of the level-set value, and they are initially assigned with \( {LSV}_{upper}=\max \left({\alpha}_j^n\right) \) and \( {LSV}_{lower}=\min \left({\alpha}_j^n\right) \). Then LSVupper and LSVlower are updated according to (34), until the difference between LSVupper and LSVlower is small enough, e.g., LSVupper − LSVlower < 10−5:

$$ \left\{\begin{array}{c} LS{V}_{upper}= LSV\; if\;V< Obj{V}_l\\ {} LS{V}_{lower}= LSV\; if\;V> Obj{V}_l\end{array}\right., $$
(34)

where the target volume ObjV for the current iteration can be calculated as

$$ {ObjV}_l=\left\{\begin{array}{l}\max \left({ObjV}_{l-1}\left(1- ER\right),{V}^{\ast}\right)\kern0.5em if\ {ObjV}_{l-1}\ge {V}^{\ast}\\ {}\min \left({ObjV}_{l-1}\left(1+ ER\right),{V}^{\ast}\right)\kern0.3em if\kern0.2em {ObjV}_{l-1}<\mathrm{V}{,}^{\ast}\end{array}\right. $$
(35)

obviously, the calculation method for ObjV here is the same as BESO. ER represents the evolutionary ratio. In essence, the update process of the nodal sensitivity-based level-set value is another representation of the “element removal/addition” in BESO.

As mentioned in Section 3.1.1, the grid points are classified into two categories, solid and void. According to (32), when ϕgp(o) > LSV is satisfied, the grid point is solid. By contrast, when ϕgp(o) < LSV is satisfied, the grid point is void. Since the LSF value of grid points are calculated from interpolation, if \( \min \left({\phi}_i^j\right)> LSV \) or \( \min \left({\phi}_i^j\right)< LSV \) is satisfied, then ϕgp(o) > LSV or ϕgp(o) > LSV is satisfied. Therefore, the value of \( {V}_i^f \) can be easily computed:

$$ {V}_i^f=\left\{\begin{array}{cc}1& when\kern0.5em \min \left({\phi}_i^j\right)> LSV\\ {}0& when\kern0.5em \max \left({\phi}_i^j\right)\le LSV\\ {}{N}_p/{N}_g& otherwise\end{array}\right., $$
(36)

where Np denotes the total number of grid points whose LSF value is larger than the level-set value. Then the total volume of the structure can be computed by (28).

3.1.3 The projection scheme

According to our experiments, the effect of nonlinear topology optimization based on the original ETO method is not good, e.g., when designing a long cantilever beam with minimizing the end-compliance as the optimization goal, it is difficult to obtain convergent results. Here, we introduce the projection function into the ETO method. Because in the ETO method, there are no intermediate density elements in structure except for the boundary, the introduction of projection does not aim to make element density approach 0/1 design. The projection function used in this paper is the same as Guest (Guest et al. 2004). Because the evolution of BESO/ETO is determined by the evolution rate, which means the change in structure volume fraction drives it. During the evolution of the structure, it is likely that the fine branches inside the structure cannot be generated or disappeared in one iteration, and even isolated branches may appear. In the finite element analysis, the mesh of this kind of branch often occurs very large distortion, which leads to non-convergence of the finite element analysis. Even if these fine branches can completely generate or disappear, their buckling behaviors also become a significant concern. Herein, we hope to reduce the generation and fracture of fine branches inside the structure by introducing the minimal length scale to achieve the purpose of enhancing the robustness of the optimization process. The projection function can be expressed as

$$ {\rho}_e=1-{e}^{-\beta {V}_i^f}+{V}_i^f{e}^{-\beta }, $$
(37)

where ρe is the variable of \( {V}_i^f \) after projection and β is the parameter that controls the slope of the curve. After introducing the projection scheme, (27) and (28) should be changed to

$$ {E}_e=\left(1-{\rho}_e\right){E}_{\mathrm{min}}+{\rho}_e{E}_0, $$
(38)
$$ V=\sum \limits_{i=1}^N{\rho}_e{V}_i. $$
(39)

Due to introducing the minimal length scale, the fine branches inside the structure are reduced. Therefore, the manufacturability of the structure is greatly improved, and the failure of buckling for fine branches is considerably postponed.

3.2 Optimization formulation and sensitivity analysis

Consider a general nonlinear topology optimization problem, maximize the stiffness of a structure undergoing large deformation with a volume constraint. In this paper, we use the hyperelastic material model, which means the problem is solved with considering both geometric nonlinearity and material nonlinearity. It is worth pointing out when considering the maximum stiffness of the structure under the linear assumption, it is equivalent to whether the objective is strain energy, complementary work, or end-compliance. However, in the case of nonlinearity, the three are different. In existing research based on the evolutionary method, most numerical examples use the minimization of complementary work as the optimization goal. To compensate for the lack of exploration of end-compliance, here, the end-compliance is chosen as the objective function. Problem formulation can be expressed as

$$ {\displaystyle \begin{array}{l}\underset{x}{\min}\kern0.75em C={\boldsymbol{f}}_{ext}^T\boldsymbol{u}\\ {}s.t.\kern1.25em \boldsymbol{R}\left(\boldsymbol{u},\boldsymbol{\rho} \right)=0\\ {}\kern2.25em V\left(\boldsymbol{\rho} \right)={V}^{\ast}\\ {}\kern2.25em 0\le {\rho}_e\left({V}_i^f\right)\le 1\end{array}} $$
(40)

where C is the structural end-compliance, V is the structure volume, and V∗ is the constraint value. \( {\rho}_e\left({V}_i^f\right)=1 \) represents that full of grid points in the element is solid, which means the element is solid. \( {\rho}_e\left({V}_i^f\right)=0 \) means void, and \( 0<{\rho}_e\left({V}_i^f\right)<1 \) represents boundary element, which contains solid grid points and void grid points.

Generally, sensitivity analysis should be carried out based on the design model against the design variable. However, inherited the characteristics of the ETO method, here, the design model is separated from the FEA model, which makes the analysis complicated. ρ and Vf have the same physical meaning, and after projection, Vf is transformed to ρ. Both of them are used in the FEA for analyzing the design model, and it cannot be seen as design variable because neither ρe nor \( {V}_i^f \) can be freely varied. The intermediate element is only allowed on the boundary of the structural topology, which is a combination of solid element and void element actually. Therefore, similar to the BESO, an artificial variable for the element xi is introduced. xi is used to calculate the sensitivity for topology optimization of the design model. Here, xi = 1 means that the ith element is solid in the design model, which implies the ρe = 1 in the FEA model. Similarly, xi = xmin means the element is void in the design model and ρe = 0 in the FEA model. The critical point is the boundary elements (intermediate density elements in the design model), which means 0 < ρe < 1 in the FEA model, different from the SIMP method; these elements have no exact value of xi and are just viewed as the combination of solid (xi = 1) and void (xi = xmin).

The adjoint method is utilized for computing the sensitivity of the objective. By adding a zero term to the objective function, a new objective is constructed, i.e.,

$$ {g}_0={\boldsymbol{f}}_{ext}^T\boldsymbol{u}+{\boldsymbol{\lambda}}^T\boldsymbol{R}, $$
(41)

where λ is the adjoint variable vector. Differentiating the objective function g0 with respect to the artificial design variable x:

$$ \frac{\partial {g}_0}{\partial \boldsymbol{x}}=\left({\boldsymbol{f}}_{ext}^T+{\boldsymbol{\lambda}}^T\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{u}}\right)\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{x}}+{\boldsymbol{\lambda}}^T\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{x}}, $$
(42)

eliminating the unknown displacement term ∂u/∂x, that is,

$$ {\boldsymbol{K}}_T\boldsymbol{\lambda} ={\boldsymbol{f}}^{ext}\kern1.5em {\boldsymbol{K}}_T=-\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{u}}=\frac{\partial {\boldsymbol{f}}^{int}}{\partial \boldsymbol{u}}, $$
(43)

then the sensitivity can be expressed as

$$ \frac{\partial {g}_0}{\partial \boldsymbol{x}}={\boldsymbol{\lambda}}^T\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{x}}=-{\boldsymbol{\lambda}}^T\frac{\partial {\boldsymbol{F}}^{int}}{\partial \boldsymbol{x}}. $$
(44)

According to (38), the material elasticity tensor of each element is relating to ρ, i.e.,

$$ {\boldsymbol{D}}_e=\left(\left(1-{\rho}_e\right){x}_{\mathrm{min}}^p+{\rho}_e\right){\boldsymbol{D}}_0, $$
(45)

where \( {x}_{\mathrm{min}}^p{E}_0={E}_{\mathrm{min}} \), in this paper, xmin = 0.001 and p = 3. Consider (44) and (45), the sensitivity number of the ith element can be expressed as

$$ {\alpha}_i^e={\lambda}^T\frac{\left(1-{\rho}_e\right){x}_{\mathrm{min}}^{p-1}+{\rho}_e}{\left(1-{\rho}_e\right){x}_{\mathrm{min}}^p+{\rho}_e}{f}_e^{int}\frac{\partial {\rho}_e}{\partial {V}_i^f}. $$
(46)

After projection, Vf is transformed to ρ. Therefore, we need to calculate \( \frac{\partial \rho }{\partial {V}_f} \) in the sensitivity analysis. When ρe strictly take the value 0/1, the elemental sensitivity numbers can be expressed as follows, which is similar to BESO:

$$ {\alpha}_i^e=\left\{\begin{array}{l}{\lambda}^T{f}_e^{int}\frac{\partial {\rho}_e}{\partial {V}_i^f}\kern3.25em when\kern0.5em {\rho}_e=1\\ {}\frac{x_{\mathrm{min}}^{p-1}}{x_{\mathrm{min}}^p}{\lambda}^T{f}_e^{int}\frac{\partial {\rho}_e}{\partial {V}_i^f}\kern1.25em when\kern0.5em {\rho}_e=0.\end{array}\right. $$
(47)

In order to construct the LSF, the elemental sensitivity numbers are converted to nodal sensitivity numbers \( {\alpha}_j^n \) through the filter scheme:

$$ {\alpha}_j^n=\frac{\sum \limits_{i=1}^K\omega \left({r}_{ij}\right){\alpha}_i^e}{\sum \limits_{i=1}^K\omega \left({r}_{ij}\right)}, $$
(48)

K is the total number of elements in the influence domain, \( {\alpha}_i^e \) represents the sensitivity number at the ith element, rij represents the distance between the center of the ith element and the jth node, and w(rij) is the linear weight factor defined as

$$ \omega \left({r}_{ij}\right)=\mathit{\max}\left(0,{r}_{\mathrm{min}}-{r}_{ij}\right), $$
(49)

where rmin is the filter radius. To make the optimization process more stable, the simple averaging scheme is adopted:

$$ {\left({\alpha}_j^n\right)}_k=\frac{{\left({\alpha}_j^n\right)}_k+{\left({\alpha}_j^n\right)}_{k-1}}{2}, $$
(50)

where the subscript l denotes the current iteration number. Then the nodal sensitivity numbers can be used in (29) to construct LSF.

The flowchart of the optimization process is shown as follows:

Step 1

Assign initial values to optimization parameters and discretize the design domain for the given boundary and loading conditions;

Step 2

According to the value of the design variables calculate the interpolation factor of the energy interpolation scheme;

Step 3

Using the Newton-Raphson method perform nonlinear finite element analysis;

Step 4

Calculate the objective function value and elemental sensitivity numbers;

Step 5

Convert the elemental sensitivity numbers into nodal sensitivity numbers and construct level-set function;

Step 6

Calculate elemental volume fraction of the FEA model and update the topology of the design model by the level-set value

Step 7

Repeat process 2–6, until the volume constraint and the convergence criterion are satisfied.

4 Method to handle the numerical instabilities

When solve the mathematical model proposed in (40), no matter which topology optimization method is used, the FEA problem R(u, ρ) = 0 may not converge due to excessive distortion appears in the low stiffness regions, which means too severe mesh distortion causes the tangent stiffness matrix to be indefinite or even negatively determined, resulting in the Newton-Raphson process fail to converge. In this section, the numerical methods to mitigate the excessive distortion of low stiffness regions are introduced. Here, two methods are applied, one is the adaptive step-size method, the other is the energy interpolation scheme (Wang et al. 2014).

4.1 Adaptive step-size method

The adaptive step-size method is a simple but efficient strategy, which is applied in the process of Newton-Raphson iteration. When the Newton-Raphson method is used, it means we decompose the original problem into several sub-problems. Assuming the symbol c(t) means time step, and Δt means the increment of time step. Here,

$$ c(t)=c\left(t-1\right)+\varDelta t. $$
(51)

If a sub-problem fails to converge within 100 Newton-Raphson iterations, or the maximum residual force exceeds a set threshold, then it is considered that the sub-problem has difficulty in converging, the increment of time step should be reduced to:

$$ c(t)=c\left(t-1\right)+\frac{\varDelta t}{2}. $$
(52)

If the sub-problem converges, the increment of the time step should remain in the next generation. If the t + 1 generation converges, the increment of time step returns to its original value, which means:

$$ {\displaystyle \begin{array}{l}c\left(t+1\right)=c(t)+\frac{\varDelta t}{2}=c\left(t-1\right)+\frac{\varDelta t}{2}+\frac{\varDelta t}{2}\\ {}c\left(t+2\right)=c\left(t+1\right)+\varDelta t=c\left(t-1\right)+\frac{\varDelta t}{2}+\frac{\varDelta t}{2}+\varDelta t.\end{array}} $$
(53)

On the contrary, if the sub-problem does not converge, the increment of time step continues to decrease:

$$ c(t)=c\left(t-1\right)+\frac{\varDelta t}{4}. $$
(54)

For clarity, the FEA process after adding the adaptive step size strategy is shown in Fig. 4.

Fig. 4
figure 4

The flowchart of FEA

Full size image

4.2 Energy interpolation scheme

In the ideal case, the void element does not affect the response of the solid elements, so we can choose the finite element model for the void element to simulate as long as it does not affect the convergence of the solid element. Under such an idea, Wang et al. (2014) proposed the energy interpolation scheme, which is one of the widely used solutions to alleviate the distortion of low stiffness regions in recent years. In the energy interpolation scheme, the void elements are analyzed based on linear assumption, the solid elements are analyzed based on nonlinearity theory. To conceptualize the idea, the strain energy function in (10) should be replaced by the following equation, where the new function is equal to the interpolation of the strain energy in nonlinear theory ωneo and the strain energy under small deformation assumption ωL:

$$ {\omega}_e\left(\ {\boldsymbol{u}}_e\right)=\left({\omega}_{neo}\left({\gamma}_e\ {\boldsymbol{u}}_e\right)-{\omega}^L\left({\gamma}_e\ {\boldsymbol{u}}_e\right)+{\omega}^L\left(\ {\boldsymbol{u}}_e\right)\right){E}_e, $$
(55)

where γe is the interpolation factor, and it can be expressed as

$$ {\gamma}_e=\frac{\tanh \left({\beta}_{\gamma}\eta \right)+\tanh \left({\beta}_{\gamma}\left({\rho}_e-\eta \right)\right)}{\tanh \left({\beta}_{\gamma}\eta \right)+\tanh \left({\beta}_{\gamma}\left(1-\eta \right)\right)}, $$
(56)

where βγ and η are constants and η is a threshold used to determine the element behavior. Wang et al. (2014) suggest βγ = 500 and η = 0.01; those values are adopted in this paper.

Considering the applied energy interpolation scheme, (44) should be changed to

$$ \frac{\partial {g}_0}{\partial \boldsymbol{x}}={\boldsymbol{\lambda}}^T\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{x}}=-{\boldsymbol{\lambda}}^T\left(\frac{\partial {\boldsymbol{F}}^{int}}{\partial \boldsymbol{x}}+\frac{\partial {\boldsymbol{F}}^{int}}{\partial \boldsymbol{\gamma}}\frac{\partial \boldsymbol{\gamma}}{\partial \boldsymbol{x}}\right). $$
(57)

5 Numerical examples

In this section, two topology optimization examples considering both geometric nonlinearity and material nonlinearity are presented to illustrate the effectiveness of the proposed modified evolutionary topology optimization method based on the Neo-Hookean material model. In all the examples, Young’s modulus of the solid material is E0 = 3GPa, and Poisson’s ratio is ν = 0.4. The Heaviside parameters βγ and η used in energy interpolation scheme are fixed at βγ = 500 and η = 0.01, respectively. The penal p used in M-ETO is fixed at p = 3 in all simulations. In nonlinear finite element analysis, if there is no particular explanation, the initial setting is five analysis steps.

5.1 Long cantilever beam design

A typical long cantilever example is considered first. As shown in Fig. 5. The rectangular design domain is 0.12 m long, 0.03-m height, and 0.001-m thickness. The domain is discretized using a mesh of 120 × 30 4-node finite elements. The objective volume fraction is 0.5. The left side is fixed, and a concentrated force is applied at the mid-point of the right side. The optimization process starts with density distribution ρe = 1, and the evolution ratio is assigned as 0.02. The filter radius is rmin = 2. β = 1 is used in the M-ETO method.

Fig. 5
figure 5

Design domain for a long cantilever example

Full size image

The optimal topology layouts and the corresponding deformed configurations obtained by the proposed method with different loads of f = 1N, f = 100N, f = 300N, f = 400N, and f = 500N are given in Fig. 6, respectively. As shown in Fig. 6 (a), when the applied load is very small, the topology layout appears to be almost up and down symmetrical, which is very similar to the optimization results under the assumption of small deformations. The result also meets the expectations based on experience. As the load increases, the structure tends to be asymmetric. When the load is further increased to f = 300N, we can see the structure has a bar on the right side. From Fig. 6 (c–e), the size of the bar, which includes width and length, increases with increasing load. As shown in Fig. 6 (f–j), when a load is applied, the deformation of the rightmost bar is perpendicular to the ground in the direction of the load; it means the bar becomes the major part of bearing the load.

Fig. 6
figure 6

The comparison of optimized topologies and the corresponding deformed configurations for the cantilever under different values of loads

Full size image

In Fig. 7, we compare the results obtained based on the proposed framework with the results obtained by the SIMP method. The comparison includes three load conditions. In the SIMP optimization process, the two numerical techniques mentioned in Section 4 are also used. It can be seen that the results obtained by the two methods are similar in both the contour and the deformation of the structure; only the internal detail structure is different. Considering that the optimization results of SIMP are generally used as a baseline, this verifies the rationality of the results obtained by our method. As far as the author knows, it is the first time that using a kind of evolutionary method obtain optimization results similar to SIMP under large loads. Prior to this, when using the ESO/BESO method and their extension methods, no paper has given similar results under the large load. This proves that the modification in this paper has dramatically improved the ability of the method to solve nonlinear topology optimization problems.

Fig. 7
figure 7

Structural deformation of the long cantilever beam. a–c Based on the SIMP method. d–f Based on the M-ETO method

Full size image

In the comparison of structural performance, the optimized structure obtained by the proposed framework is numerically superior to the results produced by the SIMP method. However, considering the influence of some optimization parameters, this comparison result is not of great value. It is worth noting that one of the great advantages of the kind of evolutionary methods such as ESO/BESO is that compared to SIMP methods, fewer intermediate density elements usually make the objective function value slightly lower. Thus, we can make reasonable speculations that the result obtained by the M-ETO method has the potential to surpass the results obtained by the SIMP method in performance.

The structure obtained by the proposed framework has a clear and smooth boundary in geometric. However, considering the density-based mapping used, the description of the boundary is an approximation (Van Dijk et al. 2013). If a more accurate structural response is needed, the shape optimization with conforming mesh is still required. In addition, due to the introduction of minimal length scale, the final topology layout will not include fine branches, which significantly enhances the manufacturability of the structure. These characteristics show that the proposed framework has natural advantages in combining with additive manufacturing technology, and the optimization results are more oriented to actual production.

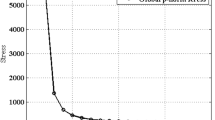
The evolutionary histories of the end-compliances and the volume fraction under f = 500N are plotted in Fig. 8. Figure 8 (a) is the evolutionary histories based on the SIMP method and the result shown in Fig. 8 (b) is based on the proposed framework. In nonlinear topology optimization, the nonlinear finite element analysis accounts for a considerable proportion of the total optimization time. When using the same finite element analysis program, the number of iteration steps directly reflects the total optimization time. Here, since the SIMP method uses the continuation scheme, it has experienced a relatively large number of iteration steps. The parameter settings in the continuation scheme are the same as Wang et al. (2014). In the M-ETO method, we use an evolution ratio of 0.02, which greatly speeds up the optimization process and significantly reduces the number of iteration steps required.

Fig. 8
figure 8

Iteration histories for the long cantilever example

Full size image

Generally speaking, the optimization efficiency of SIMP is very high. However, when using the continuation scheme and projection at the same time, because the parameter evolution of projection cannot begin until penal reaches the final value, the optimization process has increased dramatically. According to our research, when the applied load is not large, e.g., f = 300N, the optimization process of SIMP can be accelerated by changing the parameters in the continuation scheme (choose a large initial value of penal and the increment of penal). At this time, the number of iteration steps required for optimization is similar to the M-ETO method. However, when the load is relatively large, the parameter selection of the continuation scheme should not be too aggressive, which results in a large increase in the number of iteration steps required.

In M-ETO, as an extension of the BESO method, there are no intermediate density elements except for boundary elements. Meanwhile, the volume of the structure gradually decreases. These characteristics make M-ETO not need first to find a good initial solution with a large number of intermediate density elements. The value of penal does not change. Under large load conditions, even though M-ETO uses a small evolution ratio, it still has advantages in computing efficiency compared to SIMP, which uses both the continuation scheme and projection. On the other hand, compared with the previous application of the ESO/BESO method to solve nonlinear topology optimization problems, where a small evolution rate (usually less than 0.01) is often used. Here, we use a relatively large evolution rate (ER = 0.02) and can obtain convergence results under large and small loads, which fully demonstrates the effectiveness and advantages of the proposed framework in this paper.

For nonlinear topology optimization problems, the choice of evolutionary ratio is related to the finite element analysis. If the finite element analysis can be carried out smoothly, a relatively large evolutionary ratio can be chosen. In this paper, in order to ensure the finite element analysis can be successfully performed, we introduce the projection scheme, use the hyperelastic constitutive model and numerical technology (including energy interpolation scheme and adaptive step-size method). The application of these methods makes the optimization process more stable and allows to apply a relatively large evolutionary ratio.

5.2 Double clamped beam design

As shown in Fig. 9, the second example is a rectangular design domain with 0.16 m long, 0.04-m height, and 0.001-m thickness. The design domain is clamped at both the left and right sides. A concentrated force f is applied at the mid-point of the top edge. Since the structure has left-right symmetry, half of the design domain is discretized using a mesh of 80 × 40 4-node finite elements. The objective volume fraction is 0.25. The optimization process starts with density distribution ρe = 1, and the evolution ratio is assigned as 0.02. The filter radius is rmin = 3. β = 1 is used in the M-ETO method.

Fig. 9
figure 9

Design domain for a double clamped beam example

Full size image

Similar to the first example, here, we list the topology layout and the corresponding deformed configuration under three loads, f = 10N, f = 400N, f = 800N, and f = 1500N. Figure 10 (a) shows the optimization result of the double clamped beam under a small load. Compared with the optimization results shown in Fig. 10 (b–d), we can find the optimization result for f = 10N have significant differences in topology from the solution for large load. Buckling effects explain the reason for this difference, as shown in Fig. 11. The topology layouts under large load are very similar, but subtle differences can still be observed after careful observation. As the load increases, the angle between the two beams in the middle of the structure decreases, which increases the performance of the structure to resist the load.

Fig. 10
figure 10

The comparison of optimized topologies and the corresponding deformed configurations for the double clamped beam under different values of loads

Full size image
Fig. 11
figure 11

The buckling effect of the double clamped beam

Full size image

In general, most methods that can produce smooth boundaries are affected by the initial layout if no additional technology is used. However, the proposed M-ETO method does not depend on the initial guess. To prove this conclusion, here, we use M-ETO starting from initial guess designs whose volumes are close to the objective volume. As shown in Fig. 12, half of the double clamped beam is discretized into 80×40 with f = 400N. Consider two different initial guess designs, as shown in Fig. 12 (a) and (f). Initial layout A is covered with material on half of the design domain, and initial layout B is uniformly arranged holes in the design domain, which is often used in the level-set method. The initial volume fraction in both cases is 0.5, and the objective volume fraction is 0.25. Figure 12 (b–d) shows the evolution history of topology using the initial layout A. In the right column, Fig. 12 (f–i) shows the evolution history of topology using the initial layout B. Under the same load condition and parameter setting, the optimized structures without initial guess are shown in Fig. 12 (e) and (j). Obviously, different initial layouts have different evolutionary processes, but the final layouts are similar. Compared with the final topology from full material design, the angle between two beams in the middle of the structure is slightly smaller in the final topology, when optimization begins with the initial layout A. By contrast, the angle is slightly bigger when optimization begins with the initial layout B. However, these differences are not big. Next, we can perform a more quantitative analysis.

Fig. 12
figure 12

The structural deformation of the double clamped beam

Full size image

Figure 13 shows the evolutionary histories of the end-compliances and the volume fraction. Compared with the objective function values of the optimized structures in the three cases, it can be found that the difference is very small. We can use the end-compliance from full material design as a baseline, the error from using initial layout A and B is 1.097% and 0.79%, respectively. It can be considered as the impact from initial guess on structural performance is small. Since the target volume fraction is low, as shown in Fig. 13 (a), more iteration steps are required when starting with full material design. When optimization begins with an initial guess, the number of iteration steps required for optimization is reduced. Compared with Fig. 13 (b) and (c), even use the same initial volume fraction, the evolutionary histories from different initial layouts vary greatly. The number of iteration required for optimization is 77 from initial layout A, and it is only 45 from initial layout B. Obviously, the evolution process using the initial layout B is more stable, and the convergence is faster than using the initial layout A. This means that different initial layouts have different acceleration capabilities for optimization. A proper initial layout can significantly speed up the optimization process.

Fig. 13
figure 13

The evolutionary histories of the end-compliances and the volume fraction

Full size image

If the optimization procedure is forced to continue after the convergence condition is met, the value of end-compliance from initial layouts will very close to the value from full material design. The error is 0.179% from initial layout A and 0.208% from B. At the same time, the differences in topology layout are almost indistinguishable, as shown in Fig. 14. Now the conclusion is very clear, and the initial layout dependency is eliminated from the proposed framework.

Fig. 14
figure 14

The structural deformation of the 150th iteration

Full size image

6 Conclusion

This paper has presented a modified evolutionary topology optimization (M-ETO) method for nonlinear topology optimization of continuum structures. By constructing a level-set function based on the nodal sensitivity number, the structural boundaries can be clearly and smoothly expressed. With introducing the Projection scheme, the M-ETO method can effectively solve the nonlinear topology optimization problem and at the same time achieve the minimal length scale. The constitutive model used in this paper is the Neo-Hookean material model, which is known better to represent the physics of a body under large deformations. The use of hyperelastic material model enhances the stability of the optimization process to a certain extent. Combining with the energy interpolation scheme and the adaptive step-size method, the numerical instability of the low stiffness regions in the finite element analysis is greatly alleviated.

Two numerical examples are presented for illustrating the validity of the M-ETO method. The examples of long cantilever beam and double clamped beam show the five advantages of the M-ETO method. Firstly, compared to the original BESO/ETO method, the ability to solve nonlinear topology optimization problems is improved. Secondly, the M-ETO method can use a large evolution rate, which significantly reduces the time required for optimization. Thirdly, the structure obtained by the M-ETO method has clear and smooth boundary, and no additional smoothing is required. Fourth, the initial layout dependency of the M-ETO method is eliminated. Finally, the M-ETO method achieves the minimal length scale, which significantly enhances the manufacturability of the structure.

The proposed M-ETO method for nonlinear topology optimization is straightforward and effective. Considering other constraints and goals is the focus of further research, e.g., consider additive manufacturing constraints and stress constraints.