1 Introduction

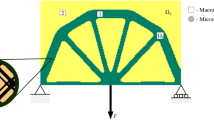
Featured by geometrical characteristics at the mesoscale, metamaterials have special mechanical properties that cannot be found in traditional materials. The property of metamaterial can be engineered by tailoring the design of mesoscale unit cells. Additive Manufacturing (AM) of metamaterial opens up new opportunities for the development of next-generation lightweight, functional vehicle components. The metamaterial infilled structure (mesostructure-structure system) has two scales of geometrical features (Fig. 1). At the lower scale, each metamaterial cell is designed to achieve special local properties. At the higher scale, the structural product is created by assembling the metamaterials cells. Design variables are defined at both scales for the optimization of system performances. In prior arts, topology optimization (e.g., homogenization method or the SIMP method) has been employed to generate macroscale structure designs that contain “gray” elements of various density levels. The “gray” elements are converted to mesostructures of predefined patterns (Cheng et al. 2018). However, different mesostructure designs of the same density level may have very different properties. To resolve this issue, a parameterized level set method has been developed to optimize the structure and the infilled metamaterial cells concurrently (Jiang et al. 2019). All the aforementioned approaches rely on gradient-based optimization algorithms, but analytical gradients are not available for structure optimization considering transient nonlinear behaviors such as impact, crash, and blast, because the high nonlinearity of transient dynamic simulation is exacerbated by numerical and physical noises and bifurcations. Several non-gradient approaches (Tovar et al. 2006; Wehrle et al. 2015) have been proposed for structure optimization under transient dynamic loads. Due to the low efficiency, those methods are only applicable to the design of single-scale structure components. In this work, we aim at developing an efficient, non-gradient design optimization method for mesostructure-structure system under transient dynamic loads. Given the structure design (infilled envelop) at the macroscale, we propose an informatics-based approach to solve the infill optimization problem: establish a cellular metamaterial database (cell designs and transient dynamic properties) firstly, and then find the optimal selection for each unit inside the infill envelop.

Fig. 1
figure 1

An example of the mesostructure-structure system. It is to be noted that regions of the same density level can be filled with cellular metamaterials of very different properties. Selecting the optimal mesostructure design for each element is a critical step in system optimization. The density level is represented by volume fraction (VF) of the material phase in a unit cell

Full size image

A simple way to optimize the mesostructure-structure system is the brute-force strategy. During the optimization process, all design evaluations are conducted by running expensive, high-fidelity simulations (e.g., fully validated, high-resolution model). However, this strategy is not realistic for real world engineering problems due to the high computational cost. To resolve this issue, many scholars propose to use simplified low-fidelity models for optimization and high-fidelity models for design verification (Zhao et al. 2018; Zhao et al. 2019). However, this method has two major weaknesses. First, the low-fidelity model leads to designs of low performances. Second, the high-fidelity data points are not fully utilized in optimal search. For better design performance and lower computational cost, a multi-fidelity approach is proposed in this paper. Two types of numerical models are established for the mesostructure-structure system: (1) A high-fidelity, high-resolution model that captures the mesoscale geometry of each metamaterial cell, and (2) a low-fidelity, low-resolution model, in which each mesostructure cell is represented by one element. Each element in the coarse model is assigned with homogenized effective properties of the corresponding metamaterial cell. The fine model provides an accurate prediction of the system responses at a high computational cost, while the coarse model provides a fast yet less accurate emulator. Our goal is to predict the system response with reasonable accuracy and acceptable computational cost by fusing information obtained from a small set of high-fidelity sample points and a sufficient number of low-fidelity sample points. To this end, a Probabilistic Multi-Phase Sampling-Based Global Optimization strategy is proposed. This strategy improves the predictability of the surrogate model with minimal additional sampling points. Furthermore, a modified Particle Swarm Optimization (PSO) algorithm is employed to overcome the difficulty in searching the global optimum of a high nonlinear, high-dimensional design problem.

The remainder of this paper is organized as follows. Section 2 introduces the technical background. Section 3 presents the proposed design optimization method. In Section 4, comparative studies on two engineering benchmark problems are presented to demonstrate the effectiveness of the proposed method. Section 5 concludes this paper.

2 Technical backgrounds

2.1 Multi-fidelity models

In engineering practices, designers may have access to a variety of analysis models with different levels of fidelity. Here, “fidelity” indicates how accurately the physical principles are captured, and how close are the model assumptions to the actual situation. Usually, the high-fidelity model provides a more accurate and reliable description of the real physics but requires more resources (e.g., computational time).

There are three categories of multi-fidelity approaches: adapting, fusion, and filtering. For the adapting approach, the multi-fidelity predictor is created by multiplying or adding a correction function to the low-fidelity model. The correction function represents the difference between the low-fidelity and the high-fidelity models. The additive and multiplicative correction functions are shown in (1) and (2) respectively, where δ(x) is equal to yHF − yLF and ρ(x) is equal to yHF/yLF (Son and Choi 2016; Liu et al. 2016).

$$ {\hat{y}}_{\mathrm{add}}={\hat{y}}_{LF}\left(\boldsymbol{x}\right)+\delta \left(\boldsymbol{x}\right) $$
(1)
$$ {\hat{y}}_{\mathrm{multi}}=\rho \left(\boldsymbol{x}\right)\cdotp {\hat{y}}_{LF}\left(\boldsymbol{x}\right) $$
(2)

A comprehensive correction (Keane 2012; Perdikaris et al. 2015) can be created by combining the additive correction and the multiplicative correction, as shown in (3).

$$ {\hat{y}}_{\mathrm{com}}=\rho \left(\boldsymbol{x}\right)\cdotp {\hat{y}}_{LF}\left(\boldsymbol{x}\right)+\delta \left(\boldsymbol{x}\right) $$
(3)

Fischer et al. (Fischer et al. 2017) proposed a hybrid correction model, which is a weighted function of additive and multiplicative correction functions:

$$ {\hat{y}}_{\mathrm{hyrid}}=\omega \left(\boldsymbol{x}\right)\cdotp \left[{\hat{y}}_{LF}\left(\boldsymbol{x}\right)+\delta \left(\boldsymbol{x}\right)\right]+\left(1-\omega \left(\boldsymbol{x}\right)\right)\cdotp \left[\rho \left(\boldsymbol{x}\right)\cdotp {\hat{y}}_{LF}\left(\boldsymbol{x}\right)\right] $$
(4)

The second category is the fusion-based methods. CoKriging surrogate modeling (Sinclair 1977; Howarth 1979) is one of the most popular fusion methods. Kennedy and O’Hagan (Kennedy and O'Hagan 2000) proposed a CoKriging approach to correct the prediction by low-fidelity computer simulation with high-fidelity simulation results. CoKriging is widely employed in various engineering fields such as aerospace (Qian and Wu 2008; Han et al. 2010). Like the Kriging model, CoKriging model predicts the epistemic uncertainty at locations without a sample point, which provides a basis for sample replenishment.

For the third category, filtering-based methods, the high-fidelity models are invoked only if certain criteria (filtered by the low-fidelity model) are met. Several multi-fidelity optimization algorithms have been proposed based on this type of methods (Bekasiewicz and Koziel 2015; Bahrami et al. 2016). The high-fidelity model is only used to evaluate new designs in the promising design regions, which are identified using the low-fidelity model.

2.2 Adaptive Surrogate Model-based Global Optimization

Surrogate Model-based Global Optimization (SBO) reduces the computational cost of optimization by replacing the expensive simulation with a surrogate model. The training data of the surrogate model can be collected either using a one-shot Design of Experiments (DoE), which means that all DoE points are generated upfront by space-filling sampling methods, or using adaptive sequential sampling approaches. The adaptive sampling approaches have the advantage of allocating resources to critical design sub-regions, which are identified based on the performances of existing designs (Dong et al. 2016). For example, the Expected Improvement criterion (EI, (5)) has been employed in Efficient Global Optimization (EGO) to identify the most promising sampling locations for the next iteration of optimal search (Jones et al. 1998):

$$ {f}_{EI}\left(\boldsymbol{x}\right)=\max \left(\sigma \left(\boldsymbol{x}\right)\frac{{\hat{y}}_{\mathrm{min}}-\hat{y}\left(\boldsymbol{x}\right)}{\sigma \left(\boldsymbol{x}\right)}\Phi \left(\frac{{\hat{y}}_{\mathrm{min}}-\hat{y}\left(\boldsymbol{x}\right)}{\sigma \left(\boldsymbol{x}\right)}\right)+\sigma \left(\boldsymbol{x}\right)\upphi \left(\frac{{\hat{y}}_{\mathrm{min}}-\hat{y}\left(\boldsymbol{x}\right)}{\sigma \left(\boldsymbol{x}\right)}\right)\right) $$
(5)

Φ(x) and ϕ(x) are the Cumulative Distribution Function (CDF) and the Probability Density Function (PDF) of the standard normal distribution. Another example of the adaptive SBO approach is the Space Exploration and Unimodal Region Elimination method (Younis and Dong 2010). The design space is divided into unimodal sub-regions based on the DoE data. A Kriging surrogate model is established for each unimodal sub-region, and additional high-fidelity sample points will be added to the critical sub-regions to refine the Kriging surrogate model for optimal search. Both performance improvement and space-filling properties are considered in adaptive sampling (Long et al. 2015; Jie et al. 2014; Chung et al. 2018).

All the aforementioned methods only involve high-fidelity design evaluators. It will be problematic when the design problem has a high-dimensional input space, because a huge amount of sample points is required to establish an accurate surrogate model. In this work, we propose to resolve this issue by employing the multi-fidelity approach.

2.3 Particle Swarm Optimization

Particle Swarm Optimization (PSO) was firstly proposed by Eberhart and Kennedy in 1995 (Kennedy and Eberhart 1995). The basic concept is to simulate the searching behavior of a flock of foraging birds. Each particle (i.e., search agent) in the N-dimensional design space has two attributes: speed and position. The optimal solution found by each particle is called the individual optimum, and the best value found by the swarm at present is called the current global optimum. The search history is recorded with a memory function. PSO has demonstrated its advantage over the traditional gradient optimization algorithms or local search strategies in solving engineering design problems. However, premature convergence occurs when PSO is applied to the highly nonlinear, non-convex design problem with multiple local optimums. To overcome this issue, three types of methods have been developed: neighborhood topological structure, parameter selection, and algorithm hybrid (Zhan et al. 2009). The neighborhood topology structure refers to the information exchange among adjacent particles. Godoy et al. proposed the Complex Neighborhood Particle Swarm Optimizer (CNPSO), in which the neighborhood of the particles is organized through an evolving complex network (Godoy and Zuben 2009). The premature convergence problem can also be resolved by setting the control parameters properly. The inertia weight has been identified as one of the most significant parameter for improving the search capability (Shi and Eberhart 1998; Gao and Duan 2007; Alfi and Fateh 2011). Algorithm hybrid refers to combination of several different speed updating modes under certain management strategy to leverage the advantages of different updating modes (Xin et al. 2012). New optimization algorithms are also created by hybridizing PSO with other heuristic algorithms (Gou et al. 2017). In this work, a modified PSO will be employed to overcome the premature convergence problem.

3 The proposed approach: probabilistic multi-phase surrogate-based multi-fidelity optimization

In this section, we will firstly introduce two pillars of the proposed optimization framework: the Probabilistic Multi-Phase (PMP) sampling strategy, and a modified Particle Swarm Optimization algorithm. Then, we will present the proposed optimization framework in Section 3.3.

3.1 Probabilistic Multi-Phase Sampling Strategy

The PMP sampling strategy is shown as the flowchart in Fig. 2. The pseudocode is presented in Algorithm 1.

Fig. 2
figure 2

Flowchart of the PMP sampling process. SM stands for surrogate model

Full size image

In the first step, DoE is conducted to gain initial knowledge of the relationship between design variables and design responses. A variety of DoE methods can be employed in this step, such as full factorial experimental design, orthogonal experimental design, uniform experimental design, and Latin Hypercube Sampling (LHS). Here we adopt LHS, which ensures that the set of random samples is representative of the real variability. The initial number of sampling points is determined by (6), where dim represents the number of design variables.

$$ \mathrm{initial}\ \mathrm{number}\ \mathrm{of}\ \mathrm{SP}=\min \left(\frac{\left(\dim +1\right)\left(\dim +2\right)}{2},5\times \dim \right) $$
(6)

During the sampling iterations, additional samples are generated either by a local sampler or by a global sampler. When the local sampler is activated, new training data will be collected inside a certain sub-region of the design space (i.e., important design region) to improve the accuracy of local prediction. If the global sampler is activated, new training data will be collected in the entire design space to improve the global accuracy of the surrogate model. During the iterative sampling process, the switch between the local and global samplers is controlled by the probabilistic multi-phase switch criterion. This criterion enables maximization of information gain by allocating sample points to the most promising design sub-regions.

Algorithm 1: PMP sampling strategy.

figure a

3.1.1 Local sampler

The purpose is to allocate sampling resources to important design regions to improve the local prediction accuracy. The important design region is defined as

$$ {\displaystyle \begin{array}{c}{\boldsymbol{x}}_L^k=\max \left({\boldsymbol{x}}_C^k-0.5{\boldsymbol{V}}^k,{\boldsymbol{x}}_L\right)\\ {}{\boldsymbol{x}}_U^k=\max \left({\boldsymbol{x}}_C^k-0.5{\boldsymbol{V}}^k,{\boldsymbol{x}}_U\right)\end{array}} $$
(7)

\( {\boldsymbol{x}}_L^k \) and \( {\boldsymbol{x}}_U^k \) are the lower and upper bounds of the important design sub-regions in the \( {\boldsymbol{k}}^{\mathrm{th}} \)iteration, \( {\boldsymbol{x}}_C^k \) presents the optimal design in the database in the \( {\boldsymbol{k}}^{\mathrm{th}} \) iteration, and \( {\boldsymbol{v}}^k \) on the ith variable dimension is defined in (8), where η presents a constant defined as a reduction coefficient. According to our tests, we recommend to use 0.2 as the value of η.

$$ {V}_i^k={\upeta}^{\frac{1}{\dim }}\times \left({x_U}_i-{x_L}_i\right) $$
(8)

xUi and xLi are upper and lower bounds in the ith dimension. Given the important design region, the local search criterion is defined in (9), where \( \hat{y}\left(\boldsymbol{x}\right) \) is a surrogate model trained with all previous data points,

$$ {\displaystyle \begin{array}{c}\mathrm{find}\ \boldsymbol{x}={\left[{x}_1,{x}_2\dots {x}_3\right]}^T\\ {}\min\ \hat{y}\left(\boldsymbol{x}\right)\\ {}\mathrm{S}.\mathrm{T}.{\boldsymbol{x}}_L^k\le \boldsymbol{x}\le {\boldsymbol{x}}_U^k\end{array}} $$
(9)

The optimal solution \( {\boldsymbol{x}}_{\mathrm{Loc}}^k \) is taken as the additional sampling location to enrich the local training data set. The response of \( {\boldsymbol{x}}_{\mathrm{Loc}}^k \) is obtained by running the high-fidelity simulation model.

3.1.2 Global sampler

The purpose is to improve the average accuracy of the surrogate model globally in the entire design space by adding sample points to the design region of a high epistemic uncertainty (lack of sample points). The epistemic uncertainty of an unknown point in the design space is represented by a Gaussian distribution:

$$ f\left(\boldsymbol{x}\right)\sim N\left(\hat{f}\left(\boldsymbol{x}\right),\operatorname{var}\left(\hat{f}\left(\boldsymbol{x}\right)\right)\right) $$
(10)

where the mean \( \hat{f}\left(\boldsymbol{x}\right) \) and variance \( \operatorname{var}\left(\hat{f}\left(\boldsymbol{x}\right)\right) \) is obtained from the Kriging surrogate model. The mathematical formula of global search criterion is shown in (11), where xL and xU present the upper and lower bounds of the design variables.

$$ {\displaystyle \begin{array}{c}\mathrm{find}\ \boldsymbol{x}={\left[{x}_1,{x}_2\dots {x}_3\right]}^T\\ {}\min \operatorname {var}\left(\hat{f}\left(\boldsymbol{x}\right)\right)\\ {}\mathrm{S}.\mathrm{T}.{\boldsymbol{x}}_L\le \boldsymbol{x}\le {\boldsymbol{x}}_U\end{array}} $$
(11)

The optimal solution \( {\boldsymbol{x}}_{GLO}^k \) is the updated sampling location. High-fidelity simulation is conducted to obtain the response of \( {\boldsymbol{x}}_{\mathrm{GLO}}^k \).

3.1.3 Probabilistic multi-phase switch criterion

Probabilistic multi-phase switch criterion is the core of the proposed PMP sampling strategy (Fig. 3). It controls the switch between the local sampler and the global sampler. If there is a strong evidence that the global optimum is likely to be inside the local sub-region, more resources will be allocated to generate more samples in the same sub-region. If there is a strong evidence that the global optimum is outside the local sub-region, the global sampler is activated. If there is no strong evidence to support neither side, both global and local sampling will be conducted.

Fig. 3
figure 3

Probabilistic multi-phase switch criterion. The optimal design within the important design region (OPI) and the optimal design outside the important design region (OPO) are found by surrogate model-based optimization. The comparison between OPI and OPO determines the sampling locations in the next iteration

Full size image

During each iteration, the most promising point inside the important design region (OPI) and the most promising point outside the important design region (OPO) are identified. The responses of the two points are marked as \( {f}_{\mathrm{opt}}^{\mathrm{in}}\left(\boldsymbol{x}\right) \) and \( {f}_{\mathrm{opt}}^{\mathrm{out}}\left(\boldsymbol{x}\right) \), respectively. So the probability that OPI is better than OPO is evaluated as:

$$ {\mathrm{Pro}}_{\mathrm{flag}}=P\left( OPI< OPO\right)=\Phi \left(\frac{\ {f}_{\mathrm{opt}}^{\mathrm{out}}\left(\boldsymbol{x}\right)-{f}_{\mathrm{opt}}^{\mathrm{in}}\left(\boldsymbol{x}\right)}{\sqrt{{\mathrm{MSE}}_{\mathrm{opt}}^{\mathrm{out}}\left(\boldsymbol{x}\right)+{\mathrm{MSE}}_{\mathrm{opt}}^{\mathrm{in}}\left(\boldsymbol{x}\right)}}\right) $$
(12)

Φ(x) is the CDF of standard normal distribution. Given the value of Proflag, the multi-phase switch criterion is established:

$$ \mathrm{Search}\ \mathrm{Phase}=\left\{\begin{array}{c}\mathrm{Global}\ \mathrm{sampling},\kern1.75em \mathrm{if}\ \Pr {\mathrm{o}}_{\mathrm{flag}}>{\varepsilon}_{\mathrm{glo}}\\ {}\mathrm{Local}\ \mathrm{sampling},\kern2em \mathrm{if}\ \Pr {\mathrm{o}}_{\mathrm{flag}}<{\varepsilon}_{\mathrm{loc}}\ \\ {}\mathrm{Both},\kern1em \mathrm{otherwise}\end{array}\right. $$
(13)

where εglo and εloc are constants defined as a critical coefficient. We recommend to use εglo = 0.75 and εloc = 0.5 based on our empirical tests.

3.1.4 Distance control criterion

It is well known that when some of the sample points are very close to each other, numerical issues will occur in fitting the Kriging model. To resolve this problem, a remedy (Algorithm 2) is proposed and integrated into the sequential sampling search process, where NSP presents the number of sampling points.

Algorithm 2: Distance control of sampling locations.

figure b

3.2 Modified Particle Swarm Optimization

Swarm intelligence algorithms are employed to solve the optimization problem with a nonlinear design landscape and multiple local optimums. PSO is selected, as it has better performance than the traditional gradient-based algorithms in high-dimensional nonlinear problems (Kennedy 2010). In order to avoid premature convergence induced by the stagnation of particle search motion, appropriate random perturbations are injected into the search process. The stagnant particles are reactivated to escape from the local optimum. In 2018, Liu et al. (Liu et al. 2019) proposed an adaptive reset operator to reset the speed of stagnant particles:

$$ {\boldsymbol{V}}_{\mathrm{reset}}=\mu \cdotp rw\cdotp {\boldsymbol{V}}_{\mathrm{rand}} $$
(14)
$$ \mu =\sqrt{1-\frac{{\mathrm{iter}}_{\mathrm{current}}}{{\mathrm{iter}}_{\mathrm{max}}}} $$
(15)
$$ rw=\left({rw}_{max}-{rw}_{min}\right)\cdotp \mu +{rw}_{min} $$
(16)

where μ is the generation correlation coefficient, rw is the velocity correlation coefficient, rwmax and rwmin are preset constants, and Vrand is a random value for speed reset.

3.3 PMP sampling-based optimization (PMP-SBO) framework

A new design framework is proposed by integrating the addition correction-based multi-fidelity surrogate model, PMP sampling, and the modified PSO. The multi-fidelity surrogate model provides an efficient and accurate tool for design evaluation. PMP sampling strategy is employed to enrich the dataset for training surrogate models. The modified PSO algorithm is employed to explore the design space and find the global optimum based on the multi-fidelity surrogate model.

The pseudo code of the framework is presented as Algorithm 3. The first step in each iteration is to establish an addition correction-based multi-fidelity surrogate model, which is shown in (1), using all existing sampling points. At each sampling location with both high-fidelity and low-fidelity data, the bias is calculated. Based on the bias dataset, another Kriging model is established as the addition bias correction term δ(x). The second step is to determine the important sub-regions for sampling in the next iteration. The objective is to add new points to the sub-region that possibly contains the optimal design or the sub-regions that lead to maximum improvements in the predictability of the multi-fidelity model. The sampling sub-regions are determined based on the optimal designs found by the multi-fidelity model within and without the current important sub-region (\( {f}_{\mathrm{opt}}^{\mathrm{in}}(x) \) and \( {f}_{\mathrm{opt}}^{\mathrm{out}}(x) \)). The sampling location in the next iteration is generated following the proposed PMP strategy. The performance of the new sample point is evaluated by both the high-fidelity and the low-fidelity models. Finally, the multi-fidelity model is updated with the new sample point, and an optimal design is obtained with the updated multi-fidelity model.

Algorithm 3. PMP-SBO framework.

figure c

4 Application cases

The proposed design framework is employed to optimize the metamaterial infill inside a fixed macroscale design envelop. Two case studies are presented in this section: optimization of a 2D planar cellular metamaterial structure under static loads and optimization of a pseudo 3D cellular metamaterial structure under transient dynamic load such as crash impact. Assuming that we have already determined the density of a structural region by topology optimization, the objective of this work is to select proper cellular mesostructure designs from the database as the infill material.

As a demo, the design envelops of the two case studies are predetermined as 0.6. We have established a metamaterial database, which includes three cellular mesostructure designs of the same density (VF = 0.6), as shown in Fig. 4. The base material of metamaterial (solid phase) is assigned with the property of steel. Topology optimization methods can be employed to obtain an initial structure design, i.e., macroscale structural envelop and the density of each element, under static loads; the proposed approach further expands the design space and enable the selection of the optimal mesostructure cell from the database to improve both static and transient dynamic performances. As shown in the exemplar database, cellular mesostructures of the same density may have very different elastic moduli, Poisson’s ratios, and nonlinear behaviors under dynamic loads. The stress-strain curves under different compression strain rates are used as the homogenized effective dynamic properties in the low-fidelity model. The dynamic properties are evaluated at ten different strain rates: quasi-static, 0.0001, 0.0005, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, and 1. It is to be noted that the proposed method can be extended to design problems with more choices of cellular designs of different volume fractions. We can also relieve the density constraint to enable the selection of metamaterial cells of different density levels in the database, as the initial density distribution pattern obtained by static topology optimization may not be optimal for transient dynamic load cases.

Fig. 4
figure 4

A database of mesostructure cells of the same density (VF = 0.6)

Full size image

For the large-scale real world engineering problems that involve hundreds or thousands of infill elements, high dimensionality of the design space poses a significant challenge to infill optimization. The large-scale problems can be addressed by implementing dimension reduction before conducting infill optimization. One example is the metamaterial frontal impact absorber shown in Fig. 1. To reduce the dimension of the problem, the large structure is divided into different zones, and each zone is infilled with the same cellular metamaterial design. Thus, only one selection variable is needed for each zone.

4.1 Multiscale plate in 2D plane

A 2D rectangular plate is constructed by infilling a rectangular design envelop with 3×4 mesostructure cells (Fig. 5). The high-fidelity model has a sufficiently high resolution such that it can capture the mesoscale geometric characteristics of each cell. The property of base material (steel) is assigned to each element of the fine model. In the low-fidelity model, each mesostructure cell is represented by one element, which is assigned with homogenized effective properties of the corresponding mesostructure cell. Two load cases are considered. First, a compression load of 10,000 N is applied to the top surface. The design objective is to minimize the compression deformation. Second, a shear load of 100 N is applied to the top surface. An upper bound of shear deformation is defined as the design constraint.

Fig. 5
figure 5

The fine model and the coarse model of a 2D rectangular plate under compression or shear loads

Full size image

One design variable is defined for each cell to enable independent selection of a cellular mesostructure design from the database. There are 12 discrete design variables in total, one for each unit cell. Then, the optimization problem is formulated as follows:

$$ {\displaystyle \begin{array}{c}\mathrm{find}\ x={\left[{x}_1,{x}_2\dots {x}_{12}\right]}^T\\ {}\min\ \mathrm{displacement}\ \mathrm{in}\ \mathrm{Case}\ 1\\ {}\mathrm{S}.\mathrm{T}.\mathrm{displacement}\ \mathrm{in}\ \mathrm{Case}\ 2>0.68\end{array}} $$
(17)

where x1, x2…x12 are the design variables. The initial dataset includes 100 low-fidelity sample points and 20 high-fidelity sample points. The proposed PMP-SBO method is tested for 20 times. On average, 82 additional sample points are generated for both low-fidelity and high-fidelity design evaluations during the search process. In total, 182 low-fidelity design evaluations and 102 high -fidelity design evaluations are incurred. Convergence history curves of five tests are plotted in Fig. 6.

Fig. 6
figure 6

The convergence history of PMP-SBO optimization on the 2D plate case

Full size image

The proposed method is compared with a traditional multi-fidelity surrogate model-based optimization approach, where a CoKriging surrogate model is established based on the same set of low-fidelity and high-fidelity samples. A reference solution of the optimization problem is obtained with an accurate surrogate model established on a sufficiently large training dataset (i.e., 500 fine sample points) that fully covers the design space. The results of the comparative study are presented in Table 1. It is observed that the PMP-SBO method finds a much better design than the traditional multi-fidelity surrogate model-based approach. This case study also demonstrates the efficiency of the PMP-SBO method, which achieves the same design performance with much fewer high-fidelity samples than the accurate surrogate model.

Table 1 Optimal solution found by PMP-SBO and CoKriging
Full size table

4.2 Pseudo-3D energy absorber

A pseudo-3D energy absorber is constructed by assembling mesostructure-infilled 2D plates in the 3D space (Fig. 7). The absorber consists of four plates in the X-Y plane, and four plates in the X-Z plane. Each plate consists of 3 ×5 mesostructure cells. This structure system is rotationally symmetric with respect to the X-axis, so only 36 out of 120 cells are considered as independent design variables. The process of axial crush is simulated using dynamic explicit FEA. The total impact energy absorbed by the structure is defined as the system response.

Fig. 7
figure 7

Pseudo-3D energy absorber under impact loads: a the high-fidelity model; b the low-fidelity model; c top view of the structure. As it is a rotational symmetric structure with respect to X-axis, the independent design region is marked with red lines in (c)

Full size image

Then, the optimization problem is formulated as:

$$ {\displaystyle \begin{array}{c}\mathrm{find}\ x={\left[{x}_1,{x}_2\dots {x}_{36}\right]}^T,\kern0.5em \mathrm{s}.\mathrm{t}.\\ {}\max\ \mathrm{the}\ \mathrm{total}\ \mathrm{energy}\ \mathrm{aborption}\end{array}} $$
(18)

where x1, x2…x36 are the design variables. One variable is defined for one unit cell. Three optimization approaches are compared in this study. (1) Cokriging multi-fidelity surrogate model-based optimization. (2) EGO with the correction multi-fidelity model, and (3) the proposed method based on multi-fidelity modeling and PMP-SBO. For Approach (1), two CoKriging surrogate models are trained on two different datasets: (i) a smaller dataset of 80 high-fidelity sample points and 400 low-fidelity sample points, and (ii) a larger dataset of 100 high-fidelity sample points and 400 low-fidelity sample points. For Approaches (2) and (3), the initial dataset contains 80 high-fidelity sample points and 400 low-fidelity sample points. Each approach is tested independently for 20 times, and the average performance of each method is presented in Table 2. yopt is the “virtual” response of the optimal design, which is obtained from the surrogate model. yver is the verified response (i.e., “true” response), which is obtained by conducting high-fidelity simulation on the optimal design. Figure 8 compares the convergence history curves of different optimization approaches. For each approach, one representative convergence curve is plotted.

Table 2 Optimal value of the pseudo-3D energy absorber system
Full size table
Fig. 8
figure 8

Comparison of the convergence rates of EGO and PMP-SBO. The design objective is to maximize the energy absorption. 60 designs are evaluated in each iteration

Full size image

Although the best virtual performance (yopt) is obtained with the CoKriging multi-fidelity surrogate model, its true responses yver is much worse than the virtual response. It indicates that the CoKriging surrogate model has a large error when it is applied to the highly nonlinear, high-dimensional design problems. The optimal designs obtained by CoKriging may not be even close to the true global optimum. Both Approaches (2) and (3) employ the idea of updating the surrogate model by adaptive sampling during optimal search. These two methods achieve better yver values than the traditional multi-fidelity surrogate model-based approach. It is also observed that PMP-SBO shows better performances than EGO at the same computational cost.

5 Conclusions

In this paper, an optimization framework is proposed for the design optimization of mesostructure-structure systems under static or transient dynamic load conditions. This framework integrates multi-fidelity surrogate modeling, Probabilistic Multi-Phase Sampling Strategy, and a modified PSO algorithm to enhance the efficiency of optimization. Our major conclusions are summarized as follows.

  1. 1.

    A probabilistic multi-phase switch criterion is proposed to improve the accuracy of the multi-fidelity model by adding sampling points sequentially during the optimization process. This approach provides an effective tool for allocating sampling resources.

  2. 2.

    Compared with the optimization approaches that only use high-fidelity analysis, the proposed approach achieves an equal or similar performance at lower computational costs.

  3. 3.

    The proposed approach shows its advantage over the traditional CoKriging multi-fidelity surrogate model-based optimization method, because the proposed approach allocates more computational resources to improve the predictability at the critical design regions.

However, the application of the proposed approach is limited to infill design at the current stage. The shape of the structure envelop is predetermined. In the future work, we will integrate this method with the optimization of the structure envelop. We will also further enrich the mesostructure database to provide more options for the infill design.