1 Introduction

Frame structures composed of beams and columns are used in numerous applications within the field of structural engineering. One such application is the rear structure of a wind turbine nacelle which is the starting point of the work presented in this paper. The design process is often iterative and involves many choices. Conflicting criteria like for instance low mass and high stiffness in addition to the occurrence of load redistribution adds to the complexity. This has led researchers to apply optimization techniques.

Continuous optimization of circular bar members in trusses has been studied since the 1960s, see Dorn et al. (1964). Defining a ground structure where members connect to nodes in all possible combinations, simultaneous sizing and topology optimization can be carried out if bar areas are allowed to reach zero. See e.g. Zhang et al. (2013) for a more recent publication also dealing with discrete bar areas.

For frame structures made from standard cross sections, e.g. Rectangular Hollow Sections (RHS) and I-sections, the sizing (candidate selection) problem is always discrete. The optimization methods previously applied to solve the problem include the Branch and Bound method (Huang and Arora 1997) and heuristic methods such as Simulated Annealing (Balling 1991), Genetic Algorithm (Jenkins 1992), and Particle Swarm algorithms (Jármai et al. 2006).

A completely different approach to solution of discrete problems is employed in topology optimization of continuum structures. Using the direct density approach (Bendsøe 1989), the material/void selection in each finite element is relaxed using a continuous density design variable. Thus, the discrete problem can be solved with gradient-based methods. Intermediate densities are made unfavorable with a penalization. This method was extended to three phases by Sigmund and Torquato (1997) and Gibiansky and Sigmund (2000) and used for the design of microstructures with extreme properties. Based on this work Stegmann and Lund (2005) developed the Discrete Material Optimization (DMO) method for optimization of laminated composites with an arbitrary number of candidate materials. The parameterization is based on generalized weight functions from continuum topology optimization (Hvejsel and Lund 2011). Bruyneel (2011) developed the Shape Functions with Penalization (SFP) parameterization scheme based on shape functions from a four node finite element which reduced the number of design variables.

Yu-pin et al. (2013) used the SFP method for cross section selection in frame structures with a mass objective function and constraints on the displacements. For this simple case the gradient-based method outperformed the Genetic Algorithm in terms of computational efficiency. To the authors’ knowledge this is the only paper in the open literature on gradient-based cross section selection in frame structures based on density approaches.

The approach in this paper is to apply the DMO method for cross section selection in frame structures. As will be shown, the parameterization is very simple and easy to implement. The objective is a preliminary design tool which can be used to quickly generate a first estimate of a design. In Section 2 the discrete problem is formulated mathematically. In Section 3 the methodology is explained and mass, compliance and stress criteria are defined. Also joint stiffnesses and implementation are discussed. Section 4 presents numerical examples that demonstrate the applicability of the proposed method. Section 5 discusses various issues related to optimization and analysis of frame structures.

2 Problem formulation

Given an input frame model consisting of members connected at master nodes (see Fig. 1), the task is to find the optimal combination of candidate cross sections for the members from a catalog of standard RHS and I-sections. This is done by altering the binary design variables x which are linked to the entries in the catalog.

Fig. 1
figure 1

Design parameterization of three member frame with two candidates

Full size image

The binary design variables are defined as:

$$\begin{array}{@{}rcl@{}} x_{ij} = \left\{\begin{array}{ll} 1 & \text{If candidate}~i~\text{is chosen in member}~j \\ 0 & \text{Otherwise} \end{array}\right. \end{array} $$
(1)

The design variables are stored in the vector x and the double index ij is merely convenient notation. In a Finite Element (FE) environment the optimization problem is mathematically formulated as:

$$\begin{array}{@{}rcl@{}} \underset{\mathbf{x}}{\text{minimise}}&&f\left( m(\mathbf{x}),C(\mathbf{x})\right) \\ \text{subject to}&&(1)~[\mathbf{K}]\mathbf{D} = \mathbf{R} \\ &&(2)~\boldsymbol{\sigma_{\text{VM}}} \leq \boldsymbol{\sigma_{\max}} \\ &&(3)~\sum\limits_{i=1}^{nCand} x_{ij} = 1 \quad \forall~j \\ &&(4)~x_{ij} \in \{0,1\} \\ &&,~i=1,...,nCand \\ &&,~j=1,...,nMemb \end{array} $$
(2)

The objective function to be minimized includes mass, m, and compliance, C, criteria. The first constraint dictates that the solution must be at the equilibrium state and is handled using a nested analysis and design (NAND) formulation. The second constraint ensures that von Mises stresses sampled at various locations in the structures, σ VM , are below a maximum allowable value. The third and fourth constraints facilitate the selection of exactly one candidate in each member with nCand and nMemb referring to the number of candidates and members respectively. In the work presented in this paper all members are assigned the same catalog but member specific candidates can easily be included. Note that if the third constraint is changed such that design variables in a member are allowed to sum to less than or equal to one, simultaneous candidate selection and topology optimization can be performed. That is, it is possible to remove all candidates as well. Other prevalent criteria used in optimization of frame structures include local and global stability and natural frequencies. These are not included in this paper but a discussion is given in Section 5.

3 Methodology

Following the framework set up by Hvejsel and Lund (2011) the starting point in the DMO method is to relax the design variables to continuous quantities. Next, properties are interpolated between 0 (no candidate) and 1 (full candidate) using weight functions. Note that this approach permits mixtures of candidate cross sections. To push the design variables to integers, intermediate designs with mixtures of candidate cross sections are made unfavorable by means of a penalization introduced through the interpolation scheme. If the optimizer outputs non-integer solutions the results must be rounded off.

3.1 Relaxation and interpolation

In a mathematical sense the relaxation simply implies that the fourth constraint in (2) changes to x i j ∈ [0,1]. The interpolation is carried out by the well-known SIMP (Solid Isotropic Material with Penalization, Bendsøe and Sigmund (2003) and RAMP (Rational Approximation of Material Properties (Stolpe and Svanberg 2001)) schemes from continuum topology optimization:

$$\begin{array}{@{}rcl@{}} \text{SIMP:} && w(x_{ij}) = x_{ij}^{p} \end{array} $$
(3a)
$$\begin{array}{@{}rcl@{}} \text{RAMP:} && w(x_{ij}) = \frac{x_{ij}}{1 + r (1 - x_{ij})} \end{array} $$
(3b)

Although the names suggest a physical interpretation of intermediate designs, the sole purpose of the schemes in this paper is mathematical manipulation. That is, only integer solutions are of interest.

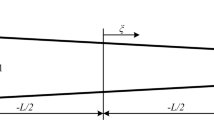
In the following, the interpolation schemes employed in the paper will be elaborated. Both below- and above-linear penalizations will be employed. Figure 2 depicts the SIMP scheme with various values of the penalty parameter p. For p > 1 the penalization will be below-linear. Note that SIMP also offers an above-linear penalization with 0 < p < 1, but due to the gradient approaching \(\infty \) when x i j approaches 0 this is not employed. Figure 3 depicts the RAMP scheme. With r > 0 the penalization is below-linear whereas with − 1 < r < 0 the penalization is above-linear. For a more convenient updating of the above-linear penalization, the parameter s e q is introduced such that e.g. s e q = 2 penalizes with the same magnitude as r = 2. The magnitude is measured using the arrows in Fig. 3 about which the RAMP function is symmetric.

Fig. 2
figure 2

SIMP interpolation with various values of the penalty parameter p

Full size image
Fig. 3
figure 3

RAMP interpolation with various values of the penalty parameters r and s e q

Full size image

To summarize, the three interpolation schemes used in this paper with their appertaining penalty parameters are:

  1. 1.

    SIMP, below-linear (p)

  2. 2.

    RAMP, below-linear (r)

  3. 3.

    RAMP, above-linear (s e q )

The values of the penalty parameters are controlled through a continuation method (Bendsøe and Sigmund 2003). The penalty is chosen such that the interpolation is initially linear or slightly penalized. Through iterations the penalty is increased such that the final design hopefully is an integer solution. In each iteration the optimized design from the previous iteration is used as a starting point. If the penalty starts too high, the risk of ending in a local minimum is increased.

In previous work on the DMO method, interpolation is carried out with the constitutive tensor of each candidate. The approach in this paper is different: Overall quantities containing constitutive properties are interpolated. There are two reasons for this: a) The parameterization is simpler and b) Shape functions in Timoshenko beam elements depend on the Young’s modulus, shear modulus, moments of inertia, area and length of the beam (Bazoune et al. 2003). Thus, if those properties were interpolated for each candidate, the shape functions of a particular beam element would be dependent on the design variables. This, in turn, would make the Design Sensitivity Analysis (DSA) very tedious.

The DMO element stiffness matrix in this work is thus obtained as:

$$\begin{array}{@{}rcl@{}} [\mathbf{k_{DMO}}] = [\mathbf{k_{0}}] + \sum\limits_{i=1}^{nCand} w_{c}(x_{ij})\left( [\mathbf{k}]_{i} - [\mathbf{k_{0}}] \right) \end{array} $$
(4)

[k] i is the stiffness matrix of the i th candidate. w c (x i j ) is the constitutive weight function evaluated with the design variable x i j . [k 0] is the stiffness matrix of a weak material and is included to avoid a singular stiffness matrix in case of topology optimization.

For the DSA the derivative of the element stiffness matrix is needed. It is simply obtained as:

$$\begin{array}{@{}rcl@{}} \frac{\partial [\mathbf{k_{DMO}}]}{\partial x_{kl}} = \frac{\partial w_{c}(x_{ij})}{\partial x_{kl}} \left( [\mathbf{k}]_{i} - [\mathbf{k_{0}}] \right) \end{array} $$
(5)

Here x k l is the design variable corresponding to the k th candidate in the l th member. Note that each weight function is only dependent on one design variable x i j . Thus, only the condition k = i ∧ l = j corresponds to a non-zero derivative.

When computing element stresses a constitutive interpolation must also be employed for consistency. For the beam elements used in this work, stresses are computed from section forces and moments which in turn are computed from nodal displacements, see e.g. Cook et al. (2002). These computations are contained in a stress-displacement function, g σ, i :

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}_{i} = w_{c}(x_{ij})~g_{\sigma,i}(\mathbf{d}) \end{array} $$
(6)

Here the subscript i on the g σ, i function indicates that the properties of the i th candidate are used in the calculation, and d is the element displacement vector.

3.2 Mass and compliance criteria

The mass and compliance criterion functions are defined as follows:

$$\begin{array}{@{}rcl@{}} m(\mathbf{x}) &=& \sum\limits_{j=1}^{nMemb}~~\sum\limits_{i=1}^{nCand} w_{d}(x_{ij})~\rho_{i}~A_{i}~L_{j} \end{array} $$
(7a)
$$\begin{array}{@{}rcl@{}} C(\mathbf{x}) &=& \mathbf{R}^{\mathrm{T}}\mathbf{D} \end{array} $$
(7b)

The mass is interpolated using candidate and member properties and the density weight function w d (x i j ). The compliance is calculated using the global load vector R which in the case of design dependent inertial loads is linearly interpolated and displacements D obtained from the global system of equations, [K DMO ]D = R.

The DSA of the mass criterion function is trivial. The compliance counterpart is effectively handled using the adjoint method, see for instance Tortorelli and Michaleris (1994). It can be shown that the displacements D satisfy the adjoint problem whereby each sensitivity can be computed as:

$$\begin{array}{@{}rcl@{}} \frac{\partial C(\mathbf{x})}{\partial x_{kl}} = -\mathbf{D}^{\mathrm{T}}\frac{\partial [\mathbf{K_{DMO}}]}{\partial x_{kl}}\mathbf{D} + 2~ \mathbf{D}^{\mathrm{T}}\frac{\partial \mathbf{R}}{\partial x_{kl}} \end{array} $$
(8)

Note that the compliance DSA can be conducted without solving the global system of equations since the displacements are readily available. For design independent loads the rightmost term vanishes.

The problem treated in traditional continuum topology optimization is minimization of the compliance with a constraint on the total amount of material, i.e. mass. In the following this formulation is used to study the effect of penalization with the approach presented in this paper.

Consider a 6 m long, 1 kN tiploaded cantilever beam with two candidate materials and thus two design variables. In this example the design with the 2nd candidate is infeasible in terms of mass. Figure 4 presents the design space with the constitutive properties interpolated with the SIMP scheme and p = 1, i.e. linear interpolation. The compliance objective function is represented by the level curves. Notice how it goes to infinity when both design variables approach zero. The mass constraint, i.e. infeasible region, is represented by the grey colored area enclosed by the solid black line. The red dashed line is the design variable equality constraint and the solution must be found on this line.

Fig. 4
figure 4

2D design space for cantilever beam with two candidates and SIMP interpolation with p = 1

Full size image

By inspection it is possible to locate the global optimum to approximately {x 1, x 2} = {0.63,0.37}, where the compliance objective function assumes a value of 20 Nm (green cross in the figure). This is however not an integer solution and does not represent a physically sensible design. Rounding the design variables to the nearest integer will obviously give the wanted integer solution and in this case it is also feasible. However, depending on the sensitivity of the constraint, rounding can have a detrimental effect on feasibility and an integer output from the optimizer is preferred.

The design space from the same example with a penalty parameter of p = 2 is shown in Fig. 5. The penalization makes the objective function concave and moves the global optimum to the integer solution {x 1, x 2} = {1,0}.

Fig. 5
figure 5

2D design space for cantilever beam with two candidates and SIMP interpolation with p = 2

Full size image

Numerical studies with minimization of compliance subject to a mass constraint have shown that this formulation lacks robustness in terms of obtaining integer solutions. Moreover, in an industrial context the formulation of a hard mass constraint on the entire structure is less useful. Thus, the mass criterion is implemented in the objective function in (2) using a weighted sum formulation:

$$\begin{array}{@{}rcl@{}} { f\left( m(\mathbf{x}),C(\mathbf{x})\right) = \alpha C(\mathbf{x})^{\text{norm}} + (1-\alpha) m(\mathbf{x})^{\text{norm}} }\end{array} $$
(9)

The parameter α ∈ [0,1] controls how the mass and compliance criterion functions are weighted. In order to add the mass and compliance criterion functions, i.e. quantities with different units and possibly different orders of magnitudes, the criterion functions are normalized with their respective values obtained with the initial guess x 0, e.g. C(x)norm = C(x)/C(x 0).

In minimum mass topology optimization (e.g. with stress constraints), the mass is not penalized (Bendsøe and Sigmund 2003). However, e.g. París et al. (2009) report that a penalized mass objective function can be used as an aid to obtaining integer solutions. This will also be the procedure in this paper and w d (x i j ) in (7a) is an above-linear interpolation with the penalty parameter s e q .

3.3 Stress constraints

In traditional continuum topology optimization, stress constraints are introduced on the following form in order to make them simple and physically consistent (Bendsøe and Sigmund 2003):

$$\begin{array}{@{}rcl@{}} \sigma_{\text{VM}} \leq w_{s}(x) \sigma_{\max} \end{array} $$
(10)

The design variable x is the density in topology optimization. w s (x) is a stress weight function used to interpolate the maximum allowable stress. There are two main challenges in regard to stress constraints in topology optimization. The first is whether to use local or globally aggregated stress constraints. Since beam elements are used in this paper an appropriately low number of local constraints can be defined and this approach is used. The second challenge is the singularity problem. Studies using simple trusses have shown that the global optimum can be located in degenerate subdomains of the design space which gradient-based optimizers cannot enter (Kirsch 1990). A remedy is to relax the constraint, i.e. to enlarge the degenerate subdomain as employed with the ε-approach (Cheng and Guo 1997) and the qp-method (Bruggi 2008). The latter has the advantage that the relaxation vanishes with integer designs and will therefore be considered in this paper.

The qp-method uses SIMP interpolation with the following penalty parameters:

$$\begin{array}{@{}rcl@{}} w_{c}(x_{ij}) &=& x_{ij}^{p} \quad,~p\geq 1 \end{array} $$
(11a)
$$\begin{array}{@{}rcl@{}} w_{s}(x_{ij}) &=& x_{ij}^{q} \quad,~q\geq 1,~q\leq p \end{array} $$
(11b)

The problem can be solved with a q initially smaller than p. Through continuation iterations q is increased until the condition q = p, which corresponds to the original problem. Whether there is a singularity problem in the present optimization problem has not been confirmed but the qp-method has proven effective as mathematical manipulation to relax the stress constraints yielding better solutions. This is also evident from Fig. 6 which depicts the 2D design space of a cantilever beam with two candidates where the design with the 1st candidate is infeasible.

Fig. 6
figure 6

2D design space for cantilever beam with two candidates and SIMP interpolation. Left with p = 3, q = 3, right with p = 3, q = 1. Notice that the contours indicate the value of the stress constraint

Full size image

For a given cross section eight evaluation points are defined which are depicted in Fig. 7. Notice that points 4 and 8 on an RHS section are not coincident with points 4* and 8* on an I-section. For the RHS section, the shear stresses from torsion and normal stresses from bending about the z-axis are maximum at points 4 and 8. Both of these stresses are negligible in the web of the I-section, i.e. at points 4* and 8*.

Fig. 7
figure 7

Points in a cross section where stresses are evaluated. Notice that points 4 and 8 on an RHS section are different from points 4* and 8* on an I-section since the geometry is not coincident there

Full size image

If only point loads at the master nodes are present in the model it suffices to evaluate stresses at the end of each member whereby the number of stress constraints is 16 per member. In the optimization with inertia loads, stresses will also be evaluated at the midspan of each member whereby the total number of stress constraints reaches 24 per member.

A local constraint is defined at each of the eight points in Fig. 7 in a given member. It is defined using a scalar stress criterion function, Ψ:

$$\begin{array}{@{}rcl@{}} {\Psi}(\mathbf{x}) \leq 0 \end{array} $$
(12)

Ψ(x) must be a sum of contributions from the different candidates available for the particular member analogous to the interpolation of stiffness matrices in (4). The starting point for the criteria applied in this paper is (10). Dividing by the maximum allowable stress to normalize and afterwards summing over all candidates the following is obtained:

$$\begin{array}{@{}rcl@{}} {\Psi}(\mathbf{x}) = \sum\limits_{i=1}^{nCand} \left[\frac{\sigma_{\text{VM},i}}{\sigma_{\text{Y},i}} - w_{s}(x_{ij})\right] \end{array} $$
(13)

Here σ VM, i is the von Mises stress at the point of consideration in the i th candidate calculated from interpolated stress components cf. (6). σ Y, i is the yield stress of the i th candidate. Note that if any of the fractions σ VM, i /σ Y, i is greater than 1 the constraint will be violated since \(\sum w_{s} \leq 1\).

Consider now the DSA of the stress constraints using the Direct Differentiation Method (DDM). Differentiating (13) the following is obtained:

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d} {\Psi}(\mathbf{x})}{\mathrm{d} x_{kl}} = \sum\limits_{i=1}^{nCand} \left[ \frac{1}{\sigma_{\text{Y},i}} \frac{\mathrm{d}\sigma_{\text{VM},i}}{\mathrm{d} x_{kl}} - \frac{\partial w_{s}(x_{ij})}{\partial x_{kl}} \right] \end{array} $$
(14)

The differentiation can be done w.r.t. any design variable in x. With the weight function w s (x i j ) given as a simple analytical expression, the calculation of its derivative is a trivial task. The derivative of the von Mises stress in the i th candidate is more cumbersome to obtain. Using the chain rule and vectorizing it is given as:

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d} \sigma_{\text{VM},i}}{\mathrm{d} x_{kl}} = \frac{\partial \sigma_{\text{VM},i}}{\partial \boldsymbol{\sigma}_{i}^{\mathrm{T}}} \frac{\mathrm{d} \boldsymbol{\sigma}_{i}}{\mathrm{d} x_{kl}} \end{array} $$
(15)

Partial derivatives of the von Mises stress w.r.t. the individual stress components can be obtained analytically using the expression for the von Mises criterion. Derivatives of the individual stress components w.r.t. a design variable are obtained with basis in (6). Differentiation yields:

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d} \boldsymbol{\sigma}_{i}}{\mathrm{d} x_{kl}} = \frac{\partial w_{c}(x_{ij})}{\partial x_{kl}}~g_{\sigma,i}(\mathbf{d}) + w_{c}(x_{ij})~g_{\sigma,i} \left( \frac{\mathrm{d} \mathbf{d}}{\mathrm{d} x_{kl}} \right) \end{array} $$
(16)

The derivative of the displacement vector is found implicitly using the pseudo load problem (obtained by differentiating the equilibrium equation):

$$\begin{array}{@{}rcl@{}} [\mathbf{K_{DMO}}]\frac{\mathrm{d}\mathbf{D}}{\mathrm{d} x_{kl}} = \frac{\partial \mathbf{R}}{\partial x_{kl}} - \frac{\partial [\mathbf{K_{DMO}}]}{\partial x_{kl}}\mathbf{D} \end{array} $$
(17)

The solution to this equation is the derivative of the global displacement vector. By means of bookkeeping the element displacement vector derivative can be found. Using DDM, the sensitivity (17) must be solved for each design variable in the stress DSA. This is more efficient than an adjoint DSA since the number of stress constraints in this work exceeds the number of design variables.

3.4 Joint stiffnesses

Joints between the frame members are commonly designed as either welded or bolted, which impose a rotational stiffness reduction on the joint. This must be taken into account when designing a structure according to Eurocode 3: Part 1-8: Design of Joints (CEN 2007a). Joints are divided into three categories depending on joint stiffnesses, S: nominally pinned, semi-rigid, and rigid:

$$\begin{array}{@{}rcl@{}} { \begin{array}{l l c c c l} \text{Nom. pinned:~~~} & 0 & \leq &S&\leq& 0.5EI/L \\ \text{Semi-rigid:} & 0.5EI/L &\leq &S& \leq& 8EI/L \\ \text{Rigid:} & 8EI/L & \leq &S& \leq & \infty \\ \end{array}} \end{array} $$
(18)

Here length L, Young’s modulus E, and moment of inertia I belong to the member going into the joint. Thus there will be a joint stiffness for each member in the joint.

In this paper, the rotational stiffnesses of joints are controlled by continuous design variables to give an indication of whether the joint should be rigid, semi-rigid or pinned. For each master node, one design variable scale the joint stiffnesses to be in the semi-rigid interval. For a joint stiffness at the transition to the rigid interval the design variable is equal to 0, and for the transition to the pinned region the design variable is equal to 1. Joint strength is not considered. A similar approach was taken by Fredricson et al. (2003). The implementation is straight forward and the approach allows for modeling load redistribution in the structure. That is, when the joint stiffness goes toward zero, so does the bending moment in the members connected in the joint. In order to maintain equilibrium the forces and moments elsewhere in the structure will change. Thus, in a complicated frame structure with beams, columns and bracings, the structural response is heavily dependent on the joint stiffnesses.

Huber and Tschemmernegg (1998) suggest to model a joint as an equivalent beam stub to account for the physical dimensions of the joint (Fig. 8). The moment of inertia of the joint stub I joint is determined such that the response is equivalent to that of a rotational spring with stiffness S, i.e. M = S 𝜃. Using the rotation angle of a cantilever beam with a constant moment, the joint moment of inertia is determined as:

$$\begin{array}{@{}rcl@{}} I_{joint} = \frac{S\,L_{joint}}{E} \end{array} $$
(19)

E and A of the equivalent beam stub are assigned the same values as those of the member with which it is connected. Changing S and thereby I j o i n t a joint response in the semi-rigid interval can be obtained. The joint stubs have a length L joint equal to half the height of the smallest candidate in the member. Note that this can yield some overlapping members, both due to joint angles other than 0 ∘ and 90 ∘ but also due to the fact that the joint length is kept fixed during optimization.

Fig. 8
figure 8

Modeling from Huber and Tschemmernegg (1998) applied on a K-joint. Corner stress evaluation points are indicated by a cross

Full size image

The inclusion of joint stiffnesses introduces extra design variables in the optimization, whose design sensitivities must be found. This is rather tedious and details are left out. They are also determined using DDM.

3.5 Implementation

The parameterization and criteria elaborated previously in this section are implemented in a MATLAB program. The baseline is an FE-routine with 3D linear elastic Timoshenko beam elements with an analytical stiffness matrix from Cook et al. (2002). Structural loads are input as point loads in the master nodes and linear accelerations, angular accelerations and angular velocities in the global coordinate system. Multiple load cases are included using a weighted sum formulation.

The code enables access to all relevant information for e.g. the DSA. The optimization is carried out with MATLAB’s intrinsic fmincon using a Sequential Quadratic Programming (SQP) algorithm. The initial guess of candidate selection variables x i j is taken as x i j = 1/n C a n d in order not to favor any candidates a priori while obeying the design variable equality constraint (Stegmann and Lund 2005). Joint design variables are initialized as 0.5 corresponding to a stiffness halfway between rigid and pinned. The continuation approach is implemented with p, r and s eq increasing by 1 in each continuation iteration and q increasing by 1.11. With the starting value of p being equal to q + 1, a maximum of 10 continuation iterations can be carried out before the condition p = q is fulfilled. The convergence of the SQP optimizer is monitored using a first-order optimality measure with a tolerance of 10−6. By the end of each continuation iteration the DMO convergence is checked: If each member has one design variable with a value greater than 0.95 the optimization is terminated.

The FE-routine is verified against the commercial FE-code ANSYS while the analytical gradients are verified using Finite Difference (FD) approximations - both with satisfactory results.

An interesting consequence of the inertial loads is that the structural behavior no longer is monotonic as also noted by Bruyneel and Duysinx (2005). This behavior is depicted in Fig. 9 with the same setup as in Fig. 4 but with added gravity.

Fig. 9
figure 9

The linearly interpolated compliance objective function shows non-monotonic behavior when inertia loads are imposed

Full size image

4 Numerical examples

In the following, results are presented with three different benchmark frame models.

4.1 Benchmark models

The benchmark models and their catalog of candidates used in this section are depicted in Figs. 10, 11 and 12. In the models, the blue arrows indicate the orientation of the local z-axis (major axis) of the cross section. Numbers refer to members and numbers in brackets refer to master nodes. The material is structural steel with a Young’s modulus of 210 GPa and a yield stress of 235 MPa. Cross section properties can be found in DIN 1025-1 (I-sections) and EN 10210-2 (RHS).

Fig. 10
figure 10

Benchmark model 1: 2D Tower and appertaining catalog

Full size image
Fig. 11
figure 11

Benchmark model 2: 3D Frame and appertaining catalog

Full size image
Fig. 12
figure 12

Benchmark model 3: 3D Box. This model uses the same catalog as 3D Frame, Fig. 11

Full size image

4.2 Mapping the pareto front

This example considers the 2D Tower model with only mass and compliance criteria and rigid joints. Varying the parameter α in (9) the Pareto front can be mapped in the criterion space. A sweep through 20 values of α yielded 12 unique solutions. A full factorial design exploration has also been conducted with evaluation of all 58 = 390,625 combinations (computation time: 25 minutes). The results along with the utopia point is depicted in Fig. 13. The DMO approach effectively predicts the Pareto front. Each optimum is found within a few seconds on a standard laptop with all outputs from the optimizer being integer solutions.

Fig. 13
figure 13

Pareto front in the criterion space of benchmark model 2: 2D Tower

Full size image

Two DMO solutions from Fig. 13 are presented in Table 1 along with the number of iterations.

Table 1 Mass and compliance optimization of 2D Tower
Full size table

4.3 Simultaneous candidate selection and topology optimization

Consider again the 2D Tower model with mass, compliance and rigid joints with the same settings as the previous example. As previously mentioned, simultaneous candidate selection and topology optimization can be performed if the design variables are allowed to sum to less than or equal to one in a member. Thus the third constraint in (2) is changed to:

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{nCand} x_{ij} \leq 1 \quad \forall~j \end{array} $$
(20)

This form of the constraint has shown to be less robust in terms of obtaining integer solutions; When design variables must sum to unity, an increase in the amount of one candidate always means a decrease in the amount of other candidates. This balance is not enforced with (20). Another approach is to include a candidate with insignificant mass and stiffness. This introduces an extra design variable per member and thus is slower but more robust. Notice that the topology of the frame structure is limited to the input model to the program. Thus, only members defined before the optimization can be removed.

With α = 0, i.e. pure mass minimization, both approaches yield the trivial solution with all members removed. Two other results with the inequality constraint approach, (20), are given in Table 2. Consider α = 0.2 and compare to Table 1: By removing member 2, the mass is lowered by 60 kg, while the compliance is almost unaffected. With α = 0.3 two members are removed which significantly increases the compliance. Using the approach with an extra design variable and the original unity-sum constraint in (2), only member 2 is removed from the two cases of α presented.

Table 2 Simultaneous candidate selection and topology optimization results from 2D Tower using the inequality constraint approach. Settings are given in Table 1
Full size table

4.4 Optimization with stress constraints and rigid joints

This example is used to demonstrate the effect of the implemented stress constraints. Consider the benchmark model 3D Frame with rigid joints and with the objective of minimizing the mass, i.e. α = 0 in (9). Two different Factors of Safety (FoS) for stresses are used as constraints for the results in Table 3. Also the number of iterations and the global optimum found using a full factorial design exploration are presented. The second design in the table, which is also the global optimum, is depicted in Fig. 14 (left). For both DMO optima, the stress constraint is inactive. The stress constraints work well although the computational time does increase substantially.

Table 3 Stress constrained minimum mass optimization of 3D Frame
Full size table
Fig. 14
figure 14

Stress constrained minimum mass optimized design of 3D Frame with FoS = 2.5. Numbers refer to the candidate number, numbers in brackets refer to joint stiffnesses (0: rigid, 1: pinned). Member numbers are repeated in upper left corner for convenience. The cross sections are scaled by 150 %. Left: rigid joints, compliance is 298.8 Nm. Right: joint stiffness design variables, compliance is 370.1 Nm

Full size image

4.5 Optimization with stress constraints and joint design variables

Consider again the 3D Frame with the same setup as previously only this time the joint stiffnesses are also included as design variables. Results are given in Table 4. The first design with FoS = 2.0 is in fact identical to the global optimum with rigid joints. Thus, the optimized joint stiffnesses can be set to rigid and the design will still be feasible in stresses. For this particular example where the global optimum has an active stress constraint, the enlargement of the design space due to the joint stiffness design variables is beneficial for the optimizer. The second design with FoS = 2.5 is depicted in Fig. 14 (right). By replacing the I-section (candidate 4) in member 3 with a slightly smaller RHS (candidate 8) and manipulating the joint stiffnesses, the forces and moments in the structure are redistributed. For instance, the lowest FoS in member 2 is decreased from 15.5 to 6.2. The result is that the mass is lowered by 9.8 kg or 4.7 % while the stresses are still below their maximum allowable values. The compliance is increased by 71.2 Nm or 24 %, however this was not a criterion in the present problem. If the optimization is carried out with fixed pinned joints the optimizer selects the same candidates cross sections as in Fig. 14 (right). The compliance, however, increases by 36 %. This indicates that the variable joint stiffnesses enable better utilization of the material in the structure. As will become evident in the next example, some optima are more sensitive to the joint stiffnesses and require certain combinations of stiffnesses in the semi-rigid interval.

Table 4 Stress constrained minimum mass optimization of 3D Frame including joint stiffness design variables and candidate selection. Settings are given in Table 3
Full size table

4.6 Elaborate optimization of benchmark model 3: 3D box

To prove that the DMO method applied to frame structures is suitable to larger scale problems with industrial applicability the third benchmark model, 3D Box, is subjected to mass, compliance and stress criteria in addition to joint stiffness design variables and two load cases with inertia loads. The parameter α is 0.1, i.e. 90 % mass and 10 % compliance minimization. Apart from providing some stiffness to the design, it was found that a small amount of compliance in the objective function increases the robustness when stress constraints are imposed. The nodal point loads defined in Fig. 12 in combination with gravity will form load case 1. Load case 2 consists of a linear acceleration a, angular acceleration \(\boldsymbol {\dot {\omega }}\) and angular velocity ω applied to the global coordinate system:

$$\begin{array}{@{}rcl@{}} \mathbf{a} = \left\{\begin{array}{lll} 0.0 \\ 0.0 \\ 5.0 \end{array}\right\} ~;\quad \boldsymbol{\dot{\omega}} = \left\{\begin{array}{lll} 2.0 \\ 9.0 \\ 1.5 \end{array}\right\} ~;\quad \boldsymbol{\omega} = \left\{\begin{array}{lll} 0.0 \\ 3.5 \\ 1.0 \end{array}\right\} \end{array} $$
(21)

The inertia loads require a discretization of each member into multiple finite elements. Convergence in terms of maximum stress was reached with 10 elements per member yielding a total of 1,226 degrees of freedom. With 10 candidates and 18 members a total of 180 DMO design variables exist plus 8 joint design variables. The number of stress constraints is 432.

The maximum allowable stresses are calculated with basis in the Eurocode standard (CEN 2007b): Load case 1 is considered an ultimate limit state (\(\sigma _{\max } = 138\) MPa) and load case 2 is considered as fatigue (\(\sigma _{\max } = 87\) MPa).

The optimizer converged to an integer solution in 4 continuation iterations. The mass is 955 kg, compliance for load case 1 is 4,123 Nm and 8.1 Nm for load case 2. The maximum stresses are 138 MPa for load case 1 and 26.7 MPa for load case 2. The optimized design is depicted in Fig. 15.

Fig. 15
figure 15

Stress constrained minimum mass and compliance optimized design of 3D Box with joint stiffness design variables. Numbers refer to candidate numbers and numbers in brackets refer to the joint stiffness design variables: 0: Rigid, 1: Pinned. The settings were: constitutive interpolation: SIMP, p = 2, q = 1 (increasing), density interpolation: RAMP, s eq = 2 (increasing)

Full size image

Notice how large I-sections are chosen for the bracings in member 17 and 18. From Fig. 12 it is evident that the local z-axes of all horizontal members also point in a horizontal direction. Thus, the bracings are the only options for aligning the strong axes of cross sections with the major load direction. Preferably the orientation of the cross sections should be included in the optimization to avoid making limiting decisions a priori. This could be realized by expanding the catalog with rotated candidates or letting a design variable control the rotation in each member.

Post processing of the design indicates that it is a local minimum. If for instance candidate 10 in member 1 is substituted with candidate 9, the mass is lowered by 70 kg while the compliance is increased insignificantly. In addition, the maximum stresses are lowered by 1 MPa. Setting all the joint stiffnesses to either rigid or pinned does, however, not yield feasible solutions. The former increases the maximum stress to 139 MPa, while the latter will cause the maximum stress to attain 155 MPa. If instead, each joint stiffness is rounded to either rigid or pinned the result is a maximum stress of 146 MPa. Thus, the current design is very sensitive to the joint stiffnesses.

Consider the continuation iteration history of members 1 and 2 in Fig. 16. It can be concluded that no new candidates are selected after iteration 2. This observation is in fact valid for all members in the model. Thus, for the present problem, the penalization could potentially increase faster.

Fig. 16
figure 16

Continuation iteration history of member 1 (left) and member 2 (right) of the 3D Box. Four continuation iterations have been carried out before all members have converged with a tolerance of 95 %. Iteration 0 corresponds to the initial guess

Full size image

Figure 17 presents the development of the mass and compliance objective functions as well as the maximum stress constraint. The continuation iterations are indicated with vertical dashed lines where the effect of increasing penalization is evident as spikes in the graphs. As seen the problem converges monotonically.

Fig. 17
figure 17

The iteration history of mass, compliance and maximum stress for 3D Box

Full size image

4.7 Comparison to discrete search methods

This subsection presents results obtained with MATLAB’s intrinsic ga Genetic Algorithm (GA) optimizer on the 3D Box benchmark model. The optimization is carried out with default settings which implies that the generation of random numbers is based on the Mersenne Twister algorithm with seed 0.

The setup is as described in Section 4.6. The optimized design is depicted in Fig. 18 and has, as the DMO design, large I-sections for the bracings. A comparison of key figures to the DMO solution is presented in Table 5. From the table it is evident that both solutions are feasible in stresses. The GA solution is 15 % lighter but the compliance is 22 % higher. Thus, both solutions are reasonable in terms of fulfilling the objective. The DMO method converges in less than two thirds of the time spent by GA and uses 97 % fever function evaluations. Since the code was not performance optimized it is believed that even more computational efficiency can be gained for the DMO method - especially in the DSA. Furthermore, if more design variables and/or more degrees of freedom are included in the model, the difference is expected to be greater.

Fig. 18
figure 18

Genetic Algorithm stress constrained minimum mass and compliance optimized design of 3D Box with joint stiffness design variables. Numbers refer to candidate numbers and numbers in brackets refer to the joint stiffness design variables: 0: Rigid, 1: Pinned

Full size image
Table 5 Comparison between DMO and GA optimizations on 3D Box benchmark model. The computational time was measured on a standard laptop with an Intel Core i7 2.6 GHz processor and 8 GB RAM
Full size table

5 Discussion

With an output from a preliminary design tool as the one presented in this paper, some additional steps are required in order to reach a final design. Although more criteria can be included in the optimization, different standards and norms can make this task challenging.

The first logical step is to make detailed joint designs. The optimal joint stiffnesses can be difficult to realize in practice but they do provide useful information for the designer. Artificial explicit penalization of joint design variables could be a way of pushing joint stiffnesses to either rigid or pinned. With a detailed joint design, the stresses including stress concentrations from e.g. welds or bolts must be calculated. This might very well involve solid Finite Element (FE) modeling. If solid FE models of all possible joint configurations are made before the optimization, a joint catalog can be implemented in the optimization analogously to the selection of cross sections. However, the number of combinations for each joint in the model is the number of candidates raised to the power of the number of members in the joint. For the 3D Box benchmark model a rigid and a pinned joint type for all eight joints would then result in 880,000 entries in the joint catalog.

If members in the structure are subjected to twist about the longitudinal axis, the effects of warping torsion can also be considered with the proper boundary conditions. Stability - both local and global - should be assessed wherever compressive stresses exist. In an optimization framework, Torii et al. (2015) proposed to use a single global stability constraint that can also capture local instability, i.e. on member level. While this can be implemented in the present approach, the Eurocode standard has specific requirements. As also noted by Jármai et al. (2006) the Eurocode formulae include a variety of parameters that depend on the stiffness conditions and the moment distribution in the member. Therefore fixed approximations must be used during optimization. Yet another difficulty is the case of topology optimization where members can be removed, thereby changing the effective length of other members.

Finally, the dynamic response of the frame model should be assessed. The fundamental natural frequency of the structure must be well away from the frequency of excitation loads, e.g. the rotor frequency in the case of a wind turbine nacelle. Here, the joint stiffnesses also play a vital role, in that different joint types will introduce varying amount of hysteresis and viscous damping. Decreasing joint stiffnesses also tend to reduce especially the lower natural frequencies of the system as shown by Sekulovic et al. (2002). It was also shown that a nonlinear joint stiffness model should be used to properly account for the dynamic response.

The requirements set forth by the standards may seem tedious but this underlines the usefulness of a good preliminary design.

6 Conclusion

The DMO method has been succesfully applied to 3D frame structures for selection of candidate cross sections subjected to mass, compliance and stress criteria. In addition, the MATLAB implementation can take into account joint stiffness as design variables, inertia loads and multiple load cases.

The well-known SIMP and RAMP interpolation schemes from continuum topology optimization serve as the basis in the relaxation of the discrete problem. By means of penalization all of the presented optimizations converged to integer solutions. To this end the inclusion of the mass criterion in the objective function and the penalization hereof proved useful albeit slightly unconventional in continuum topology optimization. The amount of mass and compliance in the weighted sum objective function is controlled by a linear scaling parameter. Regarding the stress criteria, a modified version of the qp-method was implemented as it provided a sufficient relaxation of the design space.

In the numerical examples the usefulness of the method was demonstrated. Mapping of the Pareto front is a quick and effective way of outlining the design space. It was successfully validated using a full factorial design exploration. Simultaneous candidate selection and topology optimization enabled for members to be removed. Thus, the input to the program can be a ground structure.

Allowing the joint stiffness of each master node to continuously scale within the semi-rigid interval yielded designs that are lighter than their rigid joint counterparts. Finally, all criteria, joint stiffnesses, inertia loads and two load cases were included in an optimization of a complicated 3D frame model. The comparison to the Genetic Algorithm showed promise in that both the DMO and GA optimized designs are on the Pareto front. The latter has a lower mass but also a proportionally lower stiffness. With the successful output from the optimizer it is clear that also problems with industrial applicability can be handled.