1 Introduction

Sheet metal forming is an important industrial technology for producing light weight products with high productivity. There are many process parameters for the successful sheet metal forming, such as material properties, blank shape, die geometry, and blank holder force (BHF). Low BHF leads to wrinkling, whereas high BHF results in tearing. Both wrinkling and tearing are major defects in sheet metal forming, and they should be strongly avoided. To avoid these defects, the BHF plays a crucial role in sheet metal forming. Recently, variable blank holder force (VBHF) that controls the BHF through the stroke is recognized as an attractive and innovative approach for the successful sheet metal forming (Obermeyer & Majlessi 1998), and many papers to determine the VBHF trajectory in deep drawing have been published.

Two approaches are mainly used to determine the VBHF trajectory: One is to develop a closed-loop type algorithm, and the other is to use a design optimization technique. One of the representative papers using the closed-loop type algorithm can be found in Ref. (Sheng et al. 2004), in which a proportional plus integral (PI) controller was developed. Lo and Yang (Lo & Yang 2004), Wang et al.(Wang et al. 2007), and Lin et al.(Lin et al. 2007) developed a proportional, integral, and differential (PID) controller for the VBHF trajectory in deep drawing. In their papers, wrinkling was evaluated by the distance between the die and the blank holder, and tearing was evaluated by the maximum thinning. The gain coefficients in the PI and PID controller were then adjusted to avoid the wrinkling and tearing. Yagami et al. developed a closed-loop type algorithm in deep drawing to avoid wrinkling (Yagami et al. 2007), in which both the BHF and the punch motion was controlled. We also developed a simple closed-loop type algorithm without the PI and PID controller (Kitayama et al. 2010), in which the thickness deviation as well as the wrinkling and tearing were considered. Through the numerical simulation and the experiments, the validity was examined. The closed-loop type algorithm is easy to carry out, but a large number of simulations are required. In particular, the trial-and-error method is required to determine the several parameters in the algorithm. In general, numerical simulation in deep drawing is so intensive that it is preferable to determine the VBHF trajectory with a small number of simulations for a practical engineering application.

To determine the VBHF trajectory with a small number of simulations, response surface approach is valid. In particular, a sequential approximate optimization (SAO) that the response surface is repeatedly constructed and optimized is recognized as one of the powerful tools available in design optimization. Chengzhi et al. determined the optimal BHF (Chengzhi et al. 2005), in which both the wrinkling and the tearing were evaluated by the forming limit diagram (FLD), and were approximated with the quadratic polynomial. Note that the BHF is constant through the punch stroke, and VBHF approach is not employed in this paper. Jakumeit et al. used the Kriging to determine the optimal VBHF trajectory (Jakumeit et al. 2005), in which the stroke was divided, and the BHF was taken as the design variables. In addition, the FLD was used to evaluate the objective functions. As Ingarao and Di Lorenzo suggest (Ingarao & Di Lorenzo 2010), the FLD is a useful tool to evaluate the wrinkling and tearing. To determine an optimal VBHF trajectory, one of the simplest approaches is to divide the stroke into sub-stroke steps. The BHF of sub-stroke step is then taken as the design variables. We also determined the optimal VBHF trajectory in deep drawing with the SAO using a radial basis function (RBF) network (Kitayama et al. 2012), in which the thickness deviation was minimized under the wrinkling and tearing constraints. Design optimization using the SAO for drawbead forces can be found in Refs. (Breitkopf et al. 2005; Jansson et al. 2003; Liu & Yang 2008; Sun et al. 2011; Wang et al. 2009a; Wang et al. 2010), in which note that a constant BHF is used. Optimization of VBHF trajectory using the SAO is recognized as an attractive and crucial approach for successful sheet metal forming in industry (Kitayama et al. 2013; Wang et al. 2008), but the practical application is rarely reported. Fortunately, servo press can freely control the BHF through the stroke, we use it for an optimal VBHF trajectory in experiment.

In addition to VBHF approach, blank shape is an important factor for successful sheet metal forming. Wrinkling will be easily generated with a large blank shape, whereas it is difficult to obtain the desirable product with a small blank shape. In deep drawing, earing that is often defined as the area above the trimmed contour is generated, and the earing is discarded. Since the blank shape directly leads to the cost reduction, it is much important to determine an optimal blank shape minimizing earing as well as the optimal VBHF trajectory. To determine an optimal blank shape, there are mainly two approaches: One is to develop a closed-loop type algorithm, and the other is to use a response surface approach. A typical approach using a closed-loop type algorithm is to adopt the geometrical shape error (GSE) (Park et al. 1999; Vafaeesefat 2011; Wang et al. 2009b) and the target shape error (TSE) (Oliveira et al. 2009), in which finite element analysis (FEA) is repeatedly carried out until the GSE and TSE value becomes very small. The approach using the GSE and the TSE are valid, but a large number of simulations are required to determine an optimal blank shape. Since it is preferable to determine an optimal blank shape with a small number of simulations, the SAO to determine an optimal blank shape is an important method in practical application in industry. Several papers to determine an optimal blank shape using the SAO can be found in Refs. (Hino et al. 2006; Kitayama et al. 2015; Liu et al. 2013; Naceur et al. 2008).

Here, we would like to summarize our motivation of this paper.

  1. (1)

    Blank shape directly affects the material cost. To reduce the material cost, it is important to determine an optimal blank shape minimizing the earing.

  2. (2)

    VBHF approach is recognized as an attractive and crucial technology for successful sheet metal forming, but the practical application is rarely reported. We use AC servo press (H1F150, Komatsu Industries, Corp.) for the VBHF approach. Unfortunately, optimal VBHF trajectory is unknown in advance. The optimal VBHF trajectory is then determined.

  3. (3)

    As described above, blank shape optimization and optimization of variable blank holder force trajectory was separately performed. Simultaneous optimization of both blank shape and VBHF trajectory is one of the crucial issues in industrial requirement, but this is rarely discussed. To meet this requirement, simultaneous optimization of both blank shape and VBHF trajectory is performed, where the SAO using the RBF network is adopted (Kitayama et al. 2011). The simultaneous optimization is one of the most challenging issues in industry. The validity should be examined through numerical and experimental result.

The rest of paper is organized as follows: In section 2, the FEA model based on the experimental results is developed. The validity of the FEA model is discussed. In section 3, the simultaneous design optimization of both blank shape and VBHF trajectory is described. The SAO using the RBF network is also briefly described. In section 4, numerical and experimental result is shown and the validity of the proposed approach is discussed.

2 Experiments and finite element analysis model

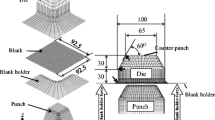
In our case study, a tray-type product shown in Fig. 1 is considered. First, the experiment for the formability is carried out. Based on the experimental results, the FEA model is developed. SUS304 is used as the blank, and the material property is listed in Table 1. The detailed numerical simulation model is discussed in section2.2, and here let us explain about the forming process using the FEA model shown in Fig. 2. For the symmetry, only a half model is considered. The punch is fixed, and the die drops to the negative z direction with 580 mm/s. Note that the velocity of the die with 580 mm/s is used to shorten the computational time (Mass scaling is not used). We have already confirmed that there was no strain rate dependency during developing the FEA model. The BHF is applied to the positive z direction, and the stroke length is 58 mm for the successful sheet forming. The stress–strain curve is shown in Fig. 3, which can be obtained through an experiment. LS-DYNA, which is one of the dynamic explicit FEA codes, is used in the numerical simulation.

Fig. 1
figure 1

Tray-type product

Full size image
Table 1 Material property of SUS304
Full size table
Fig. 2
figure 2

Finite element analysis model for numerical simulation

Full size image
Fig. 3
figure 3

Stress–strain curve

Full size image

2.1 Experiment for formability

To investigate the formability, several constant BHFs are applied under lubrication condition. No tearing can be observed under the lubrication condition, and the aim is to identify the wrinkling region. Note that the tearing is observed without lubrication. The result is shown in Fig. 4, in which the gray zone represents the wrinkling region. Let us explain about Fig. 4, in which the triangles represent the critical point that the wrinkling is observed. For example, in the case of 50 kN, no wrinkling can be observed till the stroke of 20 mm. However, the wrinkling is observed after the stroke of 20 mm.

Fig. 4
figure 4

Formability window of wrinkling under lubrication condition

Full size image

2.2 Finite element analysis model

Based on the experimental results, the FEA model shown in Fig. 2 is developed. In Fig. 2, the symbol nelm denotes the number of finite elements. The rigid element is used to the punch, the die, and the blank holder. Note that the drawbead is modeled in the die and the blank holder for the accurate numerical simulation. The Belytschko-Tsay shell type element with seven integration points across the thickness is used for the blank. The friction coefficient and the penalty coefficient for contact in the interfaces (blank/punch, blank/blank holder, and blank/die) are set to 0.05 and 0.10, respectively. Note that the low friction coefficient is used for the lubrication condition. The experimental and numerical result at point A is shown in Fig. 5.

Fig. 5
figure 5

Experimental and numerical result at point A in Fig. 4

Full size image

2.3 Forming limit diagram

In this paper, the forming limit diagram (FLD) (Storen & Rice 1975) is used to numerically evaluate the wrinkling and the tearing. In the FLD, the strain states of all elements of the blank are plotted on a major-minor strain plane. The FLD at point A in Fig. 3 is shown in Fig. 6, in which the solid curve represents the critical limit for the tearing, and the dashed line the critical limit for the wrinkling. In other words, the tearing can be observed when the strain states are plotted above the critical curve for the tearing, and the wrinkling can be observed when the strain states are plotted below the critical line for the wrinkling. It is clear from Fig. 6 that several points are plotted below the critical line for the wrinkling, and the FEA model is then valid. Then, we use this FEA model for the simultaneous optimization of blank shape and variable blank holder force trajectory.

Fig. 6
figure 6

Forming limit diagram at points A in Fig. 4

Full size image

3 Simultaneous optimization of blank shape and variable blank holder force trajectory

Simultaneous optimization of blank shape and variable blank holder force trajectory is one of the challenging issues in industry. Numerical simulation in sheet metal forming is so intensive that the SAO using the RBF network is used for the simultaneous optimization. First, we briefly the SAO using the RBF network, and the design optimization is formulated.

3.1 Sequential approximate optimization using radial basis function network

The general procedure of SAO is shown in Fig. 7, from which it is found that the response surface is repeatedly constructed and optimized. In addition, new sampling points are added for improving the response surface. The effectiveness using multiple surrogate techniques is discussed in Ref. (Viana et al. 2013), but the RBF network is used throughout the SAO procedure in this paper. Therefore, the RBF network is used to construct the response surface. In addition, the density function which is constructed by the RBF network is used to find an unexplored region. In the following, the RBF network is briefly described.

Fig. 7
figure 7

General procedure of a sequential approximate optimization

Full size image

The RBF network is a three-layer feed-forward network. Let m be the number of sampling points, and the training data is given by {x j , y j }(j = 1, 2, ⋯, m). The response surface is constructed by the following equation:

$$ \tilde{y}\left(\boldsymbol{x}\right)={\displaystyle {\sum}_{j=1}^m{w}_j{h}_j\left(\boldsymbol{x}\right)} $$
(1)

where h j (x) is the j-th basis function, and w j denotes the weight of the j-th basis function. The Gaussian kernel given by (2) is widely used as the basis function:

$$ {h}_j\left(\boldsymbol{x}\right)= \exp \left(-\frac{{\left(\boldsymbol{x}-{\boldsymbol{x}}_j\right)}^T\left(\boldsymbol{x}-{\boldsymbol{x}}_j\right)}{r_j^2}\right) $$
(2)

where r j is the width of the j-th basis function. In the RBF network, in order to determine the weight vector w, the following equation is minimized:

$$ E={\displaystyle {\sum}_{j=1}^m{\left({y}_j-\tilde{y}\left({\boldsymbol{x}}_j\right)\right)}^2}+{\displaystyle {\sum}_{j=1}^m{\lambda}_j{w}_j^2}\to \min $$
(3)

where the second term is introduced for the regularization, and λ j which have a sufficiently small value (e.g. λ j  = 1.0 × 10− 3) is introduced. The necessary condition of (3) results in the following equation:

$$ \boldsymbol{w}={\left({\boldsymbol{H}}^T\boldsymbol{H}+\boldsymbol{\varLambda} \right)}^{-1}{\boldsymbol{H}}^T\boldsymbol{y} $$
(4)

where H, Λ, and y are given as follows:

$$ \begin{array}{cc}\hfill \boldsymbol{H}=\left[\begin{array}{cccc}\hfill {h}_1\left({\boldsymbol{x}}_1\right)\hfill & \hfill {h}_2\left({\boldsymbol{x}}_1\right)\hfill & \hfill \cdots \hfill & \hfill {h}_m\left({\boldsymbol{x}}_1\right)\hfill \\ {}\hfill {h}_1\left({\boldsymbol{x}}_2\right)\hfill & \hfill {h}_2\left({\boldsymbol{x}}_2\right)\hfill & \hfill \cdots \hfill & \hfill {h}_m\left({\boldsymbol{x}}_2\right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill {h}_1\left({\boldsymbol{x}}_m\right)\hfill & \hfill {h}_2\left({\boldsymbol{x}}_m\right)\hfill & \hfill \cdots \hfill & \hfill {h}_m\left({\boldsymbol{x}}_m\right)\hfill \end{array}\right]\hfill & \hfill \hfill \end{array} $$
(5)
$$ \boldsymbol{\varLambda} =\left[\begin{array}{cccc}\hfill {\lambda}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {\lambda}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda}_m\hfill \end{array}\right] $$
(6)
$$ \boldsymbol{y}={\left({y}_1,{y}_2,\cdots, {y}_m\right)}^T $$
(7)

It is clear from (4) that the learning of the RBF network can be achieved by the matrix inversion (H T H + Λ)− 1. The additional learning is also reduced to the incremental calculation of the matrix inversion (Nakayama et al. 2002), and the RBF network is suitable for SAO.

In order to easily determine the width, the following simple estimate is proposed (Kitayama et al. 2011):

$$ \begin{array}{cc}\hfill {r}_j=\frac{d_{j, \max }}{\sqrt{n}\sqrt[n]{m-1}}\hfill & \hfill j=1,2,\cdots, m\hfill \end{array} $$
(8)

where r j denotes the width of the j-th Gaussian kernel, and d j,max denotes the maximum distance between the j-th sampling point and the other sampling points. (8) is applied to each Gaussian kernel individually, and can deal with the non-uniform distribution of the sampling points.

3.2 Density function to find the unexplored region

One of the key issues for successful SAO is to add a new sampling point around an unexplored region for global approximation. In other words, it is important to find an unexplored region effectively. To find an unexplored region, we have developed the density function using the RBF network (Kitayama et al. 2011). The basic idea has been described in Ref. (Kitayama et al. 2011), and the numerical procedure for the density function is described below:

  1. (D-STEP1)

    The vector y D = (1, 1, ⋯, 1) T m × 1 is prepared at the sampling points.

  2. (D-STEP2)

    The weight vector w D of the density function D(x) is calculated as:

    $$ {\boldsymbol{w}}^D={\left({\boldsymbol{H}}^T\boldsymbol{H}+\boldsymbol{\varLambda} \right)}^{-1}{\boldsymbol{H}}^T{\boldsymbol{y}}^D $$
    (9)
  3. (D-STEP3)

    The density function D(x) is minimized to determine the unexplored region.

    $$ D\left(\boldsymbol{x}\right)={\displaystyle {\sum}_{j=1}^m{w}_j^D{h}_j\left(\boldsymbol{x}\right)}\to \min $$
    (10)
  4. (D-STEP4)

    The point minimizing D(x) is taken as the new sampling point.

Figure 8 is an illustrative example of the density function in one dimension, and the black dots denote the sampling points. It is clear from Fig. 8 that local minima are generated around the unexplored region. Note that points A and B in Fig. 8 represent the lower and upper bounds of the design variable x 1 of the density function. The optimal points minimizing the density function are taken as new sampling points for global approximation. Since it is difficult to find several optimal points simultaneously, the following iterative procedure is introduced:

Fig. 8
figure 8

Illustrative example of the density function in one dimension

Full size image
  1. (1)

    A global minimum of the density function can be determined, and this point is added as a new sampling point.

  2. (2)

    The density function is constructed from all sampling points, and return to (1).

By introducing this iterative processes, it is expected that the uniform distribution of the sampling points can be achieved.

3.3 Evaluation of wrinkling and tearing using forming limit diagram

Tearing and wrinkling are the major defects that typically occur in deep drawing, and are handled as the design constraints in this paper. In order to evaluate the degree of tearing and wrinkling, the strains in the formed element are analyzed and compared against the forming limit curve (FLC, as shown in Fig. 9). The following FLC was defined in the principal plane of logarithmic strains proposed by Hillman and Kubli (Hillmann & Kubli 1999).

$$ \begin{array}{cc}\hfill {\varepsilon}_1={\varphi}_T\left({\varepsilon}_2\right)\hfill & \hfill {\varepsilon}_1={\varphi}_W\left({\varepsilon}_2\right)\hfill \end{array} $$
(11)

where φ T is the FLC that controls tearing, and φ W is the FLC that controls wrinkling. Then, the following safety FLC is defined:

$$ \left.\begin{array}{l}{\theta}_T\left({\varepsilon}_2\right)=\left(1-s\right){\varphi}_T\left({\varepsilon}_2\right)\\ {}{\theta}_W\left({\varepsilon}_2\right)=\left(1+s\right){\varphi}_W\left({\varepsilon}_2\right)\end{array}\right\} $$
(12)

where s represents the safety tolerance, and is defined by the engineers (in this paper, s is set to 0.2). If an element comes to or lies above FLC, it is expected that a risk of tearing can be observed. Similarly, a risk of wrinkling can be assumed if an element lies in the wrinkling region. Unlike previous studies (Wang et al. 2008; Wang et al. 2009a; Wang et al. 2010), the risk of both wrinkling and tearing were evaluated according to the following two constraints (Kitayama et al. 2012):

Fig. 9
figure 9

Forming limit diagram for evaluating tearing and wrinkling

Full size image

For tearing:

$$ \begin{array}{cc}\hfill {g}_1\left(\boldsymbol{x}\right)={\left({\displaystyle {\sum}_{j=1}^{nelm}{T}_j}\right)}^{1/p}\hfill & \hfill \left\{\begin{array}{cc}\hfill {T}_j={\left({\varepsilon}_1^j-{\theta}_T\left({\varepsilon}_2^j\right)\right)}^p\hfill & \hfill {\varepsilon}_1^j>{\theta}_T\left({\varepsilon}_2^j\right)\hfill \\ {}\hfill {T}_j=0\hfill & \hfill otherwise\hfill \end{array}\right.\hfill \end{array} $$
(13)

For wrinkling:

$$ \begin{array}{cc}\hfill {g}_2\left(\boldsymbol{x}\right)={\left({\displaystyle {\sum}_{j=1}^{nelm}{W}_j}\right)}^{1/p}\hfill & \hfill \left\{\begin{array}{cc}\hfill {W}_j={\left({\theta}_W\left({\varepsilon}_2^j\right)-{\varepsilon}_1^j\right)}^p\hfill & \hfill {\varepsilon}_1^j<{\theta}_W\left({\varepsilon}_2^j\right)\hfill \\ {}\hfill {W}_j=0\hfill & \hfill otherwise\hfill \end{array}\right.\hfill \end{array} $$
(14)

Based on the literature (Wang et al. 2008; Wang et al. 2009a; Wang et al. 2010), p is set to 4. Also, nelm represents the number of finite elements of the blank.

3.4 Objective function, design constraint, and design variables for blank shape and variable blank holder force trajectory

Blank shape has a direct influence on the material cost as well as the product quality. A large blank produces a large flange part that is trimmed off as waste, whereas a desirable product cannot be obtained with a small blank. In addition, the BHF affects the product quality. Therefore, simultaneous optimization of blank shape and BHF is one of the crucial issues. First, let us explain about the objective function and the design constraint for the blank shape. The deformation with the initial blank shape (the thickness of 0.38 mm, the width of 430 mm, and the length of 125 mm) is shown in Fig. 10, in which the solid line denotes the exact shape, the dashed line the trimmed contour, and the area above the trimmed contour the earing, respectively. Note that only a half model is shown in this figure. The trimmed contour is set to 10 mm from the exact shape. It is found from Fig. 10 that a large earing is produced with the initial blank size, and our objective is to determine the optimal blank shape minimizing earing. Therefore, the area above the trimmed contour is taken as the objective function.

Fig. 10
figure 10

Deformation in numerical simulation (only a half model)

Full size image

To determine the optimal blank shape minimizing the earing, the five nodes denoted by black circles in Fig. 11 are taken as the design variables. Nodes 1 and 5 move along the horizontal line (x-axis), and Node 3 moves along the vertical line (y-axis), respectively. In addition, Nodes 2 and 4 move along the vertex of the initial blank shape. Considering the blank cutting with a laser processing, these nodes are connected by straight line as shown in Fig. 11, and the optimal blank shape is then determined.

Fig. 11
figure 11

Design variables for blank shape

Full size image

The area above the trimmed line is taken as the objective function, and it completely depends on the blank shape. Figure 12 shows an example of the undesirable product, from which it is found that the area below the trimmed line is generated after the sheet metal forming. It is strongly needed from a design requirement that the area below the trimmed contour should not be generated. To avoid the undesirable product, the area below the trimmed contour is taken as the design constraint g 3(x). When the area below the trimmed contour is not generated as shown in Fig. 10, zero is assigned to g 3(x).

Fig. 12
figure 12

Illustrative example of undesirable product

Full size image

For the variable blank holder force trajectory, total stroke L max is partitioned into M sub-stroke steps and the BHF of each sub-stroke is taken as the design variables. An illustrative example of the design variables is shown in Fig. 13, where it should be noted that the design variable for VBHF starts from x 6.

Fig. 13
figure 13

Design variables for variable blank holder force trajectory

Full size image

3.5 Flow of sequential approximate optimization using radial basis function network

The flow of the SAO using the RBF network is shown in Fig. 14. The detailed procedure is summarized as follows:

Fig. 14
figure 14

Flow of sequential approximate optimization using radial basis function network

Full size image
  1. (STEP1)

    Several initial sampling points are generated by the latin hypercube design (LHD).

  2. (STEP2)

    Numerical simulation at the sampling points is carried out. Then, the objective function (f(x): the area above the trimmed line), and the design constraints (g 1(x): tearing, g 2(x): wrinkling, and g 3(x): the area below the trimmed contour) are calculated.

  3. (STEP3)

    Response surface by the RBF network is developed and optimized.

  4. (STEP4)

    If the terminal criterion is satisfied, the SAO using the RBF network will be terminated. Otherwise, the optimal solution obtained in STEP3 is added as a new sampling point for improving the local accuracy. In this paper, the error at the optimal solution is adopted as the terminal criterion, which is set to 5.0 %.

  5. (STEP5)

    The density function is developed and optimized for the global approximation. This step is repeated till the terminal criterion is satisfied, as shown in Fig. 13. Then, the algorithm returns to STEP 2.

4 Numerical and experimental results

Through numerical simulation, the simultaneous optimization of blank shape and variable blank holder force trajectory is performed. Based on the numerical result, the experiment using an AC servo press (H1F150, Komatsu Industry Corp.) is carried out. Considering the availability of the AC servo press, the total stroke is divided into 4. The side constraints are set as follows:

$$ \left.\begin{array}{l}\begin{array}{ccc}\hfill 15\le {x}_1\le 43\left[ mm\right]\hfill & \hfill 18\le {x}_2\le 77\left[ mm\right]\hfill & \hfill 37\le {x}_3\le 56\left[ mm\right]\hfill \end{array}\\ {}\begin{array}{cc}\hfill 40\le {x}_4\le 108\left[ mm\right]\hfill & \hfill 34\le {x}_5\le 43\left[ mm\right]\hfill \end{array}\\ {}\begin{array}{ccc}\hfill 50\le {x}_6\le 130\left[kN\right]\hfill & \hfill for\hfill & \hfill 0\le {L}_1\le 20\left[ mm\right]\hfill \end{array}\\ {}\begin{array}{ccc}\hfill 50\le {x}_7\le 200\left[kN\right]\hfill & \hfill for\hfill & \hfill 20\le {L}_2\le 32\left[ mm\right]\hfill \end{array}\\ {}\begin{array}{ccc}\hfill 50\le {x}_8\le 200\left[kN\right]\hfill & \hfill for\hfill & \hfill 32\le {L}_3\le 44\left[ mm\right]\hfill \end{array}\\ {}\begin{array}{ccc}\hfill 50\le {x}_9\le 200\left[kN\right]\hfill & \hfill for\hfill & \hfill 44\le {L}_4\le 58\left[ mm\right]\hfill \end{array}\end{array}\right\} $$
(15)

Fifteen initial sampling points are first generated with the LHD, and the optimal blank shape and VBHF trajectory is determined. The terminal criterion is satisfied at 26 sampling points, and the SAO algorithm using the RBF network is terminated. The optimal blank shape and VBHF trajectory are shown in Figs. 15 and 16. Table 2 shows the optimal BHF. The FLD at the optimal solution is also shown in Fig. 17, from which it is found that no tearing and wrinkling can be observed.

Fig. 15
figure 15

Optimal blank shape and deformed shape in numerical simulation

Full size image
Fig. 16
figure 16

Optimal VBHF trajectory in numerical simulation and experiment

Full size image
Table 2 Optimal BHF
Full size table
Fig. 17
figure 17

Forming limit diagram at optimal solution

Full size image

Based on the numerical result, the experiment using AC servo press (H1F150, Komatsu Industries, Corp.) is carried out. The average die speed in the experiment is approximately 80 mm/s. The overview is shown in Fig. 18. The optimal blank shape and the deformed shape in the experiment are shown in Fig. 19. Note that the optimal VBHF trajectory is shown in Fig. 16 with the red line. It is clear from the experimental result that the successful sheet metal forming is performed. In addition, the AC servo press has a high performance for the VBHF trajectory.

Fig. 18
figure 18

Overview of punch, blank holder, and drawbead

Full size image
Fig. 19
figure 19

Optimal blank shape and deformed shape in experiment

Full size image

Let us examine the effectiveness of optimal blank shape and optimal VBHF trajectory. Conventionally, the full blank size shown in Table 1 and a constant BHF (140kN) is used to produce this tray-type product. When the optimal blank shape is used, the area of 20.10 % can be reduced. This directly leads to the material cost reduction, and therefore the material cost of 20.10 % can be reduced with the optimal blank shape. Next, let us consider the VBHF trajectory. One of the objectives using VBHF approach is to minimize the energy consumption in the successful sheet metal forming, and the energy consumption of the AC servo press is evaluated. The total stroke for the successful sheet metal forming is 58 mm, and the product between the constant BHF (140kN) and the total stroke (58 mm) is then simply defined as the forming energy. The forming energy using the optimal VBHF trajectory is calculated as:

$$ {\displaystyle {\sum}_{i=1}^M{x}_{5+i}{L}_i} $$
(16)

Therefore, the gray area in Fig. 13 is simply regarded as the forming energy. When the optimal VBHF trajectory is used, the forming energy of 20.30 % is reduced. The summary is listed in Table 3. Finally, as shown in Fig. 20, five lengths are examined for the dimension accuracy. The result is summarized in Table 4, from which it is clear that the error is small except for l 3. Fortunately, as shown in Fig. 13, the area below the trimmed line is not generated with the optimal blank shape in the experiment. We confirm from these results that the simultaneous optimization of both blank shape and VBHF trajectory is valid.

Table 3 Comparison between conventional and proposed approach
Full size table
Fig. 20
figure 20

Evaluation for dimension accuracy

Full size image
Table 4 Dimension accuracy between numerical simulation and experiment
Full size table

5 Concluding remarks

Blank shape optimization and optimization of variable blank holder force trajectory was separately performed in previous papers. Simultaneous optimization of both blank shape and VBHF trajectory is recognized as one of the important issues in industrial requirement, but this is not rarely discussed. To meet this requirement, simultaneous optimization of both blank shape and VBHF trajectory is performed. First, we carried out the experiment to identify the wrinkling region. Based on the experimental results, the FEA model is developed. The validity of the FEA model is examined by using the FLD. After that, numerical optimization with the SAO using the RBF network is performed, and the optimal blank shape and the optimal VBHF trajectory are then determined. Based on the numerical optimization result, the experiment using the AC servo press (H1F150, Komatsu Industries, Corp.) is carried out. It is found from the experimental results that the successful sheet metal forming is performed. In addition, we can confirm from the numerical and experimental result that both the material cost and the forming energy are simultaneously reduced by using design optimization technique.