1 Introduction

Surrogate-based analysis (SBA) plays an increasingly significant role in most scientific and engineering applications (Queipo et al. 2005). In recent years, as the computer aided engineering (CAE) develops rapidly (e.g. Finite-Element Analysis and Computational Fluid Dynamic Analysis), SBA is employed in various areas which involve structural design (Degroote et al. 2012), aerodynamic shape optimization (Yu et al. 2011; Eves et al. 2012) and multidisciplinary design optimization (MDO, Yao et al. 2011). By using SBA, the computational burden can be greatly reduced, as the efforts involved in constructing and optimizing the surrogate model are much lower than the standard approach that directly couples the simulation codes with the optimizer (Forrester and Keane 2009). Besides, it can be utilized to find the global optimal solution of black-box problems, realize parallel optimization and filter numerical noise. The surrogate model (Wang and Shan 2007; Tenne and Armfield 2009) is often referred to as “approximation model” or “response surface”. There are various techniques for constructing a SM. Polynomial response surface (RSM, Box and Draper 1987a, b) is the classical regression method, which is widely used in engineering design but hard to deal with non-linear and multimodal models (Forrester and Keane 2009). Radial basis functions (RBF, Broomhead and Loewe 1988) and kriging (also referred to as Gaussian process) are most prominent and commonly used for interpolation (Li et al. 2008; Simpson et al. 2001). The RBF is represented as a sum of basis functions each associated with an appropriate coefficient to emulate complicated design landscapes and kriging treats the system response as a realization of a stochastic process to predict the unexplored region. Among these techniques, the kriging model is increasingly popular (Paz et al. 2014; Cadini et al. 2014). This is because kriging has the capability of predicting highly non-linear responses, and meanwhile it can directly provide a significant estimation of the uncertainty of the predictor.

Multi-fidelity methods (also called variable-fidelity methods) have been developed to enhance the efficiency of constructing an accurate SM (Kennedy and O’Hagan 2000; Forrester et al. 2007; Robinson et al. 2008; Zadeh et al. 2009; Sun et al. 2011; Yelten et al. 2012; Koziel and Ogurtsov 2013). With computational capabilities improving, the range of numerical analysis models increases and one same problem always has multiple analysis models with various fidelities. Generally, the low-fidelity (LF) model is a computationally cheap model, such as calculated by panel methods, empirical equations, or simple beam theory. Nevertheless, the high-fidelity (HF) model is commonly a more accurate but relatively computationally expensive model, which may be solved by computational fluid dynamics or finite element analysis. Responses from HF analysis are always more difficult to obtain than that from the LF model. Generally, a multi-fidelity surrogate-based method always utilizes a large number of cheap data coupled with a small quantity of expensive data to improve the accuracy of the expensive problem’s SM. Chang et al. (1993) proposed a kind of multi-fidelity method which constructed a “bridge function” to correct the low-fidelity surrogate model and the accuracy was enhanced. Balabanov and Venter (2004) introduced a novel approach to multi-fidelity optimization which employs the gradient information from a LF model to improve the performance of a HF SM. Koziel et al. (2006) advised a “Space-mapping framework” concept, which iteratively updates and optimizes SMs based on a fast physically based “coarse model” to minimize the number of expensive “fine model” evaluations. Xiong et al. (2008) combined the multi-fidelity analysis with objective-oriented sequential sampling to improve a design objective. Han et al. (2010) presented a new cokriging method for multi-fidelity surrogate-based analysis and proved its validity in aerodynamic examples. Koziel and Leifsson (2013) provided a surrogate-based optimization algorithm for transonic airfoil design, which replaced the direct optimization of the HF model by an iterative reoptimization of a LF model. To sum up, most of these methods aim to solve how to fuse the useful information from different models to improve the overall approximation accuracy. However, there are few methods considering the uncertainty of the system and utilizing the uncertainty information synthetically.

In this paper, a kriging-based SM was constructed to predict the expensive function. Considering the uncertainty of the different fidelities’ models and the uncertainty of the kriging-based predictor, we implemented mathematical modeling to obtain the integral uncertainty of a HF model and that of a LF model, respectively. The inadequacy of the analysis model is qualified to denote the model uncertainty in the form of probability. Presently, many techniques for assigning model probabilities are introduced. Zio and Apostolakis (1996) and Reinert and Apostolakis (2006) utilized expert assessment to qualify the uncertainty. Link and Barker (2006) and Burnham and Anderson (2002) discussed the Akaike information criterion and Bayesian statistical criterion. Allaire et al. (2010) used the maximum entropy theory to analyze uncertainty of models. This paper just employed the expert opinion to give the probabilities of various analysis models and didn’t pay more attention to how to obtain uncertainty assessment of some specific engineering problem. As above, the uncertainty of the kriging-based predictor was also qualified in the form of probabilities by estimating its mean square error. Subsequently, based on a kind of filtering algorithm, the independent information from different models was fused and a new SM with depressed uncertainty was obtained. As the previous discussion, the SM is helpful to realize the engineering design, and the fused SM will be a more efficient tool to help engineers finish their design.

The remainder of the paper is organized as follows: Section 2 gives a detailed introduction about how to confirm the integral uncertainty of SMs. Section 3 explains the fusion strategy. Several numerical cases and one engineering example are implemented in Section 4. Finally, Section 5 summaries our conclusions and discusses the future research.

2 Uncertainty analysis

2.1 Prediction uncertainty of kriging-based SMs

As our previous discussion, kriging is an interpolation method to predict the value of a function at an untested point by computing a weighted sum of the known values of the function in the neighborhood of the point (Jones et al. 1998).

In this section, the kriging predictor and its mean square error (MSE) function are directly given as follows:

$$ \widehat{f}\left(\boldsymbol{x}\right)=\widehat{\mu}+{\boldsymbol{r}}^T\left(\boldsymbol{x}\right){\boldsymbol{R}}^{-1}\left(\boldsymbol{f}-\mathbf{1}\widehat{\mu}\right) $$
(1)
$$ {\widehat{s}}^2\left(\boldsymbol{x}\right)={\widehat{\sigma}}^2\left[1-{\boldsymbol{r}}^{\mathrm{T}}\left(\boldsymbol{x}\right){\boldsymbol{R}}^{-1}\boldsymbol{r}\left(\boldsymbol{x}\right)+\frac{{\left(1-{\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{r}\left(\boldsymbol{x}\right)\right)}^2}{{\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\mathbf{1}}\right] $$
(2)

Where, r(x) is a N-dimensional vector. The i-th element of r(x) is R(Θ, x, x (i)) where x is the any location to be estimated. R is a N × N correlations matrix whose element in the the j-th column of the i-th line is defined as R(Θ, x (i), x (j)). The parameters \( \widehat{\mu},\kern0.5em {\widehat{\sigma}}^2,\kern0.5em \varTheta \) are obtained by maximum likelihood estimation (MLE). The details are demonstrated in Appendix A.

The MSE function ŝ 2(x) reflects the uncertainty of the predictor \( \widehat{f}\left(\boldsymbol{x}\right) \). The approximation accuracy depends on the distance between the untested location and the given sample points. Intuitively, the kriging predictor \( \widehat{f}\left(\boldsymbol{x}\right) \) will perform better if the untested location is closer to the sample points.

In this paper, any location to be predicted by a kriging-based SM has a Gaussian distribution \( N\left(\widehat{f}\left(\boldsymbol{x}\right),\widehat{s}{\left(\boldsymbol{x}\right)}^2\right) \). The predictor is \( \widehat{f}\left(\boldsymbol{x}\right) \) and its variance is ŝ 2(x). As Fig. 1 shows, the uncertainty of the given sample point x (i) is zero, and the untested location far away from the sample points has a larger prediction error. The blue area in Fig. 1 denotes the region of the prediction error.

Fig. 1
figure 1

The kriging model with prediction uncertainty

Full size image

2.2 Uncertainty of analysis models

Modeling and computational simulation are becoming more and more prevalent in a wide variety of engineering, economic, governmental, and business activities. Commonly, a complex physical system can be modeled in various kinds of mathematical forms. The similarity between the mathematical formulation and the physical nature determines the accuracy of the model (OberKampf and Roy 2010).

The uncertainty assessment of models is critically and quantitatively to determine the ability of the mathematical model and its embodiment in a computer code to simulate a well-characterized physical process. The uncertainty of these mathematical models includes: parameter uncertainty, parametric variability, residual variability, observation error, and model inadequacy. Among these, the model inadequacy usually comes from the incomplete knowledge, improper modeling, or the omission of computation complexity, which will be focused on in this paper (Kennedy and O’Hagan 2001).

As George Box (Box and Draper 1987a, b) said two decades ago, “All models are wrong. Some are useful”. A model could be inaccurate but close enough for its purpose. Similarly, even a highly accurate model may be not appropriate if a high-performance system had higher accuracy requirements. Hence, for a specific physical problem, assessment of the model inadequacy relays on the inherent characteristics of the physical system. This paper defines that analysis models with different fidelities have various probability distributions which will be provided by experts. The HF model will have a smaller variance, and the LF model will have a larger one.

As Fig. 2 shows, the analysis model obtains a response value Y. The real result is assumed as y*. Due to the uncertainty of AM, a random variable associated with y* is defined as Y* with a Gaussian distribution. The Gaussian distribution is expressed as follows:

Fig. 2
figure 2

Analysis model with model uncertainty

Full size image
$$ p\left(Y*\right)=\frac{1}{\delta \sqrt{2\pi }}\ast \exp \left(-\frac{1}{2{\delta}^2}{\left(Y*-Y\right)}^2\right) $$
(3)

Where, δ 2 is the model variance. If a model performs better, |Y − y * | is always smaller. According to the principle of statistics, |Y − y * | will not be much greater than δ. For a specific problem, experts need to define a suitable standard deviation δ to satisfy the basic conditions P(|Y * − Y| < δ) > 0.68, P(|Y * − Y| < 2δ) > 0.95 and P(|Y * − Y| < 3δ) > 0.99. Eventually, the probability distribution N(Y, δ 2) is obtained.

2.3 The expression of integral uncertainty

Section 2.1 has introduced the uncertainty of the kriging-based SM. Generally, the prediction variance of the SM at the sample location is zero. When the uncertainty of the analysis model is considered, the variance of the known interpolating point should denote the model variance. In order to realize this thought, the prediction uncertainty of the SM and the inherent uncertainty of the analysis model are combined. Since the prediction distribution \( N\left(\widehat{f}\left(\boldsymbol{x}\right),\widehat{s}{\left(\boldsymbol{x}\right)}^2\right) \) and the model uncertainty distribution N(Y, δ 2) possess the same mean value at the sample points, the combination of variances is entirely focused on.

Assume that δ 2 AM and δ 2 pred are the model variance and prediction variance at the same test location X, respectively. The integral variance is defined as follows:

$$ {\delta}_{Integral}^2={\delta}_{AM}^2+{\delta}_{pred}^2 $$
(4)

Utilizing Formula (4), the kriging-based SM can reflect the inherent model uncertainty and its prediction uncertainty together. The new probability distribution of the SM turns out to be \( N\left(\widehat{f}\left(\boldsymbol{x}\right),\widehat{s}{\left(\boldsymbol{x}\right)}^2+{\delta}_{AM}^2\right) \) as Fig. 3 shows.

Fig. 3
figure 3

The kriging model with integral uncertainty

Full size image

3 Information fusion

As previously discussed, the core concept of multi-fidelity methods is how to fuse the useful information from various models. Especially, in this paper, when the model uncertainty is considered, it is imperative to find a new fusion method.

At the mention of information fusion, many scholars may think of the Kalman filter (KF) (Kalman 1960). To put it simply, the KF is an optimal recursive data processing algorithm (Foytik et al. 2011). This paper defines the HF SM (constructed by HF data) SMh as the measuring system and the LF SM (constructed by LF data) SMl as the predicted system. According to the equations of the KF, the independent information from SMh and SMl is fused. In addition, the integral uncertainty of the fused SM is decreased based on the theory of the KF algorithm.

Essentially, the KF is composed of five equations to minimize the estimated error covariance. Firstly, a discrete-time controlled process needs to be introduced, which can be described by a linear stochastic difference equation.

$$ \boldsymbol{X}(k)=\boldsymbol{AX}\left(k-1\right)+\boldsymbol{B}\boldsymbol{U}(k)+\boldsymbol{W}(k) $$
(5)

In addition, the measured value is defined as follows:

$$ \boldsymbol{Z}(k)=\boldsymbol{H}\boldsymbol{X}(k)+\boldsymbol{V}(k) $$
(6)

In the two Equations (5) and (6), X (k) is the state variable of the system at the time step k and U (k) is the controlled variable at the time step k. A and B are system parameters, which are matrixes for multi-model systems. Z (k) is the measured value, and H is the parameter of the measuring system. X (k) and Z (k) are two kinds of independent information. W (k) and V (k) denote the process noise and measurement noise at the time step k, respectively, and they are assumed to be white Gaussian noise with W~N (0,Q) and V~N (0,R). Q and R are referred to as covariance.

Assume that the current time step is k. According to the process system, the current state variable can be predicted by the last system state.

$$ \boldsymbol{X}\left(k\left|k-1\right.\right)=\boldsymbol{AX}\left(k-1\left|k-1\right.\right)+\boldsymbol{B}\boldsymbol{U}(k) $$
(7)

Where, X(k|k-1) is the result obtained based on the last state. X(k-1|k-1) is the previous optimal state value.

Likewise, the covariance is updated as follows:

$$ \boldsymbol{P}\left(k\left|k-1\right.\right)=\boldsymbol{A}\boldsymbol{P}\left(k-1\left|k-1\right.\right){\boldsymbol{A}}^T+Q $$
(8)

Here, P(k|k-1) is the covariance of X(k|k-1) and P(k-1|k-1) is the covariance of X(k-1|k-1). Among the five equantions of the KF, Equations (7) and (8) denote the prediction of system.

After the prediction result is obtained, combining the measurement result, the optimal estimated result can be expressed as follows:

$$ \boldsymbol{X}\left(k\left|k\right.\right)=\boldsymbol{X}\left(k\left|k-1\right.\right)+Kg(k)\left(\boldsymbol{Z}(k)-\boldsymbol{H}\boldsymbol{X}\left(k\left|k-1\right.\right)\right) $$
(9)

Where, Kg(k) is referred to as Kalman Gain.

$$ Kg(k)=\frac{\boldsymbol{P}\left(k\left|k-1\right.\right){\boldsymbol{H}}^T}{\left(\boldsymbol{H}\boldsymbol{P}\left(k\left|k-1\right.\right){\boldsymbol{H}}^T+\boldsymbol{R}\right)} $$
(10)

Up to now, the optimal estimation X(k|k) has been achieved at the time step k. Meanwhile, the covariance of X(k|k) also needs to be updated to finish the circular flow.

$$ \boldsymbol{P}\left(k\left|k\right.\right)=\left(\boldsymbol{I}-Kg(k)\boldsymbol{H}\right)\boldsymbol{P}\left(k\left|k-1\right.\right) $$
(11)

In Equation (11), P(k|k) denotes the updated covariance of X(k|k) and I is 1for a single model system. Thus, Equations (7)–(11) are the classical KF equations.

Intuitively, the KF fuses the information from two independent systems (predicted state system and measuring system) to get the optimal estimated result. Likewise, the KF can be utilized to fuse the useful information from the LF model and HF model to get a better SM. In this paper, the information from HF and LF SM should be also independent. The dependence between HF and LF information ultimately comes from the two analysis models. That is, the observed sample values from the HF and LF analysis models should be solved by two independent solvers. For instance, the same physical models by two programmers with different implementations results in somewhat different answers.

As discussed in Section 2.3, a SM considering the analysis model uncertainty will give a predicted value Y at some location with N(Y, δ 2 integral ). At this moment, the SM has great similarities with a state system or a measuring system but it can’t be updated as time goes on. According to the condition of the KF, Y can be regarded as the predicted state value X(k) or the measured value Z(k) and δ 2 integral can be regarded as their covariance.

Since SMs just provide predicted data and don’t depend on time series, this paper doesn’t pay more attention to Equations (7) and (8) which are employed to update time in the KF. Equations (9)–(11) which are utilized for measurement update are focused on. Here, the estimated result X(k|k-1) is replaced by the response value from LF SM. The measured result Z(k) is also replaced by the HF result. The observation matrix H is defined as an identity matrix. The proposed multi-fidelity Kalman filtering (MFKF) equations are summarized as:

$$ {Y}_{fused}={Y}_{SMl}+Kg\left({Y}_{SMh}-{Y}_{SMl}\right) $$
(12)
$$ Kg=\frac{\delta_{SMl}^2}{\delta_{SMl}^2+{\delta}_{SMh}^2} $$
(13)
$$ {\delta}_{fused}^2=\left(1-Kg\right)\cdot {\delta}_{SMl}^2 $$
(14)

At the same predicted location, the SMh will get a result with a normal distribution N(Y SMh , δ 2 SMh ). In a similar way, the SMl gets a response with N(Y SMl , δ 2 SMl ). Here, Kg is the Kalman Gain. In According with Equations (12)–(14), the fused result Y fused and variance δ 2 fused can be obtained. In particular, Equations (12)–(14) are applicable, just when the information from HF and LF SM is independent. In this paper, the HF and LF functions of mathematical examples are independent and the HF and LF observed values of engineering examples are obtained by independent solvers.

4 Example demonstrations

4.1 One-dimensional graphical example

In order to demonstrate the MFKF method, a one-dimensional mathematical example from the reference provided by Han et al. (2010) is considered here. Figure 4 shows the function expressions and shapes of the LF model and HF model.

Fig. 4
figure 4

The original function diagram

Full size image

Sample x-locations from LF model and HF model are S 1 = {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0} and S 2 = {0.0, 0.3, 0.5, 0.7, 1.0},respectively. Figure 5 shows the kriging-based SMs constructed at S 1 and S 2. Figure 6a and b show the mean square error (MSE) of the HF and LF kriging predictor. The results from Fig. 6a and b indicate that the size of the MSE depends on the number of sample points. As Section 2.1 has discussed, if there are more sample points, the kriging-based SM will have a better approximation performance.

Fig. 5
figure 5

SMs of multi-fidelity functions

Full size image
Fig. 6
figure 6

Comparison chart of the kriging-based MSE

Full size image

As Equation (4) suggests, the integral uncertainty of a SM involves model uncertainty and prediction uncertainty. Now, assume that the model variance of the HF model and LF model are 4 and 25, respectively. Combining the MSE shown in Fig. 6a and b, the integral variance can be acquired and the fusion algorithm is implemented by means of Equation (12)–(14).

From Fig. 7a and b, the fused SM with its variance can be seen. The response value of the fused SM is more close to that of the SM with the lower variance at the same x-location. In addition, the variance of the fused SM is lower than both of that of the previous SM models.

Fig. 7
figure 7

Comparison chart of SMs before and after information fusion

Full size image

In order to explore how the model uncertainty and prediction uncertainty affect the fused results, we give different model variances and change the number of sample points, respectively.

Figure 8 gives three sets of results. The number of sample points is the same with Fig. 7. While the model variances of the HF and LF model are 0 and 25 in Fig. 8a and b. Likewise, model variances in Fig. 8c and d are 4 and 9. In Fig. 8e and f, the model variances are 4 and 49. The results from Figs. 8 and 7 suggest that there is a positive correlation between the model variance and the integral variance. With the model variance increases, the integral variance will heighten. The fused SM will be close to the SM with lower variance. In addition, Fig. 8b shows that if the model variance of HF model is zero (It means the high-fidelity model is the perfect model), the variance of the fused results at S 2 is zero too. It suggests that the fused SM at these sample x-locations has the true response values, which is consistent with the actual situation.

Fig. 8
figure 8

Comparison chart of results with different model variances

Full size image

On the other hand, we change the prediction uncertainty of the multi-fidelity SMs to observe the fused results. Since the number of sample points affects the prediction uncertainty, the HF models with 3 points and seven points are provided in Fig. 9.

Fig. 9
figure 9

Comparison chart of results with different number of sample points

Full size image

Combining Fig. 7 with Fig. 9, it can be found that the prediction uncertainty of the SM will increase with the number of sample points reducing. Besides, if prediction performance is worse, the integral variance will get higher. As Fig. 9a shows, the HF SM with three sample points can’t predict better than the LF one with 11 points. Furthermore, the prediction variance of the SM is positively correlated with the integral variance. To sum up, whatever the variances of multi-fidelity SMs are, the variance of the fused SM is always the lowest.

4.2 Numerical cases

For further demonstrating the proposed MFKF method, five numerical examples (Zheng et al. 2013) are employed. These examples are constructed based on Six-hump camel-back (SC), Branin (BR), Booth (BT), Bohachevsky (BC) and Himmelblau (HM) functions which are introduced in Appendix B. Since co-kriging has been widely used in engineering optimization and proved to be a good fusion method for multi-fidelity problems (Forrester et al. 2007; Wankhede et al. 2011; Huang et al. 2013), we decide to compare it with the MFKF method in Section 4.2.

Co-kriging doesn’t consider the model uncertainty and commonly treats the high-fidelity model as the “true model”. For a fair comparison, the proposed method in this paper defines the HF model variance as zero (Refer to Fig. 8b). The two methods are implemented on six numerical cases which involve the one-dimensional (OD) function introduced in Section 4.1 and the five numerical examples demonstrated in Appendix B.

According to the statistical theory discussed in Section 2.2, the standard deviations of the LF models on the six test examples (OD, SC, HM, BT, BR, BC) are defined as 7.15, 24, 45, 280, 1025, 4660, respectively. For both of the two fusion methods, the optimal Latin hypercube sampling (OLHS, Morris and Mitchell 1995) strategy is employed to finish the DOE process. The co-kriging method is realized by Forrester’s surrogate toolbox (Forrester et al. 2008). Three kinds of model accuracy measurements are adopted to compare the two methods: the RMSE, the maximum absolute error (MAX) and the R 2 value.

$$ RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum_{i=1}^N{\left({y}_i-{\widehat{y}}_i\right)}^2}} $$
(15)
$$ MAX= \max \left|{y}_i-{\widehat{y}}_i\right|\kern0.5em ,\kern1em i=1,\kern0.5em \dots \kern0.5em ,N $$
(16)
$$ {R}^2=1-\frac{{\displaystyle {\sum}_{i=1}^N{\left({y}_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle {\sum}_{i=1}^N{\left({y}_i-{\overline{y}}_i\right)}^2}} $$
(17)

Here, N denotes the total number of validation points, \( {\overline{y}}_i \) denotes the mean value of the observed value y i and ŷ i is defined as the predicted value. RMSE is employed to gauge the overall accuracy of the model; MAX is utilized to evaluate the local accuracy of the model; R 2 is computed to reflect the overall performance of SMs. For the three measurements, larger values of R 2 indicate that the SM have a better performance and lower values of RMSE/MAX suggest that the accuracy of the SM is high.

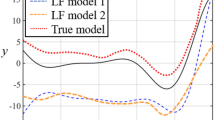
Table 1 shows the RMSE, MAX and R 2 values of the six numerical cases. Meanwhile, the real and approximation contours are present in Fig. 10. From Table 1 and Fig. 10, it can be found that MFKF has a better approximation performance on BT and BC than co-kriging. Nevertheless, co-kriging obtains more accurate models on HM and BR. For the SC function, MFKF constructs a SM with the higher local approximation accuracy but the global accuracy is worse than co-kriging. As Fig. 10c shows, the local maximum value of the SM constructed by MFKF is more close to the true value but the overall accuracy looks bad. Figure 11 demonstrates the approximation effect of the two multi-fidelity methods on the one-dimensional example. From Table 1 and Fig. 11, it can be clearly found that MFKF constructs a more accurate SM than co-kriging on this problem. In summary, MFKF can provide a kind of excellent modeling capability.

Table 1 Approximation performance comparison of the six numerical cases
Full size table
Fig. 10
figure 10

Approximation and real contours of the five two-dimensional test functions

Full size image
Fig. 11
figure 11

SMs constructed by the two method

Full size image

As our previous discussion, the MFKF method can not only fuse the useful information from different models but also can decrease the integral uncertainty of the SM. Table 2 provides the mean and maximum values of the standard deviations which come from 50 sample points. What’s more, the results from SMs with different fidelities are compared. Figures 12, 13 and 14 show a 3d graphic example (HM) to demonstrate the fusion process. Here, the grey surfaces are the boundaries of δ Integral . From Table 2 and Figs. 12, 13 and 14, it is clear that the fused standard deviations are decreased. To sum up, the MFKF method provides a novel strategy to construct the multi-fidelity SM. In addition, the uncertainty of the SM can be reduced based on the KF theory.

Table 2 The mean and maximum values of the standard deviations from different SMs
Full size table
Fig. 12
figure 12

Low-fidelity SM with error

Full size image
Fig. 13
figure 13

High-fidelity SM with erro

Full size image
Fig. 14
figure 14

The fused SM with error

Full size image

4.3 Engineering example

The MFKF method can be widely used in computer aided engineering (CAE) designs. In this paper, an engineering example about strength and stability analysis of autonomous underwater vehicles’ (AUVs) hull is introduced. As Fig. 15 shows, the hull has eight design variables which involve: the thickness t, the distance between ribs l, and the six basic parameters of the rib: x 1, x 2, x 3, y 1, y 2, y 3. The material property is shown in Table 3. The depth of the water is set as 700 m and the radius of the hull is the standard size 162 mm. Now there are two models with independent solvers. The HF model possesses the fine grid, every element of which is smaller than 20 mm, and the total number of nodes is about 66,000. In addition, the HF model is solved by ANSYS finite solver. The LF model utilized the traditional empirical formula to estimate the response and the process is realized by C program. Figure 16 provides the mesh graphs of the HF model.

Fig. 15
figure 15

AUVs’ hull structure diagram

Full size image
Table 3 Material properties
Full size table
Fig. 16
figure 16

The diagram of high-fidelity grids

Full size image

Through strength and linear buckling analysis, the maximum von Mises stress and the maximum critical load of the HF and LF models are obtained. Here, a complete analysis on the HF and LF models averagely spends about 12 min and several seconds, respectively. Since the LF data is cheap, there are 80 LF sample points. On the contrary, the HF data is precious and only 40 points are sampled. When the strength analysis is implemented, Experts assign the HF and LF model variances with 225 and 2025 Mpa2, respectively. When the maximum critical load is computed, the HF and LF model variances are assigned with 25 and 400 Mpa2. Now, two kriging-based SMs with model uncertainty are constructed. In order to demonstrate the details of the process, 16 sample points obtained by OHLS are provided in Tables 4 and 5.

Table 4 Sixteen sets of strength analysis results (maximum von Mises stress) of the high-fidelity model, low-fidelity model and the fused model (Here, Str represents the maximum von Mises stress)
Full size table
Table 5 Sixteen sets of stability analysis results (Maximum critical load) of the high-fidelity model, low-fidelity model and the fused model (Here, Pcr represents the maximum critical load)
Full size table

The strength and stability analysis results from Tables 4 to 5 suggest that the proposed kriging-based MFKF method can also be employed in engineering problem. The 16 sets of sampling values reflect that the fused SM can provide a prediction result with lower variance than the previous SMs. According to the theory of the KF, the useful information from different models is utilized synthetically. Thus, the fused results are more close to the true response. It’s convenient for engineers to analyze the whole problem and find the optimal solution under model uncertainty by the fused SM.

5 Conclusions and outlook

In this paper, a novel kriging-based multi-fidelity method has been proposed. The MFKF method firstly combines the model uncertainty with kriging-based prediction error to obtain the integral uncertainty. Simultaneously, the kriging-based SMs are constructed through data from different models (HF model or LF model). After the HF and LF SMs with the integral uncertainty are obtained, a fusion algorithm is implemented. The fusion algorithm refers to the KF’s idea of optimal estimation to synthetically utilize the information from different SMs. Eventually, the fused SM with lower variance is acquired. The one-dimensional graphical example demonstrates that the model variance and kriging-based prediction variance are positively correlated with the integral variance and the fused SM is more close to the SM with the lower integral variance. The two-dimensional numerical cases further indicate that the MFKF method can provide a kind of excellent modeling capability. The engineering example proves that the multi-fidelity method is feasible in practice. In summary, this paper gives the mathematical model of integral uncertainty of SMs and brings the idea of optimal estimation into multi-fidelity SM area. In addition, it provides a convenient approach for engineers to analyze an engineering problem with model uncertainty. Furthermore, the fused SM will be a helpful tool for engineers to implement reliability optimization and it will be potentially applied in Multi-fidelity optimization and Multidisciplinary design optimization. Since the MFKF method in this paper can just fuse the information from independent systems, more future work will focus on other advanced filtering algorithms to solve non-Gaussian distributions and multi-fidelity models with dependence. In addition, according to the similarities between time update of the KF method and the infill update of the SM, the further work will be carried out on this part.