Moisture-induced stresses in glulam frames

Abstract

Wood is a hygroscopic and moisture-sensitive material that seeks to achieve equilibrium moisture content (EMC) with its surrounding environment. For softwood timber structures exposed to variations in climate throughout their service life, this behaviour results in variable moisture-content gradients that cause moisture-induced stresses in the direction of and perpendicular to the fibres. Although Eurocode 5 (EC5) states that moisture-induced stresses should be considered, they are often not adequately dealt with in building design due to the difficulties in predicting the stresses involved by hand. Accordingly, there is a need for advanced computer tools to study how the long-term stress behaviour of timber structures is affected by creep and cyclic variations in climate. A beam model to simulate the overall hygro-mechanical and visco-elastic behaviour of (inhomogeneous) glulam structures is presented. A two-dimensional transient, non-linear moisture transport model for wood is also developed and linked with this beam model. The combined models are used to study the long-term deformations and stresses in a curved frame structure exposed to both mechanical loading and cyclic climate conditions. It is shown that the moisture-induced deformations and stresses are of such magnitude that the design codes employed should take them into account. Thus it is argued that climate-related loads should be treated as separate load contributions that can be included in different load combinations.

1 Introduction

Most timber structures consist of solid or composite beams, columns and frames that can be of different types; see e.g. Thelandersson and Larsen (2003), Porteous and Kermani (2007), Larsen and Enjily (2009), and Thelandersson et al. (2011). The lamination and finger jointing of wood has enabled timber beams and frames of virtually any length and curve to be produced; see DS EN 14080:2013 (0000) and Glulam handbook (2001). Wood is an inhomogeneous, hygroscopic, moisture-sensitive and orthotropic material that needs to be carefully analysed, especially in the case of softwood timber structures exposed to varying climate conditions. Numerous advanced two and three dimensional finite element models of moisture-induced stresses in individual timber boards and glulam structures have been presented during the last few decades; see e.g. Svensson (1997), Angst and Malo (2010), Angst and Malo (2013), Svensson and Toratti (2002) for 2D simulations and Ormarsson (1999), Fortino et al. (2009), Fortino and Toratti (2010), Ormarsson et al. (1999) for 3D simulations. The numerical results show that moisture-induced stresses can be of significant size and for glulam they can become quite big depending on the geometrical configuration of the laminates. It was also stated in Angst and Malo (2010) that geometrical configuration and material parameters affect the stress development more than the selection of a certain numerical formulation of mechano sorption. Further experimental and numerical works dealing with moisture-induced stresses, creep and fracture in wood and glulam are for example Jönsson (2005), Häglund (2010), Fragiacomo et al. (2011), Mohager and Toratti (1993), Srpcic et al. (2009), Hanhijärvi et al. (1998), Zhou et al. (2009), and Qiu et al. (2014). In recent decades, extensive research on the material and physical properties of wood has been carried out; see e.g. Bodig and Jayne (1982), Kollmann and Côté (1968), Dinwoodie (1981), Dahlblom et al. (1999) and Yamashita et al. (2009). For Norway spruce, the modulus of elasticity (MOE) often increases rather linearly (up to a factor of two) from pith to bark, whereas the shrinkage coefficient usually decreases (Wormuth 1993; Dahlblom et al. 1999). The inhomogeneity for softwood timber containing reaction wood becomes stronger and the shrinkage or swelling is considerably greater than for normal wood (Ormarsson et al. 2000). Clearly, material knowledge of this kind should be better accounted for in the design of softwood timber structures. In EC5 EN 1995-1-1 - Eurocode 5 (1995), the inhomogeneity and the moisture sensitivity of wood are only dealt with in terms of encapsulation in connection with certain safety and modification factors. The dynamics of the moisture climate can result in solid timber and laminated timber products becoming markedly distorted (twisted, bowed, cupped or crooked) when exposed to climatic variations; see e.g. Johansson and Kliger (2002), Ormarsson and Cown (2005), Astrup (2009), and Gereke et al. (2010).

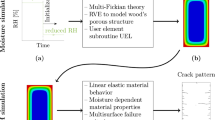
A moisture transport model is needed to estimate the variation in moisture to which a wooden structure would be subjected during its lifetime. Moisture transport in wood is a highly complex process that involves several dependent variables and different modes of transport for the various phases of water within the wood, see e.g. Frandsen and Svensson (2007). From a structural engineering standpoint, moisture transport below fibre saturation point (FSP) is of most interest, since this is the span of MC a wooden structure will experience over its service life. Below FSP, sufficient accuracy can be obtained by using a total moisture transport model governed by the laws of diffusion, without full consideration of the coupled behaviour of the different moisture transport phases. In the present paper, a transient non-linear moisture transport model governed by Fick’s law is used. The model has been verified to some extent on the basis of analytical and experimental results. For more details of the theory and the implementation procedure employed here, see Gíslason (2014) and Siau (1995).

2 Material and methods

Moisture-induced stresses in timber structures are difficult to predict by hand because of the generally complex hygro-mechanical material behaviour of wood, though they can be predicted through use of a three-dimensional simulation model that includes a full 3D-material formulation for the wood material. In the case of large timber structures, however, a three-dimensional computer model is too computationally expensive for practical usage. The modelling approach presented here combines a transient non-linear moisture transport model with a hygro-mechanical beam model to simulate cheaply and effectively the moisture-induced deformation and stresses that occur in large timber structures during their service life.

2.1 Geometry and material data

The timber structure studied here was a glulam structure exposed to climatic conditions corresponding to an outdoor structure protected against direct contact with rain. A static model, together with the boundary conditions, dead load, climate load and the cross-sectional dimension involved, is shown in Fig. 1. The timber structure is assumed to be built during the summer when it is in a stress-free condition with a 12 % initial moisture content. The variations in moisture content (MC) on the frame surface considered are those based on the climate data for one year as shown in Fig. 2, repeated over the course of 50 years. It is assumed that the cross section is that applied to a typical composite beam having no slip deformation between the lamellae. Figure 1 shows curves that represent the variations found here in the modulus of elasticity E(y) and in the longitudinal shrinkage coefficient $\alpha (y)$ over the cross-section of the frame. The mechano sorption parameter used is 0.1 × 10⁻⁹ [1/Pa]. In addition to these material data, the creep parameters are the same as those in Ormarsson et al. (2010).

Fig. 1

Structural geometry, whereby the static system, loads, variations in MC and in modulus of elasticity E(y) as well as in the shrinkage coefficient $\alpha (y)$ are shown

2.2 Modelling

Four different computer simulations based on the structural geometry and the material data presented above were performed.

• 1. A two-dimensional transient non-linear moisture transport analysis of the cross-section of the frame. The prescribed time history of the boundary moisture content shown in Fig. 1 is based on the climate data obtained in Fig. 2.

• 2. A frame analysis used to simulate the long-term visco-elastic and hygro-mechanical flexure and the axial deformations of the timber frame structures. An extended beam theory was developed to model the longitudinal stresses found in inhomogeneous timber composites exposed to a combination of mechanical loads and strong variations in the environmental conditions involved. The variations in moisture gradient over the height of the cross section are the drivers of the moisture-induced stress generation that takes place. The moisture gradients involved are predicted by the transient moisture flow model referred to above.

• 3. The frame model referred to above does not calculate the stresses found perpendicular to the direction of the grain. To study these stresses, a two-dimensional distortion model of the cross-section of the frame was created. The model consists of a transient linear diffusion model coupled with the distortion model described in Ormarsson (1999).

• 4. The timber frame being studied is a statically indeterminate curved structure made of an orthotropic wood material. When a frame of this type is loaded either in bending or in exposure to climatic variations, significant stresses perpendicular to the grain can occur in the curved part of the frame. The moisture-induced stresses are generated by the structural constraints found when involving the free straightening or free bending of the curved part of the frame during moistening or drying of the frame. A two-dimensional stress model of the frame structure was created to study this stress phenomenon.

3 Moisture transport

A key component in predicting the moisture-induced stresses that a wooden structure will be subjected to during its service life, is a complete history of its varying MC over time. Modelling moisture-induced stresses is a two-step process that involves sequential coupling between the MC and the stresses that arise. The MC time history in its entirety is calculated first and the stresses subsequently. This is valid because changes in MC will affect the stresses whereas the change in stresses has virtually no affect on the MC.

3.1 Climate variation

The outdoor climate worldwide varies appreciably on both a daily and a yearly basis. Nordic countries are no exception to this, where typical variations in the average daily relative humidity (RH) range from about 90 % in the winter to around 65 % in the summer, along with widely varying temperatures. An example of such changes is shown in Fig. 2, which depicts the changes in RH and temperature occurring at a weather station in the town of Drammen, (Norway Weather 2014).

Fig. 2

Daily RH and temperature values obtained in Drammen, Norway, see Weather (2014)

Wooden structures exposed to such varying conditions experience considerable changes in MC. As a hydroscopic material, wood seeks to achieve equilibrium in its internal MC in relation to the surroundings. When such a state is reached, the wood neither gains nor loses moisture, and thus has an equilibrium moisture content (EMC). The EMC depends mainly on the RH and the temperature that the wood is exposed to. In the present study, the expression for EMC used in Wood Handbook (2010) is employed and shown in Eq. 1 as

$$\begin{aligned} EMC = \frac{1800}{W_{emc}} \left( \frac{KH_{Rh}}{1- K H_{Rh}} + \frac{K_1K \ H_{Rh} + 2K_1K_2K^2 H_{Rh}^2}{1+K_1K H_{Rh} + K_1K_2K^2 H_{Rh}^2} \right) \end{aligned}$$

(1)

where

$$\begin{aligned}&W_{emc} = 349 + 1.29 T_c + 0.0135 T_c^2 \nonumber \\&K = 0.805 + 0.000736 T_c - 0.00000273 T_c^2 \nonumber \\&K_1 = 6.27 - 0.00938 T_c - 0.000303 T_c^2 \nonumber \\&K_2 = 1.91 + 0.0407 T_c - 0.000293 T_c^2 \end{aligned}$$

(2)

and $H_{Rh}$ is the relative humidity [%] and T_c is the temperature in degrees Celsius [°C]. The relationship between RH, temperature and EMC is depicted in the contour plot presented in Fig. 3, in which the EMC values are shown as contour lines.

Fig. 3

Contour plot of EMC [%] as a function of RH and temperature, obtained using the USDA method, see (Wood Handbook 2010)

Using the expression for EMC presented above, the RH and temperature values shown in Fig. 2 can be used to form an EMC time history for a whole year. Since the changes in the MC of the wood represent a relatively slow process, the EMC values obtained can only accurately depict the MC found at the boundaries of the cross section of the frame. Therefore, they can serve as input to subsequent calculations of moisture-flow as a transient boundary condition.

Fig. 4

Daily boundary EMC values and the linear fit of the data for modelling

To accommodate the 6 month time-step obtained with the use of the hygro-mechanical frame program, the daily boundary EMC values shown in Fig. 4 are fitted linearly to half-year increments. The linearly fitted data serve as input to further calculate the moisture transport instead of using the scattered daily values. The same methodology is used to calculate the time-history of the temperature. This observation data for the period of one year only strictly applies to the period 2013–2014, though it is assumed here that the patterns involved will largely repeat themselves throughout the course of the next 50 years. This introduces certain inaccuracies, since the yearly climate varies somewhat over time.

3.2 Moisture transport modelling

Moisture transport in wood is actually a complex process that varies considerably with the direction of the material and the state of the moisture being transported. Water is transported through wood either as free liquid water in the lumina and cavities of the cell, as bound liquid water in the cell wall, or as water vapour in a gaseous state. Each state has its own characteristics and properties. Below FSP, a reasonable approximation is to consider all of these states together in a total moisture transport model using Fick’s law of diffusion (Krabbenhoft 2003).

$$\begin{aligned} \dot{w} = \nabla (\mathbf {D} \nabla w) \end{aligned}$$

(3)

Fick’s second law of diffusion describes the flow of water over time ($\dot{w}$) through a medium, as expressed in terms of the moisture-content gradient($\nabla w$) within it, times a proportionality factor (in this case a non-constant diffusion coefficient $\mathbf {D}(w,T)$).

3.2.1 Diffusion coefficients

The diffusion coefficient quantifies how rapidly, for a given moisture content gradient, moisture diffuses over a cross section. The diffusion coefficient of wood varies greatly with such factors as MC, temperature, the specific gravity of the wood in question, and pressure.

The present study uses the transverse diffusion coefficient model in (Siau 1995). This model has separate expressions for the transport of different water phases within wood, which are combined to obtain a total moisture transport diffusion coefficient. The results obtained with the use of the model under a variety of different isothermal conditions are shown in Fig. 5.

Fig. 5

Transverse diffusion coefficients for various isothermal conditions using the Siau model (Siau 1995)

The diffusion coefficient is non-linear and varies considerably with differences in temperature and MC, as seen in Fig. 5. Since MC can vary greatly at any given time within the cross section of the beam, the diffusion coefficients also vary considerably within the spatial domain.

3.2.2 FEM formulation

The finite element method (FEM) is employed to solve the governing equation, resulting in a first-order differential eq. (4) that contains solution-dependent variables, since the diffusion coefficients depend upon the MC, making the system non-linear as

$$\begin{aligned} \mathbf {C} \dot{\mathbf {w}} + \mathbf {K}_w(w) \mathbf {w} = 0 \end{aligned}$$

(4)

where $\mathbf {w}$ is the unknown MC vector, $\mathbf {C}$ is the capacity matrix and $\mathbf {K}_w$ is the diffusivity matrix.

The equation is solved incrementally, using time-step increments of $\Delta t$ so as to obtain an overall solution at time $t_{n+1} = t_n + \Delta t$. A general family of algorithms emerges when defining a parameter $\alpha$ for this purpose, such that $t_{n+\alpha } = t_n + \alpha \Delta t$ within the interval $0 \le \alpha \le 1$. The governing equation at time $t_{n+\alpha }$ becomes (Huebner et al. 1995):

$$\begin{aligned} \mathbf {C} \dot{\mathbf {w}}_{n+\alpha } + (\mathbf {K}_w)_{n+\alpha } \mathbf {w}_{n+\alpha } = 0 \end{aligned}$$

(5)

Fig. 6

2D MC variation over the cross section and average 1D center-line values used as input to the hygro-mechanical frame model

The two following approximations are then introduced:

$$\begin{aligned} \dot{\mathbf {w}}_{n+\alpha } = \frac{\mathbf {w}_{n+1} - \mathbf {w}_{n}}{\Delta t} \end{aligned}$$

(6)

$$\begin{aligned} \mathbf {w}_{n+\alpha } = (1-\alpha ) \mathbf {w}_{n} + \alpha \mathbf {w}_{n+1} \end{aligned}$$

(7)

Inserting these approximations into eq. (5) results in:

$$\begin{aligned} \underbrace{ \left[ \frac{1}{\Delta t} \mathbf {C} + \alpha (\mathbf {K}_w)_{n+\alpha } \right] }_{\mathbf {\widetilde{K}}_x} \mathbf {w}_{n+1} = \underbrace{ \left[ -(1-\alpha ) (\mathbf {K}_w)_{n+\alpha } + \frac{1}{\Delta t} \mathbf {C} \right] \mathbf {w}_{n} }_{\mathbf {\widetilde{F}}_x} \end{aligned}$$

(8)

In this equation, the unknowns are $\mathbf {w}_{n+1}$ and $\mathbf {w}_{n+\alpha }$, whereas $\mathbf {w}_{n}$ is known from the prior time step. As demonstrated in Hughes (1977), this particular algorithm is unconditionally stable for $\alpha \ge {1}/{2}$, meaning that the algorithm has no critical time step size. Since it is also accurate at the second-order level for $\alpha = {1}/{2}$, the value of $\alpha$ is preferred for the solution algorithm.

To solve this system of equations, the terms involved are summed so as to obtain new “stiffness” $\mathbf {\widetilde{K}}_x$ and “force” $\mathbf {\widetilde{F}}_x$ terms. The terms stiffness and force are used here solely for reasons of convention and familiarity, and are defined in eq. (8). Defining them this way results in the familiar FEM equation. Here they represent a coupled algebraic equation system that can be solved so as to determine $\mathbf {w}_{n+1}$ as

$$\begin{aligned} \mathbf {w}_{n+1} = \mathbf {\widetilde{K}}_x \ \backslash \ (\mathbf {\widetilde{F}}_x - \mathbf {f}_{BC}) \end{aligned}$$

(9)

where $\mathbf {f}_{BC}$ is a vector containing the prescribed boundary conditions. To solve this equation, the unknown parameter $\mathbf {w}_{n+\alpha }$ is initially set equal to the known parameter $\mathbf {w}_{n}$. The Newton–Rhapson iteration scheme is used to correct for this approximation and account for the non-linearity of the system. The final result is a transient non-linear moisture transport model governed by Fick’s law of diffusion. For further details regarding this, see Gíslason (2014).

3.3 Implementation

The time history of the moisture transport is calculated for the cross section in 2D; it is assumed that the moisture flow at the ends of the beam can be neglected, since the beam is relatively slender. Isoparametric four-node elements are used here; the diffusion coefficient for each element being calculated at each time step, since it depends upon the variations in MC and in temperature that occur. Gauss quadrature is employed for integrating across the elements.

The results obtained in 2D need to be adjusted to 1D to be used as input to the 1D beam model. For this purpose, a simple weighted average is calculated across each row of nodal points to obtain a center-line average of the 2D cross sections. An example of a 2D result and its 1D weighted average is shown in Fig. 6.

4 Moisture-induced stresses

This section describes the simulation results obtained for each of the three stress models described in Sect. 2.2.

4.1 Beam modelling of inhomogeneous composite structures

The derivation of the extended finite element theory for inhomogeneous composite beams with two nodal points is given in its entirety in Ormarsson and Dahlblom (2013) and Steinnes (2014). The rheological model used is based on a mechano sorption model for beams in Leicester (1971). When beam elements of this type are exposed to both mechanical and moisture related load actions simultaneously, higher-order beam elements are needed to simulate the non-linear section-force variations along the length of the element. The formulation presented here is a finite element formulation for a beam element having four nodal points.

4.1.1 Geometric description of a beam element

The beam geometry, degrees of freedom, and loads involved, and illustrations of a possible cross-sectional geometry with varying sizes of the lamellae are shown in Fig. 7. The longitudinal modulus of elasticity E(y) and the longitudinal shrinkage coefficient $\alpha (y)$ are allowed to vary piecewise and linearly over the height of the beam (in the y-direction). Each of the material parameters is assumed constant along the length and across the width (in the z-direction) of a beam element. A given beam element can be subjected to axial loading $q_x(x,t)$ and uniaxial bending-loading $q_y(x,t)$, as well as to environmental loading, in terms of variations in moisture content w(y, t) as shown in Fig. 7. The degree of variation in moisture content changes over the cross section, which is affected for example, by climate conditions at the beam surface, by different MC states of the lamellae directly after gluing, and by different EMC states of the lamellae. The material model employed deals with such phenomena as linear elasticity, shrinkage or swelling, mechano-sorption and visco-elastic wood behaviours, see Ormarsson and Dahlblom (2013).

Fig. 7

a Beam geometry, mechanical load variation $q_x(x,t)$ and $q_y(x,t)$, moisture-related load variation w(y, t) and degrees of freedom of the beam element, b Illustrations of possible cross-sectional geometry and variations in the parameters E(y), $\alpha (y)$ and w(y, t)

4.1.2 Finite element formulation

An incremental finite element formulation in matrix form for a beam element becomes

$$\begin{aligned} \mathbf {K}^e\dot{\mathbf {a}}^e = \dot{\mathbf {f}}^e_b + \dot{\mathbf {f}}^e_l + \dot{\mathbf {f}}^e_p \end{aligned}$$

(10)

where

$$\begin{aligned} \mathbf {K}^e = \int _a^b {\mathbf {B}^e}^T \mathbf {D} \mathbf {B}^e dx \end{aligned}$$

(11)

$$\begin{aligned} \dot{\mathbf {f}}^e_b = \left[ (\hat{\nabla }\mathbf {N}^e)^T \dot{\mathbf {F}}\right] ^b_a - \left[ {\mathbf {N}^e}^T \dot{\mathbf {V}}\right] ^b_a \end{aligned}$$

(12)

$$\begin{aligned} \dot{\mathbf {f}}^e_l = \int _a^b {\mathbf {N}^e}^T \dot{\mathbf {q}} dx \end{aligned}$$

(13)

$$\begin{aligned} \dot{\mathbf {f}}^e_p = \dot{\mathbf {f}}^e_w + \dot{\mathbf {f}}^e_m + \dot{\mathbf {f}}^e_c = \int _a^b {\mathbf {B}^e}^T \dot{\mathbf {F}}_p \ dx = \int _a^b {\mathbf {B}^e}^T (\dot{\mathbf {F}}_w + \dot{\mathbf {F}}_m + \dot{\mathbf {F}}_c) \ dx \end{aligned}$$

(14)

The matrix $\mathbf {K}^e$ is the element stiffness matrix, $\dot{\mathbf {f}}^e_b$ is the boundary vector, $\dot{\mathbf {f}}^e_l$ is the load vector and $\dot{\mathbf {f}}^e_p$ is the pseudo-load vector. The vectors $\dot{\mathbf {f}}^e_w$, $\dot{\mathbf {f}}^e_m$ and $\dot{\mathbf {f}}^e_c$ are the pseudo-load vectors for free shrinkage $\dot{\mathbf {f}}^e_w$, mechano-sorption $\dot{\mathbf {f}}^e_m$, and creep strain $\dot{\mathbf {f}}^e_c$. For a planar beam element (with 12 degrees of freedom; see Fig. 7a, the element displacement/rotation vector $\mathbf {a}^e$, the element shape function matrix $\mathbf {N}^e$ and the associated strain/curvature matrix $\mathbf {B}^e$ are given as

$$\begin{aligned} \mathbf {a}^e = \left[ \begin{array}{llllllllllll} u_1 &{} u_2 &{} u_3 &{} u_4 &{} u_5 &{} u_6 &{} u_7 &{} u_8 &{} u_9 &{} u_{10} &{} u_{11} &{} u_{12} \\ \end{array}\right] ^T \end{aligned}$$

(15)

$$\begin{aligned} \mathbf {N}^e = \left[ \begin{array}{cccccccccccc} N_{1}^e &{} 0 &{} 0 &{} N_{4}^e &{} 0 &{} 0 &{} N_{7}^e &{} 0 &{} 0 &{} N_{10}^e &{} 0 &{} 0 \\ 0 &{} N_{2}^e &{} N_{3}^e &{} 0 &{} N_{5}^e &{} N_{6}^e &{} 0 &{} N_{8}^e &{} N_{9}^e &{} 0 &{} N_{11}^e &{} N_{12}^e \\ \end{array}\right] \end{aligned}$$

(16)

$$\begin{aligned} {\mathbf {B}^e}^T = (\tilde{\nabla }\mathbf {N}^e)^T = \left[ \begin{array}{cc} \frac{dN_{1}^e}{dx} &{} 0\\ 0 &{} \frac{d^2N_{2}^e}{dx^2}\\ 0 &{} \frac{d^2N_{3}^e}{dx^2}\\ \frac{dN_{4}^e}{dx} &{} 0\\ 0 &{} \frac{d^2N_{5}^e}{dx^2}\\ 0 &{} \frac{d^2N_{6}^e}{dx^2}\\ \frac{dN_{7}^e}{dx} &{} 0\\ 0 &{} \frac{d^2N_{8}^e}{dx^2}\\ 0 &{} \frac{d^2N_{9}^e}{dx^2}\\ \frac{dN_{10}^e}{dx} &{} 0\\ 0 &{} \frac{d^2N_{11}^e}{dx^2}\\ 0 &{} \frac{d^2N_{12}^e}{dx^2}\\ \end{array}\right] \end{aligned}$$

(17)

The element shape functions $N_{i}^e$ can be calculated as

$$\begin{aligned} \mathbf {N}^e_x = \left[ \begin{array}{cccc} N_{1}^e &{} N_{4}^e &{} N_{7}^e &{} N_{10}^e \\ \end{array}\right] = \bar{\mathbf {N}}_x\mathbf {C}_x^{-1} \end{aligned}$$

(18)

$$\begin{aligned} \mathbf {N}^e_y = \left[ \begin{array}{cccccccc} N_{2}^e &{} N_{3}^e &{} N_{5}^e &{} N_{6}^e &{} N_{8}^e &{} N_{9}^e &{} N_{11}^e &{} N_{12}^e \\ \end{array}\right] = \bar{\mathbf {N}}_y\mathbf {C}_y^{-1} \end{aligned}$$

(19)

where

$$\begin{aligned} \bar{\mathbf {N}}_x = \left[ \begin{array}{cccc} 1 &{} x &{} x^2 &{} x^3 \\ \end{array}\right] \end{aligned}$$

(20)

$$\begin{aligned} \bar{\mathbf {N}}_y = \left[ \begin{array}{cccccccc} 1 &{} x &{} x^2 &{} x^3 &{} x^4 &{} x^5 &{} x^6 &{} x^7 \\ \end{array}\right] \end{aligned}$$

(21)

$$\begin{aligned} \mathbf {C}_x = \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} \frac{L}{3} &{} \left(\frac{L}{3}\right)^2 &{} \left(\frac{L}{3}\right)^3 \\ 1 &{} 2\frac{L}{3} &{} \left(2\frac{L}{3}\right)^2 &{} \left(2\frac{L}{3}\right)^3 \\ 1 &{} L &{} L^2 &{} L^3 \\ \end{array}\right] \end{aligned}$$

(22)

$$\begin{aligned} \mathbf {C}_y = \left[ \begin{array}{cccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} \frac{L}{3} &{} \left(\frac{L}{3}\right)^2 &{} \left(\frac{L}{3}\right)^3 &{} \left(\frac{L}{3}\right)^4 &{} \left(\frac{L}{3}\right)^5 &{} \left(\frac{L}{3}\right)^6 &{} \left(\frac{L}{3}\right)^7 \\ 0 &{} 1 &{} 2\left(\frac{L}{3}\right) &{} 3\left(\frac{L}{3}\right)^2 &{} 4\left(\frac{L}{3}\right)^3 &{} 5\left(\frac{L}{3}\right)^4 &{} 6\left(\frac{L}{3}\right)^5 &{} 7\left(\frac{L}{3}\right)^6 \\ 1 &{} 2\frac{L}{3} &{} \left(2\frac{L}{3}\right)^2 &{} \left(2\frac{L}{3}\right)^3 &{} \left(2\frac{L}{3}\right)^4 &{} \left(2\frac{L}{3}\right)^5 &{} \left(2\frac{L}{3}\right)^6 &{} \left(2\frac{L}{3}\right)^7 \\ 0 &{} 1 &{} 2\left(2\frac{L}{3}\right) &{} 3\left(2\frac{L}{3}\right)^2 &{} 4\left(2\frac{L}{3}\right)^3 &{} 5\left(2\frac{L}{3}\right)^4 &{} 6\left(2\frac{L}{3}\right)^5 &{} 7\left(2\frac{L}{3}\right)^6 \\ 1 &{} L &{} L^2 &{} L^3 &{} L^4 &{} L^5 &{} L^6 &{} L^7 \\ 0 &{} 1 &{} 2L &{} 3L^2 &{} 4L^3 &{} 5L^4 &{} 6L^5 &{} 7L^6 \\ \end{array}\right] \end{aligned}$$

(23)

4.1.3 Numerical example

A curved statically indeterminate glulam structure was employed to study how hygro-mechanical and long-term visco-elastic deformations and stresses develop during the lifetime of the structure. The structure in question is shown in Fig. 1. The figures that follow illustrate how the presence of the dominant mechanical loads $q_x(x,t)$ and $q_y(x,t)$, together with a cyclically varying moisture load, as shown in Fig. 1, affect the deformation, the moment and the longitudinal stress that occur in the structure. Figure 8 shows how the long-term deflection increases markedly over time, due to both creep and the mechano-sorption phenomenon. Note that the frame is exposed to the climate conditions associated with outdoor structure protected against direct contact with water.

Fig. 8

Deformations of the frame structure during the winter after 1, 10, 20, 30, 40, and 50 years in service

Figures 9 and 10 show how the moment and stresses on the upper surface vary non-linearly along the direction of the frame. The curved corner part of the frame is exposed to a strong negative moment that results, in turn, in significant tension on the outer surface of the frame.

Fig. 9

Moment distribution of the frame structure during the winter after 1, 10, 20, 30, 40, and 50 years in service

Fig. 10

Variations in the longitudinal stress on the outer surface of the frame structure during the winter after 1, 10, 20, 30, 40, and 50 years in service

Stress distributions within a cross-section of the curved corner part are shown in Fig. 11. As can be seen, the stresses vary noticeably, both over a given year and over time in general. The stress distributions in the lamellae at the top and bottom are non-linear because of the significant moisture gradient in these lamellae. The discontinuity in the stress profile is caused by discontinuous variations in the modulus of elasticity and in the shrinkage properties, as shown in Fig. 1.

Fig. 11

Variations in the longitudinal stress found during the winter in a cross-section located in the curved corner parts of the overall structure

4.2 2D-modelling of the cross section

When a timber structure is exposed to variations in moisture, a moisture gradient of considerable size arises over the cross section. This moisture gradient, in combination with internal deformation constraints, can result in significant stresses perpendicular to the direction of the grain. To study this phenomenon, MC results pertaining to the two dimensional transient moisture flow model serve as input data to a two-dimensional distortion model of the cross-section of the frame when it is exposed to variations in climate similar to those used in connection with the frame analysis involved. The moisture model employed here is a linear model that uses the average value of the diffusion coefficient involved.

4.2.1 Geometry of the cross section

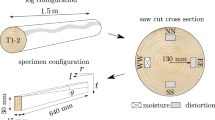
The geometry of the cross section is shown in Fig. 1. The cross section consists of 26 lamellae, each set of two lamellae being cut from flat-sawn timber boards, each of similar type and with a thickness of 45 mm. The pith is located on the side of the board, as shown in Fig. 1.

4.2.2 A numerical example

Figure 12 presents color plots of the deformed cross sections at the ends of several different months during the first period when the structure was in service, so as to provide insight into how the moisture gradient, the cross-sectional deformations and the tangential stresses within the structures develop. As seen in Fig. 4, the cross section here is assumed to have a constant initial MC of 12 % and to be exposed to the climatic variations shown in Fig.1, which act on all of the surfaces of the cross section in question.

Fig. 12

Variations in the moisture content and the tangential stresses over the cross section of the frame

The results shown in Fig. 12 indicate that a cross section of this size does not attain the moisture content equilibrium (EMC). As well, moisture-content gradients and stresses of considerable sizes are shown to occur inside the cross sections during various months involved. This illustrates how the moisture flow, stress generation and mechano-sorption phenomena are ongoing throughout the year. The maximum swelling deformation of the cross section comes after 8 months have passed. Note that all of the deformations shown in Fig. 12 are magnified by a factor of 5.

4.3 2D-modelling of the frame structure

A 2D analysis of the frame was performed to study how structural constraints in the statically indeterminate frame structure affect the transverse stresses found in the curved corner parts. Both the material data and the moisture loading were based on the simulations conducted.

4.3.1 2D-geometry of the frame structure

Figure 13 shows the two-dimensional frame geometry, element mesh and boundary conditions used for the simulations. Since the frame is a symmetric structure and is exposed to symmetric loading, only half of the frame structure needs to be analysed. To obtain an even stress distribution over the curved corner area, it was necessary to use a cylindrical coordinate system and a rather fine element mesh.

Fig. 13

Geometry, boundary conditions, and element mesh for the 2D-frame structure

4.3.2 A numerical example

To study how the mechanical and moisture loads affect the transverse stresses in the curved corner area, two separate simulations were performed, when the frame was loaded with simply a mechanical load, and when the structure was exposed to a pure moisture load. Figure 14 shows, for each of these two load cases, both the maximum deformations and the distribution of the transverse stresses within the curved corner area.

Fig. 14

Deformations and variations in the transverse stress found in the curved corner part of the frame during the summer (the deformations are magnified by a factor of 10): a Moisture loading, b Mechanical loading

5 Results and discussion

The beam simulation presented in Sect. 4.1.3 shows the maximum degree of deflection to occur during the winter, increasing from 30 to 153 [mm] during years 1–50. The results presented in Figs. 9 and 10 show how the moments in the curved corner area decreased slightly, and the tensile stress on the outside surfaces decreased significantly. These moment variations over time occurred because the frame, being a statically indeterminate structure, was exposed to cyclic moisture loading during its lifetime. Figure 11 shows that the maximum tensile stress (7.7 MPa) occurred after 50 years in the first glueline counted from the upper side of the cross section. Note that the stresses on the top and the bottom surfaces decreased significantly, whereas those inside the cross section increased. The strong decreases in stresses on the upper and the bottom surface resulted in a decrease in the moments involved, as shown in Fig. 9. The strongest stress that was involved in the compression here was −11.5 MPa on the bottom surface, already during the first winter period.

Figure 12 shows that, for the 2D-simulation presented in Sect. 4.2, the maximum tangential tensile stresses (of approx. 1.0 MPa) occurred after eight months at the upper surface and after ten months on the sides of the cross section. This stress level is twice as high as the characteristic tension strength perpendicular to the direction of the grain, and thus implies a high risk for fractures to occur. The figure also shows a maximum compression stress (about 1.0 MPa) to occur after 2 and 14 months. The stress level involved is lower than the characteristic compression strength of the material (GL32h).

Figure 14, based on the 2D-simulation of the frame structure presented in Sect. 4.3, shows clearly that the mechanical load results in a larger degree of bending deformation than the environmental load, whereas the size of the maximum stress in the curved corner part is of the same order of magnitude (about 0.2 MPa) but with a different sign. Moisture loading is seen to cause tension perpendicular to the grain and mechanical loading to produce compression. Note that the maximum positive and negative stresses occur at different locations in the curved area and thus fail to balance each other out.

6 Conclusion

The combination of moisture flow models with relatively simple stress models appears to be highly promising for the practical designing of wooden structures in a manner conducive to the maintenance of their long-term behaviour. Although the effects of variations in moisture loading should clearly be considered in structural timber design, this matter has not yet been dealt with adequately.

The modelling results presented here indicate that curved statically indeterminate frame structures can readily show adverse deformations and stresses when exposed to a combined action of mechanical loading and variations in moisture over time. Curved corner areas have a high probability of cracks developing due to the appreciable moisture-induced stresses caused by moisture content gradient over the cross section and because of the structural constraints concerning free bending of the curved sections. Because these sections are strongly loaded in bending, the question arises as to whether the cracked cross sections have sufficient load-carrying capacity.

When designing in wood, one should strive to develop moisture-related solutions to be able to effectively, safely and economically design the wooden structures of tomorrow.

7 Future work

The beam model presented here appears to have a strong potential for further development. The future beam models should simulate mechanical- and moisture-induced stresses in curved beams and frames, beams connected with eccentric normal force actions, beams exposed to both biaxial bending and twist-distortion. The simulation of stresses perpendicular to the direction of the grain should be considered in beam elements of these types. In addition, the beam model employed can be expanded to include non-linear visco-elastic models and geometrical non-linear models involving lateral torsional buckling.

Further experimental verification of variations in moisture and of moisture-induced deformations of wooden beams of larger size should be performed in typical outdoor environments.

Comparative studies of different designing practices, particularly in relation to the Eurocodes and with the use of the beam model, should be carried out. These should encompass case studies of different structures, ranging from simple statically determinate frames to highly complex structures, each designed based on the Eurocode and compared with results from the beam analyses.