1 Introduction

Digital differentiator (DD) is used to compute the time rate of change of any real-time applied or measured input. Unlike the analog differentiators, digital differentiator implementation is composed of delays, adders, and multipliers in place of inductors, capacitors, and resistors, which provide flexibility in the configuration. The extensive applicability of the digital differentiator designs in image processing, radar signaling, and in different aspects of biomedical engineering makes it a convincing field for researchers and designers [2, 21]. Like other types of filters, digital differentiators can be designed as finite impulse response (FIR) or infinite impulse response (IIR) filters. However, both techniques have their own merits and demerits but, in applications where the linear phase is not required, IIR digital differentiators are preferred over FIR digital differentiators due to their low filter order [16].

Researchers have proposed several low-order differentiator designs based on fractional delays, numerical integration methods, and direct pole-zero optimization, which reasonably approximates the DD’s ideal magnitude response [2,3,4, 8, 9, 12, 22]. Some evolutionary and intelligent algorithms have also been developed to provide the optimum designs by direct coefficient optimization of the generalized transfer function of different orders [5, 11, 13]. These metaheuristic algorithms are applied to the fitness function based on the error difference function formulated using \(L_2\) norm. These optimizations incorporated the associated drawbacks of ripples in the pass-band and high overshoots at discontinuity points. However, recent research shows that \(L_1\) fitness function-based designs provide a flatter response in both pass- and stop-band. Furthermore, integration of different objective functions and hybrid optimization algorithms have been utilized to propose the low-order differentiator design with better approximations [1, 10, 19]. Apart from it, some new implementation techniques have also been developed to provide superior noise behavior and overflow stability which makes the designs computationally efficient [14, 17].

Generally optimizing algorithms are based on the concept of exploration and exploitation. In the first exploration phase, the algorithm performs the extensive search for the possible search space whereas in next exploitation phase, the algorithm emphasizes on local search and convergence towards promising areas obtained in the first phase. As these are two conflicting stages, the algorithm must possess the optimum balance. The algorithm multiverse optimizer (MVO) formulated by Mirjalili et al. in 2016 efficiently balances exploration and exploitation, and provides the highly competitive results during optimization. Due to local optima avoidance, MVO outperforms PSO, GA, GSA and other optimizing algorithms [15].

In this paper, the integrated and comprehensive study of MVO with \(L_1\)-norm is exercised for the design of IIR digital differentiator. First, the direct wave form (DWF)-based generalized transfer function is derived as it provides less coefficient sensitivity and low quantization noise in its implementation [18]. It is then followed by optimization of the \(L_1\)-norm error objective function by utilizing the multiverse optimizer algorithm. The proposed design has also been compared with the existing designs to show its efficacy.

The rest of this paper is prepared as follows: Sect. 2 outlines the proposed digital differentiator’s design. Section 3 manifests the short description of the multi-verse optimization algorithm used in the paper. Section 4 discusses the simulation results of the proposed design and comparison with the existing designs. Section 5 concludes the paper.

2 Problem Formulation and Design of Digital Differentiator

The ideal digital differentiator is defined by

$$\begin{aligned} H_d(\omega )=j\omega \quad -\pi \le \omega \le \pi \end{aligned}$$
(1)

which can be approximated using Nth-order IIR digital system. For second order, the generalized transfer function can be written as:

$$\begin{aligned} H(z)=\frac{B_0z^2+B_1z+B_2}{{z^{2}-A_1z-A_2}} \end{aligned}$$
(2)

or

$$\begin{aligned} H(z)=B_0+\frac{\alpha _1z+\alpha _2}{{z^{2}-A_1z-A_2}} \end{aligned}$$
(3)

where \(\alpha _1\) = \(B_1+A_1B_0\) and \(\alpha _2\) = \(B_2+A_2B_0\). The system function H(z) has five degrees of freedom, which can be utilized to obtain any IIR-based system design. The proposed approach is first to convert Eq. (3) into its corresponding state-space representation. After that, the similarity transformation is applied to acquire the corresponding direct wave-form representation [17, 18]. Finally, their respective coefficients have been optimized.

The general state-space representation can be written as:

$$\begin{aligned} \mathbf{s}[n+1]=\mathbf {A}s[n]+\mathbf {B}x[n],\quad y[n]=\mathbf {C}s[n]+\mathbf {D} u[n] \end{aligned}$$
(4)

where \(\mathbf{s}[n]\) is the N-dimensional state vector of state variables for the input x[n] and, y[n] is the corresponding output. Hence, to represent Eq. (3) in the state-space form, it must satisfy the relation \(H(z)=\mathbf {D}+\mathbf {C}(z\mathbf {I}-\mathbf {A})^{-1}\mathbf {B}\). Therefore, the corresponding matrices can be calculated as:

$$\begin{aligned} \mathbf{A} =\begin{bmatrix} A_1&{}A_2\\ 1&{}0 \end{bmatrix};\quad \mathbf{B}=\begin{bmatrix} 1\\ 0 \end{bmatrix};\quad \mathbf{C}=\begin{bmatrix} \alpha _1&{}\alpha _2\\ \end{bmatrix}; \mathbf{D}=[B_0] \end{aligned}$$
(5)

To obtain the DWF, the state plane rotation is applied to Eq. (5), which establishes the relation as [7]:

$$\begin{aligned}{}[\mathbf{A_w}]= & {} [\mathbf{T}^{-1}\mathbf{AT}]; \quad [\mathbf{B_w}] = [\mathbf{T}^{-1}\mathbf{AB}]; \end{aligned}$$
(6)
$$\begin{aligned}= & {} [\mathbf{CT}]; \quad [\mathbf{D_w}] = [\mathbf{B}_0] \end{aligned}$$
(7)

where

$$\begin{aligned} \mathbf{T} =\begin{bmatrix} \frac{1}{2}&{}\frac{-1}{2}\\ \frac{1}{2}&{}\frac{1}{2}\end{bmatrix} \end{aligned}$$
(8)

Therefore, the obtained state-space matrices for the DWF are as follows:

$$\begin{aligned} \mathbf{A_w}= & {} \begin{bmatrix} 1-\gamma _1&{}-\gamma _2 \\ \gamma _1&{}-1+\gamma _2\end{bmatrix};\quad \mathbf{B_w}=\begin{bmatrix} 1\\ -1 \end{bmatrix} \end{aligned}$$
(9)
$$\begin{aligned} \mathbf{C_w}= & {} \begin{bmatrix} \eta _1-\gamma _1B_0&\eta _2-\gamma _2B_0 \end{bmatrix}; \mathbf{D_w}=[B_0] \end{aligned}$$
(10)

where

$$\begin{aligned} \gamma _1=\frac{1}{2}(1-A_1-A_2),\quad \gamma _2=\frac{1}{2}(1+A_1-A_2) \end{aligned}$$
(11)

and

$$\begin{aligned} \eta _1=\frac{1}{2}(B_0+B_1+B_2),\quad \eta _2=\frac{1}{2}(B_0-B_1+B_2) \end{aligned}$$
(12)

Therefore, the corresponding DWF-based transfer function can be written as:

$$\begin{aligned} H_w(z)= & {} \mathbf{D}_w + \mathbf {C_w}( z \mathbf{I}- \mathbf{A}_w)^{-1}\mathbf{B}_w \end{aligned}$$
(13)
$$\begin{aligned} H_w(z)= & {} k\frac{B_0z^2+(\eta _1-\eta _2)z+(\eta _1+\eta _2-B_0)}{z^2+{(\gamma _1-\gamma _2)}z+(\gamma _1+\gamma _2-1)} \end{aligned}$$
(14)

The five coefficients \(\gamma _1, \gamma _2, \eta _1, \eta _2\) and \(B_0\) of the obtained transfer function in Eq. (14) can be optimized to approximate the ideal digital differentiator. The \(L_1\)-norm fitness function provides the flat response, low overshoot, and ripples at the discontinuity points [1]. Therefore, \(L_1\)-norm-based error objective function is utilized to minimize the error between the ideal and the approximated response. It is defined as:

$$\begin{aligned} ||E ||=\sum _\omega |\big (|H_d(\omega )|-|H_w(z)|)|_{z=e^{j\omega }} \end{aligned}$$
(15)

where \(||. ||\) provides norm of function.

3 \(L_1\)-MVO for the Design of Digital Differentiator

The multi-verse optimizer utilized for the optimization is described in this section. The \(L_1\)-norm-based error objective function given in Eq. (15) is minimized and evaluated at each iteration to get the best possible outcome.

MVO Algorithm is a nature-inspired and stochastic population-based algorithm. It is inspired by the theory of multiple parallel universes based on the three key factors: white holes, black holes, and wormholes. White holes play a part in the expansion, created during big-bang or from the universes’ collision. Black holes are the opposite of the white hole and attract everything, even the light, under strong gravitational pull. The wormholes act like time-space tunnels for traveling from one part of the universe to any other or between universes. Besides, each universe shows its inflation rate to result in the expansion. These three concepts are formulated in a mathematical model to evaluate exploration, exploitation, and local re-search. For exploring search spaces, MVO uses black and white hole concepts, and for exploiting the search spaces, it uses wormholes. Each solution and variable is interpreted as a universe and object in the search space, respectively. The inflation rate is proportional to the corresponding fitness function [15, 20].

The algorithm follows the following rules for its successful operation.

  • The higher inflation rate leads to a high probability of white holes and a low probability of having black holes.

  • The objects tend to move from a higher inflation rate to a lower inflation rate through white holes and black holes.

  • The objects may show random movement to get the possible best universe, irrespective of the inflation rate.

Table 1 Control parameters of MVO for the design
Full size table

The optimization process begins with creating a set of universes randomly. With each iteration, objects move from a higher inflation rate to a lower inflation rate through white holes and black holes. Meanwhile, wormholes teleport objects randomly to get the best universe. The updating process relies on the following equation: [6].

$$\begin{aligned} x_{i}^{j}= {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} x_j+TDR+((ub_j-lb_j)*r_4+lb_j), &{} \text {if}\ r_3< 0.5 \\ x_j-TDR+((ub_j-lb_j)*r_4+lb_j), &{} \text {if}\ r_3 \ge 0.5 \\ \end{array}\right. } &{} \text {if}\ r_2 < WEP \\ x_{RW}^{j} &{} \text {if}\ r_2\ge WEP\\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(16)

Here, \(x_j\) represents the jth parameter of the best individual universe. \(lb_j\) and \(ub_j\) indicate the lower and upper bounds of jth variable. \(x_{i}^{j}\) represents the jth parameter of ith universe with \(r_2, r_3, r_4\) are random numbers ranges from 0 to 1. TDR and WEP are Traveling Distance Rate and Wormhole Existence. TDR and WEP are defined as:

$$\begin{aligned} \mathrm{WEP}=\bigg (a+t * \bigg (\frac{b-a}{T}\bigg )\bigg ) \end{aligned}$$
(17)

where a, b, t are the minimum, maximum and current iterations. T represents the maximum number of allowed iterations.

$$\begin{aligned} TDR=\bigg (1-\frac{t^{1/p}}{T^{1/T}}\bigg ) \end{aligned}$$
(18)

where p indicates the exploitation accuracy [6, 15]. Table 1 enlists all the essential parametric values for the optimization process. The coefficients of lower and upper bound are restricted within the limit of − 0.5 and 1 to maintain the IIR design’s stability.

4 Simulation Analysis and Comparison With the Existing Designs

The optimized values for \(\gamma _1, \gamma _2, \eta _1, \eta _2\) and \(B_0\) are obtained as 0.88678, 0.17933, − 0.00032, − 0.31687 and − 0.67014, respectively. The corresponding transfer function of the proposed digital differentiator is obtained as:

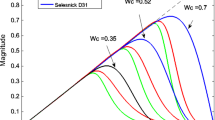
$$\begin{aligned} H_\mathrm{proposed}(z)=1.72247\frac{-0.67014+0.31655z^{-1}+0.35295z^{-2}}{1+0.707454z^{-1}+0.066108z^{-2}} \end{aligned}$$
(19)

The proposed differentiator’s magnitude response is plotted along with the ideal in Fig. 1. It approximates the ideal differentiator considerably well over the complete Nyquist interval. Figure 2 compares the absolute magnitude error of the proposed \(L_1\)-MVO-based differentiator design with the recently published designs to evaluate its efficacy.

Fig. 1
figure 1

Magnitude response of the ideal and proposed digital differentiator

Full size image
Fig. 2
figure 2

Absolute magnitude error comparison of existing digital differentiator designs with the proposed design

Full size image

In 2011, the third-order segment-based digital differentiator was proposed by Al-Alaoui [2]. The standard numerical integration techniques followed by the simulated annealing (SA) optimization algorithm provide an excellent approximation to the ideal differentiator. The utilization of genetic algorithm approximation has been done by Jain et al. to propose the design of digital differentiators with considerable improvement [12]. Upadhyay optimized pole-zeros locations to provide the second-order digital differentiator [22]. Furthermore, the designs provided by Aggarwal integrate the \(L_1\)-norm with different optimization techniques and approximate the ideal digital differentiator with low magnitude error [1]. Table 2 enlists the transfer functions of the existing designs of digital differentiators.

Table 2 Transfer functions of existing IIR digital differentiators
Full size table

It can be seen in Fig. 2 that the proposed DD performs better than the designs mentioned above for the complete Nyquist interval. The proposed \(L_1\)-MVO-based design provides less error than the Upadhyay et al. [22] in the high-frequency range and outranges the design proposed by the Al-Alaoui, Gupta et al. Aggarwal et al. (\(L_1\)-PSO). At the same time, it remains comparable with the design offered by Aggarwal et al. (\(L_1\)-BA). Yet, for the complete Nyquist frequency range, the proposed \(L_1\)-MVO design provides considerable improvement to all the designs taken for comparison. Table 3 gives the statistical comparison, which further confirms that the sum of absolute magnitude error (SAME) and mean absolute magnitude error (MAME) attain by the proposed designs are the least compared to others.

Table 3 Comparison of errors of the existing digital differentiators designs with the proposed design
Full size table

5 Conclusion

This paper has presented the optimum design of the second-order IIR digital differentiator. The design involves optimizing direct wave-form-based coefficients with \(L_1\)-norm-based error objective function after utilizing the multiverse optimizing algorithm. The proposed design gives SAME and MAME as 1.5998 and − 45.8842 dB, respectively, which performs better than the existing IIR differentiator designs. Therefore, the proposed DD design can be used as the alternative to the existing ones.