1 Introduction

Time delay, which is generally viewed as a main source of oscillation, degradation of system performance and instability, is frequently encountered in practical engineering systems, such as networked systems, suspension systems, biological systems and chemical processes systems [1, 3, 9, 19, 37, 41, 45]. Therefore, the problem of stability analysis and controller design for time-delay systems has been one of the hottest issues in control society. Depending on whether or not the stability criteria include the information about delay, most of the existing works on time delay systems are based on two approaches: delay-independent criteria [24] and delay-dependent criteria [47], of which the later one takes the delay information into account and gives less conservative results. In past decades, various methods, such as Jensen’s inequality [16], free-weighting matrices [44], the reciprocally convex approach [30], delay-partitioning approach [10, 12], the augmented Lyapunov functional [49], relaxed Lyapunov functional [42] and Wirtinger-based inequality [33], have been introduced to find a maximal allowable delay as large as possible for a given time-delay system. Furthermore, time-delay theory has been applied widely in practical engineering systems [15, 22, 28], and good results have been acquired.

It should be pointed out that the results aforementioned are based on systems with one single delay. It is well known that in many practical systems, however, physical plant, controller, sensors and actuator are difficult to locate at the same place, meaning that signals must be transmitted from one place to another. So, the signals may experience two different network segments with different properties such as one from sensor to controller and the other from controller to actuator(as Fig. 1) [14, 23]. Meanwhile, the properties of these two delays may not be identical due to the difference between the network transmission conditions; hence, it is not reasonable to regard the two additive delays as a whole. Since it has a strong application background in bilateral teleoperation systems(as Fig. 2) and networked control [8, 31], the research on this model has received considerable attentions and various approaches have been applied for it to obtain less conservative results [7, 27, 32, 35]. Yet the order of time-varying delays is taken into account, there still leaves some room to improve the results.

Fig. 1
figure 1

Networked control system

Full size image
Fig. 2
figure 2

Bilateral teleoperation system

Full size image

In fact, almost all of the studies aforementioned focus on Lyapunov asymptotic stability, which is defined over an infinite-time interval. However, in practical, our interests are always concerned on the behavior of the system over a prescribed time interval. For instance, in the presence of saturation or controlling the trajectory of a space vehicle from a given point to a final one in a fixed short time interval. That is, the state of the system does not exceed a bound over a given finite time interval. To deal with such situations, the concept of finite-time stability was proposed by P. Dorato [6]. Specifically, a system is said to be finite-time stable if, given a bound on the initial condition, its state remains within a prescribed bound in a fixed time interval. With the development of Lyapunov–Krasovskii-like function(LKLF) approach and LMI techniques, a great number of results on finite-time stability were obtained for various sorts of systems, such as neural network systems [29, 51], impulsive systems [4], switch systems [25, 40, 52], T-S fuzzy systems [18, 26] and time-delay systems [5, 20, 21, 43, 48]. However, there is still room for further research to reduce the conservatism of these results. Further, to the best knowledge of authors, the problem of finite-time stability for system with additive varying delays has been received little attention, which motivates our research.

In this paper, the problems of finite-time stability and finite-time stabilization for continuous systems with additive time-varying delays are investigated. Main contributions of this paper are threefold: (1) the problem of finite-time stability and stabilization for a class of continuous system with additive time-varying delays is studied, while little previous works have centered on it; (2)the interval of additive time delays has been studied, and a new LKLF, which splits the whole delay interval into proper subintervals, is constructed to derive the conditions; and (3) to reduce the conservatism, we take the LKLF as a whole to examine its positive definite so that the requirements of conditions are relaxed and the loss of information is diminished when estimating the bound of LKLF. Finally, some numerical examples are provided to demonstrate the less conservative and the effectiveness of the proposed design approach.

The remainder of this paper is organized as follows: In Sect. 2, the considered system is stated, and some preliminaries are provided for preparations. Delay-dependent finite-time stability conditions are presented in Sect. 3.1. In Sect. 3.2, delay-dependent finite-time stabilization conditions are provided based on the finite-time stability results. Numerical simulation results are given in Sect. 4 to illustrate the effectiveness of the proposed approach. Finally, conclusion is drawn in Sect. 5.

Notation Throughout this paper, \(\mathbb {R}^{n}\) is the n-dimensional Euclidean vector space, and \(\mathbb {R}^{m\times n}\) denotes the set of all \(m\times n\) real matrices. For symmetric matrices X and Y, \(X>Y\) (respectively,\(X\ge Y)\) means that \(X-Y\) is positive definite (respectively, positive semi-definite). The superscript “T” represents the transpose. The symmetric terms in a symmetric matrix are denoted by “\({*}\)”. Moreover, we use \(\lambda _{\max } \left( \cdot \right) (\lambda _{\min } \left( \cdot \right) )\) to denote the maximum (minimum) eigenvalue of a symmetric matrix.

2 Preliminaries

Consider the following linear continuous system with two additive time-varying delay components in the state

$$\begin{aligned} \dot{x}\left( t \right) =Ax\left( t \right) +A_d x\left( {t-d_1 \left( t \right) -d_2 \left( t \right) } \right) +Bu\left( t \right) \end{aligned}$$
(1)

where \(x\left( t \right) \in \mathbb {R}^{n}\) is the state vector and \(u\left( t \right) \in \mathbb {R}^{m}\) is the control input signal. \(A\in \mathbb {R}^{n\times n}\),\(A_d \in \mathbb {R}^{n\times n}\) and \(B\in \mathbb {R}^{n\times m}\) are constant matrices. The time delays of \(d_1 \left( t \right) \) and \(d_2 \left( t \right) \) are different time-varying functions that satisfy

$$\begin{aligned} 0\le d_1 \left( t \right) \le d_1 , \quad 0\le d_2 \left( t \right) \le d_2 \end{aligned}$$
(2)

and

$$\begin{aligned} \dot{d}_1 \left( t \right) \le \mu _1 , \quad \dot{d}_2 \left( t \right) \le \mu _2 \end{aligned}$$
(3)

where \(d_1\), \(d_2\) and \(\mu _1\), \(\mu _2\) are constant.

To simplify the system, we set \(d\left( t \right) =d_1 \left( t \right) +d_2 \left( t \right) \) and the system (1) can be rewritten as

$$\begin{aligned} \dot{x}\left( t \right) =Ax\left( t \right) +A_d x\left( {t-d\left( t \right) } \right) +Bu\left( t \right) \end{aligned}$$
(4)

where

$$\begin{aligned} 0\le d\left( t \right) \le d, \quad d=d_1 +d_2, \quad \mu =\mu _1 +\mu _2 \end{aligned}$$
(5)

Remark 1

In the system (1) as Fig. 1, the control signal first experiences the delay \(d_1 \left( t \right) \) and then experiences the delay \(d_2 \left( t \right) \) [34], so the system must contain the subinterval \(\left[ {0,d_1 \left( t \right) } \right] \) and \(\left[ {d_1 \left( t \right) ,d\left( t \right) } \right] \). In many previous papers, this fact has been ignored and it will lead to some conservatism or even mistakes.

Our objective is to derive some sufficient conditions that guaranteeing the finite-time stability and finite-time stabilization of system (1). In the sequel, following lemmas are introduced which will be applied to prove the results in the later.

Lemma 1

(Wirtinger inequality) [33] For any matrix \(P>0\) and a differentiable signal x in \(\left[ \alpha \right. ,\left. \beta \right] \rightarrow \mathbb {R}^{n}\), the following inequality holds

$$\begin{aligned} -\int _\alpha ^\beta {\dot{x}\left( s \right) ^{T}P\dot{x}\left( s \right) }\text {d}s\le \frac{1}{\beta -\alpha }\varpi ^{T}\Pi \varpi \end{aligned}$$
(6)

where

$$\begin{aligned} \Pi= & {} \left( {{\begin{array}{ccc} {-4P}&{} \quad {-2P}&{} \quad {6P} \\ {*}&{} \quad {-4P}&{} \quad {6P} \\ {*}&{} \quad {*}&{}\quad {-12P} \\ \end{array} }} \right) \\ \varpi= & {} \left[ {{\begin{array}{ccc} {x^{T}\left( \beta \right) }&{}\quad {x^{T}\left( \alpha \right) }&{}\quad {\frac{1}{\beta -\alpha }\int _\alpha ^\beta {x^{T}\left( s \right) } \text {d}s} \\ \end{array} }} \right] ^{T} \end{aligned}$$

Lemma 2

(Jensen inequality) [16] For any matrix \(P>0\) and a vector function x in \(\left[ \alpha \right. ,\left. \beta \right] \rightarrow \mathbb {R}^{n}\), if the integrals concerned are well defined, then the following inequality holds

$$\begin{aligned} -\int _\alpha ^\beta {x^{T}\left( s \right) Px\left( s \right) }\text { d}s\le -\frac{1}{\beta -\alpha }\left( {\int _\alpha ^\beta {x^{T}\left( s \right) } \text {d}s} \right) P\left( {\int _\alpha ^\beta {x\left( s \right) } \text {d}s} \right) \end{aligned}$$
(7)

Now the definition of finite-time stability of system with additive time delays will be given as follow.

Definition 1

(Finite-Time Stability (FTS))[2]. Given a positive matrix R and three positive constants \(c_1 \) ,\(c_2 \) ,T,with \(c_1 <c_2 \),the time-delay system described by Eq. (1) with \(u\left( t \right) =0\) is said to be finite-time stability with respect to \(\left( {{\begin{array}{cccccc} {c_1 }&{} {c_2 }&{} T&{} {d_1 }&{} {d_2 }&{} R \\ \end{array} }} \right) \), if the state variables satisfy the relationship: \(\sup _{-d\le \theta \le 0} \left\{ {x^{T}\left( \theta \right) Rx^{T}\left( \theta \right) ,\left. {\dot{x}^{T}\left( \theta \right) R\dot{x}^{T}\left( \theta \right) } \right\} } \right.<c_1 \Rightarrow x^{T}\left( t \right) Rx^{T}\left( t \right) <c_2 ,\forall t\in \left[ {0,T} \right] \).

Remark 2

In the framework of asymptotic stability for time-delay systems, researches aim to find a maximal allowable delay as large as possible [11, 13, 50]. For FTS, however, it is of interest to minimize the trajectory bound \(c_2 \). The smaller the \(c_2 \) is, the less conservative the system is [53].

Remark 3

It should be pointed out that there is difference between finite-time stability and finite-time attractiveness. The first one is about the bound of system states in a specified time interval, while the later one aims that system state reaches the equilibrium of system in a finite time.

3 Main Results

3.1 Finite-Time Stability Analysis

In this section, sufficient conditions for the FTS of system (1) will be established in the following theorem.

Theorem 1

The system (1) is finite-time stable with respect to \(\left( {{\begin{array}{cccccc} {c_1 }&{} {c_2 }&{} T&{} {d_1 }&{} {d_2 }&{} R \\ \end{array} }} \right) \) if there exist a positive matrix P, symmetric matrices \(Q_1 \) ,\(Q_2 \) ,\(Q_3 \) where \(Q_1>Q_2 >Q_3 \) and scalars \(\theta _1 \) ,\(\theta _2 \) ,\(\theta _3 \) ,\(\theta _4 \) ,\(\theta _5 \) ,\(\gamma \) satisfying the following conditions.

$$\begin{aligned}&\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} \quad {Q_i +P} \\ \end{array} }} \right) >0\quad \left( {i=1,2,3} \right) \end{aligned}$$
(8)
$$\begin{aligned}&\left( {{\begin{array}{cc} {\bar{{\Omega }}}&{} \quad {\Psi ^{T}} \\ {*}&{} \quad \quad {-P^{-1}} \\ \end{array} }} \right) <0 \end{aligned}$$
(9)
$$\begin{aligned}&c_1 \theta _2 +c_1 d_1 \theta _3 +c_1 \text {d}\theta _4 +c_1 \text {d}\theta _5 +\frac{1}{2}c_1 d^{2}\theta _2 \le \theta _1 e^{-\gamma T}c_2 \end{aligned}$$
(10)

where

$$\begin{aligned} \bar{{\Omega }}_{11}= & {} A^{T}P+PA+Q_1 -\left( {4+\gamma d+\gamma } \right) P, \bar{{\Omega }}_{13} =PA_d ,\\ \bar{{\Omega }}_{14}= & {} -2P, \bar{{\Omega }}_{15} =6P+\gamma dP,\\ \bar{{\Omega }}_{22}= & {} -\left( {1-\mu _1 } \right) \left( {Q_1 -Q_2 } \right) , \bar{{\Omega }}_{33} =-\left( {1-\mu } \right) \left( {Q_2 -Q_3 } \right) ,\\ \bar{{\Omega }}_{44}= & {} -4P-Q_3 , \bar{{\Omega }}_{45} =6P,\\ \bar{{\Omega }}_{55}= & {} -12P-\gamma dQ_3 -\gamma dP, \bar{{\Omega }}_{12} =\bar{{\Omega }}_{23} =\bar{{\Omega }}_{24} =\bar{{\Omega }}_{25} =\bar{{\Omega }}_{34} =\bar{{\Omega }}_{35} =0\\ \Psi= & {} \left( {{\begin{array}{ccccc} {\textit{dPA}}&{} 0&{} {{\textit{dPA}}_d }&{} 0&{} 0 \\ \end{array} }} \right) , \lambda _1 =\lambda _{\min } \left( {\tilde{P}} \right) , \lambda _2 =\lambda _{\max } \left( {\tilde{P}} \right) , \lambda _3 =\lambda _{\max } \left( {\tilde{Q}_1 } \right) ,\\ \lambda _4= & {} \lambda _{\max } \left( {\tilde{Q}_2 } \right) , \lambda _5 =\lambda _{\max } \left( {\tilde{Q}_3 } \right) , \tilde{P}=R^{{-1}/2}PR^{{-1}/2},\\ \tilde{Q}_i= & {} R^{{-1}/2}\tilde{Q}_i R^{{-1}/2}, i=1,2,3,\\ \theta _1>&0, \theta _2>0, 0<\theta _1 I<P<\theta _2 I, Q_1<\theta _3 I, Q_2<\theta _4 I, Q_3 <\theta _5 I, \gamma >0. \end{aligned}$$

Proof

Construct the following LKLF

$$\begin{aligned} V_1 \left( t \right)= & {} x^{T}\left( t \right) Px\left( t \right) \nonumber \\ V_2 \left( t \right)= & {} \int _{t-d_1 \left( t \right) }^t {x^{T}} \left( s \right) Q_1 x\left( s \right) \text {d}s+\int _{t-d\left( t \right) }^{t-d_1 \left( t \right) } {x^{T}\left( s \right) Q_2 x\left( s \right) } \text {d}s \nonumber \\&+\quad \int _{t-d}^{t-d\left( t \right) } {x^{T}\left( s \right) Q_3 x\left( s \right) } \text {d}s \nonumber \\ V_3 \left( t \right)= & {} d\int _{-d}^0 {\int _{t+\theta }^t {\dot{x}^{T}\left( s \right) P\dot{x}\left( s \right) \text {d}s\text {d}\theta } } \end{aligned}$$
(11)

First, we should prove the positive definiteness of the candidate LKLF under the condition of Theorem 1.

By using Lemma 2, it follows that

$$\begin{aligned} V_3 \left( t \right)\ge & {} \int _{-d_1 \left( t \right) }^0 {\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) ^{T}P\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) \text {d}\theta } \nonumber \\&+\quad \int _{-d\left( t \right) }^{-d_1 \left( t \right) } {\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) ^{T}P\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) \text {d}\theta } \nonumber \\&+\quad \int _{-d}^{-d\left( t \right) } {\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) ^{T}P\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) \text {d}\theta } \end{aligned}$$
(12)

Noticing that

$$\begin{aligned} V_2 \left( t \right)= & {} \int _{-d_1 \left( t \right) }^0 {x^{T}\left( {t+\theta } \right) Q_1 x\left( {t+\theta } \right) } \text {d}\theta +\int _{-d\left( t \right) }^{-d_1 \left( t \right) } {x^{T}\left( {t+\theta } \right) } Q_2 x\left( {t+\theta } \right) \text {d}\theta \nonumber \\&+\quad \int _{-d}^{-d\left( t \right) } {x^{T}\left( {t+\theta } \right) Q_3 x\left( {t+\theta } \right) } \text {d}\theta \end{aligned}$$
(13)

Combining (12) and (13), we have

$$\begin{aligned} V_2 \left( t \right) +V_3 \left( t \right)= & {} \int _{-d_1 \left( t \right) }^0 {\left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) } ^{T}\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} {Q_1 +P} \\ \end{array} }} \right) \left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) \text {d}\theta \nonumber \\&+\quad \int _{-d\left( t \right) }^{-d_1 \left( t \right) } {\left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) } ^{T}\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} {Q_2 +P} \\ \end{array} }} \right) \left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) \text {d}\theta \nonumber \\&+\quad \int _{-d}^{-d\left( t \right) } {\left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) } ^{T}\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} {Q_3 +P} \\ \end{array} }} \right) \left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) \text {d}\theta \quad \quad \quad \end{aligned}$$
(14)

If (8) is satisfied, we can ensure the positive definiteness of LKLF we construct.

Then, calculating the time derivative of the function along the trajectory with the system (1)

$$\begin{aligned} \dot{V}_1 \left( t \right)= & {} \dot{x}^{T}\left( t \right) Px\left( t \right) +x^{T}\left( t \right) Px\left( t \right) \end{aligned}$$
(15)
$$\begin{aligned} \dot{V}_2 \left( t \right)\le & {} x^{T}\left( t \right) Q_1 x\left( t \right) -\left( {1-\mu _1 } \right) x^{T}\left( {t-d_1 \left( t \right) } \right) \left( {Q_1 -Q_2 } \right) x\left( {t-d_1 \left( t \right) } \right) \nonumber \\&-\left( {1-\mu } \right) x^{T}\left( {t-d\left( t \right) } \right) \left( {Q_2 -Q_3 } \right) x\left( {t-d\left( t \right) } \right) \nonumber \\&-x^{T}\left( {t-d} \right) Q_3 x\left( {t-d} \right) \end{aligned}$$
(16)
$$\begin{aligned} \dot{V}_3 \left( t \right)= & {} d^{2}\dot{x}^{T}\left( t \right) P\dot{x}\left( t \right) -d\int _{t-d}^t {\dot{x}^{T}\left( \theta \right) P\dot{x}\left( \theta \right) } \text {d}\theta \end{aligned}$$
(17)

By using Lemma 2, we have

$$\begin{aligned} \dot{V}_3 \left( t \right)\le & {} d^{2}\left( {Ax\left( t \right) +A_d x\left( {t-d\left( t \right) } \right) } \right) ^{T}P\left( {Ax\left( t \right) +A_d x\left( {t-d\left( t \right) } \right) } \right) \nonumber \\&+\hat{{\varpi }}^{T}\left( t \right) \hat{{\Pi }}\hat{{\varpi }}\left( t \right) \end{aligned}$$
(18)

where

$$\begin{aligned} \hat{{\varpi }}^{T}\left( t \right)= & {} \left( {{\begin{array}{ccc} {x^{T}\left( t \right) }&{} {x^{T}\left( {t-d} \right) }&{} {\frac{1}{d}\int _{t-d}^t {x^{T}\left( s \right) }\text {d}s} \\ \end{array} }} \right) ^{T}\\ \hat{{\Pi }}= & {} \left( {{\begin{array}{ccc} {-4P}&{} {-2P}&{} \quad {6P} \\ {*}&{} {-4P}&{} \quad {6P} \\ {*}&{} {*}&{} \quad {-12P} \\ \end{array} }} \right) \end{aligned}$$

Combining the (15)–(18), we have

$$\begin{aligned} \dot{V}\left( t \right) \le \xi ^{T}\left( t \right) \Omega \xi \left( t \right) \end{aligned}$$
(19)

where

$$\begin{aligned} \xi \left( t \right)= & {} \left( {{\begin{array}{ccccc} {x\left( t \right) }&{} {x\left( {t-d_1 \left( t \right) } \right) }&{} {x\left( {t-d\left( t \right) } \right) }&{} {x\left( {t-d} \right) }&{} {\frac{1}{d}\int _{t-d}^t {x\left( s \right) } \text {d}s} \\ \end{array} }} \right) ^{T},\\ \Omega= & {} \left( {\Omega _{\textit{ij}} } \right) _{5\times 5} , \Omega _{11} =A^{T}P+PA+Q_1 -4P+A^{T}\left( {d^{2}P} \right) A,\\ \Omega _{13}= & {} PA_d +A^{T}\left( {d^{2}P} \right) A_d , \Omega _{14} =-2P,\\ \Omega _{15}= & {} 6P, \Omega _{22} =-\left( {1-\mu _1 } \right) \left( {Q_1 -Q_2 } \right) ,\\ \Omega _{33}= & {} -\left( {1-\mu } \right) \left( {Q_2 -Q_3 } \right) +A_d ^{T}\left( {d^{2}P} \right) A_d ,\\ \Omega _{44}= & {} -4P-Q_3 , \Omega _{45} =6P, \Omega _{55} =-12P,\\ \Omega _{12}= & {} \Omega _{23} =\Omega _{24} =\Omega _{25} =\Omega _{34} =\Omega _{35} =0. \end{aligned}$$

Given a positive scalar \(\gamma \), it follows as

$$\begin{aligned} \dot{V}\left( t \right) -\gamma V\left( t \right)= & {} \xi ^{T}\left( t \right) \Omega \xi \left( t \right) -\gamma x^{T}\left( t \right) Px\left( t \right) -\gamma \left( {V_2 \left( t \right) +V_3 \left( t \right) } \right) \end{aligned}$$
(20)
$$\begin{aligned} -\gamma V_2= & {} -\gamma \left( {\int _{t-d_1 \left( t \right) }^t {x^{T}} \left( s \right) Q_1 x\left( s \right) \text {d}s+\int _{t-d\left( t \right) }^{t-d_1 \left( t \right) } {x^{T}\left( s \right) Q_2 x\left( s \right) } \text {d}s} \right. \nonumber \\&+\quad \left. {\int _{t-d}^{t-d\left( t \right) } {x^{T}\left( s \right) Q_3 x\left( s \right) } \text {d}s} \right) \nonumber \\\le & {} -\gamma \left( {\int _{t-d_1 \left( t \right) }^t {x^{T}} \left( s \right) Q_3 x\left( s \right) \text {d}s+\int _{t-d\left( t \right) }^{t-d_1 \left( t \right) } {x^{T}\left( s \right) Q_3 x\left( s \right) } \text {d}s} \right. \nonumber \\&+\quad \left. {\int _{t-d}^{t-d\left( t \right) } {x^{T}\left( s \right) Q_3 x\left( s \right) } \text {d}s} \right) \nonumber \\= & {} -\gamma \int _{t-d}^t {x^{T}\left( s \right) Q_3 x\left( s \right) } \text {d}s \end{aligned}$$
(21)

This together with (12) follows

$$\begin{aligned} -\gamma \left( {V_2 \left( t \right) +V_3 \left( t \right) } \right)\le & {} -\gamma \int _{-d}^0 {x^{T}\left( {t+\theta } \right) Q_3 x\left( {t+\theta } \right) \text {d}\theta }\nonumber \\&-\gamma \int _{-d}^0 {\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) ^{T}P\left( {x\left( t \right) -x\left( {t+\theta } \right) } \right) } \text {d}\theta \nonumber \\= & {} -\gamma \int _{-d}^0 {\left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) ^{T}\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} {Q_3 +P} \\ \end{array} }} \right) } \left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \end{array} }} \right) \text {d}\theta \nonumber \\ \end{aligned}$$
(22)

By using Lemma 2 under the condition of (8), we have

$$\begin{aligned} -\gamma \left( {V_2 \left( t \right) +V_3 \left( t \right) } \right)\le & {} -\gamma \frac{1}{d}\left( {\int _{-d}^0 {\left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) \text {d}\theta } } \right) ^{T}\left( {{\begin{array}{cc} P&{} {-P^{T}} \\ {*}&{} {Q_3 +P} \\ \end{array} }} \right) \nonumber \\&\times \left( {\int _{-d}^0 {\left( {{\begin{array}{c} {x\left( t \right) } \\ {x\left( {t+\theta } \right) } \\ \end{array} }} \right) \text {d}\theta } } \right) \nonumber \\= & {} -\gamma \frac{1}{d}\left( {{\begin{array}{c} {\text {d}x\left( t \right) } \\ {\int _{t-d}^t {x\left( s \right) } \text {d}s} \\ \end{array} }} \right) ^{T}\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} {Q_3 +P} \\ \end{array} }} \right) \nonumber \\&\times \left( {{\begin{array}{c} {\text {d}x\left( t \right) } \\ {\int _{t-d}^t {x\left( s \right) } \text {d}s} \\ \end{array} }} \right) \end{aligned}$$
(23)
$$\begin{aligned} -\gamma V\left( t \right)\le & {} -\gamma x^{T}\left( t \right) Px\left( t \right) -\gamma \left( {{\begin{array}{c} {x\left( t \right) } \\ {\frac{1}{d}\int _{t-d}^t {x\left( s \right) } \text {d}s} \\ \end{array} }} \right) ^{T} \nonumber \\&\times \left( {{\begin{array}{cc} {dP}&{} {-dP} \\ {*}&{} {d\left( {Q_3 +P} \right) } \\ \end{array} }} \right) \left( {{\begin{array}{cc} {x\left( t \right) } \\ {\frac{1}{d}\int _{t-d}^t {x\left( s \right) } \text {d}s} \\ \end{array} }} \right) \nonumber \\= & {} -\xi ^{T}\left( t \right) \hat{{\Omega }}\xi \left( t \right) \end{aligned}$$
(24)

where

$$\begin{aligned} \hat{{\Omega }}= & {} \left( {\hat{{\Omega }}_{\textit{ij}} } \right) _{5\times 5} , \hat{{\Omega }}_{11} =\gamma \left( {1+d} \right) P, \hat{{\Omega }}_{15} =-\gamma dP, \hat{{\Omega }}_{55} =\gamma d\left( {Q_3 +P} \right) ,\\ \hat{{\Omega }}_{12}= & {} \hat{{\Omega }}_{13} =\hat{{\Omega }}_{14} =\hat{{\Omega }}_{22} =\hat{{\Omega }}_{23} =\hat{{\Omega }}_{24} =\hat{{\Omega }}_{25} =\hat{{\Omega }}_{33} =\hat{{\Omega }}_{34} =\hat{{\Omega }}_{35} \\= & {} \hat{{\Omega }}_{44} =\hat{{\Omega }}_{45} =0. \end{aligned}$$

Combining (19) and (24) together, we have

$$\begin{aligned} \dot{V}\left( t \right) -\gamma V\left( t \right) \le \xi ^{T}\left( t \right) \tilde{\Omega }\xi \left( t \right) \end{aligned}$$
(25)

where

$$\begin{aligned} \tilde{\Omega }= & {} \Omega -\hat{{\Omega }}, \quad \tilde{\Omega }_{11} =A^{T}P+PA+Q_1 +A^{T}\left( {d^{2}P} \right) A-\left( {4+\gamma d+\gamma } \right) P,\\ \tilde{\Omega }_{13}= & {} PA_d +A^{T}\left( {d^{2}P} \right) A_d ,\\ \tilde{\Omega }_{14}= & {} -2P, \tilde{\Omega }_{15} =6P+\gamma dP, \tilde{\Omega }_{22} =-\left( {1-\mu _1 } \right) \left( {Q_1 -Q_2 } \right) ,\\ \tilde{\Omega }_{33}= & {} -\left( {1-\mu } \right) \left( {Q_2 -Q_3 } \right) +A_d ^{T}\left( {d^{2}P} \right) A_d , \quad \tilde{\Omega }_{44} =-4P-Q_3 , \tilde{\Omega }_{45} =6P,\\ \tilde{\Omega }_{55}= & {} -12P-\gamma d\left( {Q_3 +P} \right) , \tilde{\Omega }_{12} =\tilde{\Omega }_{23} =\tilde{\Omega }_{24} =\tilde{\Omega }_{25} =\tilde{\Omega }_{34} =\tilde{\Omega }_{35} =0. \end{aligned}$$

It should be pointed out that Z is coupled with A and \(A_d \) in \(\tilde{\Omega }\); hence, we aim to decouple them in the following parts. The matrix \(\tilde{\Omega }\) can be rewritten as

$$\begin{aligned} \tilde{\Omega }=\bar{{\Omega }}-\Psi ^{T}\left( {-P} \right) ^{-1}\Psi \end{aligned}$$
(26)

By using Schur complement, if (9) is satisfied, we have

$$\begin{aligned} \dot{V}\left( t \right) -\gamma V\left( t \right) <0 \end{aligned}$$
(27)

Integrating (27) from 0 to t with \(t\in ( 0 , T ]\), we obtain

$$\begin{aligned} V\left( t \right) <e^{\gamma t}V\left( 0 \right) \end{aligned}$$
(28)

The initial value of LKLF can be written as

$$\begin{aligned} V\left( 0 \right)= & {} x^{T}\left( 0 \right) Px\left( 0 \right) +\int _{-d_1 \left( 0 \right) }^0 {x^{T}\left( s \right) Q_1 x\left( s \right) } \text {d}s\nonumber \\&+\quad \int _{-d\left( 0 \right) }^{-d_1 \left( 0 \right) } {x^{T}\left( s \right) Q_2 x\left( s \right) } \text {d}s \nonumber \\&+\int _{-d}^{-d\left( 0 \right) } {x^{T}\left( s \right) Q_3 x\left( s \right) } \text {d}s+\int _{-d}^0 {\int _\theta ^0 {\dot{x}^{T}\left( s \right) P\dot{x}\left( s \right) } \text {d}s}\text {d}\theta \nonumber \\\le & {} \lambda _{\max } \left( {\tilde{P}} \right) x^{T}\left( 0 \right) Rx\left( 0 \right) +\lambda _{\max } \left( {\tilde{Q}_1 } \right) \int _{-d_1 \left( 0 \right) }^0 {x^{T}\left( s \right) Rx\left( s \right) } \text {d}s \nonumber \\&+\quad \lambda _{\max } \left( {\tilde{Q}_2 } \right) \int _{-d\left( 0 \right) }^{-d_1 \left( 0 \right) } {x^{T}\left( s \right) Rx\left( s \right) } \text {d}s\nonumber \\&+\,\lambda _{\max } \left( {\tilde{Q}_3 } \right) \int _{-d}^{-d\left( 0 \right) } {x^{T}\left( s \right) Rx\left( s \right) } \text {d}s \\&+\lambda _{\max } \left( {\tilde{P}} \right) \int _{-d}^0 {\int _\theta ^0 {\dot{x}^{T}\left( s \right) R\dot{x}\left( s \right) } \text {d}s} \text {d}\theta \nonumber \\\le & {} c_1 \lambda _{\max } \left( {\tilde{P}} \right) +c_1 d_1 \left( t \right) \lambda _{\max } \left( {\tilde{Q}_1 } \right) +c_1 \left( d\left( t \right) \right. \nonumber \\&\left. -\,d_1 \left( t \right) \right) \lambda _{\max } \left( {\tilde{Q}_2 } \right) +c_1 \left( {d-d\left( t \right) } \right) \lambda _{\max } \left( {\tilde{Q}_3 } \right) \nonumber \\&+\quad \frac{1}{2}c_1 d^{2}\lambda _{\max } \left( {\tilde{P}} \right) \nonumber \\\le & {} c_1 \lambda _2 +c_1 d_1 \lambda _3 +c_1 d\lambda _4 +c_1 d\lambda _5 +\frac{1}{2}c_1 d^{2}\lambda _2 \nonumber \end{aligned}$$
(29)
$$\begin{aligned} V\left( t \right)\ge & {} V_1 =x^{T}\left( t \right) Px\left( t \right) \ge \lambda _{\min } \left( {\tilde{P}} \right) x^{T}\left( t \right) Rx\left( t \right) \nonumber \\= & {} \lambda _1 x^{T}\left( t \right) Rx\left( t \right) \end{aligned}$$
(30)
$$\begin{aligned} \lambda _1 x^{T}\left( t \right) Rx\left( t \right)\le & {} V\left( t \right) <e^{\gamma t}V\left( 0 \right) \nonumber \\\le & {} e^{\gamma T}\left( {c_1 \lambda _2 +c_1 d_1 \lambda _3 +c_1 d\lambda _4 +c_1 d\lambda _5 +\frac{1}{2}c_1 d^{2}\lambda _2 } \right) \end{aligned}$$
(31)

Condition (10) implies that for\(\forall t\in \left( 0 \right. ,\left. T \right] \),\(x^{T}\left( t \right) Rx\left( t \right) <c_2 \). This completes the proof. \(\square \)

Remark 4

In some existing literature about additive delays, researchers divided the whole delay into many subintervals ignoring the fact that some of them may not belong to the delay interval. For example, if \(d\left( t \right) <d_1 \), the subinterval \(\left[ 0, d_2 \left( t \right) +d_1 \right] \) will not belong to the delay interval, which means the results involved such subintervals containing the wrong information and could not reflect the characteristics of this system.

Remark 5

As we know, delay interval will be divided into a lot of subintervals based on delay-partitioning, while these split points may not describe the characteristics of systems in time axis. Due to the special nature of system (1), we choose proper split points, which represent the features of system as mentioned in Remark 1, to avoid making the LKLF reduce into an incomplete delay-partitioning. For instance, \(d_2 \left( t \right) \) does not appear in time axis (as Fig. 3), so we do not choose it as a split point.

Fig. 3
figure 3

Time-delay interval of system (1)

Full size image

Remark 6

Unlike other studies about finite-time stability of time-delay systems, the positive of the LKLF has been taken into consideration in this paper. It will diminish the lost information when estimating the bound of LKLF in (30) and slack the requirement of FTS so that the conservatism can be reduced in some degree.

To show the advantage of method we proposed over existing ones since little attention has been focused on the FTS of system (1), a corollary based on a simple LKLF and Wirtinger inequality is provided here.

Corollary 1

The system (1) is finite-time stable with respect to \(\left( {{\begin{array}{cccccc} {c_1 }&{} {c_2 }&{} T&{} {d_1 }&{} {d_2 }&{} R \\ \end{array} }} \right) \) if there exist positive matrices P,\(Q_1 \) ,\(Q_2 \) ,\(Q_3 \) where \(Q_1>Q_2 >Q_3 \) and scalars \(\theta _1 \) , \(\theta _2 \) ,\(\theta _3 \) ,\(\theta _4 \) , \(\theta _5 \) ,\(\gamma \) satisfying the following conditions.

$$\begin{aligned}&\Pi =\left( {\Pi _{\textit{ij}} } \right) _{6\times 6} <0 \end{aligned}$$
(32)
$$\begin{aligned}&c_1 \theta _2 +c_1 d_1 \theta _3 +c_1 \text {d}\theta _4 +c_1 \text {d}\theta _5 +\frac{1}{2}c_1 d^{2}\theta _2 \le \theta _1 e^{-\gamma T}c_2 \end{aligned}$$
(33)

where

$$\begin{aligned} \Pi _{11}= & {} A^{T}P+PA+Q_1 -4P, \Pi _{13} =PA_d , \Pi _{14} =-2P, \Pi _{15} =6P, \\ \Pi _{16}= & {} dA^{T}P,\\ \Pi _{22}= & {} -\left( {1-\mu _1 } \right) \left( {Q_1 -Q_2 } \right) , \Pi _{33} =-\left( {1-\mu } \right) \left( {Q_2 -Q_3 } \right) , \quad \Pi _{36} =dA_d ^{T}P, \\ \Pi _{44}= & {} -4P-Q_3 ,\\ \Pi _{45}= & {} 6P, \Pi _{55} =-12P, \quad \Pi _{66} =-P, \\ \Pi _{12}= & {} \Pi _{23} =\Pi _{24} =\Pi _{25} =\Pi _{26} =\Pi _{34} =\Pi _{35} =\Pi _{46} =\Pi _{56} =0. \end{aligned}$$

Proof

We choose the same LKLF as in Theorem 1 and define that every Lyapunov matrix is positive definite. Then, similar as the Theorem 1, we can derive the Corollary 1 easily. \(\square \)

3.2 Finite-Time Stabilization

In this subsection, a state feedback controller is designed, which guarantees the following system finite-time stable.

$$\begin{aligned} \dot{x}\left( t \right)= & {} Ax\left( t \right) +A_d x\left( {t-d_1 \left( t \right) -d_2 \left( t \right) } \right) +Bu\left( t \right) \nonumber \\ u\left( t \right)= & {} Kx\left( t \right) \end{aligned}$$
(34)

Corollary 2

The closed-loop system described in Eq. (34) is finite-time stable with respect to \(\left( {{\begin{array}{cccccc} {c_1 }&{} {c_2 }&{} T&{} {d_1 }&{} {d_2 }&{} R \\ \end{array} }} \right) \) if there exist a positive matrix M, symmetric matrices \(N_1 \), \(N_2 \), \(N_3 \), \(H_1 \), \(H_2 \), \(H_3 \), \(H_4 \),\(H_5 \),where \(N_1>N_2 >N_3 \) and a positive scalar \(\gamma \), satisfying the following conditions.

$$\begin{aligned}&\left( {{\begin{array}{cc} M&{} {-M} \\ {*}&{} {N_i +M} \\ \end{array} }} \right) >0\quad \left( {i=1,2,3} \right) \end{aligned}$$
(35)
$$\begin{aligned}&\tilde{\Xi }=\left( {\tilde{\Xi }_{ij} } \right) _{6\times 6} <0 \end{aligned}$$
(36)
$$\begin{aligned}&c_1 H_2 +c_1 d_1 H_3 +c_1 dH_4 +c_1 dH_5 +\frac{1}{2}c_1 d^{2}H_2 \le H_1 e^{-\gamma T}c_2 \end{aligned}$$
(37)

where

$$\begin{aligned} \tilde{\Xi }_{11}= & {} MA^{T}+W^{T}B^{T}+AM+BW+N_1 -\left( {4+\gamma d+\gamma } \right) M, \tilde{\Xi }_{13} =A_d M, \\ \tilde{\Xi }_{14}= & {} -2M, \\ \tilde{\Xi }_{15}= & {} \left( {6+\gamma d} \right) M, \quad \tilde{\Xi }_{16} =d\left( {MA^{T}+W^{T}B^{T}} \right) , \quad \tilde{\Xi }_{22} =-\left( {1-\mu _1 } \right) \left( {N_1 -N_2 } \right) ,\\ \tilde{\Xi }_{33}= & {} -\left( {1-\mu } \right) \left( {N_2 -N_3 } \right) , \quad \tilde{\Xi }_{36} =dMA_d ^{T}, \tilde{\Xi }_{44} =-4M-N_3 , \quad \tilde{\Xi }_{45} =6M,\\ \tilde{\Xi }_{55}= & {} \left( {-12-\gamma d} \right) M-\gamma dN_3 , \tilde{\Xi }_{66} =-M,\\ \tilde{\Xi }_{12}= & {} \tilde{\Xi }_{23} =\tilde{\Xi }_{24} =\tilde{\Xi }_{25} =\tilde{\Xi }_{34} =\tilde{\Xi }_{35} =\tilde{\Xi }_{26} =\tilde{\Xi }_{46} =\tilde{\Xi }_{56} =0,\\ \lambda _1= & {} \lambda _{\min } \left( {\tilde{P}} \right) , \lambda _2 =\lambda _{\max } \left( {\tilde{P}} \right) , \lambda _3 =\lambda _{\max } \left( {\tilde{Q}_1 } \right) , \lambda _4 =\lambda _{\max } \left( {\tilde{Q}_2 } \right) , \\ \lambda _5= & {} \lambda _{\max } \left( {\tilde{Q}_3 } \right) , \tilde{P}=R^{{-1}/2}PR^{{-1}/2},\\ \tilde{Q}_i= & {} R^{{-1}/2}\tilde{Q}_i R^{{-1}/2}, i=1,2,3, 0<H_1<M<H_2 , N_1<H_3 ,\\ N_2<&H_4 , N_3 <H_5 , N_1>N_2 >N_3. \end{aligned}$$

Further, if the LMIs in Eqs. (35)–(37) have feasible solutions, the control gain matrix K can be calculated by

$$\begin{aligned} K=WM^{-1} \end{aligned}$$
(38)

Proof

The closed-loop system (34) can be rewritten as

$$\begin{aligned} \dot{x}\left( t \right) =A_K x\left( t \right) +A_d x\left( {t-d_1 \left( t \right) -d_2 \left( t \right) } \right) \end{aligned}$$
(39)

where \(A_K =A+BK\)

Then, replace A by \(A_K \) in Theorem 1, we obtain

$$\begin{aligned}&\left( {{\begin{array}{cc} P&{} {-P} \\ {*}&{} {Q_i +P} \\ \end{array} }} \right) >0\quad \left( {i=1,2,3} \right) \end{aligned}$$
(40)
$$\begin{aligned}&\Xi =\left( {\Xi _{ij} } \right) _{6\times 6} <0 \end{aligned}$$
(41)
$$\begin{aligned}&c_1 \theta _2 +c_1 d_1 \theta _3 +c_1 \text {d}\theta _4 +c_1 \text {d}\theta _5 +\frac{1}{2}c_1 d^{2}\theta _2 \le \theta _1 e^{-\gamma T}c_2 \end{aligned}$$
(42)

where

$$\begin{aligned} \Xi _{11}= & {} A_K ^{T}P+PA_K +Q_1 -\left( {4+\gamma d+\gamma } \right) P, \Xi _{13} =PA_d , \Xi _{14} =-2P, \\ \Xi _{15}= & {} 6P+\gamma dP,\\ \Xi _{16}= & {} dA_K ^{T}P, \Xi _{22} =-\left( {1-\mu _1 } \right) \left( {Q_1 -Q_2 } \right) , \Xi _{33} =-\left( {1-\mu } \right) \left( {Q_2 -Q_3 } \right) , \\ \Xi _{36}= & {} dA_d ^{T}P,\\ \Xi _{44}= & {} -4P-Q_3 , \Xi _{45} =6P, \Xi _{55} =-12P-\gamma dQ_3 -\gamma dP, \Xi _{66} =-P,\\ \Xi _{12}= & {} \Xi _{23} =\Xi _{24} =\Xi _{25} =\Xi _{34} =\Xi _{35} =\Xi _{26} =\Xi _{46} =\Xi _{56} =0. \end{aligned}$$

That is to say, if (40)–(42) are satisfied, closed-loop system (34) is finite-time stable.

It should be noted that K coupled with P in the inequality (41) which makes it non-LMI. To get rid of these nonlinearities, inequality in Eq. (41) multiplies by the following diagonal matrix from both left and right sides

$$\begin{aligned} diag\left\{ {{\begin{array}{cccccc} {P^{-1}}&{} {P^{-1}}&{} {P^{-1}}&{} {P^{-1}}&{} {P^{-1}}&{} {P^{-1}} \\ \end{array} }} \right\} \end{aligned}$$

Similarly, the inequalities in Eq. (40) multiplies by the following diagonal matrix from both left and right sides

$$\begin{aligned} diag\left\{ {{\begin{array}{cc} {P^{-1}}&{} {P^{-1}} \\ \end{array} }} \right\} \end{aligned}$$

And the inequality in Eq. (42) multiplies by \(P^{-1}\) from both left and right sides.

By defining

$$\begin{aligned} M= & {} P^{-1}, N_1 =P^{-1}Q_1 P^{-1}, N_2 =P^{-1}Q_2 P^{-1}, N_3 =P^{-1}Q_3 P^{-1}, W=KP^{-1},\\ H_1= & {} P^{-1}\left( {\theta _1 I} \right) P^{-1}, H_2 =P^{-1}\left( {\theta _2 I} \right) P^{-1}, H_3 =P^{-1}\left( {\theta _3 I} \right) P^{-1},\\ H_4= & {} P^{-1}\left( {\theta _4 I} \right) P^{-1},\\ H_5= & {} P^{-1}\left( {\theta _5 I} \right) P^{-1}, K=WM^{-1}. \end{aligned}$$

Then, we have inequalities in Eqs. (40)– (42) are equivalent to Eqs. (35)– (37). Based on Theorem 1, inequalities in Eqs. (8)–(10) are equivalent to Eqs. (35)–(37). In other word, inequalities in Eqs. (35)–(37) can guarantee the FTS of system (34).

In consequence, system in Eq. (34) with the state feedback control gain matrix K in Eq. (38) is finite-time stable with respect to\(\left( {{\begin{array}{cccccc} {c_1 }&{} {c_2 }&{} T&{} {d_1 }&{} {d_2 }&{} R \\ \end{array} }} \right) \). This completes the proof. \(\square \)

Remark 7

Finite-time controller has been applied to a variety of practice systems, such as servomechanism system and terminal guidance system [17, 46]. To show the advantage compared to the asymptotic stability (LAS) results, a set of sufficient conditions based on Lyapunov theory is established in the following.

Corollary 3

The closed-loop system described in Eq. (34) is asymptotic stable, if there exist a positive matrix M, and symmetric matrices \(N_1 \), \(N_2 \), \(N_3 \), where \(N_1>N_2 >N_3 \), satisfying the following conditions.

$$\begin{aligned} \left( {{\begin{array}{cc} M&{} {-M} \\ {*}&{}\quad {N_i +M} \\ \end{array} }} \right)> & {} 0\quad \left( {i=1,2,3} \right) \end{aligned}$$
(43)
$$\begin{aligned} \Gamma= & {} \left( {\Gamma _{\textit{ij}} } \right) _{6\times 6} <0 \end{aligned}$$
(44)

where

$$\begin{aligned} \Gamma _{11}= & {} MA^{T}+W^{T}B^{T}+AM+BW+N_1 -\left( {4+\gamma d+\gamma } \right) M,\\ \Gamma _{13}= & {} A_d M, \Gamma _{14} =-2M,\\ \Gamma _{15}= & {} \left( {6+\gamma d} \right) M, \Gamma _{16} =d\left( {MA^{T}+W^{T}B^{T}} \right) , \quad \Gamma _{22} =-\left( {1-\mu _1 } \right) \left( {N_1 -N_2 } \right) ,\\ \Gamma _{33}= & {} -\left( {1-\mu } \right) \left( {N_2 -N_3 } \right) , \quad \Gamma _{36} =dMA_d ^{T}, \Gamma _{45} =6M, \\ \Gamma _{44}= & {} -4M-N_3 , \Gamma _{55} =\left( {-12-\gamma d} \right) M-\gamma dN_3 , \Gamma _{66} =-M,\\ \Gamma _{12}= & {} \Gamma _{23} =\Gamma _{24} =\Gamma _{25} =\Gamma _{34} =\Gamma _{35} =\Gamma _{26} =\Gamma _{46} =\Gamma _{56} =0. \end{aligned}$$

Proof

We assume \(\gamma =0\) in the Theorem 1 and define the \(\Omega <0\) in Eq. (19). Then, we will obtain the asymptotic stability and asymptotic stabilization conditions easily according to the setups in Theorem1 and Corollary 2. This completes the proof. \(\square \)

Remark 8

Although the proof of Corollary 3 is same like Theorem 1 and Corollary 2, it should be emphasized that asymptotic stability and finite-time stability are independent concepts; indeed, a system can be finite-time stable but not asymptotic stable, and vice versa.

4 Numerical Examples

In this section, we present the following examples to demonstrate the effectiveness of the obtained results carried out in this paper.

Example 1

Consider system (34) with following parameters.

$$\begin{aligned} A= & {} \left( {{\begin{array}{ccccc} {1.2}&{} \quad {-0.5}&{} \quad {1.3}&{} \quad {-0.4}&{} \quad {0.2} \\ {1.3}&{} \quad {-0.4}&{} \quad {1.1}&{} \quad {0.2}&{} \quad 0 \\ {0.2}&{} \quad {0.6}&{} \quad {0.2}&{} \quad {0.1}&{} \quad {0.3} \\ {1.3}&{} \quad {0.1}&{} \quad {1.2}&{} \quad {0.5}&{} \quad {0.1} \\ 0&{} \quad {0.1}&{} \quad {0.3}&{} \quad {0.1}&{} \quad 0 \\ \end{array} }} \right) \\ A_d= & {} \left( {{\begin{array}{ccccc} 0&{} {-0.2}&{}\quad {0.1}&{} \quad 0&{} \quad 0 \\ 0&{} \quad {-0.1}&{} \quad {0.2}&{} \quad {0.1}&{} \quad {-2} \\ 0&{} \quad {0.1}&{} \quad {-0.2}&{} \quad 0&{} \quad {0.1} \\ 0&{} \quad {0.1}&{} \quad {-0.2}&{} \quad {0.1}&{} \quad 0 \\ {-0.5}&{} \quad 0&{} \quad {0.2}&{} \quad {-0.3}&{} \quad 0 \\ \end{array} }} \right) \\ B= & {} \left( {{\begin{array}{ccccc} 2&{} \quad {-0.1}&{} \quad 0&{} \quad {0.1}&{} \quad {-0.1} \\ {0.6}&{} \quad {-0.5}&{} \quad {-0.1}&{} \quad {-0.2}&{} \quad {0.1} \\ 1&{} \quad {-0.3}&{} \quad {-1}&{} \quad {0.2}&{} \quad {-0.5} \\ {0.1}&{} \quad {-0.1}&{} \quad {0.4}&{} \quad {-0.3}&{} \quad {0.2} \\ {0.1}&{} \quad {0.2}&{} \quad {-0.8}&{} \quad {0.1}&{} \quad {-0.4} \\ \end{array} }} \right) \\ d_1= & {} 0.5, d_2 =0.5, \mu _1 =0.01, \mu _2 =0.02, R=I, c_1 =1, c_2 =10, T=1.5 \end{aligned}$$

Based on Corollary 2, the corresponding controller gain matrix K can be obtained as follows.

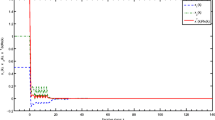
$$\begin{aligned} K=\left( {{\begin{array}{ccccc} {-3.4002}&{} \quad {1.9152}&{} \quad {0.1889}&{} \quad {-2.3719}&{} \quad {-10.7353} \\ {1.5287}&{} \quad {8.7852}&{} \quad {8.8819}&{} \quad {-12.4369}&{} \quad {-32.5924} \\ {-1.7758}&{} \quad {6.7994}&{} \quad {-23.1155}&{} \quad {11.0637}&{} \quad {72.9253} \\ {0.6136}&{} \quad {-11.7185}&{} \quad {15.0751}&{} \quad {19.6724}&{} \quad {-28.5376} \\ {-1.5851}&{} \quad {-19.8650}&{} \quad {57.1703}&{} \quad {-13.5623}&{} \quad {-162.3567} \\ \end{array} }} \right) \end{aligned}$$

Figures 4 and 5 show the state responses \(x\left( t \right) \) of system (34) and evolution of \(x^{T}\left( t \right) Rx\left( t \right) \) for an initial value \(\left( {{\begin{array}{ccccc} {0.3}&{} \quad {0.4}&{} \quad {0.5}&{} \quad {0.5}&{} \quad {0.5} \\ \end{array} }} \right) ^{T}\) It can be seen that, the state values are within a certain bound and the values of \(x^{T}\left( t \right) Rx\left( t \right) \) are less than the bound \(c_2 =10\), which concludes that system (34) is FTS with respect to \(\left( {{\begin{array}{cccccc} 1&{} \quad {10}&{} \quad {1.5}&{} \quad {0.5}&{} \quad {0.5}&{} \quad I \\ \end{array} }} \right) \).

In this example, the main purpose is to show that results considering the positive definiteness of LKLF as a whole can reduce the conservatism. Based on Remark 2, we know that the minimum allowed bound \(c_2 \) can quantitatively describe the conservatism of different methods. Table 1 shows that our results are less conservative than those set every Lyapunov matrix positive definite.

Fig. 4
figure 4

State response of the closed-loop system

Full size image
Fig. 5
figure 5

Time history of \(x^{T}\left( t \right) Rx\left( t \right) \)

Full size image
Table 1 Minimum value of \(c_2 \) for different \(c_1 \)
Full size table

Example 2

Consider the system (34) with parameters given in the succeeding text.

$$\begin{aligned} A= & {} \left( {{\begin{array}{cc} {-0.002}&{} \quad 0 \\ 0&{} {-0.009} \\ \end{array} }} \right) , A_d =\left( {{\begin{array}{cc} {-0.01}&{} \quad 0 \\ {-0.1}&{} \quad {-0.01} \\ \end{array} }} \right) , B=\left( {{\begin{array}{c} {0.2} \\ {-0.5} \\ \end{array} }} \right) \\ d_1= & {} 1, d_2 =2, \mu _1 =0.01, \mu _2 =0.02 \end{aligned}$$

Considering the state feedback controller \(u\left( t \right) =Kx\left( t \right) \) which guarantees system (34) finite-time stabilization, we choose \(c_1 =1\) ,\(c_2 =10\) ,\(T=10\) ,\(\gamma =0.01\). By using Corollary 2, the feasible solutions can be found and the controller gain (FTS) is given as follows

$$\begin{aligned} K_1 =\left( {{\begin{array}{cc} {-6.3388}&{} \quad {-0.1576} \\ \end{array} }} \right) \end{aligned}$$

As a comparison, we consider the state feedback controller to make sure system (34) asymptotic stabilization and the controller gain (LAS) based on Corollary 3 is given as follows

$$\begin{aligned} K_2 =\left( {{\begin{array}{cc} {-38.5336}&{} \quad {-1.8107} \\ \end{array} }} \right) \end{aligned}$$
Fig. 6
figure 6

State response of the closed-loop system

Full size image
Fig. 7
figure 7

Time history of \(x^{T}\left( t \right) Rx\left( t \right) \)

Full size image

Figures 6 and 7 show the state responses \(x\left( t \right) \) of system (34) and evolution of \(x^{T}\left( t \right) Rx\left( t \right) \) for an initial value \(\left( {{\begin{array}{cc} {0.6}&{} {0.8} \\ \end{array} }} \right) ^{T}\) generated by \(K_1 \). It can be seen that the state responses are within a certain bound and the values of \(x^{T}\left( t \right) Rx\left( t \right) \) are less than the bound \(c_2 =10\), which concludes that system (34) is FTS with respect to \(\left( {{\begin{array}{cccccc} 1&{} {10}&{} {10}&{} 1&{} 2&{} I \\ \end{array} }} \right) \).

Figure 8 shows that the values of \(x^{T}\left( t \right) Rx\left( t \right) \) generated by \(K_1 \) are lower evidently than that caused by \(K_2 \), while the values of \(K_1 \) are less than that of \(K_2 \) correspondingly. It means that our results based on finite-time stabilization can obtain a better dynamic performance at the cost of a lower gain.

Fig. 8
figure 8

State value comparison of \(K_1 \) and \(K_2 \)

Full size image

5 Conclusion

In this paper, the problems of finite-time stability and finite-time stabilization have been addressed for continuous systems with additive time-varying delays. First, a proper LKLF based on splitting the whole delay interval into new subintervals is presented, and by using Wirtinger inequality, a set of sufficient conditions of finite-time stability are derived in terms of LMIs. To obtain less conservative results, we take the LKLF as a whole to examine its positive definite, rather than restricting each term of it to positive definite as usual. Then, based on the stability results, the state feedback stabilization is investigated, and delay-dependent conditions are established for the state feedback controller such that the closed-loop system is FTS. Finally, examples are given to show the less conservatism of the stability results and the effectiveness of the proposed approach. As future works, it is interesting to consider the approach developed in this paper could be extended to practical engineering application with a variety of constraints [36, 38, 39].