Efficient Design of Discrete Fractional-Order Differentiators Using Nelder–Mead Simplex Algorithm

Abstract

Applications of fractional-order operators are growing rapidly in various branches of science and engineering as fractional-order calculus realistically represents the complex real-world phenomena in contrast to the integer-order calculus. This paper presents a novel method to design fractional-order differentiator (FOD) operators through optimization using Nelder–Mead simplex algorithm (NMSA). For direct discretization, Al-Alaoui operator has been used. The numerator and the denominator terms of the resulting transfer function are further expanded using binomial expansion to a required order. The coefficients of z-terms in the binomial expansions are used as the starting solutions for the NMSA, and optimization is performed for a minimum magnitude root-mean-square error between the ideal and the proposed operator magnitude responses. To demonstrate the performance of the proposed technique, six simulation examples for fractional orders of half, one-third, and one-fourth, each approximated to third and fifth orders, have been presented. Significantly improved magnitude responses have been obtained as compared to the published literature, thereby making the proposed method a promising candidate for the design of discrete FOD operators.

1 Introduction

The concept of fractional calculus is being used ever since its mention in the letters exchanged between L’Hospital and Leibniz in the year 1695. Fractional calculus, in a sense, is generalization of the integer-order calculus. As fractional calculus describes the characteristics of most of the natural systems more realistically, a renewed interest among the researchers has grown in the last three decades and the fractional calculus has found applications in numerous science and engineering disciplines [8]. Applications of fractional calculus have been explored in large number of domains such as control, signal processing, chaos theory, mechanics, physics, chemistry, electrical circuit with fractance, generalized voltage divider, viscoelasticity, fractional-order multipoles in electromagnetism, electrochemistry [4, 9, 10, 13, 17, 23].

Signal processing and control engineering are the two major thrust areas where fractional-order system applications have shown major developments. For example, fractional-order signal processing has been used at times to estimate water level elevations of north part of the Great Salt Lake, since the data distribution was heavy-tailed, i.e., needed large memory [20, 21]. Also, in image processing, fractional-order differentiator helped to improve the criterion of thin detection and immunity to noise by extending CRONE detector to fractional order. It may be noted that earlier design used integer-order operator [16]. Further, a comparison for modeling of speech signal using linear predictive coding approach based on integer-order and fractional-order models has also been reported, and it was demonstrated that fractional-order approach models speech signal more accurately [1].

In control engineering, the first choice of a control engineer is always the conventional proportional–integral–derivative (PID) controller. Making the integration and derivative terms fractional offers two more degrees of freedom to the control design engineer. Such controllers are termed as fractional PID controllers. The fractional PID controllers can be efficiently designed and tuned for a desired performance even for a complex system as compared to their conventional integer-order counterparts. Fractional-order PID controllers applied to path tracking problems in autonomous vehicles have demonstrated better results [22]. In another recent research, a fractional-order fuzzy PID controller for a two-link rigid robotic manipulator has been investigated for path tracking problem. The performance of the proposed fractional-order fuzzy PID controller was found to be superior to the fuzzy PID controller for path tracking, disturbance rejection, and noise suppression applications [19].

Despite the fact that fractional-order calculus finds its applications in numerous domains, even today, its implementation poses challenges. In modeling and analysis of systems using fractional calculus, fractional-order derivative (FOD) operator plays a key role and hence an efficient implementation of FOD operator is essential. Further, as this operator is not a standard of-the-shelf operator supplied in the various commercially available modeling and analysis tools, its effect is implemented using an equivalent standard integer-order transfer function.

One of the well-known, time-domain definitions of FOD operator is a Grünwald–Letnikov’s as defined below [6, 12].

$$\begin{aligned} \hbox {Gr}\ddot{\hbox {u}}\hbox {nwald}{-}\hbox {Letnikov's:}\,D^{n}f(t)= & {} \frac{d^{n}f(t)}{dt^{n}}\nonumber \\= & {} \lim \nolimits _{h\rightarrow 0} \frac{1}{h^{n}}\sum \nolimits _{k=0}^n (-1)^{n}\left( {{\begin{array}{l} n \\ k \\ \end{array} }} \right) f({t-kh});\quad n \epsilon R^{+}\nonumber \\ \end{aligned}$$

(1)

where

$$\begin{aligned} \left( {{\begin{array}{l} n \\ k \\ \end{array} }} \right) =\frac{n\left( {n-1} \right) \left( {n-2} \right) \cdots \left( {n-k+1} \right) }{k!} \end{aligned}$$

FOD operators can also be used to describe the fractional-order transfer function in frequency domain as in [6].

$$\begin{aligned} G(s)=\frac{Y(s)}{X(s)}=\frac{b_m s^{\beta _m }+b_{m-1} s^{\beta _{m-1} }+b_{m-2} s^{\beta _{m-2} }\cdots +b_0 s^{\beta _0 }}{a_m s^{\alpha _m }+a_{m-1} s^{\alpha _{m-1} }+a_{m-2} s^{\alpha _{m-2} }\cdots +a_0 s^{\alpha _0 }};\quad \beta , \alpha \epsilon R \end{aligned}$$

(2)

Equivalently, the transfer function in z-domain can be given by

$$\begin{aligned} G( z )= & {} \frac{b_m ( {\psi ( {z^{-1}} )} )^{\beta _m }+b_{m-1} ( {\psi ( {z^{-1}} )} )^{\beta _{m-1} }+b_{m-2} ( {\psi ( {z^{-1}} )} )^{\beta _{m-2} }\cdots +b_0 ( {\psi ( {z^{-1}} )} )^{\beta _0 }}{a_m ( {\psi ( {z^{-1}} )} )^{\alpha _m }+a_{m-1} ( {\psi ( {z^{-1}} )} )^{\alpha _{m-1} }+a_{m-2} ( {\psi ( {z^{-1}} )} )^{\alpha _{m-2} }\cdots +a_0 ( {\psi ( {z^{-1}} )} )^{\alpha _0 }};\nonumber \\&\beta ,\alpha \epsilon R \end{aligned}$$

(3)

where $\psi$ is a mapping function from s-domain to z-domain.

In order to represent an equivalent fractional-order operator using the integral powers, various power series such as Taylor’s, Maclaurin, continued fraction expansion (CFE), binomial are normally used. Essentially, these implementations, in an ideal sense, require infinite memory. Therefore, in order to implement FOD operators, theoretically, powers of z-terms range from 0 to $\infty$. Since it is impractical to implement infinite number of terms on any computing hardware, as it suffers from space and time complexity, truncation of the series becomes an inherent important consideration. Usually, the higher the number of terms or the order considered, the better the resulting transfer function approximates an ideal analog transfer function. At the same time, the higher the order of transfer function, the higher is the implementation complexity, thus requiring more resources. Therefore, researchers always search for an alternative efficient way to approximate the ideal FOD operator with an equivalent lower-order discrete transfer functions having higher accuracy, i.e., frequency response be as close as possible to the ideal operator and the order of the transfer function be as low as possible.

In designing and implementation of discrete FODs, the key step is the discretization of the fractional-order differentiator $({s^{\alpha }})$. Discretization refers to a mapping from s-domain to z-domain. It can be of two types: direct discretization and indirect discretization [28]. Indirect discretization methods involve two steps, i.e., frequency domain fitting in continuous time domain followed by discretization of the so obtained continuous time transfer function using a mapping function, whereas direct discretization methods include the application of power series expansion of Euler operator, CFE of the Tustin operator, and numerical integration-based methods. The major drawback of using these expansion techniques is that they approximate transfer function in a limited frequency range only. In [3, 5, 11, 24], $s^{\alpha }$ has been discretized using direct discretization schemes, whereas in [15], indirect discretization schemes have been implemented. In [25], modification of the Schneider and Al-Alaoui–Schneider–Kaneshige–Groutage rule has been presented for the improvement of the fractional-order differentiator in the low frequency range. In the design of discrete FODs, a recent trend has been to explore the applications of optimization techniques such as particle swarm optimization (PSO) and genetic algorithm (GA) [7]. Das et al. have expanded various discretization operators using CFE up to the desired order followed by optimization of resulting coefficients so as to minimize a predefined error function.

In this work, the proposed technique makes use of direct discretization method followed by optimization of the resulting transfer function. For discretization of the fractional-order operator, Al-Alaoui operator has been used. The numerator and the denominator components of the resulting discrete time transfer function have been further expanded using binomial expansion for the fractional power. The coefficients of transfer function thus obtained are further re-tuned using Nelder–Mead simplex algorithm (NMSA) optimization method so as to minimize root-mean-square (RMS) error in magnitude response. It may be noted that the NMSA requires a starting solution. In the present work, the expanded binomial expansion coefficients of the z-terms, for numerator as well as the denominator, are used as the starting solutions. The obtained operators, optimized using NMSA, have offered better approximations of fractional-order differentiators in all the investigated cases. Significantly enhanced performance has been demonstrated as compared to the published literature, thereby making the proposed method a promising candidate for design of discrete FODs.

This paper is organized as follows. Following a brief literature survey in Sect. 1, various discretization schemes including Al-Alaoui operator are summarized in Sect. 2. Generic discrete transfer functions for fractional-order operators of various powers have also been derived using Al-Alaoui operator and have been presented in this section. The used optimization technique, NMSA, is then described in Sect. 3 with the help of a flowchart and a supporting numerical example. Using Al-Alaoui operator for discretization, transfer functions of various orders for different powers are then obtained for binomially expanded limited terms FODs. NMSA optimization is further utilized to tune the coefficients of the resulting differentiators for minimum magnitude response RMS error. Designs of optimized differentiators are presented in Sect. 4 along with frequency responses and magnitude and phase error v/s frequency plots. Variations of fitness function v/s iteration plots are also presented to show the convergence of NMSA optimization process. Section 5 presents performance comparisons of designed differentiators with existing differentiators of same power and approximated to same order as reported in the recent literature. Frequency responses and the magnitude RMS errors have been compared, and the results are presented in this section. Further, a comparison of the optimization performance of NMSA with GA is also carried out for a half differentiator of third order. Comparison results in terms of timing aspect and achievable fitness function values along with statistical t test analysis of 50 independent runs have been presented in Sect. 6. The paper is finally concluded in Sect. 7.

2 Discretization Using Al-Alaoui Operator

Frequency response of an ideal fractional-order differentiator $({s^{\alpha }})$, of order $\alpha$, is given by

$$\begin{aligned} H({j\omega })=( {j\omega })^{\alpha } \end{aligned}$$

(4)

where $j=\sqrt{-1}$, $\omega$ is the frequency in radians/s, and $\alpha$ is the fractional power of the differentiator under consideration. Frequency response can also be written as,

$$\begin{aligned} H({j\omega })=e^{j\alpha \frac{\pi }{2}}\omega ^{\alpha } \end{aligned}$$

Magnitude and phase responses, from the above function, can be given as,

$$\begin{aligned}&\left| {H\left( {j\omega } \right) } \right| =\omega ^{\alpha } \end{aligned}$$

(5)

$$\begin{aligned}&\varPhi =\alpha 90^{\circ } \end{aligned}$$

(6)

Figure 1 illustrates frequency response up to 500 Hz of an ideal half-order $(\alpha =0.5)$ differentiator. A constant phase of $45^{\circ }$ can be clearly observed for this differentiator.

Fig. 1

Frequency response of an ideal half-order differentiator

Mapping functions are the transformations used to convert a transfer function from s-domain to z-domain. There are many mapping functions available in the literature, and some important ones are given below:

$$\begin{aligned} \hbox {Euler:}\,\frac{1}{s}= & {} \frac{Tz}{z-1} \end{aligned}$$

(7)

$$\begin{aligned} \hbox {Tustin:}\,\frac{1}{s}= & {} \frac{T}{2}\frac{z+1}{z-1} \end{aligned}$$

(8)

$$\begin{aligned} \hbox {Schneider:}\,\frac{1}{s}= & {} \frac{T}{12}\frac{5z^{2}+8z-1}{z\left( {z-1} \right) } \end{aligned}$$

(9)

$$\begin{aligned} \hbox {Simpson:}\,\frac{1}{s}= & {} \frac{T}{3}\frac{z^{2}+4z+1}{z^{2}-1} \end{aligned}$$

(10)

$$\begin{aligned} \hbox {F012:}\,\frac{1}{s}= & {} \frac{2T}{5}\frac{z\left( {z+2} \right) }{5z^{2}-4z-1} \end{aligned}$$

(11)

$$\begin{aligned} \hbox {Rectangular:}\,\frac{1}{s}= & {} \frac{T}{z-1} \end{aligned}$$

(12)

Mapping function used in this work, developed by Al-Alaoui, is described by (13). According to this mapping function, fractional-order integrator is defined as follows.

$$\begin{aligned} H_{\text {Al-Alaoui}} \left( z \right) =\frac{3}{4}H_\mathrm{Rectangular} \left( z \right) +\frac{1}{4}H_\mathrm{Tustin} \left( z \right) \end{aligned}$$

(13)

Therefore, $H_{\text {Al-Alaoui}} \left( z \right) =\frac{1}{s}=\left( {\frac{7T}{8}\frac{1+\frac{1}{7}z^{-1}}{1-z^{-1}}} \right)$.

It gives a fractional-order differentiator as,

$$\begin{aligned} s^{\alpha }=\left( {\frac{8}{7T}\frac{1-z^{-1}}{1+\frac{1}{7}z^{-1}}} \right) ^{\alpha } \end{aligned}$$

(14)

On expanding using binomial series,

$$\begin{aligned} \left( {\frac{8}{7T}\frac{1-z^{-1}}{1+\frac{1}{7}z^{-1}}} \right) ^{\alpha }=\left( {\frac{8}{7T}} \right) ^{\alpha }\left( {\frac{\mathop \sum \nolimits _{k=0}^\infty \left( {{\begin{array}{l} \alpha \\ k \\ \end{array} }} \right) \left( {-z} \right) ^{-k}}{\mathop \sum \nolimits _{k=0}^\infty \left( {{\begin{array}{l} \alpha \\ k \\ \end{array} }} \right) \left( {\frac{z}{7}} \right) ^{-k}}} \right) ^{} \end{aligned}$$

(15)

where $\left( {{\begin{array}{l} \alpha \\ k \\ \end{array} }} \right) =\frac{\gamma \left( {\alpha +1} \right) }{\gamma \left( {k+1} \right) *\gamma \left( {\alpha -k+1} \right) }$, where the symbol $\gamma$ is the gamma function.

A half differentiator, expressed up to fifth order, can now be described as:

$$\begin{aligned}&s^{\frac{1}{2}}=\sqrt{\left( {\frac{8}{7T}} \right) }\\&\quad \frac{1+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 2 \right) *\gamma \left( {0.5} \right) }\left( {-z} \right) ^{-1}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 3 \right) *\gamma \left( {-0.5} \right) }\left( {-z} \right) ^{-2}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 4 \right) *\gamma \left( {-1.5} \right) }\left( {-z} \right) ^{-3}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 5 \right) *\gamma \left( {-2.5} \right) }\left( {-z} \right) ^{-4}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 6 \right) *\gamma \left( {-3.5} \right) }\left( {-z} \right) ^{-5}}{1+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 2 \right) *\gamma \left( {0.5} \right) }\left( {\frac{z}{7}} \right) ^{-1}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 3 \right) *\gamma \left( {-0.5} \right) }\left( {\frac{z}{7}} \right) ^{-2}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 4 \right) *\gamma \left( {-1.5} \right) }\left( {\frac{z}{7}} \right) ^{-3}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 5 \right) *\gamma \left( {-2.5} \right) }\left( {\frac{z}{7}} \right) ^{-4}+\frac{\gamma \left( {1.5} \right) }{\gamma \left( 6 \right) *\gamma \left( {-3.5} \right) }\left( {\frac{z}{7}} \right) ^{-5}}\\ \end{aligned}$$

$$\begin{aligned}&s^{\frac{1}{2}}=\sqrt{\left( {\frac{8}{7T}} \right) }\\&\quad \frac{1-\frac{0.8862}{1*\left( {1.7725} \right) }\left( z \right) ^{-1}+\frac{0.8862}{2*\left( {-3.5449} \right) }\left( z \right) ^{-2}-\frac{0.8862}{6*2.3633}\left( z \right) ^{-3}+\frac{0.8862}{24*\left( {0.9453} \right) }z^{-4}-\frac{0.8862}{120*0.2701}z^{-5}}{1+\frac{0.8862}{1*1.7725}\left. {\left( {\frac{z}{7}} \right. } \right) ^{-1}+\frac{0.8862}{2*\left( {-3.5449} \right) }\left( {\frac{z}{7}} \right) ^{-2}+\frac{0.8862}{6*2.3633}\left( {\frac{z}{7}} \right) ^{-3}+\frac{0.8862}{24*\left( {-0.9453} \right) }\left( {\frac{z}{7}} \right) ^{-4}+\frac{0.8862}{120*0.2701}\left( {\frac{z}{7}} \right) ^{-5}}\\&s^{\frac{1}{2}}=\sqrt{\left( {\frac{8}{7T}} \right) }\\&\quad \frac{1-0.5z^{-1}-0.1250z^{-2}-0.0625z^{-3}-0.0390625z^{-4}-0.02734375z^{-5}}{1+0.07142857z^{-1}-0.00255102z^{-2}+0.0001822z^{-3}-0.00001626926z^{-4}+0.000001626926z^{-5}} \end{aligned}$$

For $T=0.001, s^{\frac{1}{2}}$ can be expressed as

$$\begin{aligned}&s^{\frac{1}{2}}=33.80617\nonumber \\&\frac{1-0.5z^{-1}-0.1250z^{-2}-0.0625z^{-3}-0.0390625z^{-4}-0.02734375z^{-5}}{1+0.07142857z^{-1}-0.00255102z^{-2}+0.0001822z^{-3}-0.00001626926z^{-4}+0.000001626926z^{-5}}\nonumber \\ \end{aligned}$$

(16)

Similarly,

$$\begin{aligned}&s^{\frac{1}{3}}=10.45516\nonumber \\&\frac{1-0.333333z^{-1}-0.111111z^{-2}-0.0617284z^{-3}-0.04115226z^{-4}-0.03017833z^{-5}}{1+0.04761905z^{-1}-0.002267574z^{-2}+0.000179966z^{-3}-0.0000171396z^{-4}+0.00000179558z^{-5}} \end{aligned}$$

(17)

$$\begin{aligned}&s^{\frac{1}{4}}=5.814307\nonumber \\&\frac{1-0.25z^{-1}-0.09375z^{-2}-0.0546875z^{-3}-0.03759766z^{-4}-0.02819824z^{-5}}{1+0.03571429z^{-1}-0.001913265z^{-2}+0.000159438z^{-3}-0.0000156591z^{-4}+0.000001677768z^{-5}}\nonumber \\ \end{aligned}$$

(18)

Corresponding third-order designs can be obtained by truncating the above expressions up to $z^{-3}$. From (16) to (18), we can find the following coefficients (b and a) to design the resulting fractional operators.

$$\begin{aligned} s^{\alpha }\cong \frac{b_0 +b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}\cdots +b_n z^{-\hbox {m}}}{a_0 +a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}\cdots +a_n z^{-n}};m\le n \end{aligned}$$

(19)

The coefficients of z-terms are then fed to NMSA, as the initial solutions, to minimize the real-valued RMS error of the magnitude response of the system $H(j\omega )$ defined as:

$$\begin{aligned} \hbox {RMS}\, \hbox {Magnitude}\, \hbox {Error}=\sqrt{\frac{\sum \left| {\left| {\hbox {H}\left( \omega \right) } \right| _\mathrm{Proposed} -\left| {\hbox {H}\left( \omega \right) } \right| _\mathrm{Ideal} } \right| }{n}^{2}} \end{aligned}$$

(20)

where n is the number of sampled frequency points.

3 Optimization Using Nelder–Mead Simplex Algorithm

The NMSA is a popular direct search method for unconstrained minimization [14, 27]. It aims at minimizing a real-valued function f(x) for $x \epsilon R^{\mathrm{n}}$. It is a direct search method; i.e., it does not use derivative information unlike gradient methods of optimization. In cases where it is difficult to obtain a derivative of fitness functions, direct search methods are more preferred over gradient-based methods. It may also be noted that the NMSA is a local optimization method and global optimum search is not guaranteed. Local optimization methods locate a minima, i.e., minimum value, in a region nearby the proposed starting point, whereas global optimization techniques aim at locating the global minima, i.e., lowest possible value of the fitness function. As will be seen later, the popular global optimization method GA also tends to take more time than the aforementioned method. As mentioned earlier, in the NMSA, used in this work, an initial estimation of the solution is already calculated using discretization of Al-Alaoui operator followed by binomial expansion of the numerator and the denominator. The only task left is to search for the best possible coefficient values in the nearby region without any explicit boundaries. Therefore, NMSA has worked pretty well. This method is termed as “simplex” method, but it should not be confused with the well-known simplex method for linear programming.

At the beginning of every iteration, a new simplex is given, along with its (n+1) vertices such that

$$\begin{aligned} f\left( {x_1 }\right) \le f\left( {x_2}\right) \le \cdots \le f\left( {x_{n+1}}\right) \end{aligned}$$

where $x_1 ,x_2 ,x_3, \ldots x_{n+1}$ are the arrays of n points each, n is the number of variables for which the fitness function is to be optimized, $x_1$ is referred to as the best point, and $x_{n+1}$ is referred to as the worst point. Similarly, $f\left( {x_1 } \right)$ is referred to as the best fitness function value, whereas $f\left( {x_{n+1} } \right)$ as the worst fitness function value. The next iteration defines a new simplex and generates a new set of $(n+1)$ vertices by moving the worst vertex around a centroid which is an average value of the remaining vertices. The process continues in the same manner while minimizing the worst fitness function value. To provide a big picture, NMSA “shrinks” a polygon of $(n+1)$ vertex, where n is the number of variables to be optimized. The flowchart in Fig. 2 describes the algorithm completely. Various computations for the implementation can be described as:

$$\begin{aligned} \hbox {Reflection point:}\, x_\mathrm{r}= & {} \bar{x}+{\rho }\left( {\bar{x}-x_{n+1} } \right) \end{aligned}$$

(21)

$$\begin{aligned} \hbox {Expansion point:}\, x_\mathrm{e}= & {} \bar{x}+{\chi }\left( {x_\mathrm{r} -\bar{x}} \right) \end{aligned}$$

(22)

$$\begin{aligned} \hbox {Outside contraction:}\, x_\mathrm{c}= & {} \bar{x}+{\beta }\left( {x_\mathrm{r} -\bar{x}} \right) \end{aligned}$$

(23)

$$\begin{aligned} \hbox {Inside contraction:}\,x_\mathrm{cc}= & {} \bar{x}-{\beta }\left( {\bar{x} -x_{n+1} } \right) \end{aligned}$$

(24)

Coefficient of reflection: $\rho =1$; coefficient of expansion: $\chi =2$; coefficient of contraction: $\beta =0.5$; coefficient of shrinkage: $\sigma =0.5$; and the centroid: $\bar{x} =\frac{1}{n}\sum \nolimits _{i=1}^n x_i$ .

Fitness function to be minimized, in this particular problem, is defined as follows:

$$\begin{aligned} f\left( x \right) =\hbox {RMS}_\mathrm{Magnitude} \end{aligned}$$

To demonstrate the implementation of the algorithm, a numerical example is given below. Let us assume we need to find the minima of a function defined by $f({x,y})=x^{2}+y^{2}+2x+2y+2$. It may be noted that in this case the function itself becomes the fitness function. Let the starting initial vertex be (0, 1). Since it is a function in two variables, the simplex here would be a triangle. Therefore, $x= [0, 1]$ and $x_j =x_1 +\Delta _j$, where $j=2,3$ and $\Delta _j$ is determined using the following Table 1 [2]. Length of the sides of the simplex $a =3$, $N=2$. Therefore, $p=2.84, q=0.84$. The stepwise iterative computations are shown as follows:

Fig. 2

Nelder–Mead simplex algorithm

Table 1 Definitions of variables

S. no.	Iteration no. 1	Iteration no. 2	Iteration no. 3		Iteration no. 20
1	$x_1 =[0, 1]$	$x_1 =[0, 1]$	$x_1 =[-0.84, -1.84]$		$x_1 =[-0.9988, -1.0094]$
2	$x_2 =[2.84, 1.84]$	$x_2 =[2, -1]$	$x_2 =[0, 1]$	...	$x_2 =[-1.0105, -1.0018]$
3	$x_3 =[0.84, 3.84]$	$x_3 =[2.84, 1.84]$	$x_3 =[2, -1]$		$x_3 =[-0.9846, -0.9802]$
4	$f\left( {x_1 } \right) =5$	$f\left( {x_1 } \right) =5$	$f\left( {x_1 } \right) =0.7312$		$f\left( {x_1 } \right) =0.000088923$
5	$f\left( {x_2 } \right) =11.4512$	$f\left( {x_2 } \right) =9$	$f\left( {x_2 } \right) =5$	...	$f\left( {x_2 } \right) =0.00011445$
6	$f\left( {x_3 } \right) =15.4512$	$f\left( {x_3 } \right) =11.4512$	$f\left( {x_3 } \right) =9$		$f\left( {x_3 } \right) =0.0006317$
7	$\bar{x}=[1.42, 1.42]$	$\bar{x} =[1 0]$	$\bar{x} =[-0.42,-0.42]$		$\bar{x} =[-1.0047, -1.0056]$
8	$x_\mathrm{r} =[2, -1]$	$x_\mathrm{r} =[-0.84, -1.84]$	$x_\mathrm{r} =[-2.84, 0.16]$	...	$x_\mathrm{r} =[-1.0247 -1.0310]$
9	$f\left( {x_\mathrm{r} } \right) =9$	$f\left( {x_\mathrm{r} } \right) =0.7312$	$f\left( {x_\mathrm{r} } \right) =4.6712$		$f\left( {x_\mathrm{r} } \right) =0.0016$
10		$x_\mathrm{e} =[-2.68, -3.68]$			$x_\mathrm{cc} =[-0.9946, -0.9929]$
11		$f\left( {x_\mathrm{e} } \right) =10.0048$			$f\left( {x_\mathrm{cc} } \right) =0.000079301$

As can be seen, a decreasing error is observed for successive iterations. The process continues till a convergence is obtained, which would depend upon the tolerance set by the user. In the case under consideration, at 20th iteration, the vertices of the triangle are obtained as $x_1 =[-0.9988, -1.0094], x_2 =[-1.0105, -1.0018], x_3 =[-0.9846, -0.9802]$ and an error of $f\left( {x_\mathrm{cc} } \right) =0.000079301$ against the actual result of $[-1,-1]$.

The NMSA has both been acclaimed and criticized: acclaimed, mainly because it is one of the first derivative-free optimization techniques and is very simple to understand, robust, and reliable, and criticized mainly because it has been developed heuristically and no proofs of convergence have been derived.

4 Fractional-Order Differentiator Designs Using NMSA

To demonstrate the capability of the proposed optimization technique, NMSA, six case studies have been investigated and the obtained results are presented in this section. These investigations include a half differentiator of third order, a half differentiator of fifth order, a one-third differentiator of third order, a one-third differentiator of fifth order, a one-fourth differentiator of third order, and lastly, a one-fourth differentiator of fifth order. For each of the cases under consideration, the initial starting solution, as required by NMSA, is first obtained as demonstrated in Eqs. (16)–(18) for respective values of $\alpha$. The coefficients of the respective transfer functions for differentiators of various orders are then fine-tuned for minimum RMS magnitude error with the help of the NMSA. Tables 2 and 3 present the final optimized differentiator designs with their RMS magnitude errors for various fractional-order differentiators. The magnitude responses of various differentiators are computed for a sampling time $T=0.001$ s. It may be noted that the choice of T is purely arbitrary and it is applicable to other sampling rates as well by suitably scaling the designs. As shown in Tables 2 and 3, RMS magnitude errors of 1.193117 and 0.773236 have been achieved for half differentiators of third and fifth orders, respectively. Similarly, RMS magnitude errors of 0.441906 and 0.307687 have been achieved for one-third differentiators of third and fifth orders, respectively, and RMS magnitude errors of 0.243824 and 0.175219 have been achieved for one-fourth differentiators of third and fifth orders, respectively. For these optimizations, the numbers of iterations have been kept as 200, 450, 120, 300, 100, and 250, respectively, for third- and fifth-order half differentiators, third- and fifth-order one-third differentiators, and third- and fifth-order one-fourth differentiators. These numbers have been decided after investigating the pole–zero behavior of respective differentiators and ensuring a small pole radius (${<}0.15$, in all cases). It was also observed that higher number of iterations yielded better RMS magnitude error, but the design possessed larger pole radii, thereby lengthening the transient response. Due to this reason, the numbers of iterations were kept as mentioned above.

Table 2 Designed third-order fractional differentiators

Table 3 Designed fifth-order fractional differentiators

Figure 3 presents variations of fitness function with generations for all the considered differentiators. As seen from figure, all the obtained fitness curves have flattened; therefore, it can be concluded that the best possible designs have been achieved and there is not much scope for further improvement in the NMSA optimization process. Figure 4 compares the frequency response with the ideal one for half differentiator of third and fifth orders. Figure 5 presents the corresponding absolute error v/s frequency for both designs of half differentiators. Similarly, Figs. 6, 7, 8, and 9 present the same for one-third and one-fourth differentiators. All of the proposed designs can be seen to be tracking the ideal responses very closely in these figures.

Fig. 3

Fitness function v/s generations (NMSA)

Fig. 4

Frequency responses of half differentiators of third and fifth orders

Fig. 5

Absolute error v/s frequency plots of half differentiators of third and fifth orders

Fig. 6

Frequency responses of one-third differentiators of third and fifth orders

Fig. 7

Absolute error v/s frequency plots of one-third differentiators of third and fifth orders

Fig. 8

Frequency responses of one-fourth differentiators of third and fifth orders

Fig. 9

Absolute error v/s frequency plots of one-fourth differentiators of third and fifth orders

5 Comparison with the Existing Differentiators

Several fractional-order differentiators of various orders and fractional powers, designed by various other methods, have been reported in the literature. This section presents a comparative study with the respective class of differentiators. Table 4 presents designs of half differentiators of third order recently reported in the literature along with the proposed design. Corresponding RMS magnitude and phase errors are also listed in Table 5. It can be clearly observed that the RMS magnitude error, 1.193117, of proposed half differentiator is the lowest among the compared ones. Figure 10 plots the frequency magnitude responses along with the phase responses of these designs. Figure 11 depicts the corresponding RMS magnitude errors and the RMS phase errors. Similarly, Table 6 presents the designs and Table 7 presents the corresponding performances of the half differentiators of fifth order. Again, the RMS magnitude error, 0.773236, of proposed half differentiator is the lowest among the compared ones. Figure 12 plots the frequency magnitude responses along with the phase responses of these designs. Figure 13 plots the corresponding RMS magnitude errors and the RMS phase errors. For all the comparisons made in this paper, the references have been designated by the respective serial numbers as these have appeared in the references followed by the year. In case of multiple designs from a given reference, the above syntax has been further appended with numbers, 1, 2, and so on. For example, [7] 2011 (2) refers to second design of reference number 7, published in 2011.

Table 4 Designs of third-order half differentiators

Table 5 RMS magnitude and phase errors of third-order half differentiators

Table 6 Designs of fifth-order half differentiators

Table 7 RMS magnitude and phase errors of fifth-order half differentiators

Fig. 10

Frequency responses of third-order half differentiators

Fig. 11

Comparison of magnitude and phase RMS errors of third-order half differentiators

Fig. 12

Frequency responses of fifth-order half differentiators

Fig. 13

Comparison of magnitude and phase RMS errors of fifth-order half differentiators

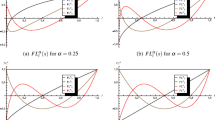
Furthermore, Table 8 presents the designs and Table 9, the corresponding performances of the one-third differentiators of third order. The RMS magnitude error, 0.441906, of proposed one-third differentiator is again the lowest among the compared ones. Figure 14 plots the frequency magnitude responses along with the phase responses of these designs. Figure 15 plots the corresponding RMS magnitude errors and the RMS phase errors. Similarly, Table 10 presents the designs and Table 11, the corresponding performances of the one-third differentiators of fifth order. Again, the RMS magnitude error, 0.307687, of the proposed one-third differentiator is the lowest among the compared ones. Figure 16 plots the corresponding frequency magnitude responses along with the phase responses. Figure 17 plots the corresponding RMS magnitude errors and the RMS phase errors of these designs.

Fig. 14

Frequency responses of third-order one-third differentiators

Fig. 15

Comparison of magnitude and phase RMS errors of third-order one-third differentiators

Fig. 16

Frequency responses of fifth-order one-third differentiators

Fig. 17

Comparison of magnitude and phase RMS errors of fifth-order one-third differentiators

Table 8 Designs of third-order one-third differentiators

Table 9 RMS magnitude and phase errors of third-order one-third differentiators

Table 10 Designs of fifth-order one-third differentiators

Table 11 RMS magnitude and phase errors of fifth-order one-third differentiators

Table 12 presents the designs and Table 13, the corresponding performances of the one-fourth differentiators of third order. Here, also it can be clearly observed that the RMS magnitude error, 0.243824, of proposed half differentiator is the lowest among the compared ones. Figure 18 plots the frequency magnitude responses along with the phase responses. Figure 19 plots the corresponding RMS magnitude errors and the RMS phase errors. Finally, Table 14 presents the designs and Table 15, the corresponding performances of the one-fourth differentiators of fifth order. Again, the RMS magnitude error, 0.175219, of proposed one-fourth differentiator is the lowest among the compared ones. Figure 20 plots the frequency magnitude responses along with the phase responses. Figure 21 plots the corresponding RMS magnitude and phase errors.

Fig. 18

Frequency responses of third-order one-fourth differentiators

Fig. 19

Comparison of magnitude and phase RMS errors of third-order one-fourth differentiators

Fig. 20

Frequency responses of fifth-order one-fourth differentiators

Fig. 21

Comparison of magnitude and phase RMS errors of fifth-order one-fourth differentiators

Table 12 Designs of third-order one-fourth differentiators

Table 13 RMS magnitude and phase errors of third-order one-fourth differentiators

Table 14 Designs of fifth-order one-fourth differentiators

Table 15 RMS magnitude and phase errors of fifth-order one-fourth differentiators

6 Comparative Study of NMSA with Genetic Algorithms

The performance of NMSA, in terms of the achievable fitness function values and the timing aspect, has been compared with the GA optimization technique using their respective MATLAB packages. Applications of NMSA for designing FODs have already been demonstrated. A sample case study considering only the half differentiator of third-order design by GA has been conducted, and the results are presented in this section. Various parameters used for GA optimization technique are listed in Table 16. To evaluate the performance comparison of these optimization methods, 50 independent trial runs of both methods were conducted and the obtained values of fitness function were recorded. NMSA was observed to produce zero standard deviation, whereas GA produced a standard deviation of 6.039116 in RMS magnitude error. The zero standard deviation in the designs by NMSA is a unique feature indicating the same result for all the 50 trial runs. Figure 22 presents variation of fitness function with number of iterations as optimized using GA as a sample design study. Comparing Figs. 3 and 22, it can be clearly seen that NMSA converges much faster and better. In this case, GA was able to achieve a best fitness value of 5.80047 in 200 iterations against 1.193116 of NMSA in 200 iterations. It should be noted that the same fitness function has been used for both the optimization methods. Also, on an average, NMSA was able to execute an iteration in 0.6795 s as compared to 26.0796 s taken by GA. Based on this input, it can be concluded that NMSA is 38 times faster than GA. The above computations were performed on an Intel Core i5 @3.2 GHz CPU with 4 GB RAM. A sample design obtained by GA optimization is given in Table 17 along with its performance in terms of the RMS magnitude error. The corresponding frequency response is shown in Fig. 23. Table 18 summarizes the comparison of GA-based designs with the NMSA-based design. Based on this study, it can be concluded that NMSA is a better option as compared to GA for the fractional-order differentiator design. Inferior results obtained by GA can be attributed to its tendency to get trapped in local minima. This is in line with the other works where GA has been claimed to yield poor convergence and solution quality [18].

Fig. 22

Fitness function v/s generations (GA)

Fig. 23

Frequency response of half differentiator of third order optimized using GA

Table 16 Used GA parameters

Table 17 Half differentiator of third-order designed using GA

Table 18 Comparison of NMSA and GA for third-order half differentiator designs

To further compare the effectiveness of NMSA and GA, a hypothetical t test was performed on the fitness function values obtained in the above-mentioned 50 independent trial runs. t test, t Student statistic or distribution t is a method for determining the statistical significance of the difference between two independent samples of an equal sample size [26]. It may be noted that the t test method is developed without mathematical proof. Higher positive t value indicates the goodness of reference result with respect to the comparing result and vice versa. On the other hand, negative t value indicates the badness of reference result with respect to the comparing result. Furthermore, for a mean minimization problem, t test value will be positive if algorithm 1’s mean is less than algorithm 2’s mean; thus, algorithm 1 is better than algorithm 2. On the other hand, t test value being negative means algorithm 1 is poorer than the algorithm 2 with respect to their means [18, 26].

The t Student statistic is described as:

$$\begin{aligned} t=\frac{\overline{X_2 } -\overline{X_1 } }{\sqrt{\frac{S_1 ^{2}}{n_1 }+\frac{S_2 ^{2}}{n_2 }}} \end{aligned}$$

(25)

where $\overline{X_1 }$ and $\overline{X_2 }$ are the means of the samples $X_1$ and $X_2$, respectively, $S_1 ^{2}$ and $S_2 ^{2}$ are the variances of sample 1 and sample 2, respectively, and finally, $n_1$ is the size of the sample 1 and $n_2$ is the size of the sample 2. In the present work, the NMSA is considered as the algorithm 1 (reference) and GA is considered as the algorithm 2, whose performance is to be compared. Table 19 presents the results of t test. The value $t=14.1710$ gives sufficient statistical information to say that NMSA outperforms GA along the realized simulations.

Table 19 Comparison of NMSA and GA using t test

7 Conclusions

This paper presented a novel application of Nelder–Mead simplex optimization technique for designing efficient fractional-order differentiators. For discretization, the well-known Al-Alaoui operator has been used. To prove the efficacy of proposed method, six case studies have been presented, namely a half differentiator of third order, a half differentiator of fifth order, a one-third differentiator of third order, a one-third differentiator of fifth order, a one-fourth differentiator of third order, and a one-fourth differentiator of fifth order. The obtained simulation results have been compared with the recently published works, and significantly reduced RMS magnitude errors have been obtained in all of the investigated cases, thereby making the proposed technique a potential optimization method for designing fractional differentiators. Further, a comparative study with genetic algorithm-based optimization technique has also been presented and the proposed method has been found to outperform GA-based designs. As a future research scope, various mapping functions, other than Al-Alaoui operator, can be chosen and corresponding performances can be investigated.