Global Adaptive Finite-Time Control for Stochastic Nonlinear Systems via State Feedback

Abstract

This paper discusses the problem of global adaptive finite-time control for a class of stochastic nonlinear systems with parametric uncertainty. Under the assumption that the drift and diffusion terms satisfy lower-triangular growth conditions, a continuous adaptive controller is designed based on the adding one power integrator technique and parameter separation principle. By constructing an adaptive law to counteract the effects of uncertain parameters, it is proved that system states can be regulated to the origin almost surely in a finite time. Two simulation examples are given to demonstrate the effectiveness of the proposed control procedure.

1 Introduction

Since stochastic noise arises in various realistic dynamic models of practical control problems frequently and inevitably, it is required to establish stochastic system models and analyze the system dynamics from the stochastic point of view. With the development of stochastic theory, some constructive controller design methods, such as Sontag’s stabilization formula and backstepping techniques, have been extended to stochastic settings [7, 14], which leads to an increasing amount of efforts toward controller design for stochastic nonlinear systems [4, 20, 28, 30] and the references therein. With respect to uncertain nonlinear systems, adaptive control is one of the effective ways to deal with parametric uncertainty [17]. For stochastic nonlinear systems driven by noise of unknown covariance, the work [5] employed the adaptive backstepping technique with tuning functions to construct a state feedback controller which makes the closed-loop system globally stable in probability. Based on stochastic LaSalle theorem [16], the result obtained in [5] has been further extended to a class of stochastic system with both unknown covariance and unknown system parameters in parametric-strict-feedback form [12] and output-feedback canonical form [13], respectively. It is worth noting that in the aforementioned results [5, 12, 13], those unknown parameters appear in the system linearly, i.e., the considered systems are linearly parameterized. As shown in [19], nonlinear parameterization commonly exists in many physical systems, such as biochemical processes and machines with friction, and exhibits more complex dynamics. Recently, many efforts have been devoted to explore the adaptive control problem toward stochastic nonlinear systems with nonlinear parameterization. Under some assumptions, a smooth adaptive state feedback controller was designed for stochastic high-order nonlinear systems to guarantee that the equilibrium of interest is globally stable in probability and the states can be regulated to the origin almost surely [24]. Then, the work [18] generalized this result by relaxing restrictions on power orders, as well as nonlinear functions. Based on switching strategy, the work [8] has solved the problem of adaptive stabilization for a class of stochastic nonholonomic system.

Note that the adaptive controller design procedures in the aforementioned works only consider the asymptotic behaviors of system trajectories as time goes to infinity. Obviously, adaptive control laws with finite-time convergence are more desirable, under which the closed-loop system exhibits faster convergence rate and better disturbance rejection properties. In the deterministic case, Haimo gave a sufficient condition for finite-time stability of continuous systems in [9]. With the improvement of finite-time Lyapunov stability theory [3] and finite-time homogeneous theory [2], the design methods for continuous finite-time controllers have developed rapidly, which leads to several results on finite-time feedback stabilization, for example, [6, 11, 26, 32, 33] and the references therein. In [22], discontinuous controllers have been designed for neural networks with discontinuous activations to achieve finite-time stabilization and the work [21] proposed a switching protocol to cover both continuous and discontinuous controllers. As a general extension, the problem of finite-time control for stochastic nonlinear systems has become an active research filed. Based on stochastic Lyapunov theorem on finite-time stability [25], several finite-time stabilization results have been achieved, for example, [1, 15, 27, 29, 31]. Specifically, a state feedback controller with a dynamic gain was designed in [1] to achieve finite-time stability in probability. Based on homogeneous domination approach, the works [29, 31] have solved the output feedback finite-time stabilization problem for both lower-triangular and upper-triangular systems. However, all the above-mentioned works do not take parametric uncertainty into consideration. Unlike the case that growth rates for nonlinear terms are constants in [29, 31] or functions of system states in [15, 27], the growth rates considered in this paper are smooth functions of system states and unknown parameters, which cannot be dominated by introducing a constant gain or just functions of system states.

Motivated by Hong et al. [10] in the deterministic case, in this paper, we aim to address the problem of adaptive finite-time control for a class of stochastic nonlinear systems with nonlinear parameterization. The main obstacles can be divided into two aspects: One is that the commonly used stochastic Barbalat’s lemma cannot be applied to finite-time stability analysis; the other one is that the inequality ${\mathcal {L}}V\le -c\cdot V^\gamma$, $c>0, 0<\gamma <1$, cannot be obtained easily, since the Lyapunov function $V$ is a positive definite function with respect to not only system states but also the parameter estimation error. To tackle this problem, we first employ the parameter separation principle [19] to set apart the nonlinear parameters from the nonlinear function, under which the nonlinearly parameterized system can be dominated by a linear-like parameterized one. Then, with the help of adding one power integrator technique, a ${\mathcal {C}}^0$ adaptive state feedback controller is obtained iteratively. Finally, based on stochastic finite-time stability theorem, the closed-loop system can be proved to be bounded in probability and the states can be regulated to the origin almost surely in a finite time.

Notations: ${\mathbb {R}}_{+}$ denotes the set of all nonnegative real numbers, and ${\mathbb {R}}^n$ denotes the real $n-$dimensional space. ${\mathbb {R}}_{\hbox {odd}}^{>2}=:\{q\in {\mathbb {R}}:q>2$ is a ratio of two odd integers$\}$. For any given vector or matrix $X$, $X^T$ represents its transpose; $Tr\{X\}$ represents its trace when $X$ is square; and $\Vert \cdot \Vert$ denotes the Euclidean norm of a vector $X$ or the Frobenius norm of a matrix $X$. For a bounded function $X:{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}^{n\times m}$, $\Vert X\Vert _\infty =\sup _{t\in {\mathbb {R}}_+}\Vert X(t)\Vert$. ${\mathcal {C}}^i$ denotes the set of all functions with continuous $i$th partial derivatives; ${\mathcal {K}}$ denotes the set of all functions, ${\mathbb {R}}_+\rightarrow {\mathbb {R}}_+$, which are continuous, strictly increasing and vanishing at zero; ${\mathcal {K}}_\infty$ denotes the set of all functions which are of class ${\mathcal {K}}$ and unbounded; and $a\wedge b$ means the minimum of $a$ and $b$.

2 Preliminaries and Problem Statement

Consider the following stochastic nonlinear system

$$\begin{aligned} \hbox {d}x=f(x)\hbox {d}t+g^T(x)\hbox {d}\omega ,\quad x(0)=x_0\in {\mathbb {R}}^n \end{aligned}$$

(1)

where $x\in {\mathbb {R}}^n$ is the system state and $\omega$ is an $r-$dimensional standard Wiener process defined on a probability space $(\varOmega ,\digamma ,\digamma _t,P)$. The Borel measurable functions $f: {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ and $g^T: {\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times r}$ are continuous in $x$ that satisfy $f(0)=0$ and $g(0)=0$.

Lemma 1

[23] Suppose that $f(x)$ and $g(x)$ are continuous with respect to their variables and satisfy the linear growth condition:

$$\begin{aligned} \Vert f(x)\Vert ^2+\Vert g(x)\Vert ^2\le K(1+\Vert x\Vert ^2) \end{aligned}$$

(2)

for $K>0$. Then given any $x_0$ independent of $\omega (t)$, (1) has a continuous solution with probability one.

Definition 1

[14] For any given $V(x)\in {\mathcal {C}}^{2}$ associated with stochastic nonlinear system (1), the infinitesimal generator ${\mathcal {L}}$ is defined as ${\mathcal {L}}V(x)=\frac{\partial V}{\partial x}f(x)+\frac{1}{2}Tr\{g(x)\frac{\partial ^2 V}{\partial x^2}g^T(x)\}$, where $\frac{1}{2}Tr\{g(x)\frac{\partial ^2 V}{\partial x^2}g^T(x)\}$ is called as the Hessian term of ${\mathcal {L}}$.

Definition 2

[15] The trivial solution of (1) is said to be finite-time stable in probability if the solution exists for any initial value $x_0\in {\mathbb {R}}^n$, denoted by $x(t;x_0)$. Moreover, the following statements hold:

• (i) Finite-time attractiveness in probability: For every initial value $x_0\in {\mathbb {R}}^n\backslash \{0\}$, the first hitting time $\tau _{x_0}=\inf \{t;x(t;x_0)=0\}$, which is called the stochastic settling time, is finite almost surely, that is, $P\{\tau _{x_0}<\infty \}=1$;

• (ii) Stability in probability: For every pair of $\varepsilon \in (0,1)$ and $r>0$, there exists a $\delta =\delta (\varepsilon ,r)>0$ such that $P\{\Vert x(t;x_0)\Vert <r, \forall t\ge 0\}\ge 1-\varepsilon$, whenever $\Vert x_0\Vert <\delta$;

• (iii) The solution $x((t+\tau _{x_0});x_0)$ is unique for $t\ge 0$.

Lemma 2

[15] For system (1), if there exist a Lyapunov function $V:{\mathbb {R}}^n\rightarrow {\mathbb {R}}_+$, ${\mathcal {K}}_\infty$ class functions $\mu _1$ and $\mu _2$, positive real numbers $c>0$ and $0<\gamma <1$ such that for all $x\in {\mathbb {R}}^n$ and $t\ge 0$,

$$\begin{aligned} \mu _1(\Vert x\Vert )&\le V(x)\le \mu _2(\Vert x\Vert ), \end{aligned}$$

(3)

$$\begin{aligned} {\mathcal {L}}V(x)&\le -c\cdot (V(x))^{\gamma } \end{aligned}$$

(4)

then the trivial solution of (1) is finite-time attractive and stable in probability.

Lemma 3

[19] For any real-valued continuous function $f(x,y)$, where $x\in {\mathbb {R}}^m$ and $y\in {\mathbb {R}}^n$, there are smooth scalar-value functions $a(x)\ge 1$ and $b(y)\ge 1$ such that

$$\begin{aligned} |f(x,y)|\le a(x)b(y). \end{aligned}$$

(5)

Lemma 4

For $x\in {\mathbb {R}}$, $y\in {\mathbb {R}}$, and $p\ge 1$, the following inequalities hold:

$$\begin{aligned} |x+y|^p&\le 2^{p-1}|x^{p}+y^p|,\\ \big (|x|+|y|\big )^\frac{1}{p}&\le |x|^\frac{1}{p}+|y|^\frac{1}{p}\le 2^{\frac{p-1}{p}}\big (|x|+|y|\big )^{\frac{1}{p}}. \end{aligned}$$

If $p\ge 1$ is an odd integer or a ratio of two odd integers,

$$\begin{aligned} |x-y|^p \le 2^{p-1}|x^p-y^p|,\ \ |x^{\frac{1}{p}}-y^{\frac{1}{p}}|\le 2^{1-\frac{1}{p}}|x-y|^{\frac{1}{p}}. \end{aligned}$$

Lemma 5

For any positive real numbers $c$, $d$, and any real-valued function $\gamma (x,y)> 0$, the following inequality holds:

$$\begin{aligned} |x|^c|y|^d \le \frac{c}{c+d}\gamma (x,y)|x|^{c+d}+\frac{d}{c+d}\gamma ^{-\frac{c}{d}}(x,y)|y|^{c+d}. \end{aligned}$$

In this paper, we consider a class of stochastic nonlinear systems described by

$$\begin{aligned} \hbox {d}x_1(t)=&(x_2(t)+f_1(\bar{x}_1(t),\theta ))\hbox {d}t+g_1^T(\bar{x}_1(t),\theta )\hbox {d}\omega (t),\nonumber \\ \vdots&\nonumber \\ \hbox {d}x_{n-1}(t)=&(x_n(t)+f_{n-1}(\bar{x}_{n-1}(t),\theta ))\hbox {d}t+g_{n-1}^T(\bar{x}_{n-1}(t),\theta )\hbox {d}\omega (t),\nonumber \\ \hbox {d}x_n(t)=&(u(t)+f_n(\bar{x}_n(t),\theta ))\hbox {d}t+g_n^T(\bar{x}_n(t),\theta )\hbox {d}\omega (t) \end{aligned}$$

(6)

where $x(t)=(x_1(t),\ldots ,x_n(t))^T \in {\mathbb {R}}^n$, $u(t)\in {\mathbb {R}}$ are the system states and the control input, respectively. $\bar{x}_i(t)=(x_1(t),\ldots ,x_i(t))^T$, $i=1,\ldots ,n$. $\omega (t)$ is an $r$-dimensional standard Wiener process defined on a probability space $(\varOmega ,\digamma ,\digamma _t,P)$ with $\varOmega$ being a sample space, $\digamma$ being a $\sigma$-field, $\digamma _t$ being a filtration, and $P$ being a probability measure. $\theta \in {\mathbb {R}}^N$ is a vector of uncertain parameters, with some integer $N>0$. The drift terms $f_i: {\mathbb {R}}^i\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}$ and the diffusion terms $g_i: {\mathbb {R}}^i\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}^r$, $i=1,\ldots ,n$, are Borel measurable, continuous with their arguments and satisfy $f_i(0,\theta )=0$, $g_i(0,\theta )=0$.

Assumption 1

For $i=1,\ldots ,n$, there exist nonnegative smooth functions $\gamma _i(\bar{x}_i,\theta )<\infty$ and $\eta _i(\bar{x}_i,\theta )<\infty$ such that

$$\begin{aligned} |f_i(\bar{x}_i,\theta )|\le&\left( |x_1|^{\frac{r_i+\tau }{r_1}}+\cdots +|x_i|^{\frac{r_i+\tau }{r_i}}\right) \gamma _i(\bar{x}_i,\theta ),\\ \Vert g_i(\bar{x}_i,\theta )\Vert \le&\left( |x_1|^{\frac{2r_i+\tau }{2r_1}}+\cdots +|x_i|^{\frac{2r_i+\tau }{2r_i}}\right) \eta _i(\bar{x}_i,\theta ) \end{aligned}$$

with $r_i=(i-1)\tau +1$, $i=1,\ldots ,n+1$, $\tau \in (-\frac{1}{n},0)$.

For simplicity, we assume $\tau =-p/q$ with $p$ being an even integer and $q$ being an odd integer. Based on this, $r_i$ will be odd in both denominator and numerator.

Remark 1

With the aid of the parameter separation principle in Lemma 3, we know that there are positive smooth functions $\gamma _{i1}(\bar{x}_i)$, $\gamma _{i2}(\theta )$, $\eta _{i1}(\bar{x}_i)$ and $\eta _{i2}(\theta )$, $i=1,\ldots ,n$, such that

$$\begin{aligned} |f_i(\bar{x}_i,\theta )|\le&\left( |x_1|^{\frac{r_i+\tau }{r_1}}+\cdots +|x_i|^{\frac{r_i+\tau }{r_i}}\right) \gamma _{i1}(\bar{x}_i)\gamma _{i2}(\theta ),\\ \Vert g_i(\bar{x}_i,\theta )\Vert \le&\left( |x_1|^{\frac{2r_i+\tau }{2r_1}}+\cdots +|x_i|^{\frac{2r_i+\tau }{2r_i}}\right) \eta _{i1}(\bar{x}_i)\eta _{i2}(\theta ). \end{aligned}$$

Remark 2

With respect to the case $dx=f(x,t)\hbox {d}t+g(x,t)\Sigma (t)\hbox {d}\omega$ in [5], we can regard the unknown covariance $\Sigma (t)$ as one part of the diffusion terms and then Assumption 1 becomes

$$\begin{aligned} \Vert g_i(\bar{x}_i,t)\Sigma (t)\Vert \le&\left( |x_1|^{\frac{2r_i+\tau }{2r_1}}+\cdots +|x_i|^{\frac{2r_i+\tau }{2r_i}}\right) \eta _{i1}(\bar{x}_i)\zeta . \end{aligned}$$

for an unknown constant $\zeta >0$. By constructing an adaptive law to estimate the unknown parameter, the results obtained in this paper can be used to deal with the adaptive finite-time control problem for stochastic nonlinear systems with unknown covariance.

3 Main Results

In this paper, the problem of global adaptive finite-time control is to find a continuous control law

$$\begin{aligned} \left\{ \begin{array}{ll} u=u(x,\hat{\varTheta }),&{}u(0,\hat{\varTheta })=0 \\ \dot{\hat{\varTheta }}=\phi (x,\hat{\varTheta }),&{}\phi (0,\hat{\varTheta })=0 \end{array} \right. \end{aligned}$$

(7)

such that the trajectory $(x(t),\hat{\varTheta })$ of system (6) under control law (7) is bounded in probability, and moreover, for any initial condition $(x(0),\hat{\varTheta }(0))$, $x(t)$ converges to zero in a finite time almost surely, where $\hat{\varTheta }$ is the estimate of $\varTheta =\max _{1\le i,j\le n}\{\gamma _{i2}(\theta ),\eta _{i2}(\theta )\eta _{j2}(\theta )\}$.

In what follows, we propose an iterative procedure to construct an adaptive finite-time controller by adopting adding one power integrator technique.

Initial Step: Choose the Lyapunov function

$$\begin{aligned} V_1=W_1+\frac{1}{2}\tilde{\varTheta }^2 \end{aligned}$$

(8)

where $W_1=\int _{x_1^*}^{x_1}(s^{\mu /r_1}-x_1^{*\mu /r_1})^{\frac{4\mu -r_1}{\mu }}$ with $x_1^*=0$, $\tilde{\varTheta }=\varTheta -\hat{\varTheta }$, and $\mu \in {\mathbb {R}}_{\hbox {odd}}^{>2}$. Under Assumption 1, one has

$$\begin{aligned} {\mathcal {L}}V_1=&\,x_1^{\frac{4\mu -r_1}{r_1}}(x_2+f_1)+\frac{4\mu -r_1}{2r_1}x_1^{\frac{4\mu -2r_1}{r_1}}\Vert g_1\Vert ^2-\tilde{\varTheta }\dot{\hat{\varTheta }}\nonumber \\ \le&\,\xi _1^{\frac{4\mu -r_1}{\mu }}x_2+\xi _1^{\frac{4\mu +\tau }{\mu }}h_{11}(x_1)\varTheta -\tilde{\varTheta }\dot{\hat{\varTheta }}-n\varTheta \xi _1^{\frac{4\mu +\tau }{\mu }}+n\varTheta \xi _1^{\frac{4\mu +\tau }{\mu }}\nonumber \\ \le&\,\xi _1^{\frac{4\mu -r_1}{\mu }}(x_2-x_2^*)+\xi _1^{\frac{4\mu -r_1}{\mu }}x_2^* +\xi _1^{\frac{4\mu +\tau }{\mu }}\hat{\varTheta }(h_{11}(x_1)+n)\nonumber \\&-\,n\varTheta \xi _1^{\frac{4\mu +\tau }{\mu }}-\tilde{\varTheta }\left( \dot{\hat{\varTheta }}-(h_{11}(x_1)+n)\xi _1^{\frac{4\mu +\tau }{\mu }}\right) \end{aligned}$$

(9)

where $\xi _1=x_1^{\mu /r_1}$ and $h_{11}(x_1)=\frac{4\mu -r_1}{2r_1}\eta ^2_{11}(x_1)+\gamma _{11}(x_1)\ge 0$ is a smooth function. Obviously, the virtual controller $x_2^*=-\xi _1^{r_2/\mu }\big (n+(h_{11}(x_1)+n)\sqrt{\hat{\varTheta }^2+1}\big ):=-\xi _1^{r_2/\mu }\rho _1(x_1,\hat{\varTheta })$ leads to

$$\begin{aligned} {\mathcal {L}}{V_1}\le -n\xi _1^{\frac{4\mu +\tau }{\mu }}-n\varTheta \xi _1^{\frac{4\mu +\tau }{\mu }}+\xi _1^{\frac{4\mu -r_1}{\mu }}(x_2-x_2^*) -\tilde{\varTheta }(\dot{\hat{\varTheta }}-\sigma _1(\cdot )) \end{aligned}$$

(10)

with $\sigma _1(\cdot )=(h_{11}(x_1)+n)\xi _1^{\frac{4\mu +\tau }{\mu }}:=\delta _1(\cdot )\xi _1^{\frac{4\mu +\tau }{\mu }}$, $\delta _1(\cdot )>0$.

Inductive Step: Suppose at step $k-1$, there are positive smooth functions $\rho _1(\cdot ),\ldots ,\rho _{k-1}(\cdot )$, a Lyapunov function $V_{k-1}$, which is positive definite and proper, and a set of virtual controllers $x_1^*,\ldots ,x_k^*$ defined by

$$\begin{aligned} x_1^*= & {} 0, \quad \xi _1=x_1^{\mu /r_1}-x_1^{*\mu /r_1},\nonumber \\ x_i^{*}= & {} -\xi _{i-1}^{r_{i}/\mu }\rho _{i-1}(\bar{x}_{i-1},\hat{\varTheta }),\quad \xi _i=x_i^{\mu /r_i}-x_i^{*\mu /r_i}, \ \ i=2,\ldots ,k \end{aligned}$$

(11)

such that

$$\begin{aligned} {\mathcal {L}}V_{k-1}\le&-\!(n-k+2)\sum _{i=1}^{k-1}\xi _i^{\frac{4\mu +\tau }{\mu }}-(n-k+2)\varTheta \sum _{i=1}^{k-1}\xi _i^{\frac{4\mu +\tau }{\mu }}\nonumber \\&+\,\xi _{k-1}^{\frac{4\mu -r_{k-1}}{\mu }}(x_k-x_k^{*}) -\left( \tilde{\varTheta }-\sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\right) (\dot{\hat{\varTheta }}-\sigma _{k-1}(\cdot )) \end{aligned}$$

(12)

with $\sigma _{k-1}(\cdot )=\sum _{i=1}^{k-1}\delta _i(\cdot )\xi _i^{\frac{4\mu +\tau }{\mu }}$ and smooth functions $\delta _i(\cdot )>0$, $i=1,\ldots ,k-1$. At the $k$th step, one chooses the following Lyapunov function

$$\begin{aligned} V_k=V_{k-1}+W_k=V_{k-1}+\int _{x_k^*}^{x_k}\left( s^{\mu /r_k}- x_k^{*\mu /r_k}\right) ^{\frac{4\mu -r_k}{\mu }}\hbox {d}s. \end{aligned}$$

(13)

The infinitesimal generator ${\mathcal {L}}$ of $V_k$ along the trajectory of (6) is

$$\begin{aligned} {\mathcal {L}}V_k=&\,{\mathcal {L}}V_{k-1}+\sum _{i=1}^k\frac{\partial W_k}{\partial x_i}(x_{i+1}+f_i)+\frac{1}{2}\sum _{i=1}^k\sum _{j=1}^k\frac{\partial ^2 W_k}{\partial x_i\partial x_j}\Vert g_i^T\Vert \Vert g_j\Vert +\frac{\partial W_k}{\partial \hat{\varTheta }}\dot{\hat{\varTheta }} \end{aligned}$$

(14)

where $\forall i,j=1,\ldots ,k-1$

$$\begin{aligned} \frac{\partial W_k}{\partial x_k}=&\,\, \xi _k^{\frac{4\mu -r_k}{\mu }},\ \ \frac{\partial W_k}{\partial x_i}=\,\frac{r_k-4\mu }{\mu } \frac{\partial {x_k^{*\mu /{r_k}}}}{\partial x_i}\int _{x_k^*}^{x_k}\left( s^{\mu /{r_k}}-x_k^{* \mu /{r_k}}\right) ^{\frac{3\mu -r_k}{\mu }}\hbox {d}s,\nonumber \\ \frac{\partial W_k}{\partial \hat{\varTheta }}=&\,\frac{r_k-4\mu }{\mu } \frac{\partial {x_k^{*\mu /{r_k}}}}{\partial \hat{\varTheta }}\int _{x_k^*}^{x_k}\left( s^{\mu /{r_k}}-x_k^{* \mu /{r_k}}\right) ^{\frac{3\mu -r_k}{\mu }}\hbox {d}s,\nonumber \\ \frac{\partial ^2W_k}{\partial x_k^2}=&\,\frac{4\mu -r_k}{r_k}\xi _k^{\frac{3\mu -r_k}{\mu }}x_k^{\frac{\mu -r_k}{r_k}},\ \ \frac{\partial ^2W_k}{\partial x_k\partial x_i}=\frac{r_k-4\mu }{\mu }\frac{\partial {x_k^{*\mu /{r_k}}}}{\partial x_i}\xi _k^{\frac{3\mu -r_k}{\mu }},\nonumber \\ \frac{\partial ^2W_k}{\partial x_i\partial x_j}=\,&\frac{r_k-4\mu }{\mu }\frac{\partial ^2{x^{*\mu /r_k}_k}}{\partial x_i\partial x_j}\int _{x_k^*}^{x_k}\left( s^{\mu /{r_k}}-x_k^{* \mu /{r_k}}\right) ^{\frac{3\mu -r_k}{\mu }}\hbox {d}s,\nonumber \\&+\,\frac{(4\mu -r_k)(3\mu -r_k)}{\mu ^2}\frac{\partial {x^{*\mu /r_k}_k}}{\partial x_i} \frac{\partial {x^{*\mu /r_k}_k}}{\partial x_j}\int _{x_k^*}^{x_k}\left( s^{\mu /r_k}-x_k^{* \mu /r_k}\right) ^{\frac{2\mu -r_k}{\mu }}\hbox {d}s \end{aligned}$$

(15)

which implies $W_k$ is ${\mathcal {C}}^2$ due to $\mu \in {\mathbb {R}}_\mathrm{odd}^{>2}$.

Based on Lemmas 4 and 5, the following four propositions are given to analyze each term of the right-hand side of (14), whose proofs are included in Appendix.

Proposition 1

There exists a smooth function $h_{k1}(\bar{x}_{k-1},\hat{\varTheta })\ge 0$ such that

$$\begin{aligned} \sum _{i=1}^{k-1}\frac{\partial W_k}{\partial x_i}x_{i+1}\le \frac{1}{3}\sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+ |\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k1}(\bar{x}_{k-1},\hat{\varTheta }). \end{aligned}$$

(16)

Proposition 2

There is a smooth function $h_{k2}(\bar{x}_{k},\hat{\varTheta })\ge 0$, satisfying

$$\begin{aligned} \sum _{i=1}^{k}\frac{\partial W_k}{\partial x_i}f_i\le \frac{1}{3}\varTheta \sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+ \varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k2}(\bar{x}_{k},\hat{\varTheta }). \end{aligned}$$

(17)

Proposition 3

There exists a nonnegative smooth function $h_{k3}(\bar{x}_{k},\hat{\varTheta })$ such that

$$\begin{aligned} \frac{1}{2}\sum _{i=1}^k\frac{\partial ^2 W_k}{\partial x_i^2}\Vert g_i\Vert ^2\le \frac{1}{3}\varTheta \sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+ \varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k3}(\bar{x}_{k},\hat{\varTheta }). \end{aligned}$$

(18)

Proposition 4

For $i\ne j$, there is a smooth function $h_{k4}(\bar{x}_k,\hat{\varTheta })\ge 0$ such that

$$\begin{aligned} \frac{1}{2}\sum _{i=1}^k\sum _{j=1}^k\frac{\partial ^2 W_k}{\partial x_i\partial x_j}\Vert g_i^T\Vert \Vert g_j\Vert \le \frac{1}{3}\varTheta \sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k4}(\bar{x}_{k},\hat{\varTheta }). \end{aligned}$$

(19)

Note that

$$\begin{aligned} \xi _{k-1}^{\frac{4\mu -r_{k-1}}{\mu }}(x_k-x_k^{*})\le&2^{1-\frac{r_k}{\mu }} |\xi _{k-1}|^{\frac{4\mu -r_{k-1}}{\mu }}|\xi _k|^{\frac{r_k}{\mu }} \le \frac{1}{3}|\xi _{k-1}|^{\frac{4\mu +\tau }{\mu }}+c_1|\xi _k|^{\frac{4\mu +\tau }{\mu }} \end{aligned}$$

(20)

with $c_1\ge 0$. Substituting (16)–(20) into (14), one has

$$\begin{aligned} {\mathcal {L}}V_k\le&-\!\left( n-k+\frac{4}{3}\right) \sum _{i=1}^{k-1}\xi _i^{\frac{4\mu +\tau }{\mu }}-(n-k+1)\varTheta \sum _{i=1}^{k-1}\xi _i^{\frac{4\mu +\tau }{\mu }}+\frac{\partial W_k}{\partial \hat{\varTheta }}\dot{\hat{\varTheta }}\nonumber \\&+\,\big (c_1+h_{k1}(\cdot )+(h_{k2}(\cdot )+h_{k3}(\cdot )+h_{k4}(\cdot ))\varTheta \big )\xi _k^{\frac{4\mu +\tau }{\mu }}+\xi _k^{\frac{4\mu -r_k}{\mu }}x_{k+1}^*\nonumber \\&+\,\xi _k^{\frac{4\mu -r_k}{\mu }}(x_{k+1}-x_{k+1}^*)-\left( \tilde{\varTheta }-\sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\right) (\dot{\hat{\varTheta }}-\sigma _{k-1})\nonumber \\ \le&-\!\left( n-k+\frac{4}{3}\right) \sum _{i=1}^{k-1}\xi _i^{\frac{4\mu +\tau }{\mu }}-(n-k+1)\varTheta \sum _{i=1}^{k}\xi _i^{\frac{4\mu +\tau }{\mu }} +\frac{\partial W_k}{\partial \hat{\varTheta }}\sigma _k\nonumber \\&+\,(c_1+h_{k1}(\cdot )+\delta _k(\cdot )\hat{\varTheta })\xi _k^{\frac{4\mu +\tau }{\mu }}+\sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _{k}(\cdot )\xi _k^{\frac{4\mu +\tau }{\mu }}\nonumber \\&-\,\left( \tilde{\varTheta }-\sum _{i=1}^{k}\frac{\partial W_i}{\partial \hat{\varTheta }}\right) (\dot{\hat{\varTheta }}-\sigma _{k})+\xi _k^{\frac{4\mu -r_k}{\mu }}(x_{k+1}-x_{k+1}^*)+\xi _k^{\frac{4\mu -r_k}{\mu }}x_{k+1}^* \end{aligned}$$

(21)

where $\sigma _k=\sigma _{k-1}+(n-k+1+h_{k2}(\cdot )+h_{k3}(\cdot )+h_{k4}(\cdot ))\xi _k^{\frac{4\mu +\tau }{\mu }}:=\sigma _{k-1}+\delta _k(\cdot )\xi _k^{\frac{4\mu +\tau }{\mu }}$, $\delta _k(\cdot )>0$. With respect to the terms $\frac{\partial W_k}{\partial \hat{\varTheta }}\sigma _k$ and $\sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _{k}(\cdot )\xi _k^{\frac{4\mu +\tau }{\mu }}$, we have the following proposition. Please refer to the Appendix for the detailed proof.

Proposition 5

There exist two nonnegative smooth functions $h_{k5}(\bar{x}_k,\hat{\varTheta })$ and $h_{k6}(\bar{x}_k,\hat{\varTheta })$ such that

$$\begin{aligned} \frac{\partial W_k}{\partial \hat{\varTheta }}\sigma _k\le&\frac{1}{3}\sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+ |\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k5}(\bar{x}_{k},\hat{\varTheta }),\nonumber \\ \sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _{k}(\cdot )\xi _k^{\frac{4\mu +\tau }{\mu }}\le&|\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k6}(\bar{x}_{k},\hat{\varTheta }). \end{aligned}$$

(22)

By choosing the $k+1$th virtual controller as $x_{k+1}^{*}=-\xi _k^{\frac{r_k+\tau }{\mu }}(n-k+1+c_1+h_{k1}(\cdot )+h_{k5}(\cdot )+h_{k6}(\cdot )+\delta _k(\cdot )\sqrt{1+\hat{\varTheta }^2}):=-\xi _k^{\frac{r_k+\tau }{\mu }}\rho _k(\bar{x}_k,\hat{\varTheta })$, it yields

$$\begin{aligned} {\mathcal {L}}V_k\le&{-}(n-k+1)\sum _{i=1}^{k}\xi _i^{\frac{4\mu +\tau }{\mu }}-(n-k+1)\varTheta \sum _{i=1}^{k}\xi _i^{\frac{4\mu +\tau }{\mu }}\nonumber \\&+\xi _k^{\frac{4\mu -r_{k}}{\mu }}(x_{k+1}-x_{k+1}^{*})-\left( \tilde{\varTheta }-\sum _{i=1}^{k}\frac{\partial W_i}{\partial \hat{\varTheta }}\right) (\dot{\hat{\varTheta }}-\sigma _{k}). \end{aligned}$$

(23)

Last Step: Based on the analysis above, one can choose the adaptive control law as

$$\begin{aligned} u=\,&x_{n+1}^*=\,-\xi _n^{\frac{r_n+\tau }{\mu }}\rho _n(x,\hat{\varTheta }),\nonumber \\ \dot{\hat{\varTheta }}=\,&\sigma _n=\sum _{i=1}^n\delta _i(\cdot )\xi _i^{\frac{4\mu +\tau }{\mu }} \end{aligned}$$

(24)

and the Lyapunov function $V_n=V_{n-1}+W_n=V_{n-1}+\int _{x_n^*}^{x_n}(s^{\mu /r_n}-x_n^{*\mu /r_n} )^{\frac{4\mu -r_n}{\mu }}\hbox {d}s$ such that

$$\begin{aligned} {\mathcal {L}}V_n\le -\sum _{i=1}^n\xi _i^{\frac{4\mu +\tau }{\mu }}-\varTheta \sum _{i=1}^n\xi _i^{\frac{4\mu +\tau }{\mu }} \end{aligned}$$

(25)

where $\delta _n(\cdot )$ and $\rho _n(\cdot )$ are positive smooth functions.

Remark 3

The Lyapunov functions $V_k$, $k=1,\ldots ,n$, are positive definite and proper with respect to $x$ and $\tilde{\varTheta }$, which can be discussed by the following two cases.

Case 1: If $x_k^*\le x_k$, with $\mu \in {\mathbb {R}}_{odd}^{>2}$ and Lemma 4, one gets

$$\begin{aligned} W_k=&\int _{x_k^*}^{x_k}\left( s^{\mu /r_k}-x_k^{*\mu /r_k}\right) ^{\frac{4\mu -r_k}{\mu }}\hbox {d}s\ge \left( 2^{1-\frac{\mu }{r_k}}\right) ^{\frac{4\mu -r_k}{\mu }}\int _{x_k^*}^{x_k}(s-x_k^* )^{\frac{4\mu -r_k}{r_k}}\hbox {d}s\nonumber \\ =&\,\left( 2^{1-\frac{\mu }{r_k}}\right) ^{\frac{4\mu -r_k}{\mu }}\frac{r_k}{4\mu }(x_k-x_k^*)^{\frac{4\mu }{r_k}}, \end{aligned}$$

(26)

$$\begin{aligned} W_k\le&\left( x_k^{\mu /r_k}-x_k^{*\mu /r_k}\right) ^{\frac{4\mu -r_k}{\mu }}(x_k-x_k^*)\le 2^{1-\frac{r_k}{\mu }}\xi _k^4; \end{aligned}$$

(27)

Case 2: If $x_k^*\ge x_k$, (26) and (27) can be proved similarly.

Therefore, $V_k=\sum _{i=1}^kW_i+\frac{1}{2}\tilde{\varTheta }^2\ge \sum _{i=1}^k(2^{1-\frac{\mu }{r_i}})^{\frac{4\mu -r_i}{\mu }}\frac{r_i}{4\mu }(x_i-x_i^*)^{\frac{4\mu }{r_i}} +\frac{1}{2}\tilde{\varTheta }^2$, which imply that $V_k$ is positive definite and proper.

Remark 4

The controller design procedure is based on adding one power integrator technique. If one uses the traditional backstepping method to design a finite-time feedback controller, singularities will occur in the derivatives of virtual controllers, because of the existence of fractional powers that are less than one. The adding one power integrator technique, which introduces integrators into the Lyapunov function, can prevent taking direct derivatives of virtual controllers so that singularities can be avoided.

Theorem 1

Under the control law (24), the problem of global adaptive finite-time control for system (6) can be solved.

Proof

First, we conclude the boundedness in probability of the closed-loop system. Let $\tilde{x}=(x_1,\ldots ,x_n,\hat{\varTheta })$, under which the closed-loop system (6)–(24) can be rewritten as

$$\begin{aligned} \hbox {d}\tilde{x}=F(\tilde{x},\theta )\hbox {d}t+G^T(\tilde{x},\theta )\hbox {d}\omega \end{aligned}$$

(28)

where $F(\tilde{x},\theta )=(x_2+f_1(\cdot ),\ldots ,u+f_n(\cdot ),\sigma _n(\cdot ))^T$ and $G(\tilde{x},\theta )=(g_1(\cdot ),\ldots ,g_n(\cdot ),0)$. For $m>0$, define the following truncation functions

$$\begin{aligned} F_m(\tilde{x},\theta )&=\left\{ \begin{array}{ll} F(\tilde{x},\theta ), &{} \hbox {if }\Vert \tilde{x}\Vert \le m; \\ F\big (m\frac{\tilde{x}}{\Vert \tilde{x}\Vert },\theta \big ), &{} \hbox {if }\Vert \tilde{x}\Vert > m. \end{array} \right. \nonumber \\ G^T_m(\tilde{x},\theta )&=\left\{ \begin{array}{ll} G^T(\tilde{x},\theta ), &{} \hbox {if }\Vert \tilde{x}\Vert \le m; \\ G^T\big (m\frac{\tilde{x}}{\Vert \tilde{x}\Vert },\theta \big ), &{} \hbox {if }\Vert \tilde{x}\Vert > m. \end{array} \right. \end{aligned}$$

(29)

which are continuous in $\tilde{x}$ and satisfy the linear growth condition in Lemma 1. Therefore, $\forall T>0$ and $\forall t\in [0,T]$, there exists a continuous solution $\tilde{x}_m(t)$ with the initial value $\tilde{x}_0$ to the equation

$$\begin{aligned} \tilde{x}_m(t)=\tilde{x}_0+\int _0^tF_m(\tilde{x},\theta )\hbox {d}s+\int _0^tG^T_m(\tilde{x},\theta )\hbox {d}\omega (s). \end{aligned}$$

(30)

Applying Dynkin’s formula, one has

$$\begin{aligned} EV_n(\tilde{x}_m(\tau '_m\wedge T))&=V_n(\tilde{x}_0)+E\int _0^{\tau '_m\wedge T}{\mathcal {L}}V_n(\tilde{x}_m(s))\hbox {d}s\le V_n(\tilde{x}_0)<+\infty \end{aligned}$$

(31)

under which

$$\begin{aligned} P(\tau '_m\le T)\inf _{\Vert \tilde{x}_m\Vert =m}V_n(\tilde{x}_m)\le EV_n(\tilde{x}_m(\tau '_m\wedge T))\le V_n(\tilde{x}_0). \end{aligned}$$

(32)

where $\tau '_m=\inf \{t;\Vert \tilde{x}_m(t;\tilde{x}_0)\Vert \ge m\}$. Since $V_n$ is positive definite and proper, one gets $\forall T>0$, $\lim _{m\rightarrow +\infty }P(\tau '_m\le T)=0$ by letting $m\rightarrow +\infty$ on both sides of (32). Define $\tilde{x}(t)=\tilde{x}_m(t)$, for $t\in [0,\tau '_m)$. Since $\tau '_m\rightarrow +\infty$ almost surely as $m\rightarrow +\infty$, $\{\tilde{x}(t)\}_{t\ge 0}$ is the continuous solution of (28). Furthermore, from (25), ${\mathcal {L}}V_n\le 0$ and $V_n$ is positive definite and proper with respect to $x,\tilde{\varTheta }$; one can obtain the boundedness in probability of $x$ and $\tilde{\varTheta }$, and therefore the solution $\hat{\varTheta }$ is also bounded in probability.

In what follows, we use two cases to analyze the finite-time convergence of $x$. Take a Lyapunov function $V_n^*=\sum _{i=1}^nW_i$, which is positive definite and proper with respect to $x$, for any fixed $\hat{\varTheta }$, and satisfies $V_n^*\le 2(\xi _1^4+\cdots +\xi _n^4)$. From (25), one has

$$\begin{aligned} {\mathcal {L}}V^*_n={\mathcal {L}}V_n+\tilde{\varTheta }\dot{\hat{\varTheta }}\le -c_2\sum _{i=1}^n\xi _i^{\frac{4\mu +\tau }{\mu }}+(\varTheta -\hat{\varTheta })\dot{\hat{\varTheta }} \end{aligned}$$

(33)

with a positive constant $c_2\ge 0$.

Case 1: If $\hat{\varTheta }(0)\ge \varTheta$, with $\dot{\hat{\varTheta }}=\sum _{i=1}^n\delta _i(\cdot )\xi _i^{\frac{4\mu +\tau }{\mu }}\ge 0$, one gets ${\mathcal {L}}V_n^*\le -c_2\sum _{i=1}^n\xi _i^{\frac{4\mu +\tau }{\mu }}$.

Case 2: If $\hat{\varTheta }(0)<\varTheta$, we suppose that there exists a finite time $T_1\ge 0$ such that $\hat{\varTheta }(t)\ge \varTheta$, $\forall t\ge T_1$, which leads to ${\mathcal {L}}V_n^*\le -c_2\sum _{i=1}^n\xi _i^{\frac{4\mu +\tau }{\mu }}$, $\forall t\ge T_1$. Otherwise, there is another finite time $T_2$ satisfying $\dot{\hat{\varTheta }}(t)=0$ and $\hat{\varTheta }(t)<\varTheta$, $\forall t\ge T_2$. Due to $\delta _i(\cdot )>0$, one can get $\xi _i(t)=0$ a.s., $i=1,\ldots ,n$, $\forall t\ge T_2$, i.e., $x(t)=0$ a.s., $\forall t\ge T_2$.

Combining the above two cases, we learn that $\forall \hat{\varTheta }(0)$, there are positive constants $c_3$ and a finite time $T_3$ such that

$$\begin{aligned} {\mathcal {L}}V^*_n\le -c_2\sum _{i=1}^n\xi _i^{\frac{4\mu +\tau }{\mu }}\le -c_3{V_n^*}^{\frac{4\mu +\tau }{4\mu }}, \quad \forall t\ge T_3. \end{aligned}$$

(34)

Since $0<\frac{4\mu +\tau }{4\mu }<1$ and $V_n^*$ is positive definite and proper with respect to $x$, it can be proved that the solution $x$ is finite-time attractive and stable in probability by Lemma 2.

Define the stopping time $\tau _m=\inf \{t\ge \tau _{x_0};\Vert x(t;x_0)\Vert \ge m,m>0\}$. It is clear that $\tau _m$ is an increasing time sequence. Applying Dynkin’s formula, one has, $\forall t\ge 0$

$$\begin{aligned} EV_n^*(x((t+\tau _{x_0})\wedge \tau _m))=&EV_n^*(x(\tau _{x_0}))+ E\int _{\tau _{x_0}}^{(t+\tau _{x_0})\wedge \tau _m}{\mathcal {L}}V_n^*(x(s))\hbox {d}s\le 0. \end{aligned}$$

(35)

Since $V_n^*(x)$ is positive definite and proper with respect to $x$, one can obtain $EV_n^*(x(t+\tau _{x_0})\wedge \tau _m))=0$, which implies that $V_n^*(x((t+\tau _{x_0})\wedge \tau _m))=0$ almost surely, $\forall t\ge 0$. Letting $m\rightarrow +\infty$, we get $x(t+\tau _{x_0})=0$ a.s., $\forall t\ge 0$, which means that system state $x(t)$ is finite-time stable in probability. This completes the proof of Theorem 1. $\square$

4 Illustrative Examples

In this section, we present two examples to illustrate the effectiveness of the design procedure.

Example 1

Consider the following uncertain stochastic nonlinear system

$$\begin{aligned} \hbox {d}x_1=&\left( x_2+\theta ^3 x_1^{\frac{7}{9}}\right) \hbox {d}t,\nonumber \\ \hbox {d}x_2=&\left( u+x_2^{\frac{5}{7}}\ln {\left( 1+x_1^2\theta ^2\right) }\right) \hbox {d}t+x_1^{\frac{2}{3}}\sin \theta \hbox {d}\omega . \end{aligned}$$

(36)

where $\theta$ is an unknown positive constant. From the drift term $x_2^{\frac{5}{7}}\ln {(1+x_1^2\theta ^2)}$, we can find that the unknown parameter $\theta$ appears nonlinearly. Based on Lemma 3, one has $\ln {(1+x_1^2\theta ^2)}\le |x_1\theta |\le x_1^2+\theta ^2\le (1+x_1^2)(1+\theta ^2)$. It is easy to verify that the drift and diffusion terms satisfy Assumption 1 with $\tau =-\frac{2}{9}$. Define $\varTheta =\max \{\theta ^3,\theta ^2,1+\theta ^2\}$ and $\tilde{\varTheta }=\varTheta -\hat{\varTheta }$, where $\hat{\varTheta }$ is the estimate of $\varTheta$.

By letting $V_1=\frac{3}{28}x_1^{\frac{28}{3}}+\frac{1}{2}\tilde{\varTheta }^2$, the infinitesimal generator ${\mathcal {L}}$ of $V_1$ along the trajectory of (36) is

$$\begin{aligned} {\mathcal {L}}V_1\le \,&x_1^{\frac{25}{3}}\left( x_2+x_1^{\frac{7}{9}}\varTheta \right) -\tilde{\varTheta }\dot{\hat{\varTheta }}\\ \le \,&\xi _1^{\frac{25}{7}}(x_2-x_2^{*})+\xi _1^{\frac{25}{7}}x_2^{*} +\varTheta \xi _1^{\frac{82}{21}}-0.113\varTheta \xi _1^{\frac{82}{21}}+0.113\varTheta \xi _1^{\frac{82}{21}} -\tilde{\varTheta }\dot{\hat{\varTheta }}\\ \le \,&\xi _1^{\frac{25}{7}}(x_2-x_2^{*})+\xi _1^{\frac{25}{7}}x_2^{*}-0.113\varTheta \xi _1^{\frac{82}{21}} +1.113\hat{\varTheta }\xi _1^{\frac{82}{21}}-\tilde{\varTheta }\left( \dot{\hat{\varTheta }}-1.113\xi _1^{\frac{82}{21}}\right) \end{aligned}$$

for $\xi _1=x_1^{\frac{7}{3}}$. With the virtual controller $x_2^{*}=-\xi _1^{\frac{1}{3}}(1.311+1.113\hat{\varTheta })$, it yields

$$\begin{aligned} {\mathcal {L}}V_1\le -0.113\varTheta \xi _1^{\frac{82}{21}}-1.311\xi _1^{\frac{82}{21}} +\xi _1^{\frac{25}{7}}(x_2-x_2^{*})-\tilde{\varTheta }\left( \dot{\hat{\varTheta }}-1.113\xi _1^{\frac{82}{21}}\right) . \end{aligned}$$

Defining $V_2=V_1+W_2=V_1+0.1\int _{x_2^*}^{x_2}(s^3-x_2^{*3})^{\frac{11}{3}}\hbox {d}s$, one obtains

$$\begin{aligned} {\mathcal {L}}V_2=\,&{\mathcal {L}}V_1+\frac{\partial W_2}{\partial x_1}\left( x_2+x_1^{\frac{7}{9}}\theta ^3\right) +\frac{\partial W_2}{\partial x_2}\left( u+x_2^{\frac{5}{7}}\ln {(1+x_1^2\theta ^2)}\right) \\&+\frac{\partial ^2 W_2}{\partial x_2^2}x_1^{\frac{4}{3}}\sin ^2\theta +\frac{\partial W_2}{\partial \hat{\varTheta }}\dot{\hat{\varTheta }}. \end{aligned}$$

With $\xi _2=x_2^3-x_2^{*3}$, one has

$$\begin{aligned} \Big |\frac{\partial W_2}{\partial x_1}x_2\Big |=\,&\Big |\frac{11}{30}\frac{\partial x_2^{*3}}{\partial x_1}x_2\int _{x_2^*}^{x_2}\left( s^3-x_2^{*3}\right) ^{\frac{8}{3}}\hbox {d}s\Big |\\ \le \,&0.3\xi _1^{\frac{82}{21}}+\left( \frac{35}{41}a_1\left( \frac{60}{41}a_1\right) ^{\frac{6}{35}}+\frac{63}{82}a_2\left( \frac{95}{82}a_2\right) ^{\frac{19}{63}}\right) \xi _2^{\frac{82}{21}}\\ :=\,&0.3\xi _1^{\frac{82}{21}}+h_1\xi _2^{\frac{82}{21}},\\ \Big |\frac{\partial W_2}{\partial x_1}x_1^{\frac{7}{9}}\theta ^3\Big |\le&\,\, 0.1\varTheta \xi _1^{\frac{82}{21}}+\frac{63}{82}a_1\left( \frac{95}{41}a_1\right) ^{\frac{19}{63}}\varTheta \xi _2^{\frac{82}{21}}\\ :=&\,0.1\varTheta \xi _1^{\frac{82}{21}}+h_2\varTheta \xi _2^{\frac{82}{21}},\\ \Big |\frac{\partial W_2}{\partial x_2}x_2^{\frac{5}{7}}\ln {(1+x_1^2\theta ^2)}\Big |\le \,&\Big |0.1\xi _2^{\frac{11}{3}}\varTheta x_2^{\frac{5}{7}}(1+x_1^2)\Big |\le 0.001\varTheta \xi _1^{\frac{82}{21}}\\&+\left( 0.1x_1^2+\frac{77}{82}a_3\left( \frac{2500}{41}a_3\right) ^{\frac{5}{77}}\right) \varTheta \xi _2^{\frac{82}{21}}\\ :=\,&0.001\varTheta \xi _1^{\frac{82}{21}}+h_3\varTheta \xi _2^{\frac{82}{21}},\\ \Big |\frac{1}{2}\frac{\partial ^2 W_2}{\partial x_2^2}x_1^{\frac{4}{3}}\sin ^2\theta \Big |\le&\, 1.1\xi _2^{\frac{8}{3}}x_2^2\xi _1^{\frac{4}{7}}\varTheta \le 0.011\varTheta \xi _1^{\frac{82}{21}}\\&+\left( 2.2438+\frac{28}{41}a_4\left( \frac{1300}{41}a_4\right) ^{\frac{13}{28}}\right) \varTheta \xi _2^{\frac{82}{21}}\\ :=&\,0.011\varTheta \xi _1^{\frac{82}{21}}+h_4\varTheta \xi _2^{\frac{82}{21}}, \end{aligned}$$

$$\begin{aligned} \big |\xi _1^{\frac{25}{7}}(x_2-x_2^{*})\big |\le&\,\, \xi _1^{\frac{82}{21}}+7.3617\xi _2^{\frac{82}{21}},\\ \Big |\frac{\partial W_2}{\partial \hat{\varTheta }}\sigma _1\Big |\le&\, \Big |0.582\frac{\partial x_2^{*3}}{\partial \hat{\varTheta }}\xi _2^3\left( 1.113\xi _1^{\frac{82}{21}}+(h_2+h_3+h_4)\xi _2^{\frac{82}{21}}\right) \Big |\\ \le&\, 0.01\xi _1^{\frac{82}{21}}+\left( \frac{63}{82}a_5\left( \frac{950}{41}a_5\right) ^{\frac{19}{63}}+a_6\right) \xi _2^{\frac{82}{21}} :=0.01\xi _1^{\frac{82}{21}}+h_5\xi _2^{\frac{82}{21}} \end{aligned}$$

under which

$$\begin{aligned} {\mathcal {L}}V_2\le&-\!0.001\varTheta \xi _1^{\frac{82}{21}}-0.001\xi _1^{\frac{82}{21}} +\left( h_1+7.3617\right) \xi _2^{\frac{82}{21}}+(h_2+h_3+h_4)\varTheta \xi _2^{\frac{82}{21}}\\&+0.1\xi _2^{\frac{11}{3}}(u-x_3^*)+0.1\xi _2^{\frac{11}{3}}x_3^*-\left( \tilde{\varTheta }-\frac{\partial W_2}{\partial \hat{\varTheta }}\right) (\dot{\hat{\varTheta }}-\sigma _1) \end{aligned}$$

where

$$\begin{aligned} a_1&=1.3581(1.311+1.113\hat{\varTheta })^3,\quad a_2=1.3581(1.311+1.113\hat{\varTheta })^4,\\ a_3&=0.1(1+x_1^2)\times (1.311+1.113\hat{\varTheta })^{\frac{5}{7}},\quad a_4=1.1(1.311+1.113\hat{\varTheta })^2,\\ a_5&=2.1631x_1^{\frac{28}{3}}(1.311+1.113\hat{\varTheta })^2,\\ a_6&=1.9435(1.311+1.113\hat{\varTheta })^2\times (h_2+h_3+h_4)|x_1|^{\frac{7}{3}}|\xi _2|^3,\\ \sigma _1&=1.113\xi _1^{\frac{82}{21}}+(h_2+h_3+h_4)\xi _2^{\frac{82}{21}}. \end{aligned}$$

Therefore, the controller can be chosen as

$$\begin{aligned} \dot{\hat{\varTheta }}=\,&\sigma _1,\nonumber \\ u=&-\!10\left( h_1+h_5+7.3618+(h_2+h_3+h_4)\hat{\varTheta }\right) \xi _2^{\frac{5}{21}}. \end{aligned}$$

(37)

Fig. 1

Responses of the closed-loop system (36) and (37)

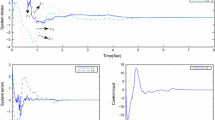
In the simulation, one chooses $\theta =0.1$. With the initial values chosen as $x_1(0)=-0.8$, $x_2(0)=1$ and $\hat{\varTheta }(0)=0.06$, Fig. 1 shows the simulation results. From Fig. 1, we can see that under the constructed adaptive controller, system states $(x_1(t),x_2(t))$ converge to zero almost surely in a finite time.

Example 2

Consider the parallel active suspension system with random noise in [15]

$$\begin{aligned} \hbox {d}x_1&=\frac{1}{A}x_2\hbox {d}t+g_1\hbox {d}\omega ,\nonumber \\ \hbox {d}x_2&=(-c_fx_2+k_fi_v)\hbox {d}t+g_2\hbox {d}\omega \end{aligned}$$

(38)

where $A=1$ is the effective surface of piston, $i_v$ is the current input that adjusts the opening of the current-controlled solenoid valve that controls the fluid flow, $k_f=5$, $g_1=0$, $c_f=2\theta$, and $g_2=0.1\theta (x_1+x_2)$, with an unknown positive constant $\theta$.

It is easy to obtain that $|f_2|\le |x_2|^{5/7}(1+x_2^2)2\theta$ and $\Vert g_2\Vert \le 0.1\theta (|x_1|^{2/3}+|x_2|^{6/7})(1+x_1^2+x_2^2)$ satisfy Assumption 1 by choosing $\tau =-\frac{2}{9}$. Let $\varTheta =\max \{2\theta ,0.01\theta ^2\}$ and $\hat{\varTheta }$ is the estimate of $\varTheta$. According to Theorem 1, one can construct the following state feedback controller by following the design procedure in Section 4

$$\begin{aligned} i_v=&\,-2\xi _2^{\frac{5}{21}}\big (7.3618+h_1+h_4+h_5+(h_2+h_3+0.1(1+x_2^2))\hat{\varTheta }\big ),\nonumber \\ \dot{\varTheta }=&\,0.013x_1^{\frac{82}{9}}+(h_2+h_3+0.1(1+x_2^2))\xi _2^{\frac{82}{21}} \end{aligned}$$

(39)

where

$$\begin{aligned} h_1&=1.9355\rho _1^{\frac{123}{35}}+2.9526\rho _1^{\frac{328}{63}},\quad \rho _1=1.031+0.013\hat{\varTheta },\\ h_2&=0.1056\rho _1^{\frac{410}{539}}(1+x_2^2)^{\frac{82}{77}},\quad h_5=0.0144\rho _1^{\frac{164}{63}}x_1^{\frac{328}{27}},\\ h_3&=0.3406(1+x_1^2+x_2^2)^{\frac{82}{35}}\left( 1+\rho _1^{\frac{12}{7}}\right) ^{\frac{41}{35}}+0.22(1+x_1^2+x_2^2)^2\\&\quad \,+\,0.3702\rho _1^{\frac{41}{14}}(1+x_1^2+x_2^2)^{\frac{41}{14}}\left( 1+\rho _1^{\frac{12}{7}}\right) ^{\frac{41}{28}}+0.3849\rho _1^{\frac{41}{17}}(1+x_1^2+x_2^2)^{\frac{41}{17}}\\ h_4&=0.0227\rho _1^2x_1^{\frac{7}{3}}\xi _2^3\big (0.1(1+x_2^2)+h_2+h_3\big ),\quad \xi _2=x_2^3+x_1^{\frac{7}{3}}\rho _1^3. \end{aligned}$$

Fig. 2

Responses of the closed-loop system (38) and (39)

In the simulation, one chooses $\theta =1$ and the initial values $x_1(0)=1.1$, $x_2(0)=-0.8$, $\varTheta (0)=0.9$. The simulation results are shown in Fig. 2, which demonstrates that the states $(x_1,x_2)$ converge to zero almost surely in a finite time and all the signals of the closed-loop system are bounded in probability.

5 Conclusion

In this note, a systematic design scheme for adaptive controller has been presented to guarantee the boundedness in probability of the closed-loop system, as well as the almost surely convergence to the origin of the system states in a finite time. Actually, for system (6) without unknown parameters, a finite-time controller has been constructed in [29], whose design procedure is consistent with the one here. By introducing the adaptive updating law, this paper extends the results to a class of stochastic nonlinear systems with parametric uncertainty existing in both drift and diffusion terms. The problem to be further studied is how to establish output feedback finite-time controllers for system (6) and nonlinear systems with even more uncertainties.

Appendix

For convenience, some generic functions $\beta _i(\bar{x}_i,\hat{\varTheta })$, $i=1,\ldots ,n$, are used throughout the paper to stand for any nonnegative smooth functions with respect to their variables and may be implicitly changed in different places.

Proof of Proposition 1

The estimate of $|\partial (x_k^{*1/r_k})/\partial x_i|$ can be done by an inductive argument. Note that

$$\begin{aligned} \Big |\frac{\partial x_2^{*\mu /r_2}}{\partial x_1}\Big |=&\Big |\frac{\partial \big (\xi _1\rho _1^{ \mu /r_2}(x_1,\hat{\varTheta })\big )}{\partial x_1}\Big |\le |\xi _1|^{\frac{\mu -r_1}{\mu }}\beta _1(x_1,\hat{\varTheta }). \end{aligned}$$

(40)

Assume that, for $i=1,\ldots ,k-2$,

$$\begin{aligned} \Big |\frac{\partial x_{k-1}^{*\mu /r_{k-1}}}{\partial x_i}\Big |\le \left( \sum _{j=1}^{k-2}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \beta _{k-2}(\bar{x}_{k-2},\hat{\varTheta }). \end{aligned}$$

(41)

Therefore, it can be verified that

$$\begin{aligned} \Big |\frac{\partial x_{k}^{*\mu /r_{k}}}{\partial x_i}\Big |\le&\Big |\xi _{k-1}\frac{\partial \rho _{k-1}^{\mu /r_k}(\cdot )}{\partial x_i}\Big |+\Big |\rho _{k-1}^{\mu /r_k}(\cdot )\frac{\partial x_{k-1}^{*\mu /r_{k-1}}}{\partial x_i}\Big |\nonumber \\ \le&\,|\xi _{k-1}|^{\frac{\mu -r_i}{\mu }}\beta _{k-1}(\cdot ) +\left( \sum _{j=1}^{k-2}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \beta _{k-2}(\cdot )\rho _{k-1}^{\mu /r_k}(\cdot )\nonumber \\ \le&\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \beta _{k-1}(\cdot ),\quad i=1,\ldots ,k-2, \end{aligned}$$

(42)

$$\begin{aligned} \Big |\frac{\partial x_{k}^{*\mu /r_k}}{\partial x_{k-1}}\Big |\le&\Big |\xi _{k-1}\frac{\partial \rho _{k-1}^{\mu /r_k}(\cdot )}{\partial x_{k-1}}\Big |+\Big |\rho _{k-1}^{\mu /r_k}(\cdot )\frac{\mu }{r_{k-1}}x_{k-1}^{\frac{\mu -r_{k-1}}{r_{k-1}}}\Big |\nonumber \\ \le&\,\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_{k-1}}{\mu }}\right) \beta _{k-1}(\cdot ) \end{aligned}$$

(43)

which implies that (41) also holds for the $k$th virtual controller. According to the definition of $\xi _i$, $i=1,\ldots ,k$, and Lemma 4, one gets

$$\begin{aligned} |x_i|\le (|\xi _i|+|\xi _{i-1}\rho _{i-1}^{\mu /r_i}(\cdot )|)^{r_i/\mu } \le |\xi _i| ^{r_i/\mu }+|\xi _{i-1}|^{r_i/\mu }\rho _{i-1}(\cdot ),\quad i=2,\ldots ,k \end{aligned}$$

(44)

which leads to $\forall i=1,\ldots ,k-1$

$$\begin{aligned} \Big |\frac{\partial W_k}{\partial x_i}x_{i+1}\Big |\le&|\xi _k|^3\big (\sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\big ) \big (|\xi _{i+1}|^{r_{i+1}/\mu }+|\xi _{i}|^{r_{i+1}/\mu }\rho _{i}(\cdot )\big )\beta _{k-1}(\cdot )\nonumber \\ \le&\,\frac{1}{3(k-1)}\sum _{j=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }}+|\xi _k|^{\frac{4\mu +\tau }{\mu }}\beta _{k-1}(\cdot ). \end{aligned}$$

(45)

Clearly, Proposition 1 follows from (45). $\square$

Proof of Proposition 2

Under Assumption 1, the drift terms can be estimated as

$$\begin{aligned} |f_i|\le&\left( |\xi _1|^{\frac{r_i+\tau }{\mu }}+\sum _{j=2}^i\left( |\xi _j| ^{\frac{r_i+\tau }{\mu }}+\rho _{j-1}^{\frac{r_i+\tau }{r_j}}(\cdot )|\xi _{j-1}|^{\frac{r_i+\tau }{\mu }}\right) \right) \gamma _{i1}(\bar{x}_i)\varTheta \nonumber \\ \le&\left( |\xi _1|^{\frac{r_i+\tau }{\mu }}+\cdots +|\xi _i|^{\frac{r_i+\tau }{\mu }}\right) \beta _i(\cdot )\varTheta ,\quad i=1,\ldots ,k. \end{aligned}$$

(46)

According to Lemmas 4 and 5, one has $\forall i=1,\ldots ,k$

$$\begin{aligned} \Big |\frac{\partial W_k}{\partial x_i}f_i\Big |\le&|\xi _k|^3\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \big (|\xi _1|^{r_{i+1}/\mu }+\cdots +|\xi _{i}|^{r_{i+1}/\mu }\big )\beta _{k}(\cdot )\varTheta \nonumber \\ \le&\,\frac{1}{3k}\varTheta \sum _{i=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }} +\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\beta _k(\cdot ), \end{aligned}$$

(47)

under which Proposition 2 holds naturally. $\square$

Proof of Proposition 3

Based on Assumption 1, one has $\forall i=1,\ldots ,k$

$$\begin{aligned} \Vert g_i\Vert \le&\left( |x_1|^{\frac{2r_i+\tau }{2r_1}}+\cdots +|x_i|^{\frac{2r_i+\tau }{2r_i}}\right) \eta _{i1}(\bar{x}_i)\eta _{i2}(\theta )\nonumber \\ \le&\left( |\xi _1|^{\frac{2r_i+\tau }{2\mu }}+\cdots +|\xi _i|^{\frac{2r_i+\tau }{2\mu }}\right) \beta _i(\cdot )\eta _{i2}(\theta ). \end{aligned}$$

(48)

Similar to the proof in Proposition 1, the estimate of $|\partial ^2(x_k^{*\mu /r_k})/\partial x_i^2|$ can also be done inductively. Specifically, for $i=1,\ldots ,k-1$

$$\begin{aligned} \Big |\frac{\partial ^2 x_{k}^{*\frac{\mu }{r_{k}}}}{\partial x_i^2}\Big |\le \left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -2r_i}{\mu }}\right) \beta _{k-1}(\cdot ). \end{aligned}$$

(49)

Combining (48) and (49), it yields that for $i=1,\ldots ,k-1$,

$$\begin{aligned} \frac{1}{2}\frac{\partial ^2 W_k}{\partial x_i^2}\Vert g_i\Vert ^2 \le&\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -2r_i}{\mu }}\right) |\xi _k|^3\left( \sum _{l=1}^i|\xi _l|^{\frac{2r_i+\tau }{2\mu }}\right) ^2\varTheta \beta _{k-1}(\cdot )\nonumber \\&+\,\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) ^2|\xi _k|^2\left( \sum _{l=1}^i|\xi _l|^{\frac{2r_i+\tau }{2\mu }}\right) ^2\varTheta \beta _{k-1}(\cdot )\nonumber \\ \le&\,\frac{1}{3k}\varTheta \sum _{j=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }}+\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\bar{h}_{k3}(\cdot ) \end{aligned}$$

(50)

where $\bar{h}_{k3}(\cdot )\ge 0$ is a smooth function of $x_1,\ldots ,x_{k-1},\hat{\varTheta }$. Moreover, for a nonnegative smooth function $\tilde{h}_{k3}(\bar{x}_k,\hat{\varTheta })$

$$\begin{aligned} \frac{1}{2}\frac{\partial ^2 W_k}{\partial x_k^2}\Vert g_k\Vert ^2\le&|\xi _k|^{\frac{3\mu -r_k}{\mu }}\left( |\xi _{k-1}|^{\frac{\mu -r_k}{\mu }}+|\xi _k|^{\frac{\mu -r_k}{\mu }}\right) \left( \sum _{j=1}^k|\xi _j|^{\frac{2r_k+\tau }{2\mu }}\right) ^2\varTheta \beta _k(\cdot )\nonumber \\ \le&\frac{1}{3k}\varTheta \sum _{j=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }}+\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\tilde{h}_{k3}(\cdot ). \end{aligned}$$

(51)

It is clear that Proposition 3 follows from (50) and (51), by letting $h_{k3}(\cdot )\!=(k\!-1)\bar{h}_{k3}(\cdot )+\tilde{h}_{k3}(\cdot )$. $\square$

Proof of Proposition 4

In a similar way, for $i,j=1,\ldots ,k-1$ and $i\ne j$,

$$\begin{aligned} \Big |\frac{\partial ^2 x_{k}^{*\mu /r_k}}{\partial x_i\partial x_j}\Big |\le \left( \sum _{l=1}^{k-1}|\xi _l|^{\frac{\mu -r_i-r_j}{\mu }}\right) \beta _{k-1}(\cdot ) \end{aligned}$$

(52)

under which

$$\begin{aligned} \frac{\partial ^2 W_k}{\partial x_i\partial x_j}\Vert g_i^T\Vert \Vert g_j\Vert \le&\frac{1}{3(k-1)(k-2)}\varTheta \sum _{l=1}^{k-1}|\xi _l|^{\frac{4\mu +\tau }{\mu }}+ \varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\bar{h}_{k4}(\bar{x}_{k-1},\hat{\varTheta }) \end{aligned}$$

(53)

where $\bar{h}_{k4}(\cdot )$ is a nonnegative smooth function. For $i=k$ and $j\ne k$, there exists a smooth function $\tilde{h}_{k4}(\bar{x}_k,\hat{\varTheta })$ satisfying

$$\begin{aligned} \frac{\partial ^2 W_k}{\partial x_k\partial x_j}\Vert g_k^T\Vert \Vert g_j\Vert \le&\frac{1}{6(k-1)}\varTheta \sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+ \varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\tilde{h}_{k4}(\cdot ). \end{aligned}$$

(54)

which leads to Proposition 4 by combining it with (53). $\square$

Proof of Proposition 5

Using (15) and the definition of $\sigma _k$, one can get

$$\begin{aligned} \frac{\partial W_k}{\partial \hat{\varTheta }}\sigma _k\le&\frac{\partial x_k^{*\mu /r_k}}{\partial \hat{\varTheta }}|\xi _k|^3\left( \sum _{i=1}^k|\xi _i|^{\frac{4\mu +\tau }{\mu }}\right) \beta _k(\cdot )\nonumber \\ \le&\,\frac{1}{3}\sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+|\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k5}(\bar{x}_k,\hat{\varTheta }) \end{aligned}$$

(55)

for a nonnegative smooth function $h_{k5}(\cdot )$. In addition, it is easy to obtain that

$$\begin{aligned} \sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _k(\cdot )\xi _k^{\frac{4\mu +\tau }{\mu }}\le \left( 1+\left( \sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _k(\cdot )\right) ^2\right) ^{1/2}\xi _k^{\frac{4\mu +\tau }{\mu }}. \end{aligned}$$

(56)

By choosing $h_{k6}(\bar{x}_k,\hat{\varTheta })=\sqrt{1+(\sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _k(\cdot ))^2}$, we complete the proof. $\square$