1 Introduction

The term elliptic curve does not refer to the geometry of an ordinary ellipse. Instead, the term elliptic in this context refers to the association of a curve with elliptic functions [1] such as the Weierstrass \(\wp .\) In [2], it was shown that the conventional Tresca yield condition represents a limiting case of an elliptic curve when expressed in Weierstrass form. By perturbing the conventional Tresca yield condition in this particular form, a family of yield criteria was generated that are true elliptic curves. Hence, the designation generalized Tresca yield condition was adopted in that paper. Additional yield criteria that can also be represented in Weierstrass form, such as [3], were also discussed there. It was further noted that any yield criterion that can be expressed in Weierstrass form could be parametrized in terms of the Weierstrass elliptic \(\wp \)-function.

Following a brief introduction to elliptic curves [2], the general and singular solutions for the conventional Tresca yield condition were presented in analytical form under plane stress loading conditions. Both solutions are necessary to derive a mode I perfectly plastic solution for the Tresca yield condition under plane stress loading conditions. However, statically admissible perfectly plastic solutions are not necessarily unique. Usually insight is required from an additional source to provide a physically meaningful solution to a problem. Here that insight comes from a limiting process based on solutions of the generalized Tresca yield condition for the mode I crack problem. Support for this approach comes from the well-known and accepted plane stress, mode I perfectly plastic solution under the von Mises yield condition [4], which is recoverable as a limiting case of this analysis.

In algebraic geometry theory, what commonly constitutes Weierstrass form is a cubic algebraic equation having the following representation [5],

$$\begin{aligned} Y^{2}=X^{3}+c_{1} X+c_{2} , \end{aligned}$$
(1)

where \(c_{1} \) and \(c_{2} \) are constants. The generalized Tresca yield condition further defines the symbols in (1) as follows

$$\begin{aligned} X=J_{2} /k^{2}-3,\quad Y=(3\sqrt{3} /2)\,J_{3} /k^{3},\quad c_{1} =-3,\quad c_{2} =2+\varepsilon , \end{aligned}$$
(2)

where \(J_{2} \) and \(J_{3} \) are the second and third invariants of the deviatoric stress tensor, k is a parameter with units of stress, and \(\varepsilon \) is a dimensionless parameter that represents a perturbation of the conventional Tresca yield condition. For the special case, \(\varepsilon =0,\) (1) and (2) reduce to the traditional Tresca yield condition [6], with k becoming the yield strength in pure shear.

Mode I crack problems [7], under plane stress loading conditions, are the intended applications for this theory. Consequently, the deviatoric stress invariants \(J_{2} \) and \(J_{3},\) as defined in [8], reduce to the following expressions

$$\begin{aligned} J_{2} =\left( {\sigma _{1}^{2} -\sigma _{1} \sigma _{2} +\sigma _{2}^{2} } \right) /3,\quad J_{3} =(\sigma _{1} +\sigma _{2} )\left( {2\sigma _{1}^{2} -5\sigma _{1} \sigma _{2} +2\sigma _{2}^{2} } \right) /27, \end{aligned}$$
(3)

where \(\sigma _{1} \) and \(\sigma _{2} \) are the first and second principal stresses, respectively, with the third principal stress \(\sigma _{3}\) being zero.

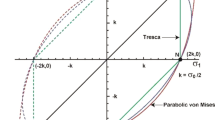
Two distinct but closely related classes of generalizations of the Tresca yield condition are now defined. The first class [2] involves those yield criteria that lie within or on the von Mises yield locus in the principal stress plane, Fig. 1. They are governed by (1) without modification. The second class of generalization involves those yield conditions whose loci lie outside or on the von Mises locus, Fig. 1. In this case, the substitution \(Y^{2}\rightarrow -Y^{2}\) in (1) produces the appropriate relationship. To distinguish between these two classes of yield criteria, the latter is designated as the modified generalized Tresca yield condition. Both generalizations of the Tresca yield condition are plotted in the normalized principal stress plane in Fig. 1, where \(\sigma _{0} \) is the yield strength in tension.

Note that the outer hexagon, shown in Fig. 1, is the boundary proposed in [6] and in [9] as the limit of convex plastic yield surfaces for isotropic materials. It was used for comparison with newly defined yield criteria in [10] and [11]. A more detailed representation of this boundary, which delineates specific lines, is depicted in Fig. 2. A relationship that expresses this outer bound compactly in \(\left( {J_{2} ,J_{3} } \right) \) is also provided for plane stress loading conditions on the figure.

Fig. 1
figure 1

Generalizations of the Tresca yield condition

Full size image
Fig. 2
figure 2

Outer boundary of convex yield surfaces

Full size image

2 Generalized Tresca yield condition

The generalized Tresca yield condition has the following representation under plane stress loading conditions [2],

$$\begin{aligned}&\left( {\sqrt{\varepsilon }-4} \right) ^{2}\left( {\sigma _{1} -\sigma _{2} } \right) ^{2}\sigma _{1}^{2} \sigma _{2}^{2} +4\left( {\sqrt{\varepsilon }-4} \right) \sigma _{0}^{2} \left( {\sigma _{1}^{2} -\sigma _{1} \sigma _{2} +\sigma _{2}^{2} } \right) ^{2}+ \nonumber \\&\quad 32\sigma _{0}^{4} \left( {\sigma _{1}^{2} -\sigma _{1} \sigma _{2} +\sigma _{2}^{2} } \right) =4\left( {\sqrt{\varepsilon }+4} \right) \sigma _{0}^{6} ,\quad 0\le \varepsilon \le 16. \end{aligned}$$
(4)

The relationships between the yield strength in tension \(\sigma _{0} \) and the yield strength in pure shear \(\tau _{0} \) in terms of the parameters k and \(\varepsilon \) of (2) are given by

$$\begin{aligned} \sigma _{0} =k\sqrt{4-\sqrt{\varepsilon }} ,\quad \tau _{0} =k\sqrt{3-2\cosh \left[ {(2/3)\sinh ^{-1}\left( {\sqrt{\varepsilon }/2} \right) } \right] } ,\quad 0\le \varepsilon <16. \end{aligned}$$
(5)

The parameter \(\varepsilon \) in (4) can be determined experimentally from the ratio of \(\tau _{0} /\sigma _{0},\) as determined from (5), after dividing the two expressions to eliminate k.

For \(\varepsilon \) equal to 16, the von Mises yield condition is recoverable from (4). This reduction in algebraic order occurs because the right hand side of (1) becomes factorable for that particular value of \(\varepsilon .\) Consequently, the von Mises yield condition is regarded as a limiting case of the generalized Tresca yield condition.

The largest possible normal stress \(\sigma _{\max }\) as a function of \(\varepsilon \) is determined by setting \(\sigma _{1} =\sigma _{\max }\) and \(\sigma _{2} =\sigma _{\max } /2\) in (4) as

$$\begin{aligned} \sigma _{\max } =2\sigma _{0} \sqrt{3-2\cosh \left( {\frac{1}{3}\cosh ^{-1}\left( {1+\frac{\varepsilon }{2}} \right) } \right) } /\sqrt{4-\sqrt{\varepsilon }} ,\quad 0\le \varepsilon <16. \end{aligned}$$
(6)

Taking the limit of (6) as \(\varepsilon \rightarrow 16\) gives the classical value \(\sigma _{\max } =2\sigma _{0} /\sqrt{3}\) of the von Mises yield condition. This limiting process is necessary, as the expression itself becomes indeterminate for \(\varepsilon \) equal to 16.

The location of \(\sigma _{\max } /\sigma _{0}\) in Fig. 1 corresponds to the largest value of \(\sigma _{1} /\sigma _{0} \) to the right of the origin of the normalized principal stress plane on a given yield surface for a particular value of \(\varepsilon .\)

3 Modified generalized Tresca yield condition

Although applications in this paper will be restricted to the generalized Tresca yield condition, some corresponding modified relationships are provided for completeness. To obtain the modified generalized Tresca yield condition, substitute \(-Y^{2}\) for \(Y^{2}\) in (1). The relationships (2) and (3) remain the same as the unmodified version regarding deviatoric stress invariants. However, the relationships for the yield strength in tension and in pure shear in terms of \(\varepsilon \) become

$$\begin{aligned} \begin{array}{l} \sigma _{0} =k\sqrt{\frac{9}{2}-3\sqrt{7} \sinh \left( {\frac{1}{3}\sinh ^{-1}\frac{13+2\varepsilon }{7\sqrt{7} }} \right) } ,-2.4355\le \varepsilon \le 16, \\ \tau _{0} =\left\{ {{\begin{array}{*{20}c} {k\sqrt{3-2\cos \left[ {(2/3)\sin ^{-1}\left( {\sqrt{-\varepsilon } /2} \right) } \right] } ,-2.4355\le \varepsilon<0} \\ {k,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,\varepsilon =0} \\ {k\sqrt{3-2\cosh \left[ {(2/3)\sinh ^{-1}\left( {\sqrt{\varepsilon }/2} \right) } \right] } ,\quad \,\,\;\,0<\varepsilon <16.} \\ \end{array} }} \right. \\ \end{array} \end{aligned}$$
(7)

In Fig. 3, the ratio \(\tau _{0} /\sigma _{0} \) is plotted as a function of \(\varepsilon \) for both classes of generalized Tresca yield conditions.

Fig. 3
figure 3

Ratio of yield strengths in shear to tension as a function of the parameter \(\varepsilon \)

Full size image

Note that in Fig. 3 the values of the ratio of \(\tau _{0} /\sigma _{0}\) exceed or else approach the limiting value of the von Mises yield condition for the modified generalized Tresca yield condition. The lower limit of \(\varepsilon ,\) shown in Fig. 3, is a consequence of Drucker’s criterion of a stable plastic material [12]. That criterion states that in order for a material to remain stable the yield surface must be convex.

The curve shown in Fig. 1, which is closest to the outer hexagonal boundary, and at specific points touches it, corresponds to \(\varepsilon =-2.4355.\) Note that any closed, smooth curve is convex if its signed curvature \(\kappa \) does not change sign along its boundary [13]. A plot of curvature for the shape of a curve just inside the convex limit is shown in Fig. 4 for a value \(\varepsilon =-2.43.\)

Fig. 4
figure 4

Curvature of yield locus shape near its convex limit

Full size image

The curvature in Fig. 4 is close to changing sign at six specific locations on the yield surface where the values of \(\kappa \) are near to zero. For values of \(\varepsilon <-2.4355,\) there are curves of this family that have concave regions and consequently are unsuitable as yield surfaces.

4 Analytical solution of governing equation

The solutions presented in this section are intended for application to mode I, perfectly plastic problems under plane stress loading conditions, as in [4, 7, 14, 15]. In this context, a stress function in polar coordinates \(\phi ,\) analogous to an Airy stress function with respect to the derived stresses [16], is introduced to solve yield condition (4) under conditions of equilibrium. As is typical of plane stress, mode I perfectly plastic solutions [17], the stress function may be simplified to just \(f\left( \theta \right) ,\) as the stresses themselves (9) are independent of radial coordinate r, i.e.,

$$\begin{aligned}&\phi \left( {r,\theta } \right) =r^{2}f\left( \theta \right) ,\quad p={f}'\left( \theta \right) , \end{aligned}$$
(8)
$$\begin{aligned}&\sigma _{\theta } =2f\left( \theta \right) ,\quad \tau _{r\theta } =-{f}'\left( \theta \right) =-p,\nonumber \\&\sigma _{r} ={f}''\left( \theta \right) +2f\left( \theta \right) =p\frac{dp}{df}+2f, \end{aligned}$$
(9)

where \(\sigma _{\theta } \) and \(\sigma _{r} \) are normal stresses, \(\tau _{r\theta } \) is the shear stress in polar coordinates, and the primes on \(f\left( \theta \right) \)denote differentiation with respect to \(\theta .\)

The principal stresses \(\sigma _{1} \) and \(\sigma _{2} \) are defined in terms of the polar coordinate stresses as

$$\begin{aligned} \left\{ {\sigma _{1} \;\sigma _{2} } \right\} =\left( {\sigma _{r} +\sigma _{\theta } } \right) /2\pm \sqrt{\left( {\sigma _{r} -\sigma _{\theta } } \right) ^{2}+4\tau _{r\theta }^{2} } /2. \end{aligned}$$
(10)

Let us now introduce the following notation as in [2, 14, 15],

$$\begin{aligned} Q=\frac{p^{2}}{2}+2f^{2},\quad q=\frac{dQ}{df}={f}''\left( \theta \right) +4f\left( \theta \right) . \end{aligned}$$
(11)

With these substitutions (8)–(11), the generalized Tresca yield condition (4) assumes the following form

$$\begin{aligned} \left( {2k^{2}+kq+fq-Q} \right) \left( {2k^{2}-kq+fq-Q} \right) \left( {4k^{2}-q^{2}+8\left( {fq-Q} \right) } \right) =\varepsilon k^{6}, \end{aligned}$$
(12)

where k is defined by the first equation appearing in (5). When \(\varepsilon \) equals zero, the governing equation for the conventional Tresca yield condition is obtained. Analytical solutions will simplify in this case because (12) becomes factorable. The general solution for the conventional Tresca yield condition is provided in [2]. Although highly nonlinear, the more general form of (12) with \(\varepsilon \ne 0\) is also solvable analytically by taking advantage of the fact that it has the form of a Clairaut equation. See [14, 18], and [19] for solution techniques for this special class of equations.

The operational procedure to solve this Clairaut equation is to treat q as a constant \(q_{c}\) and to solve (12) for Q. By reintroducing the definition of Q in terms of p and f from (11), one then solves this expression for p. At this point, after identifying p as \({f}'\left( \theta \right) ,\) the equation becomes separable in f and \(\theta ,\) which is then integrated to obtain its primitive. The primitive contains an inverse trigonometric function, which can then be inverted to provide a more convenient form of solution for evaluating stresses.

Following this procedure, the general solution of (12) is

$$\begin{aligned}&f=\left( {q_{c} -\sqrt{8c+q_{c}^{2} } \sin \left( {2\theta +\alpha } \right) } \right) /4, \nonumber \\&\quad a=144k^{4}-40k^{2}q_{c}^{2} +q_{c}^{4} ,\quad b=1728k^{6}-6480k^{4}q_{c}^{2} -540k^{2}q_{c}^{4} +q_{c}^{6} , \nonumber \\&\quad A=24\sqrt{-3k^{2}q_{c}^{2} a^{2}+3k^{6}b\varepsilon +1296k^{12}\varepsilon ^{2}} , \nonumber \\&\quad B=\root 3 \of {A-6480k^{4}q_{c}^{2} -540k^{2}q_{c}^{4} +q_{c}^{6} +864k^{6}\left( {2+\varepsilon } \right) }, \nonumber \\&\quad c=\frac{3}{2}k^{2}-\frac{q_{c}^{2} }{24}+\frac{-144k^{4}-216k^{2}q_{c}^{2} -q_{c}^{4} }{24B}-\frac{B}{24}, \end{aligned}$$
(13)

where \(\alpha \) and \(q_{c} \) are arbitrary constants.

The normalized phase plane of solution (13) is shown in Fig. 5 for the case \(\varepsilon \) equals one. For a fixed value of \(q_{c},\) an individual ellipse is traced out in the phase plane upon varying \(\theta .\)

Fig. 5
figure 5

Typical phase plane of solutions for generalized Tresca yield condition. After [2]

Full size image

The envelope of the family of ellipses shown in Fig. 5 constitutes the locus of what is known as a singular solution of (12). Singular solutions are artifacts of nonlinear equations, and they cannot be obtained directly from the general solution by selecting particular values of the arbitrary constants. Instead, they must be solved independently using other techniques.

One method of obtaining a singular solution is through a process called the principle of duality in [18]. This use of a contact transform is particularly effective in solving singular solutions of Clairaut equations related to plasticity theory [14]. The transformation chosen for solving (12) is numbered as (41.4) in [20] and defined as

$$\begin{aligned} f=\frac{dy}{dx},\quad Q=x\frac{dy}{dx}-y,\quad q=x, \end{aligned}$$
(14)

where the three contact variables are \(\left( {x,y,\frac{dy}{dx}} \right) \). The result of substituting (14) into (12) is

$$\begin{aligned} \left( {2k^{2}+kx+y} \right) \left( {2k^{2}-kx+y} \right) \left( {4k^{2}-x^{2}+8y} \right) =\varepsilon k^{6}. \end{aligned}$$
(15)

Note how the differential equation has been transformed into an algebraic equation, which is a property related to (12) having Clairaut form.

The next step in obtaining the singular solution is to differentiate (15) with respect to x under the assumption that \(y=y\left( x \right) ,\) i.e.,

$$\begin{aligned}&\left( {k+\frac{dy}{dx}} \right) \left( {2k^{2}-kx+y} \right) \left( {4k^{2}-x^{2}+8y} \right) + \nonumber \\&\quad \left( {2k^{2}+kx+y} \right) \left( {-k+\frac{dy}{dx}} \right) \left( {4k^{2}-x^{2}+8y} \right) + \nonumber \\&\quad \left( {2k^{2}+kx+y} \right) \left( {2k^{2}-kx+y} \right) \left( {-2x+8\frac{dy}{dx}} \right) =0. \end{aligned}$$
(16)

This particular operation captures information specifically related to the envelope of the general solution, which is pertinent to finding the singular solution.

Now the inverse of contact transformation (14) is given by

$$\begin{aligned} x=q,\quad y=fq-Q,\quad \frac{dy}{dx}=f. \end{aligned}$$
(17)

By substituting (17) into both (15) and (16), one generates a system of equations in the original variables. The elimination of the common variable q from this newly defined system of equations will reduce the order of the differential equation by one, i.e., from second to first. This reduction in order occurs because q, as defined by (11), is the only term of the original differential equation containing second-order derivatives of \(f\left( \theta \right) \) with respect to \(\theta \).

Perhaps the simplest way to eliminate q from this system of equations is to solve first the cubic algebraic equation [21] for q in (16) once inverse relationships (17) have been introduced. Afterward, substitute the only real-valued root for q obtained from (16) into (15) following the application of the inverse contact transformation (17), i.e., substitute q into the original ordinary differential equation (12). Following this procedure, a differential algebraic equation of order one is generated for the singular solution.

In this context, the only real-valued root for q, determined from (16), is given by

$$\begin{aligned}&q=\frac{4f^{2}+\,Q-6k^{2}}{2\left( {f^{2}-k^{2}} \right) }f+\sqrt{-\frac{G}{\left( {f^{2}-k^{2}} \right) ^{2}}} \sinh \left( {\frac{1}{3}\sinh ^{-1}\left( {\frac{3\sqrt{3} f\,H}{\left( {f^{2}-k^{2}} \right) G}\,\sqrt{-\frac{\left( {f^{2}-k^{2}} \right) ^{2}}{G}} } \right) } \right) , \nonumber \\&\quad \text {where }G=48f^{6}-24f^{4}\left( {3k^{2}+Q} \right) +2k^{2}\left( {8k^{4}-12k^{2}Q+Q^{2}} \right) + \nonumber \\&\quad \quad f^{2}\left( {20k^{4}+36k^{2}Q+Q^{2}} \right) , \nonumber \\&\quad \text { and }\quad \;\;\,H=64f^{8}-48f^{6}\left( {3k^{2}+Q} \right) +k^{2}Q\left( {8k^{4}+6k^{2}Q+Q^{2}} \right) + \nonumber \\&\quad 4f^{4}\left( {22k^{4}+27k^{2}Q+2Q^{2}} \right) -4f^{2}k^{2}\left( {4k^{4}+14k^{2}Q+5Q^{2}} \right) . \end{aligned}$$
(18)

Subsequently, the substitution of q from (18) into (12) produces the differential algebraic equation of order one for the singular solution. The differential algebraic equation, so obtained, now allows the loci of individual singular solutions to be plotted implicitly in the phase plane for the range \(0<\varepsilon <16.\)

In Fig. 6, several loci of singular solutions in the phase plane are displayed spanning three orders of magnitudes in \(\varepsilon .\) Notice how the shape of the singular solution locus of Fig. 6 for \(\varepsilon \) equals one matches the shape of the envelope of ellipses shown in Fig. 5.

Fig. 6
figure 6

Phase plane of singular solution loci of generalized Tresca yield condition

Full size image

While the differential equation for singular solutions has now undergone a reduction from second to first order, a completely analytical solution appears to be intractable because of the complicated nature of its degree. Nevertheless, the subroutine NDSolve of Mathematica®  contains a powerful differential algebraic equation solver whose capabilities may be applied to equations of this type.

In the solution of the mode I perfectly plastic crack problem under the von Mises yield condition [4], the singular solution governs the leading sector ahead of the crack tip. Incidentally, that singular solution was also associated with a fan of straight mathematical characteristics. It will be assumed here that singular solutions govern the leading sector for all cases of the generalized Tresca yield condition with the exception of the conventional Tresca yield condition. This exception is a consequence that the singular solution for the conventional Tresca yield condition does not encompass the entire locus of the family of ellipses of its general solution [2]. All other cases of the generalized Tresca yield condition do.

In order to solve the differential algebraic equation numerically for the singular solution for cases where \(0<\varepsilon <16,\) one must specify an initial condition for the function \(f\left( \theta \right) .\) In this capacity, \(\sigma _{\max } \) of (6) plays a vital role. In the leading sector directly ahead of the crack tip, designated here by \(\theta =\theta _{0},\) one may infer using symmetry arguments that \(\sigma _{\theta } =\sigma _{\max } =2f\left( {\theta _{0} } \right) .\) Consequently, the initial condition is \(f\left( {\theta _{0} } \right) =\sigma _{\max } /2,\) for \(0<\varepsilon <16,\) where \(\sigma _{\max }\) is determined by (6). Note that computationally it is necessary to use an initial value of \(f\left( \theta \right) \) slightly smaller than \(f\left( {\theta _{0} } \right) \) to avoid an extraneous solution that is constant and violates yield. The special cases, \(\varepsilon =0\) for the Tresca yield condition and \(\varepsilon =16\) for the von Mises yield condition, are solvable analytically and do not require numerical solution.

In [2], both the general solution and singular solution for the conventional Tresca yield condition \(\left( {\varepsilon =0} \right) \) were obtained analytically. The phase plane of these solutions is shown in Fig. 7. The singular solution for the Tresca yield condition is limited to the flat surfaces comprising the top and bottom extremals of the phase plane. The curved sides of the barrel shaped boundary are simply particular members of the family of ellipses of the general solution and do not constitute part of a singular solution.

Fig. 7
figure 7

Phase plane of solutions for conventional Tresca yield condition. After [2]

Full size image
Fig. 8
figure 8

Phase plane of solutions for von Mises yield condition

Full size image

In Fig. 8, the phase plane for solutions of the von Mises yield condition \(\left( {\varepsilon =16} \right) \) is shown. Note that the envelope of the family of ellipses of its general solution and correspondingly the locus of the singular solution are circular. There are also three distinct heavy curves that correspond to individual sectors of solutions for the mode I crack problem under the von Mises yield condition [4]. The corresponding physical plane is represented in Fig. 9 where mathematical characteristics of the solution form a grid pattern. Only the upper half plane needs to be considered due to symmetry.

Fig. 9
figure 9

Perfectly plastic mode I crack problem under the von Mises yield condition, after [4]. Reproduced from [17] with minor modifications with permission of the American Society of Mechanical Engineers

Full size image

The leading sector OCD of Fig. 9 corresponds to the highlighted portion of the circular boundary (red) in Fig. 8, which constitutes a portion of the singular solution locus of the phase plane. The remaining two sectors of Fig. 9, OBC and OAB, correspond to the heavy green and blue lines, respectively, of Fig. 8, which correspond to particular cases of the general solution. Along the crack line OA of Fig. 9, a state of uniaxial compression exists. Along OB, a stress discontinuity forms.

5 Numerical solution of mode I crack problems under the generalized Tresca yield condition

The crack orientation for all mode I crack problems solved in this article will be aligned similarly to that shown in Fig. 9. The semi-infinite crack will lie along the polar coordinate angle \(\theta =0\) with the angle \(\theta \) measured in the counterclockwise direction. The first two sectors for the generalized Tresca yield condition can use the analytical solution (13). The third sector, however, must solve the differential algebraic equation generated by substituting (18) into (12). Being of first order this differential algebraic equation requires a single initial condition

$$\begin{aligned} f\left( {\theta _{0} } \right) =\sigma _{\max } /2,\quad \text { where }\theta _{0} =\pi , \end{aligned}$$
(19)

and \(\sigma _{\max } \) is determined by (6). The angles separating the three distinct sectors of the upper half plane must also be determined numerically.

The first sector of the solution will assume a uniaxial state of compression \(-\sigma _{0} \) along the crack line in agreement with the solution of [4] under the von Mises yield condition. With this assumption, the stress function has the form

$$\begin{aligned} f_{1} =-\left( {\sigma _{0} /2} \right) \sin ^{2}\theta , \end{aligned}$$
(20)

which is a special case of the general solution (13).

The second sector of the solution will employ a stress function \(f_{2} \) of the form (13), where the angle between sectors 1 and 2 will be designated \(\theta _{12} .\) The third sector will solve the differential algebraic equation for the function \(f_{3} \) of the singular solution subject to (19) as the initial condition. The angle separating sectors 2 and 3 will be designated \(\theta _{23} .\)

The first step in the solution process is to solve for \(f_{3} \) using the subroutine NDSolve of Mathematica®  to establish an interpolating function over the region \(\theta =0\) to \(\theta =\pi .\) Within Mathematica®,  this interpolation function can be treated as any other analytical function including the taking of derivatives. Consequently, the stress field in regions 1, 2, and 3 can now be determined once the constants \(\alpha ,\;q_{c} ,\;\theta _{12} ,\text { and }\theta _{23} \) are evaluated. The subroutine FindRoot of Mathematica®  was used for this purpose. For equilibrium, the stresses \(\sigma _{\theta } \) and \(\tau _{r\theta } \) must agree at the interfaces \(\theta _{12} \) and \(\theta _{23} .\) Thus, there are four equations and four unknowns \(\left( {\alpha ,q_{c} ,\theta _{12} ,\theta _{23} } \right) \) to be solved simultaneously, i.e.,

$$\begin{aligned} \begin{array}{l} \left. {\sigma _{\theta } } \right| _{f_{1} ,\theta _{12} } =\left. {\sigma _{\theta } } \right| _{f_{2} ,\theta _{12} } ,\left. {\quad \sigma _{\theta } } \right| _{f_{2} ,\theta _{23} } =\left. {\sigma _{\theta } } \right| _{f_{3} ,\theta _{23} } \\ \left. {\tau _{r\theta } } \right| _{f_{1} ,\theta _{12} } =\left. {\tau _{r\theta } } \right| _{f_{2} ,\theta _{12} } ,\left. {\quad \tau _{r\theta } } \right| _{f_{2} ,\theta _{23} } =\left. {\tau _{r\theta } } \right| _{f_{3} ,\theta _{23} } . \\ \end{array} \end{aligned}$$
(21)

Table 1 summarizes the numerical results of this analysis for four specific values of \(\varepsilon .\)

Table 1 Mode I crack parameters generalized Tresca yield condition
Full size table

The stresses, so obtained from the stress functions \(\left( {f_{1} ,f_{2} ,f_{3} } \right) \), for the mode I crack problem under plane stress loading conditions and the generalized Tresca yield condition are plotted in Fig. 10. The greatest differences exhibited in the behavior of stresses associated with a change of \(\varepsilon \) in Fig. 10 occur near \(\theta =\pi \) for \(\sigma _{r} .\) For smaller values of \(\varepsilon , \sigma _{r}\) values initially tend toward zero with increasing \(\theta \) in the third sector, but then abruptly rise near \(\theta =\pi .\) This behavior in \(\sigma _{r} \) was also noted in a similar mode I crack problem [14, 15], under the yield condition in [3], for which analytical solutions were given for the ordinary differential equations for all three sectors.

Fig. 10
figure 10

Spectrum of mode I crack stresses for generalized Tresca yield condition

Full size image

6 Mode I crack solution for conventional Tresca yield condition

The behavior exhibited by the stresses in Fig. 10 gives an indication of what the stresses of the mode I crack problem might be for the conventional Tresca yield condition. As \(\varepsilon \rightarrow 0,\) the stress \(\sigma _{r} \) shows a tendency toward zero as \(\theta \rightarrow \pi .\) Because \(\tau _{r\theta } \) is also zero in front of the crack, these two together might indicate a uniaxial state of tension \(\sigma _{0} \) exists there. This possibility is related to the fact that the whole right hand face of the Tresca yield condition is equal to \(\sigma _{0} ,\) which is also equal to \(\sigma _{\max } .\) This differs significantly from other members of the family of yield surfaces of the generalized Tresca yield condition where \(\sigma _{\max } >\sigma _{0} ,\) and it may help explain the rapid rise in \(\sigma _{r} \) near \(\theta =\pi \) in Fig. 10. Another indication of the state of stress for the conventional Tresca yield condition comes from the region near \(\theta =2.\) There \(\tau _{r\theta } \) appears to remain nearly a constant over a certain interval, which is an indication of a singular solution of the Tresca yield condition [2]. Further, in agreement with the solution in [4] under the von Mises yield condition, the region near the crack face will be assumed to be in a state of uniaxial compression \(-\sigma _{_{0} } .\) Finally, adjacent to the sector of uniaxial compression is an intervening sector of the general solution that joins with the singular solution sector. All these assumptions are illustrated in Fig. 11, along with additional information that comes from the actual solution of the problem.

Fig. 11
figure 11

Mode I crack problem under Tresca yield condition

Full size image

Now the general and singular solutions for the conventional Tresca yield condition were given in [2]. The stress function and stresses in sector OAB of Fig. 11 for uniaxial compression along the crack faces are a special case of the general solution

$$\begin{aligned} \begin{array}{l} f^{OAB}=-\frac{\sigma _{0} }{2}\sin ^{2}\theta ,\quad 0\le \theta \le \theta _{OB} \\ \sigma _{\theta }^{OAB} =-\sigma _{0} \sin ^{2}\theta ,\quad \tau _{r\theta }^{OAB} =\sigma _{0} \sin \theta \cos \theta ,\quad \sigma _{r}^{OAB} =-\sigma _{0} \cos ^{2}\theta . \\ \end{array} \end{aligned}$$
(22)

Similarly, the stress function and the stresses in sector ODE for uniaxial tension ahead of the crack tip are

$$\begin{aligned} \begin{array}{l} f^{ODE}=\frac{\sigma _{0} }{2}\cos ^{2}\theta ,\quad \theta _{OD} \le \theta \le \pi , \\ \sigma _{\theta }^{ODE} =\sigma _{0} \cos ^{2}\theta ,\quad \tau _{r\theta }^{ODE} =\sigma _{0} \sin \theta \cos \theta ,\quad \sigma _{r}^{ODE} =\sigma _{0} \sin ^{2}\theta . \\ \end{array} \end{aligned}$$
(23)

The form of the singular solution is

$$\begin{aligned} \begin{array}{l} f^{OCD}=\frac{\sigma _{0} }{2}\theta -\beta ,\quad \theta _{OC} \le \theta \le \theta _{OD} , \\ \sigma _{\theta }^{OCD} =\sigma _{0} \theta -2\beta ,\quad \tau _{r\theta }^{OCD} =-\frac{\sigma _{0} }{2},\quad \sigma _{r}^{OCD} =\sigma _{0} \theta -2\beta , \\ \end{array} \end{aligned}$$
(24)

where \(\beta \) is a constant to be determined from a boundary condition on traction. It is also important to note that \(\sigma _{\theta }^{OCD} =\sigma _{r}^{OCD} ,\) as this is a key to finding a meaningful solution. In Fig. 10, \(\sigma _{\theta } \approx \sigma _{r} \) for \(\varepsilon =0.01\) in the neighborhood of \(\theta =2,\) which indicates the singular solution (24) is approached in that region for small \(\varepsilon .\) In addition, it was previously mentioned that \(\tau _{r\theta } \) is nearly a constant in this region for small \(\varepsilon \) as (24) clearly indicates.

In sector OBC, the general solution is

$$\begin{aligned} \begin{array}{l} f^{OBC}=\gamma +\frac{\sigma _{0} }{4}\sin \left( {2\theta +\delta } \right) ,\quad \theta _{OB} \le \theta \le \theta _{OC} , \\ \sigma _{\theta }^{OBC} =2\gamma +\frac{\sigma _{0} }{2}\sin \left( {2\theta +\delta } \right) ,\quad \tau _{r\theta }^{OBC} =-\frac{\sigma _{0} }{2}\cos \left( {2\theta +\delta } \right) ,\quad \sigma _{r}^{OBC} =2\gamma -\frac{\sigma _{0} }{2}\sin \left( {2\theta +\delta } \right) , \\ \end{array} \end{aligned}$$
(25)

where \(\gamma \) and \(\delta \) are constants to be determined from boundary conditions on traction.

The numerical solution for the constants \(\left( {\beta ,\gamma ,\delta ,\theta _{OB} ,\theta _{OC} ,\theta _{OD} } \right) \) of (23)–(25) was obtained in a very similar fashion as for the generalized Tresca yield condition. However, there are now six unknowns for the conventional Tresca solution instead of four unknowns previously encountered, as there are now four distinct sectors to consider rather than three. The results of the numerical analysis are displayed in Table 2.

Table 2 Mode I crack parameters under the Tresca yield condition
Full size table

Figure 7 shows the location of the mode I solution on the phase plane of the conventional Tresca yield condition by highlighting the four distinct regions associated with the four sectors of the physical plane.

The location of various sectors of Fig. 11 is shown in the Tresca yield surface in Fig. 12.

Fig. 12
figure 12

Location of mode I crack sectors (Fig. 11) on Tresca yield surface

Full size image

Note that the stresses in Fig. 12 lie either in a hyperbolic region of the Tresca yield condition, sector OBC and the fan OCD, or else on the nexus of the hyperbolic and parabolic regions, sectors ODE and OAB. The use of the words hyperbolic and parabolic here refers to the class of partial differential equations associated with those regions of the yield surface [12]. In sector OCD, a fan of slip lines exist, which is similar in appearance to those encountered in a plane strain problem. Similarly, in sector OBC an orthogonal network of straight slip lines exist, as it is also associated with a hyperbolic region of the yield surface.

For completeness, the mode I solution under the von Mises yield condition [4] will now be provided.

Region OAB of Fig. 9 has the same form of stress function and stresses (22) as the Tresca yield condition for uniaxial compression and consequently will not be repeated here. For sector OBC of Fig. 9, one has

$$\begin{aligned} \begin{array}{l} f^{OBC}=\frac{c_{3} }{4}-\frac{1}{4\sqrt{3} }\sqrt{4\sigma _{0}^{2} -c_{3}^{2} } \sin \left( {2\theta +c_{4} } \right) ,\quad \theta _{OB} \le \theta \le \theta _{OC} , \\ \sigma _{\theta }^{OBC} =\frac{c_{3} }{2}-\frac{1}{2\sqrt{3} }\sqrt{4\sigma _{0}^{2} -c_{3}^{2} } \sin \left( {2\theta +c_{4} } \right) ,\quad \tau _{r\theta }^{OBC} =\frac{1}{2\sqrt{3} }\sqrt{4\sigma _{0}^{2} -c_{3}^{2} } \cos \left( {2\theta +c_{4} } \right) , \\ \sigma _{r}^{OBC} =\frac{c_{3} }{2}+\frac{1}{2\sqrt{3} }\sqrt{4\sigma _{0}^{2} -c_{3}^{2} } \sin \left( {2\theta +c_{4} } \right) , \\ \end{array} \end{aligned}$$
(26)

where \(c_{3} \) and \(c_{4} \) are constants, which are given in Table 3 along with \(\theta _{OB} \) and \(\theta _{OC} .\) For region OCD of Fig. 9, which is the singular solution sector, one has

$$\begin{aligned} \begin{array}{l} f^{OCD}=-\frac{\sigma _{0} }{\sqrt{3} }\cos \theta ,\quad \theta _{OC} \le \theta \le \pi , \\ \sigma _{\theta }^{OCD} =-\frac{2\sigma _{0} }{\sqrt{3} }\cos \theta ,\quad \tau _{r\theta }^{OCD} =-\frac{\sigma _{0} }{\sqrt{3} }\sin \theta ,\quad \sigma _{r}^{OCD} =-\frac{\sigma _{0} }{\sqrt{3} }\cos \theta . \\ \end{array} \end{aligned}$$
(27)

Note that in the original solution in [4] the crack surfaces lie to the left of the crack tip rather than to the right as shown in Fig. 9.

Table 3 Mode I crack parameters under the von Mises yield condition
Full size table

In [4], all stresses fall within the hyperbolic region of the von Mises yield condition [12], with the exception of the line OD ahead of the crack tip, which is parabolic. See Fig. 13.

Fig. 13
figure 13

Location of mode I crack sectors (Fig. 9) on von Mises yield surface

Full size image

Figure 8 shows the location of the mode I solution of [4] on the phase plane for solutions under the von Mises yield condition by highlighting the three distinct regions associated with the three sectors of the physical plane. Compare this figure with the four regions of Fig. 7 for the mode I problem under the Tresca yield condition. In the case of the Tresca solution, it takes, in effect, two sectors (colors red and cyan) to replace the single leading sector (color red) of the singular solution of the von Mises solution.

A comparison of Tresca and von Mises stresses for the mode I crack problem follows in Fig. 14.

Fig. 14
figure 14

Comparison of mode I crack solutions, Tresca versus von Mises yield criteria

Full size image

7 Closing remarks

There have been several proposals for isotropic yield criteria over the years that span relationships between the Tresca and von Mises yield criteria, e.g., [9,10,11], and [22]. It is not the intent of this paper to judge the facility of one proposed criteria over the others. Instead, the intent here is to point out some of the desirable features of the newly proposed generalized Tresca yield condition [2]. For one thing, this criterion was originally proposed as a perturbation of the conventional Tresca yield condition based on its Weierstrass form. It was soon discovered, however, that not only was it a perturbation of the Tresca yield condition, but it also captured the von Mises yield criterion as a limiting case of its parameter. As it relies on the same second and third deviatoric stress invariants that define the conventional Tresca yield condition, it has a relatively simple mathematical form, and it serves as a natural outgrowth of that criterion.

A physically acceptable solution of a mode I crack problem under the Tresca yield condition that is analogous to the plane stress, mode I crack problem for the von Mises yield condition [4] has long eluded solution. For example, it is surprising to discover that a fan of parabolic slip lines proves inadmissible for the leading sector of such a proposed crack problem, as this would violate the yield condition near the crack tip in order to satisfy the equations of equilibrium. This situation is contrary to a similar slip line field illustrated in [23] for the mode III crack problem, which does allow a statically admissible solution without violating the yield condition. A different perfectly plastic mode I solution under the Tresca yield condition was proposed in [24], using a biaxial state of stress of magnitude \(\sigma _{0} \) as the leading sector; however, this solution does not predict a state of compression adjacent to the crack faces. This prediction is contrary to a state of stress found in linear elastic theory by the uniaxial tensile loading of elongated elliptical hole in a direction perpendicular to its major axis [16]. Thus, while statically admissible, the solution having the biaxial state of stress is not a completely satisfying solution physically.

In this investigation, information gleaned from the generalized Tresca yield condition for variations in the parameter \(\varepsilon ,\) helped to formulate a new solution of a mode I crack problem under the conventional Tresca yield condition. This solution provides a strong analogy to the plane stress solution under the von Mises yield condition [4].

There is a distinctive difference, however, between the two mode I crack solutions depending on which yield criterion is used. While fans of mathematical characteristics exist in both solutions, the fan sectors in the Tresca solution do not lie directly in front of the crack tip as in [4]. Consequently, a crack moving under steady-state conditions may have very different properties regarding strain rates depending on the particular yield condition used. In [25], it was stated that no analytical, perfectly plastic solution has been found for a slow-moving, steady-state, mode I crack under plane stress loading conditions. This is an area for future study, and the solution presented here may provide new insight about possible leading sectors.