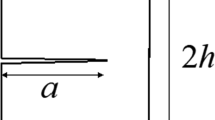Dynamic Crack Growth in Viscoelastic Materials with Memory

Abstract

In this paper we introduce a model of dynamic crack growth in viscoelastic materials, where the damping term depends on the history of the deformation. The model is based on a dynamic energy dissipation balance and on a maximal dissipation condition. Our main result is an existence theorem in dimension two under some a priori regularity constraints on the cracks.

1 Introduction

We consider the problem of crack growth in a viscoelastic cracked material with memory governed by the system

$$\begin{aligned} \ddot{u}(t) - \text {div}\big (({\mathbb {C}}+{\mathbb {V}}) Eu(t)\big ) + \text {div}\Big ( \int ^t_{-\infty } \text {e}^{\tau -t}\,{\mathbb {V}}Eu(\tau ) \, \text {d}\tau \Big ) = f(t), \end{aligned}$$

(1.1)

where u,  Eu,  and $\ddot{u},$ are the displacement, the symmetric part of its gradient, and its second derivative with respect to time, ${\mathbb {C}}$ and ${\mathbb {V}}$ are the elasticity and viscosity tensors, while f is the external load. For this model the stress at time t is given by

$$\begin{aligned} \sigma (t):={\mathbb {C}}Eu(t) + {\mathbb {V}}Eu(t) - \int ^t_{-\infty } \text {e}^{\tau -t}\,{\mathbb {V}}Eu(\tau ) \, \text {d}\tau . \end{aligned}$$

(1.2)

Moreover, as in [6, 13] we assume that we know the displacement u on $(-\infty ,0]$ and we want to solve (1.1) on [0, T],  for given $T>0.$ Under this assumption, it is convenient to write (1.1) in the form

$$\begin{aligned} \ddot{u}(t) - \text {div}(\sigma _0(t))= \ell _0(t) \quad t\in [0,T], \end{aligned}$$

(1.3)

where

$$\begin{aligned}{} & {} \sigma _0(t):={\mathbb {C}}Eu(t)+{\mathbb {V}}Eu(t) - \int ^t_{0} \text {e}^{\tau -t}\,{\mathbb {V}}Eu(\tau ) \, \text {d}\tau , \end{aligned}$$

(1.4)

$$\begin{aligned}{} & {} \ell _0(t):=f(t) - \text {div}F_0(t), \end{aligned}$$

(1.5)

$$\begin{aligned}{} & {} F_0(t):=\int ^0_{-\infty } \text {e}^{\tau -t}\,{\mathbb {V}}Eu_0(\tau ) \, \text {d}\tau \end{aligned}$$

(1.6)

and $u_0$ is a function that represents the displacement on $(-\infty ,0],$ namely $u(s)=u_0(s)$ for every $s\in (-\infty ,0].$ For physical details regarding the right-hand side of Eq. (1.4) see, e.g., [20].

When no cracks are present, problems similar to (1.1) and (1.3) were studied by Boltzmann [1, 2] and Volterra [21, 22], while recent results can be found in [12, 13, 15].

In this paper we study the problem on a bounded open set $\Omega \subset {\mathbb {R}}^2.$ The crack at time $t\in [0,T]$ is a 1-dimensional closed subset $\Gamma _t$ of $\Omega$ and the irreversibility of crack growth means that $\Gamma _t \subseteq \Gamma _\tau$ if $t \le \tau .$ For technical reasons we assume that the shape of the cracks and their dependence on time is sufficiently regular, with precise a priori estimates.

Fig. 1

Cracked domain

In the case of smooth functions, equation (1.3) is satisfied on $\Omega {{\setminus }} \Gamma _t$ (see also Fig. 1) with suitable boundary conditions (on the Dirichlet part $\partial _D\Omega ,$ on the Neumann part $\partial _N\Omega ,$ and on $\Gamma _t$) and with prescribed initial conditions. Namely, u and $\{\Gamma _t\}_{t\in [0,T]}$ satisfy

$$\begin{aligned}{} & {} \ddot{u}(t) - \text {div}(\sigma _0(t)) = \ell _0(t) \quad \text {in } \Omega {\setminus }\Gamma _t, \end{aligned}$$

(1.7)

$$\begin{aligned}{} & {} u(t) = u_D(t) \quad \text {on } \partial _D\Omega , \end{aligned}$$

(1.8)

$$\begin{aligned}{} & {} \sigma _0(t)\nu =F_0(t)\nu \quad \text {on } \partial _N\Omega , \end{aligned}$$

(1.9)

$$\begin{aligned}{} & {} \sigma ^{\pm }_0(t)\nu =F^\pm _0(t)\nu \quad \text {on } \Gamma _t, \end{aligned}$$

(1.10)

$$\begin{aligned}{} & {} u(0)=u^0\quad \text {and}\quad \dot{u}(0)=u^1 \end{aligned}$$

(1.11)

for every $t\in [0,T],$ where $u_D$ is the Dirichlet condition, $u^0$ is the initial condition for the displacement, $u^1$ is the initial condition for the velocity, $\nu$ is the unit normal, and the symbol ± in (1.10) denotes suitable limits on each side of $\Gamma _t.$ We note that, as consequence of (1.3)–(1.6), the Neumann conditions on $\Gamma _t$ are not zero. In the paper we consider a weak formulation (see Definition 2.10) which coincides with the one in (1.7)–(1.11) under suitable regularity assumptions.

When $\{\Gamma _t\}_{t\in [0,T]}$ is prescribed, problem (1.7)–(1.11) has been studied in [5, 18]. More precisely, in [18] an existence theorem is proved, while in [5] one can find results regarding uniqueness and continuous dependence of u on the data (in particular on the cracks).

In the model considered in our paper the unknown of the problem is the family of cracks $\{\Gamma _t\}_{t\in [0,T]}$ which, in the spirit of [7, 8], must satisfies the following conditions:

• (a) an energy dissipation balance (consistent with dynamic Griffith’s theory) for the solution u of (1.7)–(1.11) (see Definition 3.3): the sum of the kinetic and elastic energies and of the energies dissipated by viscosity and crack growth balances the work done by the forces acting on the system;

• (b) a maximal dissipation condition, depending on a parameter $\eta >0$ (see Definition 4.1), which forces the crack to run as fast as possible.

Condition (a) is a dynamic version of Griffith’s criterion (see [14] for the quasistatic case and [16] for the dynamic problem).

The main result of this paper is that, given initial and boundary conditions satisfying suitable hypotheses, there exists a family $\{\Gamma _t\}_{t\in [0,T]}$ satisfying (a) and (b) (see Theorem 4.3).

The proof follows the lines of [8], where a similar problem is studied for the case of pure elastodynamics. To deal with the memory term appearing in (1.4), we use the results of [5, 18]. In particular the continuous dependence on the data obtained in [5] is a fundamental tool for a compactness argument that plays a key role in the proof of Theorem 4.3.

The structure of the paper is the following:

• in Sect. 2 we give a precise formulation of the problem and we give all the preliminary results;

• in Sect. 3 we define the class of cracks $\{\Gamma _t\}_{t\in [0,T]}$ such that the energy balance described in a) is satisfied and we prove a compactness result;

• in Sect. 4 we define the maximal dissipation condition and we prove the main result of the paper (Theorem 4.3).

2 Formulation of the Problem

The reference configuration of our problem is a bounded open set $\Omega \subset {\mathbb {R}}^2,$ with Lipschitz boundary $\partial \Omega$ and we assume that $\partial \Omega =\partial _D\Omega \cup \partial _N\Omega ,$ where $\partial _D\Omega$ and $\partial _N\Omega$ are disjoint (possibly empty) Borel sets, on which we prescribe Dirichlet and Neumann boundary conditions respectively. Moreover, we fix a time interval [0, T],  with $T>0.$

We give a precise definition of the admissible cracks of our model using a suitable class of curves. The following definitions and results are based on [7, 8]. The curves are always parameterized using the arc-length parameter s and for a given curve $\gamma : [a_\gamma , b_\gamma ] \rightarrow {\mathbb {R}}^2$ we define $\Gamma ^\gamma := \gamma ([a_\gamma ,\,b_\gamma ])$ and $\Gamma ^\gamma _s:= \gamma ([a_\gamma ,\,s]),$ for every $s \in [a_\gamma ,\,b_\gamma ].$ When it is clear from the context we omit the dependence on $\gamma$ and we write $\Gamma$ and $\Gamma _s$ instead of $\Gamma ^\gamma$ and $\Gamma ^\gamma _s.$ In order to describe the initial crack, we fix a curve $\gamma _0: [a_0,\, 0] \rightarrow {\overline{\Omega }}$ such that $\gamma _0(a_0)\in \partial \Omega ,$ $\gamma _0(s)\in \Omega$ for every $s\in (a_0,0]$ and we define the initial crack as

$$\begin{aligned} \Gamma _0:= \gamma _0([a_0, 0]). \end{aligned}$$

We suppose that $\gamma _0$ is of class $C^{3,1}$ and that it is transversal to $\partial \Omega$ at $\gamma _0(a_0)$ (there exists an isosceles triangle contained in ${\overline{\Omega }}$ with vertex in $\gamma _0(a_0)$ and axis parallel to $\gamma '_0(a_0)$). We fix two constants $r>0$ and $L>0$ and we now define the space of admissible crack paths.

Definition 2.1

Let ${\mathcal {G}}_{r,L}$ be the space of simple curves $\gamma :[a_0, b_\gamma ] \rightarrow {\overline{\Omega }}$ of class $C^{3,1},$ with $a_0 < 0 \le b_\gamma ,$ such that

• (a) $\gamma (s)=\gamma _0(s)$ for every $s \in [a_0,\,0],$

• (b) $|\gamma '(s)|=1$ for every $s \in [a_0, b_\gamma ],$

• (c) the two open disks of radius r tangent to $\Gamma$ at $\gamma (s)$ do not intersect $\Gamma ,$

• (d) $\text {dist}(\gamma ([0,b_\gamma ]),\partial \Omega ) \ge 2r ,$

• (e) $|\gamma ^{(3)}(s)|\le L,$ $|\gamma ^{(3)}(s_2)-\gamma ^{(3)}(s_1)|\le L |s_2-s_1|$ for any $s,\,s_1,\,s_2\in [a_0,b_\gamma ],$

where $\gamma ^{(i)}$ denotes the i-th derivative of $\gamma .$

We fix $\gamma _0,$ r,  and L such that ${\mathcal {G}}_{r,L}\ne \emptyset .$

Remark 2.2

By (a) and (d) we have $|a_0| \ge 2r.$ Condition (c) implies $|\gamma ^{(2)}(s)| \le 1/r$ for every $s \in [a_0,\,b_\gamma ].$

Definition 2.3

Let $\gamma _k$ be a sequence of curves in ${\mathcal {G}}_{r,L}$ and let $\gamma \in {\mathcal {G}}_{r,L}.$ We say that $\gamma _k$ converges uniformly to $\gamma$ if $b_{\gamma _k} \rightarrow b_\gamma$ and for every $b\in (0,b_\gamma )$ we have $\gamma _k|_{[a_0,b]} \rightarrow \gamma |_{[a_0,b]}$ uniformly in $[a_0,b]$ as $k\rightarrow +\infty$.

We have to describe the dependence of the crack length on the time. We fix two constants $\mu >0$ and $M>0$ which bound the speed of the crack tip and some higher order derivatives of the crack length with respect to time, respectively.

Definition 2.4

Let $T_0 < T_1.$ The class ${\mathcal {S}}^{reg}_{\mu ,M}(T_0,T_1)$ is composed of all nonnegative functions satisfying the following conditions:

$$\begin{aligned} s{} & {} \in C^{3,1}([T_0,T_1]), \end{aligned}$$

(2.1)

$$\begin{aligned} 0{} & {} \le \dot{s}(t) \le \mu \end{aligned}$$

(2.2)

$$\begin{aligned} |\ddot{s}(t)| \le M,\quad |\dddot{s}(t)|{} & {} \le M,\quad |\dddot{s}(t_1) -\dddot{s}(t_2)| \le M |t_1 - t_2|, \end{aligned}$$

(2.3)

for $t, t_1, t_2 \in [T_0,T_1],$ where dots denote derivatives with respect to time. We denote by ${\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1)$ the set of all functions $s\in C^0([T_0,T_1])$ such that there exists a finite subdivision $T_0=\tau _0< \tau _1<\cdots < \tau _k = T_1$ for which $s|_{[\tau _{j-1},\tau _j]} \in {\mathcal {S}}^{reg}_{\mu ,M}(\tau _{j-1},\tau _j).$ The minimal set $\{\tau _0, \tau _1,\ldots , \tau _k \}$ for which this property holds is denoted by sing(s).

Given $0\le T_0 < T_1 \le T$, $\gamma \in {\mathcal {G}}_{r,L},$ $s\in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1) \le b_\gamma ,$ the time dependent cracks corresponding to these functions are given by

$$\begin{aligned} \Gamma ^\gamma _{{s(t)}}:=\gamma ([a_0,s(t)]) \quad \text {for all } t \in [T_0,T_1], \end{aligned}$$

and the corresponding cracked domains are

$$\begin{aligned} \Omega ^{\gamma }_{s(t)}:=\Omega {\setminus }\Gamma ^{\gamma }_{{s(t)}} \quad \text {for all } t \in [T_0,T_1]. \end{aligned}$$

For simplicity of notation we sometimes denote $\Gamma ^{\gamma }_{{s(t)}}$ by $\Gamma _{{s(t)}},$ when $\gamma$ is clear from the context. See Fig. 1.

Remark 2.5

Under our assumptions, the cracks are described by curves starting from $\partial \Omega .$ This assumption is used in several points. For example, it is necessary to apply the results of [5, 7, 8].

Remark 2.6

In [3,4,5, 9, 19] the cracks are described using a family of time-dependent diffeomorphism $\Phi , \Psi : [0, T] \times {\overline{\Omega }} \rightarrow {\overline{\Omega }}.$ Thanks to [8, Lemma 2.8] it is possible to obtain the same maps also in our case.

We now define the functional spaces that will be used in order to give the definition of weak solution of the viscoelastic problem (1.7)–(1.11).

We define ${\mathbb {R}}^{2 {\times } 2}$ as the space of real $2\times 2$ matrix and ${\mathbb {R}}^{2 {\times } 2}_{sym}$ as the space of real $2\times 2$ symmetric matrices. The Euclidean scalar product between the matrices A and B is denoted by A : B. For every $A\in {\mathbb {R}}^{2 {\times } 2}$ the symmetric part $A_{sym}\in {\mathbb {R}}^{2\times 2}$ is defined as $A_{sym}=\frac{1}{2}(A+A^T),$ where $A^T$ denotes the transpose matrix of A. For any pair of vector spaces we define ${\mathcal {L}}(X; Y)$ as the space of linear and continuous maps form X into Y. Let $0< \lambda < \Lambda$ be two fixed constants. We now define the space of tensors that satisfy suitable conditions regarding regularity and symmetry. See also [8, Definition 3.1].

Definition 2.7

We define ${\mathcal {E}}(\lambda ,\Lambda )$ as the set of all maps ${\mathbb {L}}:{{\overline{\Omega }}} \rightarrow {\mathcal {L}}({\mathbb {R}}^{2 {\times } 2}; {\mathbb {R}}^{2 {\times } 2} )$ of class $C^2$ such that for every $x\in {\overline{\Omega }}$ we have

$$\begin{aligned}{} & {} {\mathbb {L}}(x)A={\mathbb {L}}(x)A_{sym}\in {\mathbb {R}}^{2 {\times } 2}_{sym} \quad \text {for every } A \in {\mathbb {R}}^{2 {\times } 2}, \end{aligned}$$

(2.4)

$$\begin{aligned}{} & {} {\mathbb {L}}(x)A:B={\mathbb {L}}(x)B:A\quad \text {for every } A,\,B \in {\mathbb {R}}^{2 {\times } 2}, \end{aligned}$$

(2.5)

$$\begin{aligned}{} & {} \lambda |A_{sym}|^2\le {\mathbb {L}}(x)A:A \le \Lambda |A_{sym}|^2 \quad \text {for every } A \in {\mathbb {R}}^{2 {\times } 2}. \end{aligned}$$

(2.6)

We now fix the following maps

$$\begin{aligned} {\mathbb {C}},{\mathbb {V}}\in {\mathcal {E}}(\lambda ,\Lambda ), \quad {\mathbb {A}}:={\mathbb {C}}+{\mathbb {V}}\end{aligned}$$

(2.7)

where ${\mathbb {C}}(x)$ and ${\mathbb {V}}(x)$ respectively represent the elasticity and viscosity tensor at the point $x\in {{\overline{\Omega }}}.$

Given $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ and $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ we now introduce the function spaces that will be used in the precise formulation of problem (1.7)–(1.11).

We recall that $\Gamma :=\gamma ([a_0,b_\gamma ]; {\mathbb {R}}^2).$ For every $u\in H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^2)$ Du denotes jacobian matrix in the sense of distributions on $\Omega {\setminus }\Gamma$ and Eu is its symmetric part, i.e.,

$$\begin{aligned} Eu:=\tfrac{1}{2}(Du + Du^T). \end{aligned}$$

The following lemma is an extension of the second Korn’s inequality (see, e.g., [17]) to the case of cracked domain.

Lemma 2.8

Let $\gamma \in {\mathcal {G}}_{r,L}$ and let $\Gamma :=\gamma ([a_0,b_\gamma ]; {\mathbb {R}}^2).$ Then there exists a constant K,  depending only on $\Omega$ and $\Gamma ,$ such that

$$\begin{aligned} \Vert Du\Vert ^2 \le K ( \Vert u\Vert ^2 + \Vert Eu\Vert ^2 ) \end{aligned}$$

(2.8)

for every $u\in H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^2),$ where $\Vert \cdot \Vert$ denotes the $L^2$ norm.

We note that in Lemma 2.8 it is possible to find a smooth extension of $\Gamma$ up to the boundary of $\Omega .$ From this observation, we obtain that Lemma 2.8 is an immediate consequence of [5, Lemma 2.2].

Remark 2.9

Let $\gamma \in {\mathcal {G}}_{r,L}$ and let $\Gamma :=\gamma ([a_0,b_\gamma ]; {\mathbb {R}}^2).$ Then, using a localization argument (see, e.g., [5]), we can prove that the trace operator is well defined and continuous from $H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^2)$ into $L^2(\partial \Omega ;{\mathbb {R}}^2).$

We set

$$\begin{aligned} V^{\gamma }:=H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^2), \quad H:=L^2(\Omega ;{\mathbb {R}}^2{}), \quad \text {and} \quad \underline{H}:=L^2(\Omega ;{\mathbb {R}}^{2 {\times } 2}{}). \end{aligned}$$

(2.9)

Since ${\mathcal {L}}^2(\Gamma )=0,$ we have the embedding $V^{\gamma } \hookrightarrow H \times \underline{H}$ given by $v \mapsto (v,\,Dv)$ and we can see the distributional gradient Dv on $\Omega {\setminus } \Gamma$ as a function defined a.e. on $\Omega ,$ which belongs to $\underline{H}.$

For every finite dimensional Hilbert space Y the symbols $(\cdot \,,\cdot )$ and $\Vert \cdot \Vert$ denote the scalar product and the norm in the $L^2(\Omega ; Y),$ according to the context. The space $V^{\gamma }$ is endowed with the norm

$$\begin{aligned} \Vert u\Vert _{V^{\gamma }}:=\big (\Vert u\Vert ^2+ \Vert Du\Vert ^2\big )^{{1}/{2}}. \end{aligned}$$

(2.10)

For every ${\overline{s}}\in [a_0,b_\gamma ]$ we define

$$\begin{aligned} V^{\gamma }_{\overline{s}}:=H^1(\Omega {\setminus }\Gamma _{\overline{s}};{\mathbb {R}}^2) \quad \text {and} \quad V^{\gamma ,D}_{\overline{s}}:=\big \{u\in V^{\gamma }_{\overline{s}}\,\,\big |\,\,u|_{\partial _D\Omega }=0\big \}, \end{aligned}$$

(2.11)

where $\Gamma _{\overline{s}}=\gamma ([a_0,{\overline{s}}])$ and $u|_{\partial _D\Omega }$ denotes the trace of u on $\partial _D\Omega .$ We note that $V^{\gamma }_{\overline{s}}$ and $V^{\gamma ,D}_{\overline{s}}$ are closed linear subspaces of $V^{\gamma }.$ For every $s\in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1)$ and for every $t\in [T_0,T_1]$ the spaces $V^{\gamma }_{{s}(t)}$ and $V^{\gamma ,D}_{{s}(t)}$ are defined as in (2.11) with $\overline{s}=s(t).$

We define

$$\begin{aligned} {\mathcal {V}}_{\gamma ,s}(T_0,T_1):=\big \{ v\in {L^2}(T_0,T_1; V^{\gamma })\cap H^1(T_0,T_1;H)\,\big |\,v(t)\in V^{\gamma }_{{s(t)}}\!\text { for a.e. }\!t\!\in \! (T_0,T_1) \big \}, \nonumber \\ \end{aligned}$$

(2.12)

which is a Hilbert space with the norm

$$\begin{aligned} \Vert v\Vert _{{\mathcal {V}}_{\gamma ,s}}:=\big (\Vert v\Vert ^2_{{L^2}(T_0,T_1;V^{\gamma })}+\Vert \dot{v}\Vert ^2_{{L^2}(T_0,T_1;H)}\big )^{\frac{1}{2}}, \end{aligned}$$

(2.13)

where the dot denotes the distributional derivative with respect to t. Moreover we set

$$\begin{aligned} {\mathcal {V}}^D_{\gamma ,s}(T_0,T_1):=\big \{ v\in {\mathcal {V}}_{\gamma ,s}(T_0,T_1) \,\big |\,v(t)\in {V^{\gamma ,D}_{{s(t)}}}\,\text { for a.e. }\,t\in (T_0,T_1) \big \},\nonumber \\ \end{aligned}$$

(2.14)

which is a closed linear subspace of ${\mathcal {V}}_{\gamma ,s}(T_0,T_1)$ and we define

$$\begin{aligned} \!{\mathcal {V}}^\infty _{\gamma ,s}(T_0,T_1)\!:=\!\big \{ v\!\in \! L^\infty (T_0,T_1; V^{\gamma })\cap W^{1,\infty }(T_0,T_1;H)\,\big |\,v(t)\!\in \! V^{\gamma }_{{s(t)}}\!\text { for a.e. }\!t\!\in \! (T_0,T_1) \big \},\nonumber \\ \end{aligned}$$

(2.15)

which is a Banach space with the norm

$$\begin{aligned} \Vert v\Vert _{{\mathcal {V}}^\infty _{\gamma ,s}}:=\Vert v\Vert _{L^\infty (T_0,T_1;V^{\gamma })}+\Vert \dot{v}\Vert _{L^\infty (T_0,T_1;H)}. \end{aligned}$$

(2.16)

Moreover, it is convenient to introduce the space of weakly continuous functions with values in a Banach space X with topological dual $X^*,$ defined by

$$\begin{aligned} C^0_w([T_0,T_1]; X):=\big \{ v: [T_0,T_1] \rightarrow X \,\big |\, t \mapsto \langle h,\, v(t) \rangle \text { is continuous for every } h \in X^* \big \}. \end{aligned}$$

When it is clear from the context we will omit the dependence on $\gamma$ or s in the functional spaces, writing V,  $V_{{s(t)}},$ $V^{D}_{{s(t)}},$ ${\mathcal {V}}(T_0,T_1),$ ${\mathcal {V}}^D(T_0,T_1),$ and ${\mathcal {V}}^\infty (T_0,T_1)$ instead of $V^{\gamma },$ $V^{\gamma }_{{s(t)}},$ $V^{\gamma ,D}_{{s(t)}},$ ${\mathcal {V}}_{\gamma ,s}(T_0,T_1),$ ${\mathcal {V}}^D_{\gamma ,s}(T_0,T_1),$ and ${\mathcal {V}}^\infty _{\gamma ,s}(T_0,T_1).$

Since $H^1(T_0,T_1;H)\hookrightarrow C^0([T_0,T_1];H)$ we have ${\mathcal {V}}(T_0,T_1)\hookrightarrow C^0([T_0,T_1],H).$ In particular $v(T_0)$ and $v(T_1)$ are well defined elements of H,  for every $v\in {\mathcal {V}}(T_0,T_1).$

We set

$$\begin{aligned} {\tilde{H}}:=L^2(\Omega ;{\mathbb {R}}^{2 {\times } 2}_{sym}). \end{aligned}$$

(2.17)

On the forcing term $\ell (t)$ of (1.7) we assume that

$$\begin{aligned} \ell (t):= f(t) - \text {div}F(t), \end{aligned}$$

(2.18)

where

$$\begin{aligned} f\in {L^2}(0,T;H) \quad \text {and} \quad F\in H^1(0,T;{\tilde{H}}) \end{aligned}$$

(2.19)

are prescribed functions and the divergence of a matrix valued function is the vector valued function whose components are obtained taking the divergence of the rows.

The Dirichlet boundary condition on $\partial _D \Omega$ is obtained by prescribing a function

$$\begin{aligned} u_D\in H^2(0,T;\,H)\cap H^1(0,T;\,V_{0}) \end{aligned}$$

(2.20)

where $V_0$ is $V_{\overline{s}}$ for $\overline{s}=0.$ It is not restrictive to assume that for every $t\in [0,T]$

$$\begin{aligned} u_D(t)=0 \quad \text {a.e. on } \{ x\in \Omega \,|\, \text {dist}(x,\partial \Omega ) \ge r \}. \end{aligned}$$

(2.21)

We are now in a position to give the definition of weak solution for the viscoelastic problem.

Definition 2.10

(Solution for visco-elastodynamics with cracks) Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ and assume (2.7), (2.19)–(2.21). Let $u^{0} \in V_{s(T_0)}$ such that $u^{0}-u_D(T_0)\in V^D_{s(T_0)}$ and let $u^{1}\in H.$ We say that u is a weak solution of the problem of visco-elastodynamics on the cracked domains $\Omega {\setminus }\Gamma _{{s(t)}},$ $t\in [T_0,T_1],$ with initial conditions $u^{0}$ and $u^{1},$ if

$$\begin{aligned}&u\in {\mathcal {V}}(T_0,T_1) \quad \text {and} \quad u-u_D\in {\mathcal {V}}^D(T_0,T_1), \end{aligned}$$

(2.22)

$$\begin{aligned}&-\int ^{T_1}_{T_0}(\dot{u}(t),{\dot{\varphi }}(t))\,\text {d}t+ \int ^{T_1}_{T_0} ({\mathbb {A}}Eu(t),E\varphi (t)) \,\text {d}t\nonumber \\&- \int ^{T_1}_{T_0}\int ^t_{T_0} \text {e}^{\tau -t} ({\mathbb {V}}Eu(\tau ), E\varphi (t))\,\text {d}\tau \text {d}t= \int ^{T_1}_{T_0} (f(t),\varphi (t))\,\text {d}t{} \nonumber \\&+ \int ^{T_1}_{T_0} (F(t),E\varphi (t)) \,\text {d}t{} \quad \text {for all } \varphi \in {\mathcal {V}}^D(T_0,T_1) \text { with }\varphi (T_0)=\varphi (T_1)=0, \end{aligned}$$

(2.23)

$$\begin{aligned}&u(T_0)=u^{0} \quad \text {in } H \quad \text {and} \quad \dot{u}(T_1)=u^{1} \quad \text {in } (V^D_{s(T_0)})^*, \end{aligned}$$

(2.24)

where $(V^D_{s(T_0)})^*$ denotes the topological dual of $V^D_{s(T_0)}.$

Remark 2.11

If u satisfy (2.22) and (2.23), it is possible to prove that $\dot{u}\in H^1 (0,T;(V^D_{s(T_0)})^*)$ (see [18, Remark 4.6]), which implies $\dot{u}\in C^0([T_0,T_1];(V^D_{s(T_0)})^*).$ In particular $\dot{u}(T_0)$ is well defined as an element of $(V^D_{s(T_0)})^*.$

Remark 2.12

In the case of smooth functions problem (2.22)–(2.24) is satisfied in a stronger sense. Namely, u and $\{\Gamma _{{s(t)}}\}_{t\in [T_0,T_1]}$ satisfy

$$\begin{aligned}{} & {} \ddot{u}(t) - \text {div}\big (({\mathbb {C}}+ {\mathbb {V}}) Eu(t)\big ) + \text {div}\Big ( \int ^t_{T_0} \text {e}^{\tau -t}\,{\mathbb {V}}Eu(\tau ) \, \text {d}\tau \Big ) = \ell (t) \quad \text {in } \Omega {\setminus }\Gamma _{{s(t)}}, \nonumber \\ \end{aligned}$$

(2.25)

$$\begin{aligned}{} & {} u(t) = u_D(t) \quad \text {on} \partial _D\Omega , \end{aligned}$$

(2.26)

$$\begin{aligned}{} & {} \Big (({\mathbb {C}}+ {\mathbb {V}}) Eu(t) - \int ^t_{T_0} \text {e}^{\tau -t}\,{\mathbb {V}}Eu(\tau ) \, \text {d}\tau \Big )\nu =F(t)\nu \quad \text {on } \partial _N\Omega , \end{aligned}$$

(2.27)

$$\begin{aligned}{} & {} \Big (({\mathbb {C}}+ {\mathbb {V}}) Eu(t) - \int ^t_{T_0} \text {e}^{\tau -t}\,{\mathbb {V}}Eu(\tau ) \, \text {d}\tau \Big )^{\!\pm }\!\!\!\nu =F(t)^\pm \nu \quad \text {on } \Gamma _{{s(t)}}, \end{aligned}$$

(2.28)

$$\begin{aligned}{} & {} u(T_0)=u^0\quad \text {and}\quad \dot{u}(T_0)=u^1 \end{aligned}$$

(2.29)

for every $t\in [T_0,T_1],$ where $\ell (t):=f(t)-\text {div}F(t),$ $\nu$ is the unit normal, and the symbol ± in (2.28) denotes suitable limits on each side of $\Gamma _{{s(t)}}.$

Existence of the solution for the viscoelastic problem (2.22)–(2.24) is given by [18] for $\Omega \subset {\mathbb {R}}^d$ with $d\ge 1$ and under more general assumptions on the regularity of the cracks. Uniqueness and continuous dependence on the data are proved in [5] under the assumption that the constant $\mu ,$ which controls the speed of the crack tip in Definition 2.4, satisfies

$$\begin{aligned} 0< \mu < \mu _0, \end{aligned}$$

(2.30)

where the constant $\mu _0$ is not explicitly defined in terms of the data of the problem. Using the fact that $d=2$ in our work, we will prove that uniqueness and continuous dependence can be obtained under the explicit assumption

$$\begin{aligned} 0< \mu < \sqrt{\lambda }/2, \end{aligned}$$

(2.31)

where $\lambda$ are the constants that appears in Definition 2.7 respectively.

In order to prove this results, we have to define an auxiliary problem, which can be interpreted as the elastodynamics problem with elasticity tensor replaced by ${\mathbb {A}}.$

Definition 2.13

(Solution for elastodynamics with cracks) Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ and assume (2.7), (2.19)–(2.21). Let $u^{0} \in V_{s(T_0)}$ such that $u^{0}-u_D(T_0)\in V^D_{s(T_0)}$ and let $u^{1}\in H.$ We say that v is a weak solution of the problem of elastodynamics on the cracked domains $\Omega {\setminus }\Gamma _{{s(t)}},$ $t\in [T_0,T_1],$ with initial conditions $u^{0}$ and $u^{1},$ if

$$\begin{aligned}&v\in {\mathcal {V}}(T_0,T_1) \quad \text {and} \quad v-u_D\in {\mathcal {V}}^D(T_0,T_1), \end{aligned}$$

(2.32)

$$\begin{aligned}&-\int ^{T_1}_{T_0}(\dot{v}(t),{\dot{\varphi }}(t))\,\text {d}t+ \int ^{T_1}_{T_0} ({\mathbb {A}}Ev(t),E\varphi (t)) \,\text {d}t= \int ^{T_1}_{T_0} (f(t),\varphi (t))\,\text {d}t{} \nonumber \\&+ \int ^{T_1}_{T_0} (F(t),E\varphi (t)) \,\text {d}t{} \quad \text {for all } \varphi \in {\mathcal {V}}^D(T_0,T_1) \text { with } \varphi (T_0)=\varphi (T_1)=0, \end{aligned}$$

(2.33)

$$\begin{aligned}&v(T_0)=u^{0} \quad \text {in } H \quad \text {and} \quad \dot{v}(T_1)=u^{1} \quad \text {in } (V^D_{s(T_0)})^*. \end{aligned}$$

(2.34)

Remark 2.14

In the case of smooth functions problem (2.32)–(2.34) is satisfied in a stronger sense. Namely, v and $\{\Gamma _{{s(t)}}\}_{t\in [T_0,T_1]}$ satisfy

$$\begin{aligned}{} & {} \ddot{v}(t) - \text {div}\big ({\mathbb {A}}Ev(t)\big ) = \ell (t) \quad \text {in } \Omega {\setminus }\Gamma _{{s(t)}}, \end{aligned}$$

(2.35)

$$\begin{aligned}{} & {} v(t) = u_D(t) \quad \text {on } \partial _D\Omega , \end{aligned}$$

(2.36)

$$\begin{aligned}{} & {} ({\mathbb {A}}Ev(t) )\nu =F(t)\nu \quad \text {on } \partial _N\Omega , \end{aligned}$$

(2.37)

$$\begin{aligned}{} & {} ({\mathbb {A}}Ev(t) )^\pm \nu =F(t)^\pm \nu \quad \text {on } \Gamma _{{s(t)}}, \end{aligned}$$

(2.38)

$$\begin{aligned}{} & {} v(T_0)=u^0\quad \text {and}\quad \dot{v}(T_0)=u^1 \end{aligned}$$

(2.39)

for every $t\in [T_0,T_1],$ where $\ell (t):=f(t)-\text {div}F(t),$ $\nu$ is the unit normal, and the symbol ± in (2.38) denotes suitable limits on each side of $\Gamma _{{s(t)}}.$

We can state the following result.

Theorem 2.15

Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ and assume (2.7), (2.19)–(2.21) and (2.31). Let $u^{0} \in V_{s(T_0)}$ such that $u^{0}-u_D(T_0)\in V^D_{s(T_0)}$ and let $u^{1}\in H.$ Then there exists a unique solution v of problem (2.32)–(2.34). Moreover $v \in {\mathcal {V}}^\infty (T_0,T_1),$ $v\in C^0_w([T_0,T_1];V),$ and $\dot{v}\in C^0_w([T_0,T_1];H).$

Proof

The existence of the solution can be proved without any constraint on the speed of the crack tip and can be found, for instance, in [18], where the author considered a more general problem. To prove the uniqueness, it is enough to consider the case $F=0.$ Under this assumption, the proof of uniqueness is given by [8]. $\square$

With the following result we obtain a better regularity with respect to time.

Proposition 2.16

Under the same assumption of Theorem 2.15, let v be the unique solution of problem (2.32)–(2.34). Then $v\in C^0([T_0,T_1], V) \cap C^1([T_0,T_1], H).$

Proof

In the case $F=0,$ a solution for the elastodynamics with cracks in the sense of [8] is also a solution in the sense of Definition 2.13. By uniqueness, the two solutions coincide. In particular, we get that, if $F=0,$ the solution is in $C^0([T_0,T_1], V) \cap C^1([T_0,T_1], H).$

If the forcing term F is not zero, we can use same approximation argument used in [5, Lemma 4.7]. Then for every $\varepsilon >0$ there exists $F_\varepsilon \in H^1(0,T, {\tilde{H}})$ such that $F_\varepsilon (t)\in C^\infty _c(\Omega {{\setminus }} \Gamma ;\,{\mathbb {R}}^{d\times d}_{sym})$ for every $t\in [0,T]$ and

$$\begin{aligned} \Vert F_\varepsilon - F\Vert _{L^\infty (0,T;{\tilde{H}})} + \Vert \dot{F}_\varepsilon - \dot{F}\Vert _{L^2(0,T;{\tilde{H}})} < \varepsilon . \end{aligned}$$

(2.40)

We define $v_\varepsilon$ as the solution of the elastodynamic problem in Definition 2.13 with F replaced by $F_\varepsilon .$ Since $F_\varepsilon$ is regular in space we have that

$$\begin{aligned} (F_\varepsilon (t),E\psi )=-(\text {div}F_\varepsilon (t),\psi ) \end{aligned}$$

(2.41)

for all $t\in [0,T]$ and for all $\psi \in V.$ It follows that $v_\varepsilon$ is a solution in the sense of Definition 2.13 with f and F respectively replaced by $f-\text {div}F_\varepsilon$ and 0. By the results of [8] we have that $v_\varepsilon \in C^0([T_0,T_1], V) \cap C^1([T_0,T_1], H).$ Using the continuous dependence on the forcing terms given by [5, Proposition 3.5] and (2.40), we obtain that

$$\begin{aligned} \sup _{t \in [0,T]}\Vert v_\varepsilon (t)- v(t)\Vert _V + \sup _{t \in [0,T]}\Vert \dot{v}_\varepsilon (t) - \dot{v}(t) \Vert \rightarrow 0 \quad \text {as } \varepsilon \rightarrow 0. \end{aligned}$$

In particular, we get that $v\in C^0([T_0,T_1], V) \cap C^1([T_0,T_1], H).$ $\square$

We now fix the notation that will be useful in order to give the main results concerning continuous dependence on the data.

Let $0\le T_0 < T_1 \le T,$ let $\gamma _k\in {\mathcal {G}}_{r,L}$ be a sequence of cracks paths, and let $s_k \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s_k(T_1)\le b_{\gamma _k},$ be a sequence of crack lengths. We define $V^{\gamma _k},$ $\Vert \cdot \Vert _{V^{\gamma _k}},$ $V^{\gamma _k}_{s_k(t)},$ $V^{{\gamma _k},D}_{s_k(t)},$ ${\mathcal {V}}_{\gamma _k,s_k}(T_0,T_1),$ $\Vert \cdot \Vert _{{\mathcal {V}}_{\gamma _k.s_k}},$ ${\mathcal {V}}^{D}_{\gamma _k,s_k}(T_0,T_1)$ as in (2.9)–(2.14) with $\Gamma$ and $\Gamma _{{s(t)}}$ replaced by $\Gamma ^{\gamma _k}:=\gamma _k([a_0,b_{\gamma _k}])$ and $\Gamma ^{\gamma _k}_{s_k(t)}:=\gamma _k([a_0,s_k(t)]).$

Let $u^0_k\in V^{\gamma _k}_{s_k(T_0)},$ with $u^{0}_k-u_D(T_0)\in V^{\gamma _k,D}_{s_k(T_0)},$ $u^1_k,\in H,$

$$\begin{aligned} f_k\in L^2(0,T; H) \quad \text {and}\quad F_k \in H^1(0,T; {\tilde{H}}). \end{aligned}$$

(2.42)

We define $u_k$ as the weak solution of k-th viscoelastic problem on the cracked domains $\Omega {\setminus }\Gamma ^{\gamma _k}_{s_k(t)},$ $t\in [T_0,T_1],$ that is

$$\begin{aligned}&u_k\in {\mathcal {V}}_{\gamma _k,s_k}(T_0,T_1) \quad \text {and} \quad u_k-u_D\in {\mathcal {V}}^D_{\gamma _k,s_k}(T_0,T_1), \end{aligned}$$

(2.43)

$$\begin{aligned}&-\int ^{T_1}_{T_0}(\dot{u}_k(t),{\dot{\varphi }}(t))\,\text {d}t+ \int ^{T_1}_{T_0} ({\mathbb {A}}Eu_k(t),E\varphi (t)) \,\text {d}t\nonumber \\&- \int ^{T_1}_{T_0}\int ^t_{T_0} \text {e}^{\tau -t} ({\mathbb {V}}Eu_k(\tau ), E\varphi (t))\,\text {d}\tau \text {d}t= \int ^{T_1}_{T_0} (f_k(t),\varphi (t))\,\text {d}t{}\nonumber \\&+ \int ^{T_1}_{T_0} (F_k(t),E\varphi (t)) \,\text {d}t{} \quad \text {for all } \varphi \in {\mathcal {V}}^D_{\gamma _k,s_k}(T_0,T_1) \text { with } \varphi (T_0)=\varphi (T_1)=0, \end{aligned}$$

(2.44)

$$\begin{aligned}&u_k(T_0)=u^0_k \quad \text {in } H \quad \text {and} \quad \dot{u}_k(T_1)=u^1_k \quad \text {in } (V^{\gamma _k,D}_{s_k(T_0)})^*. \end{aligned}$$

(2.45)

Moreover, we define $v_k$ as the weak solution of k-th problem of elastodynamics on the cracked domains $\Omega {\setminus }\Gamma ^{\gamma _k}_{s_k(t)},$ $t\in [T_0,T_1],$ that is

$$\begin{aligned}&v_k\in {\mathcal {V}}_{\gamma _k,s_k}(T_0,T_1) \quad \text {and} \quad v_k-u_D\in {\mathcal {V}}^D_{\gamma _k,s_k}(T_0,T_1), \end{aligned}$$

(2.46)

$$\begin{aligned}&-\int ^{T_1}_{T_0}(\dot{v}_k(t),{\dot{\varphi }}(t))\,\text {d}t+ \int ^{T_1}_{T_0} ({\mathbb {A}}Ev_k(t),E\varphi (t)) \,\text {d}t= \int ^{T_1}_{T_0} (f_k(t),\varphi (t))\,\text {d}t{} \nonumber \\&+ \int ^{T_1}_{T_0} (F_k(t),E\varphi (t)) \,\text {d}t{} \quad \text {for all } \varphi \in {\mathcal {V}}_{\gamma _k,s_k}(T_0,T_1) \text { with } \varphi (T_0)=\varphi (T_1)=0, \end{aligned}$$

(2.47)

$$\begin{aligned}&v_k(T_0)=u^0_k \quad \text {in } H \quad \text {and} \quad \dot{v}_k(T_1)=u^1_k \quad \text {in } (V^{\gamma _k,D}_{s_k(T_0)})^*. \end{aligned}$$

(2.48)

We now state the result concerning continuous dependence on the data for the problem of elastodynamics. It will be used to prove the same result for the viscoelastic problem.

Theorem 2.17

Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ and assume (2.7), (2.19)–(2.21) and (2.31). Let $u^{0} \in V^{\gamma }_{s(T_0)},$ with $u^{0}-u_D(T_0)\in V^{\gamma ,D}_{s(T_0)}$ and let $u^{1}\in H.$ Let $\gamma _k\in {\mathcal {G}}_{r,L},$ let $s_k \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s_k(T_1)\le b_{\gamma _k}.$ Let $u^0_k\in V^{\gamma _k}_{s_k(T_0)},$ with $u^{0}_k-u_D(T_0)\in V^{\gamma _k,D}_{s_k(T_0)},$ $u^1_k,\in H,$ and assume (2.42). Let v be the weak solution of problem (2.32)–(2.34) on the cracked domains $\Omega {\setminus }\Gamma ^{\gamma }_{{s(t)}},$ $t\in [T_0,T_1].$ Let $v_k$ be the weak solution of problem (2.46)–(2.48) on the cracked domains $\Omega {\setminus }\Gamma ^{\gamma _k}_{s_k(t)},$ $t\in [T_0,T_1].$ Assume that

$$\begin{aligned}{} & {} \Vert f_k - f\Vert _{{L^2}(0,T;H)}\rightarrow 0, \quad \Vert F_k - F\Vert _{ H^1(0,T;{\tilde{H}})}\rightarrow 0, \end{aligned}$$

(2.49)

$$\begin{aligned}{} & {} s_k \rightarrow s \quad \text {uniformly}, \qquad \gamma _k \rightarrow \gamma \quad \text {uniformly}, \end{aligned}$$

(2.50)

$$\begin{aligned}{} & {} u^0_k \rightarrow u^0 \quad \text {in } H, \qquad Du^0_k \rightarrow Du^0 \quad \text {in } \underline{H}, \qquad u^1_k \rightarrow u^1 \quad \text {in } H, \end{aligned}$$

(2.51)

as $k\rightarrow +\infty$. Then

$$\begin{aligned}{} & {} v_k(t) \rightarrow v(t) \quad \text {in } {H}, \end{aligned}$$

(2.52)

$$\begin{aligned}{} & {} Dv_k(t) \rightarrow Dv(t) \quad \text {in } \underline{H}, \end{aligned}$$

(2.53)

$$\begin{aligned}{} & {} \dot{v}_k(t) \rightarrow \dot{v}(t) \quad \text {in } {H}, \end{aligned}$$

(2.54)

for every $t\in [T_0,T_1]$ as $k\rightarrow +\infty$.

Proof

In the case $f_k=f,$ $F_k=F=0$ for any $k\in {\mathbb {N}},$ it is a consequence of [8, Theorem 3.5]. In the general case, the result follows from the same approximation argument used in [5, Lemma 4.7, Proposition 4.9]. $\square$

Now we are in a position to obtain the same results for the viscoelastic system.

Theorem 2.18

Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ and assume (2.7), (2.19)–(2.21) and (2.31). Let $u^{0} \in V_{s(T_0)},$ such that $u^{0}-u_D(T_0)\in V^D_{s(T_0)}$ and let $u^{1}\in H.$ Then there exists a unique solution u of problem (2.22)–(2.24). Moreover $u \in {\mathcal {V}}^\infty (T_0,T_1),$ $u\in C^0_w([T_0,T_1];V),$ and $\dot{u}\in C^0_w([T_0,T_1];H).$

Proof

We can not apply directly [5, Theorem 2.7] because in general (2.30) is not satisfied. However, assuming (2.31) instead of (2.30) we can repeat all arguments of the proof of that theorem, which is based on existence and uniqueness for elastodynamics with cracks (in our case given by Theorem 2.15) and on a fixed point argument. $\square$

Proposition 2.19

Under the same assumptions of Theorem 2.18, let u be the unique solution of problem (2.22)–(2.24). Then $u\in C^0([T_0,T_1], V) \cap C^1([T_0,T_1], H).$

Proof

It is enough to apply Proposition 2.16 with F(t) replaced by

$$\begin{aligned} F(t)+\int ^t_{T_0} \text {e}^{\tau -t}{\mathbb {V}}Eu(\tau ) \text {d}\tau , \end{aligned}$$

for all $t\in [T_0,T_1].$ $\square$

The following theorem provides the continuous dependence on the data for the solution of the viscoelastic problem.

Theorem 2.20

Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma ,$ and assume (2.7), (2.19)–(2.21) and (2.31). Let $u^{0} \in V^{\gamma }_{s(T_0)},$ such that $u^{0}-u_D(T_0)\in V^{\gamma ,D}_{s(T_0)}$ and let $u^{1}\in H.$ Let $\gamma _k\in {\mathcal {G}}_{r,L},$ let $s_k \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s_k(T_1)\le b_{\gamma _k}.$ Let $u^0_k\in V^{\gamma _k}_{s_k(T_0)},$ such that $u^{0}_k-u_D(T_0)\in V^{\gamma _k,D}_{s_k(T_0)},$ $u^1_k,\in H,$ and assume (2.42). Let u be the weak solution of problem (2.22)–(2.24) on the cracked domains $\Omega {\setminus }\Gamma ^{\gamma }_{{s(t)}},$ $t\in [T_0,T_1].$ Let $u_k$ be the weak solution of problem (2.43)–(2.45) on the cracked domains $\Omega {\setminus }\Gamma ^{\gamma _k}_{s_k(t)},$ $t\in [T_0,T_1].$ Assume that

$$\begin{aligned}{} & {} \Vert f_k - f\Vert _{{L^2}(0,T;H)}\rightarrow 0, \qquad \Vert F_k - F\Vert _{ H^1(0,T;{\tilde{H}})}\rightarrow 0, \end{aligned}$$

(2.55)

$$\begin{aligned}{} & {} s_k \rightarrow s \quad \text {uniformly}, \qquad \gamma _k \rightarrow \gamma \quad \text {uniformly}, \end{aligned}$$

(2.56)

$$\begin{aligned}{} & {} u^0_k \rightarrow u^0 \quad \text {in } H, \qquad Du^0_k \rightarrow Du^0 \quad \text {in } \underline{H}, \qquad u^1_k \rightarrow u^1 \quad \text {in } H, \end{aligned}$$

(2.57)

as $k\rightarrow +\infty$. Then

$$\begin{aligned}{} & {} u_k(t) \rightarrow u(t) \quad \text {in } {H}, \end{aligned}$$

(2.58)

$$\begin{aligned}{} & {} Du_k(t) \rightarrow Du(t) \quad \text {in } \underline{H}, \end{aligned}$$

(2.59)

$$\begin{aligned}{} & {} \dot{u}_k(t) \rightarrow \dot{u}(t) \quad \text {in } {H}, \end{aligned}$$

(2.60)

for every $t\in [T_0,T_1]$ as $k\rightarrow +\infty$. Moreover there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u_k(t) \Vert + \Vert D u_k(t)\Vert + \Vert \dot{ u}_k(t) \Vert \le C \end{aligned}$$

for every $k\in {\mathbb {N}}$ and $t \in [T_0,T_1].$

Proof

As in the proof of Theorem 2.18, we cannot apply directly [5, Theorem 4.1], because in general (2.30) is not satisfied. However, assuming (2.31) instead of (2.30) we can repeat all arguments of the proof of that theorem, which is based on the continuous dependence on the data for elastodynamics with cracks (in our case given by Theorem 2.17) and on a results concerning the convergence of fixed points of a sequence of functions (see [5, Lemma 4.2]).$\square$

3 Energy Balance

In this section we study the problem of the dynamic energy-dissipation balance on a given cracked domain $\Omega {\setminus }\Gamma ^{\gamma }_{{s(t)}}$ for the solution of the viscoelastic problem.

Let $\gamma \in {\mathcal {G}}_{r,L},$ $0\le T_0 < T_1 \le T,$ $s \in {\mathcal {S}}^{piec}_{\mu ,M}(T_0,T_1),$ with $s(T_1)\le b_\gamma .$ It is convenient to define the operator ${\mathcal {L}}_{T_0}:{\mathcal {V}}(T_0,T_1)\rightarrow H^1(T_0,T_1;{\tilde{H}})$ as

$$\begin{aligned} ({\mathcal {L}}_{T_0}u)(t):= \int ^t_{T_0} \text {e}^{\tau -t}{\mathbb {V}}Eu(\tau ) \text {d}\tau , \end{aligned}$$

(3.1)

for all $u\in {\mathcal {V}}(T_0,T_1),$ for all $t\in [T_0,T_1].$ Since

it is easy to check that ${\mathcal {L}}_{T_0}$ is bounded. Indeed, using the Hölder inequality it is possible to prove that

$$\begin{aligned} \Vert {\mathcal {L}}_{T_0}u\Vert _{L^\infty (T_0,T_1;{\tilde{H}})} \le (T_1-T_0)^{1/2} \Vert {\mathbb {V}}\Vert _{\infty } \Vert u \Vert _{{\mathcal {V}}(T_0,T_1)}, \end{aligned}$$

(3.2)

(3.3)

Assume (2.7), (2.19)–(2.21) and let $v \in C^0([T_0,T_1],V)\cap C^1([T_0,T_1],H).$ For every $t \in [T_0,T_1]$ the sum of kinetic and elastic energy is given by

$$\begin{aligned} {\mathcal {E}}_v(t)=\frac{1}{2}\Vert \dot{v}(t)\Vert ^2+ \frac{1}{2}({\mathbb {C}}Ev(t),Ev(t)). \end{aligned}$$

(3.4)

For an interval $[t_1,t_2]\subset [T_0,T_1]$ the dissipation due to viscosity between time $t_1$ and $t_2$ is given by

$$\begin{aligned} {\mathcal {D}}_v(t_1,t_1)=&\,\frac{1}{2}({\mathbb {V}}Ev(t_2),Ev(t_2)) - \frac{1}{2}({\mathbb {V}}Ev(t_1),Ev(t_1))\nonumber \\&-(({\mathcal {L}}_{T_0}v)(t_2),Ev(t_2)) +(({\mathcal {L}}_{T_0}v)(t_1),Ev(t_1))\nonumber \\&+\int ^{t_2}_{t_1} ({\mathbb {V}}Ev(t),Ev(t)) \text {d}t{} - \int ^{t_2}_{t_1}(({\mathcal {L}}_{T_0}v)(t),Ev(t)) \text {d}t{}. \end{aligned}$$

(3.5)

Moreover, taking into account the dynamic Griffith’s criterion (see [14, 16]), we assume that the energy dissipated in the process of crack production on the interval $[t_1,t_2]$ is proportional to $s(t_2)-s(t_1),$ which represents the length of the crack increment. For simplicity we take the proportionality constant equal to one. Finally, the work done between time $t_1$ and $t_2$ by the boundary and volume forces is

$$\begin{aligned} {\mathcal {W}}_v(t_1,t_2)&= \int ^{t_2}_{t_1} \Big ( (f(t), \dot{v}(t) - \dot{u}_D(t)) + (({\mathbb {C}}+{\mathbb {V}})Ev(t),E\dot{u}_D(t) ) - (({\mathcal {L}}_{T_0}v)(t),E\dot{u}_D(t) ) \Big )\text {d}t{} \nonumber \\&\quad -\int ^{t_2}_{t_1}(\dot{F}(t), Ev(t)- Eu_D(t))\text {d}t{} -\int ^{t_2}_{t_1} (\dot{v}(t), \ddot{v}_D(t)) \text {d}t{} + (\dot{v}(t_2), \dot{u}_D(t_2)) \nonumber \\&\quad - (\dot{v}(t_1), \dot{u}_D(t_1)) + (F(t_2), Ev(t_2)-Eu_D(t_2))-(F(t_1), Ev(t_1)-Eu_D(t_1)). \end{aligned}$$

(3.6)

Remark 3.1

When $F=F_0$ as in (1.6) and all terms are regular enough, formulas (3.5) and (3.6) can be obtained multiplying (1.1) with $\dot{u}-\dot{u}_D$ and integrating by parts. For more details when viscosity is not present see also to [7, Section 3] and [8, Section 4].

Remark 3.2

We stress that (3.5) and (3.6) make sense for every weak solution of problem (2.22)–(2.23), thanks to Proposition 2.19.

We now define the class of cracks whose solutions of the viscoelastic problem satisfy the dynamic energy-dissipation balance.

Definition 3.3

Let $0\le T_0 < T_1 \le T,$ $s_0 \ge 0,$ and ${\overline{\gamma }}\in {\mathcal {G}}_{r,L},$ with $b_{{\overline{\gamma }}}=s_0,$ and assume (2.7), (2.19)–(2.21) and (2.31). Let $u^{0} \in V^{{\overline{\gamma }}}_{s_0},$ such that $u^{0}-u_D(T_0)\in V^{{\overline{\gamma }},D}_{s_0}$ and let $u^{1}\in H.$ The class

$$\begin{aligned} {\mathcal {B}}^{reg}(T_0,T_1)={\mathcal {B}}^{reg}(T_0,T_1,s_0,{\overline{\gamma }},{\mathbb {C}},{\mathbb {V}},f,F,u_D,u^0,u^1) \end{aligned}$$

is composed of all pairs $(\gamma ,s),$ with $\gamma \in {\mathcal {G}}_{r,L},$ $\gamma |_{[a_0,s_0]}={\overline{\gamma }}|_{[a_0,s_0]},$ $s\in {\mathcal {S}}^{reg}_{\mu ,M}([T_0,T_1]),$ $s(T_0)=s^0,$ and $s(T_1)\le b_\gamma ,$ such that the unique weak solution u of the viscoelastic problem (2.22)–(2.24) satisfies the energy-dissipation balance

$$\begin{aligned} {\mathcal {E}}_u(t_2)-{\mathcal {E}}_u(t_1) + {\mathcal {D}}_u(t_1,t_2) + s(t_2) - s(t_1) = {\mathcal {W}}_u(t_1,t_2) \end{aligned}$$

(3.7)

for every interval $[t_1,t_2]\subset [T_0,T_1].$ Similarly, the class

$$\begin{aligned} {\mathcal {B}}^{piec}(T_0,T_1)= {\mathcal {B}}^{piec}(T_0,T_1,s_0,{\overline{\gamma }},{\mathbb {C}},{\mathbb {V}},f,F,u_D,u^0,u^1) \end{aligned}$$

is defined in the same way replacing $s\in {\mathcal {S}}^{reg}_{\mu ,M}([T_0,T_1])$ by $s\in {\mathcal {S}}^{piec}_{\mu ,M}([T_0,T_1]).$

The class ${\mathcal {B}}^{reg}(T_0,T_1)$ is nonempty, as clarified by the following result, whose proof follows the lines of [11, Lemma 1] and [10, Proposition 2.7].

Proposition 3.4

Under the assumption of Definition 3.3, the pair $({\overline{\gamma }}, s),$ with $s(t)=s_0$ for every $t\in [T_0,T_1],$ belongs to ${\mathcal {B}}^{reg}(T_0,T_1).$

Proof

We prove the result in the case of homogeneous boundary condition, i.e. $u_D=0.$ Indeed, the case of non-homogeneous data can be obtained considering the equation for $u-u_D.$ It is convenient to extend our data on [0, 2T] by setting $f(t)=0$ and $F(t)=F(T)$ for $t\in (T,2T].$ It is clear that $f\in L^2(0,2T, H),$ $F\in H^1(0,2T,{\tilde{H}}),$ and that, by uniqueness, the solution u of the viscoelastic problem on $[T_0,2T]$ is an extension of the solution on $[T_0,T_1].$ Since the domain is constant with respect to time we deduce from (2.22)–(2.23) that $u\in H^2([T_0,2T]; (V^D_{s_0})^*)$ and

$$\begin{aligned} \langle \ddot{u} (t), \varphi \rangle + (({\mathbb {C}}+{\mathbb {V}})Eu(t),E\varphi )-({\mathcal {L}}_{T_0}u(t), E\varphi )=(f(t),\varphi ) + (F(t), E\varphi ) \end{aligned}$$

(3.8)

for all $\varphi \in V^D_{s_0}$ and for a.e. $t\in [T_0,2T].$

Given a Banach space X and a function $r:[T_0,2T] \rightarrow X,$ for every $h>0$ we define $\sigma ^hr,\delta ^hr:[T_0,2T-h]\rightarrow X$ by $\sigma ^hr(t):=r(t+h)+r(t),$ $\delta ^hr(t):=r(t+h)-r(t).$ For a.e. $t\in [T_0,2T-h]$ we have $\sigma ^hu(t),\delta ^hu(t) \in V^D_{s_0}.$ We consider (3.8) at time t and a time $t+h,$ in both cases with $\varphi =\delta ^h u(t).$ We sum the two expressions and we integrate on $[t_1,t_2] \subseteq [T_0,T_1].$ We get

$$\begin{aligned} \int ^{t_2}_{t_1} \big ( K_h (t) + E_h(t) + D_h(t) \big ) \, \text {d}t= \int ^{t_2}_{t_1} L_h(t) \, \text {d}t{}, \end{aligned}$$

(3.9)

where the terms that appear in (3.9) are defined as

$$\begin{aligned} K_h(t)&:=\langle \sigma ^h\ddot{u}(t), \delta ^h u(t)\rangle , \\ E_h(t)&:=(({\mathbb {C}}+{\mathbb {V}})\sigma ^hEu(t),\delta ^hEu(t)), \\ D_h(t)&:=-(\sigma ^h[{\mathcal {L}}_{T_0}u(t)], \delta ^hEu(t)),\\ L_h(t)&:=(\sigma ^hf(t), \delta ^hu(t)) + (\sigma ^hF(t), \delta ^hEu(t)). \end{aligned}$$

We have that

$$\begin{aligned}&\int ^{t_2}_{t_1} K_h(t) \, \text {d}t{} \\&\quad =- \int ^{t_2}_{t_1} (\sigma ^{h}\dot{u}(t), \delta ^{h} \dot{u}(t)) \, \text {d}t+ (\sigma ^{h}\dot{u}(t_2), \delta ^{h} u(t_2)) - (\sigma ^{h}\dot{u}(t_1), \delta ^{h} u(t_1))\\&\quad =-\int ^{t_2}_{t_1} \big ( \Vert \dot{u}(t+h) \Vert ^2 \text {d}t{}- \Vert \dot{u}(t) \Vert ^2 \big ) \text {d}t{} + (\sigma ^{h}\dot{u}(t_2), \delta ^{h} u(t_2)) - (\sigma ^{h}\dot{u}(t_1), \delta ^{h} u(t_1))\\&\quad =-\int ^{t_2+h}_{t_1+h} \Vert \dot{u}(t) \Vert ^2 \text {d}t{} + \int ^{t_2}_{t_1} \Vert \dot{u}(t) \Vert ^2 \text {d}t{} + (\sigma ^{h}\dot{u}(t_2), \delta ^{h} u(t_2)) - (\sigma ^{h}\dot{u}(t_1), \delta ^{h} u(t_1))\\&\quad = - \int ^{t_2+h}_{t_2}\!\!\!\! \Vert \dot{u}(t) \Vert ^2 \text {d}t{} + \int ^{t_1+h}_{t_1} \!\!\!\! \Vert \dot{u}(t) \Vert ^2 \text {d}t{} + (\sigma ^{h}\dot{u}(t_2), \delta ^{h} u(t_2)) - (\sigma ^{h}\dot{u}(t_1), \delta ^{h} u(t_1)) \end{aligned}$$

and dividing by h we get

Then

$$\begin{aligned} \int ^{t_2}_{t_1}\frac{K_h(t)}{h} \, \text {d}t{}\rightarrow - \Vert \dot{u}(t_2)\Vert ^2 + \Vert \dot{u}(t_1)\Vert ^2 + 2 \Vert \dot{u}(t_2)\Vert ^2 - 2 \Vert \dot{u}(t_1)\Vert ^2= \Vert \dot{u}(t_2)\Vert ^2 - \Vert \dot{u}(t_1)\Vert ^2, \nonumber \\ \end{aligned}$$

(3.10)

as $h\rightarrow 0^+,$ where we have used the fact that $u \in C^1([T_0,2T], H).$ Moreover

$$\begin{aligned} \int ^{t_2}_{t_1} E_h(t) \, \text {d}t{}&= \int ^{t_2}_{t_1} (({\mathbb {C}}+ {\mathbb {V}})Eu(t+h), Eu(t+h)) \text {d}t{} - \int ^{t_2}_{t_1} (({\mathbb {C}}+ {\mathbb {V}})Eu(t),Eu(t)) \text {d}t{} \nonumber \\&=\int ^{t_2+h}_{t_1+h} (({\mathbb {C}}+ {\mathbb {V}})Eu(t), Eu(t)) \text {d}t{} - \int ^{t_2}_{t_1} (({\mathbb {C}}+ {\mathbb {V}})Eu(t),Eu(t)) \text {d}t{} \nonumber \\&= \int ^{t_2+h}_{t_2} (({\mathbb {C}}+ {\mathbb {V}})Eu(t), Eu(t)) \text {d}t{} - \int ^{t_1+h}_{t_1} (({\mathbb {C}}+ {\mathbb {V}})Eu(t),Eu(t)) \text {d}t{} \end{aligned}$$

(3.11)

which give us

$$\begin{aligned} \int ^{t_2}_{t_1}\frac{E_h(t)}{h} \, \text {d}t{} \rightarrow (({\mathbb {C}}+ {\mathbb {V}})Eu(t_2), Eu(t_2)) - (({\mathbb {C}}+ {\mathbb {V}})Eu(t_1),Eu(t_1)) \end{aligned}$$

(3.12)

as $h \rightarrow 0^+,$ where we have used the fact that $u \in C^0([T_0,2T], V).$ Regarding the term $D_h$ we have

$$\begin{aligned} -\int ^{t_2}_{t_1} D_h(t) \, \text {d}t{}&= \int ^{t_2}_{t_1} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t+h)) \text {d}t{} - \int ^{t_2}_{t_1} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{} \nonumber \\&=\int ^{t_2+h}_{t_1+h} (\sigma ^{-h}[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{} - \int ^{t_2}_{t_1} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{} \nonumber \\&= \int ^{t_2+h}_{t_1+h} ({\mathcal {L}}_{T_0}u(t-h) - {\mathcal {L}}_{T_0}u(t+h),Eu(t)) \text {d}t{} \nonumber \\&\quad -\int ^{t_1+h}_{t_1} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{} + \int ^{t_2+h}_{t_2} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{} \nonumber \\&= \int ^{t_2}_{t_1} ({\mathcal {L}}_{T_0}u(t) - {\mathcal {L}}_{T_0}u(t+2h),Eu(t+h)) \text {d}t{} \nonumber \\&\quad -\int ^{t_1+h}_{t_1} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{} + \int ^{t_2+h}_{t_2} (\sigma ^h[{\mathcal {L}}_{T_0}u(t)],Eu(t)) \text {d}t{}, \end{aligned}$$

(3.13)

which give us

(3.14)

where we have used again that $u\in C^0([T_0,2T],V)$ and ${\mathcal {L}}_{T_0}u \in H^1(T_0,2T;{\tilde{H}})$.

With similar arguments, we have that

$$\begin{aligned} \int ^{t_2}_{t_1} \frac{L_h(t)}{h} \text {d}t{}&\rightarrow 2\int ^{t_2}_{t_1} (f(t),\dot{u}(t)) \text {d}t{} -2 \int ^{t_2}_{t_1} (\dot{F}(t), Eu(t)) \text {d}t{}\nonumber \\&\quad + 2(\dot{F}(t_2), Eu(t_1)) - 2(\dot{F}(t_1), Eu(t_1)), \quad \text {as } h\rightarrow 0^+. \end{aligned}$$

(3.15)

Dividing by h Eq. (3.9) and using Eqs. (3.10), (3.12), (3.14), and (3.15), we get the following identity

$$\begin{aligned}&\Vert \dot{u}(t_2)\Vert ^2 + (({\mathbb {C}}+ {\mathbb {V}})Eu(t_2), Eu(t_2)) + 2\int ^{t_2}_{t_1} ({\mathbb {V}}Eu(t)-{\mathcal {L}}_{T_0}u(t),Eu(t)) \text {d}t{}\nonumber \\&\quad - 2({\mathcal {L}}_{T_0}u(t_2),Eu(t_2)) = \Vert \dot{u}(t_1)\Vert ^2 + (({\mathbb {C}}+ {\mathbb {V}})Eu(t_1),Eu(t_1)) -2({\mathcal {L}}_{T_0}u(t_1),Eu(t_1))\nonumber \\&\quad + 2\int ^{t_2}_{t_1} (f(t),\dot{u}(t)) \text {d}t{} -2 \int ^{t_2}_{t_1} (\dot{F}(t), Eu(t)) \text {d}t{} + 2(\dot{F}(t_2), Eu(t_1)) - 2(\dot{F}(t_1), Eu(t_1)), \end{aligned}$$

(3.16)

that is the energy-dissipation balance (3.7) when $u_D=0$ and $s(t)=s_0$ for all $t\in [T_0,T_1].$ $\square$

The following remark deals with the concatenation of solutions on adjacent time intervals.

Remark 3.5

Under the assumption of Definition 3.3, let $0 \le T_0< T_1 < T_2 \le T,$

$$\begin{aligned}{} & {} (\gamma _1,s_1)\in {\mathcal {B}}^{piec}(T_0,T_1,s_0,{\overline{\gamma }}, {\mathbb {C}}, {\mathbb {V}}, f, F, u_D, u^0, u^1),\\{} & {} (\gamma _2,s_2)\in {\mathcal {B}}^{piec}(T_1,T_2,s_1(T_1),\gamma _1, {\mathbb {C}}, {\mathbb {V}}, f, F, u_D, u(T_1), \dot{u}(T_1)). \end{aligned}$$

Let $s :[T_0,T_2] \rightarrow {\mathbb {R}}$ be defined as

$$\begin{aligned} s(t):={\left\{ \begin{array}{ll} s_1(t) &{} \text {if } t\in [T_0,T_1],\\ s_2(t) &{} \text {if } t\in [T_1,T_2]. \end{array}\right. } \end{aligned}$$

(3.17)

Then $(\gamma _2,s)\in {\mathcal {B}}^{piec}(T_0,T_2,s_0,{\overline{\gamma }}, {\mathbb {C}}, {\mathbb {V}}, f, F, u_D, u^0, u^1).$

Using the continuous dependence Theorem 2.20 we are in a position to prove a compactness result for ${\mathcal {B}}^{reg}.$ We will use this result in the proof of Lemma 4.4, which will be crucial for the main theorem of the paper (i.e., Theorem 4.3).

Theorem 3.6

Under the assumption of Definition 3.3, let $(\gamma _k,\,s_k)\in {\mathcal {B}}^{reg}(T_0,T_1).$ Then there exists a not relabelled subsequence and there exists $(\gamma ,s)\in {\mathcal {B}}^{reg}(T_0,T_1)$ such that $\gamma _k \rightarrow \gamma$ uniformly (in the sense of Definition 2.3) and $s_k \rightarrow s$ in $C^3([T_0,T_1]).$

Proof

By [8, Lemma 2.5] there exist a subsequence (not relabelled) $\gamma _k$ and $\gamma \in {\mathcal {G}}_{r,L}$ such that $\gamma _k \rightarrow \gamma$ uniformly (in the sense of Definition 2.3). By Ascoli–Arzelà Theorem there exists $s\in C^3([T_0,T_1])$ and a further subsequence $s_k$ converging to s in $C^3([T_0,T_1]).$ Moreover, if we pass to the limit ad $k\rightarrow +\infty$ in the conditions in Definition 2.4 for $s_k,$ we get that $s\in {\mathcal {S}}^{reg}_{\mu ,M}([T_0,T_1]).$ We defined u as the solution of the viscoelastic problem (2.22)–(2.24) on the time-dependent cracked domain $t\mapsto \Omega {{\setminus }}\Gamma ^{\gamma }_{{s(t)}}$ with $t\in [T_0,T_1]$ and we define $u_k$ as the solution of the viscoelastic problem on the time-dependent cracked domain $t\mapsto \Omega {{\setminus }}\Gamma ^{\gamma _k}_{s_k(t)}$ with $t\in [T_0,T_1].$ Since $(\gamma _k,s_k)\in {\mathcal {B}}^{reg}(T_0,T_1)$ we have

$$\begin{aligned}&\frac{1}{2}\Vert \dot{u}_k(t_2)\Vert ^2 + \frac{1}{2}(({\mathbb {C}}+{\mathbb {V}})Eu_k(t_2),Eu_k(t_2))-({\mathcal {L}}_{T_0}u_k(t_2),Eu_k(t_2)) \nonumber \\&\qquad -\frac{1}{2}\Vert \dot{u}_k(t_1)\Vert ^2 - \frac{1}{2}(({\mathbb {C}}+{\mathbb {V}})Eu_k(t_1),Eu_k(t_1))+({\mathcal {L}}_{T_0}u_k(t_1),Eu_k(t_1)) \nonumber \\&\qquad -\int ^{t_2}_{t_1} ({\mathbb {V}}Eu_k(t),Eu_k(t)) \text {d}t{} - \int ^{t_2}_{t_1}({\mathcal {L}}_{T_0}u_k(t),Eu_k(t)) \text {d}t{} + s_k(t_2) - s_k(t_1) \nonumber \\&\quad = \int ^{t_2}_{t_1} \Big ( (f(t), \dot{u}_k(t) - \dot{u}_D(t)) + (({\mathbb {C}}+{\mathbb {V}})Eu_k(t),E\dot{u}_D(t) ) - ({\mathcal {L}}_{T_0}u_k(t),E\dot{u}_D(t) ) \Big )\text {d}t{} \nonumber \\&\qquad -\int ^{t_2}_{t_1}(\dot{F}(t), Eu_k(t)- Eu_D(t))\text {d}t{} + (F(t_2), Eu_k(t_2) \nonumber \\&\qquad -Eu_D(t_2))-(F(t_1), Eu_k(t_1)-Eu_D(t_1)) \nonumber \\&\qquad -\int ^{t_2}_{t_1} (\dot{u}_k(t), \ddot{u}_D(t)) \text {d}t{} + (\dot{u}_k(t_2), \dot{u}_D(t_2)) - (\dot{u}_k(t_1), \dot{u}_D(t_1)), \end{aligned}$$

(3.18)

for every interval $[t_1,t_2]\subset [T_0,T_1].$ Using Theorem 2.20 and the bounds (3.2)–(3.3), we can pass to the limit as $k \rightarrow +\infty$ in (3.18) and we get the energy-dissipation balance (3.7) for u. This proves that $(\gamma ,s)\in {\mathcal {B}}^{reg}(T_0,T_1)$ and concludes the proof. $\square$

4 Existence for the Coupled Problem

In this section we prove an existence result for the crack evolution (described by the functions $\gamma$ and s). In order to do this we define a maximal dissipation condition (see also [7, 8]), which forces the crack tip to choose a path which allows for a maximal speed.

Definition 4.1

Assume (2.7), (2.19)–(2.21) and (2.31). Let $u^{0} \in V_{0},$ such that $u^{0}-u_D(0)\in V^D_{0},$ and let $u^{1}\in H.$ Given $\eta >0$ we say that $(\gamma ,s)\in {\mathcal {B}}^{piec}(0,T)$ satisfies the $\eta -$maximal dissipation condition on [0, T] if there exists no $({\hat{\gamma }}, {\hat{s}})\in {\mathcal {B}}^{piec}(0,\tau _1),$ for some $\tau _1\in (0,T],$ such that

• (M1) $sing(\hat{s}) \subset sing({s}),$

• (M2) $\hat{s}(t)=s(t)$ and $\hat{\gamma }(\hat{s}(t))={\gamma }({s}(t))$ for every $t\in [0,\tau _0],$ for some $\tau \in [0,\tau _1),$

• (M3) $\hat{s}(t)>s(t)$ for every $t\in (\tau _0,\tau _1]$ and $\hat{s}(\tau _1)>s(\tau _1) + \eta .$

Remark 4.2

We refer to the discussions in [7, Section 5] and [8, Section 1] for some comments on the presence of the parameter $\eta >0.$

We are now in position to prove the main result of the paper. The proof follows the lines of [7, 8], devoted to the case of elastodynamics without viscosity terms.

Theorem 4.3

Under the assumption of Definition 4.1, for every $\eta >0$ there exists a pair $(\gamma , s) \in {\mathcal {B}}^{piec}(0,T)$ satisfying the $\eta$-maximal dissipation condition on [0, T].

Proof

Let us fix $\eta >0$ and a finite subdivision $0=T_0<T_1<\cdots <T_k=T$ of the time interval [0, T] such that $T_i - T_{i-1} < \frac{\eta }{\mu }$ for every $i\in \{0,1,2,\ldots ,k\}.$ We will define the solution using a recursive procedure on each subinterval $[T_{i-1}, T_i],$ for every $i\in \{0,1,2,\ldots ,k\}.$ In order to define this procedure, we set

$$\begin{aligned} {\mathcal {X}}_1:=\Big \{ (\gamma ,s) \in {\mathcal {B}}^{piec}(0,T_1,0,\gamma _0,{\mathbb {C}},{\mathbb {V}},f,F,u_D,u^0,u^1)\,|\, s \in {\mathcal {S}}^{reg}_{\mu ,M}(0,T_1),\, s(0)=0 \Big \},\nonumber \\ \end{aligned}$$

(4.1)

where $\gamma _0$ is the function that appears in Definition 2.1. By Proposition 3.4 we have that $(\gamma _0,0)\in {\mathcal {X}}_1$ and in particular we have ${\mathcal {X}}_1\ne \emptyset .$ Moreover, we choose $(\gamma _1,s_1)\in {\mathcal {X}}_1$ such that

$$\begin{aligned} \int ^{T_1}_{T_0} s_1(t)\, \text {d}t{}= \max _{(\gamma ,s)\in {\mathcal {X}}_1}\int ^{T_1}_{T_0} s(t)\, \text {d}t{}, \end{aligned}$$

where the existence of $(\gamma _1, s_1)$ is guaranteed by Lemma 4.4 below. If $k=1,$ we define $(\gamma ,s):=(\gamma _1,s_1)$ and we have to prove that this couple satisfies the $\eta$-maximal dissipation condition. Otherwise, we fix $i\in \{2,\ldots ,k\}$ and we set

$$\begin{aligned}&{\mathcal {X}}_i:=\Big \{ (\gamma ,s) \in {\mathcal {B}}^{piec}(0,T_i,0,\gamma _0,{\mathbb {C}},{\mathbb {V}},f,F,u_D,u^0,u^1)\,|\, s|_{[T_{i-1},T_{i}]} \in {\mathcal {S}}^{reg}_{\mu ,M}(T_{i-1},T_{i}),\nonumber \\&s(t)=s_{i-1}(t), \gamma (s(t))=\gamma _{i-1}(s_{i-1}(t)) \,\forall \,t\in [0,T_{i-1}]\Big \}. \end{aligned}$$

(4.2)

We note that ${\mathcal {X}}_i\ne \emptyset .$ Indeed, if we define ${\tilde{s}}_{i-1}$ as

$$\begin{aligned} {\tilde{s}}_{i-1}(t):={\left\{ \begin{array}{ll} s_{i-1}(t) &{} \text {for } t\in [0,T_{i-1}],\\ s_{i-1}(T_{i-1}) &{} \text {for } t\in [T_{i-1}, T_i], \end{array}\right. } \end{aligned}$$

we can apply Proposition 3.4 and Remark 3.5 to obtain $(\gamma _{i-1},{\tilde{s}}_{i-1})\in {\mathcal {X}}_i.$ Assume that the pair $(\gamma _{i-1},s_{i-1})\in {\mathcal {X}}_{i-1}$ has already been defined, then we choose $(\gamma _i,s_i)\in {\mathcal {X}}_i$ such that

$$\begin{aligned} \int ^{T_i}_{T_{i-1}} s_i(t)\, \text {d}t{}= \max _{(\gamma ,s)\in {\mathcal {X}}_i}\int ^{T_i}_{T_{i-1}} s(t)\, \text {d}t{}, \end{aligned}$$

(4.3)

where the existence of $(\gamma _i, s_i)$ is guaranteed by Lemma 4.4 below.

We now define $(\gamma ,s):=(\gamma _k,s_k),$ where $(\gamma _k,s_k)$ is the pair defined in the final step of the procedure defined above. It remains to prove that $(\gamma ,s)$ satisfies the $\eta$-maximal dissipation condition on the interval [0, T]. Assume, by contradiction that there exist $0 \le \tau _0 < \tau _1 \le T$ and $({\hat{\gamma }},{\hat{s}}) \in {\mathcal {B}}^{piec}(0,\tau _1)$ such that:

• (i) $sing({\hat{s}}) \subset sing(s) \subset \{ T_1,\ldots , T_{k-1} \}$

• (ii) $s(t)={\hat{s}}(t)$ and $\gamma (s(t))={\hat{\gamma }}({\hat{s}}(t))$ for every $t \in [0,\tau _0],$

• (iii) $s(t) < {\hat{s}}(t)$ for every $t\in (\tau _0,\tau _1]$ and ${\hat{s}} (\tau _1) > s(\tau _1) + \eta .$

Since $\tau _0 < T,$ there exists an index $j\in \{1,\ldots ,k\}$ such that $\tau _0\in [T_{j-1},T_j).$ We claim that $\tau _1 > T_j.$ Indeed, the using the monotonicity of s and the points (ii) and (iii), we have that ${\hat{s}} (\tau _1) > s(\tau _1) + \eta \ge s(\tau _0) + \eta = {\hat{s}}(\tau _0) + \eta$ and in particular ${\hat{s}}(\tau _1) - {\hat{s}}(\tau _0) > \eta .$ On the other hand, since ${\hat{s}} \in {\mathcal {S}}^{piec}_{\mu ,M}(0,\tau _1)$ we have ${\hat{s}}(\tau _1)- {\hat{s}}(\tau _0) \le \mu (\tau _1 - \tau _0),$ which together with the previous inequality give us $\tau _1 - \tau _0 > \eta /\mu .$ Since the subdivision of the interval was chosen such that $T_{i-1}- T_i < \eta /\mu$ for every $i\in \{1,\ldots ,k\},$ we get that $\tau _1>T_j.$

Using (i) we have that ${\hat{s}}|_{[T_{j-1},T_j]} \in {\mathcal {S}}^{reg}_{\mu ,M}(T_{j-1},T_j)$ and taking (ii) into account we get that $({\hat{\gamma }}, {\hat{s}}) \in {\mathcal {X}}_j.$ By construction $s=s_j$ on $[T_{j-1},T_j],$ where $s_j$ is the function defined in (4.3) for $i=j.$ As a consequence of (iii) we get ${\hat{s}} (t) > s(t) = s_j (t)$ for every $t\in (\tau _0, T_j],$ which contradicts (4.3). $\square$

We close this section with the following lemma used to prove Theorem 4.3. The proof follows the lines of [8, Lemma 5.3], with obvious modifications.

Lemma 4.4

For every $i=1,\ldots , k$ there exists $(\gamma _i,s_i) \in {\mathcal {X}}_i$ such that

$$\begin{aligned} \int ^{T_i}_{T_{i-1}} s_i(t)\, \text {d}t{}= \max _{(\gamma ,s)\in {\mathcal {X}}_i}\int ^{T_i}_{T_{i-1}} s(t)\, \text {d}t{}, \end{aligned}$$

(4.4)

where ${\mathcal {X}}_i$ is the space defined in (4.1) and (4.2).

Proof

Let $i\in \{1,\ldots ,k\}$ be fixed and let us define

$$\begin{aligned} S:=\sup _{(\gamma ,s)\in {\mathcal {X}}_i}\int ^{T_i}_{T_{i-1}} s(t)\, \text {d}t{}. \end{aligned}$$

For every $n\in {\mathbb {N}}$ let $(\gamma ^n,s^n) \in {\mathcal {X}}_i$ be such that

$$\begin{aligned} \int ^{T_i}_{T_{i-1}} s^n(t)\, \text {d}t{} \ge S - \frac{1}{n}. \end{aligned}$$

(4.5)

Let $u_{i-1}$ be the unique solution of the viscoelastic system (2.22)–(2.24) on the time-dependent domain $t \mapsto \Omega {{\setminus }}\Gamma ^{\gamma _{i-1}}_{s_{i-1}(t)}$ for $t\in [0,T_{i-1}].$ By Theorem 3.6 there exists a (not relabelled) subsequence of $(\gamma ^n, s^n|_{[T_{i-1},T_i]})$ and an element

$$\begin{aligned} (\gamma _i, {\tilde{s}}) \in {\mathcal {B}}^{reg}(T_{i-1},T_i,s_{i-1}(T_{i-1}),\gamma _{i-1}, {\mathbb {C}}, {\mathbb {V}}, f, F, u_D, u_{i-1}(T_{i-1}), \dot{u}_{i-1}(T_{i-1})), \end{aligned}$$

such that $\gamma ^n \rightarrow \gamma _i$ uniformly (in the sense of Definition 2.3) and $s^n|_{[T_{i-1},T_i]} \rightarrow s$ in the sense of $C^3([T_{i-1},T_i]).$ We now define

$$\begin{aligned} {s}_{i}(t):={\left\{ \begin{array}{ll} s_{i-1}(t) &{} \text {for } t\in [0,T_{i-1}],\\ {{\tilde{s}}}(t) &{} \text {for } t\in [T_{i-1}, T_i]. \end{array}\right. } \end{aligned}$$

By definition of ${\mathcal {X}}_i,$ we have that $\gamma ^n(s_{i-1}(t))=\gamma ^n(s^n(t))=\gamma _{i-1}(s_{i-1}(t))$ for all $t\in [0,T_{i-1}].$ Passing to the limit as $n\rightarrow + \infty$ we obtain that $\gamma _i(s_i(t))=\gamma _{i-1}(s_{i-1}(t))$ for all $t\in [0,T_{i-1}],$ which together to Remark 3.5, give us $(\gamma _i, s_i) \in {\mathcal {X}}_i.$ Finally, passing to the limit as $n\rightarrow + \infty$ in Eq. (4.5), we get Eq. (4.4) and this concludes the proof. $\square$

<ArticleNote Type="Misc"><Heading>Publisher’s Note</Heading><SimplePara>Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.</SimplePara></ArticleNote>