Knot reversal acts non-trivially on the concordance group of topologically slice knots

Abstract

We construct an infinite family of topologically slice knots that are not smoothly concordant to their reverses. More precisely, if $\mathcal {T}$ denotes the concordance group of topologically slice knots and $\rho$ is the involution of $\mathcal {T}$ induced by string reversal, then $\mathcal {T}/ \text {Fix}(\rho )$ contains an infinitely generated free subgroup. The result remains true modulo the subgroup of $\mathcal {T}$ generated by knots with trivial Alexander polynomial.

1 Introduction

Given an oriented knot K in $S^3$, let $K^r$ denote K with its string orientation reversed. Determining for a given knot K whether or not $K \cong K^r$ is among the most challenging problems in classical knot theory. In 1963, Trotter [24] proved that there exist knots K for which $K \not \cong K^r$. By 1983, Hartley [13] had developed the tools necessary to determine which prime knots with ten or fewer crossings are reversible. With the advent of computer programs such as SnapPy [7], deciding if a given knot is reversible is now routine. (In some settings, knots for which $K \cong K^r$ are called invertible, but in working with concordance it is better to use the word reversible to distinguish it from the inverse in the concordance group, $-K$.)

Following the discovery of Casson–Gordon invariants [2, 3], Casson observed that the techniques developed in that work were not sufficient to answer the more subtle question of whether in general K and $K^r$ are concordant; in higher dimensions it is the case that $K \cong K^r$ for all K. Since then, extensions of Casson–Gordon theory have provided means to address this question; see, for example, the successful application of twisted Alexander polynomials in [18].

In current research about knot concordance, a focus is on the smooth concordance group of topologically slice knots, $\mathcal {T}$. Since Casson–Gordon theory applies in the topological locally flat category, tools deriving from that theory cannot resolve questions about how reversal acts on $\mathcal {T}$. Our first goal is to show that string reversal acts non-trivially on $\mathcal {T}$. Notice that for a knot K, the manifolds built by p/q–surgery on K and on $K^r$, as well as the cyclic branched covers of K and $K^r$, are oriented diffeomorphic. Since surgery and branched covering constructions have been at the heart of the analysis of smooth concordance via such methods as Heegaard Floer theory, the challenges are evident.

Despite the difficulties just mentioned, we are able to find a topologically slice knot K for which K and $K^r$ are not concordant. Beyond this, we construct an infinite set of knots in $\mathcal {T}$ to demonstrate that the set of concordance classes that are fixed by reversal is relatively small. To make this precise, denote by $\rho$ the action of string reversal on the concordance group $\mathcal {C}$. The statement that the set of knots for which reversal acts trivially is small is made formal by considering the fixed set of $\rho$. Here is the main result of this paper. Let $\mathcal {T}_\Delta$ be the subgroup of $\mathcal {T}$ generated by knots with trivial Alexander polynomial.

Theorem 1.1

The quotient $\mathcal {T}/ \text {Fix\,}(\rho )$ contains an infinitely generated free subgroup. Furthermore, the quotient $\mathcal {T}/ \left( \text {Fix\,}(\rho )+\mathcal {T}_\Delta \right)$ contains an infinitely generated free subgroup.

One quick consequence concerns the relationship between slicing a knot and its branched covers. In particular, if K is slice, then all its cyclic branched covers of prime power degree bound rational homology balls. One can ask if there is a converse to such a statement. To see that Theorem 1.1 gives an answer, consider the following. For the knots we construct, $K {\#}-K^r$ is not slice, yet it has the same cyclic branched covers as $K {\#}-K$, which is slice. Hence, the following is immediate.

Corollary 1.2

There exists an infinite linearly independent set of knots in $\mathcal {T}$ with the property that for each nontrivial linear combination of knots in their span, all its cyclic branched covers of prime power degree bound rational homology balls.

This corollary is related to a result in the paper [1] by Aceto, Meier, Miller, Miller, Park and Stipsicz which builds a finite set of knots representing two-torsion in $\mathcal C$ with the property that associated cyclic branched covers bound rational homology balls.

Outline. In Sect. 2 we present slicing obstructions obtained by combining Casson–Gordon invariants and the Heegaard Floer d–invariant. In Sect. 3 we present a specific topologically slice knot K and prove that $K {\#}-\rho (K)$ is not smoothly slice. This knot K is similar to one used in [6]; there, the linking form of the 3–fold branched cover of $S^3$ branched over K has exactly two metabolizers. Separate arguments are applied related to each metabolizer, one using Casson–Gordon theory and the other Heegaard Floer theory. In the current setting, the relevant branched covering has a much larger number of metabolizers (76 to be precise) and many of these do not offer obstructions to sliceness. Thus, we first eliminate many from consideration, leaving four distinct families to consider. Once that is done, topological obstructions are derived from invariants developed in [10]; we build our computations of the relevant Heegaard Floer invariants using a specific computation of [6], but more detail is required because that paper did not address an issue of Alexander polynomial one knots which we want to include here.

In building this single example in Sects. 2 and 3, we are able to develop the key tools and notation for the general problem. Then, in Sect. 4 we build an infinite family of knots used in proving Theorem 1.1. A key ingredient is to find infinitely many topologically slice knots $K_i$ such that $K_i$ are nontrivial in $\mathcal {T}/ (\text {Fix}(\rho )+\mathcal {T}_\Delta )$ and the orders of the first homology groups of the 3–fold branched covers of $S^3$ branched over $K_i$ are relatively prime, which is done using certain number theoretic arguments (see Appendix A). Another key ingredient is computations of the Heegaard Floer d–invariants of the $K_i$, and this is accomplished using the powerful methods developed by Cha [4].

2 Slicing obstructions

2.1 Casson–Gordon invariants

Let $Y_q(K)$ denote the q–fold cyclic branched cover of $S^3$ with branch set an arbitrary knot K; we will henceforth assume that q is an odd prime power. It is then the case that $Y_q(K)$ is a ${\mathbb Q}$–homology sphere.

For each element $\chi \in H_1(Y_q(K))$ there is a Casson–Gordon invariant $\eta (K, q, \chi )$. This invariant takes values in a Witt group. Later we will describe computable invariants of this Witt group that provide slicing obstructions, and thus we will not need the precise definition of the group itself. The invariant $\eta$ was defined in [3], where it was denoted $\tau$. In that original work, $\chi$ was an element of $\text {Hom}(H_1(Y_q(K)), {\mathbb Z}_{p^r})$ for some prime power $p^r$. We have chosen $\chi \in H_1(Y_q(K))$; via the nonsingular linking form on $H_1(Y_q(K))$, such a $\chi$ determines a homomorphism in $\text {Hom}(H_1(Y_q(K)), {\mathbb Q}/{\mathbb Z})$. By restricting to elements of prime order p, the image of the homomorphism is in ${\mathbb Z}_p$, as desired. We will use Gilmer’s theorem [12] that $\eta$ is additive: $\eta (K{\#}K', q, \chi \oplus \chi ' )= \eta (K, q, \chi ) +\eta ( K', q, \chi ' )$.

2.2 Heegaard Floer invariants

If $Y_q(K)$ is a ${\mathbb Z}_2$–homology sphere, there is a Heegaard Floer invariant $\bar{d}(Y_q(K), \chi )$. Here we will summarize our notation and some of the essential properties of this invariant; further details will appear later in the exposition. The Heegaard Floer d–invariant, defined in [22], takes values in ${\mathbb Q}$. It is usually expressed as , where Y is a 3–manifold and is a Spin$^c$–structure. In the setting of ${\mathbb Z}_2$–homology spheres, Spin$^c$–structures correspond to elements of $H^2(Y) \cong H_1(Y)$, so we will work with the first homology rather than with Spin$^c$. We then have the definition $\bar{d}(Y,\chi ) =d(Y,\chi ) -d(Y,0)$. The use of $\bar{d}$ to address issues related to the presence of knots with trivial Alexander polynomial first appeared in [16]. We will use the additivity property $\bar{d}(Y{\#}Y',\chi \oplus \chi ')=\bar{d}(Y,\chi )+ \bar{d}( Y', \chi ')$. Note that $\bar{d}(Y, 0) = 0$. One key result states that if $H_1(Y, {\mathbb Z}_2) = 0$ and $Y = \partial W$, where W is a rational homology four-ball and $\chi$ is the image of a class in $H_2(W,Y)$, then $d(Y,\chi ) = \bar{d}(Y, \chi ) = 0$.

2.3 Obstructions

The main facts about the invariants $\eta$ and $\overline{d}$ that we need are stated in the next theorem.

Theorem 2.1

If K is smoothly slice and $H_1(Y_q(K), {\mathbb Z}_2) =0$, then there is a subgroup $\mathcal {M}\subset H_1(Y_q(K))$ with the following four properties: (1) $\mathcal {M}$ is a metabolizer for the linking form; (2) $\mathcal {M}$ is invariant under the order q deck transformation of $Y_q(K)$; (3) For all $\chi \in \mathcal {M}$, $\bar{d}(Y_q(K), \chi ) =0$; (4) For all $\chi \in \mathcal {M}$ of prime power order, $\eta ( K, q, \chi ) = 0$.

Recall that a metabolizer for $H_1(Y_q(K))$ is a subgroup $\mathcal {M}$ satisfying $\mathcal {M}= \mathcal {M}^\perp$ with respect to the nonsingular linking form on $H_1(Y_q(K))$. With regards to the conditions on the Casson–Gordon theorem, this result is essentially as it appeared in [3]; the equivariance of $\mathcal {M}$ was noted, for instance, in [18]. The use of d–invariants of covers to obstruct slicing was initiated in [21]. Notice that in Theorem 2.1 we actually have a stronger result that $d(Y_q(K), \chi ) =0$ for all $\chi \in \mathcal {M}$; we use that $\bar{d}(Y_q(K), \chi ) =0$, because these are the needed slicing obstructions when working modulo $\mathcal {T}_\Delta$ (see Theorem 2.2 below).

2.4 Working modulo $\mathcal {T}_\Delta$

Suppose L is a knot with trivial Alexander polynomial. Then, we have that $H_1(Y_q(L) )= 0$. Theorem 2.1 will be applied to provide a slicing obstruction. Since the first homology of $Y_q(L)$ is trivial, the presence of L does not affect the values of the $\bar{d}$–invariants or the $\eta$–invariants that we are considering. Thus $K{\#}-\rho (K){\#}L$ is not smoothly slice if we can obstruct $K {\#}-\rho (K)$ from being smoothly slice using $\eta$ and $\bar{d}$. We state this as a theorem.

Theorem 2.2

If L is a knot with trivial Alexander polynomial and Theorem 2.1 obstructs a knot $K {\#}-\rho (K)$ from being smoothly slice, then $K {\#}-\rho (K){\#}L$ is not smoothly slice.

3 A single example

In this section we construct a knot K that is nontrivial in the quotient group $\mathcal {T}/ (\text {Fix}(\rho )+\mathcal {T}_\Delta )$.

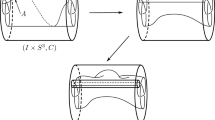
Figure 1 offers a schematic illustration of a knot $R_1$. More generally, we let $R_n$ denote the similarly constructed knot for which there are $2n+1$ half twists between the two bands. To simplify notation for now, we abbreviate $R_1$ by R in this section. We will specify a string orientation for R later. The construction of K is fairly standard. By appropriately replacing neighborhoods of the curves $\alpha$ and $\beta$ with the complements of knots $J_\alpha$ and $J_\beta$, one constructs a new knot denoted $R(J_\alpha , J_\beta )$. In effect, the bands in the evident Seifert surface for R have the knots $J_\alpha$ and $J_\beta$ placed in them. To make the notation more concise, we will sometimes abbreviate $R(J_\alpha , J_\beta )$ as $R_*$.

Fig. 1

Knot $R_1$

Let D be the knot Wh(T(2, 3), 0), the positively clasped, untwisted Whitehead double of the right-handed trefoil knot T(2, 3). Let J be the knot Wh(U, 5), the positively clasped 5–twisted Whitehead double of the unknot, having Seifert matrix

$$\begin{aligned} \begin{pmatrix} -1 &{}\quad 1 \\ 0 &{}\quad 5 \\ \end{pmatrix} \end{aligned}$$

and Alexander polynomial $5t^2 - 11t+5$. Our desired knot K is R(D, J):

Theorem 3.1

The knot $R(D, J)\ne 0 \in \mathcal {T}/ (\text {Fix}(\rho )+\mathcal {T}_\Delta )$.

The rest of this section is devoted to proving Theorem 3.1. Let $K=R(D,J)$. The knot D has Alexander polynomial $\Delta _D(t) = 1$. According to Freedman’s theorem [8, 9], D is topologically slice. A standard argument then shows that K is also topologically slice: $K \in \mathcal {T}$.

To prove Theorem 3.1 it suffices to show the following: for any knot L with $\Delta _L(t)=1$,

$$\begin{aligned} K{\#}- \rho (K){\#}L \ne 0 \in \mathcal {T}. \end{aligned}$$

By Theorem 2.2, we only need to show the following theorem:

Theorem 3.2

Theoreom 2.1 obstructs the knot $K{\#}- \rho (K)$ from being smoothly slice.

The following subsections present the proof of Theorem 3.2.

3.1 The homology of the branched cover

We will now work exclusively with $q = 3$. Recall that we are using the abbreviation $R_* = R(J_\alpha ,J_\beta )$. A standard knot theoretic computation shows that for arbitrary $J_\alpha$ and $J_\beta$, $H_1(Y_3(R_*)) \cong {\mathbb Z}[t^{\pm 1}]/\langle t-2, t^3-1\rangle \oplus {\mathbb Z}[t^{\pm 1}]/\langle 2t-1, t^3-1\rangle \cong {\mathbb Z}_7 \oplus {\mathbb Z}_7$, generated by $\widetilde{\alpha }$ and $\widetilde{\beta }$, chosen lifts of the $\alpha$ and $\beta$. Furthermore, viewing $H_1(Y_3(R_*))$ as a vector space over ${\mathbb Z}_7$, the first homology group splits into a 2–eigenspace $E_2$ and a 4–eigenspace $E_4$ with respect to the order three deck transformation of $Y_3(R_*)$. Now we make a choice of orientation of $R_*$ so that $E_2$ is generated by $\widetilde{\alpha }$ and $E_4$ is generated by $\widetilde{\beta }$.

With respect to the ${\mathbb Z}_7$–valued linking form, $\widetilde{\alpha }$ and $\widetilde{\beta }$ are eigenvectors and thus $\mathrm {lk}(\widetilde{\alpha }, \widetilde{\alpha }) = 0 = \mathrm {lk}(\widetilde{\beta }, \widetilde{\beta })$. By replacing a generator with a multiple, we can assume $\text {lk}( \widetilde{\alpha }, \widetilde{\beta }) = 1$.

If m is an oriented meridian for $R_*$, then the image of m under the map sending $R_*$ to $-R_*$ is again an oriented meridian for the latter. (Note: $-R_*$ is built by reversing the ambient orientation of $S^3$ and then reversing the orientation of $R_*$. The effect is to reverse the meridian twice.) It follows that with our choice of orientation of $R_*$, the knot $-R_*$ is oriented so that with the order three deck transformation $H_1( Y_3(-R_*))$ has the same splitting into eigenspaces, $E_2 \oplus E_4$, which are generated by $\widetilde{\alpha }$ and $\widetilde{\beta }$. Reversing the orientation of $R_*$ has the effect of inverting the deck transformation, so $H_1( Y_3(-\rho (R_*)))$ splits as a direct sum of a 2–eigenspace $E_2'$ and a 4–eigenspace $E_4'$, generated by $\widetilde{\beta }$ and $\widetilde{\alpha }$, respectively. (That is, the roles of $\widetilde{\alpha }$ and $\widetilde{\beta }$ have been reversed.) Henceforth, when we are working with $\rho (R_*)$, we will write $E_2'$, generated by $\widetilde{\beta }'$, and $E_4'$, generated by $\widetilde{\alpha }'$.

We now consider the action of the deck transformation on $H_1( Y_3(R_* {\#}-\rho (R_*)))$. It has minimal polynomial $(t-2)(t-4)$. Thus, any invariant ${\mathbb Z}_7$–subspace $\mathcal {M}$ of $H_1( Y_3(R_* {\#}-\rho (R_*)))$ splits into eigenspaces. Here are all the possibilities.

Lemma 3.3

The set of all equivariant metabolizers of $H_1(Y_3( R_* {\#}-\rho (R_*)))$ are given by the following spans:

• (1) $\left\langle \widetilde{\alpha }, \widetilde{\beta }'\right\rangle$; the 2–eigenspace.

• (2) $\left\langle \widetilde{\beta }, \widetilde{\alpha }'\right\rangle$; the 4–eigenspace.

• (3) $\left\langle \widetilde{\alpha }, \widetilde{\alpha }'\right\rangle$ or $\left\langle \widetilde{\beta }, \widetilde{\beta }'\right\rangle$; one “pure” 2–eigenvector and one “pure” 4–eigenvector.

• (4) $\left\langle \widetilde{\alpha }+ r \widetilde{\beta }', \widetilde{\beta }+ r^{-1} \widetilde{\alpha }'\right\rangle$, where $r \ne 0 \in {\mathbb Z}_7$.

Proof

Cases (1) and (2) reflect the possibility that $\mathcal {M}$ is a 2–dimensional eigenspace. The alternative is that $\mathcal {M}$ contains a 2–eigenvector and a 4–eigenvector. In general, these would be spanned by vectors of the form $x\widetilde{\alpha }+ y\widetilde{\beta }'$ and $z\widetilde{\beta }+ w\widetilde{\alpha }'$. The condition that these have linking number 0 is given by $xz - yw = 0 \mod 7$. If $x\ne 0$, then by taking a multiple we can assume $x=1$. Similarly, if $z \ne 0$, we can assume $z=1$. With this, reducing to cases (3) and (4) is straightforward. $\square$

To complete the proof of Theorem 3.2, we need to show that slicing obstructions arising from each of the metabolizers in Lemma 3.3 are nonzero. The proof of this depends on additivity and the computation of specific values of invariants. We will be able to restrict our attention to a single summand by using the next lemma which concerns reversing the orientation of an ambient space. Notice that string orientation is not relevant to these equations. The following result is then seen to be trivial; it simply states that reversing the orientation of an ambient space changes the sign of the relevant invariants.

Lemma 3.4

We have the following equalities:

• (1) $\eta (-\rho (R_*) , 3, \widetilde{\alpha }') = - \eta (R_* , 3, \widetilde{\alpha })$.

• (2) $\eta (-\rho (R_*) , 3, \widetilde{\beta }') = - \eta (R_* , 3, \widetilde{\beta })$.

• (3) $\bar{d}(Y_3(-\rho (R_*), \widetilde{\alpha }')) = -\bar{d}(Y_3(R_*), \widetilde{\alpha })$.

• (4) $\bar{d}(Y_3(-\rho (R_*), \widetilde{\beta }')) = - \bar{d}(Y_3(R_*), \widetilde{\beta })$.

Recall that $K=R_*$ with the choice $J_\alpha =D$ and $J_\beta =J$. With Lemma 3.4, we see that the proof of Theorem 3.2 is reduced to the following lemma, whose proof is postponed to the next subsection.

Lemma 3.5

For all $r \not \equiv 0 \mod 7$, we have the following:

• (1) $\eta (K, 3, r \widetilde{\alpha }) \ne 0$.

• (2) $\eta (K, 3, r \widetilde{\beta }) = 0$.

• (3) $\bar{d}(Y_3(K), r \widetilde{\beta }) \ne 0$.

We finish the proof of Theorem 3.2 modulo the proof of Lemma 3.5. It is shown that for each metabolizer listed in Lemma 3.3, the vanishing of the associated slicing obstructions arising from $\eta$–invariants and $\overline{d}$–invariants, as provided by Theorem 2.1, leads to a contradiction of Lemma 3.5.

• (1) $\left\langle \widetilde{\alpha }, \widetilde{\beta }'\right\rangle$. If $\widetilde{\alpha }$ is in the metabolizer, then the vanishing of the slicing obstructions includes the statement: $\eta (K , 3, \widetilde{\alpha }) + \eta (-\rho (K), 3, 0) = 0$. Casson–Gordon invariants for trivial characters always vanish, so this contradicts Lemma 3.5 (1).

• (2) $\left\langle \widetilde{\beta }, \widetilde{\alpha }'\right\rangle$. Here we use the element $\widetilde{\alpha }'$ and the vanishing of the slicing obstruction to conclude that $\eta (K , 3, 0) + \eta (-\rho (K) , 3, \widetilde{\alpha }') = 0$. As in the last case, this contradicts Lemma 3.5 (1) after using Lemma 3.4 to replace the $-\rho (K)$ term with one involving K.

• (3) $\left\langle \widetilde{\alpha }, \widetilde{\alpha }'\right\rangle$. This can be handled in the same way as the previous two cases.

• (4) $\left\langle \widetilde{\beta }, \widetilde{\beta }'\right\rangle$. Considering $\widetilde{\beta }$, we would have $\bar{d}(Y_3(K) , \widetilde{\beta }) + \bar{d}(Y_3(-\rho (K)) , 0) = 0$. This falls to Lemma 3.5 (3).

• (5) $\left\langle \widetilde{\alpha }+ r \widetilde{\beta }', \widetilde{\beta }+ r^{-1} \widetilde{\alpha }'\right\rangle$, where $r \ne 0 \in {\mathbb Z}_7$. In this case, this leads to the equation $\eta (K , 3, \widetilde{\alpha }) + \eta (-\rho (K) , 3, r \widetilde{\beta }') = 0$. This is addressed using Lemma 3.4 (2) and Lemma 3.5 (1) and (2).

3.2 Casson–Gordon and Heegaard Floer obstructions

In this subsection, we give a proof of Lemma 3.5, which will complete the proof of Theorem 3.2. The Casson–Gordon invariant we will use in this section is a discriminant invariant, which is determined by the value of $\eta$. Details were presented in [10]. The knots used there were almost identical to those we are considering, and [10] can serve as a complete reference. (A similar calculation arises in [6, Appendix B].)

(1) $\varvec{\eta (K, 3, r \widetilde{\alpha }) \ne 0}$: The invariant $\eta$ is conjugation invariant. Therefore $\eta (K, 3, - \widetilde{\alpha }) = \eta (K, 3, \widetilde{\alpha })$. Since $\widetilde{\alpha }$ is a 2–eigenvector of the order three deck transformation, we have $\eta (K, 3, \widetilde{\alpha }) = \eta (K, 3, 2 \widetilde{\alpha }) = \eta (K, 3, 4 \widetilde{\alpha })$. Combining these, we have reduced the proof to showing $\eta (K, 3, \widetilde{\alpha }) \ne 0$.

Observations of Gilmer [11, 12] and Litherland [20] relate the value of $\eta (K, 3, \widetilde{\alpha })$ to the value of $\eta (R(D,U), 3, \widetilde{\alpha })$ and to classical invariants of J. In the current situation, the classical invariant that will appear is $\Delta _7(J) := \sqrt{\prod _{k=1}^{6} \Delta _J(e^{2k\pi i/7})} = \sqrt{\big | H_1(Y_3(J))\big |}$.

Our next observation is that $\eta (R(D,U), 3, \widetilde{\alpha }) = 0$. Notice that R(D, U) bounds a Seifert surface of genus 1 that is obtained by tying the band dual to $\alpha$ on the evident Seifert surface for R in Fig. 1 along D. Therefore R(D, U) bounds a smooth slice disk B obtained by cutting the band dual to $\alpha$ of the Seifert surface. Since the curve $\alpha$ itself bounds a smooth slice disk in the complement of B, we have that $\eta (R(D,U), 3, \widetilde{\alpha }) = 0$. Thus, we are reduced to considering $\Delta _7(J)$ and the lemma below is the result we need. We note that by definition, a positive integer n is a d–norm if every prime factor of n which is relatively prime to d and has odd exponent in n, has odd order in ${\mathbb Z}_d^*$, the multiplicative group of units in ${\mathbb Z}_d$.

Lemma 3.6 is essentially [10, Corollary 6]. In that paper, the statement is presented as a slicing obstruction, but the obstruction is achieved by assuming that a specific Casson–Gordon invariant vanishes. Also, in that work a two-component link was being considered, but one of the components corresponds to the $\beta$ we are using here. The translation is straightforward.

Lemma 3.6

If $\eta (K,3, \widetilde{\alpha }) = 0$, then $\Delta _7(J)$ is a 7–norm.

In our case, $\Delta _J(t) = 5t^2 - 11t +5$ and a computation shows that $\sqrt{\big | H_1(Y_3(J))\big |} = (13)(97)$. The desired result is now immediate: $\gcd (7,13) =1$, 13 has odd exponent in (13)(97), and the order of 13 in ${\mathbb Z}_7^*$ is even ($13 \equiv -1 \mod 7$). Thus, $\eta (K, 3, \widetilde{\alpha }) \ne 0$ as desired.

(2) $\varvec{\eta (K, 3, r \widetilde{\beta }) = 0}$: As in Case (1), we first can reduce this to demonstrating that $\eta (K, 3, \widetilde{\beta }) = 0$. Since D is topologically slice, K is also topologically slice, bounding a slice disk B, and $\beta$ bounds a slice disk in the complement of B. It then follows from Casson–Gordon’s original theorem that $\eta (K, 3, \widetilde{\beta }) = 0$. (We are using here the fact that the Casson–Gordon theorem applies in the topological locally flat setting, which is a consequence of Freedman’s work [8, 9].)

(3) $\varvec{\bar{d}(Y_3(K), r \widetilde{\beta }) \ne 0}$: As with the previous cases, this can be reduced to the basic case that $\bar{d}(Y_3(K), \widetilde{\beta }) \ne 0$. The computation has three parts, stated as a sequence of lemmas. Our approach is closely related to the one in [6] and depends on a crucial calculation done there. Note, however, that we must work with the $\bar{d}$–invariant, rather than with the d–invariant. These results could be extracted from [6] (see Theorems 6.2 and 6.5, along with Corollary 6.6 of [6]), but in our restricted setting, much more concise arguments are available.

The proof of the following statement includes an explanation as to why the two homology groups $H_1(Y_3(K))$ and $H_1(Y_3(R(D,U)))$ can be identified. We reduce the result to a computation related to $Y_3(R(D,U))$.

Lemma 3.7

${d}(Y_3(K), x) =d (Y_3(R(D,U)), x)$ for all first homology classes x.

Proof

The knot J can be converted into the unknot by changing negative crossings to positive. Thus, there is a collection of unknots, $\{\gamma _i\}_{i=1,\ldots , r}$ (in fact, an unlink) in the complement of the natural genus one Seifert surface for K such that $(-1)$–surgery on each has the effect of unknotting the band. Each $\gamma _i$ bounds a surface in the complement of the Seifert surface. The curves $\gamma _i$ lift to $Y_3(K)$ to give a family of disjoint simple closed curves $\{\widetilde{\gamma }_{i,j}\}_{1\le i\le r, 1\le j\le 3}$. By lifting the surfaces bounded by the $\gamma _i$ in the complement of the Seifert surface for K, we see that the curves $\widetilde{\gamma }_{i,j}$ are null-homologous and unlinked.

It is now apparent that $Y_3(R(D,U))$ can be built from $Y_3(K)$ by performing $(-1)$–surgery on all the curves in $\{\widetilde{\gamma }_{i,j}\}_{1\le i\le r, 1\le j\le 3}$. There is a corresponding cobordism from $Y_3(K)$ to $Y_3(R(D,U))$ which is negative definite, has diagonal intersection form, and the inclusions $Y_3(K)$ and $Y_3(R(D,U))$ into the cobordism induce isomorphisms of the first homology. Now, basic results of [22] imply that $d(Y_3(K)) \ge d(Y_3(R(D,U)))$.

We also have that J can be unknotted by changing positive crossings to negative. The argument just given yields the reverse inequality. $\square$

Lemma 3.8

${d}(Y_3(K), r \widetilde{\alpha }) = 0$ for all $r \in {\mathbb Z}_7$. In particular, ${d}(Y_3(K), 0) = 0$.

Proof

By Lemma 3.7, we consider R(D, U) instead. This knot is smoothly slice, so $Y_3(R(D,U))$ bounds a spin rational homology ball $W^4$. The homology class $\widetilde{\alpha }$ and its multiples are null-homologous in $W^4$, so the corresponding Spin$^c$–structure extends to $W^4$. The vanishing of the d–invariant is then implied by results of [22]. $\square$

We now have our final lemma that completes the proof of Lemma 3.5.

Lemma 3.9

$\bar{d}(Y_3(K), \widetilde{\beta }) \ne 0$.

Proof

By Lemmas 3.7 and 3.8 we can switch to considering the d–invariant rather than the $\bar{d}$–invariant, as follows.

$$\begin{aligned} \begin{aligned} \bar{d}(Y_3(K), \widetilde{\beta })&= {d}(Y_3(K), \widetilde{\beta }) - {d}(Y_3(K),0) \\&= {d}(Y_3(K), \widetilde{\beta }) \\&= {d}(Y_3(R(D,U)), \widetilde{\beta }). \end{aligned} \end{aligned}$$

The argument is then completed by quoting [6, Appendix A], where it is shown that ${d}(Y_3(R(D,U)), \widetilde{\beta }) \le -3/2$. (The statement in [6] refers to a homology class denoted $4 \widehat{x_2}$. Notice that since $\widetilde{\beta }$ is a 4–eigenvector, ${d}(Y_3(R(D,U)), \widetilde{\beta }) = {d}(Y_3(R(D,U)), 4\widetilde{\beta }) = {d}(Y_3(R(D,U)), 2\widetilde{\beta })$. Also, since the d–invariant is invariant under conjugation of Spin$^c$–structure, ${d}(Y_3(R(D,U)), x) = {d}(Y_3(R(D,U)), -x)$. Thus, all d–invariants associated to nonzero elements in this eigenspace are equal.) $\square$

4 An infinite family of knots

Our goal in this section is to generalize the previous example in Sect. 3 to build an infinitely generated free subgroup of $\mathcal {T}/ (\text {Fix}(\rho )+\mathcal {T}_\Delta )$, which will prove Theorem 1.1.

We now let the two bands in the Seifert surface in Fig. 1 have $2n+1$ half-twists, and use the general notation $R_n$. For the choice of knots $J_\alpha$ and $J_\beta$, we will let $J_\alpha =\mathrm{Wh}(T(2,-3),-1)$ be the positively clasped $(-1)$–twisted Whitehead double of the left-handed trefoil, and let $J_\beta =\mathrm{Wh}(T(2,3),0)$ be the positively clasped untwisted Whitehead double of the right-handed trefoil. Notice that $J_\beta$ is topologically slice, hence so is $R_n(J_\alpha , J_\beta )$. Henceforth, we let $K_n=R_n(J_\alpha , J_\beta )$ for brevity.

The proof of Theorem 1.1 consists of selecting an appropriate set of positive integers $\mathcal {N}$ for which we can prove that the set $\{R_n (J_\alpha , J_\beta )\}_{n \in \mathcal {N}}$ represents a linearly independent set in $\mathcal {T}/( \mathrm {Fix}(\rho )+\mathcal {T}_\Delta )$. Computing the appropriate Heegaard Floer invariants of a branched cyclic cover of $R_n (J_\alpha , J_\beta )$ relies on work of Cochran-Harvey-Horn [6] and Cha [4].

Recall that we let $Y_3(K)$ denote the 3–fold cover of $S^3$ branched over an arbitrary knot K. The following is an elementary knot theoretic computation.

Lemma 4.1

$H_1(Y_3(K_n)) \cong {\mathbb Z}_{3n^2 +3n +1} \oplus {\mathbb Z}_{3n^2 +3n +1}$.

To simplify our computations, we would like to constrain the possible prime factorizations of $3n^2 +3n+1$. This is provided by a number theoretic result, the proof of which is presented in the appendix.

Theorem 4.2

There is an infinite set of positive integers $\mathcal {N}= \{n_i\}_{i\ge 1}$ such that for all i, $3n_i^2 + 3n_i +1 = p_{2i-1}p_{2i}$ where: (1) each $p_j$ is either an odd prime or equals 1; (2) if $j \ne l$ and $p_j \ne 1$, then $p_j \ne p_l$; and (3) $1\in \mathcal {N}$.

Our goal is to prove the following theorem, from which Theorem 1.1 immediately follows.

Theorem 4.3

The set of knots $\{K_n\}_{n \in \mathcal {N}}$ is linearly independent in $\mathcal {T}/(\text {Fix}(\rho )+\mathcal {T}_\Delta )$.

Elementary group theory gives the following.

Lemma 4.4

The set of knots $\{K_n\}_{n \in \mathcal {N}}$ is linearly independent in $\mathcal {T}/(\text {Fix}(\rho )+\mathcal {T}_\Delta )$ if and only if the set of knots $\{K_n{\#}-\rho (K_n) \}_{n \in \mathcal {N}}$ is linearly independent in $\mathcal {T}/\mathcal {T}_\Delta$.

Proof

It immediately follows from the following observation: ${\#}_n a_nK_n = 0$ in $\mathcal {T}/(\text {Fix}(\rho )+\mathcal {T}_\Delta )$ if and only if ${\#}_n a_nK_n = \rho ({\#}_n a_nK_n)$ in $\mathcal {T}/\mathcal {T}_\Delta$, and the latter holds if and only if ${\#}_n a_n(K_n {\#}-\rho (K_n))= 0$ in $\mathcal {T}/\mathcal {T}_\Delta$. $\square$

This in turn is easily reduced to proving the following.

Theorem 4.5

Let L be a knot with $\Delta _L(t) = 1$ and let

$$\begin{aligned} K := \left( {\#}_{n\in \mathcal {N}} a_n(K_n {\#}-\rho (K_n))\right) {\#}L. \end{aligned}$$

If $K=0\in \mathcal {T}$ for some set of $a_n$ for which all but a finite set of $a_n$ are zero, then $a_n = 0$ for all n.

The rest of this section is devoted to proving Theorem 4.5. Throughout the rest of Sect. 4, we let

$$\begin{aligned} K := \left( {\#}_{n\in \mathcal {N}} a_n(K_n {\#}-\rho (K_n))\right) {\#}L. \end{aligned}$$

where all but a finite set of $a_n$ are zero.

4.1 Proof of Theorem 4.5, first step

In this subsection we show how the argument is reduced to a statement about the d–invariants and $\eta$–invariants of $a_n(K_n {\#}-\rho (K_n))$ for each $n\in \mathcal {N}$. First, we give the following lemma.

Lemma 4.6

$d( Y_3( K_n {\#}-\rho (K_n)), 0) = 0$ and $\eta ( K_n {\#}-\rho (K_n) ,3 , 0) = 0$.

Proof

The d–invariant and $\eta$–invariant are additive under connected sums.

With regards to the d–invariant, the spaces $Y_3(K_n)$ and $Y_3(\rho (K_n))$ are orientation-preserving diffeomorphic, and orientation reversal of a 3–manifold changes the sign of the d–invariant.

With regards to the $\eta$–invariant, from results going back to Gilmer [12] and Litherland [20], the value of $\eta (K_n {\#}-\rho (K_n) ,3 , 0)$ is independent of $J_\alpha$ and $J_\beta$. In the case that $J_\alpha$ and $J_\beta$ are both unknotted, $R_n(J_\alpha , J_\beta )$ is slice, and thus the Casson–Gordon invariant vanishes. $\square$

The theorem below follows from Theorem 2.1 and Lemma 4.6; notice that the result uses the d-invariant, not the $\bar{d}$–invariant as in Theorem 2.1. Let

$$\begin{aligned} K' := \left( {\#}_{n\in \mathcal {N}} a_n(K_n {\#}-\rho (K_n))\right) , \end{aligned}$$

and now we have $K=K'{\#}L$.

Theorem 4.7

Let K and $K'$ be defined as above. If $K=0\in \mathcal {T}$, then there exists a subgroup $\mathcal {M}\subset H_1(Y_3(K'))$ for which: (1) $\big | \mathcal {M}\big |^2 = \big | H_1(Y_3(K')) \big |$; (2) $\mathcal {M}$ is a metabolizer for the linking form on $H_1(Y_3(K'))$ and $\mathcal {M}$ is invariant under the action of the order three deck transformation of $Y_3(K')$; (3) for all $z \in \mathcal {M}$, $d(Y_3(K'),z)) = 0$ and for all $z \in \mathcal {M}$ of prime power order, $\eta (K',3, z) = 0$.

Proof

Since K is smoothly slice, by Theorem 2.1 with $q=3$, there is a subgroup $\mathcal {G}\subset H_1(Y_3(K))$ for which (1) $\big | \mathcal {G}\big |^2 = \big | H_1(Y_3(K)) \big |$; (2) $\mathcal {G}$ is a metabolizer for the linking form on $H_1(Y_3(K))$ and $\mathcal {G}$ is invariant under the action of the order three deck transformation of $Y_3(K)$; (3) for all $z \in \mathcal {G}$, $\bar{d}(Y_3(K),z)) = 0$ and for all $z \in \mathcal {G}$ of prime power order, $\eta (K,3, z) = 0$.

Note that $H_1(Y_3(K)) = H_1(Y_3(K'))\oplus H_1(Y_3(L))$. Since $\Delta _L(t)=1$, it follows that $H_1(Y_3(K))=0$ and $H_1(Y_3(K)) = H_1(Y_3(K'))\oplus 0$. Now let $\mathcal {M}:= \{z\in H_1(Y_3(K'))\mid (z,0)\in \mathcal {G}\}$. Then it easily follows that the subgroup $\mathcal {M}$ satisfies the conclusions (1) and (2).

We show that $\mathcal {M}$ also satisfies the conclusion (3). Let $z\in \mathcal {M}$. Then $(z,0)\in \mathcal {G}$ and $\bar{d}(Y_3(K), (z,0))=0$. Since $\bar{d}(Y_3(K), (z,0))=\bar{d}(Y_3(K'),z) + \bar{d}(Y_3(L), 0)$ and $\bar{d}(Y_3(L), 0)=d(Y_3(L),0)-d(Y_3(L),0)=0$, it follows that $\bar{d}(Y_3(K'),z)=0$. By Lemma 4.6, $d(Y_3(K'),0)=0$ and it follows that $d(Y_3(K'),z)=0$.

Noticing that $\eta (L, 3, 0)=0$ since L is topologically slice, in a similar fashion one can show that for all $z \in \mathcal {M}$ of prime power order, $\eta (K',3, z) = 0$. $\square$

We write

$$\begin{aligned} S_n = a_n(K_n{\#}-\rho (K_n)). \end{aligned}$$

Observe that for each $n_i\in \mathcal {N}$, ${\mathbb Z}_{3n_i^2+3n_i+1}\cong {\mathbb Z}_{p_{2i-1}} \oplus {\mathbb Z}_{p_{2i}}$, and hence there is a natural decomposition

$$\begin{aligned} H_1(Y_3(S_{n_i})) \cong \big ( ( {\mathbb Z}_{p_{2i-1}} \oplus {\mathbb Z}_{p_{2i}}) \oplus ({\mathbb Z}_{p_{2i-1}} \oplus {\mathbb Z}_{p_{2i}}) \big )^{2|a_{n_i}|} . \end{aligned}$$

Since all $p_i$ are relatively prime, the metabolizer $\mathcal {M}$ obtained from Theorem 4.7 naturally splits into the direct sum of its p–primary components $\mathcal {M}_p$:

$$\begin{aligned} \mathcal {M}= \bigoplus _{i \ge 1} \left( \mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}\right) , \end{aligned}$$

where $\mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}$ is a metabolizer for the linking form on $H_1(Y_3(S_{n_i}))$. Since only a finite set of the $a_i$ are nonzero, only a finite set of the $\mathcal {M}_p$ are nonzero. We now have the following corollary of Theorem 4.7.

Corollary 4.8

Let K be defined as above. If $K=0\in \mathcal {T}$, then for all $z \in \mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}$, $d\left( Y_3(S_{n_i}), z\right) = 0$, and for all $z \in \mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}$ of prime power order, $\eta \left( S_{n_i}, 3, z\right) = 0$.

Proof

Fix $i\ge 1$. We can write

$$\begin{aligned} \mathcal {M}= \left( \mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}\right) \oplus \bigoplus _{j\ne i } \left( \mathcal {M}_{p_{2j -1}} \oplus \mathcal {M}_{p_{2j}}\right) . \end{aligned}$$

Let $z\in \mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}$. Then $(z,0)\in \mathcal {M}$, and by Theorem 4.7 it follows that $d(Y_3(K'),(z,0))=0$. By additivity of d-invariants and Lemma 4.6, it follows that $d\left( Y_3(S_{n_i}), z\right) = 0$. Similarly, one can show that $\eta \left( S_{n_i}, 3, z\right) = 0$ for all $z \in \mathcal {M}_{p_{2i -1}} \oplus \mathcal {M}_{p_{2i}}$ of prime power order. $\square$

4.2 Proof of Theorem 4.5, second step

Observe that for each $n_i=p_{2i-1}p_{2i} \in \mathcal {N}$, at least one of $p_{2i-1}$ and $p_{2i}$ is greater than one. By reordering, we can thus assume that for all i, $p_{2i -1} >1$. In the appendix, we observe that $n_1=1$, $p_1 =7$, $p_2=1$, and therefore $\mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}=\mathcal {M}_7$.

Recall that

$$\begin{aligned} K' = \left( {\#}_{n\in \mathcal {N}} a_n(K_n {\#}-\rho (K_n))\right) \text{ and } K=K'{\#}L \end{aligned}$$

and to prove Theorem 4.5 we must show that if $K=0\in \mathcal {T}$, then $a_n=0$ for all $n\in \mathcal {N}$.

In this subsection, first we will give a proof that if $K=0\in \mathcal {T}$, then $a_1=0$. Then, we will explain how that proof can be modified to show that $a_n=0$ for all $n\in \mathcal {N}$.

Proof that $\varvec{a_1=0}$: Suppose $K=0\in \mathcal {T}$. For brevity, let $a=a_1$ and $S=S_1$. Suppose $a\ne 0$. By changing the orientation if necessary, we may assume $a > 0$. Notice that

$$\begin{aligned} H_1(Y_3(S))=({\mathbb Z}_7\oplus {\mathbb Z}_7\oplus {\mathbb Z}_7\oplus {\mathbb Z}_7)^a=\bigoplus _{i=1}^a\left( \langle x_i\rangle \oplus \langle y_i \rangle \oplus \langle x_i'\rangle \oplus \langle y_i' \rangle \right) , \end{aligned}$$

where $x_i$ (respectively, $y_i$) is a lift of the curve $\alpha$ (respectively, $\beta$) to the i–th copy of $K_1=R_1(J_\alpha ,J_\beta )$ in $Y_3(S)$, and $x_i'$ (respectively, $y_i'$) is a lift of the curve $\alpha$ (respectively, $\beta$) to the i–th copy of $\rho (K_1)$ in $Y_3(S)$.

On the homology group $H_1(Y_3(S))$ the deck transformation of order three acts. Viewing $H_1(Y_3(S))$ as a vector space over ${\mathbb Z}_7$, $H_1(Y_3(S))$ splits into the direct sum of the 2–eigenspace and the 4–eigenspace. We make a choice of orientation of $K_1$ such that the 2–eigenspace is generated by the $x_i$ and $y_i'$, and the 4–eigenspace is generated by $y_i$ and $x_i'$.

Since the metabolizer $\mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}$ is invariant under the action of the deck transformations of $Y_3(S)$, one can easily see that it splits into the direct sum of the 2–eigenspace and the 4–eigenspace, $E_2\oplus E_4$, such that

$$\begin{aligned} E_2 \subset \bigoplus _{i=1}^a\left( \langle x_i\rangle \oplus \langle y_i' \rangle \right) \text{ and } E_4 \subset \bigoplus _{i=1}^a\left( \langle y_i\rangle \oplus \langle x_i' \rangle \right) . \end{aligned}$$

Lemma 4.9

If $K=0\in \mathcal {T}$, then $E_2 = \bigoplus _{i=1}^a\langle x_i\rangle$ and $E_4=\bigoplus _{i=1}^a\langle x_i'\rangle .$

Proof

Recall that we are working now only with $n_1 = 7$ and will describe the extension to all $n_i$ later. It suffices to show that $E_2 \subset \bigoplus _{i=1}^a\langle x_i\rangle$ and $E_4 \subset \bigoplus _{i=1}^a\langle x_i'\rangle$ since the order of the metabolizer $\mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}$, which is $7^{2a}$, is the same as that of the direct sum of $\bigoplus _{i=1}^a\langle x_i\rangle$ and $\bigoplus _{i=1}^a\langle x_i'\rangle$.

Suppose that $E_2$ is not contained in $\bigoplus _{i=1}^a\langle x_i\rangle$. Then, in $E_2$ there exists an element

$$\begin{aligned} h=(h_1, h_1', h_2, h_2', \ldots , h_a, h_a')\in \bigoplus _{i=1}^a\left( \langle x_i\rangle \oplus \langle y_i' \rangle \right) \end{aligned}$$

such that $h_k'\ne 0$ in $\langle y_k'\rangle ={\mathbb Z}_7$ for some $1\le k\le a$.

The Casson–Gordon invariant that we will use in this section is the Casson–Gordon signature invariant [3], which we also denote by $\eta$. Let $\sigma _r(J_\alpha )$ denote the Levine-Tristram signature function of $J_\alpha$ evaluated at $e^{2\pi r\sqrt{-1}}$. As described earlier, results of Gilmer [12] and Litherland [20] describe how the value of $\eta (S,3,h)$ is determined by the values of $\eta (R_1(U, J_\beta ),h)$ along with values of $\sigma _r(J_\alpha )$ for specified values of r. Because $J_\beta$ is topologically slice, Casson–Gordon invariants cannot distinguish $R_1(U,J_\beta )$ from $R_1(U,U)$, and for this knot all possible Casson–Gordon invariants vanish. One concludes that the relevant values of $\eta (R_1(U,J_\beta ), 3, h)$ will vanish. Combining these observations, the results of Gilmer [12] and Litherland [20] yield

$$\begin{aligned} \eta (S,3,h)= \sum _{i=1}^a \epsilon _i\left( \sigma _{b_i/7}(J_\alpha ) +\sigma _{2b_i/7}(J_\alpha )+\sigma _{4b_i/7}(J_\alpha ) \right) , \end{aligned}$$

where $b_i\in {\mathbb Z}_7$ , and $\epsilon _i=0$ if $h_i'=0$ and $\epsilon _i =1$ if $h_i'\ne 0$. Here $b_i/7=h_i'\cdot \text{ lk }(x_i,y_i')$ for the linking form $\mathrm {lk}(-,-)$ of $Y_3(S)$. The knot $J_\alpha$ has the same Seifert form as the right-handed trefoil, and therefore

$$\begin{aligned} \sigma _r(J_\alpha ) = {\left\{ \begin{array}{ll} 0 &{}0\le r< \frac{1}{3}\\ -2 &{} \frac{1}{3}<r \le \frac{1}{2}. \end{array}\right. } \end{aligned}$$

Therefore, we have $\eta (S,3,h)\le 0$. We are assuming that $h'_k \ne 0$, so $\epsilon _k=1$ and $b_k \ne 0 \in {\mathbb Z}_7$. Regardless of the value of $b_k$,

$$\begin{aligned} \sigma _{b_k/7}(J_\alpha ) +\sigma _{2b_k/7}(J_\alpha )+\sigma _{4b_k/7}(J_\alpha ) < 0. \end{aligned}$$

It follows that $\eta (S,3,h)<0$, which contradicts Corollary 4.8. One can also show $E_4 \subset \bigoplus _{i=1}^a\langle x_i'\rangle$, similarly. $\square$

Lemma 4.10

If $K=0\in \mathcal {T}$, then $a_1 = 0$.

Proof

Recall that we are assuming $a=a_1\ne 0$. By Lemma, 4.9 we obtain

$$\begin{aligned} \mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}=\bigoplus _{i=1}^a\left( \langle x_i\rangle \oplus \langle x_i'\rangle \right) . \end{aligned}$$

Therefore, the homology class $x_1$ is in $\mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}$, and hence $4x_1\in \mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}$. By Corollary 4.8, we have $d(Y_3(S), 4x_1)=0$. By additivity of d–invariants, it follows that $d(Y_3(K_1), 4x_1)=0$. By Sato [23, Theorem 1.2], a genus one knot with vanishing Ozsváth-Szabó $\tau$–invariant is $\nu ^+$–equivalent to the unknot. The knot $J_\alpha$ has genus one and $\tau (J_\alpha )=0$ by [14, Theorem 1.5]; it follows that $J_\alpha$ is $\nu ^+$–equivalent to the unknot. Now by Theorems 1.3 and 2.7 of [17], $d(Y_3(K_1), 4x_1)=d(Y_3(K_1'),4x_1)$ where $K_1'$ is the knot obtained from $K_1$ by replacing $J_\alpha$ by the unknot. Therefore, $d(Y_3(K_1'),4x_1)=0$. But in [6, p. 2141] Cochran-Harvey-Horn showed that $d(Y_3(K_1'), 4x_1)<0$. This leads us to a contradiction, and completes the proof for $a_1=0$. $\square$

General proof that $\varvec{a_{n_j} = 0}$for $\varvec{n_j\in \mathcal {N}}$: The proof for $a_{n_j}=0$ for other $n_j\in \mathcal {N}$ is easily obtained by making the following key modifications of the above proof for $a_1=0$:

• (1) For brevity, let $n=n_j$, $a=a_n$, and $S=S_n$. Replace $p_1$ and $p_2$ by $p_{2j-1}$ and $p_{2j}$, respectively. Replace $K_1=R_1(J_\alpha ,J_\beta )$ by $K_n=R_n(J_\alpha ,J_\beta )$.

• (2) $H_1(Y_3(S))={\mathbb Z}_{3n^2+3n+1}^{4a}=({\mathbb Z}_{p_{2j-1}}\oplus {\mathbb Z}_{p_{2j}})^{4a}$. Notice that each of $\langle x_i\rangle$, $\langle y_i \rangle$, $\langle x_i'\rangle$, and $\langle y_i' \rangle$ for $1\le i\le a$ is isomorphic to ${\mathbb Z}_{3n^2+3n+1}$.

• (3) For $x\in {\mathbb Z}_{3n^2+3n+1}$, let $x^*$ denote the multiplicative inverse of x in ${\mathbb Z}_{3n^2+3n+1}$, if it exists. Notice that since n and $n+1$ are relatively prime to $3n^2+3n+1$, and therefore the inverses $n^*$ and $(n+1)^*$ exist. Replace the 2–eigenspace and the 4–eigenspace by $n^*(n+1)$– and $(n+1)^*n$–eigenspaces, respectively. Then we obtain $\mathcal {M}_{p_{2j-1}}\oplus \mathcal {M}_{p_{2j}}=E_{n^*(n+1)}\oplus E_{(n+1)^*n}$.

• (4) In the proof Lemma 4.9 for $n=1$, the order of h was 7, a prime. But now the order of h in $E_{n^*(n+1)}$ is a factor of $p_{2j-1}p_{2j}$, possibly not a prime. To use the vanishing criterion for the Casson–Gordon invariant, if necessary, replace h by a multiple of h such that $h_k'\ne 0$ and h is of prime order p where p is either $p_{2j-1}$ or $p_{2j}$.

• (5) In the proof Lemma 4.9, for the computation of $\eta (S, 3, h)$ where $S=S_n$, again by the results of Gilmer [12] and Litherland [20] we have

  $$\begin{aligned} \eta (S,3,h)= \sum _{i=1}^a \epsilon _i\left( \sigma _{b_i/p}(J_\alpha ) +\sigma _{cb_i/p}(J_\alpha )+\sigma _{c^2b_i/p}(J_\alpha ) \right) , \end{aligned}$$

  where $c=n^*(n+1)\ne 0 \in {\mathbb Z}_{3n^2+3n+1}$. Recall that

  $$\begin{aligned} \sigma _r(J_\alpha ) = {\left\{ \begin{array}{ll} 0 &{}0\le r< \frac{1}{3}\\ -2 &{} \frac{1}{3}<r \le \frac{1}{2}. \end{array}\right. } \end{aligned}$$

  For the prime p, there exists $b\in {\mathbb Z}_p$ so that the set $\{ b/p, cb/p, c^2b/p\}$ contains a value at which the Levine-Tristram signature of $J_\alpha$ is $-2$. If necessary, replace h by a multiple of h such that $b_k=b\in {\mathbb Z}_p$. Then we obtain

  $$\begin{aligned} \sigma _{b_i/p}(J_\alpha ) +\sigma _{cb_i/p}(J_\alpha )+\sigma _{c^2b_i/p}(J_\alpha ) < 0. \end{aligned}$$

• (6) In the proof of Lemma 4.10, replace $4x_1\in \mathcal {M}_{p_1}\oplus \mathcal {M}_{p_2}$ by $2^*x_1\in \mathcal {M}_{p_{2j-1}}\oplus \mathcal {M}_{p_{2j}}$. Also replace $d(Y_3(K_1'),4x_1)=0$ by $d(Y_3(K_n'),2^*x_1)=0$, where $K_n'$ denotes the knot obtained from $K_n$ by replacing $J_\alpha$ by the unknot. To show $d(Y_3(K_n'),2^*x_1)\ne 0$ and derive a contradiction, instead of Cochran-Harvey-Horn’s work, we use Cha’s work in [4]: in particular, in [4, Theorem 4.2] Cha showed that $d(Y_3(K_n'), 2^*x_1)\ne 0$. (In the statement of [4, Theorem 4.2], the 3-manifold $\Sigma _r$ is our $Y_3(K_n')$ and the Spin$^c$–structure $\mathfrak {s}_{\Sigma _r} + k\hat{x_1}$ is our $2^*x_1$.)

5 Conjectures

The map $\rho$ induces homomorphisms on many subgroups and quotients of subgroups related to $\mathcal {C}$. In each case, we will continue to denote the map by $\rho$.

In [6], Cochran, Harvey and Horn defined a bipolar filtration of the knot concordance group, which, when restricted to $\mathcal {T}$, gives a filtration

$$\begin{aligned} 0 \subset \cdots \subset \mathcal {T}_{n+1} \subset \mathcal {T}_n \subset \cdots \mathcal {T}_0 \subset \mathcal {T}. \end{aligned}$$

Let $\mathcal {T}_{n, \Delta }= \mathcal {T}_n/(\mathcal {T}_n \cap \mathcal {T}_\Delta )$; notice that $\rho$ induces an involution on this quotient.

The first conjecture seems likely, based on [5].

Conjecture 1

For all $n \ge 1$, the quotient $\mathcal {T}_{n, \Delta }/\text {Fix}(\rho )$ contains an infinitely generated free subgroup.

The next conjecture also seems likely, but it is not clear that any currently available tools can address it.

Conjecture 2

The quotient $\mathcal {T}_\Delta /\text {Fix}(\rho )$ contains an infinitely generated free subgroup.

Finally, each of these conjectures can be modified to consider two-torsion. It was proved in [15] that $\mathcal {T}$ contains an infinite set of elements of order two, as does $\mathcal {T}/ \mathcal {T}_\Delta$. These knots were all reversible.

Conjecture 3

There exists a knot $K \in \mathcal {T}$ such that $2K = 0$ but $K \ne \rho (K)$ in $\mathcal {T}$.

Appendix A. Primes

We wish to prove the following, stated as Theorem 4.2 above.

Theorem A.1

There is an infinite set of positive integers $\{n_i\}_{i\ge 1}$ such that for all i, $3n_i^2 + 3n_i +1 = p_{2i-1}p_{2i}$ where: (1) each $p_j$ is either an odd prime or equals 1, and (2) if $j \ne l$ and $p_j \ne 1$, then $p_j \ne p_l$.

The proof is based on the following theorem of Lemke Oliver [19]. (The meaning of $\Gamma _G$ in the statement of the theorem will be mentioned in the following proof.)

Theorem A.2

If $G(x) = c_2x^2 + c_1x +c_o \in {\mathbb Z}[x]$ is irreducible, with $c_2 > 0$ and $\Gamma _G \ne 0$, then there exist infinitely many positive integers n such that G(n) is square free and has at most two distinct prime factors.

Proof of Theorem A.1

Let $f(n) = 3n^2 + 3n+1$ and note that f(n) is odd for all $n \in {\mathbb Z}$. Let $n_1 = 1$; then we have $p_1 = 7$ and $p_2 = 1$. Assume that a set of integers $\{n_j\}_{j=1}^k$ that satisfies the condition of the theorem has been selected. We now show how $n_{k+1}$ can be chosen.

Let $P = \prod _{i=1}^{2k} p_i$. Define $g(m) = f(Pm - 1 )$. This can be rewritten as

$$\begin{aligned} g(m) = 3P^2 m^2 -3Pm +1. \end{aligned}$$

Since g(m) is obtained from the irreducible polynomial f(n) by a linear change of coordinates, g(m) is irreducible and Theorem A.2 can be applied to find an $m_0$ for which $g(m_0)$ factors as $p_{2k+1}p_{2k+2}$. We let $n_{k+1} = Pm_0 -1$. Notice that no prime factor of P is a divisor of g(m) for any m, and thus $p_{2k+1}$ and $p_{2k+2}$ are distinct from all the primes $p_i$ for $i \le 2k$.

Finally, we need to mention the quantity $\Gamma _G$. Without going into details, $\Gamma _G = 0$ precisely when $G(n)=0$ has two solutions modulo 2. But in our case, modulo 2, $g(m) = m^2 + m +1$, which is irreducible.