Entropies of Random Transformations on a Non-compact Space

Abstract

In this paper, we present several possible natural extensions of metric and topological entropies for random transformations on a non-compact space. In particular, Brin–Katok local entropy formula and Katok $\delta$ entropy formula will be reformulated in the context of non-compact setting. Furthermore, a corresponding variational principle for non-compact systems is given.

1 Introduction

In the context of dynamical systems it is understood that both measure-theoretic entropy and topological entropy are measures of the complexity of the system. If the dynamical systems is a compact system, it was found successfully that they are good concepts and closely connected by the well known Variational Principle [21, 22]. Roughly speaking, entropies for i.i.d. random transformations [12] or stationary random transformations [2, 3] on a compact metric space share similar definitions and properties as deterministic entropies. For example, Variational Principles are true for both settings and some topological version of Shannon–McMillan–Breiman Theorem (such as Brin–Katok local entropy formula [5] and Katok $\delta$ entropy [11]) remain true for random systems [23].

When we remove the compact assumption, topological entropies of deterministic dynamical systems are studied in [8, 18, 19]. As far as we know, the metric entropies of deterministic systems in noncompact cases have not been fully addressed. However, if we remove the compact assumption, even in the deterministic setting, necessary modifications must be make to guarantee Brin–Katok local entropy formula and Katok $\delta$ entropy remain valid. Moreover, for random dynamical systems, non-compactness assumption seems more natural and has its independent interest. It worth to point out that a random compact set in a non-compact space could not be uniformly compact (in the sense that there is no compact set containing all the $\omega$-sections $\mathbf {P}$-a.s.), so it may explode and a segment of iterates of a point will always contain the moment that is out of control. Recently, some interesting examples of random systems on non-compact spaces are considered in [7, 20]. This paper is intended as an attempt to entropies of random transformations on a non-compact space. The settings and notions are introduced in Sect. 2, main results are shown in Sect. 3, and in Sect. 4, we proceed with the proofs.

2 Related Notions

2.1 Random Dynamical Systems

In this section, we review some of the standard facts on RDSs (random dynamical systems), for more information, please refer to [12, 13, 16, 17].

In this paper (X, d) will always be a (not necessarily compact) Polish space with Borel $\sigma$-algebra $\mathcal {B}(X)$. Let $(\Omega , \mathcal {F}, \mathbf {P}, \vartheta )$ be an abstract dynamical system, where $(\Omega , \mathcal {F}, \mathbf {P})$ is a probability space and $\vartheta$ is an invertible measure-preserving transformation. For the need to work with Lebesgue spaces, we will assume further that $(\Omega , \mathcal {F}, \mathbf {P}, \vartheta )$ is a Polish system, by which we mean that $\Omega$ is a Polish space and $\mathcal {F}$ is its Borel $\sigma$-algebra.

Definition 2.1

A map

$$\begin{aligned}&\phi :\mathbb {N}\times \Omega \times X\longrightarrow X\\&(n,\omega ,x)\mapsto \phi (n,\omega )x \end{aligned}$$

is called a (measurable) random dynamical system (RDS) on X over $(\Omega , \mathcal {F}, \mathbf {P}, \vartheta )$,if

• (1) $\phi$ is $(\mathcal {B}(\mathbb {N}) \otimes \mathcal {F}\otimes \mathcal {B}(X),\mathcal {B}(X))$-measurable;

• (2) The maps $\phi (n,\omega ):X \rightarrow X$ form a cocycle over $\vartheta$,i.e., they satisfy $\phi (0,\omega )=id$, $\phi (n+m,\omega )=\phi (m,\vartheta ^n\omega )\circ \phi (n,\omega )$ for all $n,m\in \mathbb {N},\omega \in \Omega .$

If in addition the maps $\phi (n,\omega ):X \longrightarrow X$ are continuous for all $n\in \mathbb {N},\omega \in \Omega ,$ then $\phi$ is called a topological RDS.

Let $\phi (\omega ):=\phi (1,\omega )$ be the time 1 map of $\phi$. Then we may write by the above cocycle property (2)

$$\begin{aligned} \phi (n,\omega ):=\left\{ \begin{array}{l@{\quad }l} id \quad &{}\text{ if }\;\;n=0\\ \phi (\vartheta ^{n-1}\omega )\circ \cdots \circ \phi (\vartheta \omega )\circ \phi (\omega )\quad &{}\text{ if }\;\;n>0. \end{array}\right. \end{aligned}$$

Moreover, for $n\in \mathbb {N}$, we call

$$\begin{aligned} \Theta ^n: \Omega \times X\rightarrow \Omega \times X, (\omega ,x)\mapsto (\vartheta ^n \omega , \phi (n,\omega )x) \end{aligned}$$

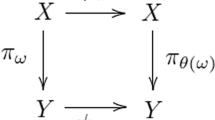
the skew-product transformation induced by $\phi$. Let $\Theta (\omega ,x):=\Theta ^1(\omega ,x)$ be the time 1 map of $\Theta$. We call any set $Y\subset \mathcal {F}\times \mathcal {B}$ with $\pi _{\Omega }Y=\Omega$ a measurable bundle over $\Omega$ (or simply a random set) with fibers $Y_{\omega }=\{x\in X:(\omega ,x)\in Y \}$ in X, where $\pi _{\Omega }$ and $\pi _{X}$ are the projections from $\Omega \times X$ onto $\Omega$ and X, respectively. If in addition, each $Y_{\omega }$ is compact and for each $x\in X$, $\omega \mapsto \text{ dist }(x, Y_{\omega })$ is measurable, where $\text{ dist }(x, A)$ is the usual distance between a point x and a set A, then Y is called a random compact set. It is called invariant if $\phi (\omega )(Y_{\omega })= Y_{\vartheta \omega },$ for all $\omega \in \Omega .$

A probability measure $\mu$ on $(\Omega \times X,\mathcal {F}\times \mathcal {B})$ is said to be $\phi$-invariant if it is invariant under $\Theta ^n$ for all $n\in \mathbb {N}$ and has marginal $\mathbf {P}$ on $\Omega$. Furthermore, $\mu$ is said to be $\phi$-ergodic if it is ergodic with respect to $\Theta$. Let $\mathcal {M}_{\phi }$ denote the set of $\phi$-invariant measures and $\mathcal {E}_{\phi }$ denote the set of ergodic elements in $\mathcal {M}_{\phi }$. Given a non-empty $\Theta$-invariant random compact set K, it was shown that there always exists $\mu \in \mathcal {M}_{\phi }$ that is supported on K , i.e. $\mu _{\omega }(K_{\omega })=1$, $\mathbf {P}$-a.e. [6]. Denote by $\mathcal {M}_{\phi }(K)$ ($\mathcal {E}_{\phi }(K)$) the set of (ergodic) probability measures $\mu \in \mathcal {M}_{\phi }$ supported on K.

2.2 Topological Entropy of Bowen Balls

Next, we shall give the definition of topological entropy with respect to a given metric. Define the following family of metrics of X,

$$\begin{aligned} d_\omega ^{n}(x,y)=\max _{0\le i\le n-1}d(\phi (i,\omega ) x,\phi (i,\omega )y),\;\;\;\;x,y\in X \end{aligned}$$

for $n\in \mathbb {N}$ and $\omega \in \Omega$. Let K be a random compact set. Note that the fact that K is random compact does not imply that it is uniformly compact. A subset E is said to be a $(\omega ,n,\varepsilon )$- separated set of $K_{\omega }$, if $x,y\in E$, $x\ne y$ implies $d_\omega ^{n}(x,y)\ge \varepsilon$. Let $s(\omega ,n,\varepsilon ,K)$ denote the largest cardinality of any $(\omega ,n,\varepsilon )$-separated set of $K_{\omega }$. A subset F is said to be a $(\omega ,n,\varepsilon )$-spanning set of $K_{\omega }$, if for any $x\in K_{\omega }$, there exists $y\in F$ such that $d_\omega ^{n}(x,y)\le \varepsilon$. Let $r(\omega ,n,\varepsilon ,K)$ denote the smallest cardinality of any $(\omega ,n,\varepsilon )$-spanning set of $K_{\omega }$.

$$\begin{aligned} h_d(\phi ,K)= & {} \lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log s(\omega ,n,\varepsilon ,K) d\mathbf {P}(\omega )\\= & {} \lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,\varepsilon ,K) d\mathbf {P}(\omega ). \end{aligned}$$

In addition, if $\vartheta$ is ergodic then above formulas remain true $\mathbf {P}$-a.e. without taking integrals. The Bowen entropy of $\phi$ with respect to the metric d is thus defined as $h_d(\phi )=\sup _{K}\{h_d(\phi ,K)\}$ where the supremum is taken over all random compact sets K and $h_d(\phi )$ can be infinite.

2.3 Metric Entropy

Definition 2.2

Let $\phi$ be an RDS and $\mu \in \mathcal {M}_{\phi }$. The conditional entropy of $\phi$ with respect to the sub-$\sigma$-algebra $\pi _{\Omega }^{-1}\mathcal {F}=\{(F\times X):F\in \mathcal {F}\}$

$$\begin{aligned} h_\mu (\phi )=h_\mu (\Theta |\pi _{\Omega }^{-1}\mathcal {F}) :=\sup \{h_\mu (\phi ,\xi ):\xi \;\text{ is } \text{ finite } \text{ partition } \text{ of }\; X\}, \end{aligned}$$

where

$$\begin{aligned} h_\mu (\phi ,\xi ):=h_\mu (\Theta |\pi _{\Omega }^{-1}\mathcal {F};\xi )= \lim _{n\longrightarrow \infty }\frac{1}{n}H_\mu \left( \bigvee _{i=0}^{n-1}\Theta ^{-i}(\pi _{X}^{-1}\xi )| \pi _{\Omega }^{-1}\mathcal {F}\right) , \end{aligned}$$

is called the metric entropy of $\phi$. We denote $\sup \{h_\mu (\phi ):\mu \in \mathcal {M}_{\phi }\}$ by $Mh(\phi )$. Since X is a Polish space, the ergodic decomposition theorem still holds, moreover, $Mh(\phi )=\sup \{h_\mu (\phi ):\mu \in \mathcal {E}_{\phi }\}$.

2.4 Brin–Katok Local Entropy

Let $A\in \mathcal {F}\otimes \mathcal {B}$, $\epsilon >0$ and K be a random invariant compact set. For $(\omega , x)\in K$ and $n\in \mathbb {N}$, define

$$\begin{aligned} B_{A, n}^{\omega }(x, \epsilon )&:=\{ y\in K_{\omega }:\ \ \text{ for }\ 0\le i\le n-1,\ \Theta ^i(\omega ,x)\in A\ \text{ iff }\ \Theta ^i(\omega , y)\in A\nonumber \\&\qquad \qquad \qquad \quad \text{ and }\ \ d(\phi (i,\omega )x, \phi (i,\omega )y)<\epsilon \ \text{ if }\ \Theta ^i(\omega ,x)\in A\}. \end{aligned}$$

It is a measurable set around x. In case $A=\Omega \times X$, $B_{A, n}^{\omega }(x, \epsilon )$ reduces to the classical random Bowen balls around x, which we shall denote by $B_{n}^{\omega }(x, \epsilon )$. Random compact set are almost uniformly in the sense of the following lemma.

Lemma 2.3

([6, Proposition 3.15]). Suppose K is a compact random set. Then for every $\epsilon >0$ there exists a compact set $K_{\epsilon }\subset X$ such that $\mathbf {P}\{\omega :\ \ K_{\omega }\subset K_{\epsilon }\}\ge 1-\epsilon$.

Let

$$\begin{aligned} \mathcal {C}_{\mathbf {P}}(K):=\{A\in \mathcal {F}\otimes \mathcal {B} :\ \exists K_{A}\subset X \ \text{ compact }\ \text{ s.t. }\ K_{\omega }\subset K_{A}\ \text{ for }\ \omega \in \pi _{\Omega }A\}.\quad \end{aligned}$$

(2.1)

For $A\in \mathcal {C}_{\mathbf {P}}(K)$, $\omega \in \Omega$ and $x\in K_{\omega }$, consider the limit

$$\begin{aligned} h_{A}(\omega ,x):=\lim \limits _{\epsilon \rightarrow 0}\varliminf _{n\rightarrow +\infty }-\frac{1}{n}\log \mu _{\omega }(B_{A, n}^{\omega }(x, \epsilon )). \end{aligned}$$

Since $B_{A, n}^{\omega }(x, \epsilon )\subset \phi (\omega )^{-1}B_{A, n-1}^{\vartheta \omega }(\phi (\omega )x, \epsilon )$, we have by invariance of $\mu _{\omega }$ that $h_{A}(\omega , x)\ge h_{A}(\vartheta (\omega ), \phi (\omega )x)$, $\mu$-a.e. So by sub ergodic theory, if $\mu$ is ergodic, there exists a constant $h_{A}\ge 0$ such that $h_{A}=h_{A}(\omega ,x)$, $\mu$-a.e.

Definition 2.4

Let $\phi$ be an RDS and $\mu \in \mathcal {E}_{\phi }(K)$. $Lh_{\mu }(\phi )=\sup _{A\in C_{\mathbf {P}}(K)}\text{ esssup }\{h_{A}(\omega ,x)\}$ is called the Brin–Katok local entropy of $\phi$ on K.

2.5 Katok $\delta$ Entropy

Let $0<\delta <1$, $\epsilon >0$ and $\mu \in \mathcal {E}_{\phi }(K)$. For any $A\in C_{\mathbf {P}}(K)$, denote $S_{A}(\omega ,n,\epsilon ,\delta ):= \min \{s_A(\omega ,n,\epsilon ,Y): Y\, \text{ is } \text{ a } \text{ measurable } \text{ bundle } \text{ with },\mu (Y)\ge 1-\delta \}$, where $s_A(\omega ,n,\epsilon ,Y)$ is the maximal number of disjoint modified Bowen balls $B_{A, n}^{\omega }(x, \epsilon )$ containing in $Y_{\omega }$. When $A=\Omega \times X$, $s_A(\omega ,n,\epsilon ,Y)=s(\omega ,n,\epsilon ,Y)$. Consider the limit

$$\begin{aligned} h_{A}^{\delta }(\omega ):=\lim \limits _{\epsilon \rightarrow 0}\varliminf _{n\rightarrow +\infty }\frac{1}{n}\log S_{A}(\omega ,n,\epsilon ,\delta ). \end{aligned}$$

Definition 2.5

Let $\phi$ be an RDS and $\mu \in \mathcal {E}_{\phi }(K)$. $h_{\mu }^{\delta }(\phi )=\sup _{A\in C_{\mathbf {P}}(K)}\{\int h_{A}^{\delta }(\omega )d\mathbf {P}(\omega )\}$ is called the Katok $\delta$ entropy of $\phi$ on K.

2.6 Topological Entropy of Proper Systems

Let X be a topological space and $T: X \rightarrow X$ be a continuous map . T is called a proper map if the pre-image by T of any compact set is compact [19].

Definition 2.6

If the maps $\phi (n,\omega ):X \longrightarrow X$ are proper for all $n\in \mathbb {N},\omega \in \Omega ,$ then $\phi$ is called a proper topological RDS.

For compact topological systems, Adler, Konheim and McAndrew introduced the concept of topological entropy and studied its properties [1]. Now, we will generalize it to any topological space for proper topological RDSs.

Definition 2.7

[19] An finite open cover $\mathcal {U}$ of X is called an admissible cover, if for each $A\in \mathcal {U}$ , the closure or the complement of A is compact.

Let $\phi$ be a proper topological RDS, and $\mathcal {U}$ be an admissible cover. For every $n\in \mathbb {N},\omega \in \Omega$ we have $\mathcal {U}_{\omega }^n=\bigvee _{i=0}^{n-1}\phi ^{-1}(n,\omega )\mathcal {U}$ is also an admissible cover. Let $N(\mathcal {U})$ denote the number of sets in a finite subcover of $\mathcal {U}$ with smallest cardinality and define the topological entropy of $\mathcal {U}$ by $H_{top}(\mathcal {U}):=\log N(\mathcal {U})$. Kingman’s subadditive ergodic theorem implies that the limit

$$\begin{aligned} h(\phi ,\mathcal {U}):=\lim _{n\rightarrow \infty }\frac{1}{n}\int H_{top}(\mathcal {U}_{\omega }^n)d \mathbf {P}(\omega )=\int \lim _{n\rightarrow \infty }\frac{1}{n} H_{top}(\mathcal {U}_{\omega }^n)d \mathbf {P}(\omega ) \end{aligned}$$

exists.

Definition 2.8

The non-negative number

$$\begin{aligned} h(\phi ):=\sup \{h(\phi ,\mathcal {U})\mid \mathcal {U} \text{ is } \text{ an } \text{ admissible } \text{ open } \text{ cover } \text{ of } X\} \end{aligned}$$

is called topological entropy of $\phi$.

Definition 2.9

A metric d is called admissible if the following conditions are satisfied:

• (1) If $\mathcal {U}_\delta =\{B(x_1,\delta ),B(x_2,\delta ),\ldots ,B(x_k,\delta )\}$ is an open cover of X for every $\delta \in (a,b)$, where $0<a<b$, then there exists $\delta _{0}\in (a,b)$ such that $\mathcal {U}_{\delta _{0}}=\{B(x_1,\delta _{0}),B(x_2,\delta _{0}),\ldots ,B(x_k,\delta _{0})\}$ is an admissible cover, where $B(x,\delta )=\{y\in X:d(x,y)<\delta \}$.

• (2) Every admissible cover of X has a Lesbesgue number.

Following [19], for the proper RDS on (X, d) with d admissible, we can define

$$\begin{aligned} h_d(\phi ,X)= & {} \lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log s(\omega ,n,\varepsilon ,X) d\mathbf {P}(\omega )\\= & {} \lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,\varepsilon ,X) d\mathbf {P}(\omega ), \end{aligned}$$

where $s(\omega ,n,\varepsilon ,X)$ and $r(\omega ,n,\varepsilon ,X)$ are the largest cardinality of any $(\omega ,n,\varepsilon )$-separated set of X and the smallest cardinality of any $(\omega ,n,\varepsilon )$-spanning set of X.

In particular, when (X, d) is compact metric space, d is admissible, any open cover of X is admissible, and any topological RDS $\phi$ is proper. Furthermore, $h(\phi )=h_d(\phi )=h_d(\phi ,X)$.

3 Main Results

We are in a situation to state our main results of this paper:

Theorem A

Let $\phi$ be an RDS on a Polish space X. For any random invariant compact set K, $0<\delta <1$ and $\mu \in \mathcal {E}_{\phi }(K)$, $h_{\mu }(\phi )=h_{\mu }^{\delta }(\phi )=Lh_{\mu }(\phi )$.

Theorem B

Let $\phi$ be a proper RDS on a locally compact Polish space X. Then

$$\begin{aligned} Mh(\phi )=h(\phi )=\min \limits _{d}h_{d}(\phi ), \end{aligned}$$

where the minimum is attained whenever d is an admissible metric.

4 Proofs

4.1 Proof of Theorem A

Let $\xi$ be a finite measurable partition of $\Omega \times X$. For $A\in \mathcal {C}_{\mathbf {P}}(K)$, $(\omega , x)\in K$, and $n\in \mathbb {N}$, consider

$$\begin{aligned} \xi _{A,-n}^{\omega }(x)&:=\{ y\in K_{\omega }:\ \ \text{ for }\ 0\le i\le n-1,\ \Theta ^i(\omega ,x)\in A\ \text{ iff }\ \Theta ^i(\omega , y)\in A\nonumber \\&\qquad \qquad \qquad \quad \text{ and }\ \phi (i,\omega ) y\in \xi ^{\vartheta ^i(\omega )}(\phi ( i,\omega )x) \ \ \text{ if }\ \Theta ^i(w,x)\in A\}. \end{aligned}$$

Let $\widetilde{\xi }=\{(\Omega \times X)\backslash A, A\cap \xi \}$. It is easy to see that

$$\begin{aligned} \widetilde{\xi }_{-n}^{\omega }(x)=\xi _{A, -n}^{\omega }(x),\ \mu \text{-a.e. } \end{aligned}$$

(4.1)

where $\widetilde{\xi }_{-n}^{\omega }=\bigvee _{i=0}^{n-1}\phi ^{-1}(i,\omega )\widetilde{\xi }^{\vartheta ^i\omega }$ and $\widetilde{\xi }_{-n}^{\omega }(x)$ is the element of $\widetilde{\xi }_{-n}^{\omega }$ that contains x. Let Z be an abstract measurable space with measurable transformation T. Let $\xi =\{C_1,\ldots , C_M\}$ be a finite Borel partition of Y. Let

$$\begin{aligned} \Sigma _M^n=\left\{ w=(w_{0},\ldots , w_{n-1}): \ w_{i}\in \{1,\ldots , M\},\ 0\le i \le n-1\right\} . \end{aligned}$$

It is easy to see that there is a natural bijection between $\xi _{-n}=\vee _{i=0}^{n-1}T^{-i}\xi$ and $\Sigma _M^n$. Hence we can identify $\xi _{-n}$ with $\Sigma _M^n$ [5].

Lemma 4.1

[15, Lemma A.1]. Let $\phi$ be an RDS and let $\mu \in \mathcal {E}_{\phi }(K)$ for some random compact set K. Let $\xi$ be a finite partition of X and let $A\in \mathcal {C}_{\mathbf {P}}(K)$ with $\mu (A)>0$. If $\mu (\pi _{X}^{-1}(\partial \xi )\cap A)=0$, then for any $\gamma >0$, there exists $0<\epsilon <\gamma$, $n_1\in \mathbb {N}$ ($n_1$ depends on $\epsilon$ and $\gamma$), and $U_{n_1, \gamma }\subset A$ with $\mu (U_{n_1, \gamma })>\mu (A)(1-\gamma )$ such that for any $(\omega ,x)\in U_{n_1, \delta }$ and $n\ge n_1$, any two elements of

$$\begin{aligned} \xi _{A, -n}^{\omega }(x, \epsilon )=\{E\in \xi _{A, -n}^{\omega }:\ E\cap B_{A, n}^{\omega }(x, \epsilon )\not =\emptyset \} \end{aligned}$$

have at most $[n\gamma /2]$ different symbols, where

$$\begin{aligned} B_{A, n}^{\omega }(x, \epsilon )&:=\{ y\in K_{\omega }:\ \ \text{ for }\ 0\le i\le n-1,\ \Theta ^i(\omega ,x)\in A\ \text{ iff }\ \Theta ^i(\omega , y)\in A\nonumber \\&\qquad \qquad \qquad \ \ \text{ and }\ \ d(\phi (i,\omega )x, \phi (i,\omega )y)<\epsilon \ \text{ if }\ \Theta ^i(\omega ,x)\in A\}. \end{aligned}$$

Consequently, given $\xi _{A, -n}^{\omega }(x, \epsilon )$ with $(\omega ,x)\in U_{n_1, \gamma }$, the possible number of $E\in \xi _{A, -n}^{\omega }(x, \epsilon )$ is bounded above by $e^{n\varphi (\gamma )}$, where $\varphi (\gamma )=\gamma \log (M-1)-r\log \gamma -(1-\gamma )\log (1-\gamma )+\gamma$ and $M=card \xi$.

Proof of Theorem A

First we show that for all $0<\delta <1$,

$$\begin{aligned} h_{\mu }^{\delta }(\phi )\le Lh_{\mu }(\phi ). \end{aligned}$$

(4.2)

Fix $\varepsilon >0$ and $0<r<1$. For any $A\in \mathcal {C}_{\mathbf {P}}(K)$, define the set $X_A(\varepsilon ,r,m)\subset \Omega \times X$, for $m\ge 1$, by $X_A(\varepsilon ,r,m)=\{(\omega ,x)\in \Omega \times X:-\frac{1}{n}\log \mu _{\omega }(B_{A, n}^{\omega }(x, \varepsilon ))\le Lh_{\mu }(\phi )+\varepsilon ,\,\text{ for } \text{ all } n\ge m\}$. Note that we can choose $r>0$ small enough, $m_0>0$ large enough such that $\mu (X_A(\varepsilon ,r,m))>1-\delta$ for every $m\ge m_0$. Let $Y\subset X_A(\varepsilon ,r,m)$ be a random compact set such that $\mu (Y)>1-\delta$. We are going to find an upper bound of $s(\omega ,m,\varepsilon ,Y)$, for every $m\ge m_0.$ Let $E_{\omega }$ be a maximal $(\omega ,m,\varepsilon )$- separated set of $Y_{\omega }$, Then for any $\omega \in \Omega$, $\mu _{\omega }(\cup _{x\in E_{\omega }}B_{A, m}^{\omega }(x, \varepsilon ))\le 1$. Since $\mu _{\omega }(B_{A, m}^{\omega }(x, \varepsilon ))\ge \exp (-m(Lh_{\mu }(\phi )+\varepsilon ))$, it follows that $card(E_{\omega })=s_A(\omega ,m,r,Y) \le \exp (m(Lh_{\mu }(\phi )+\varepsilon )).$

Hence, for every $r>0$ small enough we can find a random compact set Y such that $\mu (Y)>1-\delta$ and $\varlimsup _{n\rightarrow +\infty }\frac{1}{n}\log s_A(\omega ,m,r,Y)\le Lh_{\mu }(\phi )+\varepsilon .$ By arbitrariness of $\varepsilon$, (4.2) follows.

On the other hand, let $\xi$ be a finite partition of X with M elements. Let $A\in C_{\mathbf {P}}(K)$ be such that $\mu (A)>1-\gamma /(8M)$, where $\gamma$ is small so that $\phi (\gamma )<\gamma /4$. We claim $h_{A}^{\delta }\ge h_{\mu }(\phi ; \pi _{X}^{-1}\xi )-\gamma$. Let $\widetilde{\xi }=\{(\Omega \times X)\backslash A,\ \ A\cap \pi _{X}^{-1}\xi \}$. We first see that

$$\begin{aligned} h_{\mu }(\phi ; \pi _{X}^{-1}\xi )\le & {} h_{\mu }(\phi ; \widetilde{\xi })+\int H_{\mu _{\omega }}(\mathcal {\xi }|\widetilde{\xi }(\omega ))\ d\mathbf {P}(\omega )\nonumber \\< & {} h_{\mu }(\phi ; \widetilde{\xi })+\frac{1}{8M}\gamma \cdot \log M\nonumber \\< & {} h_{\mu }(\phi ; \widetilde{\xi })+\frac{1}{4}\gamma . \end{aligned}$$

(4.3)

The first inequality follows from the property of entropy, the second inequality follows from the definitions of $\xi$ and $\widetilde{\xi }$ as well as the property of conditional entropy. Next, consider $\xi _{A, -n}^{\omega }$ of X. Since $K_{A}$ is compact, by slightly change of $\xi \cap K_{A}$, we may assume $\mu (\pi _{X}^{-1}(\partial \xi )\cap \pi _{\Omega }^{-1}A)=0$. Now Lemma 4.1 applies. Let $\epsilon$ and $U_{n_1, \gamma }$ be as there for $\xi$ and A. Since $\xi _{A, -n}^{\omega }(x)=\widetilde{\xi }^{\omega }_{-n}(x)$ holds for $\mu$-a.e. $(\omega , x)$, we have by Shannon–McMillan–Breiman theorem [3, Theorem 2.2.5] that for $(\omega ,x)\in U_{n_1, \gamma }$ and $n\ge n_1$,

$$\begin{aligned} -\frac{1}{n}\log \mu _{\omega }\left( \xi _{A, -n}^{\omega }(x)\right) \ge h_{\mu }(\phi ; \widetilde{\xi })-\frac{1}{2}\gamma . \end{aligned}$$

(4.4)

Note that by Lemma 4.1, for each $(\omega ,x)\in U_{n_1, \gamma }$, the possible number of elements of $\widetilde{\xi }_{-n}^{\omega }=\xi _{A, -n}^{\omega }$ that intersect $B_{A, n}^{\omega }(x, \epsilon )$ is bounded above by $e^{n\varphi (\gamma )}$. Thus, we have by (4.3) and (4.4) that for $(\omega ,x)\in U_{n_1, \gamma }$, $n\ge n_1$ and $\epsilon '<\epsilon$ that

$$\begin{aligned} \mu _{\omega }\left( B_{A, n}^{\omega }(x, \epsilon ')\right)\le & {} e^{-n(h_{\mu }(\phi ; \widetilde{\xi })-\frac{1}{2}\gamma )}\cdot e^{n\varphi (\gamma )}. \end{aligned}$$

For any measurable bundle Y with $\mu (Y)\ge 1-\delta$, by (4.3), immediately gives

$$\begin{aligned} \lim \limits _{\epsilon '\rightarrow 0}\varliminf _{n\rightarrow \infty }s_A(\omega ,m,r,Y)\ge & {} h_{\mu }(\phi ; \widetilde{\xi })-\frac{1}{2}\gamma -\varphi (\gamma )\\\ge & {} h_{\mu }(\phi ; \pi _{X}^{-1}\xi )-\gamma . \end{aligned}$$

Combine with the fact that [15, Proposition 3.3] $h_{\mu }(\phi )=Lh_{\mu }(\phi )$, Theorem A follows. $\square$

4.2 Proof of Theorem B

4.2.1 $h(\phi )$ and $h_{d}(\phi ,X)$

Our first result is a generalization of the well-known result which states that, if (X, d) is compact, then the topological and the Bowen entropies coincide. In the non-compact case, we borrow the idea in [19] to restrict ourselves to admissible metric d.

Theorem 4.2

Let $\phi$ be a proper topological RDS on a metric space (X, d) where d is an admissible metric. Then it follows that $h_{d}(\phi ,X)=h(\phi )$.

Proof

We claim that, for all $\varepsilon >0$, there exists $\delta _{\varepsilon }\in (\varepsilon /2,\varepsilon )$ and a admissible open cover $\mathcal {U}_{\delta _{\varepsilon }}$ such that $N((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)\le r(\omega ,n,\varepsilon /2,X)$.

If $S=\{x_1,x_2,\ldots ,x_k\}$ is an $(\omega ,n,\varepsilon /2)$-spanning set of X, for every $\delta \in (\varepsilon /2,\varepsilon )$, we have that $\mathcal {V}_\delta =\{B(x,\delta )\cap \cdots \cap \phi ^{-1}(n-1,\omega )(B(\phi (n-1,\omega )x,\delta )):x\in S\}$ is a cover of X. Also, $\mathcal {U}_\delta =\{B(\phi (l,\omega )x,\delta ):x\in S,0\le l\le n-1\}$ is an open cover of X. Since d is an admissible metric, there exists $\delta _{\varepsilon }\in (\varepsilon /2,\varepsilon )$ such that $\mathcal {U}_{\delta _{\varepsilon }}$ is an admissible open cover of balls with radius $\delta _{\varepsilon }$. Furthermore, we have that $\mathcal {V}_{\delta _{\varepsilon }}$ is a subcover of $(\mathcal {U}_{\delta _\varepsilon })_{\omega }^n$, which implies $N((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)\le card(\mathcal {V}_{\delta _{\varepsilon }})$. Hence for each $(n,\varepsilon /2)-$spanning set S of X, there exists $\delta _{\varepsilon }\in (\varepsilon /2,\varepsilon )$ and an admissible open cover $\mathcal {U}_{\delta _{\varepsilon }}$ such that $N((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)\le card(\mathcal {V}_{\delta _{\varepsilon }})\le card(S)$. Thus it follows that $N((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)\le r(\omega ,n,\varepsilon /2,X)$, which implies

$$\begin{aligned} h(\phi ,\mathcal {U}_{\delta _{\varepsilon }})\le \limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,\varepsilon /2,X) d \mathbf {P}(\omega ). \end{aligned}$$

(4.5)

Moveover, for any admissible open cover $\mathcal {U}$, we claim that the inequality

$$\begin{aligned} \limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,|\mathcal {U}|,X) d \mathbf {P}(\omega )\le \lim _{n\rightarrow \infty }\frac{1}{n} \int H_{top}(\mathcal {U}_{\omega }^n)d \mathbf {P}(\omega ) \end{aligned}$$

(4.6)

holds, where $|\mathcal {U}|$ is the maximum of the diameters of $U\in \mathcal {U}$.

In fact, the elements of $\mathcal {U}_{\omega }^n$ are given by $U_0\cap \phi ^{-1}(1,\omega )(U_1)\cap \cdots \cap \phi ^{-1}(n-1,\omega )(U_{n-1})$, where $U_i\in \mathcal {U}$. Let $\mathcal {V}$ be a subcover of $\mathcal {U}_{\omega }^n$. For each $V\in \mathcal {V}$, take an $x_V\in V$ and let $S=\cup _{V\in \mathcal {V}}\{x_V\}$. Then S is an $(\omega ,n,|\mathcal {U}|)$-spanning set of X such that $r(\omega ,n,|\mathcal {U}|,X)\le card(S)\le card(\mathcal {V})\le N(\mathcal {U}_{\omega }^n)$. Taking logarithms, dividing by n and taking limits, (4.6) follows.

Since $|\mathcal {U}_{\delta _{\varepsilon }}|\le 2\delta _{\varepsilon }\le 2\varepsilon ,$ inequality (4.5) and (4.6), we have that

$$\begin{aligned}&\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,2\varepsilon ,X) d \mathbf {P}(\omega )\\&\quad \le \limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,|\mathcal {U}_{\delta _{\varepsilon }}|,X) d \mathbf {P}(\omega )\\&\quad \le \lim _{n\rightarrow \infty }\frac{1}{n} \int H_{top}((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)d \mathbf {P}(\omega )\\&\quad \le \limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,\varepsilon /2,X) d \mathbf {P}(\omega ) \end{aligned}$$

Taking limits with $\varepsilon \downarrow 0$, it follows that

$$\begin{aligned} h_d(\phi ,X)=\lim \limits _{\varepsilon \downarrow 0}h(\phi ;\mathcal {U}_{\delta _\varepsilon })=\sup \limits _{\varepsilon >0}h(\phi ,\mathcal {U}_{\delta _\varepsilon }). \end{aligned}$$

In order to complete the proof, it remains to show that the above supremum is equal to $h(\phi )$. For any admissible open cover $\mathcal {U}$ of X, take $\varepsilon$ be a Lebesgue number of this cover. We claim that $N(\mathcal {U}_{\omega }^n)\le N((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)$, where $\mathcal {U}_{\delta _\varepsilon }$ is given above. In fact, since every element of $(\mathcal {U}_{\delta _\varepsilon })_{\omega }^n$ is given by $U_0\cap \phi ^{-1}(1,\omega )(U_1)\cap \cdots \cap \phi ^{-1}(n-1,\omega )(U_{n-1})$, where $U_i=B(x_i,\delta _{\varepsilon })$’s are balls of radius $\delta _{\varepsilon }<\varepsilon$, there exists $\{A_0,...,A_{n-1}\}\subset \mathcal {U}$ such that $B(x_i,\delta _{\varepsilon })\subset A_i$, for each i. Hence, we get as claimed that $N(\mathcal {U}_{\omega }^n)\le N((\mathcal {U}_{\delta _\varepsilon })_{\omega }^n)$. Taking logarithms, dividing by n and taking limits, it follows that

$$\begin{aligned} h(\phi ;\mathcal {U})\le h(\phi ;\mathcal {U}_{\delta _{\varepsilon }})\le \sup \limits _{\varepsilon >0}h(\phi ;\mathcal {U}_{\delta _{\varepsilon }}), \end{aligned}$$

which shows that

$$\begin{aligned} h(\phi )=\sup \limits _{\varepsilon >0}h(\phi ;\mathcal {U}_{\delta _{\varepsilon }}). \end{aligned}$$

$\square$

4.2.2 $h(\phi )$ and $h(\widetilde{\phi })$

From now on we assume that X is a locally compact Polish space. We denote one-point compactification by $\widetilde{X}$, i.e., $\widetilde{X}$ is the disjoint union of X and $\{\infty \}$, where $\infty$ is some point not in X . The topology in $\widetilde{X}$ consists of the former open sets in X and the sets $U\cup \{\infty \}$, where the complement of U in X is compact.

Let $f:X\rightarrow X$ be a proper mapping. Define $\widetilde{f}(\widetilde{x}):\widetilde{X}\rightarrow \widetilde{X}$ by

$$\begin{aligned} \widetilde{f}(\widetilde{x})= {\left\{ \begin{array}{ll} f(\widetilde{x}), &{}\quad \text {if } \widetilde{x}\ne \infty , \\ \infty , &{}\quad \text {if } \widetilde{x}= \infty , \end{array}\right. } \end{aligned}$$

we have that $\widetilde{f}$ is also a proper map, called the extension of f to $\widetilde{X}$. Similarly,we call $\widetilde{\phi }$ is the extension of $\phi$ to $\widetilde{X}$ if we replace $\phi (\omega )$ by $\widetilde{\phi (\omega )}$ in Definition 2.1.

Theorem 4.3

Let $\phi$ be a proper RDS on a locally compact Polish space X. Let d be the metric given by the restriction to X of some metric $\widetilde{d}$ on $\widetilde{X}$, the one-point compactification of X. Then it follows that d is an admissible metric and $h_{d}(\phi ,X)=h_{\widetilde{d}}(\widetilde{\phi },\widetilde{X})$, where $\widetilde{d}$ is some metric on $\widetilde{X}$, the one-point compactification of X, and $\widetilde{\phi }$ is the extension of $\phi$ to $\widetilde{X}$. Further more, we have $h(\phi )=h(\widetilde{\phi })$.

Proof

First, by [19, Proposition 2.3], d is an admissible metric.

On one hand, let $\widetilde{S}=\{\widetilde{x_1},\ldots ,\widetilde{x_k}\}\subset \widetilde{X}$ be an $(\omega ,n,\frac{\varepsilon }{2})$-spanning set of $\widetilde{X}$, it follows that there exist an $\{x_1,\ldots ,x_k\}\subset X$, such that $\widetilde{d}_\omega ^{n}(x_i,\widetilde{x_i})<\frac{\varepsilon }{2}$. If $x\in X\subset \widetilde{X}$ , we have that $\widetilde{d}_\omega ^{n}(x,\widetilde{x_i})<\frac{\varepsilon }{2}$ , for some $\widetilde{x_i}\in \widetilde{S}$. Hence it follows that $d_\omega ^{n}(x,x_i)<\widetilde{d}_\omega ^{n}(x,\widetilde{x_i})+ \widetilde{d}_\omega ^{n}(x_i,\widetilde{x_i})<\frac{\varepsilon }{2}+\frac{\varepsilon }{2}=\varepsilon$ , showing that $S=\{x_1,\ldots ,x_k\}$ is an $(\omega ,n,\varepsilon )$-spanning set of X, and hence $r(\omega ,n,\varepsilon ,X)<\widetilde{r}(\omega ,n,\frac{\varepsilon }{2},\widetilde{X})<\infty$.

On the other hand, let $S=\{x_1,\ldots ,x_k\}\subset X$ be an $(\omega ,n,\frac{\varepsilon }{2})$-spanning set of X. By the density of X in $\widetilde{X}$ , for any $\widetilde{x}\in \widetilde{X}$ , there exists $x\in X\subset \widetilde{X}$, such that $\widetilde{d}_\omega ^{n}(x,\widetilde{x})<\frac{\varepsilon }{2}$. Since $d_\omega ^{n}(x,x_i)<\frac{\varepsilon }{2}$ for some $x_i\in S$, we have that $\widetilde{d}_\omega ^{n}(x_i,\widetilde{x})<\widetilde{d}_\omega ^{n}(x,\widetilde{x})+ d_\omega ^{n}(x_i,x)<\frac{\varepsilon }{2}+\frac{\varepsilon }{2}=\varepsilon$,i.e. $S=\{x_1,\ldots ,x_k\}$ is an $(\omega ,n,\varepsilon )$-spanning set of $\widetilde{X}$, and hence $\widetilde{r}(\omega ,n,\varepsilon ,\widetilde{X})<r(\omega ,n,\frac{\varepsilon }{2},X)<\infty$.

Therefore it follows that

$$\begin{aligned}&h_{d}(\phi ,X)\\&\quad =\lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,4\varepsilon ,X) d \mathbf {P}(\omega )\\&\quad \le \lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log \widetilde{r}(\omega ,n,2\varepsilon ,\widetilde{X}) d \mathbf {P}(\omega )\\&\quad =h_{\widetilde{d}}(\widetilde{\phi },\widetilde{X})\\&\quad \le \lim _{\varepsilon \rightarrow 0}\limsup _{n\rightarrow \infty } \frac{1}{n}\int \log r(\omega ,n,\varepsilon ,X) d \mathbf {P}(\omega )\\&\quad =h_{d}(\phi ,X). \end{aligned}$$

The last statement of the proposition now follows by applying Theorem 4.2. $\square$

4.2.3 $Mh(\phi )$ and $Mh(\widetilde{\phi })$

Theorem 4.4

Let $\phi$ be a proper RDS such that $\mathcal {M}_{\phi }\ne \emptyset$, and $\widetilde{\phi }$ is the extension of $\phi$ to the one-point compactification $\widetilde{X}$ of the locally compact separable space X. Then it follows that $Mh(\phi )=Mh(\widetilde{\phi })$, where $Mh(\widetilde{\phi })=\sup \{h_{\widetilde{\mu }}(\widetilde{\phi }):\widetilde{\mu }\in \mathcal {M}_{\widetilde{\phi }}\}$.

Proof

For any $\mu \in \mathcal {M}_{\phi }$, defining $\widetilde{\mu }(\widetilde{A})=\mu (\widetilde{A}\cap \Omega \times X )$ , we have $\widetilde{\mu }\in \mathcal {M}_{\widetilde{\phi }}$. So $h_{\widetilde{\mu }}(\widetilde{\phi })=h_{\mu }(\phi )$ and $Mh(\phi )\le Mh(\widetilde{\phi })$.

Now let $\widetilde{\mu }\in \mathcal {M}_{\widetilde{\phi }}$. Then for any $\omega \in \Omega$, there is $0\le p_{\omega }\le 1$ such that $\widetilde{\mu }_{\omega }=p_{\omega }\mu _{\omega }+(1-p_{\omega })\delta _{\infty }$ where $\mu _{\omega }$ is a probability measure on X and $\delta _{\infty }$ is the Dirac measure at $\infty$.

If $\widetilde{\xi }$ is a measurable partition of $\widetilde{X}$ then $\xi =\widetilde{\xi }|_{X}$ is a measurable partition of X. Moreover

$$\begin{aligned} h_{\widetilde{\mu }}(\widetilde{\phi };\widetilde{\xi })= & {} \int \lim _{n\rightarrow \infty }\frac{1}{n} H_{\widetilde{\mu }_{\omega }} \left( \bigvee _{i=0}^{n-1}\phi ^{-1}(i,\omega )\widetilde{\xi }\right) d \mathbf {P}(\omega )\\= & {} \int \left( p_{\omega }\lim _{n\rightarrow \infty }\frac{1}{n}H_{\mu _{\omega }}\left( \bigvee _{i=0}^{n-1}\phi ^{-1}(i,\omega )\widetilde{\xi }\right) \right. \\&\left. + (1-p_{\omega })lim_{n\rightarrow \infty }\frac{1}{n} H_{\delta _{\infty }}\left( \bigvee _{i=0}^{n-1}\phi ^{-1}(i,\omega )\widetilde{\xi }\right) \right) d \mathbf {P}(\omega )\\\le & {} \int \lim _{n\rightarrow \infty } \frac{1}{n}H_{\mu _{\omega }}\left( \bigvee _{i=0}^{n-1}\phi ^{-1}(i,\omega )\xi \right) d \mathbf {P} (\omega )\\= & {} h_{\mu }(\phi ) \end{aligned}$$

where $\mu =\int \mu _{\omega }d \mathbf {P} (\omega )\in \mathcal {M}_{\phi }$. Since $\widetilde{\mu }$ and $\widetilde{\xi }$ were chosen arbitrarily, we get that $Mh(\phi )\ge Mh(\widetilde{\phi })$. $\square$

4.2.4 The Variation Principle

In this section we give an extension of the well-known Variational Principle for proper RDSs (Theorem B). When the space X is not compact, we do not know wether $\mathcal {M}_{\phi }$ is empty or not. However when $\phi$ is a proper RDS, $M_{\widetilde{\phi }}$ is not empty.

We begin with some counting arguments. Let $\mathcal {C}=\{C_1,\ldots \,C_k\}$ be any finite collection of disjoint subsets of X, we say a finite set $E\subset X$ is $(\omega ,n,\mathcal {C})$-separated if for any pair of distinct points $x,y\in E$, there exists $0\le i<n$ and $1\le r\ne s\le k$ such that $\phi (i,\omega )x\in C_r$ and $\phi (i,\omega )y\in C_s$. Define $r(\omega ,n,\mathcal {C},K)$ to be the maximal cardinality of a $(\omega ,n,\mathcal {C})$-separated subset of $K_{\omega }$, where $K\subset \mathcal {F}\times \mathcal {B}$.

Lemma 4.5

For any $\mu \in \mathcal {E}_{\phi }$ and compact set C with $\mu (\Omega \times C)>1-\frac{\delta }{2}$ there is a random compact set $K\subset \Omega \times C$ with $\mu (K)>1-\delta$ and an N so that for every $n \ge N$ and $x\in K_{\omega }$

$$\begin{aligned} \frac{1}{n}\sum _{i=0}^{n-1}\chi _{C}(\phi (i,\omega )x)\ge 1-\delta . \end{aligned}$$

Proof

For each $N>0$, let $G_{N}(C)=\{(\omega ,x)\in \Omega \times X|\frac{1}{n}\sum _{i=0}^{n-1}\chi _{\Omega \times C}(\Theta ^i(\omega ,x)\ge 1-\delta \,\,\text{ for } \text{ every } \, n \ge N\}$ and $G_{\omega ,N}(C)=\{x\in X|\frac{1}{n}\sum _{i=0}^{n-1}\chi _{C}(\phi (i,\omega )x)\ge 1-\delta \,\,\text{ for } \text{ every } \, n \ge N\}$. It is clear that $G_{N}(C)$ is $\mu$-measurable and $\cup _{\omega \in \Omega }\{\omega \}\times G_{\omega ,N}(C)=G_{N}(C)$. Since $\mu (\cup _{N\in \mathbb {N}} G_{N}(C))=1$ and $G_{N}(C)$’s are increasing family, hence $\mu ((\Omega \times C)\cap G_{N}(C))\ge 1-\delta$, for all sufficiently large N. Then $K=(\Omega \times C)\cap G_{N}(C)$ is a random compact set follows from the fact that each $G_{N}(C)$ is a random closed set. $\square$

Lemma 4.6

Let $\xi =\{A_1,\ldots \,A_k\}$ be a Borel partition of X, let $C_r\subset A_r$ be compact subsets and let $\mathcal {C}=\{C_1,\ldots \,C_k\}$. Suppose that $K\subset \Omega \times C=\Omega \times \cup C_r$ is a random compact set and there exists $\delta >0$ so that for all $n\ge N$ and all $x\in K_{\omega }$, $\frac{1}{n}\sum _{i=0}^{n-1}\chi _{C}(\phi (i,\omega )x)\ge 1-\delta .$ Then for any $\omega \in \pi _{\Omega }(K)$,

$$\begin{aligned} \limsup _{n\rightarrow \infty }\frac{1}{n}\log r(\omega ,n,\mathcal {C},K)\ge \limsup _{n\rightarrow \infty }\frac{1}{n}\log r(\omega ,n,\xi ,K)-\varepsilon (\delta ) \end{aligned}$$

where $\varepsilon (\delta )\rightarrow 0$ as $\delta \rightarrow 0$.

Proof

If $x,y\in K_{\omega }$ and $\{x,y\}$ is not a $(\omega ,n,\mathcal {C})$-separated set, we say that x and y are $(\omega ,n,\mathcal {C})$-indistinguishable. In other words, x and y are $(\omega ,n,\mathcal {C})$-indistinguishable if for each $0\le i<n$, either both $\phi (i,\omega )x$ and $\phi (i,\omega )y$ are contained in the same element of $\mathcal {C}$ or at least one of the points $\phi (i,\omega )x$ or $\phi (i,\omega )y$ is contained in $X\backslash \bigcup _{i=1}^kC_i$. Assuming without loss of generality that $\delta$ is rational, choose $n\ge N$ so that $\delta n$ is an integer. The first step in the proof is to show that the cardinality of a $(\omega ,n,\xi )$-separated subset $S_{\omega }\subset K_{\omega }$ , all of those elements are $(\omega ,n,\xi )$-indistinguishable, is at most $k^{2\delta n} C_{n}^{2\delta n}$.

For $x\in S_{\omega }$, let $J_{\omega }(x)=\{j|0\le j<n,\phi (\omega ,j)x\in X\backslash \bigcup _{i=1}^kC_i\}$. By hypothesis, $J_{\omega }(x)$ has cardinality at most $\delta n$. Choose a collection J of $2\delta n$ integers between 0 and $n-1$. Suppose that $x,y\in S_{\omega }$ and that $J_{\omega }(x)\cup J_{\omega }(y)\subset J$. If $0\le i\le n-1$ is not an element of J, then both $\phi (i,\omega )x$ and $\phi (i,\omega )y$ are contained in the same element of $\mathcal {C}$ and hence also in the same element of $\xi$. Since $\{x,y\}$ is $(\omega ,n,\xi )$-separated, there exists $i\in J$ such that $\phi (i,\omega )x$ and $\phi (i,\omega )y$ lie in different elements of $\xi$. We conclude that there are at most $k^{2\delta n}$ points $x\in S$ with $J_{\omega }(x)\subset J$. Our claim now follows from that fact that there are at most $C_{n}^{2\delta n}$ ways to choose J.

We now know that $r(\omega ,n,\mathcal {C},K)\ge \frac{r(\omega ,n,\xi ,K)}{k^{2\delta n} C_{n}^{2\delta n}}$.

Using Stirling’s formula, we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }\frac{1}{n}\log r(\omega ,n,\mathcal {C},K)\ge \limsup _{n\rightarrow \infty }\frac{1}{n}\log r(\omega ,n,\xi ,K)-\varepsilon (\delta ) \end{aligned}$$

where $\varepsilon (\delta )=-2\delta \log k+\frac{3}{2}[(1-2\delta )\log (1-2\delta )+2\delta \log (2\delta )]$ . All terms involving $\delta$ goes to zero as $\delta$ goes to zero. $\square$

Lemma 4.7

Let $\xi =\{A_1,\ldots ,A_k\}$ be a finite measurable partition of X and $\mu \in \mathcal {E}_{\phi }$. For any $\delta >0$ and random compact set K with $\mu (K)>1-\delta$,

$$\begin{aligned} \limsup _{n\rightarrow \infty }\frac{1}{n}\int \log r(\omega ,n,\xi ,K)d\mathbf {P} \ge (1-\delta )(h_{\mu }(\phi ,\xi )-\delta ). \end{aligned}$$

Proof

Let $A_{n,\omega }=\{x\in K_{\omega }: \mu _{\omega }(\xi _n(\omega ,x))\le \frac{1}{e^{\delta n}r(\omega ,n,\xi , K)}\},$ then $\mu _{\omega }(A_{n,\omega })\le e^{-\delta n}$, where $\xi _n(\omega ,x)$ is the member of the partition $\bigvee _{i=0}^{n-1}\phi ^{-1}(i,\omega )(\xi )$ to which $x\in X$ belongs. Lemma 4.6 follows by Shannon–McMillan–Breiman theorem [3, Theorem 2.2.5], and applying the Borel–Cantelli lemma to $\mu _{\omega }$. $\square$

Theorem 4.8

For any RDS $\phi$ on a metric space (X, d), $Mh(\phi )\le h_{d}(\phi )$.

Proof

Fix a metric d , a $\mu \in \mathcal {E}_{\phi }$ , a finite Borel partition $\xi =\{A_1,\ldots \,A_k\}$ and $\delta >0$. Choose compact sets $C_r\subset A_r$ so that $C=\cup _{r=1}^k C_r$ satisfies $\mu (\Omega \times C)>1-\frac{\delta }{2}$. Choose K and N as in Lemma 4.6. For all sufficiently small $\gamma >0$

$$\begin{aligned} h_d(\phi )\ge & {} \limsup _{n\rightarrow \infty }\frac{1}{n}\int \log r(\omega ,n,\gamma ,K)d\mathbf {P}\\\ge & {} \limsup _{n\rightarrow \infty }\frac{1}{n}\int \log r(\omega ,n,\mathcal {C},K)d\mathbf {P}\\\ge & {} \limsup _{n\rightarrow \infty }\frac{1}{n}\int \log r(\omega ,n,\xi ,K)d\mathbf {P}-\varepsilon (\delta )\\\ge & {} (1-\delta )h_{\mu }(\phi ,\xi )-(\varepsilon (\delta )+\delta ). \end{aligned}$$

Since $\varepsilon (\delta )+\delta$ can be made arbitrarily small, $h_{\mu }(\phi )\le h_{d}(\phi )$ for all metrics d and all ergodic measure $\mu$. $\square$

Now, we are ready to show Theorem B for locally compact Polish space.

Proof of Theorem B

The Variational Principle for compact spaces states that

$$\begin{aligned} h(\widetilde{\phi })=Mh(\widetilde{\phi }). \end{aligned}$$

By Theorem 4.8, we have that

$$\begin{aligned} Mh(\phi )\le h_{d}(\phi ). \end{aligned}$$

Applying Theorem 4.4, it follows that

$$\begin{aligned} h(\widetilde{\phi })=Mh(\phi )\le h_{d}(\phi ). \end{aligned}$$

Applying Theorems 4.2 and 4.4, we have

$$\begin{aligned} h_{d}(\phi )\le h_{d}(\phi ,X)=h(\phi )=Mh(\phi )\le h_{d}(\phi ), \end{aligned}$$

where d is any admissible metric. $\square$