1 Introduction

The reconstruction of shallow-subsurface seismic-velocity models is of great importance in near-surface geophysics. One conventional method for the reconstruction of the P-wave velocity model is to apply first-arrival travel-time tomography to the observed data (Yilmaz, 2015). The multichannel analysis of surface waves provides an efficient way to reconstruct the S-wave velocity model by extracting and inverting surface-wave dispersion curves (e.g., Xia et al., 1999, 2012a). These methods, however, only use a portion of the observed data, i.e., the phase information of a certain wave type, and assume a plane-wave approximation in the forward problems (i.e., the eikonal equation and dispersion equation). Thus, they are usually limited by a moderate resolution.

By using and inverting the entire observed wavefield, full-waveform inversion (FWI; Tarantola, 1984) offers a high-resolution technique for the multiparameter reconstruction of the Earth model across scales (e.g., Tromp, 2020; Virieux & Operto, 2009). With the rapidly increasing computational power and the developments in the theory of FWI, it has become increasingly popular to apply FWI to shallow-seismic data for the reconstruction of near-surface models. Synthetic studies (e.g., Gélis et al., 2007; Romdhane et al., 2011; Zeng et al., 2011) have proven the relatively high resolution of shallow-seismic FWI. An increasing number of successful field applications have also proven the ability of shallow-seismic FWI in the reconstruction of accurate information of lateral/vertical heterogeneity in the model (e.g., Dokter et al., 2017; Groos et al., 2017; Köhn et al., 2019; Pan et al., 2019; Tran et al., 2013). The multiparameter shallow-seismic FWI has also been developed and applied to viscoelastic media (Gao et al., 2020, 2021), anisotropic media (Krampe et al., 2019; Manukyan & Maurer, 2020), media with an irregular free surface (Mecking et al., 2021; Nuber et al., 2016; Pan et al., 2018), and three-dimensional (3D) media (Irnaka et al., 2019; Smith et al., 2018; Teodor et al., 2021; Tran et al., 2019) in recent years.

In exploration land seismic data, surface waves are typically treated as noise and are removed in the preprocessing. The acoustic approximation is widely adopted in land-seismic FWI. On the one hand, it saves computational cost, but on the other hand, it can lead to artifacts in the P-wave velocity model by neglecting the elastic effect (changes in phase and amplitudes; e.g., Barnes & Charara, 2009; Mulder & Plessix, 2008; Solano et al., 2013). In engineering (geotechnical) land seismic data generated by a vertical-force source, Rayleigh waves are much stronger than P waves, while S waves are even weaker than P waves. Unlike exploration seismology which primarily focuses on the reconstruction of the P-wave velocity model, S-wave velocity, which provides information about the stiffness of the material, is the main targeted parameter in engineering seismology. Surface waves contain abundant information about the S-wave velocity and are treated as the main signals in engineering seismology. Because Rayleigh waves dominate the vertical component of the observed data, a shallow-seismic FWI that fits the whole recording simultaneously might result in overlooking the body-wave signal.

One way to increase the weight of P waves in land-seismic FWI is to use time windowing (e.g., Brossier et al., 2009; Sears et al., 2008) to select specific signals for inversion. Another way is to use an automatic gain control (AGC)-based objective (e.g., Mecking et al., 2021) to fit a time-weighted waveform. These approaches require predefined time windows to target the body wave in the observed data. They might damage the phase of the observed data if the windows are not designed appropriately and might fail to work if the body wave is significantly overlapping with Rayleigh waves in the recording. Since the P wave and Rayleigh wave usually interfere with each other in the time–space domain but are more separable in the frequency–velocity domain (equivalently, tau–p domain or frequency–slowness domain), alternatively, we can separate the P wave from the observed data and use the P wave alone to reconstruct the P-wave velocity model.

In this paper, we propose a wavefield-separated full-waveform inversion (WSFWI) method for the reconstruction of the near-surface model. In the WSFWI, we separate the P wave from the observed data and apply an acoustic FWI to it to reconstruct the P-wave velocity model. Then we fix the P-wave velocity model and perform an elastic FWI for the entire recording to reconstruct the S-wave velocity model. We analyze and compare the sensitivity kernels of different wave types (i.e., Rayleigh and P waves) with respect to the P-wave velocity model and show the benefits of treating Rayleigh and P waves separately. We perform a synthetic example and compare the S-wave and P-wave velocity models reconstructed by the conventional FWI and WSFWI, respectively. We apply both the conventional FWI and WSFWI to a field data set acquired in Olathe, Kansas, USA, and compare their performance in the reconstruction of the multiparameter shallow-subsurface models.

2 Methodology

We used a two-dimensional (2D) finite-difference method to solve the viscoelastic wave equation in the time domain for the simulation of shallow-seismic data (Bohlen, 2002). The least-squares misfit between the normalized observed and synthetic waveforms is defined as the objective function (Choi & Alkhalifah, 2012):

$$\Phi \left( \textbf{m} \right) = \mathop \sum \limits_{i = 1}^{ns} \mathop \sum \limits_{j = 1}^{nr} \mathop \sum \limits_{k = 1}^{nc} \left\| {\hat{s}_{i,j,k}\left( \textbf{m} \right) - \hat{d}_{i,j,k}} \right\|^{2}$$
(1)

where \(\widehat{s}\) and \(\widehat{d}\) represent the normalized synthetic and observed data in the time domain in which \(\widehat{s}_{i,j,k}=s_{i,j,k}/||s_{i,j,k}||\) and \(\widehat{d}_{i,j,k}=d_{i,j,k}/||d_{i,j,k}||\), respectively; the sums over i, j, and k represent the sums over the \({n}{s}\) source, \({n}{r}\) receivers, and \({n}{c}\) components, respectively. This normalized objective function can also be expressed as a zero-lag cross-correlation of two normalized signals (Choi & Alkhalifah, 2012). It is not sensitive to the offset-dependent amplitude decay (geometric spreading, intrinsic anelastic effects, and receiver coupling) but considers the relative amplitude difference between the signals of the same trace. Besides, it balances the contributions of near- and far-offset traces in the data and is expected to make FWI more robust compared with the least-squares objective function without normalization (Groos et al., 2014). Although we use a viscoelastic wave equation in the forward solver, we treat the QS and QP as passive parameters and do not update them. In other words, we perform elastic FWI (sometimes also called passive viscoelastic FWI) by using a viscoelastic wave equation in the forward solver. This passive viscoelastic FWI approach outperforms elastic FWI using elastic forward modeling (Groos et al., 2014), especially for near-surface models which sometimes have relatively low Q values (quality factors around/lower than 10) (e.g., Gao et al., 2020; Köhn et al., 2019; Xia et al., 2012b). We use the adjoint-state algorithm (Fabien-Ouellet et al., 2017; Plessix, 2006) to calculate the gradient of the objective function with respect to model parameters and a preconditioned conjugate gradient algorithm for optimization (Pan et al., 2020). We use the S-wave velocity, P-wave velocity, and density for model parameterization in the inversion (Köhn et al., 2012).

In FWI, Rayleigh and body waves in the observed waveform are inverted simultaneously. Because the Rayleigh wave is usually much stronger than the P wave, while the S wave is even much weaker than the P wave in the observed data, FWI mainly focuses on the fitting of the Rayleigh wave, and therefore results in poor use of the body wave. Thus, although the Rayleigh wave is less sensitive to the P-wave velocity than to the S-wave velocity, while the P-wave-dominated body waves are more sensitive to the P-wave velocity, we mainly use Rayleigh-wave signals to reconstruct the P-wave velocity model in shallow-seismic FWI, and as a result, the reconstructed P-wave velocity model might be contaminated by the crosstalk from the S-wave velocity model.

In order to make better use of the P wave in the data and to obtain a more reliable P-wave velocity model, we propose a new method, namely wavefield-separated full-waveform inversion (WSFWI), to invert the P wave and entire wavefield sequentially (Fig. 1). In the first step of WSFWI, we separate the P wave from the observed data and apply acoustic FWI to it for the reconstruction of the P-wave velocity model. In this paper, we adopt an acoustic approximation by setting S-wave velocity to zero in the viscoelastic wave equation. In the second step, we fix the reconstructed P-wave velocity model and invert the entire wavefield using elastic FWI to reconstruct the S-wave velocity model. We ignore the sensitivity of Rayleigh wave to P-wave velocity model in the second step to mitigate the possible crosstalk from the S-wave velocity to P-wave velocity models in shallow-seismic Rayleigh-wave FWI (e.g., Fig. 2 in Dokter et al., 2017). One of the key points in the WSFWI is the accurate separation of the P wave from the entire wavefield. In this work, we use a frequency filter and a velocity filter to separate the P wave (in this paper, the refracted P wave) from the Rayleigh wave because the P wave travels faster and has a higher frequency range relative to the Rayleigh wave. Other approaches, such as the Radon transform and tau–p transforms (e.g., Luo et al., 2008), can also be adopted for the wavefield separation.

Fig. 1
figure 1

Workflow of WSFWI. The body wave mentioned in the figure represents the P wave in our study. In the first step, the P wave is separated from the recording data and is used alone for the reconstruction of the P-wave velocity model via an acoustic FWI. In the second step, the full wavefield is used to reconstruct the S-wave velocity model via an elastic FWI

Full size image
Fig. 2
figure 2

Sensitivity kernels of the a full wavefield, b body (P) wave, and c Rayleigh wave with respect to the P-wave velocity. The range of the color bar in (a) and (c) is 103 higher than that in (b). d is a 1D vertical slice of the absolute value of the sensitivity kernels at the midpoint between the source (circle on the free surface) and receiver (triangle on the free surface). The gray, blue, and red lines represent the full wavefield, the P wave, and the Rayleigh wave, respectively

Full size image

2.1 Sensitivity Kernels of Different Wave Types

We use a homogeneous half-space model to compare the sensitivity kernels of different wave types with respect to the P-wave velocity model. The S-wave velocity, P-wave velocity, density, QS, and QP of the model are 200 m/s, 600 m/s, 2000 kg/m3, 100, and 200, respectively. The source and receiver are placed at the free surface with an offset of 50 m. A 30 Hz delayed Ricker wavelet is used as a vertical-force source, and both horizontal and vertical components are recorded at the receiver. Figure 2 shows the P-wave velocity sensitivity kernels (Tromp et al., 2005) of the different wave types for the homogeneous half-space model mentioned above. The sensitivity kernels of the full wavefield and Rayleigh wave (Fig. 2a, c) are calculated with a viscoelastic wave equation, while the sensitivity kernel of the P wave is calculated with a viscoacoustic wave equation (by setting S-wave velocity to zero in the viscoelastic wave equation). Because the Rayleigh wave dominates the vertical component of the observed data, the full wavefield is mainly sensitive to the shallow part of the model (Fig. 2a). The Rayleigh-wave sensitivity kernel is at a magnitude of 103 stronger than that of the body wave (Fig. 2b, c). This indicates that shallow-seismic FWI mainly uses the Rayleigh wave instead of the P wave to reconstruct the P-wave velocity model. Due to the different propagation paths, the P wave is more sensitive to the deeper part of the model, while the Rayleigh wave is more sensitive to the shallower part of the model. Figure 2d shows a vertical slice of the sensitivity kernel at the midpoint between the source and receiver. The Rayleigh-wave sensitivity decreases exponentially with depth (red curve in Fig. 2d), while the body-wave sensitivity gradually increases with depth (blue curve in Fig. 2d). Although the P wave is more sensitive to the P-wave velocity in the deep part of the model, if we invert the entire wavefield simultaneously, we will mainly update the shallow part of the P-wave velocity model (within the penetration depth of the Rayleigh wave), especially in the case when the gradient is not preconditioned appropriately. There are some differences between the sensitivities of the full wavefield and P wave in the deep part of the model (i.e., depth > 5 m in Fig. 2d), which is caused by the elastic effect (i.e., the interaction between P and Rayleigh waves, and the leaky-mode Rayleigh waves).

By separating the Rayleigh and P waves and tackling the P-wave signal alone, WSFWI can better reconstruct the P-wave velocity structure beyond the penetration depth of the Rayleigh wave. Besides, because only the P wave is used for the reconstruction of the P-wave velocity model, it can avoid (mitigate) crosstalk from the S-wave to the P-wave velocity models caused by the Rayleigh wave, and therefore improve the accuracy of the reconstructed P-wave velocity model. We did not consider the influence of converted waves here because they are usually weak in the vertical-component shallow-seismic data.

2.2 Synthetic Example

We perform a synthetic example to prove the validity of WSFWI. The true model contains a layer over the half-space with interfaces of sinusoidal shapes in the S-wave and P-wave velocity models (first row in Fig. 3). The cycle of the sinusoidal interface in the S-wave velocity model is shorter than that in the P-wave velocity model (12 m compared with 16 m), and thus the S-wave velocity model is not perfectly correlated with the P-wave velocity model. A vertical-force source and 50 vertical-component receivers are placed along the free surface, with a nearest offset of 2.4 m and a trace interval of 0.6 m. We use a roll-along manner for the data acquisition, and the whole spread is moved 1.2 m toward the end of the survey line in each new shot (Fig. 3a). A total of ten shots are used. The first and the last source points are located at 12 m and 22.8 m, respectively, and the last trace in the first and last shots are located at 43.8 m and 54.6 m, respectively. We use the same multi-scale approach (Bunks et al., 1995) in both conventional FWI and WSFWI and invert the data in a frequency range of 5 to 30 Hz, 5 to 45 Hz, and 5 to 60 Hz, progressively. A minimum of three iterations are performed at each stage, and the inversion moves to the next stage once the relative improvement in the data misfit is less than 1%. The true source wavelet, which is a delayed 40 Hz Ricker wavelet, is used in the inversion.

Fig. 3
figure 3

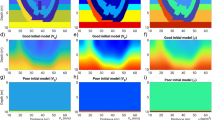
A synthetic example comparing the performance of conventional FWI and WSFWI. Two columns represent the S-wave velocity and P-wave velocity models, respectively. Four rows represent the true model (a and b), the initial model (c and d), the conventional FWI result (e and f), and the WSFWI result (g and h), respectively. Panel a shows the acquisition system in which the asterisks and triangles represent the sources and receivers, respectively. The white parts in panels e–h roughly correspond to the reconstructed interfaces between the two layers

Full size image

Figures 4 and 5 show the entire observed data and the separated P wave of the first shot. The Rayleigh wave dominates the observed wavefield, and the body-wave signal is almost invisible in the raw recording (Fig. 4), especially in the short-offset traces (Fig. 5a), due to trace normalization when displaying the data. The body-wave signal will become more visible if we only show the waveform arrivals before the Rayleigh wave. The body and Rayleigh waves share a similar frequency range in this example, and therefore, we separate the P wave from the entire recording by using a high-pass velocity filter (velocity > 350 m/s) only. The signal that arrives later than the P wave is manually muted. Figure 5b shows that the body-wave signal is nicely separated from the Rayleigh wave, thanks in part to the high Poisson ratio (or Vp/Vs ratio) of the near-surface materials (Yilmaz, 2015). Some weak artifacts are introduced in the separated body-wave data, especially in the overlapping area between the surface and P waves (e.g., first 20 traces in Fig. 5b).

Fig. 4
figure 4

Observed data of the first shot in the synthetic example

Full size image
Fig. 5
figure 5

a The entire wavefield and b the separated P wave of the first shot (Fig. 4) in the first 150 ms. The waveforms are displayed with trace normalization

Full size image

We perform the conventional FWI starting with a 1D linear-gradient model as the initial model (second row in Fig. 3). The S-wave velocity model is nicely reconstructed, and the sinusoidal shape of the interface is well delineated (Fig. 3e). The reconstructed P-wave velocity model shows the main structure of the true model, i.e., a layer over the half-space model. However, it cannot accurately delineate the shape of the interface (white part in Fig. 3f). It shows two uplifts in the interface with two peaks at around 21 m and 33 m, which correspond to the structure in the S-wave velocity model rather than the P-wave velocity model. This is caused by the crosstalk from the S-wave to the P-wave velocity models. Thus, the shape of the interface in the reconstructed P-wave velocity model is influenced simultaneously by the P-wave and S-wave velocity structures, making it difficult to reconstruct a reliable P-wave velocity model.

We perform WSFWI starting from the same 1D linear-gradient model. The first three traces in every shot are not used in the first step in WSFWI because the separated P wave is weakly contaminated by the Rayleigh wave. The sinusoidal interfaces in both the S-wave and P-wave velocity models are well resolved by the WSFWI (Fig. 3g, h). The S-wave velocity model is slightly more accurate than the conventional FWI result in the region > 45 m, while the improvement in the accuracy of the reconstructed P-wave velocity model is more notable (Fig. 3f and h). The sinusoidal shape and the correct locations of its peaks and troughs are well reconstructed, and the reconstructed P-wave velocity model is not contaminated by the crosstalk from the S-wave velocity model. The P-wave velocity of the second uplift is less accurately reconstructed compared with the first one due to the lower illumination of the P wave in the far-offset region (second uplift). Overall, both the S-wave and P-wave velocity models reconstructed by WSFWI are more accurate than the conventional FWI results with an improvement of 6% in the L2-norm model error.

The WSFWI converges after 19 (blue curve in Fig. 6a) and 46 iterations (red curve in Fig. 6b) in the two steps, respectively, while the conventional FWI converges after 43 iterations (black curve in Fig. 6b). Both the conventional FWI and WSFWI fit the observed data fairly well, and the final data fitting of WSFWI is 54% better than that with the conventional FWI (red and black curves in Fig. 6b). Although the two-step WSFWI runs more iterations than the conventional FWI, the total computational cost of WSFWI is only slightly higher (< 20%) than the conventional FWI. This is because the recording length of body-wave data is significantly shorter than the full recording (i.e., 160 ms compared with 600 ms) and the acoustic FWI is computationally cheaper than the elastic FWI. It is worth mentioning that the accuracy in the P-wave velocity model can be further improved if the P wave can be more accurately separated from the entire recording. Additionally, the accuracy of the S-wave and P-wave velocity models might be further improved if we run a conventional FWI on the WSFWI results. Overall, this synthetic example proves that WSFWI outperforms the conventional FWI, especially in the reconstruction of the P-wave velocity model.

Fig. 6
figure 6

Evolution of data misfit in the conventional FWI and WSFWI. a and b represent the data misfits in the body-wave FWI (step 1 in WSFWI) and full-wavefield FWI (conventional FWI and step 2 in WSFWI), respectively. The misfit value “jumps up” when the inversion moves to a new stage (dashed lines)

Full size image

2.3 Field Example

We applied both the conventional FWI and WSFWI to a field data set acquired at Olathe, Kansas (USA). A vertical source and 48 vertical-component receivers were placed along the survey line. The nearest offset was 3.6 m, and the trace interval was 0.6 m. Similar to the synthetic data, the field data were acquired in a roll-along manner, and the spread was moved 1.2 m toward the eastern direction (end of the survey line) in each new shot. We used a total of ten shots in this field example (shots numbered 2010 to 2019 in Miller et al., 1999). The first and the last source points were located at 12 m and 22.8 m, respectively, and the last traces in the first and last shots were located at 43.8 m and 54.6 m, respectively.

Figures 7 and 8 show the observed data of the fourth shot and its dispersion image, respectively. The Rayleigh wave dominates the wavefield, and the body-wave signal (refracted P wave) can be seen in observed data (Fig. 7). The surface-wave and body-wave energy are well separated and can be easily identified in the frequency–velocity domain (Fig. 8). The Rayleigh wave mainly dominates the low-frequency/low-velocity part of the dispersion image, while the P wave exists in the high-frequency/high-velocity part (velocity > 500 m/s and frequency > 80 Hz; red box in Fig. 8). By selecting and transforming the body-wave energy back into the time–space domain (i.e., by performing a high-pass velocity filter and a high-pass frequency filter to the data), we successfully separate the P wave from the entire recording in the time–space domain (Fig. 9). Some artifacts caused by the wavefield separation (e.g., the signal at around time zero in Fig. 9b) are manually muted before the inversion.

Fig. 7
figure 7

Observed data of the fourth shot in the field example

Full size image
Fig. 8
figure 8

Dispersion image of the fourth shot. We obtained the Rayleigh-wave dispersion image via a high-resolution linear Radon transform (Luo et al., 2008). The low-frequency low-velocity energy corresponds to Rayleigh waves, and the high-frequency high-velocity energy (red box) represents the P waves

Full size image
Fig. 9
figure 9

a The raw data and b the separated P wave of the fourth shot in the first 80 ms. The waveforms are displayed with trace normalization

Full size image

We built a 1D S-wave velocity model by inverting the Rayleigh-wave dispersion curve and a 1D P-wave velocity model by inverting the travel time of the first arrival (Fig. 10a, b). The 1D QS and QP models are built by inverting the Rayleigh-wave attenuation coefficients (Gao et al., 2018). A 3D-to-2D transform (Forbriger et al., 2014) is applied to the data, and the data are delayed by 10 ms before inversion. A multiscale strategy (Bunks et al., 1995) with a band-pass filter of 80–120 and 80–160 Hz is used in the first step of WSFWI (body-wave FWI). In both the conventional FWI and the second step of WSFWI, we progressively invert the data from 5 to 30 Hz, 5 to 45 Hz, and 5 to 80 Hz to avoid cycle skipping. A minimum of three iterations are performed at each stage, and the inversion moves to the next stage once the relative improvement in the data misfit is less than 1%. The source time functions are updated at the beginning of each stage (Groos et al., 2017).

Fig. 10
figure 10

The S-wave (left column) and P-wave (right column) velocity models in the field example. Three rows represent the initial model (a and b), the conventional FWI result (c and d), and the WSFWI result (e and f), respectively. The symbol in c represents the location of the geotechnical bedrock. The circle in f represents the location of a sewer line going across the survey line

Full size image

The S-wave velocity models estimated by the conventional FWI and WSFWI are fairly similar (Fig. 10c, e), indicating that the S-wave velocity model can be reconstructed with relatively high robustness. A borehole drilled at the horizontal distance of around 46.6 m shows that the geotechnical bedrock locates at around 4.2 m deep at this point (symbol in Fig. 10c; Miller et al., 1999), which nicely agrees with the reconstructed S-wave velocity model. The P-wave velocity models reconstructed with the conventional FWI and WSFWI are different from each other. The conventional FWI mainly updates the P-wave velocity in the shallow part of the model (above 5 m depth; Fig. 10d), while the WSFWI also updates the deeper part of the P-wave velocity model (Fig. 10f). A high P-wave velocity structure locates below 38 m at the depth of around 1 m in the WSFWI result (circle in Fig. 10f), which is not visible in the conventional FWI result. It coincides with the location of a sewer line buried across the survey line (Miller et al., 1999), indicating that this high P-wave velocity (or high Vp/Vs ratio) structure is reliable. The relatively high P-wave velocity structure might be caused by the compaction of material (granular embedment) around the sewer line. The sewer line is not visible in the reconstructed S-wave velocity model due to the relatively lower resolution (i.e., longer wavelength) of Rayleigh waves compared with P waves.

The WSFWI converges after 23 and 22 iterations in the two steps, respectively, while the conventional FWI prematurely converges after 13 iterations (Fig. 11). The final data fitting of WSFWI is 12% better than the conventional FWI (red and black lines in Fig. 11b). This difference is not notable in the waveform comparison because both the FWI and WSFWI results fit the observed data (Rayleigh wave) satisfactorily well (blue and red lines in Fig. 12a and b). If we only simulate the P waves using the FWI and WSFWI results with an acoustic-wave equation in a frequency range of 80–160 Hz, the WSFWI result fits the observed P wave better compared with the conventional FWI result (blue and red lines in Fig. 12c, d), especially in the far offset traces. We also compare P-wave data misfits (80 to 160 Hz) corresponding to the FWI and WSFWI results (e.g., data misfits in Fig. 12c, d for the fourth and eighth shots). The P-wave data fitting in the WSFWI result is on average 49% better than the conventional FWI result (blue and red curves in Fig. 13), which shows that WSFWI outperforms FWI in the data fitting, especially in the P waves. Overall, the conventional FWI mainly updates the P-wave velocity using the Rayleigh-wave signal and cannot appropriately explain the P wave in the observed data. The WSFWI result nicely fits both the Rayleigh and P waves in the observed data, leading to relatively higher reliability of the reconstructed P-wave velocity model.

Fig. 11
figure 11

Evolution of data misfit in the field example. a and b represent the data misfits in the body-wave FWI (step 1 in WSFWI) and full-wavefield FWI (conventional FWI and step 2 in WSFWI), respectively. The misfit value “jumps up” when the inversion moves to a new stage (dashed lines)

Full size image
Fig. 12
figure 12

Waveform comparison in the fourth (left column) and eighth (right column) shots. a and b represent the comparison between the entire observed data in a frequency range from 5 to 80 Hz. c and d represent the comparison between the observed and synthetic P waves simulated with an acoustic-wave equation in a frequency range from 80 to 160 Hz. Gray, red, and blue lines represent the observed data, synthetic data corresponding to the conventional FWI result, and the synthetic data corresponding to the WSFWI result, respectively. The waveforms are displayed with trace normalization

Full size image
Fig. 13
figure 13

Comparison of data misfits of the P wave (80–160 Hz) in every single shot. Blue and red curves correspond to the conventional FWI and WSFWI results, respectively. The P-wave data fitting in the WSFWI result is on average 49% better than the conventional FWI result

Full size image

3 Discussion

Herein, we chose to estimate the P-wave velocity from the P wave first and then the S-wave velocity from the Rayleigh wave. This is based on the assumption that the (refracted) P wave is less dependent on S-wave velocity compared with the Rayleigh wave on the P-wave velocity. Alternatively, we can also swap the order, which might provide results with similar accuracy. Additionally, we might jointly invert P and Rayleigh waves simultaneously with an adaptive weighting factor, which is worth further study.

We chose to use an acoustic instead of an elastic FWI in the first step so that the influence of the surface wave could be easily avoided in this step. If we want to adopt an elastic FWI in the first step, special care (e.g., time windowing) needs to be taken to remove the influence of surface wave in the synthetic data.

Near-surface materials usually have a high Poisson's ratio, and the S waves (including the converted PS wave) are usually weak in the vertical-component shallow-seismic data. Therefore, we can nicely separate P and Rayleigh waves in the observed data by simply using velocity and frequency filters. When the Poisson's ratio is low or the model is strongly heterogeneous (e.g., in exploration land seismic data), we may need to use a more sophisticated wavefield separation algorithm for the wavefield separation (Richwalski et al., 2000).

4 Conclusions

We have proposed a wavefield-separated full-waveform inversion (WSFWI) method to use the P wave and the entire (vertical-component) seismic recording sequentially for the reconstructions of near-surface P-wave and S-wave velocity models. In the WSFWI method, we firstly separate the P wave from the seismic recording and use it to reconstruct the P-wave velocity model via an acoustic FWI. Then we perform an elastic FWI on the full wavefield to reconstruct the S-wave velocity model. A synthetic example proved that WSFWI improves the accuracy of the inversion results, especially for the P-wave velocity model, and avoids crosstalk from the S-wave to P-wave velocity models. A field example showed that WSFWI can make better use of the P-wave signal, which is overlooked by the conventional FWI that focuses on fitting the Rayleigh wave, and can thereby reconstruct the P-wave velocity model with relatively higher reliability. Although we mainly focused on the first-arrival P wave and Rayleigh wave in this paper, the applications of this method to the reflected body wave and Love (SH) wave are straightforward. The WSFWI might improve the reliability of the attenuation models in viscoelastic media, which deserves further study.