1 Introduction

Rock will experience initiation and propagation of microfractures before failure, and the initiation and propagation of microfractures are associated with acoustic emissions (AEs). The AE energy radiated from rock microfractures is one of the fundamental quantization parameters that is widely used to understand the rock failure process. The AE radiation energy has been proved to be a reliable indicator warning of imminent rock failure.

For example, a significant increase of AE radiation energy before rock failure is observed in many rock types, such as granite (Přikryl et al. 2003; Zhao et al. 2014), gneiss (Zhang et al. 2004), tuff (Hall et al. 2006), saturated karst limestone (Wang et al. 2019) and coal (Xue et al. 2018). In addition, Hu et al. (2019) conducted a structural model test using 200 mm × 200 mm × 200 mm rectangular prismatic granite specimens with a horizontal central circular hole and found that a quiet period characterized by a few AE hits with high amplitude and a sharp increase in AE energy can be used as an early warning signal for overall rockburst. Jiang et al. (2019) conducted uniaxial cyclic loading tests with sandstone samples and found energy distributions can be expressed by a power law and the slope of the AE energy distribution curve decreases sharply as the number of cycles increases when close to the failure stage. Zhou et al. (2018) analyzed the AE activities induced by the excavation of the Gaoligongshan tunnel and found the AE energy resulting from slight and moderate rockbursts obeys the logarithmic normal distribution, while the AE energy of non-rockbursts obeys the Weibull distribution.

However, the radiation energy of AE sources is usually inaccurately quantified because of uncertainties in the data analysis process and limits in the data acquisition condition, such as an imprecise knowledge of the radiation pattern, uneven frequency response of AE sensors and incomplete space coverage of the AE sensor array. For example, the radiation pattern is generally assumed to be spherical for simplicity; in fact, the radiation pattern is usually butterfly-shaped and is related to the tensile angle. The tensile angle is termed the angle between the microfracture plan and the motion direction of the microfracture plan (Kwiatek and Ben-Zion 2013). For a pure shear AE source, the amplitude received by AE sensors at different azimuths and takeoff angles can differ by > 10 times, and the radiation energy can differ by > 100 times.

In the present study, we attempt to quantify the radiation energy of AE sources with different tensile angles and analyze the radiation energy evolution during the failure process of rock specimens. First, the moment tensor inversion method is used to determine the tensile angle. Then, the radiation energy of AE sources is calculated based on the relation between the radiation pattern and tensile angle. Combined with the calculation results, the spatiotemporal evolution of AE source radiation energy is analyzed during the failure process.

2 AE Radiated Energy Calculation

When the AE source is simplified to be a stationary source, the energy radiated by a given wave type from an AE source can be expressed as (Boatwright and Fletcher 1984):

$$E_{\text{C}} = 4\pi \rho V_{\text{C}} \frac{{\langle R_{\text{C}} \rangle^{2} }}{{R_{\text{C}}^{2} }}R^{2} J_{\text{C}} ,$$
(1)

where ρ is the rock density, VC is the P or SH or SV wave velocity (VSH =  VSV), RC is the radiation pattern coefficient of P or SH or SV waves at a particular AE sensor, 〈RC〉 is the average radiation pattern coefficient, R is the distance between the AE source and AE sensor, and JC is the radiation energy flux of the P or SH or SV wave.

2.1 Tensile Angle

The tensile angle has a significant impact on the radiation pattern of AE sources. To calculate the radiation pattern coefficient RC and the average radiation pattern coefficient 〈RC〉, the tensile angle should be determined in advance. In this section, the moment tensor inversion method is used to determine the tensile angle.

By assuming the microfracture is a point source, the microfracture can be characterized by a moment tensor, and the moment tensor is a real symmetric second-order tensor with nine time-dependent moment components, only six of which are independent. The relation between moment tensor M and the far-field first motion displacement u of the P wave at the sensors can be expressed as follows (Aki and Richards 2002):

$$GM = u,$$
(2)

where G is the Green function.

Assuming that there are N triggered sensors, u is a vector with dimensions of N × 1, and the vector M is composed of six independent moment components, M11, M22, M33, M12, M13 and M23. G is a matrix and has dimensions of N × 6. Hence, if N ≥ 6, the components of M can be computed using the least-squares method.

Using the simplified Green function for the moment tensor inversion method (Ohtsu 2008), the far-field first motion induced by a microfracture can be determined by

$$u\,{ = }\,C_{\text{s}} \frac{{R_{\text{e}} ({\mathbf{t}} , {\mathbf{r}} )}}{R}(r_{1}\quad {r_{2}} \quad{r_{3}} )\left( {\begin{array}{*{20}c} {M_{11} } & {M_{12} } & {M_{13} } \\ {M_{12} } & {M_{22} } & {M_{23} } \\ {M_{13} } & {M_{23} } & {M_{33} } \\ \end{array} } \right)\left( \begin{aligned} r_{1} \hfill \\ r_{2} \hfill \\ r_{3} \hfill \\ \end{aligned} \right),$$
(3)

where Cs is the magnitude of the sensor response including material constants, Re (t, r) is the reflection coefficient, t is the direction of the sensor, and r = (r1r2r3) is the direction vector from the source to the sensor.

The moment tensor can be obtained by Eq. (2) and can be decomposed according to the following equation:

$$\left( {\begin{array}{*{20}c} {M_{11} } & {M_{12} } & {M_{13} } \\ {M_{12} } & {M_{22} } & {M_{23} } \\ {M_{13} } & {M_{23} } & {M_{33} } \\ \end{array} } \right) \Rightarrow \left( {\begin{array}{*{20}c} {M_{1} } & {} & {} \\ {} & {M_{2} } & {} \\ {} & {} & {M_{3} } \\ \end{array} } \right){ = }{\mathbf{M,}}$$
(4)

where M1, M2 and M3 (M1 > M2 > M3) are the three eigenvalues of the moment tensor and represent the principal moments of the AE source.

The unit motion vector l and unit normal vector n of the microfracture plane can be deduced, as shown below (Zhao et al. 2019; Vavryčuk 2014):

$$\left\{ \begin{aligned} {\mathbf{l}} = \sqrt {\frac{{M_{1} - M_{2} }}{{M_{1} - M_{3} }}} \varvec{e}_{1} + \sqrt {\frac{{M_{1} - M_{2} }}{{M_{1} - M_{3} }}} \varvec{e}_{3} \hfill \\ {\mathbf{n}} = \sqrt {\frac{{M_{1} - M_{2} }}{{M_{1} - M_{3} }}} \varvec{e}_{1} - \sqrt {\frac{{M_{1} - M_{2} }}{{M_{1} - M_{3} }}} \varvec{e}_{3} \hfill \\ \end{aligned} \right.,$$
(5)

where e1, e2 and e3 are the corresponding eigenvectors of the eigenvalues (M1, M2 and M3), respectively.

Vectors l and n are perpendicular for pure shear microfractures but parallel for pure tensile and compression microfractures. For a microfracture (shear compression or shear tensile), vectors l and n form angles ranging between 0° and 180°. However, the vectors l and n are interchangeable for shear microfractures and mixed microfractures.

The tensile angle γ is measured between the projection of motion direction l on the microfracture plane and the motion direction l, ranging between − 90° and 90°:

$$\gamma\, { = }\,90^{ \circ } - \arccos ({\mathbf{n}} \cdot {\mathbf{l}})\frac{{180^{ \circ } }}{\pi }.$$
(6)

Even if l and n are interchanged, arccos(n·l) is still constant. Therefore, the tensile angle γ can be calculated without distinguishing between the two vectors l and n. The tensile angle is positive for shear tensile and tensile AE sources, negative for shear compression and compression AE sources, and equal to 0° for shear AE sources. The definition of microfracture plan parameters is shown in Fig. 1.

Fig. 1
figure 1

Definition of a microfracture and an AE ray out of it in Cartesian coordinates of north (N), east (E) and down (D). x1, x2 and x3 are unit vectors toward north, east and down. The microfracture and the plane it lies on are shown using a blue disk and orange oblique plane, respectively. The microfracture plane is defined by strike ϕs and dip δ. The strike ϕs of a microfracture plane is the angle measured clockwise from north to the surface intersection of the microfracture plane (0°–360°), with the microfracture hanging wall on the right when looking in the direction of the strike. The dip δ is a slope angle of the fault plane measured clockwise from the horizontal (0°–90°). n and l are the unit normal vector and unit motion vector of the microfracture plane, f is the slip vector in the fault plane, λs is the slip angle measured counterclockwise from the direction of the strike to the slip direction of the hanging wall relative to the footwall, and γ is the tensile angle measured from f toward l. r is the unit radial vector of the AE ray, which is parallel to the particle vibration direction caused by P waves. φ is the upward unit vector of the particle vibration direction caused by the SH wave, and θ is the rightward unit vector of the particle vibration direction caused by the SV wave when looking in the direction of r. R is the distance between the AE source and AE sensor. ϕ and θ are the azimuth and takeoff angle the of the AE ray

Full size image

2.2 Energy Radiation Pattern of the AE Source

The radiation pattern refers to the directional (angular) dependence of the amplitude of the radiation waves from the AE source. The radiation pattern coefficient RC is used to characterize the directional dependence of the amplitude, and the RC at a particular position is a function of the wave type (P/SH/SV), microfracture characteristics (motion direction and normal direction), relative position from the AE source (azimuth and takeoff angle) and Poisson’s ratio of rock (Ou 2008). Based on the square relation between the amplitude and energy, the energy radiation pattern coefficients of the AE source can be expressed as:

$$\begin{array}{*{20}c} {R_{P}^{2} = ({\mathbf{ {r} }}^{\text{T}} {\mathbf{S{r} }})^{2} } & {{\mathbf{ {r} }} = \sin \theta \cos \phi {\mathbf{{x} }}_{1} { + }\sin \theta \sin \phi {\mathbf{ {x} }}_{2} { + }\cos \theta {\mathbf{{x} }}_{3} } \\ {R_{SH}^{2} = ({\mathbf{{\varphi } }}^{\text{T}} {\mathbf{ S{r} }})^{2} ,} & {{\mathbf{ {\theta } }} = \cos \theta \cos \phi {\mathbf{ {x} }}_{1} { + }\cos \theta \sin \phi {\mathbf{ {x} }}_{2} - \sin \theta {\mathbf{ {x} }}_{3} } \\ {R_{SV}^{2} = ({\mathbf{{\theta } }}^{\text{T}} {\mathbf{S {r} }})^{2} } & {{\mathbf{ {\varphi } }} = \sin \theta \cos \phi {\mathbf{ {x} }}_{1} { + }\sin \theta \sin \phi {\mathbf{ {x} }}_{2} { + }\cos \theta {\mathbf{{x} }}_{3} } \\ \end{array}$$
(7)

where the super index T indicates a matrix transpose, and the symmetric S is called the source dislocation tensor for a microfracture plane. The elements of S are:

$$\begin{aligned} S_{ 1 1} = [ 2\nu /( 1- 2\nu ) + 2 {\text{sin}}^{ 2} \delta { \sin }^{ 2} \phi_{\text{s}} ]{ \sin }\gamma - ({ \sin }\delta { \cos }\lambda_{\text{s}} {\text{sin2}}\phi_{\text{s}} + {\text{sin2}}\delta { \sin }\lambda_{\text{s}} { \sin }^{ 2} \phi_{\text{s}} ){ \cos }\gamma \hfill \\ S_{ 2 2} = [ 2\nu /( 1- 2\nu ) + 2 {\text{sin}}^{ 2} \delta { \cos }^{ 2} \phi_{\text{s}} ]{ \sin }\gamma + ({ \sin }\delta { \cos }\lambda_{\text{s}} {\text{sin2}}\phi_{\text{s}} - {\text{sin2}}\delta { \sin }\lambda_{\text{s}} { \cos }^{ 2} \phi_{\text{s}} ){ \cos }\gamma \hfill \\ S_{ 3 3} = [ 2\nu /( 1- 2\nu ) + 2 {\text{cos}}^{ 2} \delta ]{ \sin }\gamma + {\text{sin2}}\delta { \sin }\lambda_{\text{s}} { \cos }\gamma \hfill \\ S_{ 1 2} = - { \sin }^{ 2} \delta {\text{sin2}}\phi_{\text{s}} { \sin }\gamma + ({ \sin }\delta { \cos }\lambda_{\text{s}} {\text{cos2}}\phi_{\text{s}} + {\text{sin2}}\delta { \sin }\lambda_{\text{s}} {\text{sin2}}\phi_{\text{s}} / 2){ \cos }\gamma \hfill \\ S_{ 1 3} = {\text{sin2}}\delta { \sin }\phi_{\text{s}} { \sin }\gamma - ({ \cos }\delta { \cos }\lambda_{\text{s}} { \cos }\phi_{\text{s}} + {\text{cos2}}\delta { \sin }\lambda_{\text{s}} { \sin }\phi_{\text{s}} ){ \cos }\gamma \hfill \\ S_{ 2 3} = - {\text{sin2}}\delta { \cos }\phi_{\text{s}} { \sin }\gamma - ({ \cos }\delta { \cos }\lambda_{\text{s}} { \sin }\phi_{\text{s}} - {\text{cos2}}\delta { \sin }\lambda_{\text{s}} { \cos }\phi_{\text{s}} ){ \cos }\gamma , \hfill \\ \end{aligned}$$
(8)

where ν is Poisson’s ratio.

Figure 2 presents the energy radiation patterns of the AE source for different tensile angles. As shown in Fig. 2, the P, SV and S wave radiation patterns of the AE source change significantly with the tensile angle, while the SH wave radiation patterns are not sensitive to the change of the tensile angle. When the tensile angles are the opposite, the energy radiation patterns of the AE source have the same shape but the opposite motion direction of the medium. For a specific tensile angle, the radiation energy of the P and SV waves in different directions changes dramatically. Therefore, the accurate tensile angle is the foundation for quantifying the radiation energy of the AE source more accurately.

Fig. 2
figure 2

Energy radiation patterns of P (a), SH (b), SV (c) and S (d) (\(R_{\text{S}}^{2} \, = \,R_{\text{SH}}^{2} \, + \,R_{\text{SV}}^{2} \,\)) waves for different tensile angles assuming rock Poisson ratio ν = 0.22 and λs = 0°. Different colors represent different motion amplitudes. The plane the microfracture lies on is shown as a subtransparent gray plane, the motion vector of the microfracture plane is marked by a red arrow, and the motion vector projected on the fault plane is shown using a black arrow

Full size image

Having the energy radiation pattern coefficients, the average energy radiation pattern coefficients 〈RC〉2 can be calculated as follows:

$$\langle R_{\text{C}} \rangle^{2} = \frac{1}{4\pi }\int_{0}^{2\pi } {\int_{0}^{\pi } {R_{\text{C}}^{2} } } \cos \delta {\text{d}}\delta {\text{d}}\phi_{\text{s}} .$$
(9)

Figure 3 presents the relation between the average energy radiation pattern coefficients 〈RC〉2 and the tensile angle for rock Poisson ratio ν = 0.22. As shown in Fig. 3, the distribution curves of 〈RC〉2 are axially symmetric with tensile angle γ = 0°. The 〈RSH〉2 and 〈RSV〉2 not only change with the tensile angle γ, but also change with the slip angle λs, while the 〈RP〉2 and 〈RS〉2 only change with the tensile angle γ. The minimum and maximum of 〈RP〉2 and 〈RS〉2 are located at tensile angle γ = 0° and γ = ± 90°, respectively. As the tensile angle γ changes from 0° to ± 90°, the 〈RP〉2 increases from 0.266 to 2.465, and the 〈RS〉2 increases from 0.399 to 0.533. The intersection of 〈RP〉2 and 〈RS〉2 is located at tensile angle γ = ± 14.7°; that is, the radiation energy of the P wave is higher than that of the S wave when the tensile angle is γ > 14.7° or γ < − 14.7°, while the radiation energy of the P wave is lower than that of the S wave when the tensile angle is − 14.7° < γ < 14.7°.

Fig. 3
figure 3

Relation between the average energy radiation pattern coefficients (〈RP〉2, 〈RSH〉2, 〈RSV〉2, 〈RS〉2) (〈RS〉2 = 〈RSH〉2 + 〈RSV〉2) and the tensile angle for rock Poisson ratio ν = 0.22. The coefficients 〈RP〉2 and 〈RS〉2 are shown using solid lines, and 〈RSH〉2 and 〈RSV〉2 are shown using thin dotted and thick chain dashed lines, respectively

Full size image

2.3 AE Source Radiation Energy Calculation

Having the energy radiation pattern coefficient R2C and average energy radiation pattern coefficients of P, SH and SV waves 〈RC〉2, we can use them together with the radiation energy flux received by an AE sensor to assess the radiation energy of the AE source.

The AE sensor used in the laboratory experiment is uniaxial, so the radiation energy flux received by AE sensor i can be expressed as follows:

$$J_{\text{ti}} = J_{\text{Pi}} \cos^{2} \alpha_{\text{Pi}} + J_{\text{SHi}} { \cos }^{2} \alpha_{\text{SHi}} + J_{\text{SVi}} { \cos }^{2} \alpha_{\text{SVi}} ,$$
(10)

where Jti is the radiation energy flux received by AE sensor i; JPi, JSHi and JSVi are the radiation energy flux of the P, SH and SV waves at the position of the AE sensor i; αPi, αSHi and αSVi are the angle between t (direction vector of AE sensor i) and r, φ, θ.

For a specific AE source, the radiation energy flux of the P, SH and SV waves at the position of the AE sensor i only depend on the distance between the AE source and the AE sensor and the corresponding radiation pattern; therefore, the relation between JPi, JSHi and JSVi can be expressed by

$$J_{\text{ai}} = \frac{{R_{\text{i}}^{2} }}{{R_{\text{Pi}}^{2} }}J_{\text{Pi}} = \frac{{R_{\text{i}}^{2} }}{{R_{\text{SHi}}^{2} }}J_{\text{SHi}} = \frac{{R_{\text{i}}^{2} }}{{R_{\text{SVi}}^{2} }}J_{\text{SVi}} ,$$
(11)

where Ri is the distance between AE source and AE sensor i; Jαi is a parameter set for the subsequent convenience of calculation, and it represents the radiation energy flux when both Ri and RPi, RSHi, RSVi are equal to 1.

Substituting Eq. (11) into Eq. (10), we can obtain Jαi by Eq. (12) as follows:

$$J_{\text{ai}}\, { = }\,{{J_{\text{ti}} R_{\text{i}}^{2} } \mathord{\left/ {\vphantom {{J_{\text{ti}} R_{\text{i}}^{2} } {\sum\limits_{{C = {\text{P,SH,SV}}}} {R_{\text{Ci}}^{2} { \cos }\alpha_{\text{Ci}} } }}} \right. \kern-0pt} {\sum\limits_{{C = {\text{P,SH,SV}}}} {R_{\text{Ci}}^{2} { \cos }\alpha_{\text{Ci}} } }}.$$
(12)

Having Jαi and substituting Eq. (11) into Eq. (1), the energy radiated by a given wave type from an AE source can be calculated as follows:

$$E_{\text{C}} = 4\pi \rho \bar{J}_{\text{ai}} (V_{\text{C}} \langle R_{\text{C}} \rangle^{2} ),$$
(13)

where \(\bar{J}_{\text{ai}}\) is the average of the \(J_{\text{ai}}\). For the small denominator in Eq. (12) (e.g., the AE sensor is close to the nodal plane), a small error would result in a large error in the calculation of AE source radiation energy. Therefore, if the denominator in Eq. (12) is < 0.2, the sensor would be not used to calculate \(\bar{J}_{\text{ai}}\).

3 AE Tests of Granitic Gneiss Specimen

3.1 Experimental System

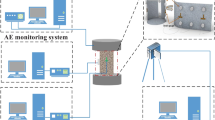
The experimental system consists of the load device and monitoring apparatus. The load device used the computer-controlled electrohydraulic Servo Press TAW-2000KN. The PCI-2 AE test apparatus produced by Physical Acoustics Corp. was applied to collect the AE signals induced by granitic gneiss. Since an insufficient frequency bandwidth would result in a severe underestimation of the radiation energy, eight wideband Nano30 sensors were arranged on the specimen surface. The sensor coordinates are shown in Table 1. In this experiment, petroleum jelly was used to lubricate the loading plates of the press machine; to reduce the end friction effect, a 45-dB threshold was selected for all sensors, and the preamplifier gain was 40 dB. Each waveform was digitized into 1024 samples at a sampling rate of 1 MHz.

Table 1 Sensor coordinates (the center point of the bottom surface of the rock specimen is the origin of the coordinates)
Full size table

3.2 Rock Specimen and Loading Control

The granitic gneiss specimen (50 × 50 × 100 mm) used in the AE experiment was collected from the Shirengou iron mine, Tangshan City, Hebei Province, China. A relatively detailed description of the mine and the mineral composition of the granitic gneiss can be found in the literature (Zhang et al. 2015, 2018). Uniaxial loading was conducted on the specimen, and the loading rate was 0.001 mm/s. The elasticity modulus, Poisson ratio, uniaxial compressive strength, P wave velocity and S wave velocity are 25.88 GPa, 0.22, 110.84 MPa, 4892 m/s and 2970 m/s, respectively.

3.3 Anisotropy of the Rock Specimen

To measure the anisotropy of the unstressed granitic gneiss rock and the stress-induced anisotropy, the velocity in vertical and horizontal directions is measured before and during the loading of another granitic gneiss specimen. The array of wave velocity transducers and the change of wave velocity during the loading process are shown in Fig. 4.

Fig. 4
figure 4

Wave velocity measurement experiment. a The array of the wave velocity transducers and wave propagation path between transducers in vertical and horizontal directions. b The change of wave velocity during the loading process for the granitic gneiss specimen. The gray cylinders represent wave velocity transducers, and the solid differently colored lines are the wave propagation path between transducers in vertical and horizontal directions. The wave velocity is measured once every 20 MPa. Because the failure of this granitic gneiss specimen occurred at 86 MPa, the last wave velocity measurement is at 80 MPa

Full size image

During the loading process, the wave velocity in both the vertical and horizontal directions increases at first and then decreases. The variation amplitudes of the wave velocity in the vertical and horizontal directions are approximately 76 m/s, 54 m/s and 88 m/s, respectively. The variation amplitudes are < 2% of the initial velocity (unstressed specimen); therefore, the wave velocity can be assumed as constant for simplification. The maximum wave velocity ratio of the unstressed specimen is 1.018. The maximum wave velocity ratio of the stressed specimen is 1.032 and occurs at 80 MPa. For unstressed rock and stressed rock, the maximum wave velocity ratios are both close to 1. Therefore, both the anisotropy of the unstressed rock specimen and the stress-induced anisotropy are not obvious, and the rock can be considered as isotropy for simplification.

3.4 Failure Mode of the Granitic Gneiss Specimen

When the specimen is in failure, two macroscopic fracture surfaces (indicated by I and II in Fig. 4) are formed and divide the specimen into three parts. The I fracture surface extends from the upper left to lower right. The morphology of the upper half part of the fracture surface (55–100 mm in elevation) is complex, while the morphology of the lower half part (0–55 mm in elevation) is close to the a plane and its dip angle is approximately 50°. The II fracture surface extends from the top surface to the I fracture surface; the morphology is close to a plane, and the dip is close to 90° (Fig. 5).

Fig. 5
figure 5

Failure mode of the rock specimen. a Photos of the ruptured specimen. b Morphology of macroscopic fracture surfaces. The solid line is the intersection line between the fracture surfaces and the specimen surface, the dashed line is the intersection line of the two macroscopic fracture surfaces, and the small gray cylinders represent AE sensors

Full size image

4 Experimental Results

4.1 The Stability Estimation of the Moment Tensors

To estimate the stability of the AE source moment tensors, a jackknife test was conducted. The error of the moment tensor is calculated by

$${\text{ERR}} = \frac{1}{N}\mathop \sum \limits_{j = 1}^{N} \frac{{\sqrt {\mathop \sum \nolimits_{i = 1}^{3} (M_{i} - M_{ij}^{t} )^{2} } }}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{3} M_{i}^{2} } }},$$
(14)

where Mi (i = 1, 2, 3) is the eigenvalue of the moment tensor inverted by all the sensors; \(M_{ij}^{t}\) (j = 1, 2,…, N) is the eigenvalue of the moment tensor inverted without the sensor j in the jackknife test.

The ERR of AE sources for the jackknife test ranges from 1.64 × 10−5 to 7.36, and the ERR of most AE sources is < 0.4 (Fig. 6). The AE sources poorly covered by the sensor array account for 53.8%. Among the AE sources with an ERR < 0.2, the poorly covered AE sources account for 50.7%, which is a little lower than their proportion to the AE sources. This indicates that the poor coverage of sensors on the AE sources indeed has some negative effects on the AE source moment tensors and results in a higher ERR. However, the difference in ERR between the well and poorly covered AE sources is still small. Therefore, whether the AE sources are well covered by the sensor array or not, the AE sources with an ERR < 0.2 are used to analyze the failure process of the rock specimen.

Fig. 6
figure 6

ERR distributions of the AE source moment tensors in the jackknife test. The AE sources inside the sensor array and > 5 mm away from the surface of the rock specimen can be considered as well covered by the sensor array. The other AE sources are considered as poorly covered by the sensor array. The ERR distributions of well covered and poorly covered AE sources are shown by light blue and yellow, respectively

Full size image

4.2 Evolution of the Radiation Energy During the Rock Failure Process

Using the method presented in Sect. 2, the radiation energy of AE sources can be calculated. Then, the evolution of the radiation energy during the rock failure process can be analyzed.

The changes in stress and accumulative radiation energy with time are shown in Fig. 7. During the failure process of the specimen, the accumulative radiation energy of AE sources experiences a sudden seven times increment; they successively occurred at 460.5 s, 498.9 s, 504.0 s, 514.9 s, 542.2 s, 599.8 s and 615.0 s. The proportions of the seven sudden increments to the total radiation energy are 6.9%, 6.2%, 54.3%, 5.0%, 20.2%, 1.4% and 2.2%, respectively. The energy release of the rock specimen is characterized by an intermittent sudden increment, suggesting the obvious brittleness of the rock specimen.

Fig. 7
figure 7

Changes of stress and AE accumulative radiation energy with time. The time nodes (a), (b), (c) and (d) correspond to 463 s, 515 s, 543 s and 630 s, respectively

Full size image

The spatial distribution of AE sources with different radiation energies during the rock failure process is shown in Fig. 8. The different colors indicate the different radiation energies and the radiation energy change from 1.25E − 6 to 0.52 J as the colors turn from purple to red. The high radiation energy AE source is colored red and yellow, the intermediate radiation energy AE source is colored green, and the low radiation energy AE source is colored blue and purple. The deadline for the time range in Figs. 8a and 6b–d correspond to the time nodes (a), (b), (c) and (d) in Fig. 7.

Fig. 8
figure 8

Spatial distribution of AE sources with different radiation energies during the failure process of the specimen. The spheres represent the AE sources, and the different colors of spheres indicate the different radiation energies

Full size image

According to the location results (Fig. 8), the AE sources trended from the top and bottom to the middle of the specimen. Before 463 s, AE sources are mainly concentrated in the top and bottom of the specimen (Fig. 8a). At 460.5 s, the first AE source with a high radiation energy occurred (Figs. 8a, 9a), corresponding to approximately 78% of the peak strength (Fig. 7). Then, several high-radiation-energy AE sources successively occurred around the first AE source with a high radiation energy, forming a high-radiation-energy cluster region in the bottom of the specimen (Fig. 8b). From 463 s, the number of AE sources with intermediate radiation energy begins to increase in the middle of the specimen (Fig. 8b, c). At 542.2 s, another AE source with a high radiation energy occurred in the high-radiation-energy cluster region (Figs. 8c, 9b); in the meantime, a significant stress drop (approximately 29 MPa) was observed in Fig. 7, suggesting the lower part of fracture I has partially formed (Fig. 5). The partially formed fracture I would transfer partial stress from the lower part to the middle and upper parts of the specimen, resulting in the AE sources migrating to the middle and upper parts of the specimen (Fig. 8d). At 615.0 s, the last AE source with a high radiation energy occurred in the middle of the specimen (Figs. 8d, 9c). After approximately 1.9 s, the specimen failure occurred (Fig. 7d).

Fig. 9
figure 9

Spatial distribution of part AE sources. a AE sources in the area outlined by solid lines in Fig. 8a. b AE sources in the area outlined by solid lines in Fig. 8c. c AE sources in the area outlined by solid lines in Fig. 8d

Full size image

Comparing the fracture surfaces and AE source locations (Fig. 8d) shows that AE sources with low or intermediate radiation energy were not only located near the fracture surfaces, but also far away from them, while the AE sources with high radiation energy were only located near the fracture surfaces. This kind of phenomenon was also observed by Chang et al. (2004), who suggest these AE sources with high radiation energy greatly affect the formation of the fracture surfaces. According to the spatiotemporal evolution process of these AE sources with high radiation energy, it can be inferred that the macroscopic fractures might propagate from the lower to upper part of the specimen.

Figure 10 presents the number of AE sources and accumulative radiation energy in each radiation energy interval. The radiation energy of AE sources span seven orders of magnitude; 94% AE sources are within the range of 10−7 to 10−2 J, while their accumulative radiation energy is only 0.07 J, which accounts for approximately 7.3% of the total radiation energy. On the contrary, the number of AE sources with radiation energy > 0.02 J is only 6, while their accumulative radiation energy is 0.91 J, which accounts for approximately 94.8% of the total radiation energy. The maximum AE source radiation energy is 0.52 J, accounting for > 50% of the total radiation energy. This indicates that the radiation energy is mainly released by a few high-radiation-energy AE sources rather than many low-radiation-energy AE sources. Combined with the change of radiation energy in the time domain (Fig. 7), it can be further inferred that the sudden increment of radiation energy in time domain is mainly due to the occurrence of high-radiation-energy AE sources rather than the occurrence of many low-radiation-energy AE sources in a short time.

Fig. 10
figure 10

Number of AE sources (red squares) and accumulative radiation energy (blue rhombuses) in each radiation energy interval. Each interval ranges from logE − 0.5 to logE + 0.5

Full size image

5 Discussion

Based on the tensile angle, the microfractures can be classified into five types as follows:

$$\left\{ {\begin{array}{*{20}c} &{ - 90^{ \circ } \le \gamma < - 60^{ \circ } ,\quad {\text{Compression }}} \\ &{ - 60^{ \circ } \le \gamma < - 30^{ \circ } ,\quad {\text{Shear-compression }}} \\ &{ - 30^{ \circ } \le \gamma \le 30^{ \circ } ,\quad {\text{Shear }}} \\& {30^{ \circ } < \gamma \le 60^{ \circ } ,\quad {\text{Shear-tensile }}} \\& {60^{ \circ } < \gamma \le 90^{ \circ } ,\quad {\text{Tensile }} . } \\ \end{array} } \right.$$
(15)

The statistical distribution of AE sources with different tensile angles is shown in Fig. 11, and the different fracture types are indicated by different background colors. The compression, shear compression, shear and shear tensile are shown in red, yellow, green and purple background colors, respectively. The tensile angles of the AE sources range from − 70° to 60°, and the shear microfractures are in the majority, accounting for > 70%. Therefore, the microfractures of specimens under the uniaxial compression condition are dominated by shear type.

Fig. 11
figure 11

Number of sources in each tensile angle interval. Each interval ranges from γ − 5° to γ + 5°. The compression, shear compression, shear and shear tensile are shown in red, yellow, green and purple background colors, respectively

Full size image

According to the classification result, the ratios of different fracture type changes with time during the failure process of the specimen are shown in Fig. 12, and the spatial distribution of AE sources with different fracture types is shown in Fig. 13. At the beginning of loading, the shear compression microfractures are in the majority (Figs. 12a, 13a). However, the ratio of shear compression microfractures rapidly decreases as the stress increases, and the ratio of shear-type microfractures increases rapidly (Fig. 12a). Then, the decreasing rate of the shear compression microfracture ratio and the increasing rate of the shear microfracture ratio start to slow down (Fig. 12b). At approximately 224 s (38.2% peak stress), the ratio of shear microfractures begins to exceed the shear compression microfractures, and shear becomes the dominant microfracture mechanism. The transformation of the main fracture mechanism can also be observed by the significantly decreased number of shear compression AE sources in Fig. 13a, b. As the stress continues to increase, the ratio of shear compression microfractures rapidly increases again, and the ratio of other types of microfractures continues to decrease in a fluctuating way (Fig. 12c, d). After the peak stress, the ratio of shear and shear compression microfractures tends to be stable (Fig. 12e).

Fig. 12
figure 12

Stress and ratios of different fracture type changes with time. The time nodes (a), (b), (c), (d) and (e) correspond to 78 s, 429 s, 515 s, 543 s and 630 s, respectively

Full size image
Fig. 13
figure 13

Spatial distribution of AE sources with different tensile angles during the failure process of the specimen. The AE sources with a high radiation energy are enlarged. The first AE source with a high radiation energy occurred during the significant stress drop, and the last AE source with a high radiation energy is marked by black arrows in c, d and e, respectively

Full size image

There are six AE sources with high radiation energy occurring at the high stress level, and four of them are shear type (the larger spheres in Fig. 13c–e), indicating the microfracture mechanism of the AE sources with a high radiation energy is also dominated by shear.

From the above, it can be seen that the main microfracture mechanism is shear compression at the low stress level, while it changes to shear as the stress increases.

6 Conclusions

In this article, the radiation energy of AE sources is calculated based on the relation between the radiation pattern and tensile angles. Then, the spatiotemporal evolution of the AE source radiation energy and microfracture mechanism are analyzed during the failure process of the granitic gneiss specimen. The following conclusions can be drawn.

1. A basic theoretical calculation is conducted to model the influence of tensile angles on the energy radiation pattern and the average energy radiation pattern coefficients of the AE source. The energy radiation patterns and average energy radiation pattern coefficients of the P and S wave change significantly with the tensile angle. An accurate tensile angle is the foundation for quantifying the radiation energy of the AE source more accurately.

2. During the failure process of the granitic gneiss specimen, the radiation energy release of the rock specimen is characterized by an intermittent sudden increment in the time domain, showing the specimen is obviously brittle. The sudden increment of radiation energy in time domain is mainly due to the occurrence of high-radiation-energy AE sources rather than the occurrence of many low-radiation-energy AE sources in a short time.

3. Under the uniaxial compression condition, the main microfracture mechanism of the granitic gneiss specimen is shear compression at the low stress level; as the stress increases the main microfracture mechanism changes to shear. When the specimen is at failure, the shear microfractures account for > 70%.