Simulating Hydraulic Fracturing: Failure in Soft Versus Hard Rocks

Abstract

In this contribution we discuss the dynamic development of hydraulic fractures, their evolution and the resulting seismicity during fluid injection in a coupled numerical model. The model describes coupling between a solid that can fracture dynamically and a compressible fluid that can push back at the rock and open fractures. With a series of numerical simulations we show how the fracture pattern and seismicity change depending on changes in depth, injection rate, Young’s Modulus and breaking strength. Our simulations indicate that the Young’s Modulus has the largest influence on the fracture dynamics and the related seismicity. Simulations of rocks with a Young’s modulus smaller than 10 GPa show dominant mode I failure and a growth of fracture aperture with a decrease in Young’s modulus. Simulations of rocks with a Young’s modulus higher than 10 GPa show fractures with a constant aperture and fracture growth that is mainly governed by a growth in crack length and an increasing amount of mode II failure. These results are very important for the prediction of fracture dynamics and seismicity during fluid injection, especially since we see a transition from one failure regime to another at around 10 GPa, a Young’s modulus that lies in the middle of possible values for natural shale rocks.

1 Introduction

Hydraulic fracturing is the process of creating cracks within a rock volume by increasing the fluid pressure until the rock fractures (Hubbert and Rubey 1959; Nordgren 1972; Valko and Economides 1995). It plays an important role in the geophysical, geomechanical and structural mechanics of the Earth’s crust in a wide variety of geological settings (Fyfe 2012) and has a growing interest in geotechnical and industrial applications (Baria et al. 1999; Urbancic et al. 1999; Warpinski et al. 1999). A hydrofracture develops if the fluid overpressure exceeds the sum of the least compressive stress and the tensile strength of the rock (Cobbold and Rodrigues 2007). During industrial hydrofracturing large quantities of fluid are pumped into a finite pore volume generating an overpressure and an outward push, which will lead to brittle failure and the development of fractures (Pearson 1981; Zoback and Harjes 1997; Niebling et al. 2012).

Fractures typically grow once the critical stress intensity factor is reached for materials (Inglis 1913; Griffith 1921; Irwin 1953). The stress intensity factor can be viewed as the prefactor of the stress singularity around a crack tip in an elastic rock, which is dependent on the crack length and its opening width or aperture (Anderson 2005). At this point the rock properties such as the Young’s modulus and Poisson ratio become important because they will influence the elastic response of the rock to the stress around the crack (Ohta et al. 1992; Tandaiya et al. 2008). Especially the Young’s modulus is very variable depending on the rock type. It can vary from around 6 GPa for clay minerals (Prasad et al. 2002), to up to 8 GPa–50 GPa for shale (Sayers 2013) and up to 70 GPa for limestones (Sachpazis 1990). The Young’s modulus is the main component, which defines the compressibility of the material and thus has a major role in controlling the shape of the fracture. If the rock is very soft the crack will become elliptical with a large aperture, whereas it remains thin when the rock is hard.

Fracturing usually occurs in extensional or shear mode depending on the setting and balance between the differential stress τ = σ¹− σ³ as well as the least compressive stress in a rock if it becomes tensile (Cobbold and Rodrigues 2007). In most cases in the Earth’s crust, a triaxial stress distribution due to the gravitational loading prompts shear opening and for tensile fractures to develop an additional stress is required. This stress is thought to come from fluid overpressure that builds up in the pore space and pre-existing fractures in the rock (Sachau et al. 2015), or is increased during hydraulic pumping.

Stresses that build up in a fluid saturated rock must be divided into stresses that act on the solid and fluid and those that act only on the solid (Von Terzaghi 1925). Stresses acting only on the solid are termed effective stress $\left( {\sigma_{ij}^{'} } \right)$ and can be described by Terzhagi’s law:

$$ \sigma_{ij}^{'} = \sigma_{ij} - P_{f} \delta_{ij}, $$

(1)

where $\sigma_{ij}$ is the stress tensor, $P_{f}$ is fluid pressure and $\delta_{ij}$ is Kronecker delta with positive sign conversion. The most common way to illustrate the 2D stress state within a rock is by using a Mohr diagram plotting shear against normal effective stress, with σ¹ and σ³ at the right hand side of the diagram in the compressive state. $P_{f}$ reduces the value of the effective stress and pushes the Mohr circle towards the left hand side. Once the circle transects the Mohr–Coloumb failure envelope in the tensile regime, the rock will fail (Fig. 1).

Fig. 1

a Standard Mohr circle diagram of effective stress showing how an increase in fluid pressure shifts the Mohr circle from its initial compressive stress state at the right hand side to the left into the tensile regime leading to failure; note that the differential stress remains constant. b Mohr circle diagram of effective stress in the model illustrating the anisotropy of stress changes when fluid overpressure or pressure gradients are taken into account. Locally the system will fluidize, the differential stress goes to zero or becomes very small leading to mainly mode I failure

However, this representation is an oversimplification and Cobbold and Rodrigues (2007) and Ghani et al. (2015) have shown with experiments and simulations that an increase in fluid overpressure in a simple sedimentary basin will lead to a local decrease of the differential stress of the effective stress tensor due to seepage forces. In this case the fluid overpressure has an anisotropic effect on the effective stresses. The Mohr circle for the effective stress state as such is still moving towards the left hand side into the regime of tensile failure, however the circle is shrinking at the same time.

Hydrofracturing is a complex interaction process and consists of at least a two way feedback between the fluid and the solid. Typically rocks are porous and thus the fluid overpressure can diffuse into the rock. According to Biot’s poroelastic theory (Detournay and Cheng 1993) this pressure diffusion influences the effective stress, since the fluid overpressure is reduced. Ghani et al. (2013) have shown that the feedback between fluid and solid leads to an initial build-up of fluid overpressure and diffusion of fluid into the rock, an increase in pressure gradient and final fracturing. The fractures in turn enhance the permeability and allow the fluid overpressure to be reduced. Existing fractures may even be pushed open by the developing fluid pressure gradients leading to a more dynamic system of overpressure release (Sachau et al. 2015). It is important to understand the full scope of this dynamic feedback in order to understand hydrofracture dynamics.

When studying active hydrofractures in the Earth’s crust, microseismic activity has been used to map the fracture’s height, extent, orientation as well as magnitude of the fracturing event in order to monitor fractures during geothermal energy extraction (Baria et al. 1999), reservoir stimulation (Urbancic et al. 1999), and waste reinjection (Warpinski et al. 1999). Laboratory experiments of acoustic emission observation during hydrofracturing (Scott Jr et al. 2000; Groenenboom and van Dam 2000) as well as modelling of such emissions (Guest and Settari 2010; Murphy et al. 2013; Rutqvist et al. 2013) can also be used to better understand the fracturing process and its aspects such as direction of fracture propagation and fluid injection induced static stress perturbation. Inversion of seismic data allows to determine the moment tensor during hydrofracturing and thus the movement of the fracture walls relative to each other (Hazzard and Young, 2002; Guest and Settari 2010; Vavryčuk 2011). It is of vital importance to understand how different rock types break during hydrofracturing, what seismic signals are emitted during this process and in turn how microseismicity can be used to monitor fluid movement and hydrofracturing.

In order to understand the solid–fluid feedback and associated seismic signals during hydrofracturing in a variety of rock types we are using a numerical model (Ghani et al. 2013, 2015) to analyse seismic aspects associated with fracture opening, mode of fracturing as well as magnitude of fracture events under variable extrinsic (overburden load, fluid flux) as well as intrinsic (Young’s Modulus, breaking strength) parameters. A more detailed account of the initial model design can be gained from Ghani et al. (2013, 2015). In this work we equipped the given model with a code module designed to track individual particles and thus analyse dynamics of the fracture opening and associated seismicity.

2 Methodology

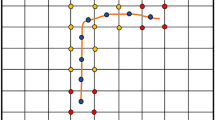
In order to numerically simulate the development of hydrofractures we employ a discrete element model (Latte), which is built upon a 2D triangular setup coupled with a square grid representing the fluid (Fig. 2) and is part of the “Elle” package (Bons et al. 2007).

Fig. 2

Schematic illustration of the DEM (discrete element model) grid overlying the fluid pressure nodes. The DEM grid is triangular whereas the fluid grid is square and larger than the DEM. Both grids are mapped onto each other using tent functions to minimize grid effects. The fluid grid is stationary whereas the DEM grid can move

In the model the triangular network is constructed of disk-shaped particles of constant radius interconnected by springs (discrete element model or DEM). Such model configuration in 2D mimics the isotropic elastic behavior of solid materials and can be used to model deformation problems in systems described by linear elastic theory (Flekkøy et al. 2002). The intrinsic stiffness coefficient k is governed by the macro-scale parameters E and v (Young’s modulus and Poisson ratio) through the consistency measures of strain energy between the 2D elastic lattice of the triangular network and solid continua (Flekkøy et al. 2002):

$$ k = \frac{\surd 3}{2}El, $$

(2)

where l stands for the thickness of the two-dimensional model. The model runs as a step function and therefore plain strain deformation is produced for each time step Δt. At the end of every time step all springs are checked and if the predetermined stress threshold for a spring is reached, it breaks releasing elastic energy, the spring is removed from the lattice and a fracture forms. The elastic energy contained in the removed spring is further redistributed among the neighboring springs via the relaxation algorithm. The breakage occurs once either the critical tensile normal stress σ₀ or the critical shear stress τ₀ is reached. In order to include combinations of tensile and shear failure it is assumed that the critical strain value E_c is seen as a sum of tensile (U_t) and shear (U_c) energies (Sachau and Koehn 2014). There are separate critical values for both tensile (Ec, σ) and shear (Ec, τ) criterions and their relationship can be expressed as (Fig. 3):

Fig. 3

Calculation of the Moment Tensor after failure takes place (spring between particles breaks). The figure shows the decomposition of total particle displacement (U_tot) into shear (U_s) and tensile components (U_t), which are respectively parallel and perpendicular to the imagined failure surface. The failure surface lies perpendicularly to the broken elastic spring. Lastly, as we have both pure tensile and pure shear movements, we introduce the concept of movement mode ratio which is defined as U_s/U_t. In this case ratios smaller than 1 are dominated by extensional fracturing whereas ratios larger than 1 become shear fracture dominated

$$ \frac{{U_{s} }}{{E_{c} }} + \frac{{U_{t} }}{{E_{c} }} = \left( {\frac{{\sigma_{n} }}{{\sigma_{0} }}} \right)^{2} + \left( {\frac{\tau }{{\tau_{0} }}} \right)^{2} = 1, $$

(3)

which describes an ellipse in σ_n–τ space (Sun and Jin 2012). Therefore, the failure can occur as a combination of both shear and tensile factors, or if one of the two components is absent, it will be equivalent to pure tensile or pure shear failure.

The 2D DEM lattice is overlain by a square grid of fluid pressure nodes. The fluid pressure diffusion is derived from mass conservation of the fluid and solid using Darcy’s law to express the seepage velocity through the porous medium (Ghani et al. 2013, 2015):

$$ \phi \beta \left( {\partial_{t} P + u_{s} \nabla \cdot P} \right) = \nabla \cdot \left[ {\left( {1 + \beta P} \right)\frac{K}{\mu }\nabla P} \right] - \left( {1 + \beta P} \right)\nabla \cdot u_{s}, $$

(4)

where φ is the porosity, β is the fluid compressibility, P is the fluid pressure deviation from hydrostatic, and u_s is the solid velocity field. K and μ stand for permeability and fluid viscosity respectively. The left hand side of the equation is the Lagrangian derivative of pore pressure following the solid matrix, the first term on the right expresses the Darcy fluid pressure diffusion relative to the particles, the last term is a source term. The source term expresses pressure change as a function of a change in the solid if particles move apart in the local reference of the Darcy flow (Ghani et al. 2013). The Kozeny-Carman relation is used to express K as a function of local porosity φ:

$$ K\left( \rho \right) = \frac{{d^{2} \left( \phi \right)^{3} }}{{180\left( {1 - \phi } \right)^{2} }}, $$

(5)

where d is the particle diameter and 1/180 is an empirical constant for packing of spheres (Carman 1937; Ghani et al. 2013, 2015).

Deformation mechanics are driven by the momentum exchange between the two phases, solid and fluid. The total force applied on the particles is compiled from three main constituents:

$$ F_{n}^{i} = f_{e} + f_{p} + f_{g}, $$

(6)

where $f_{e}$ is the interaction force between the particles (either due to a connection with the spring or repulsive), fluid pressure force $f_{p}$ and external force $f_{g}$ applied due to the gravity and large scale tectonic strain on the external boundaries. In this instance $f_{e}$ is expressed as a function of the spring elasticity constant k and an equilibrium distance between particles a, which equals the sum of the initial radii of the two connected particles:

$$ f_{e} = \mathop \sum \limits_{j} k_{ij} \left( {\left| {\vec{a}_{ij} } \right| - \left| {\vec{x}_{i} - \vec{x}_{j} } \right|} \right) \cdot \hat{n}_{ij}, $$

(7)

where x_i and x_j are the positions of the connected particles, $k_{ij}$ is the elastic (spring) constant of their contact, $\hat{n}_{ij}$ is unit vector pointing from the centroid of particle i to particle j and the sum runs over all the connected neighbours j. Once the change in relative particle positions occurs, the resulting force can be decomposed into tensile and shear components. Further details on this methodology can be found in work by Sachau & Koehn (2014).

The fluid force f_p that acts on the surface normal dA of the unit cell is a function of the fluid flow due to the pressure gradient and is described as:

$$ f_{p} = - \int P_{0} \hat{n}dA ,$$

(8)

where P₀= P + ρ_fgz is the local total fluid pressure, z depth, ρ_f density of the fluid and g gravity constant. It is the sum of a term due to viscous forces arising in the case of fluid flow through the solid, $- \smallint P\hat{n}dA$, and a buoyancy term, $- \smallint \rho f gz \hat{n}dA$.

Lastly the gravity force that is acting on every particle is calculated according to:

$$ f_{i}^{g} = \rho_{s} \pi R_{i}^{2} gC ,$$

(9)

where $\rho_{s}$ denotes the solid mass density, $R_{i}^{2} = r_{i}^{2} S$, where S is the dimension of the real system (1000 m), g is the gravitational acceleration vector and C = 2/3 is a scale factor (after Ghani et al. 2015) used to acquire a compatible one dimensional lithostatic stress that can be applied to an isotropic 2D linear elastic solid.

The buoyancy term itself can be written according to Ostrogradsky’s theorem as $- \int \rho f gz \hat{n}dA = - \rho_{f} \pi R_{i}^{2} gC$ (Mory 2013), so that the total effect of gravity, the direct one plus the buoyancy effect, is $\left( {\rho_{s} - \rho_{f} } \right)\pi R_{i}^{2} gC$, which incorporates the effects that gravity has on both solid and fluid: this drives the effective stress field σ’ = (ρ_s− ρ_f)gz in the system in a hydrostatic situation (Niebling et al. 2010a).

The solid porosity that is used for the fluid pressure evolution in the fluid lattice is described by the solid mass fraction of solid particles within a fluid cell and changes due to compression, solid movement or fracturing. The solid movement itself between two deformation steps affects the source term in Eq. 4.

Finally, the model is set up in a way that the fluid continuum grid overlies the DEM so that their boundaries coincide. Since the fluid grid is set to be twice as large as the DEM matrix, the model uses the “cloud in the cell” method to facilitate the two-way interaction between the porous matrix and the hydrodynamic phase (Ghani et al. 2013; Johnsen et al. 2006; Vinningland et al. 2007, 2012). The interaction between the porous solid and hydrodynamic phases is accomplished through the projection operator from the discrete space to the fluid grid space by the help of the smoothing function s(r_i− r₀), which distributes the weight of the particle over the four nearest fluid grid nodes:

$$ s\left( {r - r_{0} } \right) = \left\{ {\begin{array}{l} {\left( {1 - \frac{{w_{1} }}{\Delta x}} \right)\left( {1 - \frac{{w_{2} }}{\Delta z}} \right) \quad if \, \, w_{1} < \Delta x, w_{2} < \Delta z} \\ {0 \quad otherwise } \\ \end{array} } \right. ,$$

(10)

where r(x, z) and r_o(x_o, z_o) are the positions of the particle and the continuum node respectively, w₁= |x − x_o| and w₂= |z − z_o| are the relative distances.

Once a fracture occurs, it is possible to calculate the seismic moment of the event. To do this we assume that the fracture plane lies perpendicular to the midpoint of the spring connecting the two fracturing particles. The total amount of movement can be calculated and then subdivided into u_t and u_s which represent pure tensile and pure shear movement respectively. For simplicity we assume that the fracture area is equal to the sum of radii of particles broken across the plane times l, the thickness of the two-dimensional model. These values allow us to calculate the seismic moment (M₀) according to:

$$ M_{0} = A*\mu *u ,$$

(11)

where A represents the area of the fracture, $\mu$ is a shear modulus and $u$ the total movement (Aki and Richards 2002). Further we can convert this value to fit the moment magnitude M_w (Hanks and Kanamori 1979) scale using the equation:

$$ M_{w} = \frac{2}{3}log_{10} \left( {M_{0} /1 J} \right) - 10.7. $$

(12)

The numerical models have been extensively used in the literature and have been shown to reproduce experimental and analytical solutions for fracturing (Niebling et al. 2012), roughness growth (Koehn et al. 2003, 2012) and solid fluid interactions in granular (Niebling et al. 2010a, b) and solid media (Flekkøy et al. 2002; Ghani et al. 2013, 2015) as well as in landslides (Parez et al. 2016) or soil liquefaction (Clément et al. 2018; Zeev et al. 2017).

Since time steps in the model are discrete they had to be calibrated in order to avoid overstepping the breaking threshold by unreasonably large amounts, which would lead to the model stepping controlling the behavior. The time step was decreased until changes in stress and magnitudes as well as fracturing behavior became independent of the model step size. Therefore, we assume that at these small time steps the model behaves quasi-continuously.

3 Results

3.1 Parameters of Interest

The model has the following parameters: it is assumed to simulate a system that is 1 km² in area represented by 400 × 400 particles. The sides and the bottom of the model box are represented by fixed walls that are frictionless. The upper boundary is open, and force is applied controlled as a function of gravity of the overlying rock units. Fluid is injected in one fluid cell at the centre of the lower part of the model (Fig. 4). Time steps in the model are 30 s each and the models typically run 10’000 time steps. The fluid has a density of 1000 kg/m³ and a viscosity of 8.90 × 10⁻⁴ Pa s, which are the properties of water at temperature of 25 °C. Variables that were changed include depth (overload varying from 1 to 3 km with a density of overlying sediments of 2.5 × 10³ kg/m³), initial porosity, fluid injection rates, Young’s modulus and brittleness (breaking strength and its distribution) of the rock. The aim was to study how these changes affect the tensile/shear movement ratio distribution, the magnitude and the fracture pattern. A setting with 3 km depth, 0.33 Poisson’s ratio, 6 GPa Young’s modulus, ~ 1% porosity, 34 MPa tensile strength and 80000 Pa/30 s injection rate was our default setting. This setting was chosen because the mechanical properties of the rock are close to those of a typical shale, yet the increased depth guaranteed an increased principal stress and thus a larger amount of fracturing, which provides more data. Variations of these settings were performed in order to study the effects of the different variables on the hydrofracturing (Table 1).

Fig. 4

The setup of the numerical model is 2D, bounded by fixed walls on the right and left hand sides and the bottom while a stress corresponding to the weight of the overburden is applied from the top. Fluid is injected at the centre of the lower part of the model

Table 1 The default setting for the hydrofracturing experiments was set to 3 km depth, 0.3 Poisson’s ratio, 6 GPa Young’s modulus, ~ 1% porosity, 34 MPa tensile strength and 8000 Pa/30 s injection

3.2 Hydrofracture Evolution in Single Events

The model follows a similar behaviour and fracturing pattern in all presented cases that show hydrofracturing. In cases where the injection rate is too low or the porosity too high the fluid just seeps away and no fractures develop. Hydrofracturing typically takes place in four distinct stages: (1) build up of stress, (2) fracturing, (3) residual fracturing, (4) seeping (Fig. 5). In the first stage the fluid is injected at the centre of the model in several intervals. The fluid pressure diffuses into the pore space slower than the injection rate so that sufficient fluid pressure gradients build up that lead to fracturing. Stage two resembles the active hydro-fracturing where most of the seismic events can be observed. This stage typically lasts for about 2500–3000 model steps. During the third stage residual fracturing takes place. In this stage the overall porosity and permeability of the system have increased enough due to fracturing and fracture opening for the fluid to seep away. At this point it takes quite long to build up enough pressure to overcome the tensile breaking strength of the rock so that only minor fracturing events take place. In the fourth and final stage the system reaches a steady state where porosity and permeability have increased enough for the fluid to seep away and no additional fractures develop.

Fig. 5

a The model shows four stages of fracture evolution: (1) build up of stress, (2) fracturing, (3) residual fracturing, ((4) seeping. Timing and intensity of the fracturing depends upon the parameters, for the default setting time step intervals for these stages are (1) 0–1000, (2) 1000–4000, (3) 4000–7500, (4) > 7500. Changing the parameters of the model moderates the timing and intensity of the fracturing, however the overall pattern is preserved in all cases. b Figure shows changes in the vertical fluid pressure gradient averaged over the entire system. The model starting parameter is hydrostatic pressure. 10 kPa value is calculated as a difference between top and bottom boundary of the simulation box, which is 3 and 4 km. In the default setting the fluid pressure gradient is less susceptible to changes due to a low initial porosity and relatively high fluid injection rate. Once the injection rate is lowered or seepage is increased via increase in porosity, it becomes more sensitive to further overall porosity increase through fracturing

Looking at the vertical component of the fluid pressure gradients averaged over the entire system, one can observe (Fig. 5b) that in the default case the fluid pressure gradient changes coincide with fracturing. In this case once fracturing occurs the overall porosity increases and seepage intensifies, thus decreasing the gradient. In the two other cases shown in Fig. 5 the gradient is lower from the beginning of the experiment on as the model was run with (a) a lower injection rate in the experiment and (b) a shallower depth, where there is lower compaction, which allows for greater porosity and thus greater seepage. In the latter two cases the gradient is more susceptible to change as its slope decreases just as the fracturing is initiated. All three cases shown in Fig. 5b illustrate a decrease in fluid pressure gradient growth from the initial gradient produced by the injection rate to the final gradient in the system once steady state is reached, the rock has fractured and the fluid is seeping.

Figure 6a shows the moment Magnitude of fracturing events in a simulation versus the mode of fracturing ratio (shear divided by tensile). Most of the fracturing events in the simulations were mode I dominated (mode of fracturing ratio < 1) with the mode II fracture proportion increasing with the magnitude of the event (Fig. 6a). However, this trend is not linear and it can be seen that there are some mixed mode I − mode II events that have a very low magnitude. Figure 6 further illustrates the bulk of the events record on the negative side of the magnitude scale. The few events that do record on the positive side do not overstep a magnitude of 0.5 and thus are very low. Figure 6b illustrates the evolution of moment magnitude values as a function of time for a model run. Fracturing events with higher magnitudes occur early at stages of most active fracturing and magnitudes decrease towards the later stages of the fracture development.

Fig. 6

a Figure shows the moment magnitude of the fracturing events in a model versus the mode of fracturing in a default setup. All results produce an observable trend of an initial moment magnitude increase as fracturing becomes more shear-like followed by a decrease of magnitude and increase of shear component. This shows that there is no simple linear relationship between the amount of shear in the fracture and the moment magnitude of the event. b Figure illustrates the evolution of moment magnitude values as a function of time for a model run in a default setup. The greatest moment magnitude values can be observed during the phase of the most active fracturing (time-step 1000–4000) and tend to decrease towards the later phases of the model evolution

3.3 Aseismic Component

The given model is limited in the possibility to observe aseismic events due to logging only the position of the particles at the end of each time step. Therefore, the dynamics of the particle movement during the relaxation phase of the lattice are not observed or recorded. There is however significant potential for aseismic activity. To illustrate this we recorded the average amount of movement of particles located along the fracture walls during the time steps when no active fracturing takes place (Fig. 7). Figure 7 shows results from the default model setup but identical trends are observable in all control parameter configurations. The amount of movement is an order of magnitude lower than that during time steps when bond breakage occurs, however it follows the same pattern where there is greater increase in values in the initial stages of fracturing and subsequent decline in the later stages. This would be indicative of the hypothesis that large amounts of energy are being released aseismically alongside the energy released during active fracturing and may not be directly observed.

Fig. 7

Average displacement of particles during the time steps when active fracturing (seismic) takes place versus average displacement of all the particles across the fracture walls during time steps when no active fracturing is occurring (aseismic)

3.4 Variation of Parameters

Each of the following results is represented by stacked data points obtained from up to ten consecutive runs of the model with the same parameters. This is done in order to better illustrate the outcome and to minimize the uncertainties of the results. The following results are shown using the logistic distribution which is similar to the normal distribution with a more convenient choice of parameters where mode and mean is described by the same parameter. The logistic distribution is also more efficient in dealing with datasets that have greater spread of values. Histrograms in Fig. 8 show the percentage of the total data points falling into every binning interval. Logistic probability density curve (PDF) is then calculated for the given result distribution. Complete data in Fig. 9 is represented using only logistic PDFs in order to avoid clutter. In the first set of experiments the Young’s modulus (E) was varied from 4.5 GPa to 6, 7, 8, 9, 10, 12.5, 15, 20, 30 and 40 GPa. In order to illustrate the model behavior we studied 4 parameters, the moment magnitude release during model runs (Fig. 9a), the distribution of fracture wall displacement or aperture (Fig. 9b), the distribution of the amount of broken bonds for single fracture events (Fig. 9c) and the distribution of movement mode ratios in model runs (mode I versus mode II, Fig. 9d). The plots on the right hand side of the figure show the evolution distributions’ modes/means when changing Young’s modulus from soft rock setting through to hard rock setting.

Fig. 8

Displacement data for experiments with E = 4.5 GPa (left) and E = 30.0 GPa is binned according to the percentage of the total data falling within each of the intervals. Logistic distribution probability density functions are then calculated for data point distributions

Fig. 9

Logistic distribution curves on the left hand side and means on the right hand side as a function of changes in Young’s Modulus for the simulations after 10,000 time steps. Soft, intermediate and hard rocks are indicated. a Moment magnitude variation shows a decrease from soft to intermediate rock followed by an increase towards the hardest rocks. b Displacement or aperture of fracture shows a clear trend from a uniform very thin crack for hard rocks followed by a non-linear increase of the displacement or aperture towards soft rocks. c The area of the fracture or amount of broken bonds shows a relatively stable value for soft to intermediate rocks and then an increase in area towards hard rocks. d The movement mode ratio or the amount of extensional versus shear fracture shows an increase in shear fracturing towards harder rock whereas intermediate and soft rocks show dominant extensional fracturing

The moment magnitude (Fig. 9a) changes in a complicated, non-linear manner as a function of changes in the Young’s Modulus. From 4.5 to 10 GPa the moment magnitude decreases followed by an increase towards higher Young’s modulus values. The average displacement of the fractures shows clearly that the displacement median/mode is becoming smaller with an increase of the Young’s Modulus until 12.5 GPa from where it stays constant (Fig. 9b). The overall distribution becomes smaller with increasing Young’s modulus leading to a constant displacement at high values. The fracture area shows a minor initial decrease from 4.5 to 10 GPa and then an increase in area (Fig. 9c). The increase in fracture area is most pronounced from 20 to 30 and 40 GPa. Simulations with the highest elastic constants seem to have events where a larger amount of bonds break accounting for longer fractures and thus a larger fracture area. A change of the Young’s modulus has a strong influence on the fracture mode ratio during the simulations (Fig. 9d). At low Young’s modulus (from 4.5 to 10 GPa) the fracture mode is mainly extensional with a relatively narrow distribution whereas higher Young’s moduli (12.5 to 40 GPa) show a much higher amount of shear fractures in addition to mixed extensional/shear failure. The transition between these two regimes is very rapid between the values of 10 and 12.5 GPa followed by unchanging behaviour at greater values. The mean value of the logistic distribution is almost constant, around 1–3 (0.3–0.5) ratio of shear versus tensile movement, for the lower Young’s moduli, and becomes constant again, around 1–1 (1.0) ratio, once the fracture mode changes at higher Young’s moduli. In summary an increase in Young’s modulus has a strong influence on the mode of fracturing changing from extensional mode dominated at Young’s moduli below 10 GPa to mixed mode with a higher amount of shear fractures at higher values. The behaviour of the moment magnitude as a function of Young’s modulus is complex. Fracture wall displacement or aperture of the fractures decreases with an increase of Young’s modulus and becomes stationary at high values (> 20 GPa). The amount of broken bonds or the fracture area is not changing much for small Young’s modulus values but increases from values of 20 GPa and higher.

To see how the change in overburden pressure would influence the fracturing process, the depth of the simulation was changed from 3 to 1 km and the Young’s modulus was varied between the simulations in a similar fashion to the default case. Reducing the overburden produced a significant decrease in fracturing in general, so that sometimes the results yielded as much as ten times less fractures than at 3 km. The lower overburden stress led to an increased porosity, which also meant that the fluid pressure gradients were lower and less fractures developed (Fig. 5b). This resulted in a smaller amount of data points and thus more noise in the data. However, when analysing the fracture displacement or aperture data, a very similar trend to the 3 km cases can be observed where there is a rapid decrease of wall displacement with an increase in Young’s modulus followed by a steady aperture with the turning point at around 15 GPa (Fig. 10).

Fig. 10

Logistic distribution curves showing average fracture wall displacements for a series of Young’s moduli at depth of 1 km. The behaviour is very similar to the 3 km deep reference case

The other parameters (moment magnitude, mode ratio, fracture area), when analysed, produced a high amount of noise in the results and thus showed very high uncertainty and no clear relation with changes in Young’s modulus.

In a third set of simulations we changed the Young’s modulus in simulations with a lower injection rate of 50000 Pa/30 s.

Changing the injection rate from 80,000 Pa/30 s to 50,000 Pa/30 s did not change the behaviour of the simulations much. Both displacement and area change trends showed the same pattern that was observed at higher injection rate with a change in behaviour at 10 GPa. The moment magnitude pattern was almost identical in both cases with differing injection rates. The only significant change was the movement mode pattern where the behaviour changes at 9 GPa rather than 10 GPa.

In a final set of experiments we varied the breaking strength of the springs and compared the effect of breaking strength and Young’s modulus variation on the overall amount of broken bonds in single simulations. Figure 11 shows the number of broken bonds as a function of Young’s modulus divided by breaking strength. The different colours indicate runs with constant breaking strength but a variation in Young’s modulus. Breaking strength and Young’s modulus do not have the same effect on the amount of broken bonds. An increase in Young’s modulus shows a roughly linear increase in the amount of broken bonds. This behaviour is irrespective of the breaking strength. A decrease in breaking strength increases the amount of broken bonds, however in contrast to the Young’s modulus this trend is not linear. At a breaking strength of 44.2 and 54.4 MPa the amount of fractures is equally low, whereas at a low breaking strength of 27.2 MPa the amount of fracturing has increased 5 times.

Fig. 11

The figure shows the amount of bonds broken during an experiment for a series of Young’s moduli normalized by the tensile breaking strength of the rock. Increasing Young’s modulus and decreasing the breaking strength both lead to more fractures

4 Discussion

Our simulations indicate that a change in the Young’s modulus has a pronounced effect on the fracture behaviour. At a lower Young’s modulus the fracture mode is dominated by extension, the amounts of broken bonds is low and the fracture wall movement or aperture is large. At higher Young’s moduli the fracture mode becomes mixed with a larger amount of shear fractures, the fracture aperture becomes constant while the amount of broken bonds and thus the fracture area increase. The fracture behaviour changes quite abruptly at around 10 GPa. Below 10 GPa the rock is quite soft and forms elliptical shaped fractures which almost “inflate” and do not really propagate. Above 10 GPa the rock is tougher, thus it is much more prone to tensile movement and stress is relieved through propagation of fractures and thus more shear like movement.

To explain this behaviour we look at the effective stress increase at the tip of a mode I fracture. The effective stress at the crack tip $\sigma '$, is a function of $\sigma_{0}$, the external stress (as a function of the fluid pressure gradient), length L of the crack and the radius of curvature r at the crack tip (Irwin 1957):

$$ \sigma ' = 2\sigma_{0} \sqrt {\frac{L}{2r}}.$$

(13)

Figure 12 shows a plot of the solid effective stress at crack tips in the simulations that was calculated using the average opening and amount of broken bonds for different Young’s moduli. Two distinctly different regimes appear, a steep slope below an elastic constant of 10 GPa–12 GPa and a shallower slope above. A smaller elastic constant produces larger r values (aperture) and smaller l values (fracture length). It can be seen that r changes much more than l, therefore large elastic constants have a smaller r and a slightly larger l. This means that the ratio below the square root in Eq. 13 is smaller for smaller values of the elastic constant but it changes a lot with a significant change of r towards an elastic constant of about 10–12 GPa. Then the r value seems to saturate and stay more or less constant and only the length changes increase. This effect is overprinted by the square root function.

Fig. 12

Figure shows the calculated crack tip stress from the crack aperture and length as a function of Young’s Modulus (E). Both crack aperture and length values are derived as means/modes using the logistic distribution function for all the data. The plot shows two regimes, below 10 to 11 MPa Young’s Modulus the crack tip stress increases rapidly, whereas at Young’s Moduli higher than 11 MPa the crack tip stress increase is only minor. These two regime represent two failure regimes, below the critical Young’s Modulus the fractures are soft and open whereas at higher values the aperture is constant the crack propagates by an increase in length

Two different geometrical factors affect the effective stress at the crack tip, the aperture and the fracture length. Soft rocks have larger elasticity and tend to be more easily compressed leading to wide open fractures. The change in fracture aperture being strongly sensitive to changes in elasticity. In this regime, fracture length is fairly stable and in fact slowly decreases with increasing Young’s Modulus. At larger Young’s Moduli the change in fracture aperture halts, whereas the change in fracture length becomes important.

To better understand the dynamics at the fracture tip we have reconstructed the σ_xx and σ_yy stress net change between the initial and final time steps in a profile line orientated vertically and horizontally through the simulated fractured area (Figs. 13, 14).

Fig. 13

Figure shows schematic placement of the profiles used to calculate the difference in σ_xx (horizontal) and σ_yy (vertical) stress between the first and last time steps in the experiments. The profiles cover fracture networks rather than single fractures and thus show fluctuations in stress

Fig. 14

Profiles of change in σ_xx (horizontal) and σ_yy (vertical) stress throughout the experiment along the horizontal (left) and vertical (right) lines of profile. The horizontal profile shows an increase in σ_xx stress on each side of the fractured area representing a compaction zone, which is much more pronounced in the soft rock. The vertical profile shows a significant difference of σ_xx stress for soft versus hard rocks with hard rocks showing only compression whereas soft rocks have a tensile region at the top of the fracture. Both vertical profiles are anisotropic reflecting gravity

The data line is uneven as rather than going through a single fracture, it crosses a fracture network and this causes fluctuations. After performing this procedure multiple times for several cases we can observe certain patterns emerge, which are schematically depicted in Fig. 15.

Fig. 15

Figure shows schematic illustration of stress in soft and hard rocks. Arrows pointing towards the centre of fracture indicate compressive stress while arrows pointing outwards—extensional

Both cases (soft and hard rock fractures) have isotropic (explosive) behavior at the injection point and tend to have stress changes on left and right hand side. The σ_xx (horizontal) stress in both cases shows an increase on both sides of the crack representing a compaction zone of elevated local stress field. This compaction zone is much more pronounced in the soft rock. The σ_yy (vertical) stress behavior is different for soft and hard rocks. In the case of a soft rock it tends to be slightly extensional at the boundary of the fracture and then changes to compressive further away. When looking at the hard rock, the stress is mainly compressive with a small tensile area at the very center and the switch from tensile to compressive is more abrupt. At the crack tip soft and hard rocks behave quite differently, especially at the top of the fractured area. Both soft and hard rock scenarios show a bimodal behavior where both σ_xx and σ_yy stresses change from extensional to compressive closer to the end of the fractured area. However, in the case of soft rocks, the σ_xx stress becomes sharply extensional just outside the fractured area, while in the case of the hard rock scenario, no sudden change in stress is observed. This backs up the theory that fracture development in the case of soft rocks is mostly governed through lateral extension and increase of the fracture aperture as the stress regimes readily allow for lateral expansion at the crack tip. The relatively higher σ_xx stress values at the sides of the fracture suggest extensive expansion in that direction. In the case of the hard rock, the length is the key value behind the crack growth. In the case of the soft rock the fracture tip is already in extension before the crack propagates and the fluid pushes outwards to pull the solid apart for further fracturing. This behavior is very similar to fracturing in granular media where grains are being pushed apart (Eriksen et al. 2017, 2018; Niebling et al. 2012) and would represent mode I extensional failure. In contrast the hard rock fracture tip is actually under compression. The stress concentration in the hard rock case is very high at the crack tip, so that almost any tensile stress at the tip exceeds the breaking strength and leads to fracture propagation. The effect of these different mechanisms results in different slopes for hard rocks in Fig. 12.

Figure 15 illustrates that in soft rocks the cracks are shorter and have rounder shape. In this case the fluid is potentially filling the whole crack and pushing at the walls (creating gradients depending on seepage) for further fracturing. In the case of hard rocks the upper fracture tip is quite far from the injection point. In this case the fluid overpressure may not reach the tip for fracturing to occur. This leads to a low fluid pressure crack tip in the case of saturated rocks (as modeled here), and would lead to a dry crack tip if the solid is not water saturated.

The resolution of the model (amount of particles in the simulation) has an influence on the amount of fractures that can be produced in the model but the crack tip stress is not directly dependent on the particle size. The stress at the crack tip is given by the extension or shearing of springs which is only determined by the relaxation threshold that is used to solve the stress field, which is in the order of four magnitudes smaller than the particle size. Figure 16 shows that the fracture network itself does not change in geometry at different resolutions, except for the fact that a higher resolution simulation produces a more detailed fracture network with more branches.

Fig. 16

Figure shows the fracture patterns (blue particles) in detail for a hard (50 GPa) versus a soft (5 GPa) rock. a Simulation of a soft rock with four distinct shear fractures and a central mode I region. b Simulation of a hard rock with a much more pronounced central fractured area in comparison to the soft rock. c Details of the central parts where distinct openings can be seen in the soft rock in the central part representing an opening elliptical crack when the rock is soft. d A high resolution simulation of the hard rock. In this case the ratio between the fluid input area and the particle size is changed to twice the size in the horizontal and vertical direction, meaning that fluid is injected in four cells and not only in one cell as is the case with ((a) and (b). The fracture pattern in the high resolution simulation is the same as in (b) but twice the size illustrating that the scale and pattern of the fracture network is not dependent on the resolution of the model

5 Conclusions

In this contribution we show numerically how hydrofracturing during fluid injection develops in 4 distinct stages: (1) build up of stress, (2) fracturing, (3) residual fracturing, (4) seeping. The Young’s modulus of rocks and their breaking strength change the fracturing behavior resulting in two predominant fracturing mechanisms. In the cases when the fractured rock is soft, fracturing occurs due to a critical tensile strength or cohesion being exceeded, change in the stress at the crack tip as a function of the Young’s Modulus is then governed by the change in the fracture aperture and the fracture tip is constantly under extension. When the rock is hard, the fracture aperture is small and constant and the fracture length becomes the key driver of the stress change. The fracture tip is under compression and fracturing is driven strongly by stress intensification at the tip, causing fractures to propagate in more shear like failure.

We show that the relationship between Young’s modulus and the failure mechanism works independently of the tensile strength of the rock as changes in Young’s modulus for rocks with different tensile strengths produce the same relative increase in the amount of fracturing. The number of fractures that develop is a non-linear function of the breaking strength.

Changes in secondary parameters such as the amount of overburden or fluid injection rate have an impact on the amount of fractures that develop but have little to no effect on the described failure mechanisms. The transition between the failure due to a critical tensile strength for soft rocks versus a strong dependence on stress intensification for hard rock lies at a Young’s modulus of about 10 GPa in the simulations. Since Young’s moduli for natural shales vary from 8 to 50 GPa one has to be careful to use the right failure criterion depending on the shale type.