Preconditioned Inversion of 3D Borehole to Surface Electromagnetic for Reservoir Exploration

Abstract

The accurate interpretation of three-dimensional borehole to surface electromagnetic (BSEM) data has two challenging problems: the accuracy of forward modeling and the efficiency of the inversion process. In this paper, we used the least squares method to develop a preconditioned algorithm combined parametric inversion and resistivity image to overcome these difficulties for reservoir exploration. To improve accuracy, we suggest using the full integral equation (IE) solution for forward modeling. Taking into account that the IE method requires the mesh discretization of an anomalous body only, the parametric inversion based on the IE method would provide an preconditioned inverse domain consisting of the complex structure via a few parameters. Based on the predicted preconditioned inverse domain, the conventional Green’s functions can be recomputed only once and kept unchanged in iterative inversion process of resistivity image, which increases significantly the size of the inverse domain and the computation for IE modeling. The resistivity of background and complex structures embedded in layered stratum are considered to simulate the practical application in preconditioned inversion. Synthetic examples with noise studies are conducted to demonstrate that the preconditioned algorithm can be applied quickly and effectively in a complex structure inversion for BSEM in reservoir exploration.

1 Introduction

Based on the high resistivity and chargeability contrasts existing between reservoir and water, borehole to surface electromagnetic (BSEM) technology has the potential ability to monitor the distribution of reservoir, especially due to the small difference in densities between reservoir and water for seismic and gravity technologies (Wang et al. 2015; Cao et al. 2015; Zhan et al. 2017, 2019a). In BSEM measurement, the sources are located inside the borehole, while the receivers (including electric dipoles and magnetic sensors) are buried under the ground surface (He et al. 2005; Li et al. 2016; Li et al. 2017). As there has been significant progress in BSEM technology in recent years, BSEM technology is widely and efficiently applied in reservoir exploration (He et al. 2005; Marsala et al. 2011, 2013; Liu et al. 2018).

As many researchers have put tremendous efforts into the improvement of the integral equation (IE) method for the 3-D EM problem (Hohmann 1975; Wannamaker et al. 1984; Xiong 1992; Hursan and Zhdanov 2002; Zhan et al. 2019b), a few pilot tests of BSEM applications based on IE method have been carried out (Le Masne and Poirmeur 1988; Wang et al. 2007a). Such pilot tests used various numerical examples to demonstrate that the IE method provides us the ability to simulate the BSEM fields accurately. In the framework of the IE method, only the anomalous areas need to be calculated during the forward process, which greatly speeds up the calculation processes. However, exploration in complex structures with inhomogeneous background still leads to calculations too large for practical exploration, in which the domain of integration may become too large and require greater computer memory and computational time for IE modeling (Zhdanov et al. 2006; Marsala et al. 2014). As a result, in some practical applications, one of the problems faced in conventional inversion based on the IE method is that it is difficult to describe a reservoir using regular model (Li et al. 2014; Li and Liu 2016).

The improvement and development of high-resolution BSEM technologies to enhance oil recovery have been motivated by the requirement of detailed reservoir mapping for oil producing companies (Daniels 1983; Wang et al. 2006, 2007b). Such research applied the Born approximation and Quasi-analytical approximation based on the IE method into the BSEM inversion (Zhdanov and Fang 1996; Zhdanov and Hursan 2000; Zhdanov and Tartaras 2002). Although the approximation inversion significantly decreases computer memory and computational time in practical applications, the limited precision widely restricts approximation inversion for application in irregular models. The natural choice for accurately solving complex structures inversion problems would be an integral equation forward with analytical solution, provided we can determine that the moderate inversion domain contains the complex structure. When this situation occurs, it is greatly helpful to compute the inversion iteratively as the parameters are changed within only one limited and objective domain. Taking into account that the predetermined inversion domain would be described as a regular cubic structure with a few parameters, the parametric inversion method would allow us to effectively define the objective domain. Such predetermined domain maybe also applied to be a precondition in sequential resistivity image process.

In some practical applications for reservoir explorations, the reservoir was sealed away in certain areas, such that the shapes of the reservoirs maybe tilted or curved. For these reasons, a new preconditioned algorithm of parametric inversion and resistivity image has been developed using the full IE forward and least squares inversion for three-dimensional borehole to surface electromagnetic fields in complex structures. In this paper, we consider inclined reservoir models with different sizes in three dimensions, which are embedded in half homogeneous space or layered background. We take into account that the background resistivity was estimated artificially, depending on other geology or exploration information, which sometimes led to the wrong inversion result. In particular, we consider the background resistivity in the parametric inversion. We demonstrate that the background resistivity is predicted faster and more accurately than the anomalous parameters as the background space becomes larger than the anomalous area. In the framework of inversion based on IE method forward, one has to compute the field in a cubic domain, which significantly increases the required computer memory and computational time as the traditional domain of integration may become too large. The remarkable fact is that the parametric inversion provides us an estimated objective domain that will overcome the huge computation in traditional inversion, and then, the resistivity image based on IE method just needs to precompute the Green’s vector function once and keeps it unchanged during the entire inversion process. By considering synthetic examples with Gaussian noise, this paper aims to demonstrate that the preconditioned algorithm can be applied quickly and effectively in complex structure inversion for BSEM.

2 Forward Modeling

The well-known IE method has been widely used in numerical simulation. In a 3-D geoelectrical model area with a background conductivity $\sigma^{b}$ and inhomogeneity D with the arbitrary spatial variations of conductivity $\Delta \sigma = \sigma^{a} - \sigma^{b}$, for completeness, the total electric field E and the magnetic field H can be represented as a sum of background fields and anomalous fields (Hohmann 1975; Weidelt 1975):

$$\begin{aligned} \varvec{E}(\varvec{r}) &= \iiint_{D} {\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E} (\varvec{r}|\varvec{r^{\prime}})}\Delta \sigma (\varvec{r^{\prime}})\varvec{E}^{a} (\varvec{r^{\prime}})dv + \varvec{E}^{b} (\varvec{r}) \hfill \\ &=\varvec{G}_{E} \left[ {\Delta \sigma (\varvec{r^{\prime}})\varvec{E}^{a} (\varvec{r^{\prime}})} \right] + \varvec{E}^{b} (\varvec{r}) \hfill \\ \end{aligned}$$

(1)

$$\begin{aligned} \varvec{H}(\varvec{r}) &= \iiint_{D} {\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{H} (\varvec{r}|\varvec{r^{\prime}})}\Delta \sigma (\varvec{r^{\prime}})\varvec{E}^{a} (\varvec{r^{\prime}})dv + \varvec{H}^{b} (\varvec{r}) \hfill \\ &= \varvec{G}_{H} \left[ {\Delta \sigma (\varvec{r^{\prime}})\varvec{E}^{a} (\varvec{r^{\prime}})} \right] + \varvec{H}^{b} (\varvec{r}) \hfill \\ \end{aligned}$$

(2)

where $\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E} (\varvec{r^{\prime}}|\varvec{r})$, $\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{H} (\varvec{r^{\prime}}|\varvec{r})$ represent the electric and magnetic Green tensors of infinity conducting medium $\sigma^{b}$ respectively. $\varvec{r}$ and $\varvec{r^{\prime}}$ are the vector lengths of transmitter to receivers outside and inside the inhomogeneity D, respectively. $\varvec{G}_{E}$ and $\varvec{G}_{H}$ are the corresponding Green linear operators. $\varvec{E}^{a}$ is the total anomalous field at the center of discrete volume in 3-D body. And $\varvec{E}^{b}$ is the background electric field. Equations (1) and (2) are needed to discretize while the numerical simulation is performed on a computer. The 3-D body is approximated by N rectangular prismatic cells of arbitrary aspect ratio with constant conductivity in each cell. A linear matrix equation for the unknown total electric field $\varvec{E}^{a}$ in the 3-D body is derived based on the electromagnetic forward of the Eq. (1), written as:

$$\sum\limits_{n = 1}^{N} {\left( {\frac{{\sigma_{n}^{a} - \sigma^{b} }}{{\sigma^{b} }}\varGamma_{mn} - \delta_{mn} } \right)E_{n}^{a} = -\, E_{m}^{b} }$$

(3)

where

$$\delta_{mn} = \left\{ {\begin{array}{*{20}c} {I\begin{array}{*{20}c} {} & {(m = n)} \\ \end{array} } \\ {0\begin{array}{*{20}c} {} & {(m \ne n)} \\ \end{array} } \\ \end{array} } \right.$$

(4)

$$\varGamma = k^{2} \sigma^{b} \int_{vn} {g(\varvec{r},\varvec{r^{\prime}})Idv^{\prime}} + \sum\limits_{l = 1}^{2} {( - 1)^{l} \int_{sn} {\sum\limits_{i = 1}^{3} { - \nabla g(\varvec{r},\varvec{r^{\prime}}) \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ds^{\prime}} } }$$

(5)

$$g(\varvec{r},\varvec{r^{\prime}}) = \frac{{e^{{ - ik_{{}} \left| {\varvec{r} - \varvec{r^{\prime}}} \right|}} }}{{4\pi \left| {\varvec{r} - \varvec{r^{\prime}}} \right|}}$$

(6)

where $k_{{}}^{2} = - iwu_{0} \sigma^{b}$ is the wave index of background medium, $u_{0} = 4\pi \times 10^{ - 7} {\text{Hm}}^{ - 1}$ is the free space magnetic permeability, $g(r,r^{\prime})$ is the scalar Green’s function of free space, $\varvec{I}$ is the unit vector, and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}$ is the unit vector along the axis at the center of discrete volume in 3-D body.

$$\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E}^{mq} (\varvec{r},\varvec{r^{\prime}}) = \frac{{k_{q}^{2} }}{{k_{m}^{2} }}(k_{m}^{2} \varvec{I} + \nabla \nabla \cdot )\varvec{G}_{A}^{mq} (\varvec{r},\varvec{r^{\prime}})$$

(7)

One also can calculate the field according the green’s function in layered medium as presented in Eq. (7). The electric dyadic Green’s function $\varvec{G}^{mq}$ relates a vector field at observation point $\varvec{r}$ in layer $m$ to a source current element at $\varvec{r^{\prime}}$ in layer $q$, including $m = q$. The dyadic Green’s function $\varvec{G}_{A}^{mq}$ represents the magnetic vector potential in layer $m$ due to a unit strength, arbitrarily oriented electric dipole in layer $q$. The cell’s total field in 3-D body can be calculated using the biconjugate gradient stabilized method to solve the Eq. (3), the anomalous field in surface can also be gained from Eqs. (1) and (2).

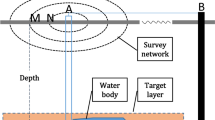
In this paper, we consider a complex tilted conductive model to test the efficiency of IE method for BSEM, as shown in Fig. 1. The transmitter well is located at the origin of coordinates outside the model excited by two vertical wire sources up and down the model at different depths, as shown in Fig. 2. The frequency is 500 Hz for the irregular tilted model shown in Fig. 3. The results of numerical experiments are presented in Fig. 4 based on different transmitter depths. In the framework of the electromagnetic field excited by vertical source, the skin depth is dependent on the length of the wire source. As a result, one can note that the model near the well was efficient at 0 ~ − 200 m depth source, while the entire rough sketch of the model was presented at 0 ~ − 500 m depth source in Fig. 4. Meanwhile, we can also note that the Hy component is more effective than the Ex component in mapping the boundary of the model herein.

Fig. 1

Three-dimensional geoelectrical model of irregular conductive prism embedded in a homogeneous half space

Fig. 2

Top plane of transmitter and receivers for irregular conductive prism

Fig. 3

Sections of irregular conductive prism embedded in a homogeneous half space in different axis direction

Fig. 4

Electromagnetic contour maps of irregular conductive prism excited at a frequency of 500 Hz

3 Preconditioned Inversion Based on the Least Square Method

3.1 Parametric Inversion

It is well known that the actual BSEM inverse problem is total nonlinear problem while one can treat the inverse domain in infinite domain and take all unknown parameters in the processing. As one of approximately treated optimization processes, parametric inversion is used to reconstruct the resistivity and the depth of layered media for providing an preconditioned inverse domain consisting of the complex structure via a few parameters. The BSEM parametric inversion problem can be approximately expressed as

$$\Delta \varvec{d} = \varvec{A}\Delta \varvec{M}$$

(8)

where $\Delta \varvec{d}$ is the vector of differences between predicted responses and measured data, and $\varvec{A}$ is the Jacobian matrix. In the framework of preconditioned inversion, the matrix will have two different derivatives of the modeled response with respect to the model parameters or resistivity. $\Delta \varvec{M}$ is the correction vector to the last model parameters.

In the first step of preconditioned inversion for BSEM, for providing an preconditioned domain, we derivate an algorithm of parametric inversion based on resistivity and depth parameters inside a given approximate domain. And an approximate model resistivity distribution within a half homogeneous or layered background is obtained, in which the resistivities of layers are considered into the inversion parameters. For completeness, Eq. (8) is based on the least squares method and can be defined as the following objective function

$$\varphi = \sum\limits_{i = 1}^{NS} {\left\| {\rho_{ai} - \rho_{ci} \left( M \right)} \right\|^{2} }$$

(9)

where $\left\| \cdot \right\|$ denotes the Euclidean norm, $\rho_{a}$ and $\rho_{c}$ represent the measured data and modeled responses, respectively, $NS$ represents the number of measured data, and $\varvec{M}$ is the matrix of the cubic model parameters, including the lengths of the cubic along the axis, location of the cubic, model resistivity, inclined angles along the axis and background resistivities. One can compute the Taylor series of the second term on the right-hand side and ignore the higher order term than two orders. And the Eq. (8) may be defined as

$$\varphi = \sum\limits_{i = 1}^{NS} {\left\| {\rho_{ai} - \rho_{ci} - \sum\limits_{j = 1}^{NM} {\frac{{\partial \rho_{ci} }}{{\partial M_{j} }}\Delta M_{j} } } \right\|^{2} }$$

(10)

where $NM$ is the number of model parameters. Minimization of Eq. (10) is written as

$$\sum\limits_{j = 1}^{NM} {\frac{{\partial \rho_{ci} }}{{\partial M_{j} }}\Delta M_{j} } = \rho_{ai} - \rho_{ci} .$$

(11)

To compute the $\frac{{\partial \rho_{ci} }}{{\partial M_{j} }}$ term, the algorithm of the difference is used, and the length of the difference step is 0.01 based on the tests. The logarithms of modeled responses and measured responses are used so that the inversion has a stable process, and then, Eq. (12) produces the system of linear equations

$${\mathbf{AX}} = {\mathbf{B}}$$

(12)

where

$$\begin{aligned} A_{ij} &= 100\left[ {\frac{{\rho_{ci} \left( {M_{1} ,M_{2} , \ldots ,1.01M_{j} , \ldots ,M_{NM} } \right)}}{{\rho_{ci} \left( {M_{1} ,M_{2} , \ldots ,M_{j} , \ldots ,M_{NM} } \right)}} - 1} \right] \hfill \\ i &= 1 \ldots NS,j = 1 \ldots NM \hfill \\ X &= \lg (\Delta M) \hfill \\ B &= \lg (\rho_{a} ) - \lg (\rho_{c} ). \hfill \\ \end{aligned}$$

One can note that there are no dimensions in the Eq. (11) so that the potential error caused by different dimensions between model parameters is avoided. Taking into account that the measured data include some variability, and the number of the parameters is far less than the number of measured data when we divide a model into blocks of unknown constant resistivity, it is necessary to impose some form of constraint to ensure stability of the iterative process by using the regularization in this paper

$$({\mathbf{A}}^{T} {\mathbf{A}} + \lambda \varvec{I}){\mathbf{X}} = {\mathbf{A}}^{T} {\mathbf{B}}$$

(13)

where $\lambda$ is a Lagrange multiplier, and $\varvec{I}$ is the unit vector. Solving Eq. (13) by using the singular value decomposition method, one can update the model parameters

$$\tilde{\varvec{M}} = \varvec{M}_{l} \cdot \exp (\varvec{X})$$

(14)

where $\tilde{\varvec{M}}$ and $\varvec{M}_{l}$ are the updated and last matrix of model parameters, respectively.

3.2 Resistivity Image

In the second step of preconditioned inversion, the algorithm of the resistivity image is used based on the preconditioned resistivity matrix $\tilde{M}$ in the parametric inversion. To have a stable inversion for BSEM, the scale of the model parameters and the measured data are also considered. As the number of the resistivity parameters is far less than the number of measured data when we divide a model into blocks of unknown constant resistivity, the inversion problem is generally ill-posed for BSEM in resistivity image. A common approach for ensuring the stability of the iterative process is to impose some form of constraint on $\Delta M$, and Eq. (7) to be minimized as the objective function

$$\varphi = \left\| {\Delta d - \tilde{A}\Delta \tilde{M}} \right\|^{2} + \lambda \left\| {w\Delta \tilde{M}} \right\|^{2}$$

(15)

where the second term on the right-hand side represents the smoothness weighted by a Lagrange multiplier $\lambda$, $w$ is the smoothness vector whose entries are either − 1, 0 or 1. Minimization of the above objective function becomes the system of linear equations as

$$(\tilde{A}^{T} \tilde{A} + \lambda w_{{}}^{T} w)\Delta \tilde{M} = \tilde{A}^{T} \Delta d$$

(16)

where $\tilde{A}$ is the Jacobian matrix of resistivity image. To compute term $\tilde{A}$, we apply the algorithm of partial derivatives introduced in Ruan’s (2001) paper and take the logarithm of Eq. (16) as

$$\tilde{A}_{ij} = \frac{{\partial \lg u_{{_{j} }} }}{{\partial \lg \sigma_{i} }} = \frac{{\sigma_{i} }}{{u_{{_{j} }} }}\frac{{\partial u_{{_{j} }} }}{{\partial \sigma_{i} }},\begin{array}{*{20}c} {} & {i = 1 \ldots MS,\;j = 1 \ldots NS} \\ \end{array}$$

(17)

where $u$ is the measured data, $\sigma$ is the model conduction, and $NS$ and $MS$ are the number of measured data and model resistivities, respectively. To compute the partial derivatives $\frac{{\partial u_{{_{j} }} }}{{\partial \rho_{i} }}$ term, one can get the derivative with respect to $\sigma$ of Eq. (1) and the $j$ th measured electric field respective to the $i$ th model block resistivity can be written as

$$\frac{{\partial E(r_{{_{j} }}^{'} )}}{{\partial \sigma_{i} }} = \int\limits_{vi} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E} (r_{{_{j} }}^{'} |r_{i}^{{}} )dv} \cdot E^{a} (r_{i}^{{}} ) + \sum\limits_{n = 1}^{N} {\int\limits_{vn} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E} (r_{{_{j} }}^{'} |r_{n}^{{}} )dv^{{}} } \cdot } \Delta \sigma_{n} \cdot \frac{{\partial E^{a} (r_{n} )}}{{\partial \sigma_{i} }}.$$

(18)

In the framework of IE method, the total electric field inside the model is also expressed as Eq. (1):

$$E^{a} (r_{a}^{'} ) = \iiint_{D} {\bar{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E} }(r_{a}^{'} |r_{a} )\Delta \sigma (r_{a} )E^{a} (r_{a} )dv + E^{b} (r_{a}^{'} )$$

(19)

where the $\bar{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E}$ is the electric Green tensor inside the model. The subscript “a” in the Eq. (19) denotes the computation domain inside the model. The derivation with respect to $\sigma$ of Eq. (19) and the $n$th measured electric field respective to the $i$th model block resistivity can be written as

$$\frac{{\partial E^{a} (r_{n}^{{}} )}}{{\partial \sigma_{i} }} = - (\Delta \sigma_{n} \cdot \bar{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E} )^{ - 1} \cdot \frac{{\partial (\Delta \sigma_{n} \cdot \bar{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E} )}}{{\partial \sigma_{i} }} \cdot E^{a} (r_{n}^{{}} ).$$

(20)

In the process of preconditioned algorithm with a given domain in the parametric inversion, one can precompute the Green function $\bar{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }_{E}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E}$ terms only once and keep them unchanged during the entire inversion process. We can solve the Eq. (15) by using the values of Eqs. (16), (17) and (19) to update the model resistivities by the following equation:

$$\sigma_{u} = \sigma_{l} \cdot \exp (\Delta \tilde{M})$$

(21)

where $\sigma_{l}$ is the final inversion model conduction. The preconditioned inversion will end until the error of fitting meets the requirement of accuracy. If not, we repeat the preconditioned inversion process. One can find a detailed description of conduction inversion based on IE method in “Appendix”.

4 Model Studies

4.1 Model Embedded in Homogeneous Half Space

We considered a complex tilted model with resistivity of 250 Ω m embedded in a homogeneous half space with the resistivity of 25 Ω m shown in Figs. 1 and 2. The inhomogeneous body represents a tilted irregular dyke structure shown in Fig. 3. In the framework of preconditioned inversion algorithm in this paper, one can use a cubic domain to present the tilted model shown in Fig. 1. The field is excited by a vertical electric current bipole with 200 m and 500 m electrode separations. To consider the practical application, the synthetic field is contaminated with 5% Gaussian noise.

The transmitter well is located 217 m from the center of the anomalous body, and the source used alternating currents with four frequencies: 1, 10, 500 and 2500 Hz. The inverted area is a homogeneous mesh consisting of 10 × 10 × 10 cubic cells with a dimension of 100 m in the axis directions and surrounding the tilted model shown in Fig. 1. The sketch of the transmitter and receivers system is shown in Fig. 2, which is enough well discretization for the highest frequency in this case. The vertical slices of the model shown in Fig. 3 are inverted, and the inverted results are shown in Figs. 5 and 6.

Fig. 5

Vertical cross-sections of the high resistivity true model and predicted model from noisy synthetic BSEM data

Fig. 6

Slices of the high resistivity true model and predicted model from noisy synthetic BSEM data

In the first step of preconditioned inversion process, the parametric inversion was used to estimate the preconditioned inverted cubic domain consisting of tilted model and the conduction of irregular dyke, together with the background conduction. The first model for parametric inversion is an arbitrary small cubic with resistivity of 100 Ω m embedded in a homogeneous half space with the resistivity of 50 Ω m. As we can expect, parametric predicted results provide us an estimated image which has spread around the location of the true model shown in Figs. 5 and 6. As the noise is presented, the parametric inversion iterates 15 times with a misfit error of 11%. It is very difficult to map the boundary of irregular model accurately, but one can precompute the objective domain and keep it unchanged during the resistivity image inverse process. Based on the diffuse and unclear predicted model provided by the parametric inverse, the resistivity inverse image better defines the boundary of the tilted irregular dyke by iterating 10 times with a misfit error of 6%.

We also designed a low resistivity model of 4 Ω m compared with the background resistivity of 25 Ω m to simulate the mixed liquor filled in reservoir stratums after oil recovery. For completeness, we used the same tilted dyke shown in Fig. 1 as the space of reservoir stratum is not changed during the entire process of the inject water recovery. One can note that the predicted results of the low resistivity model provide a clear image of tilted irregular dyke by using preconditioned inverse shown in Figs. 7 and 8.

Fig. 7

Vertical cross-sections of the low resistivity true model and predicted model from noisy synthetic BSEM data

Fig. 8

Slices of the low resistivity true model and predicted model from noisy synthetic BSEM data

In the framework of parametric inverse in this paper, the inclined model was dominated by different lengths and dip angles of a horizontal regular cuboid in three dimensions. As a result, we can obtain the symmetry sections or slices about the center of the model shown in figures. In some practical applications for BSEM, it is easy to estimate the depth information of rock formation by logging technology or geologic information. Thus, we do not consider the depth herein. It is difficult to obtain an accurate inverse result with an artificial resistivity of the background mediums for the entire inversion process. Although there are differences between the predicted resistivity and true resistivity of the model in high or low resistivity models caused by the contaminated noise, the preconditioned inversion algorithm provides a perfect reconstruction of the true model.

4.2 Model Embedded in Layered Background

The preconditioned inversion algorithm is also tested on a typical geoelectrical model with a layered background. It may find wide application in the oil exploration inversion problem with layered reservoir stratum, where we must consider the large range of layered background during the iterative inversion in order to approximate the practical situation accurately. The traditional resistivity image inverse based on the IE method forward considers the anomalous body and the layered background together in a local cubic to decrease the required computer memory and computational time, allowing us to overcome the large computation as the parametric inversion provides an objective layered background and keeps it unchanged during the entire inversion process, thereby significantly increasing the size of the inversion domain.

The layered background consists of three layers with a thickness of 250 m and 60 m. The true resistivities of three layers are 50 Ω m, 10 Ω m and 150 Ω m respectively. The tilted irregular dyke model and the observation system of BSEM are exactly the same as in Figs. 1 and 2. In this case, we consider a model with resistivity of 25 Ω m embedded in layered background. To simulate the complex geoelectrical situation, we design different sections of the model with layered background, such as model adjacent to formation interface, filled in interlayer and cross three layers background, as shown in Figs. 9 and 10. Again, the BSEM data used in preconditioned inversion for layered medium background model is added the Gaussian noise of 5%.

Fig. 9

Vertical cross-sections of the low resistivity true model and predicted model with layered background from noisy synthetic BSEM data

Fig. 10

Slices of the low resistivity true model and predicted model with layered background from noisy synthetic BSEM data

As expected, the parametric predicted results reconstruct the layered background with resistivities of 45 Ω m, 8 Ω m and 160 Ω m by iterating 15 times. For the BSEM data with 5% noise, while the misfit is 13% as the parametric inversion provides only a diffuse and unclear predicted model. One can also observe that the normal level of 5% is not sensitive to the inverted results as the parameters of layered background considered in parametric inversion. However, the parametric predicted model will be helpful in resistivity image inverse, which reconstructs the true model efficiently. Once the resistivity of layered medium is preconditioned, one long outstanding problem with iterative-based inversion schemes is solved with the accuracy of first guess values. Like other least square techniques, BSEM requires the first guess values to be as close as possible to the actual solution in order to guarantee stable convergence. As shown in Figs. 9 and 10, the misfit is 8% and the inverted results by resistivity image based on the first guess values is reasonable for the complex reservoir exploration interpretation, even in that case with noise interference. Therefore, the parametric inversion method proposed in this paper offers one potential solution for the long outstanding problem in iterative-based inversion schemes.

5 Conclusions

A preconditioned inversion algorithm of three-dimensional borehole to surface electromagnetic based on the IE method forward and least squares inversion has been developed and demonstrated in complex structure with homogeneous half space and layered background. Take full advantage of the IE method as it needs fewer grids covering the anomalous domain with only a few parameters, and the background resistivity can be considered into the inversion process. We have presented a parametric inversion for BSEM exploration based on the IE method, which provides an preconditioned inversion domain which can be kept unchanged during the entire inverse process. The remarkable property of the preconditioned algorithm is that one can precompute the Green’s function vector only once and keeping them unchanged, update the Jacobin matrix just by submitting the updated electromagnetic fields and the updated resistivity model. As a result, the preconditioned inversion based on IE method is very efficient for BSEM. Synthetic noisy examples of three dimensional BSEM in tilted irregular structures with homogeneous and layered background suggest that the preconditioned inversion algorithm provides a clear image of the true model. To widely apply BSEM technology in oil field exploration, it is necessary to develop the parallel algorithm for the preconditioned inversion in the future.

Appendix: Some Values of Partial Derivatives \(\frac{{\partial u_{{_{j} }} }}{{\partial \sigma_{i} }}\)

In the framework of IE method, taking into account that the model parameterization is to divide a model into blocks of unknown constant conduction, the Eq. (17) can also be written as

$$\frac{{\partial E(r_{{_{j} }}^{'} )}}{{\partial \sigma_{i} }} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E}^{i} \cdot E^{a} (r_{i}^{{}} ) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E} \cdot \Delta \sigma \cdot \frac{{\partial E^{a} (r)}}{{\partial \sigma_{i} }}$$

(21)

where

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E}^{i} = \left[ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{1i} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{1i} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{1i} } \\ \vdots & \vdots & \vdots \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{Mi} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{Mi} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{Mi} } \\ \end{array} } \right],\;E^{a} (r_{i} ) = \left[ {\begin{array}{*{20}c} {E_{x}^{a} (r_{i} )} \\ {E_{y}^{a} (r_{i} )} \\ {E_{z}^{a} (r_{i} )} \\ \end{array} } \right]$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{E} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{11} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{11} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{11} } \\ \end{array} } & \ldots & \ldots & {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{1N} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{1N} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{1N} } \\ \end{array} } \\ \vdots & \cdots & \cdots & \vdots \\ \vdots & \cdots & \cdots & \vdots \\ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{M1} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{M1} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{M1} } \\ \end{array} } & \cdots & \cdots & {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{MN} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{MN} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{MN} } \\ \end{array} } \\ \end{array} } \right]$$

$$\frac{{\partial E^{a} (r)}}{{\partial \sigma_{i} }} = \left[ {\begin{array}{*{20}c} {\frac{{\partial E_{x}^{a} (r_{1}^{{}} )}}{{\partial \sigma_{i} }}} & {\frac{{\partial E_{y}^{a} (r_{1}^{{}} )}}{{\partial \sigma_{i} }}} & {\frac{{\partial E_{z}^{a} (r_{1}^{{}} )}}{{\partial \sigma_{i} }}} & \cdots & {\frac{{\partial E_{x}^{a} (r_{N}^{{}} )}}{{\partial \sigma_{i} }}} & {\frac{{\partial E_{y}^{a} (r_{N}^{{}} )}}{{\partial \sigma_{i} }}} & {\frac{{\partial E_{z}^{a} (r_{N}^{{}} )}}{{\partial \sigma_{i} }}} \\ \end{array} } \right]^{T}$$

The Eq. (19) can be expressed as

$$\frac{{\partial E^{a} (r)}}{{\partial \sigma_{i} }} = - M^{ - 1} \cdot \frac{\partial M}{{\partial \sigma_{i} }} \cdot E^{a} (r)$$

(22)

where

$$M = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\Delta \sigma_{1} G_{xx}^{11} - 1} & {\Delta \sigma_{1} G_{xy}^{11} } & {\Delta \sigma_{1} G_{xz}^{11} } \\ {\Delta \sigma_{1} G_{yx}^{11} } & {\Delta \sigma_{1} G_{yy}^{11} - 1} & {\Delta \sigma_{1} G_{yz}^{11} } \\ {\Delta \sigma_{1} G_{zx}^{11} } & {\Delta \sigma_{1} G_{zy}^{11} } & {\Delta \sigma_{1} G_{zz}^{11} - 1} \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {\Delta \sigma_{N} G_{xx}^{1N} } & {\Delta \sigma_{N} G_{xy}^{1N} } & {\Delta \sigma_{N} G_{xz}^{1N} } \\ {\Delta \sigma_{N} G_{yx}^{1N} } & {\Delta \sigma_{N} G_{yy}^{1N} } & {\Delta \sigma_{N} G_{yz}^{1N} } \\ {\Delta \sigma_{N} G_{zx}^{1N} } & {\Delta \sigma_{N} G_{zy}^{1N} } & {\Delta \sigma_{N} G_{zz}^{1N} } \\ \end{array} } \\ \vdots & \ddots & \vdots \\ {\begin{array}{*{20}c} {\Delta \sigma_{1} G_{xx}^{N1} } & {\Delta \sigma_{1} G_{xy}^{N1} } & {\Delta \sigma_{1} G_{xz}^{N1} } \\ {\Delta \sigma_{1} G_{yx}^{N1} } & {\Delta \sigma_{1} G_{yy}^{N1} } & {\Delta \sigma_{1} G_{yz}^{N1} } \\ {\Delta \sigma_{1} G_{zx}^{N1} } & {\Delta \sigma_{1} G_{zy}^{N1} } & {\Delta \sigma_{1} G_{zz}^{N1} } \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {\Delta \sigma_{N} G_{xx}^{NN} - 1} & {\Delta \sigma_{N} G_{xy}^{NN} } & {\Delta \sigma_{N} G_{xz}^{NN} } \\ {\Delta \sigma_{N} G_{yx}^{NN} } & {\Delta \sigma_{N} G_{yy}^{NN} - 1} & {\Delta \sigma_{N} G_{yz}^{NN} } \\ {\Delta \sigma_{N} G_{zx}^{NN} } & {\Delta \sigma_{N} G_{zy}^{NN} } & {\Delta \sigma_{N} G_{zz}^{NN} - 1} \\ \end{array} } \\ \end{array} } \right]$$

$$E^{a} (r) = \left[ {\begin{array}{*{20}c} {E_{x}^{a} (r_{1}^{{}} )} & {E_{y}^{a} (r_{1}^{{}} )} & {E_{z}^{a} (r_{1}^{{}} )} & \cdots & {E_{x}^{a} (r_{N}^{{}} )} & {E_{y}^{a} (r_{N}^{{}} )} & {E_{z}^{a} (r_{N}^{{}} )} \\ \end{array} } \right]^{T}$$

where $E_{x}^{a} (r_{i}^{{}} )$, $E_{y}^{a} (r_{i}^{{}} )$ and $E_{z}^{a} (r_{i}^{{}} )$ are the three electrical field components of i th anomalous cell, which can be computed by solving the Eq. (3), the ‘T’ denotes the transposition of matrix, the $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{x}^{{}}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{y}^{{}}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}_{z}^{{}}$ are the three components of the Green function correspond to receivers, and the $G_{xx}^{{}}$, $G_{xy}^{{}}$ and $G_{xz}^{{}}$ are the components of the Green function correspond to the receivers inside the anomalous body.