1 Introduction

The possibility of fault reactivation during fluid injection activities represents one of the most important aspects that have to be accurately estimated to reduce the risk of leakage and hence to maintain the integrity of a storage aquifer. Indeed, faults can represent excellent impermeable barriers that constrain the fluids to remain inside the reservoir or storage aquifer. However, if the critical frictional strength is overcome, faults reactivate triggering slips (e.g. earthquake). During this phase, the fault permeability could suddenly increase and hence, faults could become preferential pathways for the migration of fluids away from the reservoir (Caine et al. 1996; Wiprut and Zoback 2000; Uehara and Shimamoto 2004). Recent works have demonstrated a strict correlation between the increase of microseismicity rates and fluid injection (Weingarten et al. 2015). Only few evidences of moderate earthquakes have been linked to fluid injection, in particular by injection of wastewater where large volumes of fluids are involved (Keranen et al. 2013; Rubinstein et al. 2014). Understanding the fault mechanics and the architecture of the fault zone became hence a fundamental issue to be considered during fluid injection activities. Slip tendency, maximum expected slip magnitude and Coulomb stress change analysis have been used to understand the behavior of natural earthquakes and hence can be applied also to the study of induced and triggered earthquakes (Moeck et al. 2009; Catalli et al. 2013; Troiano et al. 2013; McGarr et al. 2014; Sumy et al. 2014). However, only coupled fluid flow and geomechanical deformation models can aim at successfully understanding the evolution of pore pressure and rock deformation due to fluid injection in the subsurface. For this reason, an accurate numerical model for the faults is fundamental (Rutqvist et al. 2008; Cappa and Rutqvist 2011a, b; Jha and Juanes 2014). Two main approaches have been proposed in the literature to model the fault deformation: explicit representation of the fault plane with interface elements (e.g. Aagaard et al. 2013 and references therein) and equivalent continuum representation of the fault zone with solid elements (Cappa and Rutqvist 2011a, b). The first one has the advantage to constrain the slip along a surface through realistic friction constitutive law [e.g. rate and state friction (Dieterich 1979)], and the second one is better suited for the simulation of the evolution of the deformation across the fault zone during the interseismic and postseismic phases of the seismic cycle. However, in the equivalent continuum method, the displacement is computed as a continuum function, yielding a poor approximation of the slip itself and, thus, also a poor approximation of the magnitude of the triggered earthquake compared to the one obtained with the explicit representation. These approaches generally do not take into account changes in the hydromechanical properties within the fault zone. In fact, two main hydromechanical layers characterize a fault zone: the fault core and the damage zone. The fault core is composed mainly of breccia and gouge, and is characterized by fine-grain material that is continuously crumbled during several earthquakes. This layer represents the part of the fault zone with the lowest permeability. Most of the coseismic slip occurs along rupture surfaces inside the fault core (Sibson 2003). The damage fault zone is a wider layer that surrounds the fault core and features lenses of breccia and a network of macroscopic fractures. This is the most permeable layer of the fault zone. Experimental results show that the permeability of the damage zone can be one to three orders of magnitude greater than the permeability of protolith and four to six orders of magnitude greater than the permeability of the core, both in dip and in normal direction with respect to the fault plane (Talwani and Acree 1984; Oda et al. 1987; Bruhn et al. 1994; Caine et al. 1996; Wibberley and Shimamoto 2003; Townend and Zoback 2000; Mitchell and Faulkner 2012; Lockner et al. 2009). The variability strictly depends on the lithology and its level of chemical and physical alteration (Caine et al. 1996).

In this work, we perform three-dimensional coupled fluid flow and geomechanical deformation simulations of fault reactivation by water injection. We aim at studying the behavior of the reservoir system in simultaneous presence of two factors: the frictional contacts of the faults, modelled by interface elements, and the spacial variability of the permeability in the fault zones. To the best of our knowledge, no pre-existing published work focused on the effects of these two important factors. Moreover, we let the fault zone permeability vary both in the dip and in the normal direction with respect to the fault plane and we consider different permeability contrast between protolith rocks and damage zone and between damage zone and caprock. We demonstrate that the anisotropy of the fault zone permeability has a strong impact both on the timing and on the magnitude of triggered earthquakes.

2 Hydro-Mechanical Modelling of Faulted Storage Aquifers

2.1 Governing Equations in Porous Media

Assuming small deformations and isothermal conditions, the governing equations for coupled flow and geomechanics are derived from conservation of mass and balance of linear momentum. The quasi-static governing equations for linear momentum balance of the solid/fluid system on a 3D spatial domain \(\Omega\) can be expressed as

$$\begin{aligned} \nabla \cdot \varvec{\sigma }+ \rho _\mathrm{b} \varvec{g} = \varvec{0} \quad \text{ in } \Omega \end{aligned}$$
(1)

with \(\varvec{\sigma}\) the Cauchy total stress tensor, \(\varvec{g}\) the gravity acceleration vector, \(\phi _\mathrm{b} = \phi \rho _\mathrm{f} + (1 - \phi )\rho _\mathrm{s}\) the bulk density, \(\rho _\mathrm{f}\) the total fluid density, \(\rho _\mathrm{s}\) the solid-phase density and \(\phi\) the porosity, that is the ratio of voids to the total volume. In this work, we consider an isothermal single-phase flow of a fluid (water) with no stress dependence on permeability in the bulk, so that the single fluid mass conservation equation reduces to

$$\begin{aligned} \dfrac{\mathrm{d} m}{\mathrm{d} t} + \nabla \cdot \varvec{w} = \rho _\mathrm{f} f, \end{aligned}$$
(2)

where m is the fluid mass, f is the volumetric source, \(\varvec{w} = \rho _\mathrm{f} \ \varvec{v}\) is the fluid mass flux and \(\varvec{v}\) is the fluid velocity given by Darcy law:

$$\begin{aligned} \varvec{v} = - \dfrac{\varvec{k}}{\mu _f}(\nabla p_f - \rho _f \varvec{g}), \end{aligned}$$
(3)

where \(\varvec{k}\) is the permeability, \(\mu _\mathrm{f}\) is the fluid dynamic viscosity and \(p_\mathrm{f}\) is the pore fluid pressure (Bear 1972). Variations of pore fluid pressure affect the effective stress. We assume that the porous medium is fully saturated with water. In this way, the relationship between effective stress (\(\varvec{\sigma }'\)), total stress (\(\varvec{\sigma }\)) and pore pressure (\(p_\mathrm{f}\)) reduces to the Terzaghi effective stress principle:

$$\begin{aligned} \varvec{\sigma }' = \varvec{\sigma }+ p_\mathrm{f}. \end{aligned}$$
(4)

Then the deformation of the porous medium affects the fluid mass in the voids and hence, the porosity itself and the pore pressure.

2.2 Fault Zone Representation by Coupled Interface-Solid Elements

To model the deformation along the fault plane, we use an explicit representation of the fault with interface elements (see Fig. 2 for a schematic representation in a two-dimensional domain where, thus, the faults are represented by one-dimensional lines and the elements are indeed one-dimensional segments). The nodes of the mesh along the fault surfaces are duplicated, new node-IDs are assigned to the new nodes, and the mesh connectivity is updated. In this way, each fault is characterized by two surfaces (lines in 2D) that are geometrically coincident but distinct from the numerical point of view: one surface belongs to the hanging-wall block and the second one to the footwall block (Fig. 2). This split node procedure allows us to compute a different displacement for the two surfaces: we denote \(\varvec{u}_+\) the displacement of the nodes lying on the hanging wall surface and \(\varvec{u}_-\) the one of footwall surface nodes. The definition of the slip \(\varvec{d}\) on the fault surface is then straightforward:

$$\begin{aligned} \varvec{d} = \varvec{u}_+ - \varvec{u}_- . \end{aligned}$$
(5)

We are interested in modeling buried faults and, moreover, we assume that no crack propagation phenomena are occurring; thus, to avoid numerical instabilities we duplicate only the nodes that are strictly internal to the surface, thus keeping unique the ones lying on the fault boundary perimeter. This procedure is not necessary in case the fault’s perimeter lies on the boundaries of the entire domain itself.

Fig. 1
figure 1

View of the fault zone representation considered in this work.

Full size image
Fig. 2
figure 2

Two-dimensional representation of the node split for a single fault (a) and for a T-shape intersection (b). Each one of the red nodes is split into two geometrically coincident nodes, while the fault’s boundary blue nodes are kept as unique nodes. The yellow node in (b), as an internal node of the fault F1, is also split into two green nodes. The white space between the green nodes is not a physical space but rather an artificial space added for the sake of an easier graphical representation

Full size image

Furthermore, we aim at enriching our model with an additional features that augment its complexity: in fact, we are interested in modelling also intersecting faults and, in particular, T-shape intersections. These faults are treated as non-intersecting faults and the nodes along the tip line of the first fault are merged with the one along the hanging-wall or footwall surface of the second fault (depending on the location of the second fault, Fig. 2b). The fault reactivation is modeled by Amonton’s law:

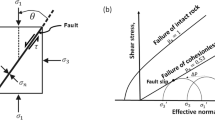
$$\begin{aligned} \tau = \mu \sigma _\mathrm{n}', \end{aligned}$$
(6)

where \(\sigma _\mathrm{n}' = (\varvec{\sigma }\varvec{n})\cdot \varvec{n}\) is the effective normal traction (\(\varvec{n}\) is the normal vector to the fault surface, \(\sigma _\mathrm{n}' = \sigma _\mathrm{n} - p_\mathrm{f}\); \(\sigma _\mathrm{n}\) is positive in compression), \(\tau = \varvec{\sigma }\varvec{n} - \sigma _\mathrm{n} \varvec{n}\) is the shear stress modulus, and \(\mu\) is the sliding friction [e.g. \(\mu = 0.6-0.8\) (Byerlee 1978); \(\mu \le 0.4\) depending on the presence of clay mineral (Saffer and Marone 2003; Brown et al. 2003; Collettini et al. 2009; Lockner et al. 2011)]. From (6), we calculate the slip tendency (ST) factor as the ratio of shear stress to normal stress acting on the plane of weakness (Streit and Hillis 2004):

$$\begin{aligned} \mathrm{ST} = \tau / \sigma _\mathrm{n}'. \end{aligned}$$
(7)

The slip tendency indicates if one fault is in a stable or unstable state of stress: if ST\(< \mu\) the state of stress is stable and no slip occurs along the fault plane. Otherwise, if ST\(\ge \mu\) the strength of the fault is overcome and slip starts to propagate along the fault plane. We use a static friction constitutive model to describe the evolution of the slip after the rupture. In this model \(\mu\) is constant, meaning that once the fault strength is overcome, the fault slips at a steady rate. To model the spatial variation of the fault zone permeability, a local mesh refinement is performed around the fault surfaces along the normal direction. The damage zone and the fault core are discretized in one elements and four elements layers, respectively (Fig. 1). Appropriate hydro-mechanical properties are associated with these elements (see Sect. 2.4).

2.3 Coupled Fluid–Solid–Fault System of Equations

We aim at writing the coupled system of equations together with the contact constrain that is needed to be solved to model a reservoir in the presence of faults. Let us denote \(\Omega\) the entire domain and \(\Gamma = \cup _i \Gamma _i\) the union of the surfaces \(\Gamma _i\) composing the fault system. After some manipulation of (1), (2), the system of equations can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} &{} \nabla \cdot (\varvec{\sigma }'(\varvec{u}) - p_\mathrm{f}) + \rho _b \varvec{g} = \varvec{0} &{} \text{ in } \Omega \\ &{} \dfrac{1}{M} \dfrac{\partial p_\mathrm{f}}{\partial t} + \dfrac{\partial \varepsilon _v(\varvec{u})}{\partial t} - \rho _f \nabla \cdot \bigg (\dfrac{\varvec{k}}{\mu _\mathrm{f}} \nabla p_\mathrm{f} - \rho _\mathrm{f} \varvec{g} \bigg ) = \rho _f f &{} \text{ in } \Omega \\ &{}\varvec{d} = \varvec{0} \quad \text{ if } \mathrm{ST} < \mu &{} \text{ on } \Gamma \\ &{}\varvec{u}_+ - \varvec{u}_- - \varvec{d} = \varvec{0} \quad \text{ if } \mathrm{ST} \ge \mu &{} \text{ on } \Gamma \end{array} \right. \end{aligned}$$
(8)

where M is the Biot modulus that depends on the fluid compressibility and the bulk modulus of the solid grain,

$$\begin{aligned} \varvec{\sigma }'(\varvec{u}) =C_\mathrm{dr} : \varvec{\varepsilon }\quad \text{ and } \quad \varepsilon _\mathrm{v}(\varvec{u}) = tr(\varvec{\varepsilon }) \end{aligned}$$
(9)

with

$$\begin{aligned} \varvec{\varepsilon }:= \dfrac{1}{2}(\nabla \varvec{u} + \nabla ^T \varvec{u}) \end{aligned}$$
(10)

and \(C_\mathrm{dr}\) is the tensor of the coefficients that define the constitutive stress strain relation of the poroelastic material. The unknowns of system (8) are indeed the displacement \(\varvec{u}\), the slip field \(\varvec{d}\), and the pore fluid pressure \(p_\mathrm{f}\). The effective and total stress fields \(\sigma\) and \(\sigma '\), as well as the deformations \(\varepsilon\) and the slip tendency ST depend on the values of the unknown fields and can be calculated once the system variables are computed. The other symbols apprearing in (8), i.e. \(\rho _\mathrm{f}\), \(\rho _\mathrm{s}\), \(\rho _\mathrm{b}\), f, \(\varvec{g}\), \(\varvec{k}\), \(\mu _\mathrm{f}\), \(C_\mathrm{dr}\), M, and \(\mu\), are parameters and/or input data and their values will be specified in Sect. 2.4.

System (8) is then endowed by boundary conditions on \(\partial \Omega\). Moreover, an equilibrium solution for \(\varvec{u}\) and \(p_f\) is computed and used as temporal initial condition. More details about boundary and initial conditions are described in Sect. 2.4.

We refer to the work of Jha and Juanes (2014) for a complete mathematical description of poroelasticity for single and multiphase fluid system and for the details about the derivation of the equations of system (8). There are two common approaches to solve the coupled balance (Eqs. 1, 2, 8). One is the sequential solution method that consists of solving first the stress balance equation and, second, using these results to solve the mass balance equation. The results of the second step are then plugged in the stress balance equation to compute again the displacement and the stress state of the system [e.g. Rutqvist et al. (2002); Kim et al. (2011); Jha and Juanes (2014)]. The second approach consists of solving the coupled system directly. This approach is used by the commercial software package ABAQUS/Standard (ABAQUS 2013) that is used in this work to perform the coupled pore pressure and stress analysis of faulted storage aquifers.

2.4 Model Setup

The geometry consists of a block of \(25 \times 25 \times 6\) km with different horizontal layers representing the permeable storage aquifer, the low-permeable cap rocks and the upper and basal aquifers (Fig. 3a, b). The storage aquifer, the cap rocks and part of the upper aquifer are cut by a fault system that is characterized by four \(45^{\circ }\) dipping faults and two vertical faults. The vertical faults are located in the central part of the block and forming a T-shaped intersection with two of the \(45^{\circ }\) dipping faults (Fig. 3c).These faults, together with the cap rocks, define the limits of the volume of storage aquifer where water injection is simulated. Two other smaller faults are present inside the storage aquifer (Fig. 3b, c). They are cutting the same horizontal multilayer domain without intersecting the vertical faults.

The simulation consists of two different steps. In the first one, we apply a gravitational loading and an initial stress field on the entire model (geostatic step). We define a compressive stress regime where the maximum (SH) and middle (Sh) stress axis are horizontal and parallel to the x-and y-axis; respectively. The minimum stress axis is vertical (Sv). The ratios between SH and Sv is 2.2 and the one between Sh and Sv is 1.5. These are chosen to obtain an initial value of slip tendency near to the critical one along the \(45^{\circ }\) dipping faults (a critical slip tendency of 0.4 is assumed). In this step, the model sides and bottom are fixed in normal direction, whereas the top of the model is free to move in all directions. We consider a hydrostatic initial pore pressure on the nodes of the entire model and this pore pressure maintained the hydrostatic value along the boundaries at all times. In this way, no variation of pore pressure can occur along the boundaries.

After this first step, the system is at equilibrium and the solution is used as the initial condition for the second step. Fluid injection is simulated (ABAQUS 2013) by applying at one node at a depth of 2250 m into the storage aquifer (Fig. 3c). The pressurized zone is located at a distance of about 1 km from the reservoir-bounding fault F1 and from the fault F2 located in the inner part of the reservoir (Fig. 3b, c). The total volume of water injected is equal to 98 m\(^3\) over 24 steps following the cubic function represented in Fig. 4. The boundary conditions are the same as the one for the geostatic step. The hydro-mechanical properties for the faulted storage aquifer-caprock system are described in Tables 1, 2 and 3. The properties that define each layer are always the same for all the different settings considered in this work. Only the permeability across the damage zone and the fault core varies depending on the distance from the fault surface (Fig. 1).

Depending on different permeability contrasts between protolith and damage zone (\(k_\mathrm{d}/k_\mathrm{p}\)) and between damage zone and fault core (\(k_\mathrm{d}/k_\mathrm{c}\)), six model sets are studied (Tables 2, 3). In Model\(_1\) the permeability of the damage zone is one order of magnitude higher than the permeability of the protolith (\(k_\mathrm{d}/k_\mathrm{p} = 10^1\)). Note that this contrast is always maintained constant depending on the type of protolith that the damage zone intersects. Concerning the fault core, its permeability is maintained constant at a value of \(10^{-22}\) m\(^2\), hence the contrast between damage zone and fault core is variable in space across layers (Tables 2, 3). As in the Model\(_1\), also in Model\(_2\), the permeability of the damage zone is one order of magnitude higher than the permeability of the protolith (\(k_\mathrm{d}/k_\mathrm{p} = 10^1\), Tables 1, 2, 3). The only difference is that, in this model, the permeability of the fault core is maintained constant at a value of \(10^{-16}\) m\(^2\) (Tables 2, 3). In Model\(_1\) and Model\(_2\), we consider only the end-member values of fault core permeability found in the literature (Forster and Evans 1991; Caine et al. 1996; Mitchell and Faulkner 2012). On the contrary in the other models, we assume a direct correlation between the fault core permeability and the permeability of the protolith rocks (Caine et al. 1996). In this way, the permeability contrasts between damage zone and fault core (\(k_\mathrm{d}/k_\mathrm{c}\)) are maintained constants depending on the type of protolith that the fault core intersects. In particular in Model\(_3\), the permeability of the damage zone is one order of magnitude higher than the permeability of the protolith (\(k_\mathrm{d}/k_\mathrm{p} = 10^1\); Tables 1, 2, 3), whereas the fault core permeability is four orders of magnitude lower than the permeability of the damage zone (\(k_d/k_c = 10^4\); Tables 2, 3). In Model\(_4\), the permeability of the damage zone is still one order of magnitude higher than the permeability of the protolith (\(k_d/k_p = 10^1\); Table 1, 2, and 3) but the fault core permeability is in this case five orders of magnitude lower than the permeability of the damage zone (\(k_d/k_c =10^5\); Tables 2, 3). In Model\(_5\), the permeability of the damage zone is two orders of magnitude higher than the permeability of the protolith (\(k_d/k_p = 10^2\); Tables 1, 2, and 3) and the fault core permeability is five orders of magnitude lower than the permeability of the damage zone (\(k_d/k_c = 10^5\); Tables 2, 3). In the last model (Model\(_6\)), the permeability of the damage zone is two orders of magnitude higher than the permeability of the protolith (\(k_\mathrm{d}/k_\mathrm{p} = 10^2\); Tables 1, 2, and 3) and the fault core permeability is in this case six orders of magnitude lower than the permeability of the damage zone (\(k_\mathrm{d}/k_\mathrm{c} = 10^6\); Tables 2, 3).

Fig. 3
figure 3

a Model geometry for the coupled simulation of water injection and fault slip. b Cross-sections along the xz-plane and c xy-plane crossing the water injection point. Note that the F1 and F4 faults form T-shape intersections with the F6 and F5 faults. The hydro-mechanical properties are described in Table 1. The black points on the F1, F2, F3 and F4 faults represent the location where \(\Delta \sigma _\mathrm{n}'\), \(\Delta \tau\) and slip are calculated in Figs. 5 and 7

Full size image
Fig. 4
figure 4

Volume of water injected for every simulation step. The total volume of water injected at the end of the numerical simulation is 98 m\(^3\)

Full size image
Table 1 Material properties used to simulate water injection in a faulted storage aquifer–caprock system
Full size table
Table 2 Variation of permeability across the damage zone for different models considered
Full size table
Table 3 Variation of permeability across the fault core for different models considered
Full size table

3 Results

Figure 5 shows the variation of the effective normal stress (\(\Delta \sigma _\mathrm{n}'\)) and shear stress (\(\Delta \tau\)) calculated on the faults F1, F2, F3 and F4 for different models. The points where \(\Delta \sigma _\mathrm{n}'\) and \(\Delta \tau\) are calculated have the same y and z coordinates as the injection point and hence are located in the storage aquifer (the location is shown in Fig. 2c). \(\Delta \sigma _\mathrm{n}'\) and \(\Delta \tau\) are obtained as the difference of the values \(\sigma _\mathrm{n}'\) and \(\tau\) calculated in the injection step minus the values of \(\sigma _\mathrm{n}'\) and \(\tau\) calculated at the initial geostatic step (squares along the color lines in Fig. 5).

Fig. 5
figure 5

Evolution of the effective normal stress \(\Delta \sigma _\mathrm{n}'\) and shear stress \(\Delta \tau\) variations along F1, F2, F3 and F4 faults for different models. Note the drop of shear stress when the faults reach the failure

Full size image

For all the faults in Fig. 5, we observe that \(\Delta \sigma _\mathrm{n}'\) always decreases as a consequence of an increase in the pore pressure. The only difference is that the magnitude of this drop depends mainly on the contrast of permeability between damage zone and protolith rock. In fact, by considering fault F1 (Fig. 5a) we observe that the evolution of \(\Delta \sigma _n'\) is very similar for the Model\(_1\), Model\(_2\), Model\(_3\) and Model\(_4\). At the end of the simulation, the effective normal stress decreases of almost 3.5 MPa. These models present the same ratio \(k_\mathrm{d}/k_\mathrm{p} = 10^1\). On the contrary, for Model\(_4\) and Model\(_5\) \(\Delta \sigma _\mathrm{n}'\) is close to 1.5 MPa. In these models, the contrast of permeability \(k_\mathrm{d}/k_\mathrm{p}\) is equal to \(10^2\). If on one hand, the contrast of permeability \(k_\mathrm{d}/k_\mathrm{p}\) determines the evolution of \(\Delta \sigma _\mathrm{n}'\) on the fault plane, on the other hand the contrast of permeability \(k_\mathrm{d}/k_\mathrm{c}\) affects the evolution of \(\Delta \tau\).

Fig. 6
figure 6

Variation of pore pressure after 98 m\(^3\) of injected water

Full size image

Let us consider again the trends of \(\Delta \sigma _n'\) and \(\Delta \tau\) on the fault F1 (Fig. 5a). Model\(_1\) and Model\(_2\) have the same contrast of permeability between damage zone and protolith rock (\(k_\mathrm{d}/k_\mathrm{p}= 10^1\)) but different contrasts of permeability between damage zone and fault core. Note that this contrast \(k_\mathrm{d}/k_\mathrm{c}\) is not constant along the dip of the faults, because in these models we assume uniform permeability values of the fault core in the direction of the fault dip. For this reason, the contrast \(k_\mathrm{d}/k_\mathrm{c}\) varies depending on the type of protolith that the fault intersects (Tables 2, 3). For example, the contrast of permeability \(k_\mathrm{d}/k_\mathrm{c}\) inside the storage aquifer is equal to \(10^1\) and \(10^4\) for the Model\(_1\) and Model\(_2\), respectively, while the contrast of permeability \(k_\mathrm{d}/k_\mathrm{c}\) inside the caprock is equal to \(10^4\) and \(10^2\) for the Model\(_1\) and Model\(_2\), respectively. Hence in the Model 1, water is well compartmentalized both in the normal direction and along the dip direction respect to the fault plane. For this reason, the shear stress increases more in Model\(_1\) than in Model\(_2\) where the fault F1 never reaches the failure (Fig. 5a). Model\(_3\) and Model\(_4\) have the same contrast of permeability between damage zone and protolith rock (\(k_\mathrm{d}/k_\mathrm{p} = 10^1\)) but different contrasts of permeability between damage zone and fault core. In these cases, the contrast \(k_\mathrm{d}/k_\mathrm{c}\) is constant along the dip of the faults. Indeed, the contrast of permeability \(k_\mathrm{d}/k_\mathrm{c}\) inside the storage aquifer and caprock is always equal to \(10^4\) and \(10^5\) for Model\(_3\) and Model\(_4\), respectively. In Model\(_4\), the fault F1 reaches failure before Model\(_3\) with a trend very similar to that obtained for the Model\(_1\) (Fig. 5a). The evolution of \(\Delta \sigma _n'\) and \(\Delta \tau\) is very similar for the other faults (Fig. 5b–d) but with different times of failure depending on the distance between the injection point and the faults. F2 fault is the only one that reaches failure in all the models. The effects of the contrast of permeability between the fault core and damage zone on \(\Delta \tau\) are well visible also by analyzing the trend of Model\(_5\) and Model\(_6\) on the fault F2 (Fig. 5b). In these models, the ratio \(k_\mathrm{d}/k_\mathrm{p}\) is the same (\(10^2\)) but the ratio \(k_\mathrm{d}/k_\mathrm{c}\) is equal to \(10^5\) and \(10^6\) for Model\(_5\) and Model\(_6\), respectively. Also in these cases, by considering the same \(\Delta \sigma _n'\), the fault F2 reaches the failure earlier in Model\(_6\) than Model\(_5\). Note that \(\Delta \tau\) increases until the strength of the fault is overcome and then it decreases continuously following the static friction law.

Fig. 7
figure 7

Slip evolution along the F1, F2, F3 and F4 faults for different models

Full size image

Figure 6 shows the variation of the pore pressure after 98 m\(^3\) of injected water. It is well visible that the contrast of permeability between the damage zone and protolith rock has a larger effect on the pore pressure distribution than the contrast of permeability between the damage zone and fault core. In fact in Model\(_5\) and Model\(_6\) (Fig. 6e, f) where \(k_\mathrm{d}/k_\mathrm{c} = 10^2\), the variation of pore pressure on the injection point is less than the other models where \(k_\mathrm{d}/k_\mathrm{c} = 10^1\). This effect is partially due to the proximity of the injection point to the damage zone and partially to the larger thickness of the damage zone with respect to the fault core.

Fig. 8
figure 8

Cumulative slip along the F1, F2 and F3 faults for different models

Full size image

Figure 7 shows the slip evolution along the F1, F2, F3 and F4 faults for different models. Slip is calculated on points located in the central part of each fault inside the storage aquifer (Fig. 3c). In this figure, we observe the steps where the faults starts to slip. Slip on one fault occurs before than others in the models where the fluids are well compartmentalized by the fault core, both in the normal and dip direction to the fault plane (Model\(_1\), and Model\(_4\)). In other models, no slip occurs because large values of permeability of the damage zone allow the fluids to move freely into the storage aquifer, without generating high values of pore pressure (e.g. Model\(_5\) and Model\(_6\) on fault F1 and F2). The distribution of the slip is very similar in the Model\(_1\) and Model\(_4\) (Fig. 8a, d). Note that the slip propagates outside the storage aquifer into the caprock and in same models also into the upper aquifer (Fig. 8a, c, d). In fact, fault F2 fails before the others and for this reason accumulates more slip during the different injection steps. In addition, fault F2 is narrow along the strike direction and hence the slip propagates mainly along the dip. Finally, Fig. 9 shows the vertical displacement along the xz plane cutting the injection point. Also in this case, we show the results for the last injection step and hence the vertical displacement includes the contributions both from the injected water and from the fault slip. The thrust-fault regime governs the kinematic of the faults, with the hanging wall moving up with respect to the footwall. This is also visible on the fault F2 (Fig. 9a–d).

Fig. 9
figure 9

Final vertical displacement along a x–z plane across the water injection point

Full size image

4 Discussion

Before interpreting the results, it is necessary to discuss briefly the limitations of the models. First, in all these models, a quasi-static approximation is considered to simulate the evolution of the slip along the fault. Hence no transient effects are considered. In fact, during the coseismic phase, the inertial term could be significant due to the propagation of seismic waves and hence affect the slip along the fault plane. In addition, a static friction constitutive model is used to describe the slip evolution along the fault planes. This friction model does not permit the drop between a static to a dynamic friction value [e.g. slip weakening friction (Ida 1973)] typical of earthquakes, neither the evolution of the friction during the interseismic phase of the seismic cycle [rate and state friction (Dieterich 1979)]. For this reason, the earthquake magnitude calculations will be discussed with caution. A second limitation concerns the elastic properties that, in this study, are assumed constants. Different measurements on fault rock sample demonstrate that the Young modulus and Poisson ratio can change significantly and hence can affect the stress build-up along the fault planes (Gudmundsson 2004; Faulkner et al. 2006). This choice was made consciously to estimate only the contribution of the permeability variation across the fault zone. A final limitation is related to the time-evolution of the permeability across the fault zone. Indeed, different geological (Sibson 1981; Chester et al. 1993) and seismological observations (Guglielmi et al. 2015; Improta et al. 2015) show that the permeability can vary during different phases of the seismic cycle. For example, the permeability estimated from seismicity distribution in Improta et al. (2015) reports values of \(10^{-13}\) \(m^{2}\) along a fault zone that became a preferential pathway for the migration of fluids during the first phase of wastewater injection in the Costa Molina well in the Val d’Agri oil reservoir (Southern Italy). Other real cases report coseismic permeability on the order of \(10^{-12}\) \(m^{2}\) along normal faults ruptured by \(M_w\)6 earthquakes in the Central Apennines of Italy (Antonioli et al. 2005; Malagnini et al. 2012). Well-known permeability–porosity relationships are considered in the literature Scheidegger (1974); TD (1982); Chin et al. (2000) and used in coupled fluid flow and geomechanical models [e.g. Cappa and Rutqvist (2011b)]. However, this work is more devoted to the understanding of the static aspects of triggered seismicity (e.g. timing of fault reactivation) than to the dynamic processes involved in this phenomena. However, in spite of these limitations, a number of interesting statements can be inferred on the basis of the present results. The variation of permeability along the normal direction of the fault plane affects the failure time of the faults that in these synthetic tests is expressed in terms of different steps of water injected. In particular, considering the same contrast of permeability between damage zone and protolith inside the storage aquifer, it is necessary to inject more water to reach the failure in the case where the contrast of permeability between damage zone and fault core is lower (e.g. Model\(_3\), Fig. 7). Otherwise considering the same contrast of permeability between damage zone and fault core (e.g. Model\(_4\) and Model\(_5\)), also inside the storage aquifer, it is necessary to inject more water to reach the failure in the case where the contrast of permeability between damage zone and protolith is largest (e.g. Model\(_5\)). This is because, depending on its absolute permeability, the fault core acts as a barrier to the fluid flow. More precisely, the smaller the absolute permeability is, the larger the increase of the pore pressure across the fault, which leads to a large decreasing of the effective normal stress for the same volume of water injected (Fig. 5). However, also the variation of permeability inside the fault core layer and along the tangential direction of the fault plane has a strong effect on the timing of the triggered earthquakes. Indeed by considering inside the storage aquifer the same contrast of permeability between damage zone and protolith and damage zone and fault core (Model\(_2\) and Model\(_3\)), it is necessary to inject more water to reach the failure in the case where the permeability does not change in the fault core along the tangential direction of the fault plane (Model\(_2\); Fig. 7b). This behavior is due to a different hydrological response of the fault zones. In fact in Model\(_3\), the fluids are well compartmentalized inside the reservoir due to the increase of the fault core permeability versus the caprocks layers. This leads to the increase of pore pressure relatively to the Model\(_2\) (Fig. 5), where the fault core permeability is maintained constant in the fault dip direction. Of course, this effect is more evident if the absolute permeability of the fault core is low. In the other cases, when the permeability inside the fault core is large and homogeneous, the effects of the variation of permeability along the tangential direction of the fault plane are negligible because the fault core acts like a barrier to the fluid flow. Few data of fault zone hydrological properties are available in the literature and are often based on the analysis of exhumed fault zones (Caine et al. 1996; Faulkner and Rutter 2001; Wibberley and Shimamoto 2003; Faulkner et al. 2006). However, the present models demonstrate that the spatial variation of the permeability inside the fault zone (including fault core and damage zone) affects the timing of the triggered earthquakes. This could explain the variability of cases where fluids injection does not generate relevant seismicity [e.g. Frohlich et al. (2015)]. The different contrast of permeability affects the magnitude of the triggered earthquakes (Table 4). We consider the magnitude of the final slip \(\Vert \varvec{d} \Vert\) at the last injection step to calculate the earthquake magnitude:

$$\begin{aligned} M_\mathrm{w} = \dfrac{2}{3}\log _{10}M_0 - 6.0, \end{aligned}$$
(11)

where \(M_0 = \int _{\Gamma } G \Vert \varvec{d} \Vert d\Gamma\) is the seismic moment and G is the shear modulus (Hanks and Kanamori 1979). We remark that our simulations are quasi-static. For this reason, earthquake refers to the seismic event producing an equivalent amount of slip (Jha and Juanes 2014). In Table 4, it is evident that for the same volume of injected fluid and considering the same fault, an earthquake with larger magnitude is expected when the faults act as a barrier (very low permeability) to the fluid flow both along the normal and tangential direction with respect to the fault plane (Model\(_1\) and Model\(_4\)). This aspect is fundamental to estimate the maximum earthquake magnitude expected during fluid injection. On the basis of the analysis of numerous case histories of earthquake sequences induced by fluid injection, McGarr et al. (2014) has demonstrated that the maximum earthquake magnitude is correlated to the total volume of fluid injected times the modulus of rigidity. If, on the one hand, it could be considered a fast method to estimate the maximum magnitude of the induced earthquake, on the other hand our results demonstrate that the initial state of stress along the faults as well as the hydrological properties of the fault zone could be decisive in estimating the effective magnitude of the triggered earthquakes. For this reason, we suggest that these variables should be included in new relationships devoted to estimate the effective magnitude of the induced and triggered earthquakes.

Table 4 Earthquake magnitude (\(M_w\)) calculations on well-orientend dipping faults for different models
Full size table

5 Conclusions

In this work, we studied the effects of the spatial variation of the fault zone permeability on the timing and magnitude of triggered earthquakes by water injection in synthetic faulted storage aquifers. Considering the variation of permeability along the normal direction of the fault plane, large contrasts of permeability between damage zone and protolith rocks can increase the recurrence time of the triggered earthquake. Conversely, large contrasts of permeability between damage zone and fault core can reduce the time of the triggered earthquake. However, the effects of the permeability contrast between damage zone and fault core are depending also on the absolute permeability of the fault core. The lower the absolute permeability of the fault core is, the lower the dependency of the timing of the triggered earthquake on the contrast of permeability across the damage zone and fault core. This is because the fault core acts as a localized barrier. In addition, another important conclusion is that the variation of fault core permeability along the tangential direction of the fault plane can also affect significantly the pore pressure distribution along the fault plane. This effect is evident when the permeability along the fault core varies from larger values for the part of fault core cutting the storage aquifer to lower values for the parts of fault core cutting the caprocks. In this way, the fluids are well compartmentalized, increasing the pore pressure along the fault surface. We conclude that the complex architecture of the fault zone should be included in fluid-flow and geomechanical simulations devoted to the evaluation of the stability of the faults during fluid injection. This is a fundamental step towards the understanding of the timing and magnitude of induced and triggered earthquakes.