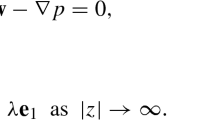Stationary Solutions to the Navier–Stokes System in an Exterior Plane Domain: 90 Years of Search, Mysteries and Insights

Abstract

In this survey, we study the boundary value problem for the stationary Navier–Stokes system in planar exterior domains. With no-slip boundary condition and a prescribed constant limit velocity at infinity, this problem describes stationary Navier–Stokes flows around cylindrical obstacles. Leray’s invading domains method is presented as a starting point. Then we discuss the boundedness and convergence of general D-solutions (solutions with finite Dirichlet integrals) in exterior domains. For the Leray solutions of the flow around an obstacle problem, we study the nontriviality, and the justification of the limit velocity at small Reynolds numbers. Further, under the same assumption of small Reynolds numbers the global uniqueness theorem for the problem is established in the class of D-solutions, its proof deals with the accurate perturbative analysis based on the linear Oseen system, inspired by classical Finn-Smith technique; the classical Amick and Gilbarg–Weinberger papers are involved here as well. The forced Navier–Stokes system in the whole plane is also presented as a closely related problem. A list of unsolved problems is given at the end of the paper.

1 Introduction

The famous Millennium problem asks, does there exist a regular global solution to the Navier–Stokes system with “good” (smooth & fast decaying) initial data? The problem is posed for three dimensional space, but for the two dimensional case the affirmative answer is well-known due to the classical results by Ladyzhenskaya. This is quite consistent with our general intuition that the three-dimensional case should be “harder” than the two-dimensional one. Surprisingly, this general intuition completely breaks down for another significant task of mathematical fluid mechanics—steady-state flow around an obstacle problem, solved for 3d case almost a century ago, but still open for 2d case:

$$\begin{aligned} \left\{ \begin{array}{l} - \Delta \textbf{w} + (\textbf{w} \cdot \nabla ) \textbf{w} + \nabla p = 0 \quad \textrm{in} \; \Omega ,\\ \nabla \cdot \textbf{w} = 0 \quad \textrm{in} \; \Omega ,\\ \textbf{w}|_{\partial \Omega } = \textbf{0}, \\ \textbf{w} \rightarrow \textbf{w}_\infty =\lambda \textbf{e}_1 \quad \text {as}\quad |z| \rightarrow \infty . \end{array} \right. \end{aligned}$$

(OBS)

Here $\Omega = {\mathbb {R}}^2 {\setminus } \bar{U}$ is an exterior plane domain, U is the corresponding bounded open set (not necessarily connected) with smooth boundary in ${\mathbb {R}}^2$; ${\textbf{w}}, p$ are the unknown velocity and pressure fields of the fluid, while ${\textbf{w}}_\infty$ is the far field constant velocity. With no loss of generality, we have set the viscosity coefficient of the fluid to be 1. The parameter $\lambda > 0$ will be referred to as the Reynolds number. Here $\textbf{e}_1=(1,0)$ is the unit vector along x-axis. Physically, the system (OBS) describes the stationary motion of a viscous incompressible fluid flowing past a rigid cylindrical body. The existence of solutions to (OBS) with arbitrary $\lambda$ was included by Professor Yudovich in the list of “Eleven Great Problems in Mathematical Hydrodynamics” [39].

The story has an initial point in the 19th century, starting with the classical paper of Stokes [37], where the famous paradox of his name was discovered, i.e., that the corresponding linearized system

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta \textbf{w} + \nabla p = 0, \\ \nabla \cdot \textbf{w} = 0, \\ \textbf{w}|_{\partial \Omega } = 0, \\ \textbf{w}(z) \rightarrow \textbf{e}_1 \quad \text {as}\quad |z| \rightarrow \infty \end{array} \right. \end{aligned}$$

(1.1)

has no solution for the considered 2d case, in contrast to the 3d situation.¹ The mathematical nature of the Stokes paradox was a subject for many investigations, see, e.g., [6, 33].

The celebrated Leray’s paper [30] can be considered as a landmark point in the study of the nonlinear problem (OBS). There, among many other results, Leray suggested the following elegant approach which was called “the invading domains method”. Denoting by ${\textbf{w}}_k$ the solution to the steady Navier–Stokes system in the intersection of $\Omega$ with the disk $B_{R_k}$ of radius $R_k\ge k$ under boundary conditions

$$\begin{aligned} {\textbf{w}}_k|_{\partial \Omega }={\textbf{0}},\quad {\textbf{w}}_k|_{S_{R_k}}=\lambda \textbf{e}_1, \end{aligned}$$

Leray showed that the sequence ${\textbf{w}}_k$ satisfies the estimate

$$\begin{aligned} \int _{\Omega \cap B_{R_k}}|\nabla {\textbf{w}}_k|^2\le c, \end{aligned}$$

(1.2)

for some positive constant c independent of k. Hence, he observed that it is possible to extract a subsequence ${\textbf{w}}_{k_n}$ which weakly² converges to a solution ${\textbf{w}}_L$ of problem (OBS)${}_{1,2,3}$ with $\int _\Omega |\nabla {\textbf{w}}_L|^2<+\infty$. This solution was later called Leray’s solution (see, e.g., [13]). This achievement of Leray immediately raises two crucial questions:

• (1) Is the constructed solution ${\textbf{w}}_L$ nontrivial, i.e., can we exclude the identity ${\textbf{w}}_L\equiv \textbf{0}$? This question is rather natural, since if we apply the Leray “invading domains” method to the corresponding Stokes system (1.1) (or even to the simplest Laplace equation), then the limiting solution will be identically zero.

• (2) If ${\textbf{w}}_L$ is nontrivial, what can we say about its behavior at infinity? Namely, can we guarantee the desired convergence

  $$\begin{aligned} \textbf{w}_{L}(z) \rightarrow {\textbf{w}}_\infty \quad \text {as}\quad |z| \rightarrow \infty \quad ? \end{aligned}$$

  (1.3)

  Both questions remained open for many decades, until recently.

Consider the problem in a more general setting:

$$\begin{aligned} \left\{ \begin{array}{l} - \Delta \textbf{w} + (\textbf{w} \cdot \nabla ) \textbf{w} + \nabla p = 0,\\ \nabla \cdot \textbf{w} = 0,\\ \textbf{w}|_{\partial \Omega } = \textbf{a}, \\ \textbf{w}(z) \rightarrow \textbf{w}_\infty =\lambda \textbf{e}_1 \quad \text {as}\quad r = |z| \rightarrow +\infty . \end{array} \right. \end{aligned}$$

(GEN)

The boundary data ${\textbf{a}}$ is an arbitrary (smooth) vector-valued function on the finite curve $\partial \Omega$. In comparison with (OBS), additional difficulties and ambiguities arise here. Namely, even the existence of a solution for the first three equations (GEN)$_{1,2,3}$ (without the limit velocity condition at infinity) is open when the flux of $\textbf{a}$ through $\partial \Omega$ is nonzero.

For the simpler case when the flux of ${\textbf{a}}$ across each connected component of $\partial \Omega$ vanishes, that is, for each component $\Gamma _i$ of $\partial \Omega$,

$$\begin{aligned} \int _{\Gamma _i} {\textbf{a}}\cdot \textbf{n}= 0, \end{aligned}$$

(1.4)

where $\textbf{n}$ is the unit outward (with respect to $\Omega$) normal vector, a solution to (GEN)$_{1,2,3}$ can be produced by the same Leray method, namely, the boundedness condition (1.2) still holds [30]. Further, this boundedness result was extended to the case when

$$\begin{aligned} \int _{\partial \Omega } {\textbf{a}}\cdot \textbf{n}= 0, \end{aligned}$$

(1.5)

i.e., when the total flux of $\textbf{a}$ through $\partial \Omega$ vanishes [26]. However, if (1.5) is not fulfilled, even the boundedness condition (1.2) is not proved in general, so, it is not clear whether Leray’s method gives solutions at least for problem (GEN)$_{1,2,3}$.

In view of all these difficulties, it sounded then astonishing the discovery of Finn and Smith in 1967 [8] the existence of a solution to both problems (OBS) and (GEN) without any compatibility relation between ${\textbf{a}}$ and ${\textbf{w}}_\infty$, only under smallness assumption on $\lambda$ or $|{\textbf{a}}-{\textbf{w}}_\infty |$ respectively.

In addition to problems (OBS) and (GEN), which looked almost insurmountable in the general case (without smallness assumptions), another direction of research was proposed in the classical papers by Gilbarg and Weinberger [13, 14], namely, the study of the asymptotic properties of general D-solutions (= solutions with finite Dirichlet integral $\int _\Omega |\nabla {\textbf{w}}|^2<\infty$) to (GEN)$_{1,2}$; this direction was further developed in the deep paper of Ch.Amick [1]. In particular, by construction, Leray solutions are D-solutions.³ The considered question is not at all simple, in view of the important fact that the finiteness of the Dirichlet integral on the plane does not guarantee the boundedness of the function itself even in the mean integral sense. For instance, for $f(z)=\bigl (\log (2+|z|)\bigr )^{\frac{1}{3}}$ we have $\int _{{\mathbb {R}}^2}|\nabla f|^2<\infty$, but $f(z)\rightarrow +\infty$ as $|z|\rightarrow \infty$. This is in a sharp contrast to the 3d case, where by the Sobolev Embedding theorem one has

$$\begin{aligned} \left( \int \limits _{{\mathbb {R}}^3}|\nabla f|^2<\infty \right) \Rightarrow \left( \int \limits _{{\mathbb {R}}^3}|f-c|^6<\infty \right) \end{aligned}$$

for some constant $c\in {\mathbb {R}}$. Really, the lack of the corresponding Embedding Theorem bears the main responsibility for the difficulties in the flow around an obstacle problem (OBS) in 2d case.⁴ Nevertheless, Gilbarg and Weinberger proved in [14] the uniform boundedness and the uniform convergence of the pressure for arbitrary D-solution; below we discuss the further extension of their results.

Another problem to study is the forced Navier–Stokes system in the whole plane:

$$\begin{aligned} \left\{ \begin{array}{l} - \Delta \textbf{w} + (\textbf{w} \cdot \nabla ) \textbf{w} + \nabla p = \textbf{f} \quad \textrm{in} \; {\mathbb {R}}^2,\\ \nabla \cdot \textbf{w} = 0 \quad \textrm{in} \; {\mathbb {R}}^2,\\ \textbf{w} \rightarrow \textbf{w}_\infty =\lambda \textbf{e}_1\quad \text {as}\quad |z| \rightarrow \infty . \end{array} \right. \end{aligned}$$

(FOR)

We shall assume that ${\textbf{f}}$ has compact support and enjoys $W^{-1,2}$ regularity. Hence solutions to (FOR) are unforced Navier–Stokes flows in the exterior domains ${\mathbb {R}}^2 {\setminus } \overline{B_R}$ with large $R>0$. Given any solution to (GEN) with zero total flux

$$\begin{aligned} \int _{\partial \Omega } {\textbf{a}}\cdot \textbf{n}= 0, \end{aligned}$$

(1.6)

one can take a divergence free extension of ${\textbf{w}}|_{{\mathbb {R}}^2 {\setminus } \bar{B}_R}$ (R large such that $\partial \Omega \subset B_R$) to the whole plane ${\mathbb {R}}^2$, which solves (FOR) with certain compactly supported ${\textbf{f}}$. Thus (GEN) and (FOR) are closely related problems. However, the constructions of solutions with arbitrary data for (GEN) and (FOR) are far from equivalent.

Since the work of Leray, through the effort of many researchers, there has been a lot of progress in the study of the systems (GEN), (OBS) and (FOR). In the rest of this paper, we attempt to give a rough overview of both the classical results and the recent advances, in particular, the following items:

• (1) Every D-solution is uniformly bounded, and, moreover, uniformly convergent to some constant vector at infinity (see [1] under some additional assumptions, and [25, 26] for general case). Further, if this uniform limit is nonzero, then the solution has the same asymptotic behavior at infinity as the linear Oseen system [34], i.e., it is physically reasonable in the sense of Finn and Smith.

• (2) Every Leray solution constructed for the problem (OBS) is nontrivial [27]. Moreover, it attains the required limit at infinity in case of small Reynolds numbers (= small $\lambda$) [21].

• (3) In case of small Reynolds numbers, solutions to (OBS) are globally unique in the class of all D-solutions [20].

• (4) For the forced system in the whole plane (FOR), Leray method always produces a solution to (FOR)$_{12}$ with finite Dirichlet integral. The limiting condition at infinity (FOR)$_{3}$ is verified in two different scenarios: (I) the limiting velocity ${\textbf{w}}_\infty$ is sufficient large with respect to the external force ${\textbf{f}}$, (II) both the total integral of force $\int _{{\mathbb {R}}^2}{\textbf{f}}$ and the limiting velocity ${\textbf{w}}_\infty$ vanish. Moreover, if the limiting velocity ${\textbf{w}}_\infty$ is sufficient large with respect to the external force ${\textbf{f}}$, then solutions to (FOR) are globally unique in the class of all D-solutions [17].

In particular, the results mentioned in the last paragraph produce large class of new solutions with prescribed zero spatial limits. Note, for comparison, that the existence of solutions to the system

$$\begin{aligned} \left\{ \begin{array}{l} - \Delta \textbf{w} + (\textbf{w} \cdot \nabla ) \textbf{w} + \nabla p = 0\quad \textrm{in} \; \Omega ,\\ \nabla \cdot \textbf{w} = 0 \quad \textrm{in} \; \Omega ,\\ \textbf{w}|_{\partial \Omega } = \lambda \textbf{e}_1, \\ \textbf{w} \rightarrow \textbf{0} \quad \text {as}\quad |z| \rightarrow \infty . \end{array} \right. \end{aligned}$$

(OBS')

is an open question even for the case of small $\lambda$! Besides, nothing is known concerning the asymptotic behavior of D-solutions having zero spatial limit at infinity. Moreover, even the simplest question,—does the problem (OBS’) have only trivial zero D-solution for $\lambda =0$?—is quite open until now.

One of the main tools in our research are two new estimates for general Navier–Stokes solutions, which have rather simple forms [17]. They control the difference between mean values of the velocity ${\textbf{w}}$ over two concentric circles in terms of the Dirichlet integral in the annulus between them. The first estimate claims that

$$\begin{aligned} |\bar{\textbf{w}}(r_1)-\bar{\textbf{w}}(r_2)|\le C_*\sqrt{\log (2+\mu )D(r_1,r_2)}, \end{aligned}$$

(1.7)

where

$$\begin{aligned} \mu =\frac{1}{r_1\mathfrak {m}}, \quad \mathfrak {m}:=\max \bigl \{|\bar{\textbf{w}}(r_1)|,|\bar{\textbf{w}}(r_2)|\bigr \},\quad D(r_1,r_2):=\int \limits _{r_1\le |z|\le r_2}|\nabla {\textbf{w}}|^2 \end{aligned}$$

(1.8)

and $C_*$ is some universal positive constant (does not depend on ${\textbf{w}}, r_i$, etc.). This estimate is qualitatively precise, since for a solution to (OBS) in case of small $\lambda$ the opposite inequality

$$\begin{aligned} \int \limits _\Omega |\nabla {\textbf{w}}|^2\le C\,\frac{1}{\log \left( 2+\frac{1}{\lambda }\right) }\lambda ^2. \end{aligned}$$

(1.9)

holds with $C=C(\Omega )$ [20]. Nevertheless, the estimate (1.7) can be strengthened in the asymptotic case when both $r_1,r_2$ tend to infinity, this is very useful for the Leray method (see Proposition 14).

The paper is organized as follows. In Sect. 2, we present Leray’s invading domains method as a starting point. The extensions of this method to the general boundary data (with nontrivial fluxes across $\partial \Omega$) and to the whole plane problem (FOR) are also discussed.

In Sect. 3, we study the boundedness and convergence of general Navier–Stokes D-solutions in exterior domains.

In Sect. 4, we study more detailed properties of the Leray solutions. For the flow around an obstacle problem, it is recently shown that Leray solutions are always nontrivial (when $\lambda \ne 0$), and they achieve the correct limit velocity when $|\lambda |$ is small. The latter result can be generalized to (FOR) in certain scenarios.

In Sect. 5, we study the asymptotics of D-solutions with nonzero limit velocity, and then discuss the construction and the unconditional uniqueness of Finn–Smith solutions to (OBS) with small nonzero $\lambda$. Finally, in last Sect. 6, we summarize the open problems mentioned in the previous sections.

2 The Invading Domains Method

We use the notation $z = x+yi= r e^{i\theta }$ for an arbitrary point $(x,y)\in {\mathbb {R}}^2$. The open discs and circles centered at the origin will be denoted by $B_r = \{|z|<r\}$ and $S_r = \partial B_r = \{|z| = r\}$.

2.1 Leray’s Argument by Contradiction

Leray [30] proposed an elegant approach to construct solutions for the flow around obstacle problem (OBS), now known as the invading domains method. The idea is to first solve the Navier–Stokes system on a sequence of bounded domains $\Omega _k = B_{R_k} \cap \Omega , k = 1,2,3, \ldots$, and then send $R_k \rightarrow +\infty$ (the choice of $R_k$ is arbitrary). To be precise, we consider the solutions ${\textbf{w}}_k$ to the following boundary value problems:

$$\begin{aligned} \left\{ \begin{array}{ll} - \Delta {{\textbf{w}}_k}+({\textbf{w}}_k\cdot \nabla ){\textbf{w}}_k+ \nabla p_k =\textbf{0}&{}\quad \hbox {in}\; \Omega _k, \\ \nabla \cdot {{\textbf{w}}_k} =0&{}\quad \hbox {in}\; \Omega _k, \\ {{\textbf{w}}_k} = \textbf{0}&{}\quad \hbox {on}\; \partial \Omega , \\ {\textbf{w}}_k ={\textbf{w}}_\infty &{}\quad \text{ for }\; r = R_k. \end{array}\right. \end{aligned}$$

(2.1)

Of course, we assume that $R_k$ is sufficiently large so that $\partial \Omega \cap S_{R_k} = \emptyset$. Note that the limit velocity condition (OBS)$_4$ is now replaced by the constant boundary condition on $S_{R_k}$. In the same paper, Leray introduced the topological fixed-point arguments now known as the Leray–Schauder theory, based on which he showed the existence of solutions to (2.1) for each k. Moreover, he showed that the Dirichlet integrals of ${\textbf{w}}_k$ are uniformly bounded for all k, that is,

$$\begin{aligned} \int _{\Omega _k} |\nabla {\textbf{w}}_k|^2 \,\le C \end{aligned}$$

(2.2)

for a finite constant C depending only on $\partial \Omega$ and ${\textbf{w}}_\infty$. As a consequence, there exists a subsequence of ${\textbf{w}}_k$ which converges in the sense of distributions to a function ${\textbf{w}}_L$ in $\Omega$, which also has bounded Dirichlet integral:

$$\begin{aligned} \int _\Omega |\nabla {\textbf{w}}_L|^2 \,\le C. \end{aligned}$$

(2.3)

By the standard regularity theory of the stationary Navier–Stokes system (see, e.g., [29, 35]), the local $C^m$-norms ($m \ge 1$) of ${\textbf{w}}_k$ are uniformly bounded. Hence, up to taking further subsequences, $\nabla ^m {\textbf{w}}_k$ convergences to $\nabla ^m {\textbf{w}}_L$ uniformly on any bounded subset of $\Omega$, for any $m \ge 1$. Consequently, ${\textbf{w}}_L$ is a smooth solution to the equations (OBS)$_{1,2,3}$. We refer to ${\textbf{w}}_L$ as a Leray solution. As already mentioned in the Introduction, whether ${\textbf{w}}_L$ achieves the limit velocity condition (OBS)$_4$ (in other words, whether the approximate solutions ${\textbf{w}}_k$ still “remember” the boundary data (2.1)$_4$ after the limiting process) is the most important and challenging problem for our study.

Leray’s method has been successful for the three dimensional flow around an obstacle problem (see [29, 30]). It is also useful for the construction of forward-in-time self-similar solutions for the 3-d instationary Navier–Stokes equations [22], whose existence was first shown in [18] using Leray–Schauder degree theory. The main difficulty in the two dimensional setting is that the Dirichlet integral is too weak to control the asymptotic behaviour of functions at infinity. For example, it is well-known that a function having finite Dirichlet integral can grow at infinity as $\log ^\alpha r$ for $\alpha < 1/2$. Nevertheless, as we will see later, the elegant nonlinear structure of the Navier–Stokes system allows one to obtain surprisingly better asymptotic estimates for D-solutions, and even determine the limit velocity of the Leray solutions in certain scenarios.

We mention that Fujita [9] and, independently Vorovich and Yudovich [38], using a method different from that of Leray, based on a Galerkin scheme, were able to prove the existence of a D-solution to (OBS). The same problem of determining the limit velocity is also open for their approach. We will focus on Leray’s method which we find more intuitive.

Leray’s proof of the crucial estimate (2.2) is based on an elegant argument by contradiction, which is often referred to as Leray’s argument reductio ad absurdum. Suppose (2.2) is false, that is, there exists a sequence of $R_k \rightarrow +\infty$ and corresponding solutions ${\textbf{w}}_k$ such that the Dirichlet integrals blow up: $J_k^2 = \int _{\Omega _k} |\nabla {\textbf{w}}_k|^2 \,\rightarrow +\infty$. Consider the normalized solutions ${\widetilde{{\textbf{w}}}_k}= J_k^{-1} {\textbf{w}}_k$ with $\int _{\Omega _k}|\nabla \widetilde{{\textbf{w}}}_k|^2 \,= 1$. By compactness, there exists a subsequence of $\widetilde{{\textbf{w}}}_k$ which weakly converges to some function $\textbf{u}$ with $\int _{\Omega } |\nabla \textbf{u}|^2 \,\le 1$. The equations satisfied by $\widetilde{{\textbf{w}}}_k$ read

$$\begin{aligned} \left\{ \begin{array}{l} - J_k^{-1} \Delta {\widetilde{{\textbf{w}}}_k}+(\widetilde{{\textbf{w}}}_k\cdot \nabla )\widetilde{{\textbf{w}}}_k+ \nabla (J_k^{-2} p_k) = 0, \\ \nabla \cdot \widetilde{{\textbf{w}}}_k = 0. \end{array}\right. \end{aligned}$$

(2.4)

Passing to the limit, we find that $\textbf{u}$ solves the Euler equations for some function q (in the sense of distributions) in $\Omega$,

$$\begin{aligned} \left\{ \begin{array}{l} (\textbf{u}\cdot \nabla )\textbf{u}+ \nabla q = 0, \\ \nabla \cdot \textbf{u} = 0. \end{array}\right. \end{aligned}$$

(2.5)

Using (2.1)$_3$, we also know that $\textbf{u} = 0$ on $\partial \Omega$. Using (2.5)$_1$, we deduce that $q\equiv$ const on each connected component $\Gamma _i$ of $\partial \Omega$ (see, e.g., [19] for the accurate proof of this identity). Let these constants be $q_i$. Suppose $\partial \Omega \subset B_R$ for some $R>0$ and let $\textbf{A}$ be a smooth extension of the boundary data (2.1)$_{3,4}$ satisfying,

$$\begin{aligned} \textbf{A}&= 0 \quad \hbox {on}\; \partial \Omega , \quad \textbf{A} \equiv {\textbf{w}}_\infty \quad \text{ for }\;|z| > 2R,\\ \nabla \cdot \textbf{A}&= 0 \end{aligned}$$

(see, e.g., [28] for the constructions of solenoidal extensions under minimal smoothness assumptions). Denote ${{\textbf{u}}}_k = {\textbf{w}}_k - \textbf{A}$, then by (2.1) we have

$$\begin{aligned} - \Delta {{{\textbf{u}}}_k} - \Delta \textbf{A} + ({\textbf{w}}_k\cdot \nabla ){{\textbf{u}}}_k + ({\textbf{w}}_k\cdot \nabla )\textbf{A} + \nabla p_k = 0. \end{aligned}$$

(2.6)

Testing (2.6) with ${{\textbf{u}}}_k$ and using that ${{\textbf{u}}}_k$ vanishes on both $\partial \Omega$ and $S_{R_k}$, we obtain

$$\begin{aligned} \int _{\Omega _k} |\nabla {{\textbf{u}}}_k|^2 + \int _{\Omega _k} \nabla {{\textbf{u}}}_k \cdot \nabla A + \int _{\Omega _k} ({\textbf{w}}_k \cdot \nabla \textbf{A}) \cdot {{\textbf{u}}}_k=0. \end{aligned}$$

(2.7)

By compact embedding, up to taking further subsequences, we have $\widetilde{{\textbf{w}}}_k$ converge to $\textbf{u}$ strongly in $L^2$ norm on every bounded subset of $\Omega$. Multiplying (2.7) with $J_k^{-2}$ and passing to the limit, we obtain

$$\begin{aligned} \int _{\Omega } (\textbf{u} \cdot \nabla \textbf{A}) \cdot \textbf{u} = -1. \end{aligned}$$

In particular, this identity shows that $\textbf{u}$ is nontrivial. On the other hand, testing (2.5) with $\textbf{A} - {\textbf{w}}_\infty$, we get

$$\begin{aligned} \int _{\Omega } (\textbf{u} \cdot \nabla \textbf{A}) \cdot \textbf{u} = -\sum _{i} q_i \int _{\Gamma _i} {\textbf{w}}_\infty \cdot \textbf{n} = 0, \end{aligned}$$

where $\textbf{n}$ is the outward (with respect to $\Omega$) unit normal on $\partial \Omega$. We have arrived at a contradiction, hence the Dirichlet integrals $\int _{\Omega _k} |\nabla {\textbf{w}}_k|^2 \,$ must be uniformly bounded.

2.2 General Boundary Values

The above proof of (2.2) also works for the general boundary value problem (GEN) under the condition that the flux of $\textbf{a}$ through each component $\Gamma _i$ vanishes, see (1.4). Without this condition, it is much harder to prove the existence of D-solutions to (GEN)$_{1,2,3}$. First of all, the invading domains method should be modified in the general case. Let $\Theta = \int _{\partial \Omega } {\textbf{a}}\cdot \textbf{n}$ be the total flux, then it is natural to consider the following system

$$\begin{aligned} \left\{ \begin{array}{ll} - \Delta {{\textbf{w}}_k}+({\textbf{w}}_k\cdot \nabla ){\textbf{w}}_k+ \nabla p_k =\textbf{0}&{}\quad \hbox {in}\; \Omega _k, \\ \nabla \cdot {{\textbf{w}}_k} =0&{}\quad \hbox {in}\; \Omega _k, \\ {{\textbf{w}}_k} = {\textbf{a}}&{}\quad \hbox {on}\; \partial \Omega , \\ {\textbf{w}}_k ={\textbf{w}}_\infty - \frac{\Theta \,\textbf{e}_r}{2\pi r}&{}\quad \text{ for }\;|z|=R_k. \end{array}\right. \end{aligned}$$

(2.8)

By adding the term $- \frac{\Theta \,\textbf{e}_r}{2\pi r}$ in the last condition, the boundary values have zero total flux across $\partial \Omega \cup S_{R_k}$ which is compatible with (2.8)$_2$. The solvability of the boundary value problem for the stationary Navier–Stokes system on bounded multiply-connected domains under the minimal compatibility condition that the total flux of the boundary data vanishes was, in fact, open for nearly 90 years since the work of Leray [30]. In 2015 [24], it was solved in the two-dimensional setting and the three-dimensional axi-symmetric setting. Based on this nontrivial result, (2.8) can be solved for each k. The next step is to show (2.2).

First, consider the case $\Theta = 0$. If $\partial \Omega$ is connected, then Leray’s proof still works as we have remarked. If $\partial \Omega$ is not connected, so that the flux through each connected component of $\partial \Omega$ may be nontrivial, the proof is harder, involving the methods in [24] which develop Leray’s argument reductio ad absurdum.

Theorem 1

[26]. If the total flux $\Theta$ vanishes, then (2.2) holds for the solutions ${\textbf{w}}_k$ to (2.8). As a consequence, there exists a subsequence of ${\textbf{w}}_k$ which converges weakly to a D-solution ${\textbf{w}}_L$ solving (GEN)$_{1,2,3}$.

Next, consider the general case $\Theta \ne 0$. The uniform boundedness of $\int _{\Omega _k} |\nabla {\textbf{w}}_k|^2$, and the existence of a D-solution to (GEN)$_{1,2,3}$ are still open in general, with the following partial results available.

Theorem 2

[32]. Suppose that $|\Theta | < 2\pi$ and $\partial \Omega$ is connected, then (2.2) holds for the solutions ${\textbf{w}}_k$ to (2.8). As a consequence, there exists a subsequence of ${\textbf{w}}_k$ which converges weakly to a D-solution ${\textbf{w}}_L$ solving (GEN)$_{1,2,3}$.

The proof in [32] also develops Leray’s argument reductio ad absurdum. Note that [32] only considered ${\textbf{w}}_\infty = 0$, but it works for nonzero ${\textbf{w}}_\infty$ with some minor modifications. It is also conceivable that the condition of $\partial \Omega$ being connected may be removed with the help of [26].

A crucial estimate used in [32] is

$$\begin{aligned} \xi = \sup _{\Vert {\textbf{u}}\Vert _H \le 1} \left| \int _{{\mathbb {R}}^2} \left( \textbf{u} \cdot \nabla \textbf{u} \right) \cdot \frac{\textbf{e}_r}{r} \right| < +\infty \end{aligned}$$

where the space $H = \{\textbf{u} \in W^{1,2}_{\textrm{loc}}({\mathbb {R}}^2): \, \text{ div }\, \textbf{u} = 0, \ \Vert \textbf{u}\Vert _H:= \Vert \nabla \textbf{u}\Vert _{L^2({\mathbb {R}}^2)} < +\infty \}.$ In fact, we have the exact equality $\xi = 1$. $\xi \le 1$ follows from a classical argument of Gilbarg–Weinberger [14, Lemma 4.1], using the following identity

$$\begin{aligned} \int _{{\mathbb {R}}^2} \left( \textbf{u} \cdot \nabla \textbf{u} \right) \cdot \frac{\textbf{e}_r}{r} \,= \int _{{\mathbb {R}}^2} \frac{1}{r^2} \big [ (u_2 - \bar{u}_2(r)) \partial _\theta u_1 - (u_1 - \bar{u}_1(r)) \partial _\theta u_2\big ] \,, \end{aligned}$$

(2.9)

where $\bar{u}_i(r)$ are the mean values of $u_i$ on the circle $S_r$, $i=1,2$. To show $\xi \ge 1$, we consider the divergence free field $\textbf{u} = f(r) \textbf{e}_\theta$ with a function f(r) compactly supported on $(0,+\infty )$. By computation, the Dirichlet integral is given by

$$\begin{aligned} \int _{{\mathbb {R}}^2} |\nabla \textbf{u}|^2 \,= 2\pi \int _0^{+\infty } \left( r (\partial _r f)^2 + r^{-1} f^2 \right) dr. \end{aligned}$$

On the other hand,

$$\begin{aligned} \int _{{\mathbb {R}}^2} \left( \textbf{u} \cdot \nabla \textbf{u} \right) \cdot \frac{\textbf{e}_r}{r} \,&= - 2 \pi \int _{0}^{+\infty } \partial _r (f^2) \log r \, dr \\&= 2\pi \int _0^{+\infty } r^{-1} f^2 dr \end{aligned}$$

It is well-known that there exist functions $f_k$ such that

$$\begin{aligned} \frac{ \int _0^{+\infty } r^{-1} f_k^2 dr }{\int _0^{+\infty } r (\partial _r f_k)^2 dr} \rightarrow +\infty , \quad k \rightarrow +\infty . \end{aligned}$$

As a consequence, we obtain for $\textbf{u}_k = f_k \textbf{e}_\theta$,

$$\begin{aligned} \frac{ \int _{{\mathbb {R}}^2} \left( \textbf{u} \cdot \nabla \textbf{u} \right) \cdot \frac{\textbf{e}_r}{r} \,}{\int |\nabla \textbf{u}_k|^2 \,} \rightarrow 1, \quad k \rightarrow +\infty , \end{aligned}$$

which gives $\xi \ge 1$.

For arbitrary total flux $\Theta$, the existence of a D-solution to (GEN)$_{1,2,3}$ has been proved under certain symmetry assumptions. In [23], the authors considered the case when $\Omega$ and $\textbf{a}$ are symmetric with respect to the x-axis, and each connected component of $\partial \Omega$ intersects the x-axis. Precisely, it is assumed that

$$\begin{aligned} (x, y) \in \Omega \iff (x, -y) \in \Omega \end{aligned}$$

(2.10)

and

$$\begin{aligned} a_1(x, y) = a_1(x, -y), \quad a_2(x, y) = -a_2(x, -y) \end{aligned}$$

(2.11)

and for each connected component $\Gamma _i$ of $\partial \Omega$,

$$\begin{aligned} \Gamma _i \cap \{y=0\} \ne \emptyset . \end{aligned}$$

(2.12)

Theorem 3

[23]. Suppose that $\Omega$ and the boundary data $\textbf{a}$ satisty the conditions (2.10)–(2.12), then there exists a symmetric D-solution in $\Omega$ to (GEN)$_{1,2,3}$.

Here, a solution ${\textbf{w}}$ is said to be symmetric if

$$\begin{aligned} w_1(x, y) = w_1(x, -y), \quad w_2(x, y) = -w_2(x, -y). \end{aligned}$$

(2.13)

The key step of the proof is to construct, given any small number $\delta > 0$, a divergence free symmetric extension $\textbf{A}$ for $\textbf{a}$, verifying

$$\begin{aligned} \textbf{A}|_{\partial \Omega } = \textbf{a}, \quad \Vert \textbf{A}\Vert _{L^4(\Omega )} + \Vert \nabla \textbf{A}\Vert _{L^2(\Omega )} < +\infty , \end{aligned}$$

and the Leray–Hopf inequality

$$\begin{aligned} \left| \int _\Omega (\textbf{u} \cdot \nabla \textbf{u}) \cdot \textbf{A} \right| \le \delta \int |\nabla \textbf{u}|^2, \quad \forall \ \textbf{u} \in H_S(\Omega ). \end{aligned}$$

Here $H_S(\Omega ):= \{\text {symmetric vector fields}\,\textbf{u} \; \text{ on } \; \Omega : \textbf{u}|_{\partial \Omega } = 0, \; \text{ div }\, \textbf{u} = 0, \, \Vert \nabla \textbf{u}\Vert _{L^2(\Omega )} < +\infty \}.$ Then, the theorem is proved using the invading domain systems (2.8), but with the boundary value on $\partial B_{R_k}$ replaced by $\textbf{A}|_{\partial B_{R_k}}$. The resulting symmetric invading domain solutions ${\textbf{w}}_k$ are shown to satisfy (2.2). Note that $\textbf{A}|_{\partial B_{R_k}}$ is different from $-\frac{\Theta }{2\pi r} \textbf{e}_r$, hence the uniform boundedness of Dirichlet integrals for (2.8) is still unsolved even in the symmetric case.

The difficulty of working with (2.8) in the non-symmetric case is reflected by a simple example which is a special case of the well-known Hamel flows (see [11, Section XII.2]). For a fixed (big) parameter $R>1$ consider the boundary value problem

$$\begin{aligned} \left\{ \begin{array}{ll} - \Delta {\textbf{w}}+({\textbf{w}}\cdot \nabla ){\textbf{w}}+ \nabla p =\textbf{0}&{}\quad \hbox {in}\; 1\le r \le R, \\ \nabla \cdot {{\textbf{w}}} =0&{}\quad \hbox {in}\; 1\le r \le R, \\ {{\textbf{w}}} = \textbf{a}&{}\quad \hbox {on}\; S_1, \\ { {\textbf{w}}} = \textbf{b}&{}\quad \textrm{on}\; S_R. \end{array}\right. \end{aligned}$$

with

$$\begin{aligned} \textbf{a}= & {} -3 \textbf{e}_r + \textbf{e}_\theta ,\\ \textbf{b}= & {} -3R^{-1} \textbf{e}_r + (R^{-\frac{1}{2}} - R^{-\frac{3}{2}} + R^{-2}) \textbf{e}_\theta . \end{aligned}$$

Hence, $\textbf{a}$ is fixed and $\textbf{b}$ is uniformly small (of size $R^{-\frac{1}{2}}$). There is an explicit solution to this system,

$$\begin{aligned} {\textbf{w}}= -3 r^{-1} \textbf{e}_r + (R^\frac{1}{2} r^{-1} + (1-R^\frac{1}{2}) r^{-2}) \textbf{e}_\theta . \end{aligned}$$

Note that ${\textbf{w}}\cdot \textbf{e}_\theta \rightarrow + \infty$ for any fixed $r>1$, if we send $R \rightarrow + \infty$! This shows that a (pointwisely) small perturbation for the boundary value on $S_{R}$ could result in a huge change for the solution ${\textbf{w}}$.

2.3 The Whole-Plane Problem

Consider the problem (FOR). In order to construct a Leray D-solution to (FOR) $_{1,2}$, it is natural to use the invading domain systems:

$$\begin{aligned} \left\{ \begin{array}{ll} - \Delta {{\textbf{w}}_k}+({\textbf{w}}_k\cdot \nabla ){\textbf{w}}_k+ \nabla p_k =\textbf{f}&{}\quad \hbox {in}\; B_{R_k}, \\ \nabla \cdot {{\textbf{w}}_k} =0&{}\quad \hbox {in}\; B_{R_k}, \\ {\textbf{w}}_k ={\textbf{w}}_\infty &{}\quad \text{ for }\;|z|=R_k. \end{array}\right. \end{aligned}$$

(2.14)

Testing (2.14)$_1$ with ${\textbf{w}}_k-{\textbf{w}}_\infty$, we get the energy equality

$$\begin{aligned} \int _{B_{R_k}} |\nabla \textbf{w}_k|^2 = \int _{B_{R_k}} \textbf{f} \cdot (\textbf{w}_k - \textbf{w}_\infty ). \end{aligned}$$

(2.15)

As in the previous sections, we need to show the uniform bound (2.2) with $\Omega = {\mathbb {R}}^2$. When the total force ${\mathcal {F}} = \int _{{\mathbb {R}}^2} \textbf{f} \textrm{d}x\textrm{d}y$ vanishes, this is not very difficult, since we can write $\textbf{f} = \nabla \cdot {\mathbb {F}}$ for some tensor ${\mathbb {F}} \in L^2({\mathbb {R}}^2)$ (see [16, Lemma 3.6] or [17, Lemma 2]), and then using (2.15) and integration by parts we have

$$\begin{aligned} \int _{B_{R_k}} |\nabla \textbf{w}_k|^2 \textrm{d}x\textrm{d}y = \int _{B_{R_k}} {\mathbb {F}}: \nabla \textbf{w}_k \textrm{d}x\textrm{d}y \end{aligned}$$

(2.16)

where ${\mathbb {F}}: \nabla \textbf{w}_k$ stands for $\sum _{i,j} {\mathbb {F}}_{ij} \partial _j w_{k,i}$. Using Hölder’s inequality we get a nice bound on the Dirichlet integral,

$$\begin{aligned} \int _{B_{R_k}} |\nabla \textbf{w}_k|^2 \textrm{d}x\textrm{d}y \le \int _{{\mathbb {R}}^2} |{\mathbb {F}}|^2 \textrm{d}x\textrm{d}y. \end{aligned}$$

However, for a general force $\textbf{f}$, such a direct estimate is unavailable. Moreover, even if the uniform boundedness of $\int _{B_{R_k}} |\nabla {\textbf{w}}_k|^2$ is assumed, it is not clear whether the local $L^p$ norms of $\textbf{w}_k$ are uniformly bounded. (For the exterior domain problems, uniform local $L^p$ estimates follow directly from (2.2) and the boundary condition on $\partial \Omega$.) These new difficulties for the whole plane problem are settled in [17].

Theorem 4

[17]. Suppose that $\textbf{f}$ is compactly suppoted in $B_R$ for some $R>0$ and $\Vert f\Vert _{W^{-1,2}(B_{2R})} < \infty$, then for the solutions ${\textbf{w}}_k$ to (2.14), $|\bar{\textbf{w}}_k(R)|$ and $\int _{{B_{R_k}}} |\nabla \textbf{w}_k|^2$ are uniformly bounded. Consequently, there exists a subsequence of $\textbf{w}_k$ which converges weakly to a D-solution ${\textbf{w}}_L$ in the whole plane solving the equations (FOR)$_{1,2}$.

The problem of determining the limit velocity of the D-solution is also challenging, and will be tackled in Sect. 4 in two different scenarios. The proof of Theorem 4 is based on the recent basic estimate (1.7) which controls the difference between the mean values of the velocity over two concentric circles in terms of the Dirichlet integral in the annulus between them (see the next section).

We also mention that, in [16], Guillod and Wittwer proposed a modified invading domains method which could, for zero total force, produce infinitely many distinct solutions parametrized by their mean values in the unit disc, while the limit velocity of these solutions at infinity is not clear.

3 Asymptotic Behaviour of D-Solutions

In this section, we shall consider an arbitrary D-solution ${\textbf{w}}$ to the (unforced) Navier–Stokes equations (GEN)$_{1,2}$ in the exterior domain $\Omega$, with associated pressure field p. By the definition of a D-solution, we have the bound

$$\begin{aligned} \int _{\Omega } |\nabla {\textbf{w}}|^2 \,< + \infty . \end{aligned}$$

(3.1)

Note that Leray solutions are examples of D-solutions (see (2.2)–(2.3)). After suitable rescaling if necessary, we can always assume that ${\mathbb {R}}^2 {\setminus } B_1 \subset \Omega$.

The main goal of this section is

Theorem 5

[25]. Let ${\textbf{w}}$ be a D-solution to the Navier–Stokes equations in the exterior domain $\{r \ge 1\}$, then there exists a constant vector ${\textbf{w}}_0 \in {\mathbb {R}}^2$ such that ${\textbf{w}}$ converges uniformly to ${\textbf{w}}_0$ at infinity. In particular, ${\textbf{w}}$ is uniformly bounded in a neighbourhood of infinity.

Before discussing the key ideas on which Theorem 5 is based, let us recall some elementary facts about the behavior of general D-functions (= functions with bounded Dirichlet integral). For the proof of the next Lemma, see, e.g., the section 2 in [25].

Lemma 6

Let $f \in W^{1,2}_{\textrm{loc}}(\Omega )$ and assume that

$$\begin{aligned} D(r_1,r_2):= \int _{\Omega _{r_1, r_2}} |\nabla f|^2 < \infty \end{aligned}$$

for some ring $\Omega _{r_1, r_2} = \{ z \in {\mathbb {R}}^2: 0< r_1< |z| < r_2 \} \subset \Omega$. Then we have

$$\begin{aligned} |\bar{f}(r_2) - \bar{f}(r_1)| \le \frac{1}{\sqrt{2\pi }}\left( D(r_1,r_2)\ln \frac{r_2}{r_1}\right) ^\frac{1}{2}. \end{aligned}$$

(3.2)

Further, if $r_2 > \beta r_1$, then there exists a number $r \in [r_1, r_2]$ such that

$$\begin{aligned} \sup _{|z| = r} |f(z) - \bar{f}(r)| \le C_\beta \sqrt{D(r_1,r_2)} \end{aligned}$$

(3.3)

with constant $C_\beta =\sqrt{\pi \frac{\beta +1}{\beta -1}}$ depending on $\beta$ only.

The circles $S_r$ in Lemma 6 with uniform estimate of the variation are often called good circles.

The inequality (3.2) demonstrates the well-known fact: the D-function in general case may have a logarithmic growth (for example, $f(z)=\bigl (\ln (2+|z|)\bigr )^{\alpha }$ with $\alpha \in (0,\frac{1}{2})$). Nevertheless, the brilliant structures of Navies–Stokes system allow to obtain much better estimates presented in the next section.

3.1 Three Important Lemmas

First of all, we recall two lemmas, discovered by Gilbarg–Weinberger [13, 14], which have played fundamental roles in the study of D-solutions.

The first lemma states that the difference between the mean values of pressure on concentric circles can be controlled by the Dirichlet integral. Let $\Omega _{r_1, r_2} = B_{r_2}\setminus B_{r_1}$.

Lemma 7

[14].

$$\begin{aligned} |\bar{p}(r_1) - \bar{p}(r_2)| \le \frac{1}{2\pi } \int _{\Omega _{r_1, r_2}} |\nabla \textbf{w}|^2 \, dxdy. \end{aligned}$$

(3.4)

The proof uses $\textbf{e}_r$ component of the Navier–Stokes equation, and the identity (2.9).

The second lemma controls the direction of the mean value of the velocity over concentric circles using the Dirichlet integral. Let $\bar{\textbf{w}}(r)$ be the mean value of $\textbf{w}$ over the circle $S_r$ and let $\varphi (r)\in S^1 = [0,2\pi ]/\sim$ be the argument of the complex number associated with the vector $\bar{\textbf{w}}(r) = (\bar{w}_1(r), \bar{w}_2(r))$, i.e., $\bar{\textbf{w}}(r)=|\bar{\textbf{w}}(r)|\,(\cos \varphi (r),\sin \varphi (r))$.

Lemma 8

[14]. Suppose that $|\bar{\textbf{w}}(r)| \ge \sigma > 0$ for some constant $\sigma$ and for all $r \in [r_1, r_2]$, then we have (the left hand size is understood as the distance in $S^1)$

$$\begin{aligned} |\varphi (r_2) - \varphi (r_1)| \le \frac{1}{4\pi \sigma ^2} \int _{\Omega _{r_1, r_2}} \left( \frac{1}{r}|\nabla \omega | + |\nabla \textbf{w}|^2 \right) \, dxdy. \end{aligned}$$

(3.5)

Here, $\omega = \partial _2 w_1 - \partial _1 w_2$ is the vorticity (we follow the sign convention in [1, 14]). The proof uses the elegant structure hidden in the $\textbf{e}_\theta$-component of the Navier–Stokes equation, see [14, p. 399].

Based on Lemma 7 and the div-curl structure in the equation

$$\begin{aligned} \Delta p = - \nabla {\textbf{w}}\cdot (\nabla {\textbf{w}})^\intercal = - \sum _{i,j=1,2} w_{i,j} w_{j,i}, \end{aligned}$$

(3.6)

Gilbarg and Weinberger proved a fundamental result on the convergence of pressure.

Proposition 9

[14]. For any D-solution in an exterior domain, the pressure p has a uniform (finite) limit at infinity.

Since the pressure can be redefined up to adding constants, one can assume that $p \rightarrow 0$ at infinity without loss of generality.

Denote by $\bar{\textbf{w}}(r)$ the average of $\textbf{w}$ on the circle $S_r$. The analog of Lemma 7 for the velocity turns out to be much harder to obtain; it was discovered only recently.

Lemma 10

[17]. Let ${\textbf{w}}$ be the D-solution to the Navier–Stokes equations (GEN)$_{1,2}$ in the annulus $\bar{\Omega }_{r_{1},r_{2}} = \{z \in {\mathbb {R}}^2: r_1\le |z|\le r_2\}$. Then we have

$$\begin{aligned} |\bar{\textbf{w}}(r_2)-\bar{\textbf{w}}(r_1)|\le C_*\sqrt{\ln (2+\mu ) \,D(r_1,r_2)}, \end{aligned}$$

(3.7)

where

$$\begin{aligned} \mu =\frac{1}{r_1\mathfrak {m}}, \quad \mathfrak {m}:=\max \bigl \{|\bar{\textbf{w}}(r_1)|,|\bar{\textbf{w}}(r_2)|\bigr \}, \quad D(r_1,r_2):=\int \limits _{\Omega _{r_1,r_2}}|\nabla {\textbf{w}}|^2 \,\end{aligned}$$

(3.8)

and $C_*$ is some universal positive constant (independent of ${\textbf{w}}, r_i$, etc.).

Note that, for $r_2 \gg r_1$, (3.7) significantly improves the direct estimate (3.2) obtained without using the Navier–Stokes equations. The estimate (3.7) is precise and can not be improved in general (see (1.9)). However, it can be improved in the asymptotic case $r_1 \rightarrow +\infty , \frac{r_2}{r_1} \rightarrow +\infty$ (see below Proposition 14 in Sect. 4).

Using the elementary formula (3.2), the validity of (3.7) can be reduced easily to the proof of the following simpler version:

$$\begin{aligned} |\bar{\textbf{w}}(r_1)-\bar{\textbf{w}}(r_2)|\le C_*(1+\mu )\sqrt{D}, \end{aligned}$$

(3.9)

where we denote $D=D(r_1,r_2)$ (really, exactly the last inequality was presented in [17] as “the first basic estimate for the velocity”). However, the proof of (3.9) is rather nontrivial; it is based on the classical methods in [1, 14] as well as the recent progress in [27]. Namely, by Lemma 7 the pressure is under control of the Dirichlet integral. So, assuming that the estimate (3.9) fails, we obtain the existence of two nested levels sets of the Bernoulli pressure $\Phi =p+\frac{1}{2}|{\textbf{w}}|^2$, and the difference of the values of $\Phi$ on these level sets is much bigger than $(1+\mu )\sqrt{D}$. Recall, that

$$\begin{aligned} \nabla \Phi =-\nabla ^\bot \omega +\omega {\textbf{w}}^\bot , \end{aligned}$$

(3.10)

where $\omega =\partial _2w_1-\partial _1w_2$ is the corresponding vorticity and we use the notation $(a_1 \textbf{e}_1 + a_2 \textbf{e}_2)^\bot$ for the rotated vector $-a_2 \textbf{e}_1 + a_1 \textbf{e}_2$. By the results of [14], the line integrals of the first term $\nabla \omega$ along certain good rays are small with respect to D (see, e.g., (3.21)), moreover, the variation of the direction of the velocity ${\textbf{w}}$ between our $\Phi$-level sets is under control of the Dirichlet integral as well (see Lemma 8). The crucial fact is that the vorticity $\omega$ does not change sign between levels sets of $\Phi$ (it was proved in [27] based on the elegant ideas of [1]). So  the direction of $\nabla \Phi$ is almost a constant (in some integral sense) between the concentric level sets of $\Phi$, a contradiction.

Of course, now main Theorem 5 follows directly from the basic estimate (3.7) with (3.3) and from the simple fact that

$$\begin{aligned} |\nabla {\textbf{w}}(z)|\rightarrow 0\quad \text{ as }\quad |z|\rightarrow +\infty \end{aligned}$$

(3.11)

(see [14]). But in reality Theorem 5 was proved in [25] much earlier than estimate (3.7). Anyway, the key role in the proof of all these results is played by several maximum principles for the functions associated with the Navier–Stokes system discussed in the next subsection.

3.2 Maximum Principles

The two-dimensional stationary Navier–Stokes equations enjoy a number of important maximum principles.

• 1. The vorticity $\omega = \partial _2 w_1 - \partial _1 w_2$ satisfy the two-sided strong maximum principle, due to the well-known vorticity equation

  $$\begin{aligned} -\Delta \omega + {\textbf{w}}\cdot \nabla \omega =0. \end{aligned}$$

  (3.12)

  In particular, for any domain U,

  $$\begin{aligned} \max _{\bar{U}} \omega = \max _{\partial U} \omega , \quad \min _{\bar{U}} \omega = \min _{\partial U} \omega . \end{aligned}$$

  (3.13)

• 2. The Bernoulli function $\Phi = \frac{|{\textbf{w}}|^2}{2} + p$ satisfies the one-sided strong maximum principle, due to the equation

  $$\begin{aligned} -\Delta \Phi + {\textbf{w}}\cdot \nabla \omega = - \omega ^2 \le 0. \end{aligned}$$

  (3.14)

  In particular, for any domain U,

  $$\begin{aligned} \max _{\bar{U}} \Phi = \max _{\partial U} \Phi . \end{aligned}$$

  (3.15)

  This is particularly useful in controlling the size of $|{\textbf{w}}|$, when combined with estimates for p.

• 3. In [1], Amick introduced a remarkable new function $\gamma = \Phi - \omega \psi$, which also enjoys the two-sided strong maximum principle. Here, $\psi$ is the stream function defined (up to adding constants) by the relation

  $$\begin{aligned} \nabla \psi = {\textbf{w}}^\perp = -w_2 \textbf{e}_1 + w_1 \textbf{e}_2. \end{aligned}$$

  (3.16)

  Note that for $\psi$ to be well-defined in the exterior domain $r \ge 1$, we require that the total flux $\int _{r=1} {\textbf{w}}\cdot \textbf{e}_r$ vanishes. (When the total flux is nonzero, $\psi$ and $\gamma$ can still be defined in simply-connected subdomains of $\Omega$.) Recall that the gradient of Bernoulli function satisfies (this is just (GEN)$_1$ in a different form)

  $$\begin{aligned} \nabla \Phi = - \nabla ^\perp \omega + \omega \nabla \psi , \end{aligned}$$

  (3.17)

  which gives

  $$\begin{aligned} \nabla \gamma = - \nabla ^\perp \omega - \psi \nabla \omega . \end{aligned}$$

  (3.18)

  Equivalently, we also have the relations

  $$\begin{aligned} \nabla ^{\perp } \gamma = \nabla \omega - \psi \nabla ^\perp \omega , \quad \nabla \omega = \frac{- \psi \nabla \gamma + \nabla ^\perp \gamma }{\psi ^2+1}. \end{aligned}$$

  (3.19)

  In particular,

  $$\begin{aligned} \nabla \gamma \cdot \nabla ^\perp \omega = - |\nabla \omega |^2. \end{aligned}$$

  (3.20)

  Applying $\nabla \cdot$ to (3.18) we get

  $$\begin{aligned} -\Delta \gamma&= \nabla \psi \cdot \nabla \omega + \psi \Delta \omega \\&= ({\textbf{w}}^\perp + \psi {\textbf{w}}) \cdot \nabla \omega \\&= \frac{ (- \psi ^2 + 1) {\textbf{w}}- 2\psi {\textbf{w}}^\perp }{\psi ^2+1} \cdot \nabla \gamma . \end{aligned}$$

  This implies the two-sided strong maximum principle for $\gamma$. Using (3.20) and the strong maximum principle for $\omega$, Amick also observed that along regular level curves of $\omega$, $\gamma$ is strictly monotone. Similarly, $\omega$ is also strictly monotone along regular $\gamma$-level curves. A particular consequence is that, in a domain where $\gamma$ is well-defined, regular level curves of $\omega$ and $\gamma$ cannot be closed.

Based on these observations and elegant topological arguments, Amick established the detailed structures of the $\omega$-level sets for D-solutions with zero total flux across the inner boundary.

Proposition 11

[1]. Suppose ${\textbf{w}}$ is a D-solution in $r\ge 1$ with zero total flux, then

• $\omega$ is not one-signed at infinity, that is, there exist two sequences of points $z_n, z_n' \rightarrow \infty$ such that $\omega (z_n) > 0$, $\omega (z_n')<0$ for all n.

• The set $\{\omega > 0\}$ contains at least one, and at most a finite number of unbounded connected components. Each of these components is simply connected. (The same result holds true for the set $\{\omega < 0\}$.)

• There exist two unbounded continuous curves ${\mathcal {C}}_i \subset \{\omega = 0\}$, parametrized by arc length as ${\mathcal {C}}_i = \{(x_i(s), y_i(s): s \in [0, +\infty ))\}, \, i=1, 2$. The functions $x_i(\cdot )$ and $y_i(\cdot )$ are piecewise real-analytic on $[0, +\infty )$, and they satisfy $(x_i(0), y_i(0))$ $\in \{|z| = 1\}$ and $|(x_i(s), y_i(s))| \rightarrow +\infty$ as $s \rightarrow +\infty$. Moreover, the function $s \rightarrow \Phi (x_1(s), y_1(s))$ is strictly decreasing, while the function $s \rightarrow \Phi (x_2(s), y_2(s))$ is strictly increasing.

3.3 Boundedness and Uniform Convergence of the Velocity

As we have already mentioned, the main Theorem 5 follows directly from the basic estimate (3.7) with (3.3) and from the uniform convergence of the gradient $|\nabla {\textbf{u}}|$ to zero (see [14]). But in reality the proof of Theorem 5 went along a completely different, longer and tortuous path.

Based on Lemma 8 and the maximum principle for Bernoulli function, Gilbarg and Weinberger [14] were able to prove that for any D-solution in the exterior domain $\Omega$, either $\int _{S_r} |{\textbf{w}}(r,\theta )|^2 d\theta \rightarrow \infty$ as $r\rightarrow \infty$, or ${\textbf{w}}$ has a finite limit ${\textbf{w}}_0$ in the $L^2$ integral sense, that is,

$$\begin{aligned} \lim _{r\rightarrow \infty } \int _{S_r} |{\textbf{w}}(r, \theta ) - {\textbf{w}}_0|^2 d \theta = 0. \end{aligned}$$

For the vorticity, they also proved the very useful decay estimates assuming that the D-solution is bounded:

$$\begin{aligned} \omega (z) = o(r^{-3/4}), \quad \int _\Omega r|\nabla \omega |^2 <+\infty . \end{aligned}$$

(3.21)

In an earlier paper [13], they proved that the Leray solution for (OBS) is uniformly bounded in $\Omega$.

Based on Proposition 11, Amick [1] showed that for a D-solution ${\textbf{w}}$ in $\Omega$ with zero total flux,

• ${\textbf{w}}$ is uniformly bounded (in $\{r \ge 1\}$).

• $\psi \nabla \omega , \nabla \gamma \in L^2(\{r\ge 1\}).$

• $\psi \omega \rightarrow 0$ and $\gamma \rightarrow \frac{|{\textbf{w}}_0|^2}{2}$ at infinity. (The uniform limit of p is set as 0.)

• $|{\textbf{w}}| \rightarrow |{\textbf{w}}_0|$ at infinity.

Furthermore, in the symmetric case (see (2.13)), Amick proved the full uniform convergence ${\textbf{w}}\rightarrow {\textbf{w}}_0$ at infinity.

In the recent papers [25, 26], the first author together with Pileckas and Russo finally proved Theorem 5. Namely, the zero total flux and symmetry constraints used in [1] are removed, and any D-solution in $\Omega$ must be bounded and has a uniform limit at infinity. The proof develops the ideas of Gilbarg–Weinberger and Amick. When the total flux is nonzero, the level sets of $\omega$ could separate infinity from the origin, in which case [25] obtained the fast decay estimate for vorticity $|\omega | = o(r^{-1})$ using the coarea formula. Such decay implies the convergence of velocity with the help of the Biot–Savart law. On the other hand, if the level sets of $\omega$ do not separate infinity from the origin, then the method of Amick [1] still applies, which still leads to the convergence of $|{\textbf{w}}|$. The full convergence of ${\textbf{w}}$ is established in [25] by combining Lemma 8 with Amick’s arguments.

4 Further Properties of the Leray Solutions

Recall that in Sect. 2, we have shown the construction of Leray solutions using the invading domains method for the systems (OBS) and (FOR) (see Sects. 2.1 and 2.3). For (FOR), we assume that ${\textbf{f}}$ has compact support. By Theorem 5, the Leray solution for either of these systems has a uniform limit velocity at infinity. Hence, the remaining problem is to verify that this limit is equal to ${\textbf{w}}_\infty$.

4.1 The Flow Around Obstacle Problem

4.1.1 Nontriviality

In [1], using energy estimates, Amick showed that if one applies the invading domains method to the Stokes system in exterior domain

$$\begin{aligned} \left\{ \begin{array}{l} - \Delta \textbf{w} + \nabla p = 0 \quad \textrm{in} \; \Omega ,\\ \nabla \cdot \textbf{w} = 0 \quad \textrm{in} \; \Omega ,\\ \textbf{w}|_{\partial \Omega } = 0, \\ \textbf{w} \rightarrow \textbf{w}_\infty = \textbf{e}_1 \quad \text {as}\quad |z| \rightarrow \infty , \end{array} \right. \end{aligned}$$

(4.1)

the resulting “Leray solution” will be trivial, i.e., identical to 0. More specifically, he showed that the solutions ${\textbf{w}}_k$ to

$$\begin{aligned} \left\{ \begin{array}{ll} - \Delta {{\textbf{w}}_k} + \nabla p_k =\textbf{0}&{}\quad \hbox {in}\; \Omega _k, \\ \nabla \cdot {{\textbf{w}}_k} =0&{}\quad \hbox {in}\; \Omega _k, \\ {{\textbf{w}}_k} = \textbf{0}&{}\quad \hbox {on}\; \partial \Omega , \\ {\textbf{w}}_k =\textbf{e}_1&{}\quad \text{ for }\;|z|=R_k. \end{array}\right. \end{aligned}$$

(4.2)

satisfy the estimate

$$\begin{aligned} \int _{\Omega _{R_k}} |\nabla {\textbf{w}}_k|^2 \,\le \frac{C}{\log R_k} \rightarrow 0, \ \textrm{as} \ R_k \rightarrow + \infty , \end{aligned}$$

(4.3)

where C is independent of $R_k$. This is consistent with the Stokes paradox, which states that the only D-solution to (4.1)$_{1,2,3}$ is the zero solution. Naturally, one may ask whether Leray’s solution for the flow around obstacle problem (OBS) is also trivial or not.

Remarkably, for the Navier–Stokes invading domain systems (2.1) with $\lambda \ne 0$, in the symmetric case (see (2.10), (2.13)), Amick showed that

$$\begin{aligned} \int _{\Omega _{R_k}} |\nabla {\textbf{w}}_k|^2 \,\ge c > 0, \end{aligned}$$

(4.4)

with c independent of $R_k$. Based on (4.4), Amick proved that the Leray solution ${\textbf{w}}_L$ as a limit of ${\textbf{w}}_k$ is nontrivial in the symmetric case.

In a recent paper [27], the symmetry assumption in Amick’s result is removed, so that the nontriviality of the Leray solutions for (OBS) is established in the general case.

Theorem 12

[27]. When $\lambda \ne 0$, the Leray solution ${\textbf{w}}_L$ constructed in Sect. 2.1 for the flow-around-obstacle problem (OBS) is not identical to 0.

To prove (4.4), Amick used two special level curves of the vorticity $\omega _k$ of ${\textbf{w}}_k$ similar to those given by Proposition 11, both travel from a circle $S_{R_0} \subset \Omega$ with $R_0$ fixed, to the outer boundary $S_{R_k}$, see [1, Section 4.2]. To prove the existence of such level curves, Amick had to work in the symmetric case so that the connected components of $\{\omega \ne 0\} \cap ({\mathbb {R}}^2 {\setminus } \bar{B}_1)$ are simply connected. In comparison, the paper [27] avoids the use of such $\omega$-level curves, and instead, it develops a new argument based on the level curve structure of the Bernoulli function $\Phi _k = \frac{|{\textbf{w}}_k|^2}{2} + p_k$. A crucial observation in [27] is that vorticity cannot change sign in an annulus type domain whose boundary consists of two closed $\Phi$-level curves. The important identity (which is, in fact, (OBS)$_1$ in a different form)

$$\begin{aligned} \nabla \Phi = - \nabla ^\perp \omega +\omega {\textbf{w}}^\perp \end{aligned}$$

is then used to estimate the difference of $\Phi$ over the two level curves. A contradiction is derived assuming that (4.4) fails. Note that the proof of the general estimate Lemma 10 we mentioned earlier is largely based on this argument.

It should be emphasized that, despite Theorem 12, it is still open whether the limit velocity of ${\textbf{w}}_L$ could be zero. In [1, p.99], Amick conjectured that the zero solution is the unique D-solution to (OBS) with $\lambda =0$. In [10], for the symmetric case, Galdi showed that if this conjecture holds true (so that the Leray solutions have nontrivial limits), then there exists a sequence of $\lambda _k \rightarrow +\infty$, such that for each $\lambda _k$, (OBS) has a solution.

4.1.2 Justification of the Limit Velocity

It turns out, when the Reynolds number $\lambda$ is small (with smallness depending only on $\Omega$), the limit condition (OBS)$_4$ holds for the Leray solution, and thus ${\textbf{w}}_L$ solves the full system (OBS). The solutions to (OBS) for small Renolds numbers were first constructed in the classical work [8] of Finn and Smith in 1967. They used another approach, very different from Leray’s invading domains method, based on delicate Oseen system estimates in the exterior domain and perturbative arguments. The uniqueness of the Finn–Smith solution in the class of D-solutions is recently proved in [20], see Sect. 5 for more details. The following theorem unifies the approaches of Leray and Finn–Smith for small $\lambda$, in the sense that they produce exactly the same solutions.

Theorem 13

[21]. There exists a constant $\lambda _1>0$ depending only on $\Omega$ such that, for any $0 < \lambda \le \lambda _1$, the Leray solution ${\textbf{w}}_L$ for (OBS) is equal to the unique D-solution to (OBS). Moreover, the convergence of ${\textbf{w}}_k$ to ${\textbf{w}}_L$ holds true without the need of taking subsequences.

The proof starts with an explicit bound on the Dirichlet integral:

$$\begin{aligned} \int _{\Omega _k} |\nabla {\textbf{w}}_k|^2 \,\le \frac{C\lambda ^2}{|\ln \lambda |}. \end{aligned}$$

(4.5)

Hence, when $\lambda$ is small, we have $\int _{\Omega _k} |\nabla {\textbf{w}}_k|^2 \,\ll \lambda ^2$. Then the methods in [27] is adapted to derive a contradiction assuming (OBS)$_4$ fails. The main novelty here is a blow-down argument which leads to the crucial asymptotic estimates for the velocity and pressure near the outer boundary.

For the blow-down method, we consider the rescaled functions $\tilde{{\textbf{w}}}_k(z) = \lambda ^{-1} {\textbf{w}}_k(R_k z)$ which are defined in the domains $\frac{1}{R_k}{\Omega }_k$. Sending k to infinity and taking suitable converging subsequences, we obtain a limiting D-solution $\textbf{u}_E$ to the Euler system on the unit disc with constant boundary condition, that is,

$$\begin{aligned} {\left\{ \begin{array}{ll} \textbf{u}_E \cdot \nabla \textbf{u}_E + \nabla p_E = 0, \\ \nabla \cdot \textbf{u}_E = 0, \\ \textbf{u}_E|_{S_1} = \textbf{e}_1. \end{array}\right. } \end{aligned}$$

(4.6)

Surprisingly, $p_E$ satisfies an implicit Neumann boundary condition

$$\begin{aligned} \partial _n p_E = 0 \end{aligned}$$

(4.7)

on $S_1$. By the classical div-curl lemma [5] and (4.6)$_3$, the right hand side of

$$\begin{aligned} \Delta p = - \nabla \textbf{u}\cdot (\nabla \textbf{u})^\intercal = - \sum _{i,j=1,2} u_{i,j} u_{j,i} \end{aligned}$$

(4.8)

belongs to the Hardy space ${\mathcal {H}}^1({\mathbb {R}}^2)$ (after extension by zero into ${\mathbb {R}}^2 \setminus \bar{B}_1$). Using the theory on local Hardy spaces and elliptic boundary value problems developed in the paper [4], (4.7) and (4.8) together lead to the pointwise estimate

$$\begin{aligned} \sup _{z_1, z_2 \in \bar{B}_1} |p_E(z_1) - p_E(z_2)| \le C \int _{B_1} |\nabla \textbf{u}_E|^2 \,. \end{aligned}$$

which then implies certain asymptotic estimates for the pressure $p_k$ associated with the Navier–Stokes solutions ${\textbf{w}}_k$. The latter estimates play important roles in adapting the method in [27] (see also the next subsection for further discussions).

4.2 The Whole-Plane Problem

The blow-down method of [21] is further developed by [17] into a general asymptotic estimate which improves Lemma 10 when the Dirichlet integral is small.

Proposition 14

Let ${\textbf{w}}_k$ be a sequence of D-solutions to the Navier–Stokes equations (GEN)$_{1,2}$ in the annulus domains $\bar{\Omega }_{r_{1k},r_{2k}} = \{z: r_{1k} \le |z| \le r_{2k} \}$. Suppose, in addition, that

$$\begin{aligned} r_{1k}\rightarrow +\infty ,\quad \frac{r_{2k}}{r_{1k}}\rightarrow +\infty , \end{aligned}$$

(4.9)

and there exist two vectors ${\textbf{w}}_0$, ${\textbf{w}}_\infty \in {\mathbb {R}}^n$ such that

$$\begin{aligned} \max _{z\in S_{r_{1k}}}|{\textbf{w}}_k(z)-{\textbf{w}}_0|\rightarrow 0, \quad \max _{z\in S_{r_{2k}}}|{\textbf{w}}_k(z)-{\textbf{w}}_\infty |\rightarrow 0\quad \textrm{as}\quad k\rightarrow +\infty . \end{aligned}$$

(4.10)

Then

$$\begin{aligned} |{\textbf{w}}_0-{\textbf{w}}_\infty |\le C_{**}\frac{D_*}{\mathfrak {m}}, \end{aligned}$$

(4.11)

where $\mathfrak {m}=\max \bigl \{|{\textbf{w}}_0|,|{\textbf{w}}_\infty |\bigr \}$, $D_* =\varliminf \limits _{k\rightarrow \infty }\int _{\Omega _{r_{1k},r_{2k}}}|\nabla {\textbf{w}}_k|^2$, and $C_{**}$ is some universal positive constant (does not depend on ${\textbf{w}}_k$, etc.)

Apparently, this estimate is very useful in comparing the prescribed limit velocity and the actual limit velocity of the Leray solution. In [17], Proposition 14 is used to prove, in the following two different scenarios, the validity of (FOR) $_3$ for the Leray solutions, and thus the existence of solutions to (FOR).

Theorem 15

Suppose that $\textbf{f}$ is compactly supported in $B_R$ for some $R>0$ and $\Vert f\Vert _{W^{-1,2}(B_{2R})} < +\infty$. There exists a universal constant $\varepsilon _1>0$ such that, if

$$\begin{aligned} \Vert \textbf{f}\Vert _{H^{-1}(2R)} \le \frac{\varepsilon _1}{\ln ^\frac{1}{2} \left( 2 + \frac{1}{\lambda R}\right) }\lambda , \end{aligned}$$

(4.12)

then the Leray solution $\textbf{w}_L$ satisfies $\textbf{w}_0 = \textbf{w}_\infty = \lambda \textbf{e}_1$. If, in addition, the total force ${\mathcal {F}}:=\int _{{\mathbb {R}}^2} \textbf{f} \,= 0$, then the factor $\ln ^{-\frac{1}{2}} \left( 2+\frac{1}{\lambda R}\right)$ in (4.12) can be removed.

Theorem 16

Suppose that $\textbf{f}$ is compactly supported in $B_R$ for some $R>0$ and $\Vert f\Vert _{W^{-1,2}(B_{2R})} < +\infty$. Assume that the total force $\int _{{\mathbb {R}}^2} \textbf{f} \,= \textbf{0}$, and $\textbf{w}_\infty = 0$. Then the Leray solution $\textbf{w}_L$ satisfies $\textbf{w}_0 = \textbf{w}_\infty = 0$.

The main idea of the proof of these theorems is rather simple. Denote by $D_*$ the “tail” of the Dirichlet integrals:

$$\begin{aligned} D_* = \lim _{r \rightarrow \infty } \overline{\lim _{k \rightarrow \infty }} \int _{\Omega _k \cap \{|z| \ge r\}} |\nabla \textbf{w}_k|^2. \end{aligned}$$

(4.13)

In case ${\textbf{w}}_0\ne 0$, using standard integration by parts and asymptotic properties of D-solutions applied to ${\textbf{w}}_L$ (see, e.g., the next section or [17, Lemma 16]), we have

$$\begin{aligned} D_* = - {\mathcal {F}} \cdot (\textbf{w}_\infty - \textbf{w}_0). \end{aligned}$$

(4.14)

In case ${\textbf{w}}_0=0$, under (4.12) assumption, also using integration by parts and (3.7), we get

$$\begin{aligned} D_*\le \liminf _{k\rightarrow \infty }\int \limits _{\Omega _k}|\nabla {\textbf{w}}_k|^2 \lesssim {\varepsilon }_1\lambda ^2 \end{aligned}$$

(4.15)

On the other hand, by (4.11),

$$\begin{aligned} |{\textbf{w}}_\infty -{\textbf{w}}_0|\lesssim \frac{1}{\lambda +|{\textbf{w}}_0|}D_*. \end{aligned}$$

This definitely implies ${\textbf{w}}_\infty ={\textbf{w}}_0$ whenever ${\mathcal {F}}={\textbf{w}}_\infty =0$ or when ${\varepsilon }_1$ is small enough.

5 Perturbative Analysis and Uniqueness

5.1 Asymptotic form of D-Solutions with Nonzero Limit Velocity

In Sect. 3, we have discussed that for an arbitrary D-solution in the exterior domain, the velocity field converges uniformly to some finite limit ${\textbf{w}}_0$ at infinity. Naturally, we hope to obtain more detailed information about the asymptotic behaviour, for example, the convergence rate. It turns out, when $|{\textbf{w}}_0| \ne 0$, a rather accurate asymptotic form of ${\textbf{w}}$ near infinity can be proved. In comparison, when $|{\textbf{w}}_0| = 0$, to the best of our knowledge no convergence rate of the velocity or pressure has been obtained for general D-solutions.

In [36], D. Smith introduced the class of physically reasonable solutions in exterior domains, that is, solutions satisfying the convergence rate

$$\begin{aligned} |{\textbf{w}}- {\textbf{w}}_0| \le C r^{-1/4-\varepsilon }, \end{aligned}$$

(5.1)

for some positive $\varepsilon$. Using detailed estimates for the convolution of functions with the fundamental solution of the Oseen system, he showed that the asymptotic behaviour of physically reasonable solutions with nonzero limit velocity $|{\textbf{w}}_0| \ne 0$ are essentially controlled by the Oseen system

$$\begin{aligned} \left\{ \begin{array}{l} \Delta \textbf{v} - \partial _1 \textbf{v} - \nabla q = 0, \\ \nabla \cdot \textbf{v} = 0, \end{array} \right. \end{aligned}$$

(5.2)

(see [36, Theorem 5]). The fundamental solution of the Oseen system $(\textbf{E},\textbf{e})$, first introduced by Oseen [31], consists of a symmetric tensor of rank two $E_{ij}$ and a vector $e_j$, such that

$$\begin{aligned} \Delta E_{ij} - \partial _1 E_{ij} - \partial _i e_j&= \delta _{ij} \delta _0, \nonumber \\ \sum _{i=1,2} \partial _i E_{ij}&= 0, \end{aligned}$$

(5.3)

where $i, j = 1, 2$ and $\delta _0$ is the delta function supported at the origin. Explicitly, $(\textbf{E}, \textbf{e})$ are given by

$$\begin{aligned} \textbf{E} = \left[ \begin{matrix} \partial _1(H+L) - L &{}\partial _2 (H + L)\\ \partial _2(H + L) &{}-\partial _1(H+L) \end{matrix}\right] , \quad \textbf{e} = -\nabla H, \end{aligned}$$

(5.4)

where $\Delta H = \delta _0$ and $- \Delta L + \partial _1 L = \delta _0$. More explicitly, H and L are given by

$$\begin{aligned} H = \frac{1}{2\pi } \ln r, \quad L = \frac{1}{2\pi } e^{r\cos \theta /2} K_0(r/2) \end{aligned}$$

(5.5)

where $K_0$ denotes the modified Bessel function of the second kind (i.e., the MacDonald function). Asymptotically, there holds

$$\begin{aligned} K_0(\rho ) = \sqrt{\frac{\pi }{2}} \left( \frac{1}{\rho ^{1/2}} + O\left( \frac{1}{\rho ^{3/2}}\right) \right) e^{-\rho } \end{aligned}$$

(5.6)

as $\rho \rightarrow \infty$. A special feature of the Oseen system in two dimensions is that, the component $E_{11}$ exhibits a parabolic wake region $\{(x,y): x \ge 0, |y| \le \sqrt{x} \}$ in which the decay at infinity is slower than outside. For a physically reasonable solution ${\textbf{w}}$, the first component $w_1$ also exhibits such a parabolic wake region at infinity in the direction of ${\textbf{w}}_\infty$, interior to which $|{\textbf{w}}-{\textbf{w}}_{\infty }| < Cr^{-1/2}$, while completely exterior to this wake $|{\textbf{w}}-{\textbf{w}}_{\infty }| < Cr^{-1}$ as $r \rightarrow \infty$.

The asymptotic expansions of the velocity (in whole space) and the vorticity (in the wake region) with leading terms given exactly by the Oseen system is obtained by Babenko [3]. We recall the net force vector

$$\begin{aligned} \textbf{F} = - \int _{\partial \Omega }(\textbf{T}({\textbf{w}},p) - \textbf{w} \otimes \textbf{w}) \cdot \textbf{n}, \end{aligned}$$

where $\textbf{T}$ is the stress tensor given by

$$\begin{aligned} \textbf{T}(\textbf{u},p) = \nabla \textbf{u} + (\nabla \textbf{u})^\intercal - p \textbf{I}. \end{aligned}$$

(5.7)

Interestingly, the leading terms obtained by Babenko depend only on ${\textbf{w}}_\infty$ and $\textbf{F}$. A more precise asymptotic expansion for vorticity (outside the wake region) is obtained recently by Guillod and Wittwer [15], where the reader can find more details on this subject.

Remarkably, in the symmetric case by Amick [2], and in the general case by Sazonov [34], it is proved that any D-solution with nonzero limit velocity must be physically reasonable! Sazonov’s proof is based on $L^p$-estimates for the velocity in an exterior domain ${\mathbb {R}}^2 \setminus B_R$ with sufficiently large R such that $\int _{{\mathbb {R}}^2 {\setminus } B_R} |\nabla {\textbf{w}}|^2 \,$ and $\sup _{{\mathbb {R}}^2 {\setminus } B_R} |{\textbf{w}}- {\textbf{w}}_0|$ are both sufficiently small. Such estimates were already carried out in the work of Galdi and Sohr [12]. Then the pointwise convergence rates of ${\textbf{w}}$ are obtained with the help of Biot–Savart law. A difficulty in the proof is to show that $|{\textbf{w}}- {\textbf{w}}_0| \in L^p$ with some $p<+\infty$ as a initial step, for which Sazonov used a delicate weighted integral estimate for the Bernoulli function.

5.2 Construction and Uniqueness of the Finn–Smith Solutions

As we have discussed in the previous sections, Leray’s invading domains method provides a starting point for studying the problems (GEN), (OBS) and (FOR) in a general setting. An alternative approach, namely perturbative analysis based on the Oseen system, was initiated by Finn and Smith [8]. Remarkably, they constructed the first nontrivial solutions to (OBS) (the limit velocity condition is satisfied), for the small Reynolds numbers case. These solutions remain the only known full solutions to (OBS) to this day. Their construction also works for (GEN) if the boundary data $\textbf{a}$ is a small perturbation of ${\textbf{w}}_\infty$.

Theorem 17

[8]. Let ${\textbf{w}}_\infty \ne 0$ and $\textbf{a} = |{\textbf{w}}_\infty | \textbf{b} + {\textbf{w}}_\infty$, and assume that $\textbf{b}$ and its first two derivatives (on the curve $\partial \Omega$) are sufficiently small (depending on ${\textbf{w}}_\infty$ and $\Omega$) in the pointwise sense, then there exists a solution ${\textbf{w}}$ to (GEN) in $\Omega$.

In the case that $\lambda = |{\textbf{w}}_\infty |$ is small, and

$$\begin{aligned} \Vert \textbf{b}\Vert _{C^2(\partial \Omega )} = o(|\ln \lambda |), \end{aligned}$$

there exists a solution ${\textbf{w}}$ to (GEN) in $\Omega$.

Note that the second statement applies to the flow-around-obstacle problem (OBS) when $\lambda$ is small, since $\textbf{b} = - \frac{{\textbf{w}}_\infty }{|{\textbf{w}}_\infty |}$ is of fixed size independent of $\lambda$.

Let us briefly recall the ideas of Finn and Smith, focusing on the system (OBS). The reader may also consult Galdi [11, Section XII.5] for another approach based on Sobolev norms instead of pointwise bounds. As we have mentioned, the linearized Stokes equations

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta \textbf{w} + \nabla p = 0, \\ \nabla \cdot \textbf{w} = 0. \end{array} \right. \end{aligned}$$

(5.8)

has no solutions for general boundary data and limit velocity. As a counterpart to the Stokes system, Finn and Smith take the Oseen system as a starting point. Let $\textbf{v}(z) = \lambda ^{-1} \textbf{w}(z) - \textbf{e}_1$. To find a solution $\textbf{w}$ for (OBS), it is equivalent to finding $\textbf{v}$ as a solution to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta \textbf{v} + \lambda \partial _1 \textbf{v} + \nabla q = -\lambda \textbf{v} \cdot \nabla \textbf{v}, \\ \nabla \cdot \textbf{v} = 0, \\ \textbf{v}|_{\partial \Omega } = - \textbf{e}_1, \\ \textbf{v} \rightarrow 0 \quad \text {as}\quad |z| \rightarrow \infty . \end{array} \right. \end{aligned}$$

(5.9)

In turn, this is reduced to solving the integral equation

$$\begin{aligned} \textbf{v}(z) = \textbf{v}_{\ell }(z;\lambda ) - \lambda \int _{\Omega } \left( \textbf{v}(z') \cdot \nabla _{z'} \right) \textbf{G}(z,z';\lambda ) \cdot \textbf{v}(z') dx' dy' =: T_\lambda \textbf{v}, \end{aligned}$$

(5.10)

where $\textbf{G}$ is the Green tensor with Dirichlet boundary conditions for the linearized Oseen system in $\Omega$ and $\textbf{v}_{\ell }(z;\lambda )$ is the linear solution to (5.9) with zero right-hand side in (5.9${}_1$) and with the same boundary conditions as $\textbf{v}$ (both $\textbf{G}$ and $\textbf{v}_{\ell }$ were constructed and studied in detail in another paper [7]). It is proved in [8] that, when $\lambda$ is sufficiently small, $T_\lambda$ is a contraction mapping for $\textbf{v}$ belonging to a small ball centered at 0 in the Banach space

$$\begin{aligned} X_\lambda = \left\{ \textbf{v}\in C(\Omega ,{\mathbb {R}}^2): \Vert \textbf{v}\Vert _{X_\lambda }:=\max _{z\in \Omega ; i=1,2} \frac{|\textbf{v}_i(z)|}{h_i(\lambda z)}<+\infty \right\} . \end{aligned}$$

(5.11)

Here the majorant functions $h_i(\xi )$ are taken as

$$\begin{aligned} 0 < |\xi | \le 1&: h_i(\xi ) = \log \frac{2}{|\xi |},\quad i = 1,2, \end{aligned}$$

(5.12)

$$\begin{aligned} |\xi |>1&: {\left\{ \begin{array}{ll} h_1(\xi ) = |\xi |^{-\frac{1}{2}}\\ h_2(\xi ) = |\xi |^{-\frac{1}{2}-\mu }, \end{array}\right. } \end{aligned}$$

(5.13)

with $0<\mu <\frac{1}{2}$ chosen arbitrarily. Then, using standard perturbative arguments, the existence and local uniqueness for fixed points of $T_\lambda$ under the conditions of Theorem 17 can be obtained.

A basic question left unanwsered in [8] is the (unconditional) uniqueness of solution. For (OBS), uniqueness in the class of D-solutions is recently proved in [20].

Theorem 18

There exists a positive constant $\lambda _2$ depending only on $\partial \Omega$ such that, for $0<\lambda <\lambda _2$, the Finn–Smith solution given by Theorem 17 is the unique D-solution to (OBS).

The main idea is to prove the smallness of $\Vert {\textbf{w}}\Vert _{X_\lambda }$ for arbitrary D-solution when $\lambda$ is small, thus reducing the uniqueness in the class of D-solutions to the local uniqueness in $X_\lambda$ which is already obtained by Finn and Smith. The proof starts with a very useful result stating that any D-solutions to (OBS) have extra small Dirichlet energy when $\lambda$ is small:

$$\begin{aligned} \int _\Omega |\nabla \textbf{w}|^2 \,\le \frac{ C\lambda ^2}{\sqrt{|\log \lambda |}}. \end{aligned}$$

(5.14)

The presence of the logarithmic factor here is, in fact, closely related to the Stokes paradox. We have mentioned in Sect. 4.1.1 that a similar logarithmic smallness is proved in [1, Theorem 22] for the Dirichlet integrals of the Stokes solutions in bounded domains. See [20, Remark 10] for more explanations on this point. Using (5.14), a crucial observation is made: outside the critical circle $\{r = \frac{1}{\lambda }\}$, pressure is uniformly small in the sense that $|p(z)| \ll \lambda ^2$. Then, the desired pointwise estimate for ${\textbf{w}}$ outside the critical circle is obtained by developing the method for proving uniform convergence of D-solutions (see Sect. 3) and the asymptotic analysis based on the Oseen system (see the previous section). On the other hand, the region inside the critical circle can be viewed as a boundary layer in which the flow is dominated by the Stokes system (instead of the Oseen system), and the pointwise estimate follows from (5.14) and local regularity estimates for the Stokes system.

5.3 Uniqueness for the Whole-Plane Problem

For the forced problem (FOR), an unconditional uniqueness result can also be obtained when the external force is sufficiently small (with respect to the limit velocity).

Theorem 19

[17]. Suppose that $\textbf{f}$ is compactly supported in $B_R$ for some $R>0$ and $\Vert f\Vert _{W^{-1,2}(B_{2R})} < +\infty$. There exists a universal constant $\varepsilon _2>0$ such that if

$$\begin{aligned} \Vert \textbf{f}\Vert _{W^{-1,2}(B_{2R})} \le \frac{\varepsilon _2}{(1+\lambda R)^3\ln ^\frac{1}{2} \left( 2+\frac{1}{\lambda R}\right) } \lambda , \end{aligned}$$

(5.15)

then the problem (FOR) is uniquely solvable in the class of D-solutions. If, in addition, the total force $\int _{{\mathbb {R}}^2}\textbf{f} \,= 0$, then the factor $\ln ^{-\frac{1}{2}} \left( 2+\frac{1}{\lambda R}\right)$ in (5.15) can be removed.

We emphasize that the condition (5.15) for uniqueness is quite different from the condition (4.12) for the existence of solutions. In particular, with R fixed, if $\textbf{f}$ is sufficiently large then (5.15) fails for arbitrary ${\textbf{w}}_\infty$. The proof is similar to that of Theorem 18, with a suitable change in the definition of the Banach space $X_\lambda$.

6 Conclusive Remarks

As we have seen, the study of the two-dimensional Navier–Stokes system has developed into a rich subject with many interesting ideas and methods. However, many fundamental questions are still unanswered. The following list contains some problems that we find rather important.

• The existence of D-solutions to the systems (GEN), (OBS) and (FOR) for general data. It is sufficient to prove, that the Leray “invading domain method” produce the required solution. Of course, this purpose seem to be very ambitious, so even a partial success in any of these problems will be highly appreciated, for example,

• The existence of D-solutions to the systems (GEN${}_{1-3}$) for general data with nonzero total flux $\int _{\partial \Omega }{\textbf{a}}\cdot \textbf{n}\ne 0$. Of course, it is sufficient to prove the uniform boundedness (2.2) of the corresponding Leray sequence (2.8).

• The asymptotic behaviour of D-solutions with zero velocity limit. The existence of a wide family of such solutions is guaranteed by Theorem 16, but their asymptotic behavior is a real “terra incognita”. Again, even a partial success here will be highly appreciated, for example, a solution of the following “Liouville type” question:

• Does the problem (OBS’) have only trivial identically zero solution for $\lambda =0$?

The methods developed in previous works turned out to be insufficient for solving these problems. Thus, a difficult but interesting struggle lies ahead.