Abstract
We prove quantitative regularity and blowup theorems for the incompressible Navier–Stokes equations in \({{\mathbb {R}}^d}\), \(d\ge 4\) when the solution lies in the critical space \(L_t^\infty L_x^d\). Explicit subcritical bounds on the solution are obtained in terms of the critical norm. A consequence is that \(\Vert u(t)\Vert _{L_x^d({{\mathbb {R}}^d})}\) grows at a minimum rate of \((\log \log \log \log (T_*-t)^{-1})^c\) along a sequence of times approaching a hypothetical blowup at \(T_*\). We use a quantitative framework inspired by Tao (in: Kechris, Makarov, Ramakrishnan, Zhu (eds) Nine Mathematical Challenges: An Elucidation, American Mathematical Society, Providence, 2021), with some new elements to deal with the lack of Leray’s epochs of regularity in the high-dimensional setting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we consider the incompressible Navier–Stokes equations in \({{\mathbb {R}}^d}\), \(d\ge 4\). In the standard manner, we normalize to unit viscosity and project the system onto the space of divergence-free vector fields. This yields
where \(u:[0,T)\times {{\mathbb {R}}^d}\rightarrow {{\mathbb {R}}^d}\) is an unknown vector field and \({\mathbb {P}}=1-\Delta ^{-1}\nabla {{\,\textrm{div}\,}}\) is the Leray projection. We will occasionally refer to the pressure \(p=-\Delta ^{-1}{{\,\textrm{div}\,}}{{\,\textrm{div}\,}}(u\otimes u)\) which is well-defined in \(L_t^\infty L_x^\frac{d}{2}\) assuming that \(u\in L_t^\infty L_x^d\). Note that \(u\in L_t^\infty L_x^d\) is a natural setting to study regularity and blowup of (1) because the associated norm is critical, i.e., \(\Vert u\Vert _{L_t^\infty L_x^d}\) and (1) are both invariant under the scaling \(u(t,x)\mapsto \lambda u(\lambda ^2t,\lambda x)\).
Let us consider, say, a finite-energy solution u of (1) arising from divergence-free Schwartz initial data. If u is smooth on \([0,T_*)\), we say that u blows up at time \(T_*\) if there exists no smooth extension to \([0,T_*]\). It is natural to ask what necessary conditions exist for u to blow up at \(T_*\), particularly those in the form of a norm of u becoming unbounded or diverging to \(+\infty \). An early result of this type is due to Leray [12] who proved (originally for only \(d=3\)) that if \(T_*\) is the blowup time, then
where \(c=c(d,p)>0\) is an absolute constant and \(d<p\le \infty \). In a similar spirit, the classical work of Prodi, Serrin, and Ladyzhenskaya [11, 15, 17] implies a blowup criterion in which the pointwise lower bound is replaced by an average in time, in such a way that the spacetime norm becomes critical. Specifically, if \(T_*\) is the blowup time, then
Both of these results degenerate at the \(p=d\) endpoint which raises the natural question of whether the critical norm \(\Vert u\Vert _{L_x^d({{\mathbb {R}}^d})}\) must become unbounded or diverge as \(t\,\uparrow \,T_*\). This is a more difficult question in view of the fact that the spatial norms \(\Vert u\Vert _{L_x^p}\), \(p>d\) are subcritical; thus if u concentrates at increasingly fine scales, one should expect these norms to become large. On the other hand, for the critical norm to grow, it is more likely due to many small concentrations of the solution scattered throughout space, not just the blowup profile itself. For this reason, one needs a genuinely different strategy to address the case \(p=d\).
The breakthrough on this problem came in the paper of Escauriaza et al. [9] who proved the three-dimensional result
which was later improved to a pointwise limit as \(t\uparrow T_*\) by Seregin [16] (which, notably, is still open in the case \(d\ge 4\)). The most important new tool was the backward uniqueness for the heat equation proved in [8] which is applied to a weak limit of solutions which “zoom in” on a potential blowup point. In order to apply backward uniqueness, one needs pointwise bounds on u and \(\nabla u\) in a large region away from the blowup point which the authors obtained using a Caffarelli–Kohn–Nirenberg-type \(\epsilon \)-regularity lemma. This appears to be the main reason that [9] is limited to \(d=3\).
In the general case \(d\ge 3\), Dong and Du [6] attempt to avoid this issue by defining a local scale-invariant quantity whose smallness, combined with \(\Vert u\Vert _{L_t^\infty L_x^d}<\infty \), implies local regularity of the solution.Footnote 1 Tools inspired by theirs will prove useful in our quantitative setting as well; see Sect. 3.2 for details.
In contrast to the classical blowup criteria above, the results using the compactness approach such as [1, 6, 9, 10, 14, 16], etc. do not imply any quantitative information on the blowup rate of any critical norm. Recently, Tao [19] gave what appears to be the first quantitative rate for a critical quantity, namely that
for \(d=3\), where \(c>0\) is an absolute constant. Instead of proceeding by contradiction as in [9] and similar works, the idea is to assume the solution is concentrating near a blowup and show directly—using, for example, Carleman estimates instead of their qualitative derivatives like backward uniqueness—that there must be mild \(L_x^3\) concentrations at an increasing number of spatial scales. Subsequent authors have used similar schemes to extend (2); for instance Barker and Prange quantify the improvement in [16] and prove a theorem for type-1 blowups [3], while the author shows that the denominator in Theorem 1.1 can be replaced by \((\log \log \frac{1}{T_*-t})^c\) in the case that u is axisymmetric [13].
In this work we are able to prove a quantitative blowup rate analogous to (2) for \(d\ge 4\), answering a question of Tao, see Remark 1.6 in [19]. As in [19], we assume for convenience that u is a classical solution, meaning it is smooth with derivatives in \(L_t^\infty L_x^2([0,T]\times {{\mathbb {R}}^d})\). Since our results depend quantitatively on only \(\Vert u\Vert _{L_t^\infty L_x^d}\), they can in principle be extended, for instance to the Leray–Hopf class as in [9].
Theorem 1.1
Suppose u is a classical solution of (1) that blows up at \(t=T_*\) and \(d\ge 4\). Then
for a constant \(c=c(d)>0\) depending only on the dimension.
This is a straightforward consequence of our other main theorem which asserts that a solution satisfying the critical bound
is regular; in particular we can quantify its subcritical norms in terms of A. Let us take A to be at least 2.
Theorem 1.2
If u is a classical solution of (1) on [0, T] satisfying (3) with \(d\ge 4\), then
for \(t\in (0,T]\), where \(C=C(j,d)\) depends only on \(j\ge 0\) and the dimension.
Remark 1.3
Using ideas from [13], particularly Proposition 8, it is possible to improve the bounds in Theorems 1.1 and 1.2 if some mild symmetry assumptions are made on u. For example, suppose u is axisymmetricFootnote 2 about the \(x_3,x_4,\ldots ,x_d\)-plane. When \(d=4\), one \(\log \) and one \(\exp \) can be removed from Theorems 1.1 and 1.2 respectively. When \(d\ge 5\), we may remove two \(\log \)s and two \(\exp \)s. In the latter case, in the proof of Proposition 5.1, we find the desired concentration at length scale \(\ell =A^{-O(1)}\) using the slightly improved energy bound (9), while when \(d=4\), we resort to pigeonholing the energy over \(A^{O(1)}\)-many length scales which yields an \(\ell \) as small as \(\exp (-A^{O(1)})\). An argument similar to Proposition 8 in [13] allows one to avoid losing additional exponentials when locating annuli of regularity as in Proposition 3.6.
Let us summarize why the approach in [19] breaks down in greater than three dimensions. The first set of difficulties arises when one would use the “bounded total speed” property, i.e., control on \(\Vert u\Vert _{L_t^1L_x^\infty }\), see Proposition 3.1(ii) in [19]. One expects (for example, based on the heuristics following Proposition 9.1 in [18]) that this property fails when \(d\ge 4\). In other words, one cannot expect any kind of “speed limit” for elements convected by u. Instead, we derive a procedure to propagate concentrations of the velocity and pressure from fine to coarse scales, encapsulated in Proposition 3.2, which is a quantitative version of Lemma 3.2 in [6]. From this we can extract several important results including an \(\epsilon \)-regularity criterion (Proposition 3.4) and the backward-propagation lemma (Proposition 3.7).
The second and more significant challenge in high dimensions is due to the lack of quantitative epochs of regularity as in Proposition 3.1(iii) in [19]. In the qualitative analysis, it suffices to use epochs of regularity for which one has absolutely no lower bound on the length, nor any explicit upper bound on |u|, \(|\nabla u|\), etc. (For example, see the use of Proposition 2.4 in the proof of Proposition 5.3 in [6].) This becomes a problem when one needs to propagate concentrations of vorticity through space and into a distant annulus of regularity, as the width of the time interval on which one has regularity determines the lower bound one can extract from unique continuation for the heat equation. We will remedy this by substituting spacetime partial regularity in place of epochs of regularity. This creates some new difficulties; first that when one propagates a high frequency concentration of the solution backward in time, a priori there is no guarantee that the resulting concentration has any of its \(L_{t,x}^2\) mass inside the regular region. There is a particular fractal arrangement of concentrations in spacetime which is consistent with this obstruction; indeed the objective of Proposition 5.1 is to locate a scale where we may rule it out.
The second difficulty faced when propagating the vorticity using only partial regularity is the following: the usual Carleman inequality for unique continuation has as its domain a large ball in space (compared to the length of the time interval); however we wish to propagate the vorticity for a great distance through a thin spacetime slice. We are able to accomplish this without the bounds suffering too badly (losing only one additional exponential compared to the \(d=3\) case) by repeatedly applying the Carleman inequality in a series of moving and expanding balls lying in an expanding slice of spacetime. We show that the iteration of unique continuation accelerates exponentially away from the initial vorticity concentration. The positive feedback loop this creates is essential for arriving at the claimed bounds, as unique continuation through a uniformly thin slice would lead to an unbounded number of logarithms and exponentials in Theorems 1.1 and 1.2.
The plan of the paper is as follows: in Sect. 2, we give some preliminaries including a useful decomposition for estimating solutions in high-integrability spaces. In Sect. 3, we prove some straightforward energy estimates, then introduce our quantitative analogue of the Dong–Du lemma for propagating concentrations of the solution from fine to coarse scales. Then we apply it to partial regularity and backward propagation of high frequency concentrations. In Sect. 4 we quote the high-dimensional version of the Carleman inequality from [19] for quantitative unique continuation, then show the iteration through a slice expanding in space. In Sect. 5, we prove the main propositions: first the back propagation into a regular cylinder, then the successive use of Carleman inequalities to propagate it forward to the final time. Finally, in Sect. 6, we use Propositions 5.1 and 5.2 to prove Theorems 1.1 and 1.2.
2 Preliminaries
2.1 Notation
We use asymptotic notation \(X\lesssim Y\) or \(X=O(Y)\) to mean that there is a constant C(d) depending only on the spatial dimension such that \(|X|\le C(d)Y\). Moreover \(X\sim Y\) is an abbreviation for \(X\lesssim Y\lesssim X\). A subscript on \(\lesssim \) or O indicates that the constant may depend on additional parameters. As in [19], we define the hierarchy of powers \(A_j=A^{C_0^j}\) where A is as in (3) and \(C_0\) is a large constant which depends only on the dimension d. Throughout the arguments we will freely enlarge A so that \(A\ge C_0\) and \(C_0\) so that it defeats any constants in the asymptotic notation.
If \(I\subset {\mathbb {R}}\) is a time interval, we use |I| to denote its length. If \(\Omega \subset {{\mathbb {R}}^d}\), \(|\Omega |\) will denote its d-dimensional Lebesgue measure. For a finite set E, we denote its cardinality by \(\#(E)\). If \(x_0\in {{\mathbb {R}}^d}\) and \(R>0\), we will write \(B(x_0,R)\) to denote the closed ball \(\{x\in {{\mathbb {R}}^d}:|x-x_0|\le R\}\). If \(z_0=(t_0,x_0)\in {\mathbb {R}}\times {{\mathbb {R}}^d}\) is a spacetime point, define the parabolic cylinder \(Q(z_0,R):=[t_0-R^2,t_0]\times B(x_0,R)\) and \(Q(R):=Q(0,R)\). If \(B=B(x_0,R)\) and \(Q=Q(z_0,R)\) where \(z_0=(t_0,x_0)\), we define the dilations \(\lambda B:=B(x_0,\lambda R)\) and \(\lambda Q:=Q(z_0,\lambda R)\).
For vectors \(u,v\in {{\mathbb {R}}^d}\), define the tensor products
We also make use of the Frobenius inner product \(A:B:={{\,\textrm{tr}\,}}(A^tB)\).
For \(\Omega \subset {\mathbb {R}}^n\) and \(I\subset {\mathbb {R}}\), we will use the Lebesgue norms
and
with the usual modifications if \(p=\infty \) or \(q=\infty \). When \(p=q\) we use the abbreviation \(L_{t,x}^p:=L_t^pL_x^p\).
For a Schwartz function \(f:{{\mathbb {R}}^d}\rightarrow {\mathbb {R}}^n\), we define the Fourier transform
and the Littlewood–Paley projection by the formula
where \(\varphi :{\mathbb {R}}^3\rightarrow {\mathbb {R}}\) is a radial bump function supported in B(0, 1) such that \(\varphi \equiv 1\) in B(0, 1/2). Then let
etc. Any sums indexed by capital letters such as \(\sum _N\) or \(\sum _{N>A}\) should be taken to have indicies ranging over the dyadic integers \(2^{\mathbb {Z}}\).
2.2 Bernstein-Type Inequalities
The following bounds on frequency-localized Fourier multipliers will prove useful, see Lemma 2.1 in [19].
Lemma 2.1
Let \(m\in C^\infty ({{\mathbb {R}}^d}\rightarrow {\mathbb {C}})\) be a multiplier supported in B(N) for some frequency \(N>0\), obeying
for all \(0\le j\le 100d\) for some \(M>0\). Then the Fourier multiplier \(\widehat{T_mf}(\xi ):=m(\xi )f(\xi )\) satisfies the bound
assuming \(1\le p\le q\le \infty \) and \(f\in L^p({{\mathbb {R}}^d})\) is smooth.
Let us record a useful application of Lemma 2.1. Taking \(P_Ne^{t\Delta }\) and summing, we obtain
for \(t>0\), \(j\ge 0\), and \(1\le p\le q\le \infty \). Moreover, combining Lemma 2.1 with (1) and (3), the following bounds on the frequency-localized vector fields are immediate.
Lemma 2.2
If u solves (1) on \([-T,0]\) and admits the bound (3), then we have
for all \(j\ge 0\), \(N>0\).
As in [19], Lemma 2.1 has a spatially localized version.
Lemma 2.3
Let m, N, and M be as in Lemma 2.1, \(\Omega \subset {{\mathbb {R}}^d}\) open, \(B\ge 1\), \(K\ge 10\), and \(\Omega _{B/N}:=\{x\in {{\mathbb {R}}^d}:{{\,\textrm{dist}\,}}(x,\Omega )<B/N\}\). Then we have
assuming \(1\le p_1\le q_1\le \infty \), \(1\le p_2\le q_2\le \infty \), and \(q_2\ge q_1\).
If f admits a decomposition \(\sum f_i\), the same proof found in [19] allows the second term on the right-hand side in the Bernstein inequality to be estimated separately for each \(f_i\), each with its own choice of \(p_2\) and \(q_2\). (This will be useful when paired with Proposition 2.5.)
In a similar spirit, the following simple result will be useful.
Lemma 2.4
If \(N,K>0\), \(j\ge 0\), \(p\le q\), \(0<r_1<r_2\), \(f\in C^\infty ({{\mathbb {R}}^d})\), and \(\phi \in C_c^\infty ({{\mathbb {R}}^d})\) with \(\phi \equiv 1\) in \(B(r_2)\), then
Proof
With \(\psi (\xi )\) the Fourier multiplier for \(P_1\), we have
as long as x is restricted to \(B(r_1)\) and c is chosen sufficiently small compared to \(r_2-r_1\). The first term is exactly \(P_N(\phi \nabla ^jf)(x)\) and the second term is straightforward to estimate using integration by parts, polynomial decay of \({{\check{\psi }}}\) and its derivatives, and Hölder’s inequality. \(\square \)
2.3 Sharp-Flat Decomposition of the Solution
A difficulty of working in \(L_x^d\) is that while one would wish to make use of energy methods, the solution does not have enough decay to be in any \(L_x^2\)-based spaces. In the cases \(d=3,4\) one can avoid this problem by some manner of splitting u into one flow solving a linear equation and another that solves a complementary nonlinear equation, see [4, 19]. For example, the method in [19] of considering \(u(t)-e^{(t-t_0)\Delta }u(t_0)\), i.e., removing the heat flow part of the evolution, leaves the remaining nonlinear flow in \(L_t^\infty L_x^p\) for \(p\in [\frac{d}{2},d]\). Unfortunately when \(d\ge 5\), this range excludes the important energy space \(L_t^\infty L_x^2\).
In the general case \(d\ge 3\) we address this difficulty using the following decomposition of u very similar to the one in [13]. We remark that decompositions based on a Picard-type iteration in the same spirit have also appeared in [2, 5, 10]. The idea is essentially to subtract off a Picard iterate starting from an initial condition \(u(t_0)\). The critical bound (3) implies good subcritical estimates on the iterate thanks to smoothing from the heat propagator, and one can show inductively using Duhamel’s formula that the difference lies in lower integrability spaces including \(L_t^\infty L_x^2\). Moreover, the difference satisfies a Navier–Stokes-type equation which leads to estimates that will be useful later.
Proposition 2.5
Suppose u is a classical solution of (1) on \([-T,0]\) with the bound (3). Then for every \(T_1\in [0,T/2]\), there exist \(u^{\flat }\) and \(u^{\sharp }\) such that the following hold:
-
We have the decomposition
$$\begin{aligned} u=u^{\flat }+u^{\sharp }\text { on }[-T_1,0]. \end{aligned}$$ -
If \(d\le p\le \infty \) and \(j\ge 0\), then
$$\begin{aligned} \Vert \nabla ^ju^{\flat }\Vert _{L_t^\infty L_x^p([-T_1,0]\times {{\mathbb {R}}^d})}&\le A^{O_j(1)}T_1^{-\frac{1}{2}(1+j-\frac{d}{p})}, \end{aligned}$$(5)$$\begin{aligned} \Vert P_Nu^{\flat }\Vert _{L_{t,x}^\infty ([-T_1,0]\times {{\mathbb {R}}^d})}&\le A^{O(1)}e^{-T_1N^2/O(1)}T_1^{-\frac{1}{2}}. \end{aligned}$$(6) -
If \(1\le p\le d\) and \(1<q<\infty \), thenFootnote 3
$$\begin{aligned} \Vert u^{\sharp }\Vert _{L_t^\infty L_x^p([-T_1,0]\times {{\mathbb {R}}^d})}&\le A^{O(1)}T_1^{\frac{1}{2}(\frac{d}{p}-1)}, \end{aligned}$$(7)$$\begin{aligned} \Vert \nabla u^{\sharp }\Vert _{L_{t,x}^2([-T_1,0]\times {{\mathbb {R}}^d})}&\le A^{O(1)}T_1^{\frac{d}{4}-\frac{1}{2}},\end{aligned}$$(8)$$\begin{aligned} \Vert \nabla u^{\sharp }\Vert _{L_t^qL_x^\frac{d}{2}([-T_1,0]\times {{\mathbb {R}}^d})}&\lesssim _q A^{O(1)}T_1^{\frac{1}{q}}. \end{aligned}$$(9) -
\(u^{\sharp }\) solves
$$\begin{aligned} \partial _tu^{\sharp }+\mathbb {P}{{\,\textrm{div}\,}}(u^{\sharp }\otimes u^{\sharp }+2u^{\flat }\odot u^{\sharp })-\Delta u^{\sharp }=f \end{aligned}$$(10)where f obeys estimates
$$\begin{aligned} \Vert \nabla ^jf\Vert _{L_t^\infty L_x^p([-T_1,0]\times {{\mathbb {R}}^d})}&\le A^{O_j(1)}T_1^{-\frac{1}{2}(3+j-\frac{d}{p})} \end{aligned}$$(11)for \(\frac{d}{2}\le p\le \infty \) and \(j\ge 0\).
Proof
Starting with
we inductively define for \(n\ge 1\)
where we have chosen a sequence of O(1)-many times \(-2T_1<\tau _1<\tau _2<\cdots <-T_1\) such that \(\tau _i-\tau _{i+1}=T_1/O(1)\). We prove (5) on the shrinking time intervals \([\tau _n,0]\) with \(u^{\flat }\) replaced by \(u^{\flat }_n\) by induction on n. For \(n=0\) it is trivial. Suppose the claim for some \(n-1\ge 0\). Then, for \(t\in [\tau _n,0]\),
which gives the desired bound. Then (6) follows similarly by induction using Duhamel’s principle and a paraproduct decomposition.
Next, it is convenient to decompose \(u^{\sharp }_n=u^{\sharp ,1}_n+u^{\sharp ,2}_n\) where
We claim the bound in (7) for \(u^{\sharp }_n\), specifically in the range \(\max (\frac{d}{n+1},1)\le p<d\) and on the time interval \([\tau _n,0]\). Thus we will obtain the desired result by taking n large depending on d. Note that the \(p=d\) case is immediate from (3) and (5). As a base case, we consider \(n=1\) for which \(u^{\sharp ,1}_1=0\). For \(u^{\sharp ,2}_1\),
which yields the desired result using (3) assuming \(\frac{d}{2}\le p<d\). Now assume the desired inequality for some \(n-1\ge 1\). Then
assuming \(\frac{1}{p}\le \frac{1}{s}+\frac{1}{r}\). This is integrable in time, and furthermore we can apply (5) and (7), by taking \(r=\frac{dp}{d-p}\) and \(s=d\), and assuming additionally that \(\max (\frac{d}{n+1},1)\le p<\frac{d}{2}\). If instead we take \(r=\frac{d}{2}\) and \(\frac{1}{s}=\max (\frac{1}{p}-\frac{2}{d},0)\), we obtain the same result but instead for \(\frac{d}{3}\le p<d\). Combining these, we have the full range of p. Next we consider \(u^{\sharp ,2}\). With \(\frac{1}{r}=\frac{1}{2}(\frac{1}{d}+\frac{1}{p})-\epsilon \),
implies the desired bound upon taking \(\epsilon \) sufficiently small depending on p and d. (5)–(8) therefore hold upon setting \(u^{\flat },u^{\sharp }:=u^{\flat }_d,u^{\sharp }_d\).
One readily computes (10) with \(f=\mathbb {P}{{\,\textrm{div}\,}}(u^{\flat }_{d-1}\otimes u^{\flat }_{d-1}-u^{\flat }_d\otimes u^{\flat }_d)\). Then (11) follows by Hölder’s inequality and (5). Multiplying (10) by \(u^{\sharp }\) and integrating over \({{\mathbb {R}}^d}\), we have
and therefore we can apply (7), (5), and (11) to find
which proves (8).
Finally, we note that
Thus by (4) and maximal regularity for the heat equation,
We conclude (9) by (5), (3), and Hölder’s inequality. \(\square \)
3 Tools for Controlling Spacetime Concentrations
3.1 Local Energy Estimates
We will make use of three slightly different consequences of the local energy equality for (1). The second is an extension of Lemma 2.2 in [6], now with the dependence on A made explicit. (See below for the definitions of C and D.)
Lemma 3.1
Let u be a smooth solution of (1) satisfying (3) on \([-T,0]\), \(r>0\), and \(I\subset [-T,0]\). Then we have
and, for \(t_0\le t\le t_0+10r^2\),
Proof
All three estimates are elementary applications of the local energy equality
along with Hölder’s inequality, (3), integration by parts, and the Calderón–Zygmund estimate for the pressure. \(\square \)
3.2 Propagation from Small to Large Scales
Define the local scale-invariant quantities
and
For brevity, if \(Q=Q(z_0,R)\), we write C(Q) in place of \(C(R,z_0)\). These quantities appear in [6], although here we have defined them slightly differently so they are proportional to the norm of u. The following proposition is closely related to Proposition 3.1 in [6]. Their method of proof is by contradiction and uses a compactness argument to find suitable values \(\eta \) and \(\epsilon \). Thus such an approach does not give any information on how they depend on A; see also the comments in footnote 1.
Proposition 3.2
Let u be a smooth solution of (1) satisfying (3). Then for any \(\epsilon \le A^{-d^3}\), if \(z_0\in [-T/2,0]\times {{\mathbb {R}}^d}\), \(\rho \le T/4\), and
then
for any \(z_1\in Q(z_0,\rho /2)\) and \(r\in (0,\rho /2)\).
As in [6], Proposition 3.2 is obtained by iteratively applying Lemma 3.3 below. The point is that given a lower bound \(C(r,z_1)+D(r,z_1)>\epsilon \) in a small cylinder, the lemma implies the same lower bound in a cylinder dilated by a factor of A. This step can be iterated until it yields a cylinder \(Q'\) that is comparable in length to \(Q(z_0,\rho )\), the ratio depending on A. Since \(Q'\) can be smaller than \(Q(z_0,\rho )\), the scaling factors in the definition of C and D lead to the loss of \(A^{O(1)}\).
Lemma 3.3
Let \(\epsilon \), u, \(\rho \), and \(z_0\) be as in Proposition 3.2. Then, with \(\eta =A^{-1}\),
implies
Proof
We translate and rescale so that \(z_0=0\) and \(\rho =1\). By (13),
Fix the large frequency scale \(N=\epsilon ^{-\frac{1}{d}}\). By interpolation and Lemma 2.3,
Fix a spatial cutoff \(\varphi \in C_c^\infty (B(1/2))\) with \(\varphi \equiv 1\) in B(1/3). By Lemma 2.4, Plancherel, and (17),
and by the same reasoning
Therefore, by Hölder’s inequality, the main term is
The remaining terms all involve the small global Bernstein error and can be estimated similarly to find
To study the low frequencies, let \(\phi \in C_c^\infty (Q(1/2))\) be a spacetime cutoff function satisfying \(\phi \equiv 1\) in Q(1/3). Using Duhamel’s formula we decompose u into local and global parts,
By Hölder, Lemma 2.1, (4), (17), fractional integration, and (15),
Next observe that \(P_{\le N}u^g\) solves the heat equation in Q(1/3) so by Hölder’s inequality and well-known parabolic theory,
Clearly \(P_{\le N}u^g=u-P_{>N}u-P_{\le N}u^l\). The first piece can be estimated using (15), while the other two we have already addressed. (Note that the estimates are unaffected by changing the domain to \(Q(\frac{1}{4})\) except for the heat propagator part of \(P_{\le N}u^l\); however even the worse bound \(\epsilon A^\frac{1}{2}\) without the improvement from using Hölder on \(Q(\eta )\) suffices.) In total,
Next we consider the pressure. From the decomposition
we have
by Lemma 2.3 and (3). By the same calculations by which we estimated C above and the large choice of N, this implies
For the other term we have
again by Lemma 2.3 and the calculations above.
Next we turn to the low frequencies. With \(\varphi \in C_c^\infty (Q(\frac{1}{5}))\) a new spacetime cutoff satisfying \(\varphi \equiv 1\) in \(Q(\frac{1}{6})\), define
where \({\mathcal {N}}\) is the Newton potential. To estimate the local contribution we employ the paraproduct decomposition
The calculations above imply that \(P_{\le N}u\) can be decomposed as \(v+w\) where
for any \(q\ge 1\). (For example, let w be the nonlinear part of \(P_{\le N}u^l\) and v the rest.) Thus, using the Calderón–Zygmund estimate for \({\mathcal {N}}\),
where q is taken large but finite to avoid the unboundedness of \({\mathcal {N}}{{\,\textrm{div}\,}}{{\,\textrm{div}\,}}\) at the endpoint. By the calculations for \(P_{>N}u\),
Finally, observe that \(P_{\le N}p^g\) is harmonic in \(Q(\frac{1}{6})\). Therefore
Then the decomposition \(P_{\le N}p^g=p-P_{>N}p-P_{\le N}p^l\) along with the above estimates and (15) implies the desired bound. This completes the estimate of \(D(\eta )\). \(\square \)
3.3 Annuli and Slices of Regularity
The first application of Proposition 3.2 is that the smallness of C and D implies good pointwise bounds on the solution. We state Proposition 3.4 as a slightly more quantitative variant of Theorem 4.1 in [6].
Proposition 3.4
Let u, \(z_0\), and \(\rho \) be as in Proposition 3.2 and suppose that for every \(z_1\in Q(z_0,\rho _1/2)\), \(\rho \in (0,\rho _1/2)\) we have
Then, for \(j=0,1,2\),
Proof
Let us normalize \(\rho _1=1\) and \(z_0=0\). By the argument in the proof of Theorem 4.1 in [6] using the bound on p coming from (3), one finds
We may bootstrap the estimates for higher derivatives using Duhamel’s formula. Let us fix a decreasing sequence of O(1)-many lengths \(\frac{1}{3}>r_1>r_2>r_3>\cdots >\frac{1}{4}\) satisfying \(r_n-r_{n+1}=1/O(1)\). For a frequency \(N\gg 1\) to be specified, (18), (5), Lemma 2.3, and Duhamel’s formula for (1) starting from \(t=-1/3\) imply
Clearly with N large enough, the first term (from the linear propagator) is negligible compared to the third (the global contribution to Bernstein). Therefore, again by Duhamel’s formula, (18), and a paraproduct decomposition of \(P_N(u\otimes u)\),
Thus, once again by Duhamel’s formula and (4), for any \(N_0>0\),
By taking \(N_0\) to be a suitable power of \(\epsilon ^{-1}\), we arrive at
Proceeding in the same way, one can obtain the higher order estimates as well. \(\square \)
Taking Propositions 3.2 and 3.4 together, we obtain the useful fact that if \(C(Q)+D(Q)\le A_1^{-1}\), then we have good pointwise bounds for u in Q/2. (Clearly we may also replace Q/2 with, say, 9Q/10 by trivially modifying the proofs.) As an application, we prove the first partial regularity result. As discussed in more depth in Sect. 4, by letting the region of regularity expand in space (as opposed to taking, say, \(Q_0\times {\mathbb {R}}^{d-k}\) for some small \(Q_0\subset {\mathbb {R}}^k\)), we obtain better estimates upon iterating unique continuation. We remark that we do not claim this to be the optimal result; indeed one should expect that regular regions exist that are unconstrained in up to three of the \(d+2\) parabolic dimensions, (cf. epochs of regularity when \(d=3\) which are unbounded in all three spatial dimensions). In this case, the region is unbounded in only one spatial dimension, i.e., radially toward \(\theta \).
Proposition 3.5
(Slices of regularity). Assume u is smooth and satisfies (1) and (3) on \([-T,0]\), \(z_0\in [-T/2,0]\times {{\mathbb {R}}^d}\), and \(R^2\le T/4\). Then there exist a direction \(\theta \in S^{d-1}\) and a time interval \(I\subset [t_0-R^2,t_0]\) with \(|I|=A_2^{-2}R^2\) such that within the slice
for \(j=0,1,2\), we have
Proof
We normalize \(R=1\) and \(z_0=0\), then apply Proposition 2.5 on the interval \([-2,0]\). Let \({\mathcal {S}}_0\) be the collection of all spacetime regions of the form
ranging over all \(\theta \in S^{d-1}\) and \(I=[-10A_2^{-2}k,-10A_2^{-2}(k-1)]\) where \(k\in [1,A_2^2/10]\cap {\mathbb {N}}\). Clearly we may find a disjoint subcollection \({\mathcal {S}}_1\) containing \(\gtrsim A_2^{d+1}\) such slices. We seek to find one where we can apply Propositions 3.2 and 3.4. To find a region where D is small, observe that by the Calderón–Zydmund estimate for \({{\,\textrm{div}\,}}{{\,\textrm{div}\,}}/\Delta \), Hölder’s inequality, Sobolev embedding, and (8),
By interpolation with the \(L_t^\infty L_x^\frac{d}{2}\) bound from (7),
As a result, of the \(\gtrsim A_2^{d+1}\) slices in \({\mathcal {S}}_1\), at least 99% must have
Using (5) and Hölder’s inequality, it is easy to see that the same can be said for \(u^{\flat }\odot u^{\sharp }\) and \(u^{\flat }\otimes u^{\flat }\). Let \(\mathcal S_2\subset {\mathcal {S}}_1\) be the collection of all such slices. Combining these estimates and applying Hölder’s inequality, we have
for every parabolic cylinder \(Q\subset S\) of length \(\sim A_2^{-1}\) and every \(S\in {\mathcal {S}}_2\). By the same argument along with (8), most of the \(S\in {\mathcal {S}}_2\) satisfy
so in fact the family \({\mathcal {S}}_3\) of slices satisfying both (19) and (20) has \(\#({\mathcal {S}}_3)\ge C_0^{-1}A_2^{d+1}\). Each of these slices occupies one of \(\sim A_2^{2}\) time intervals, so by the pigeonhole principle, there is an interval \(I=[t_0,t_0+A_2^{-2}]\) which contains at least \(C_0^{-2}A_2^{d-1}\) slices in \({\mathcal {S}}_3\). By (3), there must be one of these slices \(S_0\) such that
where \(S_{0,x}\subset {{\mathbb {R}}^d}\) is the projection of \(S_0\) to the spatial components. Then by Hölder’s inequality, for every ball of length \(A_2^{-1}\) inside \(S_{0,x}\),
By (14), (19), and (20), for any \(Q\subset S_0\) of length \(A_2/2\),
Note that the bound (20) on \(u^{\sharp }\) can be restricted to any such \(Q\subset S_0\) and extended to the full solution u using (5) and Hölder’s inequality. We conclude from the above and the local Gagliardo–Nirenberg inequality (see eg. Lemma 2.1 in [6]) that
for any \(Q\subset S_0\) of length \(A_2/2\). This along with (19) leads to the claimed bounds by Propositions 3.2 and 3.4. \(\square \)
The next proposition should be compared to Proposition 3.1(vi) in [19]. In the case \(d\ge 4\) it will be necessary locate even wider annuli where the solution enjoys good subcritical bounds, at the expense of needing to search a larger range of length scales. Note that in [19] a key ingredient of the proof is the bounded total speed property which is unavailable in high dimensions. For this reason we proceed in the manner of Barker and Prange who use an \(\epsilon \)-regularity criterion to find quantitative annuli of regularity; see [3, Section 6].
Proposition 3.6
(Annuli of regularity). Let u be a smooth solution of (1) satisfying (3) on \([-10,0]\). For any \(R_0\ge 2\), there exists a scale \(R\in [R_0,R_0^{\exp (A_4)}]\) such that for \(j=0,1,2\),
Proof
Since, by (3),
the pigeonhole principle implies that there exists R in the desired range such that
and therefore, by Hölder’s inequality, for every parabolic cylinder \(Q\subset [-10,0]\times \{R/10\le |x|\le 10R^{2A_4}\}\),
This implies that the region \([-1,0]\times \{R\le |x|\le R^{2A_4}\}\) can be covered by a collection of cylinders \(Q_j/2\) such that \(Q_j\subset [-10,0]\times \{R/10\le |x|\le 10R^{2A_4}\}\) and \(C(Q_j)+D(Q_j)\lesssim A_4^{-\frac{1}{2}}\). Successively applying Propositions 3.2 and 3.4 in all the \(Q_j\) yields the desired bounds. \(\square \)
3.4 Backward Propagation of Concentrations
Next we prove a high-dimensional analogue of Proposition 3.1(v) in [19]. The proof given there is obtained by iterating a lemma for very short back-propagation, with the bounded total speed property (Proposition 3.1(ii) in [19]) preventing the sequence of concentrations from traveling too far through space. Although the bounded total speed is unlikely to hold when \(d\ge 4\), Proposition 3.2 is a suitable replacement.
Proposition 3.7
Suppose u is smooth and satisfies (1) and (3) on \([-T,0]\) where \(T\ge 100\). If \(N_0\ge 10A_1\) and
then there exist \(z_1\in [-1,-A_2^{-1}]\times B(A_2)\) and \(N_1\in [A_2^{-1},A_2]\) such that
Proof
Using Lemma 2.2 to deduce that there must be a parabolic cylinder about \(z=0\) where we still have the lower bound on \(|P_{N_0}u|\), we have
with \(r= A_1^{-2}N_0^{-1}\), using Lemma 2.3. Rearranging, this implies
Because \(N_0\ge 10A_1\), we can apply Proposition 3.2 in the contrapositive to find
Suppose first that \(C(1,0)\ge \frac{1}{2}A_1^{-4d}\). Using some large parameter M to be specified, we split u into three pieces to estimate C(0, 1): low frequencies
intermediate frequencies
and high frequencies
Here we have used the decomposition from Proposition 2.5 on, say, \([-2,0]\times {{\mathbb {R}}^d}\) followed by Lemma 2.3 and Hölder’s inequality in space and interpolation in time. For the first term, by (6),
For the second, by Hölder’s inequality, Plancherel, (7), and (8),
Combining the above estimates, we conclude
With \(M=A_1^{O(1)}\), we obtain \(z_1\in Q(1)\) and \(N_1\in [A_2^{-1},A_2]\) such that
Suppose instead that \(D(1,0)\ge \frac{1}{2}A_1^{-4d}\). By Hölder’s inequality, Lemma 2.3, and (3), also using the fact that \(p=-\Delta ^{-1}{{\,\textrm{div}\,}}{{\,\textrm{div}\,}}(u\otimes u)\), we have
To handle the intermediate and high frequencies, we use the paraproduct decomposition
For the first term, by Hölder’s inequality, Lemma 2.1, and (3),
Next, by Proposition 2.5, Hölder’s inequality, (3), (6), and estimating \(P_{>M}u^{\sharp }\) using Plancherel and (8) as above, we have
Finally, by Hölder’s inequality, Lemma 2.3, and (3),
In total,
Once again with \(M=A_1^{O(1)}\), we obtain \(N_1\) and \(z_1\) with the claimed properties. Finally we address the possibility that this \(t_1\) falls in \([-A_2^{-1},0]\) instead of the desired interval. By the fundamental theorem of calculus and Lemma 2.2,
which implies we can redefine \(t_1\) to be in \([-1,-A_2^{-1}]\) while maintaining the lower bound on \(|P_{N_1}u|\). \(\square \)
4 Carleman Inequalities for Unique Continuation
For the reader’s convenience, we begin by quoting the quantitative unique continuation Carleman inequality from [19], which has a straightforward generalization to d dimensions.
Proposition 4.1
(Unique continuation). With \(T,r>0\), assume \(u\in C^\infty ([0,T]\times B(r)\rightarrow {\mathbb {R}})\) admits the differential inequality
while the parameters satisfy
Then
where
Clearly this Carleman inequality as written is incompatible with the geometry of Proposition 3.5 since B(r) would have to be contained in the thin slice in order to guarantee (22), while simultaneously we need \(r^2\gg t_0\) in order for the first error term to be suppressed. Instead we iteratively apply the Carleman inequality outward in space, starting near the vertex of the slice. The point is that as the iteration proceeds, the center for the Carleman inequality moves further in the \(\theta \) direction, so r can be taken to be larger, which makes the Carleman inequality stronger. Thus combining Propositions 3.5 and 4.2 leads to a feedback loop which leads to substantially better estimates; specifically, only \(\sim \log (R_2/R_1)\) iterations of Proposition 4.1 (by way of Lemma 4.3) are neededFootnote 4 to propagate a concentration from length scale \(R_1\) to \(R_2\).
Proposition 4.2
(Iterated unique continuation Carleman inequality). Suppose \(T_1>0\), \(0<\eta \le C_0^{-1}\), and u is smooth on S with
for \(j=0,1\), where, for some direction \(\theta \in S^{d-1}\),
Moreover, assume that for every \(t\in [-\eta T_1,0]\), we have
where \(20T_1^\frac{1}{2}\le R_0\le \eta ^{-2}T_1^\frac{1}{2}\) and \(\epsilon \le \eta ^8\). Then for every \(t\in [- \eta T_1/2,0]\) and \(R\ge 2R_0\), we have
Given the following lemma, Proposition 4.2 will follow by iteration.
Lemma 4.3
Assume u, \(T_1\), and \(\eta \) are as in Proposition 4.2 and that there is some \(R\ge 20T_1^\frac{1}{2}\) and \(a\in (\frac{1}{2},1)\) such that for every \(t\in [-aT_1,0]\),
where
Then for every \(t\in [-aT_1+2\eta ^5R^2\log ^{-1}\frac{1}{\epsilon _0},0]\),
where \(R':=(1+\eta ^3)R\).
Proof of Proposition 4.2
Let us normalize \(T_1=1\). One iterates Lemma 4.3 on the time intervals \([-a_k,0]\) for \(k=0,1,\ldots ,n\), where \(n=\lceil \log _{1+\eta ^3}(R/R_0)\rceil \). Specifically, the kth application of the lemma is centered at the point \(R_k\theta \in {{\mathbb {R}}^d}\) and uses the lower bound \(\epsilon _k\), where
One computes that
Recall that \(R_0\le \eta ^{-2}\) and \(\epsilon \le \eta ^8\). Thus, with \(\eta \) sufficiently small, \(a_k\ge \frac{\eta }{2}\) so the claimed bound holds on \([-\frac{\eta }{2},0]\). The final lower bound resulting from the iteration is given by
With \(\eta \) sufficiently small, we have \(\frac{\log \eta ^{-2}}{\log (1+\eta ^3)}\le \eta ^{-\frac{7}{2}}\) and \(\eta ^{-2}\le (R/R_0)^{\eta ^{-\frac{1}{2}}}\), using that \(R\ge 2R_0\). Thus \(\epsilon _n\ge \epsilon ^{(R/R_0)^{\eta ^{-4}}}\) as claimed. \(\square \)
Proof of Lemma 4.3
Again, we rescale so that \(T_1=1\). Fix any \(t'\in [-a+2\eta ^5R^2\log ^{-1}\frac{1}{\epsilon _0},0]\). We apply Proposition 4.1 to the function
on the time interval \([0,T_c]\) with the parameters
Clearly (23) implies (22) is satisfied. Consider the three terms in the Carleman inequality which takes the form \(Z\le X+Y\). For the left-hand side, since \(B(R'\theta ,\eta ^2R/2)\supset B(R\theta ,\eta ^5R)\),
using that \(\eta \) and \(\epsilon _0\) are small, \(R\ge 20\), and \(\eta \ge \epsilon _0^\frac{1}{8}\). Next, by (23),
which is negligible compared to Z due to the constraint \(\eta \le C_0^{-1}\). For the remaining term in the Carleman inequality,
By (23), the contribution to this term from the region where \(|x-R'\theta |>\eta ^5R'\) is negligible compared to Z:
using that \(\epsilon _0\le R^{-100d\eta }\). Thus Z is bounded by the contribution to Y from \(B(R'\theta ,\eta ^6R')\) which proves the lemma. \(\square \)
5 Main Propositions
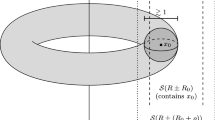
Next we proceed to the main propositions of this paper. The philosophy is similar to [19] but as discussed in Sects. 1 and 3, in higher dimensions we do not have quantitative epochs of regularity. As a result, given a spacetime point where u has a high frequency concentration, it is far from clear that the vorticity lower bound implied by Proposition 3.7 intersects at all with a spacetime region where the solution is regular, let alone an entire epoch \(I\times {{\mathbb {R}}^d}\) as in the three-dimensional case. From a qualitative perspective, since \(\omega \) is locally \(L_{t,x}^2\) and the measure of the spacetime set where \(|\nabla ^ju|\lesssim \ell ^{-1-j}\) shrinks to zero as \(\ell \rightarrow 0\), there must be some small \(\ell \) and cylinders \(Q'\subset \subset Q\) of length \(\sim \ell \) such that \(|\nabla ^ju|\lesssim \ell ^{-1-j}\) holds in Q while \(\int _{Q'}|\omega |^2dxdt\) is bounded from below (see Fig. 1). The problem is that in order to prove a quantitative theorem, we need an effective lower bound on this \(\ell \).
We schematize some key steps in the proof of Proposition 5.1. The high frequency concentration at \(z_0\) is propagated backward in time to \(z_1\). The concentration of \(P_{N_1}u\) persists in a parabolic cylinder (red) which we convert into a lower bound on \(\Vert \omega \Vert _{L_{t,x}^2}\) (blue). The objective is to locate a small cylinder Q such that u obeys subcritical bounds in the interior and the vorticity concentrates on a smaller subcylinder \(Q'\)(color figure online)
As one sees in the proof of Proposition 5.1, the worst-case scenario is that at each small scale \(\ell \), there are \(\sim \ell ^{-d+2}\) parabolic cylinders of length \(\sim \ell \) where \(\int |\omega |^2dxdt\gtrsim \ell ^{d-2}\), and in the complement the solution obeys \(|\nabla ^ju|\lesssim \ell ^{-1-j}\). At each scale, this fractal configuration is consistent with the energy inequality. We rule out this scenario in dimensions \(d\ge 5\) by applying the improved energy bound (9) at a sufficiently small scale \(\ell =A^{-C}\). In \(d=4\) we cannot quite use this improvement and are forced to take \(\ell \) as small as \(\exp (-A^C)\). Here the idea is that each scale \(\ell \) contributes roughly a fixed amount to the energy. A significant fraction of the contribution comes from the frequencies around \(\ell ^{-1}\), so by summing over many scales we can contradict this scenario.
In the proof of Proposition 5.2 we begin with a vorticity concentration in a parabolic cylinder \(Q'\), which in turned is contained in a Q/2 where u possesses subcritical bounds. We use Proposition 4.1 to propagate the vorticity lower bound into a slice of regularity obtained from Proposition 3.5. Then we iteratively apply Proposition 4.1 to locate a vorticity concentration in a distant annulus where u is regular. In this annulus we may apply a backward uniqueness Carleman inequality to conclude the existence of a \(\Vert u\Vert _{L_x^d}\) concentration at the final time
Note that the exponential smallness of \(\ell \) when \(d=4\) does not affect the final estimates because it contributes in parallel with exponentials appearing at other points in the argument.Footnote 5
Proposition 5.1
(Backward propagation into a regular region). Suppose u is a classical solution of (1) on \([t_0-T,t_0]\) satisfying (3), and that there are \(x_0\in {{\mathbb {R}}^d}\) and \(N_0>0\) such that at the point \(z_0=(t_0,x_0)\),
Then for any \(T_1\in [A_1^2N_0^{-2},T/100]\), there exist \(\ell >0\) and \(Q=Q(z_0',\ell /2)\subset [-T_1,-A_2^{-1}T_1]\times B(A_3T_1^\frac{1}{2})\) such that
for \(j=0,1,2\) and
where \(Q'=Q(z_0'-(\ell ^2/8,0),\delta \ell )\). We may take \(\delta =A_4^{-1}\) and \(\ell \) such that
Proof
Without loss of generality we may let \(z_0=0\) and \(T_1=1\). Let us begin with the case \(d\ge 5\). By Proposition 3.7, there exists a point \(z_1\in [-1,-A_2^{-1}]\times B(A_2)\) and a frequency \(N_1\in [A_2^{-1},A_2]\) such that
Combining this with Lemma 2.2, we find that the lower bound persists in a parabolic cylinder:
We apply Proposition 2.5 on \([t_1-2A_2^{-4},t_1]\) to obtain a decomposition \(u=u^{\flat }+u^{\sharp }\). Let I be the contraction of the time interval \([t_1-A_2^{-4},t_1]\) by a factor of \(\frac{1}{5}\) about its center. By (9), Hölder’s inequality, and (5),
Defining the vorticity \(\omega :=dv\) where d is the exterior derivative on \({{\mathbb {R}}^d}\) and v is the covelocity field of u, we apply the codifferential \(\delta \) to obtain \(-\Delta v=\delta \omega \). Thus we have a version of the Biot–Savart law,
It follows from (27) and Lemma 2.3 that for all \(t\in I\),
Taking the \(L_t^2(I)\) norm, bounding the \(u^{\sharp }\) global error term with (8), and the \(u^{\flat }\) term with (5), we obtain
Consider the collection of parabolic cylinders
of which there are \(\sim A_2^{-5}A_3^{d}(\delta \ell )^{-d-2}\). (Once again 2I denotes dilation of the interval about its center.) We seek to understand in which cylinders u is regular. By the \(L^p\)-boundedness of \({{\,\textrm{div}\,}}{{\,\textrm{div}\,}}/\Delta \), Hölder’s inequality, Sobolev embedding, and (8),
By interpolation with the \(L_t^\infty L_x^\frac{d}{2}\) bound coming from (7),
since the sets in \({\mathcal {C}}_0\) can overlap up to \(O(\delta ^{-d-2})\) times. Define
From (30), we clearly have
Consider an arbitrary \(Q_0=I_0\times B_0\in \mathcal {C}_0\setminus {\mathcal {C}}_1\). Additionally using (5) and (7), we have
Then by Hölder’s inequality
Next we address \(C(Q_0)\). Let \(I_{1/10}\) be the first \(\frac{1}{10}\) of the interval \(I_0\). Using again that \(Q_0\in {\mathcal {C}}_0\setminus {\mathcal {C}}_1\),
and so by the pigeonhole principle and Hölder’s inequality, there exists a \(\tau _0\in I_{1/10}\) such that
With this we can apply (14), (31), and the fact that \(Q_0\notin {\mathcal {C}}_1\) (along with Hölder’s inequality and (5) for the \(u^{\flat }\) part) to obtain
A bound for \(\Vert \nabla u\Vert _{L_{t,x}^2(3Q_0/4)}\) similarly follows from the definition of \({\mathcal {C}}_1\) and (5). Then by Gagliardo–Nirenberg interpolation,
With this and (31), we arrive at (24) in \(Q_0/2\) by Propositions 3.2 and 3.4.
For every \(Q=Q(z,\ell )\in {\mathcal {C}}_0\), let \(Q':=Q(z-(\ell ^2/8,0),\delta \ell )\). Since \(\{Q':Q\in {\mathcal {C}}_0\}\) covers \(I\times B(R)\), (29) implies
There are two cases. First, suppose
By the pigeonhole principle, since the family \(\mathcal {C}_0\setminus {\mathcal {C}}_1\) has cardinality \(A_3^{O(1)}(\delta \ell )^{-d-2}\), there is a \(Q\in \mathcal {C}_0\setminus {\mathcal {C}}_1\) such that
This pair \(Q,Q'\) satisfies the conclusion of the proposition. In the other case,
If so, we seek to derive a contradiction with (28). We compare the lower bound (33) with
from (12), and the fact that \({\mathcal {C}}_1\) contains at most \(A_3^3\delta ^{-d-2}\ell ^{-d+2}\) cylinders. Indeed, defining the family of disjoint cylinders
we have, using that the contracted cylinders \(\{Q'\}_{Q\in \mathcal {C}_0}\) are disjoint,
It follows that
For all \(Q'\in {\mathcal {C}}_2\) and \(p\ge 2\), by Hölder’s inequality,
Summing over \({\mathcal {C}}_2\),
With \(\ell \) sufficiently small as in (26), this is in contradiction with (28).
Next consider the case \(d=4\). We define
There are two cases: first, suppose \(\bigcup _{Q\in {\mathcal {C}}_0\setminus {\mathcal {C}}_3}5Q\) projected to the time axis does not cover I. Then there exists an interval \(I'\subset I\) of length \(\ell ^2\) such that
for \(j=0,1,2\). The existence of a large slab of regularity makes this case relatively straightfoward so we argue briefly. One appeals once again to (27) and repeats the calculations leading to (29); however now when we take the \(L_t^2\) norm of the Bernstein inequality it is only over \(I'\) which yields the lower bound \(\Vert \omega \Vert _{L_{t,x}^2(I'\times B(A_3))}\ge A_2^{-O(1)}\ell \). Analogous to the definition of \({\mathcal {C}}_0\), we partition a slight dilation of \(I'\times B(A_3)\) into overlapping parabolic cylinders of length \(\ell \) offset by length \(\delta \ell \). Using the regularity assumed within \(I'\) and applying the pigeonhole principle to the vorticity lower bound, it is clear that there exist Q and \(Q'\) obeying (24) and (25).
Otherwise, suppose \(\bigcup _{Q\in {\mathcal {C}}_0\setminus \mathcal {C}_3}5Q\) when projected to the time axis does cover I. Then we may take a \({\mathcal {C}}_4\subset {\mathcal {C}}_0\setminus {\mathcal {C}}_3\) such that the projections of \(\{5Q\}_{Q\in {\mathcal {C}}_4}\) form a subcover which is minimal in the sense that no more than two intersect at once. It follows that
Due to our definition of \({\mathcal {C}}_3\), for every \(Q\in {\mathcal {C}}_4\), applying Propositions 3.2 and 3.4 in the converse yields
By the argument from the proof of Proposition 3.7, there exist \(N\in [A_3^{-1}\ell ^{-1},A_3\ell ^{-1}]\) and \(z\in A_3Q\) such that
It follows by Lemmas 2.2 and 2.3, as well as Hölder, (5), and (8) to estimate the global Bernstein error, that
Using Hölder’s inequality and (6), one computes that the contribution from \(u^{\flat }\) is negligible thanks to the smallness of \(\ell \). (Note that we continue to refer to the decomposition obtained by applying Proposition 2.5 on \([t_1-2A_2^{-4},t_1]\).) By the properties of \({\mathcal {C}}_4\), particularly the at most \(A_3^{O(1)}\)-fold boundedness of the overlap, we obtain
On the other hand, by Plancherel and (8),
If (36) holds for all \(\ell \in [\exp (-A_4),A_4^{-1}]\), we reach a contradiction by summing over a geometric sequence of scales in this range. Thus the proposition is satisfied by fixing \(\ell \) to be any scale for which (36) fails. \(\square \)
Having obtained a suitable vorticity concentration within a cylinder where the solution is regular, we need only to propagate this lower bound back to time \(t_0\) using a series of Carleman inequalities (Fig. 2). For every scale \(T_1\) between \(N_0^{-2}\) and T, this scheme leads to a triple-exponentially small amount of \(L_x^3\) mass at \(t_0\). Summing over \(\log (TN_0^2)\)-many geometrically separated scales and comparing the result to (3), we will conclude the following.
Proposition 5.2
(Propagation forward to the final time). Suppose u, \(z_0\), and \(N_0\) are as in Proposition 5.1. Then
Proof
Let us once again fix an arbitrary \(T_1\in [A_1^2N_0^{-2},T/100]\). For now, we normalize \(z_0=0\) and \(T_1=1\). We continue to use the notation of Proposition 5.1 and its proof; in particular let us take Q and \(Q'\) satisfying the the conclusion. Let \(z':=(t',x')\) be the center of \(Q'\). We apply Proposition 3.5 centered at \(z'+(100(\delta \ell )^2,0)\) (i.e., shifted forward in time) at length scale \(R=\delta \ell \). This yields a slice of regularity which, by rotating, we may assume has \(\theta =e_1\). Specifically, there is an \(I\subset [t'+99(\delta \ell )^2,t'+100(\delta \ell )^2]\) of length \((\delta \ell )^2A_2^{-2}\) such that within
we have for \(j=0,1,2\)
Let \(t''\in I\) be arbitrary. In order to propagate vorticity concentration into this cone, we apply Proposition 4.1 to the function
on the interval \([0,C_0(\delta \ell )^2]\) with \(t_0=75(\delta \ell )^2\), \(t_1=(A_3^{-2}\delta ^3\ell )^2\), and \(r=\ell /2\). The differential inequality (22) for \(\omega \) becomes clear from the coordinate form of the vorticity equation
combined with the estimates in (24). Considering each the terms in the Carleman inequality which takes the form \(Z\le X+Y\), by (25) the left-hand side obeys
while for the first term on the right-hand side,
The latter is negligible compared to the former given (26); thus the Carleman inequality becomes
Finally we narrow the domain of integration using the fact that the contribution from outside \(B(x'+50\delta \ell e_1,A_3^{-1}\delta \ell )\) is negligible compared to the left-hand side which follows from (24) and (26). This yields
for every \(t''\in I\).
Next we apply Proposition 3.6 to find an \(R\in [A_4,\exp \exp (A_4)]\) such that
for \(j=0,1,2\). Then define \(x_*=x'+100Re_1\) and let \(\tau =\sup I\). We apply Proposition 4.2 to the function
on the interval \([0,4(\delta \ell )^2]\) with \(R_0=50\delta \ell \), \(\eta =A_2^{-3}\), and \(\epsilon =e^{-A_4^6}\) to find
for every \(t\in [\tau -e^{-3A_4},\tau ]\). Note that the initial lower bound follows from (38) and that we have (23) thanks to (37) and the vorticity equation.
Next we propagate this concentration forward in time using a Carleman inequality for backward uniqueness, see Proposition 4.2 in [19] (the extension of which to higher dimensions was proved in [13], Proposition 9). In particular, by applying it to the function \((t,x)\mapsto \omega (-t,x)\) on the interval [0, 1] with \(r_-=5R\) and \(r_+=R^{2A_4}/10\), we have \(Z\le X+Y\) where
(Note that this and all subsequent applications of Carleman inequalities are valid because (22) is implied by (39) and the vorticity equation.) Thus there are two cases:
and
First assuming (42), we essentially follow the proof of Theorem 5.1 in [19]. By the pigeonhole principle, there exists an \(R'\in [5R,R^{2A_4}/10]\) such that
By (39), the contribution to the left-hand side from the time interval \([-e^{-(R')^2},0]\) is negligible compared to the right so essentially the same lower bound holds with the integral evaluated on \([-1,-e^{-(R')^2}]\). We apply the pigeonhole principle, now in time, to find a \(T_0\in [e^{-(R')^2},1]\) in this time interval such that
Having obtained length and time scales where the vorticity concentrates, we cover the annulus \(\{R'\le |x|\le 2R'\}\) by \(O(R'/T_0^\frac{1}{2})^d\) balls of radius \(T_0^\frac{1}{2}\). The pigeonhole principle then provides an \(x_0\in \{R'\le |x|\le 2R'\}\) such that
Finally we may apply Proposition 4.1 on \([0,1000dT_0]\) to the function
with \(t_0=T_0\), \(t_1=C_0^{-3}T_0\), and \(r=C_0R'T_0^\frac{1}{2}\). The Carleman inequality becomes
With a sufficiently large choice of \(C_0\), the first term on the right-hand side is negligible compared the the left. Moreover, the contribution to the second term on the right from outside \(B(x_0,R'/2)\) is also negligible by (39). Thus
In both cases (41) and (42), we can thus conclude
Now let us fix an \(x_*\in \{2R\le |x|\le R^{2A_4}/4\}\) where
By repeating the simple mollification argument from [19] to convert the concentration of vorticity into the critical space, we obtain
At this point we undo the original rescaling so that \(T_1\) is explicit. This estimate can be summed over geometrically separated scales \(T_1\in [A_1^2N_0^{-2},T/100]\) to conclude
which implies the result when compared to the upper bound (3). \(\square \)
6 Proof of Theorems 1.1 and 1.2
As in [19], Theorem 1.1 is obtained easily from Theorem 1.2 combined with, say, the Prodi–Serrin–Ladyzhenskaya blowup criterion.
Proof of Theorem 1.2
We increase A so that \(A\ge C_0\) and rescale so that \(t=1\). By Propositions 5.1 and 5.2 in the converse, we have that
for all
Starting with the decomposition \(u=u^{\flat }+u^{\sharp }\) on [0, 1] and differentiating to reach \(\omega =\omega ^{\flat }+\omega ^{\sharp }\), we define the enstrophy-type quantities
and compute
Here we have defined \(\langle \nabla u,\omega \rangle _{ij}:=(\partial _iu_k)\omega _{kj}-(\partial _ju_k)\omega _{ik}\) for a vector field u and 2-form \(\omega \) so that we may represent the Lie derivative as \({\mathcal {L}}_u\omega =\langle \nabla u,\omega \rangle +u\cdot \nabla \omega \).
Clearly \(X_1\ge 0\). By Littlewood–Paley decomposition and Plancherel we have
Applying Lemma 2.2 and (43) for \(N_3\) smaller or larger than \(N_*\) respectively, we arrive at
By Hölder’s inequality, (5), (7), and (11), we have for \(t\in [\frac{1}{2},1]\)
Integrating in time using (8) and Gronwall’s inequality, we find that for any \(\frac{1}{2}\le t_1\le t_2\le 1\),
At the same time, by (8), there exists a \(t_0\in [1/2,3/4]\) such that \(E_0(t_0)\le A^{O(1)}\). Thus
Next we compute using (10)
where
We then take the Littlewood–Paley decompositions and estimate
where we decompose based on whether the top order derivatives that fall on the high frequency factors. Specifically, by Hölder, Lemma 2.1, (3), and (43),
and
Next, \(Y_3(t)\) contains essentially the same terms and admits the same bounds (note crucially the exclusion of \(k=0\) by incompressiblity). By Cauchy–Schwarz and (5),
Finally, by (5), (7), (11), and integration by parts,
In total, combining some terms with Young’s inequality,
Inductively applying Gronwall’s inequality (at each step using the pigeonhole principle to find an initial time), starting with (44) as a base case, implies
for an increasing sequence \(t_n\in [\frac{1}{2},1]\). The claimed \(L_{t,x}^\infty \) estimates are immediate by (5) and Sobolev embedding, taking n sufficiently large depending on d. \(\square \)
Notes
By this we mean the following: when regarded in the coordinate system which consists of polar coordinates \((r,\theta )\) in the \(x_1,x_2\)-plane and Cartesian coordinates in the rest, we have \(u(x)=R_{\theta }(u(R_{-\theta }x))\) where \(R_{\theta }\) denotes counterclockwise rotation by \(\theta \) in the \(x_1,x_2\)-plane.
We thank the referee for bringing (9) to our attention which allows a simplification to the argument.
If instead one were to iterate the Carleman inequality through a region of the form \(Q_0\times {\mathbb {R}}^{d-k}\) for some small \(Q_0\subset {\mathbb {R}}^k\), one would need a number of iterations on the order of \(R_2/R_1\). This would lead to an extra exponential in the vorticity lower bound, which would in turn require us to ensure a much smaller error when the backward uniqueness Carleman inequality is applied in the proof of Proposition 5.2. It would be necessary then to find a much larger annulus of regularity in Proposition 3.6 which would result (rather unsatisfyingly) in tower exponential bounds in Theorem 1.2.
It is conceivable that the \(d\ge 5\) case can be handled using the same energy pigeonholing approach, although it is less straightforward because of the spatial overlaps of the concentrations caused by the fact that \(Q'\) is a factor \(\delta \) smaller than Q. As a result \(\ell \) would depend exponentially on \(\delta ^{-1}\) which would cause problems in the proof of Proposition 5.2, as the smallness of \(\delta \) is necessary to create favorable geometry for the Carleman estimates. It is preferable for other reasons to have \(\ell \) depend polynomially on A; for example see Remark 1.3.
References
Albritton, D.: Blow-up criteria for the Navier–Stokes equations in non-endpoint critical Besov spaces. Anal. PDE 11(6), 1415–1456 (2018)
Albritton, D., Barker, T.: Global weak Besov solutions of the Navier–Stokes equations and applications. Arch. Ration. Mech. Anal. 232(1), 197–263 (2019)
Barker, T., Prange, C.: Quantitative regularity for the Navier–Stokes equations via spatial concentration. Commun. Math. Phys. 385, 717–792 (2021)
Calderón, C.P.: Existence of weak solutions for the Navier–Stokes equations with initial data in \(L^p\). Trans. Am. Math. Soc. 318(1), 179–200 (1990)
Chemin, J.-Y., Planchon, F.: Self-improving bounds for the Navier–Stokes equations. Bull. Soc. Math. France 140(4), 583–597 (2012)
Dong, H., Du, D.: The Navier–Stokes equations in the critical Lebesgue space. Commun. Math. Phys. 292(3), 811–827 (2009)
Dong, H., Wang, K.: Interior and boundary regularity for the Navier–Stokes equations in the critical lebesgue spaces. arXiv preprint arXiv:1809.06712 (2018)
Escauriaza, L., Seregin, G., Šverák, V.: Backward uniqueness for parabolic equations. Arch. Ration. Mech. Anal. 169(2), 147–157 (2003)
Escauriaza, L., Seregin, G.A., Sverak, V.: On \({L}_{3,\infty }\)-solutions of the Navier–Stokes equations and backward uniqueness. Russ. Math. Surv. 58(2), 211–250 (2003)
Gallagher, I., Koch, G.S., Planchon, F.: Blow-up of critical Besov norms at a potential Navier–Stokes singularity. Commun. Math. Phys. 343(1), 39–82 (2016)
Ladyzhenskaya, O.A.: On the uniqueness and on the smoothness of weak solutions of the Navier–Stokes equations. Zapiski Nauchnykh Seminarov POMI 5, 169–185 (1967)
Leray, J.: Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 63, 193–248 (1934)
Palasek, S.: Improved quantitative regularity for the Navier–Stokes equations in a scale of critical spaces. Arch. Ration. Mech. Anal. 242(3), 1479–1531 (2021)
Phuc, N.C.: The Navier–Stokes equations in nonendpoint borderline Lorentz spaces. J. Math. Fluid Mech. 17(4), 741–760 (2015)
Prodi, G.: Un teorema di unicita per le equazioni di Navier–Stokes. Ann. Mat. 48(1), 173–182 (1959)
Seregin, G.: A certain necessary condition of potential blow up for Navier–Stokes equations. Commun. Math. Phys. 3(312), 833–845 (2012)
Serrin, J.: On the interior regularity of weak solutions of the Navier–Stokes equations. Mathematics Division, Air Force Office of Scientific Research (1961)
Tao, T.: Localisation and compactness properties of the Navier–Stokes global regularity problem. Anal. PDE 6(1), 25–107 (2013)
Tao, T.: Quantitative bounds for critically bounded solutions to the Navier–Stokes equations. In: Kechris, A., Makarov, N., Ramakrishnan, D., Zhu, X. (eds.) Nine Mathematical Challenges: An Elucidation, vol. 104. American Mathematical Society, Providence (2021)
Funding
This work was partially funded by NSF Grant DMS-1764034.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author has no relevant financial or non-financial interests to disclose.
Additional information
Communicated by R. Shvydkoy.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author is grateful to Terence Tao for many helpful discussions and comments on the manuscript. We also thank the anonymous referees for their careful reading and valuable suggestions. This work was partially funded by NSF grant DMS-1764034.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Palasek, S. A Minimum Critical Blowup Rate for the High-Dimensional Navier–Stokes Equations. J. Math. Fluid Mech. 24, 108 (2022). https://doi.org/10.1007/s00021-022-00741-z
Accepted:
Published:
DOI: https://doi.org/10.1007/s00021-022-00741-z