1 Introduction

Define the array \([m_{n,k}]_{n,k}\) for \(n,k\in {\mathbb {Z}}\) as follows. Let \(m_{k,n}=0\) unless \(0\le k\le n\). In the latter case, \(m_{0,0}=1\), and for \(n\ge 1\) the elements \(m_{n,k}\) satisfy

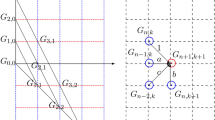
$$\begin{aligned} m_{n,k}=m_{n-1,k}+m_{n-1,k-1}+m_{n-1,k-2}. \end{aligned}$$
(1)

The zero-free part of the array has a triangular shape structurally identical to Pascal’s triangle, and it is called Motzkin triangle (A026300 and reflected version A064189 in OEIS [4]). The name comes from the fact that the right leg of the triangle coincides with the Motzkin sequence \((M_n)_{n\ge 0}\) (more precisely \(m_{n,n}=M_n\)) defined by \(M_0=M_1=1\) and for \(n\ge 2\)

$$\begin{aligned} M_n=M_{n-1}+\sum _{i=0}^{n-2}M_iM_{n-2-i}. \end{aligned}$$
(2)

Clearly, the left leg is the constant 1 sequence, i.e., \(m_{n,0}=1\) \((n\ge 0)\). Moreover, it is easy to see that \(m_{n,1}=n\) holds for any \(n\ge 0\). Figure 1 illustrates the Motzkin triangle together with the construction rule.

Fig. 1
figure 1

Motzkin triangle—A026300

Full size image

One of the first articles on Motzkin numbers (A001006 in OEIS [4]) and Motzkin triangle is the work of Donaghey and Shapiro [2]. They present some combinatorial interpretations, too. The combinatorial and algebraic properties, and generalizations of Motzkin numbers have been widely studied in several papers. For example, Oste and Van der Jeugt [3] gave a good summary on different variations based on the generalizations of the Motzkin path which is one of the combinatorial interpretations of Motzkin numbers. A well-know fact is that Motzkin numbers can be defined by Catalan numbers as well. Wang and Zhang [5] examined a type of generalized Motzkin sequence which is based on the extension of Catalan numbers. Zhao and Qi [6] also studied this sort of generalization. Recently, Chen, Wand, and Zheng [1] presented a new Motzkin triangle. The reader can find an extensive survey on several results in [1,2,3, 5, 6].

In this article, we consider, among others, the so called t-generalized Motzkin sequences \((M_n^{(t)})_{n\ge 0}\) as geometrically parallel sequences to Motzkin numbers in the Motzkin triangle (see Fig. 1 again). Their precise description is given in Sect. 4, in particular (16) provides a recursive rule, but Theorem 2 (in Sect. 3) provides a preliminary insight into their attributes. We reveal a lot of properties of the Motzkin triangle, some of them are associated to t-generalized Motzkin sequences.

The paper is organized as follows. In Sect. 2, we replace the defining rule (1) by a linear recursion among three consecutive elements of a row, where the coefficients are bivariate quadratic polynomials. The main result is given in Theorem 1. Section 3 studies linear recurrences with polynomial coefficients that refer to three arbitrary entries of the triangle forming a given structure. Here the principal observation is Theorem 3, which states the existence of linear recurrences. Another important contribution is the construction method of new recursive rules of new structures. As an application we computed the recursive description of all possible formations of three connected entries, the coefficient polynomials are collected in “Appendix” (Sect. 5). The next section (Sect. 4) goes back to Motzkin numbers and deals with t-generalized Motzkin sequences \((M_n^{(t)})\) in the sense we introduced them above. This part is based on the diagonal recurrence that can be found in the previous section. Theorem 4 is an analogue of (2) for \(t=1\). Finally, Sect. 5 considers the columns of the triangle as polynomial values, and investigates the factorization features of the aforementioned polynomials depending on the columns. Theorems 5 and 6 contain the principal results, while Conjecture 1 presumes additional speciality.

2 Recursion with three consecutive terms in rows

The following theorem provides a linear recursive relationship among three consecutive row entries of the triangle. It is a sort of spring-board, and will play an important role in our subsequent investigations.

Theorem 1

Let \(n\in {\mathbb {N}}\), and assume that \(k\le n+1\). Then the recurrence

$$\begin{aligned}&k(n-k+3)m_{n,k}=(n-k+1)(n-k+3)m_{n,k-1}\nonumber \\&\quad +(n-k+1)(2n-k+4)m_{n,k-2} \end{aligned}$$
(3)

holds in the rows of the triangle.

Proof

The statement is trivially true for arbitrary n if \(k\le 1\) or \(k=n+1\). In the sequel, we assume \(2\le k\le n\). Obviously, (3) holds when \(n=k=2\). Consequently, (3) is true for the whole 2nd row with the restriction \(k\le n+1\). Applying the technique of mathematical induction on n, we suppose that (3) holds for some \(n\ge 2\).

Now we define three quadratic bivariate polynomials according to the coefficients in (3). Put

$$\begin{aligned} p^{(0)}_{n,k}= & {} k(n-k+3),\quad p^{(1)}_{n,k}=(n-k+1)(n-k+3),\\ p^{(2)}_{n,k}= & {} (n-k+1)(2n-k+4). \end{aligned}$$

Using this notation, we will show

$$\begin{aligned} p^{(0)}_{n+1,k}m_{n+1,k}=p^{(1)}_{n+1,k}m_{n+1,k-1}+p^{(2)}_{n+1,k}m_{n+1,k-2}. \end{aligned}$$
(4)

Applying (1) for \(m_{n+1,k}\), \(m_{n+1,k-1}\), and \(m_{n+1,k-2}\), respectively, the last equation is equivalent to

$$\begin{aligned} \begin{aligned}&p^{(0)}_{n+1,k}m_{n,k}=\left( -p^{(0)}_{n+1,k}+p^{(1)}_{n+1,k}\right) m_{n,k-1}\\&\quad +\left( -p^{(0)}_{n+1,k}+p^{(1)}_{n+1,k}+p^{(2)}_{n+1,k}\right) m_{n,k-2}\\&\quad +\left( p^{(1)}_{n+1,k}+p^{(2)}_{n+1,k}\right) m_{n,k-3}+p^{(2)}_{n+1,k}m_{n,k-4}. \end{aligned} \end{aligned}$$
(5)

In order to eliminate the last term \(m_{n,k-4}\), first we use the induction hypothesis (3) with \(k-2\) and with the notation \(p^{(i)}\) to obtain

$$\begin{aligned} p^{(0)}_{n,k-2}m_{n,k-2}-p^{(1)}_{n,k-2}m_{n,k-3}=p^{(2)}_{n,k-2}m_{n,k-4}. \end{aligned}$$
(6)

Then multiply (5) by \(p^{(2)}_{n,k-2}\) and replace \(p^{(2)}_{n,k-2}m_{n,k-4}\) with the left-hand side of (6). It leads immediately to

$$\begin{aligned} P_0m_{n,k}=P_1m_{n,k-1}+P_2m_{n,k-2}+P_3m_{n,k-3}, \end{aligned}$$
(7)

where

$$\begin{aligned} P_0= & {} p^{(0)}_{n+1,k}p^{(2)}_{n,k-2},\\ P_1= & {} \left( -p^{(0)}_{n+1,k}+p^{(1)}_{n+1,k}\right) p^{(2)}_{n,k-2},\\ P_2= & {} \left( -p^{(0)}_{n+1,k}+p^{(1)}_{n+1,k}+p^{(2)}_{n+1,k}\right) p^{(2)}_{n,k-2}+p^{(0)}_{n,k-2}p^{(2)}_{n+1,k},\\ P_3= & {} \left( p^{(1)}_{n+1,k}+p^{(2)}_{n+1,k}\right) p^{(2)}_{n,k-2}-p^{(1)}_{n,k-2}p^{(2)}_{n+1,k}. \end{aligned}$$

Note that \(\deg (P_i)=4\).

Similarly to (6), the induction hypothesis with \(k-1\) implies

$$\begin{aligned} p^{(0)}_{n,k-1}m_{n,k-1}-p^{(1)}_{n,k-1}m_{n,k-2}=p^{(2)}_{n,k-1}m_{n,k-3}. \end{aligned}$$
(8)

Multiply (7) by \(p^{(2)}_{n,k-1}\). In the equality we obtain, use (8) to eliminate the term \(m_{n,k-3}\). Then we have

$$\begin{aligned}&\underbrace{P_0p^{(2)}_{n,k-1}}_{{{\mathscr {P}}}_0}m_{n,k}=\underbrace{\left( P_1p^{(2)}_{n,k-1}+P_3p^{(0)}_{n,k-1}\right) }_{{{\mathscr {P}}}_1}m_{n,k-1}\nonumber \\&\quad +\underbrace{\left( P_2p^{(2)}_{n,k-1}-P_3p^{(1)}_{n,k-1}\right) }_{{{\mathscr {P}}}_2}m_{n,k-2}. \end{aligned}$$
(9)

Here the coefficient polynomials \({{{\mathscr {P}}}_i}\) have degree 6. Since the basic polynomials \(p^{(i)}_{n,k}\) above (4) are well defined, the whole procedure can be carried out by symbolic computations, for example in Maple. It provides

$$\begin{aligned} {{\mathscr {P}}}_0= & {} k(n-k+3)R\;=\;p^{(0)}_{n,k}R, \\ {{\mathscr {P}}}_1= & {} (n-k+1)(n-k+3)R\;=\;p^{(1)}_{n,k}R, \\ {{\mathscr {P}}}_2= & {} (n-k+1)(2n-k+4)R\;=\;p^{(2)}_{n,k}R, \end{aligned}$$

where

$$\begin{aligned} R=(n-k+2)(n-k+4)(2n-k+5)(2n-k+6). \end{aligned}$$

Thus, we realize that equation (9) and the induction hypothesis (3) are proportional with the positive ratio R, and the proof is complete. \(\square \)

3 Fixed formations of three elements of the triangle

The main purpose of this section is to prove that if we fix a structure of three arbitrary elements in the triangle, then there exists a recursive rule associated to the formation. This recursion has bivariate polynomial coefficients which depend on the location (n, k) of the leading element of the triple. Here n, and k means the row, and column numbers, respectively. The leading element is the lowest element among the three. If it is not unique, then the rightmost one of the lowest row becomes the leader. For example, take three consecutive elements in a row. The leading is the rightmost one, and recursion (3) describes the corresponding rule among them. A formula is called normalized if it refers to the leading element.

In the beginning we intended to derive a recursive formula to connect \(m_{n,k}\), \(m_{n-1,k-1}\), and \(m_{n-2,k-2}\). This is a diagonal direction parallel to the right leg of the triangle, and in this sense we generalize the Motzkin sequence \((M_n)\). But it turned out that there exists a procedure which can derive a new recursive formula for new formation from two suitable structures possessing known recursive rules. This way we could construct recursive descriptions of all the 20 connected triples (see “Appendix”). Note that the procedure does not depend on the Motzkin triangle, but the recursive nexus does. The great advantage of this approach is that, knowing initial or intermediate formations, we are able to produce a new structure without making the calculations. Thus, one can apply the algorithm in other triangles as well.

Later we use this method to justify Theorem 3, which states the existence of a recursive connection of a formation of three arbitrary elements. Finally, we premise that structures with more elements can also be described similarly. For instance, we have established a recursive formula of the glider in Game of Life, where the coefficients are bivariate polynomials of degree 5 (see “Appendix”).

3.1 Construction method

Suppose that we have some known recursive rules referring to some given formations of elements. A formation is a geometrical pattern extracted from the relative locations of the elements. Note that we initially had only the defining formula (1) with four entries, and then (3) gave the second one with three elements.

A formula for a new formation can be derived if we consider one common element of the two formations. From the corresponding recursive rules, after eliminating the common term, we can create the new formula associated to the union of the two formations minus the joint element. A nice geometrical representation facilitates the application of this atomic step without carrying out the calculation itself. Accordingly, the pictogram illustrates the first known formation (1) (i.e., the formation with known recurrence), while the second known formation (3) is shown by . Put the first structure onto the second one according to Fig. 2.

Fig. 2
figure 2

Construction one

Full size image

First choose the leftmost common element to eliminate it from both (1) and (3). Equating them we obtain a new recursive rule for the formation . The notation

can shorten the description above.

Observe that this is only an abbreviation, not an operation in an algebraic sense, because (1) and (3) could yield two other formations. If we choose the middle common element, then the resulting three elements are disconnected. Thirdly, if we eliminate the rightmost common entry (see Fig. 3),

Fig. 3
figure 3

Construction two

Full size image

then the output is a new connected triple given by

In this manner, we can easily obtain what is left of the 20 connected triples. In the next subsection, we give one way to derive them in a logical order, while the “Appendix” contains their recursive identity. The sketch

(10)

shows the way to construct from and . Note that the derivations of the two inputs here were analyzed above, both are direct consequences of (1) and (3), see Figs. 2 and 3 again.

Now look at how the procedure works one layer deeper, when we are interested not only in deriving the construction, but also the precise recursive equality itself. The second phase of (10) uses the two equations

(11)

(see “Appendix”), where the two recursive formulae are normalized. Put the two formations onto each other so that the two neighbouring horizontal elements are matched pairwise. So we pushed up by one row. Hence now

$$\begin{aligned} B_{n-1,k}^{(0)}m_{n-1,k}=B_{n-1,k}^{(1)}m_{n-1,k-1}+B_{n-1,k}^{(2)}m_{n-2,k-2} \end{aligned}$$
(12)

holds. Multiply the first formula

$$\begin{aligned} A_{n,k}^{(0)}m_{n,k}=A_{n,k}^{(1)}m_{n-1,k}+A_{n,k}^{(2)}m_{n-1,k-1} \end{aligned}$$

by \(B_{n-1,k}^{(0)}\), and (12) by \(A_{n,k}^{(1)}\), which imply the common term \(A_{n,k}^{(1)}B_{n-1,k}^{(0)}m_{n-1,k}\) in the two expressions. Eliminating it we have

$$\begin{aligned}&A_{n,k}^{(0)}B_{n-1,k}^{(0)}m_{n,k}=\left( A_{n,k}^{(2)}B_{n-1,k}^{(0)}+A_{n,k}^{(1)}B_{n-1,k}^{(1)}\right) m_{n-1,k-1}\nonumber \\&\quad + A_{n,k}^{(1)}B_{n-1,k}^{(2)}m_{n-2,k-2}. \end{aligned}$$
(13)

The three coefficient polynomials are quartic, but we are lucky because their greatest common divisor is \(2(n-k)(n-k+1)\). Thus, dividing both sides of (13) by the gcd, finally we have

Theorem 2

The terms of the formation satisfy the recurrence

$$\begin{aligned} k(2n-k+2)m_{n,k}=n(2n+1)m_{n-1,k-1}+3n(n-1)m_{n-2,k-2}. \end{aligned}$$
(14)

Note that the last two coefficients are univariate polynomials in n. Hence we obtain (14) as a recursive rule which describes the directions parallel to the location of the Motzkin sequence. That was one of our main goals.

3.2 Three connected entries

In this subsection, we describe a sort of “family tree” of the 20 existing formations of three connected elements. We remark that there exist different orders to create all the objects. For example, in the (partially described) proof of Theorem 2 we used the construction (10), which could have been continued. But here we give a more transparent approach, and display the list as follows. Assume that the initial elements are and (the first one is the first triple given by Theorem 1, the second one was introduced in the previous subsection). In the first generation, we create the remaining three “corners” by

From the four “corners”, exploiting the rotation symmetry, we constitute 13 items in the second generation. Thus, we already have 18 formations.

The remaining two triples are called “diagonals”, each one can be constructed as a combination of a triple from the first, and a triple from the second generation. For instance, look at

We could compute each coefficient in each case, and it shows that the largest degree of the coefficient polynomials is 6, which occurs only in the case of the last “diagonal”. For the complete list of recursive rules see the “Appendix”. Here we have only given a of construction method of the 20 cases.

3.3 Three arbitrary entries

The main purpose of this subsection is to prove the following theorem. We fix a construction of three arbitrary elements via fixed suitable integers \(n_1\), \(k_1\) and \(n_2\), \(k_2\).

Theorem 3

Let \(0\le n_1\le n_2\) and \(k_1,k_2\) be integers. Then there exist bivariate polynomials \(f^{(0)}(n,k)\), \(f^{(1)}(n,k)\), and \(f^{(2)}(n,k)\) with integer coefficients such that

$$\begin{aligned} f^{(0)}(n,k)m_{n,k}=f^{(1)}(n,k)m_{n-n_1,k-k_1}+f^{(2)}(n,k)m_{n-n_2,k-k_2} \end{aligned}$$
(15)

holds, where

  • \(k_1>0\), if \(0=n_1<n_2\),

  • \(k_2>k_1>0\), if \(0=n_1=n_2\),

  • \(k_2>k_1\), if \(0<n_1=n_2\).

Note that the recursive formula of the theorem is normalized. It is guaranteed by the conditions given at the end of the statement in the three branches.

Proof

The case of connected triples has already been justified. Now we describe, without precise details, the way how one can derive the recurrence connection among the elements of an arbitrary triple.

First recall the construction method. It says that if we have two known triples, and we can put them onto each other so that two elements of the first cover two of the second, then after eliminating one matching, we obtain a new triple. We will use the horizontal, the vertical connected triples, and the four corners as initial constructions, and also some intermediate triples of the process. The short description is split into five steps illustrated by Fig. 4, the details are left to the reader (as we have already had a lot of experience in constructions). \(\square \)

Fig. 4
figure 4

Construction of structure of three arbitrary entries

Full size image

We note that during the procedure neither \(f^{(0)}(n,k)\), \(f^{(1)}(n,k)\), and \(f^{(2)}(n,k)\) becomes constant zero polynomial in (15). To show this the crucial point is the following statement: there are no two bivariate polynomials \(h_0(n,k)\) and \(h_1(n,k)\) such that \(h_0(n,k)m_{n,k}=h_1(n,k)m_{n,k-1}\) holds. In other words, Theorem 3 can not be reduced to two terms.

4 t-generalized Motzkin sequences

Originally, we were motivated to study the properties of t-generalized Motzkin sequences. Later we realized many related problems, some of which are the subject of this paper.

t-generalized Motzkin numbers are defined precisely as follows. Let t be a non-negative integer. Then \(M^{(t)}_n=m_{n+t,n}\) gives the nth term of the t-generalized Motzkin sequence for \(n\ge 0\). Clearly, \((M^{(0)}_n)=(m_{n,n})\) returns with the Motzkin sequence \((M_n)\). t-generalized Motzkin sequences are located parallel to \((M_n)\) in the Motzkin triangle. The substitution of (n, k) by \((n+t,n)\) in (14) provides the recursive formula

$$\begin{aligned}&n(n+2t+2)M^{(t)}_n=(n+t)(2n+2t+1)M^{(t)}_{n-1}\nonumber \\&\quad +3(n+t)(n+t-1)M^{(t)}_{n-2}, \quad n\ge 2, \end{aligned}$$
(16)

among three consecutive t-generalized Motzkin numbers. Clearly, the initial values are \(M^{(t)}_0=1\) and \(M^{(t)}_1=t+1\).

When \(t=0,1,2,\ldots , 5\) these sequences are A001006, A002026, A005322, A005323, A005324, A005325, respectively, as given in OEIS [4], but their uniformly given recurrences here,

$$\begin{aligned} (n+2)M_{n}^{}= & {} (2n+1)M_{n-1}^{}+3(n-1)M_{n-2}^{},\\ n(n+4 )M_{n}^{(1)}= & {} (n+1)(2n+3)M_{n-1}^{(1)}+3n(n+1)M_{n-2}^{(1)},\\&\vdots&\\ n(n+12 )M_{n}^{(5)}= & {} (n+5)(2n+11)M_{n-1}^{(5)}+3(n+4)(n+5)M_{n-2}^{(5)}, \end{aligned}$$

sometimes differ from the OEIS database. In case the of \(t\ge 6\), \((M^{(t)}_n)\) does not appear in [4].

Formula (2), using the terms \(M_0,M_1,\dots M_{n-1}\) provides a construction of \(M_n\). An identity having similar flavour exists for \(M_n^{(t)}\) too, but it is getting more and more complicated as we increase t. Therefore, we provide it when \(t=1\), but this treatment also indicates a hint for larger values of t.

Clearly, the defining Eq. (1) yields

$$\begin{aligned} M^{(1)}_{n}=M_{n+2}-M_{n+1}=\sum _{i=0}^{n}M_iM_{n-i}. \end{aligned}$$
(17)

Recall the recursive rule (11) with \(k=n-1\). Obviously, it gives a function to express \(M_{n-1}\) with two neighbouring terms of the 1-generalized Motzkin sequence. Indeed, by (11) we have

$$\begin{aligned} (n+3)M^{(1)}_{n-1}=4nM_{n-1}+nM^{(1)}_{n-2}, \end{aligned}$$

and, after shifting the subscripts by 1, it leads to

$$\begin{aligned} M_n=\frac{(n+4)M^{(1)}_{n}-(n+1)M^{(1)}_{n-1}}{4(n+1)}. \end{aligned}$$
(18)

Combining (18) and (17), together with \(M_{-1}^{(1)}=0\), we arrive at a new identity formulated by

Theorem 4

Let \(\mu _i=(i+4)M^{(1)}_{i}-(i+1)M^{(1)}_{i-1}\), \(i=1,2,\ldots \). We have

$$\begin{aligned} (n-2)M^{(1)}_{n}=-(n+1)M^{(1)}_{n-1}+(n+1)\sum _{i=1}^{n-1}\frac{\mu _i\mu _{n-i}}{8(i+1)(n-i+1)}. \end{aligned}$$

Moreover, formula

$$\begin{aligned}&k(n-k+2)m_{n,k}= 2(n-k+1)(2n-k+3)m_{n,k-1}\nonumber \\&\quad - 3n(n-k+2)m_{n-1,k-1} \end{aligned}$$
(19)

(refers to in Table 1 of the “Appendix”) implies a recurrence between the t-generalized and \((t+1)\)-generalized Motzkin sequences. Really, replacing (n, k) by \((n+t,n)\) in (19) we find

$$\begin{aligned} 2(t+1)(n+2t+3)M^{(t+1)}_{n-1}= n(t+2)M^{(t)}_{n} +3(n+t)(t+2)M^{(t)}_{n-1}. \end{aligned}$$
(20)

In the case of \(t=0\) identity (20) simplifies to

$$\begin{aligned} (n+3)M^{(1)}_{n-1}= n M^{}_{n} +3n M^{}_{n-1}. \end{aligned}$$

5 Columns of the Motzkin triangle

In the introduction, we mentioned that the 0th column contains only the integer 1 (i.e., \(m_{n,0}=1\)), and in the 1st column we have \(m_{n,1}=n\). This information can be interpreted so that the 0th column is described by the constant 1 polynomial \(p_0(n)=1\), while the 1st column consists of the polynomial values \(p_1(n)=n\). Going right from left, and considering n as a variable, (3) leads to the sequence of polynomials \((p_k(n))_{k\ge 0}\). Actually first we know only that \(p_k(n)\) is a rational function of n, but we can easily show by induction that \(p_k(n)\) is a polynomial indeed. That is

$$\begin{aligned}&k(n-k+3)p_k(n)=(n-k+1)(n-k+3)p_{k-1}(n)\nonumber \\&\quad +(n-k+1)(2n-k+4)p_{k-2}(n) \end{aligned}$$
(21)

holds together with the initial polynomials \(p_0(n)=1\) and \(p_1(n)=n\). Clearly, the sequence may begin with \(p_{-1}(n)=0\) as well. Note that the polynomial value \(p_k(\alpha )\) returns with \(m_{\alpha ,k}\) only if the integer \(\alpha \) satisfies \(\alpha \ge k-1\). This follows from the construction of the Motzkin triangle. The first few next polynomials are

$$\begin{aligned} p_2(n)= & {} \frac{1}{2!}(n-1)(n+2),\\ p_3(n)= & {} \frac{1}{3!}n(n-2)(n+5),\\ p_4(n)= & {} \frac{1}{4!}n(n-3)(n^2+9n+2),\\ p_5(n)= & {} \frac{1}{5!}n(n-4)(n-1)(n+2)(n+13). \end{aligned}$$

Although we are unable to give the complete rational factorization of the polynomials \(p_k(n)\) the next theorems provide important information about them.

Theorem 5

Let \(\alpha \) be a non-negative integer. Then

$$\begin{aligned} (n-\alpha )&\mid&p_{\alpha +1}(n),\quad \mathrm{and}\\ (n-\alpha )&\mid&p_{k}(n)\;\, \mathrm{for}\;\, \mathrm{all}\;\, k\ge 2\alpha +3. \end{aligned}$$

Theorem 6

If \(k\ge 0\), then

$$\begin{aligned} p_k(n)\equiv {\left\{ \begin{array}{ll} k+1 &{}\text{ if } k \equiv 0 \pmod {3}, \\ -(k+1) &{}\text{ if } k \equiv 1 \pmod {3}, \\ 0 &{}\text{ if } k \equiv 2 \pmod {3}, \end{array}\right. } \pmod {(n+2)}. \end{aligned}$$

A consequence of Theorem 6 is

Corollary 1

\((n+2)\mid p_k(n)\) if and only if k is congruent to 2 modulo 3.

Proof

(Proof of Theorem 5) It is a known fact that if f(x) is a polynomial with complex coefficients, \(\deg (f(x))=d\ge 1\), and \(\beta \in {\mathbb {C}}\), then there exists a unique complex polynomial g(x) with \(\deg (g(x))=d-1\) such that \(f(x)=(x-\beta )g(x)+f(\beta )\). Hence \(f(x)\equiv f(\beta ) \pmod {(x-\beta )}\). It immediately gives the first statement of the theorem since

$$\begin{aligned} p_{\alpha +1}(n)\equiv p_{\alpha +1}(\alpha )=m_{\alpha ,\alpha +1}=0 \;\;\pmod {(n-\alpha )}. \end{aligned}$$

Let us turn our attention to the second part. First we claim that we have

$$\begin{aligned} p_{\alpha +1-t}(n)+p_{\alpha +1+t}(n)\equiv 0 \;\;\pmod {(n-\alpha )} \end{aligned}$$
(22)

when \(t=0,1,\dots ,\alpha +2\). This is trivial if \(t=0\). For \(t=1\) let \(k=\alpha +2\) and, applying (21), we have

$$\begin{aligned}&(\alpha +2)(n-\alpha +1)p_{\alpha +2}(n)=(n-\alpha -1)(n-\alpha +1)p_{\alpha +1}(n)\\&\quad +(n-\alpha -1)(2n-\alpha +2)p_{\alpha }(n). \end{aligned}$$

Taking it modulo \((n-\alpha )\), it leads to

$$\begin{aligned} (\alpha +2)p_{\alpha +2}(n)\equiv 0-(\alpha +2)p_{\alpha }(n)\;\;\pmod {(n-\alpha )}. \end{aligned}$$

Thus, \(p_{\alpha +2}(n)+p_{\alpha }(n)\) is congruent to 0 modulo \((n-\alpha )\). Assume that (22) holds for all \(0\le t\le T\), where \(1\le T\le \alpha +1\). Then we show that (22) is true for \(T+1\). Put \(k=\alpha +1+(T+1)=\alpha +T+2\). Then (21) modulo \((n-\alpha )\) is converted to

$$\begin{aligned}&(\alpha +T+2)(-T+1)p_{\alpha +T+2}(n)\equiv (-T-1)(-T+1)p_{\alpha +T+1}(n)\nonumber \\&\quad +(-T-1)(\alpha -T+2)p_{\alpha +T}(n). \end{aligned}$$
(23)

The induction hypothesis gives \(p_{\alpha +1+T}(n)\equiv -p_{\alpha +1-T}(n)\) and \(p_{\alpha +T}(n)\equiv -p_{\alpha +2-T}(n)\) modulo \((n-\alpha )\), which together with (23) yields

$$\begin{aligned} (T+1)(\alpha&-T+2)p_{\alpha +2-T}(n)\\&\equiv (-T-1)(-T+1)p_{\alpha +1-T}(n)+(-T+1)(\alpha +T+2)p_{\alpha +T+2}(n) \\&=(T+1)(T-1)p_{\alpha +1-T}(n)+(-T+1)(\alpha +T+2)p_{\alpha +T+2}(n) \end{aligned}$$

modulo \((n-\alpha )\). The recursion formula (21) for \(k=\alpha +2-T\) provides

$$\begin{aligned}&(T+1)(\alpha -T+2)p_{\alpha +2-T}(n)\equiv (T-1)(T+1)p_{\alpha +1-T}(n)\\&\quad +(T-1)(\alpha +T+2)p_{\alpha -T}(n) \end{aligned}$$

modulo \((n-\alpha )\). Compare it with the previous formula to get \(p_{\alpha +2+T}(n)\equiv -p_{\alpha -T}(n)\).

Subsequently, assuming \(t=\alpha +2\) in (22), we have

$$\begin{aligned} p_{2\alpha +3}(n)\equiv -p_{-1}(n)=0 \;\;\pmod {(n-\alpha )}. \end{aligned}$$
(24)

Finally, consider (21) with \(k=2\alpha +4\) modulo \((n-\alpha )\). Then

$$\begin{aligned}&(2\alpha +4)(-\alpha -1)p_{2\alpha +4}(n)\equiv (-\alpha -3)(-\alpha -1)p_{2\alpha +3}(n)\\&\quad +(-\alpha -3)\cdot 0\cdot p_{2\alpha +2}(n), \end{aligned}$$

which implies \(p_{2\alpha +4}(n)\equiv 0\) modulo \((n-\alpha )\) via (24).

Thus, we have proved that \(n-\alpha \) divides \(p_k(n)\) if \(k=2\alpha +3\) and \(k=2\alpha +4\). But this property descends for larger values of \(k\ge 2\alpha +5\), since in (21) the coefficient \(n-k+3\le n-(2\alpha +5)+3=n-2\alpha -2\) is not proportional to \(n-\alpha \). Hence the proof is complete. \(\square \)

Proof

(Proof of Theorem 6) The statement is trivially true for \(k=0,1,2\). Assume that it is also true for all non-negative values as far as \(k-1\). Then simply consider (21) modulo \((n+2)\). It admits

$$\begin{aligned} -k(k-1)p_k(n)\equiv (k-1)(k+1)p_{k-1}(n)+k(k+1)p_{k-2}(n). \end{aligned}$$
(25)

Now we distinguish three cases according to the remainder of k modulo 3.

If \(k\equiv 0\pmod {3}\), then \(p_{k-1}\equiv 0\) and \(p_{k-2}\equiv -(k-1)\) modulo \((n+2)\). Hence (25) entails \(p_k(n)\equiv (k+1)\). Similarly, the other two possibilities are also easy to see. \(\square \)

Finally, based on a computer verification for \(k\le 100\) we pose

Conjecture 1

Divide the polynomial \(p_k(n)\) by the linear factors given in Theorems 5 and 6. Then the quotient polynomial is irreducible over \({\mathbb {Q}}\). The only exception is

$$\begin{aligned} \frac{p_8(n)}{n(n-1)(n-2)(n-7)(n+2)}=\frac{1}{8!}(n+11)(n^2+25n-60). \end{aligned}$$