Distributed Training of Deep Neural Networks: Convergence and Case Study

Abstract

Deep neural network training on a single machine has become increasingly difficult due to a lack of computational power. Fortunately, distributed training of neural networks can be performed with model and data parallelism and sub-network training. This paper introduces a mathematical framework to study the convergence of distributed asynchronous training of deep neural networks with a focus on sub-network training. This article also studies the convergence conditions in synchronous and asynchronous modes. An asynchronous and lock-free training version of the sub-network training is proposed to validate the theoretical study. Experiments were conducted on two well-known public datasets, namely Google Speech and MaFaulDa, using the Jean Zay supercomputer of GENCI. The results indicate that the proposed asynchronous sub-network training approach, with 64 GPUs, achieves faster convergence time and better generalization than the synchronous approach.

1 Introduction

The work presented in this paper concerns distributed and parallel machine learning with a focus on asynchronous deep learning model training. Model parallelism and data parallelism are the two primary approaches to distributed training of neural networks [1, 2]. In data parallelism, each server in a distributed environment receives a complete model replica but only a portion of the data. Locally on each server, a replica of the model is trained on a subset of the entire dataset [3]. Model parallelism involves splitting the model across multiple servers. Each server is responsible for processing a unique neural network portion, such as a layer or subnet. Data parallelism could be deployed on top of model parallelism to parallelize model training further. In a deep convolutional neural network, for instance, the convolution layer requires a big number of calculations, but the required parameter coefficient W is small, whereas the fully connected layer requires a small number of calculations, and the required parameter coefficient W is large. Consequently, data parallelism is appropriate for convolutional layers, while model parallelism is appropriate for fully connected layers.

Nevertheless, data and model parallelism approaches have numerous drawbacks. Data parallel approaches suffer from limited bandwidth since they must send the whole model to every location to synchronize the computation. A huge model with many parameters cannot meet this requirement. Model parallel approaches are not viable in most distribution settings. When data are shared across sites, model parallel computing requires that different model components can only be updated to reflect the data at a specific node. Fine-grained communication is required to keep these components in sync [4].

1.1 Objective

The study has two main objectives. Given a neural network and its partition into sub-networks, the first objective is to establish the mathematical relationship between deep learning on the complete network and deep learning on the partitioned sub-networks. The second is to use this mathematical model to clarify sufficient conditions that ensure the effective convergence, after training of the sub-networks, towards the solution that would have been obtained by the complete neural network. The research question RQ is “whether, by training and combining smaller parts of a full neural network, the convergence of the global solution to the original problem is obtained. In other words how to ensure that weight parameters obtained by training the partitioned parts of the full network reconstitute the correct weight parameters that tune the full network."

The mathematical model we introduce is general; indeed, it covers both sub-network training and federated learning approaches, as well as their execution in both synchronous and asynchronous modes. To validate our model, we conduct synchronous and asynchronous implementations of sub-network training with a coordinator and several workers and compares their performance.

Our implementation aims to validate the proposed mathematical model and its necessary conditions, rather than to offer a novel deep learning architecture for distributed deep learning. For this purpose, we present an implementation based on the Independent Subnet Training (IST), an approach proposed by Yuan et al. [5]. The experiments we conducted¹ demonstrate how asynchronous distributed learning leads to a shorter waiting time for model training and a faster model updating cycle.

1.2 Methodology

We introduce a general mathematical model to describe the sequences generated² by sub-networks partitioning-based approaches. The model considers the dependencies of the unknown variables (weights parameters) that the original neural network must tune. Consequently, different techniques can be modeled, including independent sub-network training and federated learning methods. Specifically, this mathematical model is based on a fixed-point function defined on an extended product space, see [6]: the sequences generated by the extended fixed-point function describe the aggregation of iterations produced by gradient descent algorithms applied to neural sub-networks. Using the fixed point theorem, it is possible to study the numerical convergence of sub-network-based approaches running back-propagation algorithms to the actual solution that would be obtained by original neural network.

The numerical convergence of sub-network partitioning algorithms in asynchronous mode is then examined. To this aim, we apply a classical convergence theorem of asynchronous iterations developed in [7], and in other papers such as [8, 9], to the aforementioned fixed-point function. The convergence conditions and cautious implementation details are then specified.

The rest of the paper is organized as follows: The related work to this paper is presented in Sect. 2. Section 3 recalls preliminaries on successive approximations, fixed-point principle and their usefulness to modelize sequential, synchronous and asynchronous iterations. The general mathematical model and the convergence study of the algorithms proposed by this paper are presented in Sect. 4. We first introduce the fixed-point mapping that models the behavior of a certain number of backpropagations on sub-networks of the original network. Then we prove thanks to Proposition 1 and 2 the convergence result of synchronous and asynchronous sub-networks training algorithms. Section 5 is devoted to the empirical validation of the results, the experimental use case is also presented. Section 6 discusses this paper’s results and presents future work and perspectives and Sect. 7 concludes the paper.

2 Related Work

Stochastic gradient descent (SGD) uses a randomly chosen sample to update model parameters, providing benefits such as quick convergence and effectiveness. Nodes must communicate to update parameters during gradient calculation. However, waiting for all nodes to finish before updating can decrease computing speed if there is a significant speed difference between nodes. If the speed difference is small, synchronization algorithms work well, but if the difference is significant, the slowest node will reduce overall computing speed, negatively impacting performance. Asynchronous algorithms most effectively implement it [10].

Google’s DistBelief system is an early implementation of async SGD. The DistBelief model allows for model parallelism [11]. In other words, different components of deep neural networks are processed by multiple computer processors. Each component is processed on a separate computer, and the DistBelief software combines the results. It is similar to how a computer’s graphics card can be used to perform certain computations faster than the CPU alone. The processing time is decreased because each machine does not have to wait its turn to perform a portion of the computation, but can instead work on it simultaneously. Async SGD has two main advantages: (1) First, it has the potential to achieve higher throughput across the distributed system: workers can spend more time performing useful computations instead of waiting for the parameter averaging step to complete. (2) Workers can integrate information from other workers (parameter updates), which is faster than using synchronization (every N steps). However, a consequence of introducing asynchronous updates to the parameter vector, is a new issue known as the stale gradient problem. A naive implementation of async SGD would result in a high gradient staleness value. For example, Gupta et al. [12] show that the stale value of the average gradient is equal to the number of workers. If there are M workers, these gradients are M steps late when applied to the global parameter vector. The real-world impact is that high gradient staleness values can greatly slow down network convergence or even prevent convergence for some configurations altogether. Earlier async SGD implementations (such as Google’s DistBelief system) did not consider this effect. Some ways to handle expired gradients include, among others, implementing “soft" synchronization rules such as in [13] and delaying the faster learner if necessary to ensure that the overall maximum delay is less than a threshold [14]. Researchers have proposed several schemes to parallelize stochastic gradient descent, but many of these computations are typically implemented using locks, leading to performance degradation. The authors of [15] propose a straightforward technique called Hogwild! to remove locks. Hogwild! is a scheme that enables locking-free parallel SGD implementations. Individual processors are granted equal access to shared memory and can update memory components at will using this method. Such a pattern of updates leads to high instruction-level parallelism on modern processors, resulting in significant performance gains over lock-based implementations. Hogwild! has been extended by the Dogwild! model in [16]. Dogwild! has extended the Hogwild! model to distributed-memory systems, where it still converges for deep learning problems. To reduce the interference effect of overwriting w at each step, the gradient $\nabla w$ from the training agents is transferred in place of w. The empirical evaluation of this paper is inspired by the Independent sub-network Training (IST) model [5], which decomposes the neural network layers into a collection of subnets for the same goal by splitting the neurons across multiple locations. Before synchronization, each of these subnets is trained for one or more local stochastic gradient descent (SGD) rounds. IST is better than model parallelism approaches in some ways. Given that subnets are trained independently during local updates, there is no need to synchronize them with each other. Still, IST has some of the same benefits as model parallelism methods. Since each machine only gets a small piece of the whole model, IST can be used to train models that are too big to fit in the RAM of a node or a device. This can be helpful when training large models on GPUs, which have less memory than CPUs. The following sections provide proof of convergence for partitioning-based networks in synchronous and asynchronous modes. The empirical evaluation section considers the IST model as a use case and proposes an asynchronous implementation.

3 Preliminaries: Successive Approximations. Synchronous and Asynchronous Algorithms

In the sequel, $x^{k}_{i}$ denotes the $k^{th}$ iterate of the $i^{th}$ component of a multi-dimensional vector x.

A Numerical iterative method is usually described by a fixed-point application, say T. For example, given an optimization problem $\min _{x}f(x)$, the first challenge is to build an adequate T, such that the iterative sequence $x^{k+1}=T(x^{k})$ for $k \in \textbf{N}$ converges to a fixed point $x^{*}$, solution of $\min _{x}f(x)$. Successive iterations generated by the numerical method are then described by:

$$\begin{aligned} {} \begin{array}{l} Given x^{0}=(x^{0}_{1},\ldots ,x^{0}_{n})^T \in \mathbb {R}^n\\ for i=1,\ldots ,n \\ \quad for k=1,2...\, until\,convergence\\ \quad x_{i}^{k+1}= T_{i}(x_{1}^{k},\ldots ,x_{n}^{k}) \end{array} \end{aligned}$$

(1)

Suppose that x is partitioned into m blocks $x_l$ $\in \mathbb {R}^{n_l}$ so that $\Sigma _{l=1}^{m}n_l=n$ and that m processors are respectively in charge of a block $x_l$ of components of x, then let us then define sets S(k) describing the blocks of x updated at the iteration k. The other blocks are supposed not to be updated at iteration k. Asynchronous algorithms, in which the communications between blocks are free with no synchronization between the processors in charge of the blocks, are described by the following iterations:

$$\begin{aligned} \begin{array}{l} Given x^{0}=(x^{0}_{1},\ldots ,x^{0}_{m})^T \in \Pi _{l=1}^m \mathbb {R}^{n_l}\\ \begin{array}{l} for k=1,2\ldots \, until\,convergence\\ forl=1,\ldots ,m \end{array} \\ \quad x_{l}^{k+1}=\left\{ \begin{array}{l} \begin{array}{l} T_{l}(x_{1}^{\rho _{1}(k)},\ldots ,x_{m}^{\rho _{m}(k)}) if l \in S(k)\\ x_{l}^{k}if l\notin S(k) \end{array} \end{array} \right. \end{array} \end{aligned}$$

(2)

Here $\rho _{i}(k)$ is the delay due to processor i at the $k^{th}$ iteration. Note that with this latter formulation, synchronous per-blocks iterative algorithms are particular cases of asynchronous per-blocks iterative algorithms. Indeed, one has to simply assume that there is no delay between the processors, i.e., $\forall i, k \quad \rho _{i}(k)=k$, and that all the blocks are updated at each iteration, $\forall k, S(k)=\{1,\ldots ,m \}$. In this paper, $T^{(\beta ) }$ will denote the fixed-point mapping describing the gradient descent method or its practical version SGD with learning rate $\beta$. Under suitable conditions and construction, the fixed-point application T describing the gradient descent method converges to a desired solution. In what follows, a fixed-point mapping $\mathcal {T}$ will also be introduced, this is a key function of our study on traininig deep neural netwoks. This function involves the computation of weighted parameters associated with network training, as well as combination matrices that model the aggregation of partial computations from sub-networks.

4 Convergence Study

4.1 Mathematical Modeling

Consider the general case of a feedforward neural network of some number of layers and neurons. Suppose that the number of interconnections between neurons in the network is n, so that the network is tuned by n weight vectors.

Let us consider a training set composed of inputs and targets. Consider a loss-function f (e.g. Mean Squared Error, Cross Entropy, etc.) that should be minimized on the traing set in order to fit the inputs to their targets. To do so, let $x \in \mathbb {R}^n$ be the weight vector that the neural network must tune to minimize f. Suppose that the gradient descent algorithm is used to perform this minimization. The gradient descent algorithm performs the iterations:

$$\begin{aligned} x^{k+1}=x^{k}- \beta \nabla _{x}f(x^{k}), k\in \mathbb {N}, x^{0} \in D(f) \end{aligned}$$

(3)

Under the right conditions on the function f and the learning rate $\beta$, the function $I-\nabla _{x}f$ is contractive on its definition domain D(f) and the successive iterations (Eq. 3) converge to $x^{*}$ satisfying the solution:

$$\begin{aligned} x^{*} = argmin_{x}f(x), x^* \in D(f) \end{aligned}$$

(4)

Here $\nabla _{x} f(x)={(\frac{\partial f_i}{\partial x_j})}_{ij}$ is the Jacobian matrix consisting of the partial derivatives of f with respect to weight vector x of the interconnections of the network. A Backpropagation with a learning rate $\beta _i$ applied to the network consists in computing successive iterations associated to the Descent gradient algorithm:

$$\begin{aligned} x^{0} \quad being \quad the \quad initialization \quad weights \nonumber \\ x^{k+1}=x^{k}- \beta _{i} \nabla _{x}f(x^{k}), k\in \mathbb {N}, \end{aligned}$$

(5)

Let $T^{(\beta _i)}$ denotes the fixed point application describing the iterations (Eq. 5):

$$\begin{aligned} y=T^{(\beta _i)}(x)=x-\beta _{i} \nabla _{x}f(x) \end{aligned}$$

Consider m backpropagation algorithms on the neural network $\text {Net}$ with learning rates ${\beta }_i$, $i=1,\ldots ,m$. The learning rates ${\beta }_1, ... , {\beta }_m$ are chosen in such a way that the gradient descent algorithms converge to ${x}^{*}$, solution of (4), i.e.

$$\begin{aligned} T^{(\beta _i)}(x^*)=x^*, \forall i\in \{1,\ldots ,m\} \end{aligned}$$

(6)

For a network $\text {Net}$ with n weighted vector, and m backpropagation algorithms, let us introduce the following fixed-point mapping which is called aggregation fixed point mapping:

$$\begin{aligned} \mathcal {T} :\left( \mathbb {R}^{n}\right) ^{m} \ \longrightarrow \ \ \left( \mathbb {R}^{n}\right) ^{m} \nonumber \\ \left( x^{1} ,\ldots ,x^{m}\right) \longrightarrow \left( y^{1} ,\ldots ,y^{m}\right) \nonumber \\ y^{l} =T^{(\beta _l)}\left( \sum _{k=1}^{m} E_{k} x^{k}\right) \end{aligned}$$

(7)

where $E_k$ are diagonal matrices called weight matrices so that

$$\begin{aligned} \sum _{k=1}^{m}E_k = I \end{aligned}$$

(8)

I is the identity matrix $\in \mathbb {R}^{n\times n}$. Since the weight matrices are diagonal, the aggregation fixed-point mapping modelizes the execution of m backpropagations on m sub-networks. It should be noted that condition (8) is essential for the formal convergence study.

Proposition 1

$\mathcal {T}$ is a contractive function

The aggregation fixed-point mapping $\mathcal {T}$ is contractive with constant of contraction $\alpha$ satisfying, $\alpha \le \max _{l=1}^{m}(\alpha _{l}),$ where $\alpha _l$ are the constants of contraction of $T^{(\beta _l)}$

Proof

Let $y^{l}=T^{(\beta _l)}(\Sigma _{k=1}^{m}E_{k}x^{k})$

From (6) each gradient descent converges to $x^*$ the solution of (4), so each fixed-point mapping $I-\beta \nabla _{x}J$ is contractive.

For $l\in \{1,\ldots ,m\}$, denote by $\alpha _l$ the constant of contraction of $T^{(\beta _l)}$ with respect to the $l_2$ norm $\Vert x\Vert _2$.

By (7) we have

$$\begin{aligned} \Vert y^{l}-x^*\Vert _2=\Vert T^{(\beta _l)}(\Sigma _{k=1}^{m}E_{k}x^{k})-T^{(\beta _l)}(x^{*})\Vert _2 \le \ \alpha _{l}\Vert \Sigma _{k=1}^{m}E_{k}x^{k}-x^{*}\Vert _2 \end{aligned}$$

Since $E_{k}$ are diagonal matrices and $\Sigma _{k=1}^{m}E_k=I$, we have

$$\begin{aligned} \Vert \Sigma _{k=1}^{m}(E_{k}x^{k}-x^{*})\Vert _2 =\Vert \Sigma _{k=1}^{m}E_{k}(x^{k}-x^{*})\Vert _2 \le \max _{k=1}^{m}\Vert x^{k}-x^{*}\Vert _2 \nonumber \end{aligned}$$

Thus, $\Vert y^{l}-x^*\Vert _2$ $\le$ $\alpha _{l}$ $\max _{k=1}^{m}\Vert x^{k}-x^{*}\Vert _2$

Hence we obtain, $\max _{l=1}^{m}\Vert y^{l}-x^*\Vert _2$ $\le$ $(\max _{l=1}^{m}\alpha _{l})$ $\max _{k=1}^{m}\Vert x^{k}-x^{*}\Vert _2$

Let’s define the norm, $\Vert (y^1,\ldots ,y^m)\Vert _\infty =\max _{1 \le l \le m}\Vert y^l\Vert _2$, then

$$\begin{aligned} \Vert \mathcal {T}\left( x^{1} ,\ldots ,x^{m}\right) -(x^*,\ldots ,x^*)\Vert _\infty \le (\max _{l=1}^{m}\alpha _{l}) \Vert \left( x^{1} ,\ldots ,x^{m}\right) -\left( x^*,\ldots ,x^*\right) \Vert _\infty \end{aligned}$$

This proves the claimed result.

Proposition 2

Asynchronous convergence of $\mathcal {T}$

The asynchronous iterations generated by the fixed-point mapping $\mathcal {T}$ converge to $(x^{*}, ..., x^{*})^T$.

Proof

Proposition 1 implies that we are in the framework of contractive fixed-point mapping with respect to a maximum norm on a product space. Indeed, $\mathcal {T}$ is a contractive mapping with respect to the maximum norm $\Vert ..\Vert _\infty$, on the product space $\Pi _{i=1}^{m}\mathbb {R}^{n}=\left( \mathbb {R}^{n}\right) ^{m}$. These are the required sufficient conditions for the convergence of asynchronous algorithms associated to $\mathcal {T}$. see [7]. Thus Proposition 2 is proved.

Remark 1

The aggregation fixed point mapping modelizes Independent Sub-network Training, indeed, if the neurons are disjoint then $\forall i, (E_k)_{ii}$ is equal to either 0 or 1. It should be noted that we don’t use the notion of compressed iterates and the assumptions related to the expectancy of the compression operator $\mathcal {M}(.)$ as in [5]. We prove the convergence of the iterates values instead of their convergence on expectation. To modelize federated learning like algorithms the weighted matrices become $\forall i, (E_k)_{ii} = 1/M$.

5 Empirical Validation

5.1 The Links Between the Mathematical Model and the Implementation

- To obtain asynchronous iterations produced by the aggregation of the computations of m sub-networks, it is sufficient to consider that $T=\mathcal {T}$ in (2).

- Synchronous per-blocks computations correspond to $S(k)=\{1,\ldots ,m\}$, and ${\rho _{i}}^{k}=k$, $\forall k$ (no-delays and all the blocks are updated at each iteration).

- A sub-network l is defined by all nodes j corresponding to the non-zero entries of $E_l$: $(E_l)_{jj}$ $\ne 0$, so the aggregation of the weight vectors computed by the sub-networks must be done carefully so that $\sum _{k=1}^{m}E_k = I$ is satisfied.

- Even if in the mathematical formulation $\mathcal {T}$ is defined on the product space $\Pi _{i=1}^{m}\mathbb {R}^{n}$, each sub-network l updates at each iteration only its own components, this is because the weight matrices $E_l$ are diagonal matrices and $(E_l)_{jj}=0$ if node j does not belongs into sub-network l.

- To execute the computations in asynchronous mode, it should be noted that the convergence theory requires some conditions on the block-component updates and the delays between the processors. These are listed below.

• $\forall i \in \{1,...m\}$ the set $\{k \in \mathbb {N} / i \in S(k) \}$ is infinite. This simply means that any sub-network i is guaranteed to update its computations, i.e. not to be permanently inactive.

• The delays must "follow" the iterations, the mathematical formulation for that is $\forall i, \lim _{k \rightarrow \infty }(\rho _{i}(k))=\infty$.

For more precision see the literature on asynchronous iterations, e.g. [7, 9, 17,18,19].

It can be noticed that in a practical implementation these assumptions are realistic.

5.2 Use Case: Independent Subnet Training

As a use case, let us consider the IST model for this research. Note that the proposed mathematical model is general and could also cover dependent partitioning-based networks. The publicly available Github implementation³, the clarity of the code, and the recent date of publication were among the reasons to consider this model for our use case.

In the original work, the authors suggest to regularly resample the subnets and to train them for fewer iterations between resamplings. This paper proposes that the coordinator distribute subnets only at the beginning of training to prevent blockage. Similarly to the original IST model, the following constraints are respected:

• Input and output neurons are common to all subnets.

• Hidden neurons are randomly partitioned via uniform assignment to one of n possible compute nodes.

• The complete Neural Network (NN)’s weights are partitioned based on the number of activated neurons in each subnet.

• No collisions occur because the parameter partition is disjoint.

Fig. 1.

The architecture of a distributed asynchronous training based on the partitioning-based framework.

The training process of the asynchronous IST training is as follows: (1) The coordinator distributes the sub-networks to the workers at the beginning of the training process. Contrary to the original IST, no new group of subnets is constructed to avoid synchronization. Note that during the training process, the coordinator trains a subnet, not the full neural network. (2) Each cluster (coordinator and workers) computes the loss of its local model based on its local data (i.e., forward pass). (3) Each cluster computes the gradients based on the loss (i.e., backward pass). (4) Each worker sends its parameters to the coordinator. In our asynchronous version, it is done using Pytorch’s isend method that sends a tensor asynchronously. (5) Given that the partition is disjoint, the coordinator copies the parameters into the full neural network without collisions. The asynchronous version is considered using Pytorch’s irecv method that receives a tensor asynchronously.

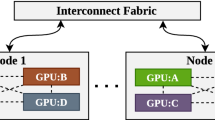
The architecture and training procedure considered in this research (Fig. 1) are comparable to frameworks such as the parameter server with centralized or federated learning techniques [20]. The local models, however, are subnets of the full model and not a replica. Note that Fig. 1 illustrates a general partitioning-based framework described by the proposed mathematical model and not necessarily the particular IST model. To represent the async IST implemented by this paper, one could ignore the transmission of the delayed parameters from the coordinator to the workers after the first partition, given that each worker has an independent subnet that does not require the parameters of other workers. One of the challenges of asynchronous training is that the asynchronous communication will be rendered meaningless if one continues to allow communication between workers: This issue is solved by avoiding parameters exchange between subnets and avoiding synchronization during local updates or the coordinator’s updates.

5.3 Experiments

The Google Speech [21] and Mafaulda⁴ [22] datasets were considered to demonstrate the advantage of asynchronous distributed training of neural networks over synchronous training. The Google Speech dataset describes an audio dataset of spoken words that can be used to train and evaluate keyword detection systems. The objective is to classify 35 labeled keywords extracted from audio waveforms. In the dataset, the training set contains roughly 76,000 waveforms, and the testing set has around 19,000 waveforms. The Mafaulda dataset is a publicly available dataset of vibration signals acquired from four different industrial sensors under normal and faulty conditions. This database is composed of 1951 multivariate time-series and comprises six different states. Similarly to [5], a three-layer MLP (multilayer perceptron) has been developed. The number of neurons in each layer is a parameter. Using subnets as mentioned in [5], the MLP is distributed across all processes and GPUs. To simplify, links between neurons are divided among all the nodes, and each link is controlled exclusively by a single node. Consequently, the coordinator node (which also participates in the training computation) and the worker node share link weights during parallel training.

In contrast to [5], where all tasks are synchronized, an implementation with asynchronous tasks and iterations has been built. In this version, there is no synchronization following the initialization. The coordinator node has a heavier workload compared to other nodes in the implementation of the IST code. It is responsible for coordinating workers, performing tests with the test dataset, sending and receiving the link weights of other nodes’ neurons. Additionally, the coordinator is also responsible for a subnet (local gradient descent) in this implementation, leading to a higher amount of calculations.

For the experiments, the French supercomputer Jean Zay of GENCI was used. This supercomputer contains more than 2,000 GPUs (most of them are NVIDIA V100).

The experiments compare the performance of three different versions of a neural network training algorithm: the old synchronous version (the training version implemented by [5]), the synchronous version with partitioning at the first iteration, and the asynchronous version with no synchronizations between the workers. The main point that the experiments aim to prove is that the asynchronous method provides better testing accuracy in a shorter time and lower execution times compared to the synchronous methods.

Fig. 2.

Experiments with the Google Speech dataset.

Table 1. Execution times for the Google Speech dataset.

The training of three models was executed ten times with 64 GPUs. A supercomputer with specialized architecture was used, resulting in minimal variations in execution times. Testing accuracy was averaged and plotted to assess the convergence of the models. Results from Figs. 2a and 3a indicate that the asynchronous method outperforms the synchronous mode due to worker nodes completing more iterations than the coordinator node (workers don’t wait for the coordinator to synchronize at the end of each epoch), while in synchronous mode, the number of iterations completed is equal to the number of epochs. The number of epochs was fixed at 100 for the Google Speech dataset and 200 for Mafaulda based on several experiments, as those values better show the difference in performance between synchronous and asynchronous training. Additionally, the average testing accuracy for 1,000 epochs was computed only for the synchronous model with one partitioning at the beginning to compare the performance of the asynchronous model with a smaller number of epochs against the synchronous model’s accuracy after 1,000 epochs. Figures 2b and 3b demonstrate that the synchronous case has lower testing accuracy even with 1,000 epochs compared to the asynchronous case. Table 1 shows the average execution times rounded to the nearest second of three versions. The maximum accuracy is shown. The last column shows the asynchronous acceleration compared to the other versions. The asynchronous training was faster than the other synchronous approaches on both Google Speech and Mafaulda datasets. The code used for the experiments is available⁵.

Fig. 3.

Experiments with the Mafaulda dataset.

6 Discussion and Perspectives

This paper aims to address numerical convergence in deep learning frameworks for large problems. To achieve this, the neural network is partitioned into subnets and back-propagation algorithms are applied to these subnets instead of the original network. The paper also raises questions about reconstituting the global solution from partial solutions of subnets and the differences between synchronous and asynchronous algorithms during convergence.

The paper presents a mathematical model that describes the behavior of partitioning-based network methods in synchronous and asynchronous modes, and proves the convergence of such methods. To validate this approach, the specific case of Independent Subnets Training is considered, and the asynchronous mode is implemented and compared to the standard synchronous mode. The study concludes that the asynchronous mode has better performance in terms of execution time and accuracy.

The presented mathematical model is general and describes various scenarios, including federated learning with workers possessing the same network architecture. Future works will investigate different concepts and distributed architectures to broaden the scope of the study.

7 Conclusion

This paper proposes a general model to investigate the convergence of distributed asynchronous training of deep neural networks. The model addresses the question of whether partial solutions of sub-networks can be used to reconstitute the global solution. Two experimentations based on the Independent sub-network Training model on different datasets are provided, demonstrating that using the asynchronous aggregation sub-networks model is interesting for reducing execution time and increasing accuracy, even on a supercomputer. The study expects a better performance from asynchronous aggregation algorithms in contexts with weak computation time to communication time ratios.