A Modified Hybrid RBF-BP Network Classifier for Nonlinear Estimation/Classification and Its Applications

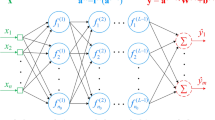
Abstract

In this work, a modified hybrid radial basis function-back-propagation (RBF-BP) supervised neural network classifier based on the works of Wen et al. [11, 12] is proposed. The modified hybrid RBF-BP network is formulated as an adaptive incremental learning algorithm for a single-layer RBF hidden neuron layer. The algorithm uses a density clustering approach to determine the number of RBF hidden neurons and it maintains the self-learning process of updating the neural network’s weights using back-propagation. For the last step of the BP neural network in the modified hybrid classifier, the centers and the width parameters of the basis functions are iteratively updated by the stochastic gradient descent algorithm. As a comparative study, some artificial and real-life datasets, for example, Double Moon, Concentric Circle, No Structure and UCI datasets, are used to test the effectiveness of our homemade implementation strategies. The experimental results showed that the implemented algorithm has significant accuracy improvement and reliability.

Supported by Department of Mathematics at CUHK and the Teaching Development and Language Enhancement Grant 2022-25 at CUHK.

1 Introduction

A combination of two neural network models, the radial basis function network (RBFN) and the back-propagation network (BPN) (e.g., [2, 5, 7]), are most widely used in nonlinear estimation/classification. RBFN is a local approximation network and the main advantage of the RBFN is that it has only one hidden layer that uses RBF as the activation function. In addition, RBFN maps nonlinearly separable problems in low-dimensional spaces to high-dimensional spaces through RBFs, making them linearly separable in high-dimensional spaces. Its disadvantage is that the classification is slow in comparison to BPN since every node in the hidden layer must compute the RBF function for the input during the classification. Another problem is the number of RBF units. Too many RBF units may result in over-fitting while too few may lead to under-fitting. This number has been manually selected on a trial-and-error basis. Some attempts have been made to decide this number adaptively [11, 12]. BPN is a global approximation neural network. During the training process, the error is propagated backward layer by layer to the input layer, and the ownership value and threshold appearing in the network are corrected. For each training sample, there is only a small number of weights and thresholds to be updated. Other hybrid classifiers, for example, the radial basis function-extreme learning machine classifier for a mixed data type and medical prediction, [6, 10, 13], perform better than the BP classifier. Further extensions of the hybrid RBF-BP network classifier (the Hybrid classifier for short) using pre-RBF kernels were found in [14, 15].

In this paper, a modified version of the hybrid classifier (the mHybrid classifier for short) is proposed based on the works of Wen et al. [11, 12]. It is formulated as an adaptive incremental learning algorithm for a single-layer RBF hidden neuron layer by fixing/shifting the center, adjusting the width parameter of the basis functions and updating the number of RBF hidden neurons, and it maintains a self-learning process of tuning a single-layer BP neural network’s weights to improve classification accuracy. In the mHybrid classifier, the center and the width parameter of the RBFs are iteratively updated by the stochastic gradient descent (SGD) algorithm.

The rest part of the paper is outlined as follows. Section 2 presents the architecture of the mHybrid network and the centers, widths and number of RBF hidden neurons interacting with the multi-layer perceptron (MLP) hidden neurons. In Algorithm 1, with optimally determined centers and width parameters, the coverage effect of each hidden neuron can be guaranteed. In Sect. 3, by passing the output of the RBF hidden neurons into an MLP neural network, backpropagation (BP) is used to update the weights of the MLP. Bridging between RBF-BP networks is shown in Algorithm 2 and their implementations are highlighted. In Algorithm 3, two SGD iterative steps are proposed for updating the centers and the width parameters of the RBF units. Section 4 examines the numerical performance of the mHybrid classifier on artificial datasets, e.g., Double Moon, Concentric Circle (e.g., [4]). No Structure [9] and real-life UCI datasets [3]. Section 5 summarizes our findings and concludes the paper.

2 Structure of the Incremental Learning Algorithm

This section describes the three sequential steps used to first find the centers for the RBFs, then find the widths for the RBFs, and to determine a new center as needed.

2.1 Finding the Centers for the Radial Basis Functions

Our aim here is to introduce an efficient technique of density clustering for balanced data. For the RBF networks, the data $\{\boldsymbol{x}\}$ of each class y is covered by circles of different sizes. To decide the optimal number of circles, a pre-selected discriminant function is designed. Then the locations and the widths of the circles are determined from the repulsive force exerted by nearby heterogeneous members, so that each circle contains many homogeneous members and few heterogeneous members. Formally, we define a set of discriminant functions $\rho _i$, one for each class i [1],

$$\begin{aligned} \rho _i(\boldsymbol{x})>\rho _j(\boldsymbol{x}) \text { for any }j\ne i\implies \boldsymbol{x} \text { belongs to class } i. \end{aligned}$$

(1)

The higher the value of $\rho _i$, the more likely that $\boldsymbol{x}$ belongs to class i. Another natural assumption is that the more members of the same class there are around $\boldsymbol{x}$, the more likely $\boldsymbol{x}$ belongs to the same class. To obtain the discriminant function, one therefore can define a potential function $\gamma$ as

$$\begin{aligned} \gamma (\boldsymbol{x},\boldsymbol{z}) = \frac{1}{1+T \Vert \boldsymbol{x}-\boldsymbol{z}\Vert ^2}, \end{aligned}$$

(2)

where $T>0$ is a distance weighting factor and $\Vert \cdot \Vert$ is the Euclidean norm. The potential $\gamma$ is a particular example of the general inverse multi-quadratic function, $(1+\epsilon ^2\Vert \boldsymbol{x}-\boldsymbol{z}\Vert ^2)^{-p/2}$ when $T=\epsilon ^2$ and $p=2$. The potential $\gamma$ is proportional to the closeness between two points $\boldsymbol{x},\boldsymbol{y}$.

Given a data set S that consists of N training samples $\{ (\boldsymbol{x}_k, y_k) \}_{k=1}^{N},$ where $\boldsymbol{x}_k \in \mathbb {R}^n$ and $y_k \in \mathbb {R}^H$, where n is the dimension of $\boldsymbol{x}_k$ and H is the dimension of $y_k$. Let $S^i=\{\boldsymbol{x}^i_k:~k=1,\cdots ,N_i\}$ be the set of training samples in the ith pattern class, $N_i$ the number of samples in class i and $S^i\,\cap \,S^j = \emptyset$ for $i\ne j$. For $\boldsymbol{x}\in \mathbb {R}^n$ and $\boldsymbol{x}^i_k\in S^i$, a discriminant function $\rho _i$ can be constructed by the superposition of such potential functions $\gamma (\cdot , \boldsymbol{x}^i_k)$:

$$\begin{aligned} \rho _i(\boldsymbol{x}) = \frac{}{}\sum _{k=1}^{N_i} \gamma (\boldsymbol{x},\boldsymbol{x}_k^i) = \sum _{k=1}^{N_i}\frac{1}{1+T \Vert \boldsymbol{x}-\boldsymbol{x}^i_k\Vert ^2}. \end{aligned}$$

(3)

As shown in Fig. 1, $T>0$ controls the width of the region of influence and the sharpness of the distribution, e.g., the larger the factor T, the sharper $\rho _i$ and the distribution of the samples will have a better shape.

It is worth mentioning that the $\rho _i$ defined here is different from that in Wen et al. [11, 12], where when evaluated at sample point ${\boldsymbol{x}^i_l}$, the summation does not consider that point (i.e., $\widetilde{\rho }_i (\boldsymbol{x}^i_l)=\sum _{k=1,k\ne l}^{N_i}\gamma (\boldsymbol{x}^i_l,\boldsymbol{x}^i_k)$). Then we have $\rho _i(x) = \widetilde{\rho }_i(x)+1$ for $x^i\in S^i$. This difference is not critical in the end (except for the choice of $\delta$) since we will only compare the values within the same class. Here are a few properties of $\gamma$ [8]:

• 1. $\gamma (\boldsymbol{x},\boldsymbol{z})$ attains maximum at $\boldsymbol{x}=\boldsymbol{z}$.

• 2. $\gamma (\boldsymbol{x},\boldsymbol{z})$ tends to 0 as $\Vert \boldsymbol{x}-\boldsymbol{z}\Vert$ increases.

• 3. $\gamma (\boldsymbol{x},\boldsymbol{z})$ is smooth and decreases monotonically as $\Vert \boldsymbol{x}-\boldsymbol{z}\Vert$ increases.

• 4. $\gamma (\boldsymbol{x}_1,\boldsymbol{z})=\gamma (\boldsymbol{x}_2,\boldsymbol{z})$ if $\Vert \boldsymbol{x}_1-\boldsymbol{z}\Vert =\Vert \boldsymbol{x}_2-\boldsymbol{z}\Vert .$

These properties allow $\rho _i$ to capture the local influence of $S^i$ at $\boldsymbol{x}$ and to correlate to the likeliness for the input $\boldsymbol{x}$ to belong to $S^i$. Finally, all that remains to be checked is whether this $\rho _i$ can classify correctly, as stated in the theorem below.

Fig. 1.

Illustration of the effect of T in a 1D example using 10 data samples.

Theorem 1

Suppose $\boldsymbol{x}^i_l\in S^i:=\{\boldsymbol{x}^i_1,\cdots ,\boldsymbol{x}^i_{N_i}\}$. Let N be the number of classes. Let $D = \min \{\Vert \boldsymbol{x}^i-\boldsymbol{x}^j\Vert ^2: \boldsymbol{x}^i\in S^i, \boldsymbol{x}^j\in S^j \text { for any }i\ne j,~ i,j\le N\}>0$. Then, there exists a continuously differentiable discriminant function $\rho _i$ such that

$$\rho _i(\boldsymbol{x}^i_l)>\rho _j(\boldsymbol{x}^i_l)\text { for any }j\ne i.$$

Proof

Suppose $S^j=\{\boldsymbol{x}_1^j,\cdots ,\boldsymbol{x}^j_{N_j}\}$. Let $T > \frac{1}{D}\left( N_j-1\right)$. Define $\rho _i$ as stated before using this T. Then,

$$\begin{aligned} \rho _j(\boldsymbol{x}^i_l) &= \sum ^{N_j}_{k=1}\frac{1}{1+T\Vert \boldsymbol{x}^i_l-\boldsymbol{x}^j_k\Vert ^2} \le N_j \max _{k=1,\cdots ,N_j} \frac{1}{1+T\Vert \boldsymbol{x}^i_l-\boldsymbol{x}^j_k\Vert ^2}\\ &\le N_j \frac{1}{\displaystyle 1+T\min _{k=1,\cdots ,N_j}\Vert \boldsymbol{x}^i_l-\boldsymbol{x}^j_k\Vert ^2} \le \frac{N_j}{1+TD} < 1 \\ &= \frac{1}{1+T\Vert \boldsymbol{x}^i_l -\boldsymbol{x}^i_l\Vert ^2} \le \sum ^{N_i}_{k=1}\frac{1}{1+T\Vert \boldsymbol{x}^i_l-\boldsymbol{x}^i_k\Vert ^2} = \rho _i(\boldsymbol{x}^i_l). \end{aligned}$$

$\square$

The value T can be selected as $T> \frac{1}{D}(N_j-1)$ for any j such that the theorem holds.

Now, using the discriminant function $\rho _i$, we can select an initial center by taking the maximum of the discriminant function over class i since the samples are concentrated/localized around it. Define the initial center

$$\begin{aligned} \boldsymbol{\mu }_k := \mathop {\mathrm {arg\,max}}\limits \{\rho _i(\boldsymbol{x}^i_l):~\boldsymbol{x}^i_l \in S^i \}. \end{aligned}$$

(4)

We now circle it with a given predetermined radius $\sigma$ with a predefined threshold $\sigma _{\min } < \sigma$. Our next goal is to move the center $\boldsymbol{\mu }_k$ and resize the circle so as to reduce the number of heterogeneous members around $\boldsymbol{\mu }_k$.

A repulsive force $\boldsymbol{F}$ from each heterogeneous member $\boldsymbol{x}^j$ in the ball $\mathcal {B}(\boldsymbol{\mu }_k,\lambda \sigma )$ $:=\{\boldsymbol{x}:~\Vert \boldsymbol{x}-\boldsymbol{\mu }_k\Vert \le \lambda \sigma \}$, where $\lambda >1$ is a width covering factor, is given by

$$\begin{aligned} \boldsymbol{F} = \exp \left( -\alpha \Vert \boldsymbol{\mu }_k-\boldsymbol{x}^j\Vert \right) \frac{\boldsymbol{x}^j-\boldsymbol{\mu }_k}{\Vert \boldsymbol{x}^j-\boldsymbol{\mu }_k\Vert }, \end{aligned}$$

(5)

where $\alpha$ is the repulsive force control factor. The exponential scale factor term is used to control the variation of the center drift due to any heterogeneous members within the ball.

The center position is updated to move away from heterogeneous members as follows:

$$\begin{aligned} \boldsymbol{\mu }_k\leftarrow \boldsymbol{\mu }_k +\boldsymbol{F}. \end{aligned}$$

(6)

The preassigned value $\alpha >0$ should not be too small otherwise it loses the purpose of maximizing the discriminant function $\rho _i$. But a very small $\alpha$ may not reduce the number of heterogeneous members in the ball. A big center shift may also result in covering new heterogeneous members. Therefore, this choice of $\alpha$ is highly dependent on the dataset. In some cases, center drifts are not sufficient to reduce the number of heterogeneous members. We, therefore, fix the maximum number of iterations $\textsf {Epo}$ allowed for testing for center drifts.

We count the number $M_{\ne i}$ of heterogeneous samples $\boldsymbol{x}\in S\backslash S^i$ in the current ball $\mathcal {B}(\boldsymbol{\mu }_k,\lambda \sigma )$ by $\Vert \boldsymbol{x}-\boldsymbol{\mu }\Vert \le \lambda \sigma$. Define $M_i$ as the number of samples in $S^i$ in $\mathcal {B}(\boldsymbol{\mu }_k,\lambda \sigma )$. The center for each ball can be adjusted by the sum of the resultant forces:

$$\begin{aligned} \boldsymbol{\mu }_k\leftarrow \boldsymbol{\mu }_k + \frac{1}{M}\sum ^{M_{\ne i}}_{p=1}\exp \left( -\alpha \Vert \boldsymbol{\mu }_k-\boldsymbol{x}_p\Vert \right) \frac{\boldsymbol{x}_p-\boldsymbol{\mu }_k}{\Vert \boldsymbol{x}_p-\boldsymbol{\mu }_k\Vert }, \end{aligned}$$

(7)

where M is the preassigned value to average all the resultant forces.

After an iteration, check the number of heterogeneous members in the ball again. If the new number $M^\prime _{\ne i}$ of heterogeneous members in the ball is reduced, the iterative process continues, otherwise the center is fixed. Once the center is positioned, the algorithm readjusts the size of the ball to mostly cover only homogeneous members. An RBF center is then selected.

2.2 Finding the Widths for the Radial Basis Functions

If heterogeneous members exist in the ball (i.e., $M^\prime _{\ne i} >0$), we shrink the ball so that it almost covers the closest heterogeneous member $\boldsymbol{x}^j$ from $\boldsymbol{\mu }_k$ by the formula below. To avoid over-shrinking, $\beta >1$ acts as a relaxation factor and $\sigma _{\min }$ as the lower bound of the size.

$$\begin{aligned} \sigma _k \leftarrow {\left\{ \begin{array}{ll} \max \{\min \{\Vert \boldsymbol{\mu }_k-\boldsymbol{x}\Vert /\beta :~\boldsymbol{x}\in S\backslash S^i\},\sigma _{\min }\} &{}\text {if } M^\prime _{\ne i} > 0\\ \sigma &{}\text {if } M^\prime _{\ne i} = 0 \end{array}\right. }. \end{aligned}$$

(8)

This $\beta$ should be slightly smaller than $\lambda$ to avoid setting too large a value on $\lambda$. Suppose $\lambda /\beta$ is less than but close to 1. Then for any $\boldsymbol{x}^{\ne i}\in (S\backslash S^i)\,\cap \,\mathcal {B}(\boldsymbol{\mu }_k,\lambda \sigma )$,

$$\begin{aligned} \sigma _{\min }\le \sigma _k\le \min \{\Vert \boldsymbol{\mu }_k-\boldsymbol{x}\Vert /\beta :~\boldsymbol{x}\in S\backslash S^i\}\le \Vert \boldsymbol{\mu }_k-\boldsymbol{x}^{\ne i}\Vert /\beta \le (\lambda /\beta )\sigma \le \sigma . \end{aligned}$$

(9)

Since the last inequality is “slightly less than”, if $M_{\ne i}^\prime >0$, the updated circle is not too large when controlled by $\beta$.

2.3 Updating the Discriminant Function

To decide if a new center is needed, the discriminant function $\rho _i$ is updated to remove the influence of the centers found so far. The processes of shifting the center and resizing the RBF balls repeat if some updated potential is above the threshold $\delta$, i.e.,

$$\begin{aligned} \max \{\rho _i^{\text {new}}(\boldsymbol{x}^i_1),\cdots ,\rho _i^{\text {new}}(\boldsymbol{x}_{N_i})\} > \delta , \end{aligned}$$

(10)

where

$$\begin{aligned} \rho _i^{\text {new}}(\boldsymbol{x})=\rho _i(\boldsymbol{x})-\rho _i(\boldsymbol{\mu }_k) \exp \left( -\frac{1}{2 \sigma _l^2}\Vert \boldsymbol{x}-\boldsymbol{\mu }_k\Vert \right) . \end{aligned}$$

(11)

If all of the new $\rho _i^{new}$ are less than $\delta$, the remaining data are not dense enough to form an effective cluster center. It is important to note that since all the terms in the discriminant function $\rho _i$ are positive, this $\delta$ is dependent on the size $N_i$ and the scaling parameter T, as shown in Fig. 1, and thus can only be determined on an empirical basis. For the overall effect of $\delta$, see Figs. (2a)–(2d). An alternative method is to normalize a new discriminant function $\widetilde{\rho }_i:= \frac{1}{N_i}\sum _k \gamma (\cdot ,\boldsymbol{x}^i_k)$. The T in the proof of Theorem 1 is then dependent on $N_i$. Future studies can then be done on the suggested selection of $\delta$ for every class i.

The whole center selection process is summarised in Algorithm 1.

3 Moving from the RBFN to the BPN

The algorithm follows the original purpose of imposing the RBF layer, which captures the relation of the classes with the points of high relative density. However, it is natural to question the relation of such a doctrine with the ultimate purpose of reducing classification error.

In MLP, a gradient-search algorithm is applied to iteratively update the weights using backpropagation in order to attain a local minimum of the error function. This simple idea comes from the fact that the infimum of a normed space is not bigger than the infimum of a subspace. The motivation for our extension comes from questioning whether extending the parameter space in the gradient-search algorithm would improve the classification. By combining the hybrid structure, we apply backpropagation to both MLP and RBF layers with the initial guess of RBF centers selected by the incremental algorithm above.

Fig. 2.

This shows an example of 10 homogeneous data points (blue). The black horizontal line marks the threshold $\delta =1$. The blue curve is the value of $\rho (x)$ with $T=1$. We pick the data point with the highest value of $\rho$ in Figure (2a) and mark it as our first cluster point $\boldsymbol{\mu }_1$ (red). (2b) The function $\rho _1$ is updated, penalizing the region around $\boldsymbol{\mu }_1$. Since some points are above the threshold, the selection continues. (2c) $\boldsymbol{\mu }_2$ is found and marked in red. Note that this showcases the importance of $\delta$ since the data point almost does not pass the test. (2d) $\boldsymbol{\mu }_3$ is found. The graph lies below the threshold and the selection process terminates. (Color figure online)

The main concern regarding this approach is the problem of hitting local minima. Here, we mainly focus on the extent to which the classifier gets stuck at the local minima after the extension of the parameter space. Therefore, we use the common stochastic gradient descent method.

Let K be the number of RBF centers. Define the output of RBF at each center $\boldsymbol{\mu }_k$ by

$$\begin{aligned} \phi _k(\boldsymbol{x};\boldsymbol{\mu }_k,\sigma _k) = \exp \left( -\frac{1}{2\sigma _k^2}\Vert \boldsymbol{x}-\boldsymbol{\mu }_k\Vert ^2\right) \text { for } k=1,2,\cdots ,K. \end{aligned}$$

(12)

The output of $\varPhi (\boldsymbol{x}) := [\phi _1(\boldsymbol{x};\boldsymbol{\mu }_1,\sigma _1),\cdots ,\phi _K(\boldsymbol{x};\boldsymbol{\mu }_K,\sigma _K)]$ is nonnegative. To facilitate computational speed, we polarise them by a mapping $\boldsymbol{x}\mapsto 2\boldsymbol{x}-1$, which becomes the input of a feedforward network with the activation function $\boldsymbol{x}\mapsto a \tanh {(b \boldsymbol{x})}$, where a and b are constants. They are updated using backpropagation, passing the error term in the output to each hidden neuron.

In Algorithm 2, $\textbf{W}= [W^{(1)},\cdots , W^{(L)}]$ is a tensor with each $W^{(l)}$ being the weight matrix between the $(l-1)$- and l-layers, where L is the number of BP hidden layers (including the output layer). $\boldsymbol{\delta }^{(l)}:=[\delta ^{(l)}_1,\cdots ,\delta ^{(l)}_{n_l}]$ is a vector recording the error passed to the $n_l$ hidden neurons of the l-th layer, $l=1,\cdots ,L$. $\boldsymbol{\delta }^{(0)}$ is the error vector for the RBF units. The error term of the first BP layer $\boldsymbol{\delta }^{(1)}$ can further be passed to the RBF layer, since $\boldsymbol{x}\mapsto \varPhi (\boldsymbol{x})$ is smooth with respect to $\boldsymbol{\mu }$ and $\boldsymbol{\sigma }$ (for strictly positive $\boldsymbol{\sigma }$). Suppose $e = \sqrt{\sum _{j=1}^{H}(y_j - \widetilde{y}^{(L)}_j)^2}$ is the error of our predicted output ${\widetilde{\boldsymbol{y}}}^{(L)}$ of the L-th layer. By the Chain rule, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \frac{\partial e}{\partial \boldsymbol{\mu }_k} &{}= \frac{\partial e}{ \partial {\widetilde{\boldsymbol{y}}}^{(0)}_k}\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}_k}{\partial \boldsymbol{\mu }_k} = \delta ^{(0)}_k \frac{\partial \widetilde{\boldsymbol{y}}^{(0)}_k}{\partial \boldsymbol{\mu }_k} =\delta ^{(0)}_k \frac{\partial }{\partial \boldsymbol{\mu }_k}\phi _k(\boldsymbol{x};\boldsymbol{\mu }_k,\sigma _k)\\ &{}=\delta ^{(0)}_k\exp \left( \frac{-\Vert \boldsymbol{x}-\boldsymbol{\mu }_k\Vert ^2}{2\sigma _k^2}\right) \frac{1}{\sigma _k^2} (\boldsymbol{x}-\boldsymbol{\mu }_k)\\ \frac{\partial e}{\partial \sigma _k} &{}= \frac{\partial e}{\partial \widetilde{\boldsymbol{y}}^{(0)}_k}\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}_k}{\partial \sigma _k} = \delta ^{(0)}_k \frac{\partial \widetilde{\boldsymbol{y}}^{(0)}_k}{\partial \sigma _k}=\delta ^{(0)}_k \frac{\partial }{\partial \sigma _k}\phi _k(\boldsymbol{x};\boldsymbol{\mu }_k,\sigma _k)\\ &{}=\delta ^{(0)}_k \exp \left( \frac{-\Vert \boldsymbol{x}-\boldsymbol{\mu }_k\Vert ^2}{2\sigma _k^2}\right) \frac{1}{\sigma ^3_k}\Vert \boldsymbol{x}-\boldsymbol{\mu }_k\Vert ^2 \end{aligned} \end{array}\right. }. \end{aligned}$$

(13)

Then, the update rules of $\boldsymbol{\mu }_k$ and $\sigma _k$ follow from SGD with learning rate $\eta$:

$$\begin{aligned} \boldsymbol{\mu }_k\leftarrow \boldsymbol{\mu }_k + 2\eta \delta ^{(0)}_k\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \boldsymbol{\mu }_k}(\boldsymbol{x}) \quad \text {and} \quad \sigma _k \leftarrow \sigma _k + 2\eta \delta ^{(0)}_k\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \sigma _k}(\boldsymbol{x}). \end{aligned}$$

(14)

Let $\mathbf {\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \boldsymbol{\mu }}} = \left[ \frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \boldsymbol{\mu }_1},\cdots ,\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \boldsymbol{\mu }_K} \right]$ and $\mathbf {\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \boldsymbol{\sigma }}} = \left[ \frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \sigma _1},\cdots ,\frac{\partial \widetilde{\boldsymbol{y}}^{(0)}}{\partial \sigma _K} \right]$. The investigated algorithm is shown as Algorithm 3, where $diag(\boldsymbol{x})$ is the diagonal matrix with the diagonal element being $\boldsymbol{x}$.

4 Numerical Results

As a comparative study, some artificial and real-life datasets were used to test the effectiveness of our implementation strategies and our homemade MATLAB codes.

4.1 Comparison of MLP and mHybrid Classifiers on Different Datasets

We used 8 datasets with classes as shown in Table 1 and all the parameters used for the mHybrid classifier are in Table 2. We set Tolerance $= 10^{-6}$. Figure 3 shows the patterns for Double Moon with 2 classes, Concentric Circles (CC), Concentric Circles with 2 extra layers (CC2) and Double Moon with 6 classes (DM6) (Each crescent is split into three sections). For each dataset, we first obtained the theoretical value $\max \{ (N_j-1)/D\}$ (the last column in Table 2), then we adjusted the T value descendingly to obtain the best result. Table 1 shows the results of the MLP and mHybrid classifiers. To assess their performance, accuracy, precision, recall, and F-score were used. Table 1 shows that the mHybrid classifier outperformed the MLP classifier.

We further examined the pendigit dataset with 10 classes. Different network architectures of MLP and mHybrid classifiers are shown in Fig. 4, where the first label refers to the number of hidden neurons of the two layers for MLP, while the second label refers to the number of RBF centers and hidden neurons used in the mHybrid classifier. According to the results, the accuracy of the mHybrid classifier is significantly better than that of the MLP classifier when the numbers of RBF centers and hidden neurons increase.

Table 1. Performance comparison of MLP and mHybrid classifiers on different datasets.

Table 2. Parameters of the mHybrid classifier used on different datasets.

Fig. 3.

(3a) Double Moon with 2 classes. (3b) Concentric Circles (CC). (3c) Concentric Circles with 2 extra layers (CC2). (3d) Double Moon with 6 classes (DM6).

Fig. 4.

Comparison of the different network architectures of two classifiers using the pendigit dataset. For MLP, the two numbers are the numbers of hidden neurons of the two hidden layers. For mHybrid, the first number is the number of RBF units and the second is the BP units.

4.2 Comparison of Hybrid and mHybrid Classifiers Using DM6 and No Structure Datasets

In what follows, we numerically analyze the effect of the center and the width parameter of the RBFs, which are iteratively updated by the SGD algorithm, referred to as Algorithm 3. Using the DM6 dataset, we observed that the mHybrid classifier outperformed the MLP and Hybrid classifiers as shown in Table 3.

Table 3. Comparison of three classifiers using DM6.

Fig. 5.

Distribution of No Structure datasets.

Fig. 6.

Comparison of two classifiers on different No Structure datasets.

Figure 5 shows the pattern of No Structure datasets, where data is labeled using agglomerative clustering algorithms with different linkages (‘Ward’, ‘Average’, and ‘Complete’) with different numbers of classes. To be more precise, ‘Ward’ minimizes the variance of each cluster, ‘Average’ uses the average of the distances of each sample pair from two clusters, and ‘Complete’ uses the maximum distances between all samples of the clusters. The datasets are tested on different initial $\sigma$ values with identical configurations. Figure 6 shows that the mHybrid classifier outperformed the hybrid classifier. In addition to that, the smaller the $\sigma$ value, the more RBF centers generated, and thus accuracy increased.

5 Conclusions

The performance of the modified hybrid RBF-BP classifier has been tested using artificial and real-life datasets. Based on the numerical results, we concluded that when using the modified classifier, including the lines for updating the last step yielded better accuracy than not including them. Although it performs better than the MLP classifier, higher computational efficiency will be required if more testing is to be done. In the future, tests may be done to fine-tune the parameters to find a set of all optimal parameters for the modified hybrid classifier. Moreover, the efficiency of combining different classifiers with the proposed classifier requires more work.