Keywords

1 Introduction

In the contemporary economy, the construction industry faces a plethora of challenges, notwithstanding its exciting growth phase. To optimize profitability, construction corporations must enhance their technical and managerial competencies. Project management is a pivotal aspect in balancing progress, cost, quality, and resources to achieve organizational objectives, which have complex interdependencies [3]. Depending on the organization's perspective, goals may include minimizing costs and time or optimizing quality control. However, to reduce project duration, the organization must relinquish human resources, raw materials, machinery, and equipment, impacting overall costs and project quality, which can be positive or negative, depending on the activity's nature [11]. Hence, project managers must allocate resources efficiently to accomplish time-cost-resource utilization optimization goals. Nonetheless, traditional methodologies, such as the Metra potential method (MPM), Critical path method (CPM), and Program evaluation and review techniques (PERT), lack realism, heavily relying on assumptions and estimates, thus hindering accurate project outcome predictions. To surmount these limitations, advanced approaches to resource allocation are imperative, involving optimal resource utilization while minimizing waste.

Time-cost-resource optimization (TCRO) is a commonly used approach that categorizes optimization methods into three groups: heuristic-based, linear program-based, and meta-heuristic-based. However, each methodology has its advantages and disadvantages. While the advantages of a particular approach may make it the most suitable option, the disadvantages include an imbalance between time and cost (TCT) for large-scale projects [2]. On the other hand, previous studies have successfully applied fuzzy logic to introduce uncertainty into the time-cost optimization model [1]. However, there is still a lack of research that uses fuzzy logic to optimize project resources and a need for a time-cost trade-off model that considers collision activities’ impact on quality costs. To address research gaps, this study aims to develop an optimal project resource balance model that considers quality and inherent uncertainty using fuzzy logic and MOSGO combined with a multi-criteria decision-making method. By taking this approach, the proposed model can account for uncertainties related to external factors that impact the project's resource allocation and quality.

2 Proposal Model for Uncertain Resource Tradeoff

This proposed study aims at building an optimal model of project resource balance with consideration of the uncertainty of input variables by applying fuzzy algorithm logic and multi-objective SGO to generalized construction projects [6]. Figure 1 depicts a schematic diagram of the entire proposed structural model incorporating MOSGO, fuzzy logic, and MCDM which were implemented in MATLAB software for the TCQT concern.

Fig. 1.
figure 1

MOSGO flowchart for the TCQT problem

Full size image

2.1 Initialization

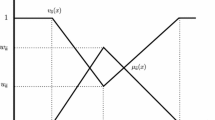
The model inputs comprise relationships and duration among tasks, the cost of each activity, and the corresponding quality. In this study, fuzzy numbers in time comprising the system have been converted to three numbers, which reflect the optimistic, most likely, and pessimistic conditions to demonstrate the uncertainty. When the execution time is measured by ambiguous numbers or uncertain lingual definitions, the solitary utility functions and the synthetic utility functions will include fuzzy mathematical operations and thus generate outcome fuzzy utility values [8, 12]. For the moment in (Fig. 2), the time is described by triangular fuzzy numbers, such as T = (153 154, 155).

Fig. 2.
figure 2

Centroid method of defuzzification

Full size image

Following, the operator needs to provide the metrics for the MOSGO issue. MOSGO utilizes a typical arbitrary technique to create the first NP individual of the population with xij ∈ [0, 1] as defined in Eq. (1).

$${X}_{i,j}^{G=0}=L{B}_{i}+{x}_{i,j}*\left({UB}_{i}-L{B}_{i}\right) ;i=\overline{1,NP}; j=\overline{1,D}$$
(1)

where LB and UB are the lower and upper bounds of decision variables. NP is the number of member in a social group; D is the decision variable number.

2.2 Decision Variables

Because the tasks in the project have much more than one realistic choice, one option would be selected randomly to be executed for each activity. As a result, we have a potential solution to the TCQT issue in construction projects depicted by the vector D.

$$X=[{X}_{i,1}, {X}_{I,2},\dots , {X}_{i,j},.., {X}_{i,D}]$$
(2)

Xi,j denotes an integer value in the intermission from 1 to Mj where Mj is the total feasible avenue for implementing activity j.

To optimize project schedule and expenses, evaluate Gantt chart works to shorten construction and select tasks to accelerate the schedule based on specific time and cost. Evaluating time for each task after identifying all project activities determines the total period necessary for project completion and specific activities [10].

$${T}_{p}=min(\underset{i=1,.., M}{\mathit{Max}}\left(F{T}_{i}\right))=min(\underset{i=1,.., M}{\mathit{Max}}\left(S{T}_{i}+{D}_{i}\right))$$
(3)

where STi, FTi are the beginning and end times of activity (i). The duration of each activity i is indicated by Di.

Transforming the quality of construction activities into a functional value of the use of various resources is challenging due to the hard to measure the impact of these performance measures on the quality of the activity. The defined quality values are inferred from performance-based models that relate the long-term performance of the finished product of each operation with its quality values [7].

$$Q= \sum_{i=1}^{N}{w}_{i}{Q}_{i}$$
(4)

where N is the number of activities and wi is the weight for activity i.

Total project costs include direct costs and indirect costs to carry out all completion of the project. Direct costs for the project include expenses for materials, human labor, equipment, and for the work of subcontractors. Direct costs are directly attributable to the object, and it is financially feasible to do so. Indirect costs are not the direct cost component of performing construction work, but nevertheless, without this cost component, there would have been no direct costs. Indirect costs are an essential component of total project costs, and they include expenses such as rent, utilities, insurance, administrative salaries, and other overhead costs that are not directly attributable to the project's physical construction work. These costs are necessary to support the project's operations and ensure its successful completion [9].

$$C= \sum_{i \in A} d{c}_{i}^{(k)}{x}_{i}^{(k)}+T \times {c}_{i}^{(k)}$$
(5)

2.3 Improving Phase

In this stage, the new solution Xi of individual is generated based on the best individual Gbest, taken directly from the set with the best individuals (first rank) of the population. The technique of quick filtration of non-outstanding values will sort out the ranks and the process of the improvement phase is revised by the formula:

$$ X_{i,j}^{new} = \frac{{\sum {F\left( {X_{i,j} } \right)} }}{{\sum {F\left( {G^{best} } \right)} }}X_{i,j}^{old} + \beta \left( {G^{best} - X_{i,j}^{old} } \right);j = 1,2, \ldots ,D $$
(6)

The optimization pathway just advances when the new individuals are better than the old individuals so \({X}_{i.j}^{new}\) is accepted if it gives better compatibility than \({X}_{i.j}^{old}\).

2.4 Acquiring Phase

During the acquiring phase, an individual in a social group interacts with the best candidate \({G}_{best}^{i}\) of that group and may also seemingly at random contact anyone else in the group to gain new knowledge. An individual acquires new understanding if he comes in direct contact with anyone who has more knowledge than himself. The one with the best knowledge (here called \({G}_{best}^{i}\)) has the greatest potential impact above others. An individual will also acquire fresh information from others when they possess more knowledge than himself [9].

$$Xi,jnew = \left\{ \begin{gathered} X_{{i,j}} ^{{old}} + \beta _{1} \left( {X_{{i,j}} - X_{{k,j}} } \right) + \beta _{2} \left( {G_{i} ^{{best}} - X_{{k,j}} } \right),f\left( {X_{i} } \right) < f\left( {X_{k} } \right) \hfill \\ X_{{i,:}} ^{{old}} + \beta 1\left( {X_{{k,:}} - X_{{i,:}} } \right) + \beta _{2} \left( {G_{i} ^{{best}} - X_{{i,j}} } \right),f\left( {X_{i} } \right) \ge f\left( {X_{k} } \right) \hfill \\ \end{gathered} \right.$$
(7)

where Xk is a random person in the current group (i ≠ k); β1 and β2 are two independent random values.

2.5 The Population Solution Selection

Throughout the optimization process, the population size remains constant at NP. To identify the NP best outcomes from the cumulative population for the next generation, this research utilized a fast non-dominated sorting technique and crowding entropy method. Non-dominated sorting is the operation of arranging the individuals according to their objective function values. Initially, the fast non-dominated sorting method is used to separate the population into non-dominant subsets {F1, …, Fn} the population numbers are considered from F1 to Fk, respectively, with Fk is assumed to be the last selected subset. Typically, the size of subsets {F1,…, Fk} is greater than NP.

Multiple-criteria decision-making (MCDM) is used to evaluate and compare options when there are multiple criteria to consider in TCQT problem. Multi-objective optimization problems involve conflicting objectives and result in a Pareto set—a set of solutions that aren't dominated by any other solution in terms of all objectives. ER method is commonly used to rank the Pareto set of non-dominated solutions in terms of project performance [4]. This process involves several steps, as described by Monghasemi et al. [5]: Step 1: Evaluate the non-dominated set of solutions to select each solution and determine the values of three attributes time, cost, and quality; Step 2: Compute the normalized weights for each attribute by Using the Shannon entropy approach; Step 3: Determine the normalized weights ωj for each basic attribute (objective); Step 4: Combine the degree of belief; Step 5: Determine the utility score of the selected solution.

2.6 Stopping Conditions

The optimization process cycle is discontinued when the halting requirements are satisfied, as indicated by the system administrator. This study utilizes the highest limit of loops to be run as the halting condition. After the methodology halts, a set of non-superior solutions (called Pareto) is generated. The meaning of the Pareto solutions, representing the average quality of the non-superior solutions, can then be calculated, and used to evaluate the performance of the optimization process (Table 1).

Table 1. Data of case study 1
Full size table

3 Case Study

The utilization and capability of the proposed model for solving the TCQT issue are evidenced by using two real case studies. The first case is a road and bridge engineering project derived from previous research intended to illustrate the application of solving the trade-off TCQ trade-off issue [10]. The above project aims to upgrade the existing two-lane highway into a four-lane highway with a length of 100 m with a total of 29 activities for a brief application in this study. The second case—a typical case in Vietnam is Spun pile of package Construction of the Test Pile and Mass Pile of “Manufacturing Facility—The Sai Gon Hi-Tech (SHTP) collected from Central Construction Joint Stock Company. The second case project consists of 46 activities with 4400 nos D600 and 360 nos D300 units on a total area of 2 zones (GFA 233000 m2). The characteristics and types of data are quantifiable and precisely defined. Tables 2 and 3 illustrate two project data, including activity logical precedence relationships, activity durations, costs, and quantities for each execution option. These cases highlight the complexities involved in large-scale construction projects and underscore the need for careful planning, precise execution, and effective project management to ensure successful project completion within the given constraints.

Table 2. Data of case study 2
Full size table

The MOSGO algorithm operates without any user-defined inputs except for two control variables, established using a trial-and-error technique. Case study 1 used a population size of 100 and ran for 50 generations, while case study 2 used a population size of 300 and ran for 100 generations. Tables 3 show the optimal solutions for case studies 1 and 2, respectively, while Fig. 3a, b present a 3D view of all the optimal solutions, highlighting trade-offs that must be considered. The model employed in case study 1 considers project quality and uncertainties related to project duration, making it superior to earlier methods of analysis. Case study 2 showcases the need to consider multiple objectives and trade-offs when making decisions. S2 offers the shortest duration, S4 is the most cost-effective option, S6 prioritizes quality, and S8 provides a balanced solution.

Table 3. Optimum solutions of both cases
Full size table
Fig. 3.
figure 3

a, b Time-cost-quality of the optimum solutions in case study 1 and case study 2

Full size image

The data shows that project duration and total project cost have an inverse relationship in both case studies. This means that as the project duration decreases, the total project cost tends to increase, and vice versa. Project duration also has an impact on project quality, as excessively short or long durations can have negative effects on quality outcomes. Higher project costs are often associated with lower-quality results, which is closely tied to the correlation between project duration and cost. Proceeding to set alpha 0.5 in a fuzzy uncertainty problem means that you are assuming equal membership and non-membership to the fuzzy set. This implies that all values in the problem are given equal consideration in terms of their membership of the fuzzy set. This could be appropriate in some cases where there is no strong preference or bias toward any particular value. Notably, when incorporating uncertainty (at a probability of 0.5) into the solution approach, the resulting findings can be intriguing and informative.

4 Conclusion

This study presented a new hybrid multi-objective algorithm that combines social group optimization, fuzzy logic, and multiple-criteria decision-making methods to solve the optimization problem requiring resources along with quality control in construction with the integration of uncertainty about the time that occurs in the actual large-scale project. The MOSGO algorithm has been updated to an unrestricted version that promotes harmony between development and optimization procedures in comparison to the existing version. The first case study's operational model demonstrates remarkable stability and yields superior outcomes compared to previous studies, particularly when optimization incorporates a novel quality objective that had not been addressed previously. In the second case study, the model's proficiency in problem-solving for realistic large-scale projects is demonstrated, underscoring its potential to effectively manage complex and expansive projects. The practical implementation of the hybrid algorithm in actual construction scenarios further substantiates the model's efficacy in significantly enhancing project outcomes.

The above-proposed MOSGO-TCQT model is adaptable, easily updatable, and can be digitized and incorporated into computer programming. Its versatility and effectiveness make it a promising tool for addressing complex and expansive problems in the primary objective of this research is to address the complex interdependence among the three critical factors of project management: time, cost, and quality.