Keywords

1 Introduction

Supply chain management aims to integrate the main business processes between each element in the chain, taking into account customer satisfaction, cycle time, and costs.

The main purpose of supply chain management is to increase customer satisfaction, reduce cycle time, and reduce inventory and operating costs. To achieve these goals, system optimization and control are required, which are primarily based on modeling the system. Various alternative methods have been proposed for modeling the supply chain [1]. Economic game-theoretical model [2], deterministic dynamic model [3,4,5,6,7,8,9,10], stochastic model [11], nonlinear dynamic model [12,13,14,15], simulation model [16, 17] can be given as examples. In the literature, the decision variables of supply chain dynamic models had been taken as “demand quantity and production quantity” [14], “stock, price and demand” [17], or “demand, stock, and production quantity” [12, 13, 15, 18]. These system dynamics, which are considered in supply chain modeling, vary according to the product type, the problem, and the size of the chain.

In this study, perishable products were taken as the focus. Perishable products lose their quality and value after a certain time period, even when used correctly throughout the supply chain. Therefore, especially food products often require specialized, more advanced transportation and storage solutions [19,20,21]. For products that are defined as perishable products, prescription drugs, pharmaceuticals (vitamins and cosmetics), chemicals (household cleaning products), batteries, photographic films, frozen foods, fresh products, dairy products, fruit and vegetables, cut flowers, blood cells can be counted. Special handling, storage techniques, and equipment are required to prevent damage, deterioration, and contamination. This includes handling, washing, rinsing, grading, storage, packaging, temperature control, and daily or hourly shelf life quality testing, and also incurs a separate cost for all these activities. Disrupting the integrity of the cold chain can destroy the entire season’s gains. For this reason, careful supply chain management of perishable products is important in terms of customer satisfaction, costs, and operating profit. Önal et al. [22] developed a mixed-integer nonlinear programming model to maximize retailer profit. Gerbecks [23] quantitatively modeled an e-retailer’s perishable supply chain, taking into account lost sales, expenditure, and operating costs. In another study, a traditional three-level supply chain consisting of the manufacturer, retailer, and customer is modeled to manage orders and stocks of perishable products [24]. In the literature, it is seen that the optimization of the activities (such as pricing, and stock) in the supply chain of perishable products has been studied. But, any study has not been found in which demand, production quantity, and stock variables are considered together, and the supply chain of perishable products is modeled with the differential equation system. In the light of this information, the supply chain of citrus products, which are considered perishable products, is modeled with a differential equation system with three decision variables [18]. The dynamic behavior of this model, which is revealed by phase portraits and bifurcation graphs, can be explained by chaos theory.

In this study, synchronization which will allow two factories connected to an enterprise to work synchronously with each other is also emphasized. The two chaotic systems discussed are synchronized using the active control technique and the system outputs are shown with time-series graphics, where the system outputs take the same values with zero error after a certain period of time.

This study is organized as follows: In Sect. 1, a new supply chain model proposed for perishable products is introduced with its notations. In Sect. 2, the system is synchronized using the active control technique. Finally, the differences between the developed new model with other models are presented in the conclusion section.

2 A Novel Supply Chain Model for Perishable Products

This section describes the main characteristics and assumptions of the model and then examines its dynamic properties using bifurcation diagram, Lyapunov exponents, and phase portraits.

2.1 Model Development and Assumptions

Food supply chains are global networks encompassing production, processing, distribution, and even sieving [25], and supply chains of perishable products are more complex and unstable than others [26]. In addition, each link of the supply chain manages its inventory and the lack of communication between each other causes the supplier’s deterioration and demand information to be delayed, thus not meeting consumer needs quickly and accurately [26].

In this study, the focus is on the supply chain model of perishable products, based on the assumption that system dynamics vary depending on the relevant processes related to each product type, such as food, oil, and consumer products [13].

The notations used in the model are given in Table 1.

Table 1. Notations used to describe the model
Full size table

x, y, and z represent state variables; m, n, and d represent parameters.

How the equations that make up the model are obtained are given in detail below, respectively. The demand for the t + 1 period depends on our production amount in the previous period and the customer satisfaction rate multiplied.

$${x}_{t+1}=\left({z}_{t}+{y}_{t}\right)*s$$
(1)

The customer satisfaction rate depends on the rate at which the customer’s demand is met by the company. In other words, customer satisfaction is achieved depending on how much of the company’s production capacity meet the demand. Even if all of the customer’s demands are met, meeting the demands of the customers in the required quality will also affect customer satisfaction. Accordingly, customer satisfaction was taken as the combined effect of demand fulfillment rate and customer satisfaction.

$$s=\left(\frac{{z}_{t}+{y}_{t}}{{x}_{t}}\right)*d$$
(2)

According to Eq. (1) and (2), Eq. (1) will take the following form:

$${x}_{t+1}=\left({z}_{t}+{y}_{t}\right)*s=\left({z}_{t}+{y}_{t}\right)*\left(\frac{{z}_{t}+{y}_{t}}{{x}_{t}}\right)*d$$
(3)

In many studies on inventory management in the literature, it is assumed that products have unlimited lifetimes and that the demand is independent of product age. However, although this assumption is not valid for short-lived, perishable products, it is seen that the demand is directly related to the age of the product [27]. Especially in the production and processing of fresh vegetables and fruits, there may be deterioration in the product during the process steps such as collecting, transmitting, processing or keeping the product. These deterioration rates are especially important for the inventory level.

In Eq. (4), the current inventory level is obtained by subtracting the amount of demand from the amount of production and the amount of deterioration.

$${y}_{t+1}={z}_{t}+{y}_{t}-{x}_{t}-{k}_{t}$$
(4)

The amount of deterioration (k) is equal to the sum of the amount of deterioration in production and the amount of deterioration in stock, as given below. The rate of deterioration in different perishable foods varies considerably. For example, canned food gradually declines in quality, while fresh fish and delicatessen products can deteriorate within a few hours. Therefore, the rate of deterioration can greatly affect the replacement policy and pricing strategy [28].

$${k}_{t}=m.{y}_{t}+n.{z}_{t}$$
(5)

According to Eq. (4) and (5), the difference equation giving the inventory level is:

$${y}_{t+1}=(1-n){z}_{t}+{\left(1-m\right)y}_{t}-{x}_{t}$$
(6)

The production amount is obtained from the difference between the demand level and the stock amount.

$${z}_{t+1}={x}_{t+1}-{y}_{t+1} +m*{y}_{t}$$
(7)

The supply chain system consisting of the continuous form of the difference equations that determine the demand, stock, and production amount explained in detail above, is given by Eq. (8).

$$\dot{x}=-x+\left(z+y\right)* \left[\left(\frac{z+y}{x}\right)*d\right]$$
$$\dot{y}=-x -m*y +\left(1-n\right)*z$$
(8)
$$\dot{z}=x-\left(1-m\right)*y-z$$

2.2 Dynamical Properties of the Proposed Model

The novel perishable product supply chain model given above was simulated in Matlab R2021 with the initial values given in Table 2 and their dynamical behavior is summarized in Table 3.

Table 2. Initial values of the new model variables
Full size table
Table 3. The dynamical behaviours summaries of the new suggested novel perishable product supply chain system according to different parameters
Full size table

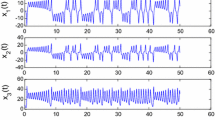
In the simulation results; the phase portraits in Fig. 1 show that the system exhibits a chaotic state when it moves away from the chaotic structure as the customer satisfaction value increases.

Fig. 1.
figure 1

3D phase portraits of the new supply chain model for (a) d = 0.302; (b) d = 0.323; (c) d = 0.33202

Full size image
Fig. 2.
figure 2

(a)The bifurcation graph of the stock disruption rate parameter, m, in the range [−2;0.5] for d = 0.302, (b) The bifurcation graph of the stock disruption rate parameter, m, in the range [−0.5;2] for d = 0.33202.

Full size image

The bifurcation graph in Fig. 2 a gives the change in the equilibrium points calculated by using 0.01 step number in the [−2;0.5] interval of parameter m for d = 0.302. In this case, it is clearly seen that the m parameter, which expresses the stock deterioration rate to which the system is sensitive, will put the system in a chaotic state as of −1.05. At the same time, in Fig. 2a, bifurcation diagram gives the change in the equilibrium points calculated by using 0.01 step number in the [−0.5;2] interval of parameter m for d = 0.33202. That is, for values of stock deterioration ratio greater than 1.05, it will put the system in order.

Fig. 3.
figure 3

Graph of Lyapunov Exponents in the range of [−5:5] of m stock decay rate parameter

Full size image

The path that a dynamic model follows when its behavior is studied in phase space is called a trajectory. The Lyapunov exponent is used as a measure of how far an orbit is away from the nearest orbit. If the Lyapunov exponent is positive, it is understood that the orbits are very close to each other at first and get further and further apart. As this positive value increases quantitatively, the rate of divergence of the orbits also increases. The negative value of the Lyapunov exponent indicates that the distant orbits approach each other over time. The increase in exponential value indicates the degree of complexity, that is, unpredictability. A system with at least one positive Lyapunov exponent in three-dimensional phase space is said to exhibit chaotic behavior [29]. As seen in Fig. 3, it is seen that a Lyapunov exponent is positive with λ1 = 4,9084, and it proves that the new supply chain system is in a chaotic structure with the given initial conditions and parameters values. Because a system with at least one positive Lyapunov exponent is chaotic [30, 31].

3 Synchronization of the New Chaotic Supply Chain Model with Active Control Method

In this study, two chaotic systems discussed are synchronized using active control. According to the active control technique, the manager and implementer systems are introduced below:

Manager System

$$\dot{{x}_{1}}=-{x}_{1}+\left({z}_{1}+{y}_{1}\right)* \left[\left(\frac{{z}_{1}+{y}_{1}}{{x}_{1}}\right)*\mathrm{0,302}\right]$$
$$\dot{{y}_{1}}=-{x}_{1}+\mathrm{1,04}*{y}_{1} +\mathrm{11,4005}*{z}_{1}$$
(9)
$$\dot{{z}_{1}}={x}_{1}-\mathrm{2,04}*{y}_{1}-{z}_{1}$$

Implementer System

$$\dot{{x}_{2}}=-{x}_{2}+\left({z}_{2}+{y}_{2}\right)* \left[\left(\frac{{z}_{2}+{y}_{2}}{{x}_{2}}\right)*\mathrm{0,302}\right]+{u}_{1}$$
$$\dot{{y}_{2}}=-{x}_{2}+\mathrm{2,04}*{y}_{2} +\mathrm{11,4005}*{z}_{2}+{u}_{2}$$
(10)
$$\dot{{z}_{2}}={x}_{2}-\mathrm{2,04}*{y}_{2}-{z}_{2}+{u}_{3}$$

\({u}_{1}\), \({u}_{2}\), \({u}_{3}\) are active control functions in the implementer system. The primary purpose of control signals is to enable the implementing system to follow the master system necessary to achieve synchronization.

For state variables, the error is defined as follows:

$${e}_{1}={x}_{2}-{x}_{1}$$
$${e}_{2}={y}_{2}-{\mathrm{y}}_{1}$$
(11)
$${e}_{3}={z}_{2}-{z}_{1}$$

Following active control design procedures, fault dynamics are obtained using manager and implementer system equations and fault definitions.

$$\dot{{e}_{1}}\text{=}-{e}_{1}+\left({e}_{3}+{e}_{2}\right)* \left[\left(\frac{{e}_{3}+{e}_{2}}{{e}_{1}}\right)*\mathrm{0,302}\right]+{u}_{1}$$
$$\dot{{e}_{2}}\text{=}-{e}_{1}+\mathrm{2,04}*{e}_{2} +\mathrm{11,4005}*{e}_{3}+{u}_{2}$$
(12)
$$\dot{{e}_{3}}= \text{ } {e}_{1}-\mathrm{2,04}*{e}_{2}-{e}_{3}+{u}_{3}$$

According to the fault dynamics, the control functions are redefined as follows:

$${u}_{1}\text{=}{-\left(\left({e}_{3}+{e}_{2}\right)* \left[\left(\frac{{e}_{3}+{e}_{2}}{{e}_{1}}\right)*\mathrm{0,302}\right]\right)+v}_{1}$$
$${u}_{2}= \text{ } {v}_{2}$$
(13)
$${u}_{3}= \text{ } {v}_{3}$$

So the error dynamics Eq. (12) becomes:

$$\dot{{e}_{1}}\text{= -}{e}_{1}\text{+}\,{v}_{1}$$
$$\dot{{e}_{2}}\text{=}-{e}_{1}+\mathrm{2,04}*{e}_{2} +\mathrm{11,4005}*z \,\text{+}\,{v}_{2}$$
(14)
$$\dot{{e}_{3}}\text{=}{e}_{1}-\mathrm{2,04}*{e}_{2}-{e}_{3}\text{+}\,{v}_{3}$$

In the active control method, a fixed matrix A is chosen to control the error dynamics (14).

$$\left[\begin{array}{c}{v}_{1}\\ {v}_{2}\\ {v}_{3}\end{array}\right]=A*\left[\begin{array}{c}{e}_{1}\\ {e}_{2}\\ {e}_{3}\end{array}\right]$$
(15)

There are several options for obtaining controller coefficients Aijs to obtain a stable closed-loop system. Here, the following matrix is processed that meets the Routh-Hurwitz criteria calculated for the stability of the synchronous state:

$$A=\left[\begin{array}{ccc}0& 0& 0\\ 1& -\mathrm{3,04}& -\mathrm{11,4005}\\ -1& \mathrm{2,04}& 0\end{array}\right]$$
(16)

Provided that the eigenvalues (λ1, λ2, λ3) are negative, (λ1, λ2, λ3) = (−1, − 1, − 1) is chosen for ease of calculation.

The error dynamical equations and control functions are given below:

$$\dot{{e}_{1}}\text{= -}{e}_{1}$$
$$\dot{{e}_{2}}\text{= -}{e}_{2}$$
(17)
$$\dot{{\mathrm{e}}_{3}}\text{=}{-\mathrm{e}}_{3}$$
$${u}_{1}\text{=}-\left(\left({e}_{3}+{e}_{2}\right)* \left[\left(\frac{{e}_{3}+{e}_{2}}{{e}_{1}}\right)*\mathrm{0,302}\right]\right)$$
$${u}_{2}= \text{ } {e}_{1}-\mathrm{3,04}*{e}_{2}-\mathrm{11,4005}*{e}_{3}$$
(18)
$${u}_{3}= \text{ } {-e}_{1}+\mathrm{2,04}*{e}_{2}$$

Numerical experiments were made using the simulation program, and the initial conditions of the manager and implementer systems were taken as x1(0) = 0,12, y1(0) =  −0,01, z1(0) =  −0,01 and x2(0) =  −5, y2(0) = -0,3 z2(0) =  −1, respectively. Numerical results are given graphically to validate the proposed method.

In Fig. 4, the change of state variables of manager and implementer systems over time is shown. Again, Fig. 4 gives the time-dependent variation of error vectors with x1 and x2, y1 and y2, z1 and z2. As seen in more detail in Fig. 5, control signals are activated at t = 0. After the control signals are activated, the error vectors rapidly approach zero from the moment t = 50. Accordingly, it is seen that the active controller synchronizes the manager and implementer systems.

Fig. 4.
figure 4

Time-dependent variation graphs of the state variables of manager and implementing systems and the differences (errors) between these variables

Full size image
Fig. 5.
figure 5

Time dependent variation of error vectors

Full size image

This study shows that synchronization of chaotic systems occurs through active control. The numerical results confirm the validity and effectiveness of the generalized active control method.

4 Conclusion and Suggestions for Future Work

We modeled a three-stage nonlinear supply chain consisting of the grower, the citrus processing plant and the customer. For perishable products, product deterioration may occur during processing or keeping the citrus. In this study, the most important difference from the supply chain dynamic models in the literature mentioned is that these deterioration rates affecting the amount of stock, production and demand are added to the model.

When customer satisfaction “d” is 0.302 in the proposed new supply chain model, the system exhibits chaotic behavior as seen in Fig. 1. The system was examined for customer satisfaction ratio is 0.302, 0.323, and 0.33202. Thus, it was revealed that a small increase in d ratio approached the system to a steady state. Moreover, it has been observed that a dynamic system of perishable products is sensitively dependent on customer satisfaction. In Fig. 3, it is seen that at least one Lyapunov exponent with λ1 = 4.9084 is positive and proves that the new supply chain system is in a chaotic structure with the given initial conditions and parameter values.

The active control method is used for chaos synchronization in the proposed model. Control signals are activated at the start time, and the error approaches zero beyond the moment t = 50. So that, the manager and implementer systems synchronize with the active control parameters. This analysis has shown us that two possible supply chain systems (for example, two factories of the firm in different cities) can operate in sync.

Consequently, obtained results are relevant for managing complex supply chain systems. In future studies, different control techniques can be used in the synchronization of the new supply chain system modeled for perishable products, as well as dynamic supply chain models for different sectors or different product types can be developed.