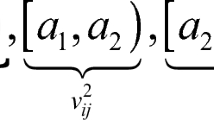Simulated Annealing for the Traveling Purchaser Problem in Cold Chain Logistics

Abstract

Transportation of perishable food in cold chain logistics systems is crucial in order to preserve the freshness of the products. Due to the extended traveling times and frequent stops, planning the distribution operations in cold chain logistics plays a vital role in minimizing the deterioration cost of the products. In order to minimize the total cost of cold chain logistics activities related to the purchase of perishable products, the route and procurement operations have to be well-planned. In this context, this paper addresses the well-known traveling purchaser problem (TPP) and extends the TPP by considering the procurement of perishable products. This is called the traveling purchaser problem in cold chain logistics (TPP-CCL). In the TPP-CCL, the demand for a number of perishable products is provided from a number of markets, where the products purchased at markets are transported by a temperature-controlled vehicle. In addition to the transportation and procurement cost, the deterioration cost of the products is taken into account in the problem. The problem is formulated as a non-linear mixed-integer programming model in which the objective is to find the best procurement and route plan for the purchaser that minimizes the total cost. Considering the complexity of the problem, a simulated annealing (SA) algorithm is proposed to solve the TPP-CCL. The SA is formed by using a number of local search procedures, where the procedures are randomly selected to find a new solution in each iteration. The proposed SA is performed for a TPP-CCL problem set that includes different-sized instances. The results of the SA are compared to the GUROBI solver results. A better result is obtained by the SA for most of the instances. The computational results show that the proposed SA outperforms the GUROBI results by finding better results in shorter computational times.

1 Introduction

The traveling purchaser problem (TPP) is the generalization of the well-known traveling salesperson problem (TSP) and aims to satisfy a number of product demands from a number of markets with minimum total cost [1]. Distinct from the TSP, TPP includes three operational decisions: the selection of the markets to be visited, the number of products purchased from each market, and the route of the purchaser.

The TPP was first introduced by Ramesh [2] in 1981 and extended with different assumptions. One of the widely studied variants of the TPP is the uncapacitated TPP, in which the amount of a product is sufficient to satisfy demand if it is available in a market [3]. Voß [4] considered a fixed market visiting cost for the uncapacitated TPP. Another variant of the TPP is the bi-objective TPP, in which the objective function includes different goals [5]. Coi and Lee [6] extended the TPP with a budget constraint for multiple vehicles. In addition to the cost-based or delivery-based constraints, a number of studies addressed the TPP with environmental concerns, such as green TPP [7], sustainable TPP [8], and solid green TPP [9]. Since the TPP belongs to the class of combinatorial optimization problems and has been shown to be NP-hard, many heuristic and meta-heuristic solution approaches have been introduced in the literature [1]. The early heuristic approaches are the solution construction methods, such as the generalized saving heuristic [10], the tour reduction heuristic [11], and the commodity adding heuristic [12]). In addition to the solution construction methods, a number of local search methods were developed to solve TPP. Recently, meta-heuristic solution approaches have been used to find better results, such as ant colony optimization [13], transgenetic algorithm [14], and variable neighborhood search [15].

In this paper, a new variation of the TPP called the traveling purchaser problem in cold chain logistics (TPP-CCL) is introduced for the procurement plan of perishable foods in cold chain logistics. The TPP-CCL takes into account the release time of the perishable foods in the markets and their additional deterioration costs during transportation. The aim of the problem is to minimize the total cost of the purchaser. The TPP-CCL is formulated as a non-linear mixed-integer programming model. To solve the considered problem, a simulated annealing (SA) algorithm is proposed. The proposed SA employs an advanced local search (LS) procedure to efficiently search the solution space. This paper contributes to the literature by introducing a new variant of the TPP by considering cold chain operational activities. Based on a non-linear deterioration cost function, which is commonly used in the cold chain literature, a non-linear mixed-integer mathematical model formulation is introduced for the problem. In addition to the deterioration costs, the mathematical formulation considers the release time of the perishable products in each market. To the best of our knowledge, the TPP has not been addressed for perishable foods with product release times. With this assumption, a more realistic operational plan can be provided for the procurement of perishable products, which are available at different times in the markets due to the fact that they are produced at different times of the day. In addition to the new variant of the TPP, this study proposes a simulated annealing algorithm in which a problem-specific local search operator is used to generate new solutions. With the help of an advanced search mechanism, the proposed SA is capable of finding effective results for the TPP-CCL.

The remainder of the paper is organized as follows. Section 2 introduces the details of the TPP-CCL and its mathematical formulation. The proposed SA is presented in Sect. 3. The computational results and performance analysis of the proposed algorithm are given in Sect. 4. Finally, the conclusions are given in Sect. 5.

2 Problem Definition and Model Formulation

In TPP-CCL, the demand for a set of perishable products is provided from a set of capacitated markets, where the available quantity of a product at a market can be less than the product demand or even zero. For each product at a market, there exists a product release time. Therefore, the purchaser can only buy a product at a market after its release time. The tour of the purchaser starts and ends at the depot node. The purchaser collects the perishable products by using a temperature-controlled vehicle, where the capacity of the vehicle is greater than the total product demand. Each market can be visited once at most. The aim of the problem is to minimize total traveling, procurement, and product deterioration costs. Deterioration of the perishable products depends on the time they stand in the vehicle and the opening time of the vehicle door for loading. The loading time of the purchaser at any market is proportional to the number of products purchased at the market. The loading operation can be carried out when all products to be purchased from the market are available. Regarding the assumptions given above, the mathematical model of the TPP-CCL is formulated by using the parameters and decision variables presented in Table 1.

Table 1. Parameters and decision variables used in the mathematical model formulation.

$$Min \sum_{i\in V}\sum_{j\in V}{c}_{ij}{x}_{ij}+\sum_{k\in K}\sum_{i\in {M}_{k}}{p}_{ik}{z}_{ik}+\sum_{k\in K}\sum_{i\in {M}_{k}}{p}_{ik}{z}_{ik}\left(1-{e}^{-{\theta }_{1}\left({r}_{0}-{r}_{i}-{{s}_{i}-w}_{i}\right)}\right)$$

$$+\sum_{i\in M}{l}_{i}\left(1-{e}^{-{\theta }_{2}{s}_{i}}\right)+\sum_{i\in M}\vartheta \left({s}_{i}+{w}_{i}\right)$$

(1)

S.t.

$$\sum_{i\in {M}_{k}}{z}_{ik}={d}_{k}\qquad k\in K$$

(2)

$${z}_{ik}\le {q}_{ik}{y}_{i} \qquad k\in K, \qquad i\in {M}_{k}$$

(3)

$${o}_{ik}\le {z}_{ik}\le {q}_{ik}{o}_{ik} \qquad k\in K, \qquad i\in {M}_{k}$$

(4)

$$\sum_{\begin{array}{c}j\in V\\ i\ne j\end{array}}{x}_{ij}={y}_{i} \qquad i\in M$$

(5)

$$\sum_{\begin{array}{c}i\in V\\ i\ne j\end{array}}{x}_{ij}={y}_{j} \qquad j\in M$$

(6)

$$\sum_{i\in M}{x}_{i0}=1$$

(7)

$$\sum_{j\in M}{x}_{0j}=1$$

(8)

$${t}_{0i}\le {r}_{i}+\gamma \left(1-{x}_{0i}\right)\qquad i\in M$$

(9)

$${t}_{0i}\ge {r}_{i}-\gamma \left(1-{x}_{0i}\right)\qquad i\in M$$

(10)

$${r}_{i}+{s}_{i}+{w}_{i}+{t}_{ij}\le {r}_{j}+\gamma \left(1-{x}_{ij}\right)\qquad i\in M,\qquad j\in V,\qquad i\ne j$$

(11)

$${r}_{i}+{s}_{i}+{w}_{i}+{t}_{ij}\ge {r}_{j}-\gamma \left(1-{x}_{ij}\right)\qquad i\in M,\qquad j\in V,\qquad i\ne j$$

(12)

$${s}_{i}=\sum_{k\in K}{h}_{i}{z}_{ik}\qquad i\in M$$

(13)

$${w}_{i}\ge {rl}_{ik}-{r}_{i}-\gamma \left(1-{o}_{ik}\right) \qquad k\in K, \qquad i\in {M}_{k}$$

(14)

$${l}_{i}+\sum_{k\in K}{p}_{ik}{z}_{ik}\le {l}_{j}+\gamma \left(1-{x}_{ij}\right)\qquad i,j\in M,\qquad i\ne j$$

(15)

$${x}_{ij}\in \left\{\mathrm{0,1}\right\}\qquad i,j\in V,\qquad i\ne j$$

(16)

$${y}_{i}\in \left\{\mathrm{0,1}\right\} \qquad i\in M$$

(17)

$${o}_{ik}\in \left\{\mathrm{0,1}\right\} \qquad k\in K, \qquad i\in {M}_{k}$$

(18)

$${z}_{ik}\ge 0 \qquad k\in K, \qquad i\in {M}_{k}$$

(19)

$${r}_{i}\ge 0 \qquad i\in V$$

(20)

$${s}_{i},{l}_{i},{w}_{i}\ge 0 \qquad i\in M$$

(21)

The objective function (1) aims to minimize total traveling, procurement, and deterioration cost. In detail, each sub-term in the objective function determines the transportation cost of the vehicle on the move (${f}_{1}$), the procurement cost (${f}_{2}$), the deterioration cost due to the waiting of products in the vehicle (${f}_{3}$), the deterioration cost due to the door-opening (${f}_{4}$), and the refrigeration cost of the vehicle while waiting at market nodes (${f}_{5}$). Here, ${f}_{1}$ and ${f}_{2}$ are the cost functions considered in the original TPP. ${f}_{3}$–${f}_{5}$ are formed regarding the existing literature related to cold chain logistics (i.e., [16,17,18]). In case there is a degree of importance among these cost items, ${f}_{1}$–${f}_{5}$ may be weighted by using importance coefficients. Constraints (2) ensure that the demand for each product is satisfied by the purchaser. Constraints (3) and (4) provide the capacity restrictions of the markets where the purchased amount of a product at any market cannot exceed the available stock. Constraints (5) and (6) guarantee that the purchaser enters and leaves each visited market exactly once. Constraints (7) and (8) assure that the route of the purchaser starts and ends at the depot node. Constraints (9)–(12) determine the arrival time of the purchaser to the visited nodes. The service time of the purchaser at market nodes is determined by constraints (13). The waiting time of the purchaser at the visited markets is computed by constraints (14). Constraints (15) determine the cumulative price of the products in the vehicle (${l}_{i}$) before it reaches a market, where ${l}_{i}$ is used to determine the deterioration cost of products while waiting in the vehicle at market nodes. Constraints (16)–(21) identify the decision variables of the model.

Based on the formulation given above, called hereafter Model 1, the purchaser is allowed to load the vehicle at any market point after all purchased products are available at the market. On the other hand, the model does not limit the purchaser for extra waiting at any market even though all products are ready. In this context, the purchaser has an opportunity to reduce deterioration costs by waiting at the markets in the route before loading the vehicle. In this way, the transportation time of the products can be reduced in case there is a potential waiting time at further market nodes. As an alternative to this situation, the extra waiting option of the purchaser can be avoided by using the constraints (22) and (23), where ${w}_{ik}^{\prime}$ is a free variable and equals to difference between the release time of product $k$ at market $i$ and the arrival time of the purchaser to the corresponding market; $k\in K$, $i\in {M}_{k}$. The extended version of the model is called Model 2.

$${w}_{ik}^{\prime}={rl}_{ik}{o}_{ik}-{r}_{i}\qquad k\in K,\qquad i\in {M}_{k}$$

(22)

$${w}_{i}=max\left\{0,{max}_{k\in K}\left\{{w}_{ik}^{\prime}\right\}\right\}\qquad i\in M$$

(23)

3 Solution Methodology

SA is a stochastic method for solving combinatorial problems proposed by Kirkpatrick, Gelatt, and Vecchi in 1983 [19]. The main feature of the SA is the solution acceptance mechanism (known as the Metropolis acceptance criterion) that allows accepting worse solutions in the search with a probability in order to escape from the local optimal. Thanks to the Metropolis criterion, SA has been successfully employed to solve many routing problems, such as capacitated vehicle routing problem with loading constraints [20], two-echelon vehicle routing problem [21], traveling salesperson problem [22], green vehicle problem [23], location routing problem [24], inventory routing problem [25], etc. Motivated by its efficiency, this study proposes a simulated annealing algorithm to solve the TPP-CCL in which the solution generation mechanism is formed by using an advanced local search procedure.

The proposed SA starts with generating an initial solution (${{\varvec{X}}}_{0}$) by iteratively selecting one of the product types and purchasing from the unvisited/visited markets according to unit insertion price. The markets with smaller unit prices are selected until the demand for the selected product is satisfied. In the main loop of the SA, a new solution (${{\varvec{X}}}^{\boldsymbol{^{\prime}}}$) is generated through the existing solution (${\varvec{X}}$) by using a number of search methods, where these methods are categorized into two groups: procurement-based search methods and route-change-based search methods. The procurement-based search methods are utilized to make a change in the procurement plan of the purchaser. In this context, an unvisited market insertion, a visited market removal, and product exchange between the visited markets are the used moves. In the route-change-based methods, the order of the visited markets is changed by using four different moves: exchanging a pair of markets, moving a market to a forward position, moving a market to a backward position, and reversing a sub-path in the route. The moves are employed in the local search procedure in a nested structure. The procedure initially starts with ${{\varvec{X}}}^{\boldsymbol{^{\prime}}}={\varvec{X}}$ and generates a new solution (${{\varvec{X}}}^{{\varvec{L}}{\varvec{S}}}$) by applying one of the procurement-based search methods. Following the procurement-based search method, one of the randomly selected route-change-based searches is carried out to improve ${{\varvec{X}}}^{{\varvec{L}}{\varvec{S}}}$. As long as an improvement is provided by the selected move, the route-change-based search is repeated. At the end of the route-change-based search, if the ${{\varvec{X}}}^{{\varvec{L}}{\varvec{S}}}$ is better than the ${{\varvec{X}}}^{\boldsymbol{^{\prime}}}$, the ${{\varvec{X}}}^{\boldsymbol{^{\prime}}}$ is updated as ${{\varvec{X}}}^{\boldsymbol{^{\prime}}}={{\varvec{X}}}^{{\varvec{L}}{\varvec{S}}}$ and the procedure continues by randomly selecting a procurement-based search to be carried out. Otherwise, the local search procedure is terminated. The methods used in the local search procedure are implemented by using the best-improvement strategy. After the local search procedure, ${{\varvec{X}}}^{\boldsymbol{^{\prime}}}$ is accepted according to the SA solution acceptance criterion where ${\varvec{X}}={{\varvec{X}}}^{\boldsymbol{^{\prime}}}$ if $f\left({{\varvec{X}}}^{\boldsymbol{^{\prime}}}\right)<f\left({\varvec{X}}\right)$ or ${e}^{\Delta/T} \ge rnd$. Here, $\Delta$ is the total cost difference between the new solution and the existing solution ($\Delta =f\left({{\varvec{X}}}^{\boldsymbol{^{\prime}}}\right)-f\left({\varvec{X}}\right)$), $T$ is the temperature, and $rnd$ is the standard uniform distributed random number. At the end of the main loop of the SA, the temperature is decreased by using a cooling coefficient ($c$). The SA is terminated if the algorithm reaches a maximum number of iterations. Based on the definition of the SA given above, the pseudo-code of the algorithm is presented in Fig. 1.

Fig. 1.

Pseudo-code of the proposed SA.

4 Computational Results

The performance of the proposed SA is analyzed by using a well-known capacitated TPP benchmark problem set introduced by Laporte et al. [26]. The TPP instances are adapted to the TPP-CCL by adding a release time for each available product in the markets. In addition to the product release time, a service time for each market is identified. The release times and service times are determined using a uniform random distribution, where the lower and upper limits of the distribution are identified according to a feasible solution obtained for the TPP instance. Finally, the deterioration costs and the refrigeration cost of the vehicle while waiting at market locations are specified. For the traveling time, it is assumed as ${t}_{ij}={c}_{ij}$. By using this scheme, 315 different-sized TPP-CCL instances are generated, where each instance characteristic is identified by three parameters: the number of nodes ($\left|V\right|=\left\{10, 20, 30\right\}$), the number of product types ($\left|K\right|=\left\{10, 20, 30\right\}$) in the instance, and $\lambda$ parameter ($\lambda =\left\{0.1, 0.5, 0.7, 0.8, 0.9, 0.95, 0.99\right\}$) that controls the number of markets in a feasible solution through the product demand. The benchmark problem set includes five different instances for each parameter combination. The generated problems are labeled as “TPP.CCL.$\left|V\right|.\left|K\right|.\lambda$.$\left[\#Instance\right]$”.

The proposed algorithm is carried out for each instance with 10 independent runs with a 10,000 iteration limit. The SA parameters are identified as ${T}_{o}=1000$, $c=0.92$, and $L=20$. In order to evaluate the performance of the proposed SA, the LS without SA and the GUROBI solver are used as competitor algorithms. As in the SA computations, the LS is run 10 times for each instance, and each run is terminated at 10,000 iterations. On the other hand, the GUROBI results are obtained with a time limit of one hour. Each computation is carried out on a personal computer with an Intel® Core™ i7-8665U CPU and 16GB of memory.

The SA, LS, and GUROBI are implemented for both Model 1 and Model 2. Table 2 and Table 3 show the summary of the computational results based on Model 1 and Model 2, respectively. The details of the results are given in Appendix Tables A1, A2, A3, A4, A5 and A6, in which each row shows the averages of the results obtained for five instances belonging to a parameter combination ($\left\{\left|V\right|, \left|K\right|, \lambda \right\}$).

In Table 2 and Table 3, the GUROBI results are presented through the best-found integer solution (${f}_{G}$), the optimality gap of the GUROBI solver (${G}_{opt}\%$), and the solution time in second (${t}_{G}$). The notations used for the LS results are the best-found solution of LS over 10 runs (${f}_{LS}^{B}$), the average solution of LS over 10 runs (${f}_{LS}^{A}$), the average computational time of LS over 10 runs (${t}_{LS}$), the percentage gap between the ${f}_{LS}^{B}$ and ${f}_{G}$ (${G}_{LS}^{B}\%$), and the percentage gap between the ${f}_{LS}^{A}$ and ${f}_{G}$ (${G}_{LS}^{A}\%$). Similar notations are used to show SA results as follows: the best-found solution of SA over 10 runs (${f}_{SA}^{B}$), the average solution of SA over 10 runs (${f}_{SA}^{A}$), the average computational time of SA over 10 runs (${t}_{SA}$), the percentage gap between the ${f}_{SA}^{B}$ and ${f}_{G}$ (${G}_{SA}^{B}\%$), and the percentage gap between the ${f}_{SA}^{A}$ and ${f}_{G}$ (${G}_{SA}^{A}\%$). The percentage gaps are calculated by using the Eq. (24) where a negative gap value indicates that a lower total cost is obtained by LS or SA compared to the GUROBI solution. Regarding the results presented in Table 2 and Table 3, it can be expressed that the proposed SA outperforms GUROBI by finding better results in less computational time. Particularly, for the large-sized instances, the average percentage gaps between the SA result and GUROBI results are greater than 20%. Similar results are provided by the LS, where a better average result is obtained for each problem size excepting the instances with the size $\left\{\left|V\right|=10, \left|K\right|=10\right\}$. On the other hand, when the SA is compared to the LS, better results are obtained by SA for almost all problem sizes.

$${G}_{LS or SA}^{B or A}\%=\frac{{f}_{LS or SA}^{B or A}-{f}_{G}}{{f}_{G}}\times 100\%$$

(24)

Table 2. Computational results for Model 1.

Table 3. Computational results for Model 2.

Another finding of the computational experiments is the effect of restricting the extra waiting before vehicle loading on the total cost. In order to compare Model 1 and Model 2, five small-sized instances ($\left|V\right|=10$ and $\left|K\right|=10$) are selected and resolved by GUROBI without a time limitation. For each instance, an optimal solution is found for both model types. Table 4 presents the selected instances and the results based on the cost items of the objective function (${f}_{1}-{f}_{5}$). In this context, the results given in Table 4 show that avoiding extra waiting for the purchaser directly affects the total cost of the purchaser. As a result, it should be expressed that less cost can be provided by allowing waiting for the purchaser at markets if waiting is allowed.

Table 4. Comparison of Model 1 and Model 2 based on the cost items.

5 Conclusion

In this study, the traveling purchaser problem in cold chain logistics (TPP-CCL) is introduced, considering the deterioration cost of perishable foods in cold chain logistics operations. TPP-CCL considers a number of perishable products to be purchased from a set of markets, where the products at markets become available at a specific time. In this context, the aim of the problem is to find the procurement and route plan for the purchaser that minimizes total traveling, procurement, and deterioration cost. Regarding the exponential computations of the deterioration rate, the problem is formulated as a non-linear mixed-integer programming model. To solve the TPP-CCL, a simulated annealing (SA) algorithm is proposed. The algorithm is formed by using a problem-specific local search (LS) procedure in which route-based and purchase-based moves are employed. In computational studies, the performance of the proposed algorithm is tested on a benchmark problem set, which includes different-sized instances. The results of the SA are compared to GUROBI results and LS results used in the SA. A better result is obtained by the proposed SA for most of the instances. As a result of the experiments, the proposed SA outperforms both the competitor algorithms. Furthermore, it is concluded from the computational experiments that allowing extra waiting for the purchaser at markets may reduce the total cost of the purchaser.

For future research, this study can be extended by considering additional restrictions of cold chain logistic activities. In this context, multiple vehicles with different cooling technologies or incompatible products can be taken into account for the purchaser. On the other hand, a maximum traveling time for each product can be considered for the perishable products. In addition to the new assumptions for the problem, problem-specific exact solution approaches can be implemented to find the optimal solution for the TPP-CCL.

Appendix

Detailed computational results for Model 1 and Model 2

Table A1. Results for the TPP-CCL instances of size $\left|V\right|=10$ for Model 1.

Table A2. Results for the TPP-CCL instances of size $\left|V\right|=20$ for Model 1.

Table A3. Results for the TPP-CCL instances of size $\left|V\right|=30$ for Model 1.

Table A4. Results for the TPP-CCL instances of size $\left|V\right|=10$ for Model 2.

Table A5. Results for the TPP-CCL instances of size $\left|V\right|=20$ for Model 2.

Table A6. Results for the TPP-CCL instances of size $\left|V\right|=30$ for Model 2.