An Ordered Flow Shop Scheduling Problem

Abstract

The subject of the study is ordered flow shop scheduling problems which were first seen in the literature in the 1970s. The main objective is to get a fast and good solution. For the purpose of the study, firstly, the ordered flow shop scheduling problems were defined. Then, a heuristic method was suggested for the ordered flow shop scheduling problems and a sample problem was solved and discussed. A genetic algorithm (GA) based on the complexity property was developed. Full enumeration was applied to determine the optimal makespan values based on Smith’s rule because Smith had specified the conditions under which circumstances the permutation can be optimum.

This study is one of the few studies in the literature to obtain optimum solutions up to 15 jobs ordered flow shop problems in a very short amount of time. The developed GA heuristic can also solve large size ordered flow shop scheduling problems very fast. The significant advantage of the proposed method is that, while Smith’s method rule not does not work with large size problems since it requires full enumeration to identify best solution to follow a convexity property where GA algorithm can find a good solution very fast.

1 Introduction

The problem of flow shop scheduling was first introduced by Johnson (Johnson 1954) 60 years ago, and since then, numerous studies have been conducted on this topic. Some of the variations of this problem have been formulated by researchers such as Dudek et al. (Dudek et al. 1992), Elmaghraby (Elmaghraby 1968), Gupta and Stafford (Gupta & Stafford, 2006) and Hejazi and Saghafianb (Hejazi and Saghafian 2005).

Scheduling involves allocating resources to different activities that have varying characteristics within a specific timeframe (Torkashvand et al. 2017). In scheduling problems, there is a set of jobs that require either single or multiple operations for completion. This is the essence of scheduling problems. Additionally, there is one workstation for each type of operation, meaning that if there are m-operation jobs, there must be m workstations. In summary, there are two types of jobs: single station and multi-station. Single and parallel machine problems fall under the category of single station shops, while flow shop and open shops belong to the multi-station shop type.

Many studies utilize a processing time matrix, in which the values are randomly selected from a predetermined distribution. To evaluate the effectiveness and efficiency of solution procedures, randomly generated problems are often employed. These problems feature processing times that are drawn from the same distribution used in job sequencing research.

There is no difference in difficulty between hypothetical and physical problems. Additionally, many industries encounter ordered flow shop problems. Therefore, instead of hypothetical problems, utilizing problems with actual processing times is more beneficial in practical situations.

The ordered flow shop scheduling problem was introduced by Smith (Smith 1968). This problem is also known as the ordered matrix problem and can be considered a subcategory of the flow shop problem with ordered processing times.

The primary objective of this study is to solve ordered flow shop problems with the makespan objective. Firstly, the flow shop scheduling problem and the ordered flow shop scheduling problem were explained. Then, the use of genetic algorithms for solving the permutation flow shop problem was outlined. Finally, the proposed method and its results were discussed.

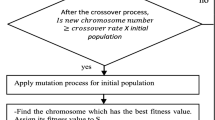
The proposed method utilized the convexity property to obtain a feasible solution, and modifications were made to the crossover and mutation processes in this method.

2 Flow Shop Scheduling Problem

Assume that there are n-jobs and m-machines, and the jobs need to be scheduled across these machines. For a problem to be classified as an m-machine flow shop problem, it needs to satisfy three requirements. Firstly, each must consist of m-operations. Secondly, each operation must require a different machine. Finally, all jobs must be processed in the same order through the machines. If these three criteria are met, that problem can be referred to as an m-machine flow shop problem (Aldowaisan and Allahverdi 2004).

Flow shop scheduling problems can be classified into two groups based on the machine characteristics: machines can have buffer spaces, or the processing is continuous without any interruptions between machines. When the processing is continuous and there are no interruptions, the problem is referred to as the no-wait flow shop problem. The no-wait flow shop problem arises when discontinuous processing is not allowed, as in the case of industries such as metal or food production, where the process must continue from start to end without interruption.

This study utilized the m-machine flow shop problem with the objective of minimizing the total completion time, which is also known as the makespan objective.

3 Ordered Flow Shop Scheduling Problem

Ordered flow shop problems must satisfy two properties. Firstly, given two jobs, A and B, with known processing times, if the processing time of A on any machine is smaller than the processing time of B, then A must also have a smaller or equal processing time on all machines compared to B.

Secondly, for ordered flow shop problems, if the processing times of several jobs are known, and if any job has its j^th smallest processing time on any machine, then every job must have their j^th smallest processing time on the same machine.

Based on these 2 properties, jobs can be sequenced in the ascending order according to their processing times, thus transforming the problem into an ordered flow shop problem with the minimum makespan criterion and permutation schedules.

There are various flow shop sequencing problems in the literature (Panwalkar and Woollam 1980), with the most interesting ones, according to the researchers, including the classical (n × m) problem, the (n × m) problem with no waiting, the (n × m) ordered problem, and the (n × m) ordered problem with no waiting.

In the classical problem, there are infinite intermediate storages between machines, meaning that there is no limitation on the number of jobs waiting in the queue between machines. Redid and Ramamoorthy (Reddy & Ramamoorthy) and Wismer (Wismer) introduced a restriction of no waiting with some justification.

The classical (n × m) problem and (n × m) problem with no waiting are considered for not only the makespan but also the mean flowtime criteria. Efficient solution procedures are not obtainable for all of these problems, but there are some exceptions. Nonetheless, both of these problems are considered unsolvable in computational complexity. However, some specialized techniques can be developed that are applicable to these problems (Coffman).

Special characteristics of processing times in flow shops have been considered in the development of the n × m ordered problem. Smith (Smith et al. 1975) and Panwalkar (Panwalkar et al. 1973) provided the practical basis for this problem.

The (n × m) ordered problem with no waiting has been considered with the makespan criterion by Panwalkar and Woollam (Panwalkar & Woollam). They have developed simple and efficient procedures for certain cases of the problem.

Smith (Smith, Dudek, & Panwalkar, 1973) demonstrated that jobs ordered in ascending or descending order based on their processing times are optimal for ordered flow shop problems if the maximum processing time for each job occurs on the first or last machine. Therefore, if the maximum processing time for each job occurs on the first machine, the jobs can be arranged in descending order. Conversely, if the maximum processing time occurs on the last machine, the jobs can be ordered in ascending order. However, if the maximum processing time occurs on an intermediate machine, Smith (Smith, Dudek, & Panwalkar, 1973) proposed an algorithm to minimize the makespan, where the minimum makespan sequence is arranged in ascending order of processing times followed by the remaining jobs in descending order.

Smith’s method generates 2ⁿ⁻¹ alternative sequences in 4 steps as follows:

Step 1: the jobs need to be ordered in terms of ascending processing times on the first machine.

Step 2: in each partial sequence, the lowest ranking job which has not been arrayed should be placed in the leftmost and rightmost unfilled array position.

Step 3: Step 2 should be repeated until the first n-1 jobs are placed into every array. The highest-ranking job has to be put only into the unfilled position.

Step 4: for makespan, the 2ⁿ⁻¹ sequences are evaluated. The sequences with the lowest makespan are the optimum ones.

4 Genetic Algorithm for Permutation Flow Shop Problem

Genetic Algorithms (GAs) are heuristic search techniques and intelligent randomized search strategies that can find near-optimal solutions for complex problems (Iyer and Barkha 2004). These algorithms are highly effective in solving problems, especially when the search space is vast and standard techniques are unable to efficiently solve the problem. GAs are based on the natural genetics and mechanics of natural selection. In GA, chromosomes represent solutions in the search space. The crossover and mutation operators are determined in each GA. How they are defined is significant.

Several steps need to be followed while applying GAs to problems. Firstly, the feasible solutions of the problems must be transformed into chromosomes, which are a string-type structures.

A standard GA starts by generating a set of presumed or randomly produced solutions, which are called chromosomes, as the initial population. Over a series of generations or iterations, it evolves different sets of solutions, i.e., chromosomes, that are better than the previous ones, with the aim of finding the optimal solution to a problem. The objective function specifies the suitability of each chromosome in each generation. A subset of the chromosomes is selected for reproduction based on their fitness value. The fitness value of each chromosome for the flow shop scheduling problems is taken as the commutual of the makespan. The number of offspring that an individual parent produces is directly proportional to its fitness value, and those with lower fitness values are eliminated via the natural selection procedure. New chromosomes, or offspring, are generated by the applying of genetic operators such as mutation and crossover to the reproduced chromosomes. The new chromosomes constitute the subsequent generation, and the process continues iteratively until a termination criterion is met.

A permutation flow shop problem involves multiple jobs and machines that need to be processed in a specific order on each machine. The primary objective of this problem is to determine a sequence for the jobs that minimizes the overall completion time.

The permutation flow shop scheduling problem is a type of assembly line problem in which there are m distinct jobs that need to be processed on n different machines. All jobs have to be processed in the same order on each machine, and the processing times for each job are predetermined and fixed. The main objective of this problem is to find a job sequence that results in the minimum completion time.

Processing time matrix of the problem:

P = (p_ij), p_ij > 0, i = 1,…,m j = 1,…,n

At any given time, each machine processes exactly one job. Moreover, each job is processed on exactly one machine. The problem is to find a sequence of jobs with the minimum makespan, where the objective is to minimize the maximum completion time among all jobs. That is, max_iC_i is minimized, where C_i is the completion time for job i.

A standard implementation exists for solving the permutation flow shop problem using a GA. The components of a standard GA can be described as follows.

The Scheme of Encoding: job sequences can be viewed as chromosomes. For example, in a five job problem, a chromosome would be represented as [12543], which also represents the alignment. Job1 is processed first on all machines, followed by job2, job5, job4 and finally job3 on all machines. This is a natural choice for this particular problem.

Initial Population: the initial population consists of N randomly generated job arrays, where N represents the size of the population.

Fitness Evaluation Function: the fitness evaluation function aims to simulate the natural process of survival of the fittest. To achieve this, the fitness evaluation function assigns a value to each member of the population that reflects their relative superiority. If r_i, where i = 1,…,N, represents the mutual of the makespan of the strings in the population, the fitness value assigned to string i would be proportional to f _i = r_i / ∑_j r_j. Our objective is to minimize the makespan.

Reproduction: based on their fitness values, individual chromosomes from the current population are replicated. That replication process is performed by randomly selecting chromosomes with a probability proportional to their fitness value. To generate the next generation, N × f _i copies of string i are expected to be present in the gene pool. This creates the mating pool, to which crossover and mutation operators are applied in order to generate the next generation.

Crossover: the primary objective of crossover is to swap information between randomly selected parental chromosomes to generate improved offspring. The crossover process combines the genetic material of two parental chromosomes to generate offspring for the next generation. This offspring retains the desirable characteristics of the parent chromosomes. This exchange is also intended to investigate superior genes.

For the crossover implementation of crossover, two parents are randomly selected from the mating pool. The parents are duplicated with a probability 1-p_c where p_c is the crossover probability. The following process is then performed.

In the standard genetic algorithm, a single point crossover is performed between two parents. This is done by randomly selecting a number k between 1 and l-1, where l is the length of the string and is greater than 1. The result of the interchanging all characters from position k + 1 to l is the creation of two new strings. It is important to note that this coding scheme can produce infeasible strings. For example, in an eight job problem with k = 3 and the crossing strings are [12345678] and [58142376].

This problem can produce [12342376] and [58145678], but these are infeasible solutions due to the recurrence of jobs. Therefore, a modification needs to be made to the standard crossover procedure. The first modification is to replicate all characters of the first parent’s chromosome until location k.

Mutation: two distinct locations of the chromosome are randomly selected, and the jobs at these locations are swapped during the crossover process. Then, the mutation operator is independently applied to each child obtained from the crossover. A small probability p_m is used when applying the mutation operator. Mutation expands the search space, preventing the selection and crossover from focusing on a narrow area of the search space and preventing the GA from getting stuck in a local optimum.

Criteria of Termination: that criterion determines the number of iterations at which the algorithm will terminate in the GA.

5 Proposed Method

This section provides a detailed explanation of the proposed method for scheduling an ordered flow shop. The method involves applying crossover and mutation operations and takes into account the requirement for a feasible solution with convexity. Each step of the approach is described in sequence.

The first step of the proposed method involved creating an ordered matrix that represented the processing times of jobs on different machines. To form the matrix, two key properties of ordered flow shop problems were taken into account and random values were assigned to its elements. The software was only provided with information on the number of jobs and machines available, such as a problem with 10 jobs and 5 machines or one with 30 jobs and 20 machines. The proposed method considers problems with a range of 10 to 30 jobs and 5 to 20 machines.

Setting the population size was another important criterion that had to be determined. In this method, the population size was fixed as 2n, where n denotes the number of jobs.

In addition, specific stopping criteria, also known as termination criteria, were defined for each distinct ordered matrix. The stopping criteria employed in the problem include 500 iterations, 1000 iterations and 2000 iterations.

The next step was to form the parents. While the parents were selected randomly, first the peak was found and then they were aligned in ascending order from the starting point to the peak, in descending order from the peak to the end. It was crucial to ensure that there was only one peak in the matrix.

The third step involved applying crossover to generate offspring from the parents. The parents were randomly divided into two parts, with the division not necessarily at the middle point. The first part of the first parent was then copied, and the second part of the second parent was inserted according to the rule described in the second step, which involved arranging the jobs in ascending order up to the highest point, and in descending order thereafter. It should be noted that ensuring the matrix had only one peak was also critical during this crossover operation.

In the fourth step, mutation was performed by randomly selecting two elements and leaving the other unchanged. The selected elements were then repositioned according to the rule described in the second step, which involved arranging the jobs in ascending order up to the highest point, and in descending order thereafter.

The parent selection process employed the Roulette Wheel Selection method. This involved randomly selecting two numbers and picking the parents whose cumulative fitness values were closest to them. It should be noted that the fitness values were calculated by dividing 1 to the C_max of parents.

In the final step, elitism was applied to generate a new population that also represented the solution. This involved forming 50% of the new population by selecting the best 25% of the current population and 25% of the child population. The remaining 50% of the new population was filled with individuals from the current and child populations that were not selected in the previous step.

6 Solutions

The population size was set to 2n, where n represented the number of jobs. The proposed method was tested for different mutation rates, stopping criteria, and varying numbers of jobs and machines. The method was implemented using the C programming language. An example problem and its corresponding results are provided below.

Table 1 displays the ordered matrix generated by the computer using random values that were generated based on certain rules explained in this study. For this problem, the mutation probability was set to 0.1 the crossover probability was set to 0.6 and the number of iterations was set to 500.

Table 1. Ordered Matrix.

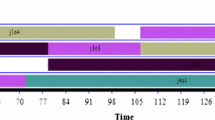
The iteration that yielded the best fitness value was the 5^th iteration, and it took 4773849 ns to obtain the result. In this context, the best fitness value refers to the lowest value achieved. For this particular problem, the best fitness value was 525, and the best alignment associated with that fitness value was [J₁, J₂, J₅, J₄, J₃].

The convexity of the result is demonstrated in Fig. 1, where the processing times for each machine are plotted according to the best alignment. The figure shows that the processing times initially increase and then decrease, indicating a convex relationship.

Fig. 1.

Convexity Property.

Tables 2 to 3 and Figs. 2–5 provide summary results for different problem sizes. The mutation probability, crossover probability, and number of iterations were set to 0.1, 0.6 and 500 respectively for all problems shown in the tables and figures. The elements of the matrix are between 1 and 800. Each matrix was executed 10 times and the minimum, maximum, and average makespan values as well as average execution times were recorded. For instance, in a 10 jobs and 5 machines problem, 10 different matrixes were created and each matrix was executed 10 times.

A new C programming language code was developed for comparison purposes. In this proposed algorithm, the jobs were sorted in ascending order based on their processing times and were then placed sequentially in the first and last empty locations of the array. For a problem with n jobs, there are 2ⁿ⁻¹ arrays generated. The makespan and processing time for each array were determined, and the best arrays were selected.

Table 2. Proposed GA Results for 20 Job Problems.

Table 3. Proposed GA Results for 30 Job Problems.

7 Result and Discussion

The proposed method improved a genetic algorithm based on the complexity property and implemented the full elimination technique based on Smith’s rule. Smith’s rule provides the conditions under which the permutation can be optimal.

The proposed method successfully generated results for problems ranging from 10 to 30 jobs and 5 to 20 machines.

On the other hand, Smith’s method could not be executed for 20 and 30 job problems due to their size and insufficient computer memory. The algorithms were executed on a computer with Intel i7 processor, 8 GB of RAM, a 500 GB hard disk, and the Windows10 operating system. The computer’s specifications can be considered a limitation for solving the problem. The results of the proposed method for 10 to 30 job problems are presented in Fig. 5.

Figure 2 compares the time performance of the proposed algorithm and Smith’s method for scheduling 10 jobs. As shown in the figure, the execution times are identical for both methods when there are up to 15 jobs to be scheduled. However, for more than 15 jobs, the proposed algorithm shows a significant improvement in execution time, thanks to its elimination approach. Time comparison between the proposed algorithm and Smith’s method for 15 jobs is shown in Fig. 3. Although the execution times are comparable for 10 jobs, the difference becomes more apparent as the number of jobs increases to 15. Notably, even though the makespan values are the same for both methods when scheduling 10 jobs, the proposed algorithm can still save time compared to Smith’s method.

Fig. 2.

Time Comparison Between two Methods (10 jobs).

Fig. 3.

Time Comparison Between two Methods (15 jobs).

Figure 4 depicts a time comparison between the two methods, for all problem sizes. As demonstrated in the figure, Smith’s method could not produce results for problems with more than 15 jobs, whereas the proposed algorithm was able to solve all problem sizes.

Figure 5 shows the makespan comparison of the two methods for all data in the study. As the figure clearly indicates, Smith’s method fails to provide solutions for problems that involve more than 15 jobs and 20 machines.

Fig. 4.

Time Comparison Between two Methods (10 to 30 jobs).

Fig. 5.

Makespan Comparison Between two Methods (10 to 30 jobs).

8 Conclusion and Future Research

Although the optimum sequencing characteristic is evident in ordered flow shop problems, finding the optimal solution becomes impossible as the problem size increases due to computational explosion.

The present study found that the proposed algorithm can achieve the optimum solution for scheduling problems with up to 15 jobs. We obtained the same optimum solutions that Smith’s method achieved for up to 15 jobs by using a genetic algorithm. While it may be possible to solve problems with 20 jobs using more powerful computers, the proposed algorithm can still produce good solutions for problems with more than 20 jobs. However, we cannot guarantee that full elimination will always yield the optimum solution on our computers beyond 15 jobs. Nevertheless, since the makespans obtained by the proposed algorithm and Smith’s method are identical, we can be confident that our algorithm can solve the problem. The proposed algorithm can quickly reach a good solution, and the fact that we found the optimum solutions for 10 and 15 jobs suggests that the algorithm should also work well for 20 and 30 jobs. Smith’s method provides a rule for achieving the optimum solution based on the convexity principle and by performing full elimination.

In summary, as the problem size increases, the proposed method outperforms Smith’s method by finding an optimal solution in less time. In addition, Smith’s method fails to provide any solution for problems with more than 15 jobs, while the proposed algorithm can handle up to 30 jobs. Overall, the proposed algorithm is superior to Smith’s method as it achieves a better makespan in less time.