Non-stationary Response of a Bridge Due to Moving Vehicle with Random Arrival Rate

Abstract

Moving vehicle excites the bridge with dynamic force which is realised as a stationary process when the vehicle velocity is constant. However, this condition is not always true when the vehicle speed varies with time while travelling over the bridge. In this paper, the bridge response to non-stationary excitation has been studied considering speed variation, uneven pavement and also random arrival rate of the vehicle. The bridge vehicle interaction has been modelled using continuum approach and the solution has been obtained using orthogonal polynomial expansion method. The generalised co-ordinates of the system response are expressed in terms of orthogonal polynomial series, which offered certain advantages to arrive at the expression of first and second order statistics of system response using the properties of the polynomial. The movement of multiple vehicles has been considered in different time windows assuming their arrival rate follows a Poisson process. Response statistics- mean and standard deviation has been studied for a single cell box girder section of single span bridge in different time windows to observe the effect of vehicle arrival rate, vehicle speed and acceleration and pavement unevenness. The amplification of maximum static flexural stress due to dynamic effect has been obtained incorporating the standard error of the mean. Sequence of accelerating vehicles is found to cause higher stress in a bridge with poor maintenance of surface. The segment of response history in an optimal time window is found to decrease the computational cost since the presence of total number of vehicles over the bridge were dependent on the vehicle speed and their arrival rate.

1 Introduction

The dynamic response of bridge considering vehicular movement has been studied by various researchers. Most of them have idealised bridge as a beam which can be simply supported or continuous [1]. In all of these models, the vehicle loads have been idealised as several concentrated loads [1]. However, in these works the effect of interaction between bridge and vehicle is not considered. In order to take the effect of bridge vehicle interaction, the vehicle has been modelled as spring mass dashpot system [2, 3] and the same has been considered in obtaining the bridge dynamic response [2, 4, 5]. In the above works, the effect of road surface roughness has not been considered, which also plays an important role in the dynamic response of the bridge. The effect of road surface roughness and bridge vehicle interaction has been considered to evaluate the dynamic response of the bridge and it has been observed from the studies that the dynamic response of the bridge is affected by the road surface roughness [6, 7].

In the above studies, the bridge response was obtained by taking deterministic vehicular loads [6,7,8,9]. However, the vehicular loads arriving on the bridge in terms of number of vehicles, axle weight, axle interval and vehicle velocity are random in nature. Hence, some of the researchers have studied the bridge dynamic response due to the random nature of the vehicles passing on the bridge assuming vehicle arrival to be a random variable [10, 11]. It was also observed from the studies that the response of vehicle induced by pavement irregularity becomes a stationary random process in time domain when the vehicle velocity is assumed to be constant. The response of vehicle induced by pavement irregularity becomes a non-stationary random process in time domain when the vehicle velocity is varying with time [12,13,14,15,16]. The non-stationary response of a vehicle travelling on homogeneous road surface has been analysed using state space approaches [12, 13]. The non-stationary response of vehicle was also obtained in which the equations of motion were first established in space domain and then covariance of the response was computed in time domain [14]. A Monte Carlo simulation technique was used to simulate the deck profile for generating input samples in numerical integration of the system equations. This was used to obtain the non-stationary response of the vehicle [16].

Thus it is evident from the studies conducted that very less work has been done to evaluate the non-stationary response of the bridge when the vehicle travels at variable velocity. In addition, it has been observed that most of the vehicular loads on the bridge are taken as deterministic in nature and have considered the effect of single vehicular movement. Hence, this paper presents a methodology to evaluate the bridge response considering random vehicular loads, multiple vehicular movement and variable velocity. Further, DAF has been evaluated for different bridge and vehicle parameters.

2 Methodology

In the present work, the vehicle arrival time is assumed as a random variable following Poisson process. The bridge response considering random vehicle arrival time and bridge vehicle interaction is obtained using Orthogonal Polynomial Expansion Method. The bridge considered in the study is a simply supported bridge with single span. It is idealised as a Euler–Bernoulli beam with uniform cross section. The vehicle is modelled as a quarter car model. The road surface roughness is assumed to be Gaussian process with zero mean and is represented by a power spectral density function. In addition to the road surface roughness, the mean surface of the bridge deck has been considered as a half sine wave. This represents the pre-chamber of the bridge.

2.1 Theoretical Formulation

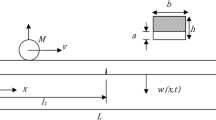
The multiple vehicle movement modelled as quarter car model on the single span bridge has been shown in Fig. 1.

Fig. 1

Vehicle movement on bridge

The deck profile is represented by,

$$h\left( {\tilde{x}} \right) = h_{mean} \left( {\tilde{x}} \right) + h_{road} \left( {\tilde{x}} \right)$$

(1)

The position of vehicle from the reference station along the bridge span at any time instant is given by

$$\tilde{x}(t) = \sum\limits_{p = 0}^{m} {a_{p} t^{p} }$$

(2)

In Eq. (2), the coefficients a_p represent different conditions of the vehicle motions. The coefficients a₀ and a₁ have non-zero values while the remaining coefficients are zero when the vehicle velocity is constant. The velocity of the vehicle at any time instant is obtained by taking the first derivative of Eq. (2) with respect to x.

A series of cosine terms with random phase angles and a certain probability density function have been used to calculate the road surface roughness [17], which is given by

$$h_{r} \left( {\tilde{x}} \right) = \sum\limits_{s = 1}^{N} {A_{s} \cos \left( {2\pi \Omega_{s} \tilde{x} + \theta_{s} } \right)}$$

(3)

The parameters A_s and Ω_s are taken from Yin et al. [17].

The governing differential equation is written after expanding C, K and F using Taylor series [18] as

$$\begin{aligned} & {\mathbf{M}}\ddot{\tilde{x}} + \left[ {{\mathbf{C}}_{mean} + {\mathbf{C}}_{{\tilde{\lambda }t_{n} }} \left\{ {\tilde{\lambda }t_{n} - \mu \left( {\tilde{\lambda }t_{n} } \right)} \right\}} \right]\dot{\tilde{x}} + \left[ {{\mathbf{K}}_{mean} + {\mathbf{K}}_{{\tilde{\lambda }t_{n} }} \left\{ {\tilde{\lambda }t_{n} - \mu \left( {\tilde{\lambda }t_{n} } \right)} \right\}} \right]\tilde{x} = \\ & {\mathbf{F}}_{mean} \left( t \right) + {\mathbf{F}}_{{\tilde{\lambda }t_{n} }} \left\{ {\tilde{\lambda }t_{n} - \mu \left( {\tilde{\lambda }t_{n} } \right)} \right\} \\ \end{aligned}$$

(4)

where, C, K and F with subscript λt_n represent the differentiation of the variable with respect to $\tilde{\lambda }t_{n}$, which is computed at $t = \tilde{\lambda }t_{n}$. M, C and K are the mass matrix consisting of bridge and vehicle mass, damping matrix consisting of bridge and vehicle damping and stiffness matrix consisting of bridge and vehicle stiffness. The response $\tilde{X}$ is expressed as the summation of product of transformed time dependent coordinate and orthogonal polynomial function as,

$$\tilde{X}_{j} \left( t \right) = \sum\limits_{l = 0}^{{N_{1} }} {Q_{jl} \left( t \right)L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right);\,j = 1,\,2,\,...,\,n_{dof} }$$

(5)

Since, the vehicle arrival time follows Poisson process, the distribution of arrival time is Gamma distribution. The probability density function of $\tilde{\lambda }t_{n}$ is given as [19]

$$p_{{\tilde{\lambda }t_{n} }} \left( {\tilde{\lambda }t} \right) = \frac{{t^{n - 1} \exp \left( { - t} \right)}}{\Gamma (n)}$$

(6)

Since the distribution of arrival time is Gamma distribution, Associated Laguerre Polynomial is the orthogonal polynomial function considered [20] in the present study which is found to satisfy the orthogonality condition. The response statistics have been found using the recurrence relationships [20] shown in Eq. (7).

$$\begin{aligned} & \tilde{\lambda }t_{n} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) = \alpha_{l - 1} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) + \beta_{l} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) + \\ & \gamma_{l + 1} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) \\ & \alpha_{l - 1} = - \left( {l - 1 + n} \right) \\ & \gamma_{l + 1} = - \left( {l + 1 + 1} \right) \\ & \beta_{l} = \left( {2l} \right) + n + 1 \\ \end{aligned}$$

(7)

Substitute Eq. (5) in Eq. (4),

$$\begin{aligned} & {\mathbf{M}}\sum\limits_{l = 0}^{{N_{1} }} {{{\ddot{Q}}}_{l} \left( t \right)} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) + \left( {{\mathbf{C}}_{mean} + {\mathbf{C}}_{{\tilde{\lambda }t_{n} }} \left\{ {\tilde{\lambda }t_{n} - \mu \left( {\tilde{\lambda }t_{n} } \right)} \right\}} \right)\sum\limits_{l = 0}^{{N_{1} }} {{\dot{\mathbf{Q}}}_{l} \left( t \right)} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) \\ & + \left( {{\mathbf{K}}_{mean} + {\mathbf{K}}_{{\tilde{\lambda }t_{n} }} \left\{ {\tilde{\lambda }t_{n} - \mu \left( {\tilde{\lambda }t_{n} } \right)} \right\}} \right)\sum\limits_{l = 0}^{{N_{1} }} {{\mathbf{Q}}_{l} \left( t \right)} L_{l}^{n} \left( {\tilde{\lambda }t_{n} } \right) = {\mathbf{F}}\left( t \right)_{mean} + {\mathbf{F}}\left( t \right)_{{\tilde{\lambda }t_{n} }} \left\{ {\tilde{\lambda }t_{n} - \mu \left( {\tilde{\lambda }t_{n} } \right)} \right\} \\ \end{aligned}$$

(8)

In order to find the response statistics of the bridge, Eq. (8) has to be multiplied by $L_{k}^{n} \left( {\tilde{\lambda }t_{n} } \right)$. Further, the recurrence relation shown in Eq. (7) has to be used and the resulting equation has to be multiplied by probability density function $p_{{\tilde{\lambda }t_{n} }} \left( {\tilde{\lambda }t} \right)$ and integrated in the domain of the random variable using the orthogonality property of the polynomial considered. The resulting equation is given as,

$$\begin{aligned} & {\mathbf{M}}\sum\limits_{l = 0}^{{N_{1} }} {{{\ddot{Q}}}_{l} \left( t \right)} d_{l}^{2} \delta_{lk} \\ & + \sum\limits_{l = 0}^{{N_{1} }} {{\dot{\mathbf{Q}}}_{l} \left( t \right)} \left[ {{\mathbf{C}}_{mean} \,d_{l}^{2} \delta_{lk} + {\mathbf{C}}_{{\tilde{\lambda }t_{n} }} \left( {\alpha_{l - 1} d_{l - 1}^{2} \delta_{l - 1k} + \beta_{l} \,d_{l}^{2} \delta_{lk} + \gamma_{l + 1} d_{l + 1}^{2} \delta_{l + 1k} } \right) - {\mathbf{C}}_{{\tilde{\lambda }t_{n} }} \mu \left( {\tilde{\lambda }t_{n} } \right)d_{l}^{2} \delta_{lk} } \right] \\ & + \sum\limits_{l = 0}^{{N_{1} }} {{\mathbf{Q}}_{l} \left( t \right)} \left[ {{\mathbf{K}}_{mean} \,d_{l}^{2} \delta_{lk} + {\mathbf{K}}_{{\tilde{\lambda }t_{n} }} \left( {\alpha_{l - 1} d_{l - 1}^{2} \delta_{l - 1k} + \beta_{l} \,d_{l}^{2} \delta_{lk} + \gamma_{l + 1} d_{l + 1}^{2} \delta_{l + 1k} } \right) - {\mathbf{K}}_{{\tilde{\lambda }t_{n} }} \mu \left( {\tilde{\lambda }t_{n} } \right)d_{l}^{2} \delta_{lk} } \right] \\ & = {\mathbf{F}}\left( t \right)_{mean} d_{0}^{2} \delta_{0k} + {\mathbf{F}}\left( t \right)_{{\tilde{\lambda }t_{n} }} \left( {\alpha_{k - 1} d_{0}^{2} \delta_{0k - 1} + \beta_{0} \,d_{0}^{2} \delta_{0k} + \gamma_{0 + 1} d_{0 + 1}^{2} \delta_{0 + 1k} } \right) - {\mathbf{F}}\left( t \right)_{{\tilde{\lambda }t_{n} }} \mu \left( {\tilde{\lambda }t_{n} } \right)d_{0}^{2} \delta_{0k} \, \\ \end{aligned}$$

(9)

where,

$$d_{l}^{2} = \frac{{\Gamma \left( {l + n + 1} \right)}}{{\Gamma \left( {l + 1} \right)\Gamma \left( {n + 1} \right)}}$$

(10)

In Eq. (10), the value of k changes from 0 to N₁. Newmark’s Method [21] has been used to solve Eq. (10) to obtain the time variation of displacement Q.

2.1.1 Expectation of the Response Vector

Using the property of orthogonal polynomial function, the expectation of the response has been evaluated and is shown below,

$$E\left[ {\tilde{X}_{i} \left( t \right)} \right] = Q_{i0} \left( t \right)d_{0}^{2} \,;\,i = 1,\,2,\,...,\,n_{dof}$$

(11)

2.1.2 Standard Deviation of the Elements of the Response Vector

The covariance of the elements of the response vector is written as,

$$Cov\left( {\tilde{X}_{i} \left( {t_{1} } \right),\tilde{X}_{i} \left( {t_{2} } \right)} \right) = E\left[ {\tilde{X}_{i} \left( {t_{1} } \right)\tilde{X}_{i} \left( {t_{2} } \right)} \right] - E\left[ {\tilde{X}_{i} \left( {t_{1} } \right)} \right]E\left[ {\tilde{X}_{i} \left( {t_{2} } \right)} \right]\,;\,i = 1,\,2,\,...,\,n_{dof}$$

(12)

In Eq. (12),

$$E\left[ {\tilde{X}_{i} \left( {t_{1} } \right)\tilde{X}_{i} \left( {t_{2} } \right)} \right] = \sum\limits_{l = 0}^{{N_{1} }} {\sum\limits_{m = 0}^{{N_{1} }} {Q_{il} \left( {t_{1} } \right)Q_{im} \left( {t_{2} } \right)} } E\left[ {L_{l}^{j} \left( {\tilde{\lambda }t{}_{j}} \right)L_{m}^{j} \left( {\tilde{\lambda }t_{j} } \right)} \right]\,;\,i = 1,\,2,\,...,\,n_{dof}$$

(13)

Equation (13) is simplified using the property of orthogonal polynomials and is given as

$$E\left[ {\tilde{X}_{i} \left( {t_{1} } \right)\tilde{X}_{i} \left( {t_{2} } \right)} \right] = \sum\limits_{l = 0}^{{N_{1} }} {\sum\limits_{m = 0}^{{N_{1} }} {Q_{il} \left( {t_{1} } \right)Q_{im} \left( {t_{2} } \right)} } d_{l}^{2} \delta_{lm} \,;\,i = 1,\,2,\,...,\,n_{dof}$$

(14)

The covariance of the elements of the response vector is written by substituting Eqs. (18) and (15) in Eq. (16) which is shown below,

$$Cov\left( {X_{i} \left( {t_{1} } \right),X_{i} \left( {t_{2} } \right)} \right) = \sum\limits_{l = 0}^{{N_{1} }} {\sum\limits_{m = 0}^{{N_{1} }} {Q_{il} \left( {t_{1} } \right)Q_{im} \left( {t_{2} } \right)d_{l}^{2} \delta_{lm} } - } Q_{i0} \left( {t_{1} } \right)Q_{i0} \left( {t_{2} } \right)d_{0}^{4} \,;\,i = 1,\,2,\,...,\,n_{d}$$

(15)

Due to the presence of Kronecker delta, Eq. (15) is simplified further and is given as,

$$Cov\left( {\tilde{X}_{i} \left( {t_{1} } \right),\tilde{X}_{i} \left( {t_{2} } \right)} \right) = \sum\limits_{l = o}^{{N_{1} }} {Q_{il} \left( {t_{1} } \right)Q_{il} \left( {t_{2} } \right)d_{l}^{2} } - Q_{i0} \left( {t_{1} } \right)Q_{i0} \left( {t_{2} } \right)d_{0}^{4} \,;\,i = 1,\,2,\,...,\,n_{dof}$$

(16)

The variance of the elements of the response vector is evaluated by substituting $t_{1} = t_{2} = t$ in Eq. (16), and is given as

$$Var\left[ {\tilde{X}_{i} \left( t \right)} \right] = \sum\limits_{l = 0}^{{N_{1} }} {\left[ {Q_{il} \left( t \right)} \right]^{2} } d_{l}^{2} - \left[ {Q_{i0} } \right]^{2} d_{0}^{4} \,;\,i = 1,\,2,\,...,\,n_{dof}$$

(17)

DAF is evaluated using the obtained response statistics of the bridge, which is the mean and standard deviation.

3 Dynamic Amplification Factor (DAF)

In bridge design, dynamic analysis is not considered. This is because several codes have suggested DAF to amplify the static effect. It is also observed that the DAF suggested in various codes only depends on the span length. However, parameters such as vehicle velocity, road surface roughness and vehicle acceleration have not been considered in the evaluation of DAF [22]. From the previous study, it is observed that DAF depends on the above parameters [23]. In the present work, the effect of DAF on the mentioned parameters has been studied.

The DAF is evaluated considering the effect of mean and standard deviation of flexural stresses, which is given as,

$$DAF = \frac{{F_{static} + F_{dynamic} }}{{F_{static} }} = 1 + \frac{{F_{dynamic} }}{{F_{static} }} = 1 + DI$$

(18)

The static response is obtained by traversing the vehicles at 5 km/hr. The maximum dynamic response is given as,

$$F_{dynamic} = \left| {\mu_{f} \left( {\tilde{x},t} \right) + E_{f} \left( {\tilde{x},t} \right)} \right|$$

(19)

where, E_f(x, t) is the standard error of the mean (SEM) defined as [23]

$$E_{f} \left( {x,t} \right) = \frac{{\sigma_{f} \left( {x,t} \right)}}{{\sqrt {{{N_{s} } \mathord{\left/ {\vphantom {{N_{s} } 4}} \right. \kern-0pt} 4}} }}$$

(20)

The maximum dynamic response in Eq. (19) takes into account the effect of mean and standard deviation of flexural stresses.

4 Numerical Study

The bridge considered for study is a single span box girder of span length 30 m with twin cell cross section. The ratio of vehicle suspension and tyre stiffness ratio is 4.0; fundamental natural frequency of the bridge is 4.5 Hz; vehicle weight is 40 tonnes; for the road surface roughness, Ω_L is taken as 0.1 cycle/m and Ω_U is taken as 2 cycle/m [24]. The mean profile is assumed to be sinusoidal with an amplitude of 0.01 m. The response is evaluated when the vehicle is at the mid-span of the bridge. The road roughness coefficient considered for good and very poor road case is 32 × 10^–6 m²/cycle/m and 1024 × 10^–6 m²/cycle/m respectively [25].

To account for multiple vehicular movement on the bridge, the flexural stresses are obtained for different time windows. The vehicle velocity considered is 20 km/hr, 40 km/hr and 60 km/hr. The window kept for vehicle movement is changed from 10 to 25 s. The comparison of mean flexural stresses for the time windows is shown in Table 1 for good and very poor road conditions. The comparison of standard deviation of flexural stresses for the above-mentioned time windows is shown in Table 2 for good and very poor road conditions. The numerical analysis has been done using MATLAB.

Table 1 Comparison of mean flexural stresses for different time windows

Table 2 Comparison of standard deviation of flexural stresses for different time windows

From Tables 1 and 2, it is observed that the mean and standard deviation of the flexural stresses do not vary significantly as time window changes from 20 to 25 secs. The time window for evaluating DAF may be reasonably taken not above 20 secs. The DAF varying the arrival rate of the vehicle, road surface roughness, vehicle velocity and acceleration of the vehicle is obtained.

4.1 Parametric Variations

The factors that are varied to observe the effect on Dynamic Amplification Factors are:

• 1. Variable vehicle velocity

• 2. Arrival rate of the vehicle

• 3. Road surface roughness.

4.1.1 Variable Vehicle Velocity

The variable vehicle velocity is obtained using Eq. (2). The vehicle is made to accelerate at 0.5 m/s², 1 m/s² and 1.5 m/s². The mean flexural stresses obtained after varying the acceleration are then compared with the mean flexural stress for a constant vehicle velocity. The comparison plot for 20 km/hr vehicle velocity and very poor road condition is shown in Fig. 2. The arrival rate of the vehicle is considered as 2 vehicles per second.

Fig. 2

Comparison of mean stress for different values of acceleration for velocity 20 km/hr and very poor road surface

The maximum value of mean stress when there is no acceleration is 19.3 MPa, 0.5 m/s² is 20 MPa, 1 m/s² is 23 MPa and 1.5 m/s2 is 28 MPa. The increase in acceleration values increases the mean flexural stresses. This is because it increases the longitudinal vibration of the bridge.

The mean flexural stresses and the standard deviation of flexural stresses for good and very poor for acceleration of the vehicle 1.5 m/s² and varying the vehicle velocity are shown in Figs. 3, 4, 5 and 6.

Fig. 3

Comparison of mean stress for varying velocity with acceleration 1.5 m/s² and good road surface

Fig. 4

Comparison of mean stress for varying velocity with acceleration 1.5 m/s² and very poor road surface

Fig. 5

Comparison of standard deviation of flexural stress for varying velocity with acceleration 1.5 m/s² and very good road surface

Fig. 6

Comparison of standard deviation of flexural stress for varying velocity with acceleration 1.5 m/s² and very poor road surface

It is observed from Figs. 3 and 4 that the mean flexural stresses are higher for lower velocity since the duration of loading is more for lower velocity as compared to higher velocity. The standard deviation of the flexural stresses does not follow the same trend as shown in Figs. 5 and 6. The DAF for varying the acceleration of the vehicle for different initial vehicle velocities and arrival rate of 2 vehicles per second for very poor road case is shown in Fig. 7.

Fig. 7

Comparison of DAF with acceleration of the vehicle for different initial vehicle velocities and arrival rate of 2 vehicles per second for very poor road conditions

It is observed from Fig. 7 that the mean flexural stresses are higher for lower velocity since the duration of loading is more for lower velocity as compared to higher velocity leading to higher DAF for lower vehicle velocity. Also, there is a significant change in the DAF when the vehicle velocity is considered constant and when the vehicle velocity is variable as seen from Fig. 7.

4.1.2 Arrival Rate of the Vehicles

The arrival rate of the vehicles is varied from 1 vehicle per second to 3 vehicles per second for initial vehicle velocity of 20 km/hr and vehicle acceleration of 1.5 m/s². The road condition considered is very poor. The mean and standard deviation of the flexural stresses for different arrival rates are shown in Figs. 8 and 9.

Fig. 8

Comparison of mean stress for varying arrival rate

Fig. 9

Comparison of standard deviation of flexural stress for varying arrival rate

It is observed from Fig. 8 that higher arrival rates signify more vehicular movement on the bridge leading to higher dynamic stresses. The standard deviation of the flexural stresses follows the same pattern as the mean flexural stresses for varying arrival rates as shown in Fig. 9. The DAF for varying arrival rates for initial vehicular velocities 20 km/hr, 40 km/hr and 60 km/hr is shown in Fig. 10.

Fig. 10

Comparison of DAF with arrival rate of the vehicle for very poor road conditions

It can be observed from Fig. 10 that the DAF increases upto 2 vehicles per second and decreases till arrival rate 3 vehicles per second. The increase in DAF can be due to an increase in the dynamic forces. However, as the arrival rate increases from 2 vehicles per second, the static forces also increase leading to a decrease in the DAF.

4.1.3 Road Surface Roughness

The deterioration in road surface condition leads to higher flexural stresses as the dynamic forces due to the vibratory motion of the vehicle on the bridge increases as shown in Figs. 3, 4, 5 and 6. The DAF for different road surface roughness for an initial vehicle velocity of 20 km/hr and arrival rate of 2 vehicles per second is shown in Fig. 11.

Fig. 11

Comparison of DAF with acceleration of the vehicle for initial vehicle velocity 20 km/hr and arrival rate of 2 vehicles per second for good and very poor road conditions

It is observed from Fig. 11 that the DAF increases with deteriorating road surface conditions. This is because bridge experiences higher dynamic forces due to very poor road surface condition.

5 Conclusions

The present study outlines an approach for the evaluation of response statistics of a single span bridge for random arrival time of the vehicles based on orthogonal polynomial expansion method. The DAF is evaluated using the response statistics obtained from the method. Parameters such as vehicle velocity, arrival rate of the vehicles, acceleration of the vehicles and road surface roughness are considered to study the effect on DAF. Based on the results obtained from the study described above, the main conclusions are as follows:

• 1 The optimum time window to evaluate the DAF is considered as 20 secs.

• 2 The mean flexural stresses are higher for lower vehicle velocity.

• 3 The DAF increases with the road surface irregularity and decreases with increase in vehicle velocity for a single span bridge.

• 4 The DAF increases for arrival rate up to 2 vehicles per second and then decreases further for a single span bridge.

• 5 The DAF increases for higher acceleration of the vehicles. Vehicle acceleration may contribute significantly to bridge response and the resulting DAF may exceed those adopted in current design codes.