Control Framework for Position Control of Three-Segment Tendon-Driven Continuum Robot

Abstract

Each continuum robots have a more flexible and bendable structure than conventional manipulators. This makes it suitable for operating in narrow and deep surgical spaces. This chapter presents a control framework for position control of the three-segment tendon-driven continuum robot. The framework includes kinematic control in configuration space with null space optimization of robot configuration, kinematic constraints, and disturbance in joint space during the tracking process. The presented framework has been successfully simulated to regulate the position error to near zero also can compensate for the joint level disturbances in the form of tendon length variation due to buckling and friction.

1 Introduction

Continuum robot is a bioinspired robot that has structures like an elephant truck, snake body, and octopus’s limb. Due to their hyper flexibility and redundancy, they have wide applications in the medical domain, mainly in Single Port Access (SPA^™) and Natural Orifice Transluminal Endoscopic Surgeries (NOTES) [1]. Conventional serial manipulators have serially connected rigid links with revolute joints, which offer more precise kinematic and dynamic control. However, the miniaturization of these robots is difficult due to the actuators being connected serially at joints. On the other hand, continuum robots are actuated passively by tendon, wire, Shape Memory Alloy (SMA), and precurved tubes for the concentric manipulator, for which the actuation unit is far from the manipulator [2]. Hence, they can be implemented for Minimally Invasive Surgery (MIS). However, these multisegment robots have more complex kinematics and dynamics than the conventional manipulator. In this chapter, a control framework has been formulated to control the tendon-driven three-segment continuum robot to follow the desired trajectory. The differential inverse kinematics [3] has been used with optimization in the null-space of Jacobian to get the unique configuration for each position.

The remaining sections are arranged as follows; Sect. 2 details the preliminary design of the three-segment tendon-driven continuum robot. The continuum robot’s kinematics is explained in Sect. 3. Section 4 exhibits the control framework for the position control and simulation results.

2 Preliminary Design

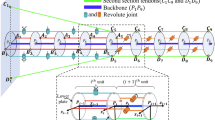
The geometric model of tendon-driven three-segment continuum robot is shown in Fig. 1. Here, the robot consists of three segments, where each continuum segment is driven by three tendons. For which the spacer discs are positioned on the continuum robot’s backbone at specific intervals, act as guides for these tendons. The continuum robot is 150 mm in length, whereas each segment is 50 mm in length and has a 10 mm diameter of spacer discs with a 4 mm distance of guiding hole from the center of the backbone. The tendons of each segment are actuated independently by some motors or linear actuators. Again referring to Fig. 1, each robot segment is characterized by the configuration parameters $(\theta ,\varnothing ,S)$. Here, $\theta$ denotes the robot’s curvature’s bending angle, $\varnothing$ represents the angle of the bending plane from positive X-axis, $S$ describe the robot’s segment’s length, which is assumed constant for each segment. The end tip position and orientation of the continuum robot is given by ${\varvec{P}}={[x, y, z]}^{T}$ and ${\varvec{R}}\in SO(3)$, which are referred to as task space parameters.

Fig. 1

Geometric model of three-segment continuum robot

3 Robot Kinematics

3.1 Forward Kinematics

In this section, to determine the kinematics of the continuum segment, a constant curvature-based method has been used [3,4,5]. Kinematics of the continuum segment is categorized in two stages, which is considered as task space to configuration space kinematic mapping and configuration space to joint (actuator) space kinematic mapping or vice versa as shown in Fig. 2 [5].

Fig. 2

Kinematic model of continuum robot segment

Configuration space to task space: The direct relation between the end tip task space parameters and the bending of continuum segments (in 3D curvature) is described by the robot independent forward kinematic mapping. Here, the end tip position ($P)$ and orientation ($R)$ of the kth continuum segment represented in homogenous transformation matrix for the kth segment is:

$${{\varvec{T}}}_{{\varvec{k}}-1}^{{\varvec{k}}}=\left[\begin{array}{cc}{{\varvec{R}}}_{{\varvec{k}}-1}^{{\varvec{k}}}& {{\varvec{P}}}_{{\varvec{k}}-1}^{{\varvec{k}}}\\ 0& 1\end{array}\right]$$

(1)

$${{\varvec{R}}}_{{\varvec{k}}-1}^{{\varvec{k}}}=\left[\begin{array}{l}{\mathrm{cos}}^{2}\,{\varnothing }_{k}(\mathrm{cos}\,{\theta }_{k}-1)+1 \\ \mathrm{sin}\,{\varnothing }_{k}\mathrm{cos}\,{\varnothing }_{k}(\mathrm{cos}\,{\theta }_{k}-1) \\ -\mathrm{cos}\,{\varnothing }_{k}\mathrm{sin}\,{\theta }_{k} \end{array} \begin{array}{c}\mathrm{ sin}\,{\varnothing }_{k}\mathrm{cos}\,{\varnothing }_{k}(\mathrm{cos}\,{\theta }_{k}-1) \\ {\mathrm{cos}}^{2}\,{\varnothing }_{k}(1-\mathrm{cos}\,{ \theta }_{k})+\mathrm{cos}\,{ \theta }_{k} \\ -\mathrm{sin}\,{\varnothing }_{k}\mathrm{sin}\,{\theta }_{k} \end{array}\begin{array}{c}\mathrm{cos}\,{\varnothing }_{k}\mathrm{sin}\,{\theta }_{k}\\ \mathrm{sin}\,{\varnothing }_{k}\mathrm{sin}\,{\theta }_{k}\\ \mathrm{cos}\,{\theta }_{k}\end{array}\right]$$

(2)

As shown in the following equation, the position vector of the segment's end tip relative to its base or the end tip of the previous segment is;

$$ P_{k - 1}^{k} = \left[ {\begin{array}{*{20}l} {x_{k} } \\ {y_{k} } \\ {z_{k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{S_{k } \cos \emptyset_{k} \left( {1 - \cos \theta_{k} } \right)}}{{\theta_{k} }}} \\ {\frac{{S_{k } \sin \emptyset_{k} \left( {1 - \cos \theta_{k} } \right)}}{{\theta_{k} }}} \\ {\frac{{S_{k } \sin \theta_{k} }}{{\theta_{k} }}} \\ \end{array} } \right] $$

(3)

where ${\varvec{T}}_{k - 1}^{k}$ is the homogenous transformation matrix. ${\varvec{R}}_{k - 1}^{k}$ is the tip orientation matrix; ${\varvec{P}}_{k - 1}^{k}$ is the position vector; $\emptyset_{k}$, $\theta_{k}$ and $S_{k}$ are considered as the configuration parameters of the kth segment of the robot. By successive multiplication of the transformation matrices corresponds to each segment, the total transformation matrix for continuum robot is obtained.

$$ \user2{ R}_{0}^{3} = {\varvec{R}}_{0}^{1} .{\varvec{R}}_{1}^{2} .{\varvec{R}}_{2}^{3} $$

(4)

where (k = 1, 2, 3).

$$ \user2{ P}_{0}^{3} = \left[ {\begin{array}{*{20}c} {\varvec{x}} \\ {\varvec{y}} \\ {\varvec{z}} \\ \end{array} } \right] = {\varvec{R}}_{0}^{1} .{\varvec{R}}_{1}^{2} .{\varvec{P}}_{2}^{3} + {\varvec{R}}_{0}^{1} .{\varvec{P}}_{1}^{2} + {\varvec{P}}_{0}^{1} $$

(5)

where ${ }{\varvec{P}}_{0}^{3}$ and ${ }{\varvec{R}}_{0}^{3}$ is the end tip position and orientation of the distal segment of the three-segment continuum robot w.r.t the robot base frame respectively.

Note: The $\theta_{i}$ = 0 the singular configuration of the robot for any $\theta_{i}$; hence it is avoided by giving some nonzero minimum scalar value.

3.2 Inverse Kinematics

Inverse kinematics for the single segment is much simpler than multisegment continuum robots due to their nonlinear kinematics. Where each segment is actuated independently by the tendons. The vector represents the tendon lengths for each segment ${\varvec{q}}_{{\varvec{i}}}$ = ${\varvec{l}}_{{{\varvec{ij}}}}$ where $l_{ij} = S_{i} - \theta_{i} d\cos (\gamma_{ij} - \emptyset_{i} )$_, j = 1, 2, and 3 (number of tendons for each segment); $i = 1 \ldots {\varvec{n}}$ no. of segments. $l_{ij}$ is the length of the jth tendon of ith segment and $\gamma_{ij}$_, the angle of the guiding hole on the spacer disk from the positive x-axis as shown in Fig. 1. These holes are at equal distances along a circle of radius $d$ on the disc. Configuration vector ${{\mathbf{\psi}}}_{{\varvec{i}}}$ $\left( {\left[ {\theta_{i} ,\emptyset_{i]} } \right]^{T} } \right)$ of each segment. Various methods are used to compute the inverse kinematics for multisegment continuum robots like differential (velocity) kinematics [3], FABRIC approach [6], and geometric approach base closed-loop inverse kinematics [7], etc. These methods have their own sets of advantages and disadvantages. To control the current three-segment robot, we employ the differential inverse kinematics approach. The end tip linear velocity of the distal segment of the robot is represented as;

$$ {\varvec{V}} = \dot{\user2{P}} = \left[ {\begin{array}{*{20}c} {\dot{\user2{x}}} \\ {\dot{\user2{y}}} \\ {\dot{\user2{z}}} \\ \end{array} } \right] = {\varvec{J}}_{{\user2{t\psi }}} \dot{\user2{\psi }} $$

(6)

$$ {\varvec{J}}_{{\user2{t\psi }}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\varvec{X}}}}{{\partial {\varvec{\theta}}_{1} }}\user2{ }} & {\frac{{\partial {\varvec{X}}}}{{\partial \emptyset_{1} }}\user2{ }} & {\frac{{\partial {\varvec{X}}}}{{\partial {\varvec{\theta}}_{2} }}\user2{ }} \\ {\frac{{\partial {\varvec{Y}}}}{{\partial {\varvec{\theta}}_{1} }}} & {\frac{{\partial {\varvec{Y}}}}{{\partial \emptyset_{1} }}} & {\frac{{\partial {\varvec{Y}}}}{{\partial {\varvec{\theta}}_{2} }}} \\ {\frac{{\partial {\varvec{Z}}}}{{\partial {\varvec{\theta}}_{1} }}} & {\frac{{\partial {\varvec{Z}}}}{{\partial \emptyset_{1} }}} & {\frac{{\partial {\varvec{Z}}}}{{\partial {\varvec{\theta}}_{2} }}} \\ \end{array} \user2{ }\begin{array}{*{20}c} {\frac{{\partial {\varvec{X}}}}{{\partial \emptyset_{2} }}\user2{ }} & {\frac{{\partial {\varvec{X}}}}{{\partial {\varvec{\theta}}_{3} }}\user2{ }} & {\frac{{\partial {\varvec{X}}}}{{\partial \emptyset_{3} }}} \\ {\frac{{\partial {\varvec{Y}}}}{{\partial \emptyset_{2} }}} & {\frac{{\partial {\varvec{Y}}}}{{\partial {\varvec{\theta}}_{3} }}} & {\frac{{\partial {\varvec{Y}}}}{{\partial \emptyset_{3} }}} \\ {\frac{{\partial {\varvec{Z}}}}{{\partial \emptyset_{2} }}} & {\frac{{\partial {\varvec{Z}}}}{{\partial {\varvec{\theta}}_{3} }}} & {\frac{{\partial {\varvec{Z}}}}{{\partial \emptyset_{3} }}} \\ \end{array} } \right] $$

(7)

Here, ${\varvec{J}}_{{{\varvec{t}}{{\mathbf{\psi}}}}}$ is the Jacobian matrix for configuration space to task space, which shows the system is over-actuated. Hence, the inverted Jacobian pseudo inverse [3, 8] has been derived. The general inverse kinematics equation is represented as;

$$ \dot{\user2{\psi }} = {\varvec{J}}_{{\user2{t\psi }}}^{{\varvec{T}}} \left( {{\varvec{J}}_{{\user2{t\psi }}} \user2{ }.\user2{ J}_{{\user2{t\psi }}}^{{\varvec{T}}} } \right)\user2{ }.\user2{ V} = \user2{ J}_{{\user2{t\psi }}}^{\# } .{\varvec{V}} $$

(8)

Now the pseudo-inverse with explicit optimization criteria is given by;

$$ \dot{\user2{\psi }} = \user2{ J}_{{\user2{t\psi }}}^{\# } .{\varvec{V}} + \left( {{\varvec{I}} - {\varvec{J}}_{{\user2{t\psi }}}^{\# } {\varvec{J}}_{{\user2{t\psi }}} } \right)\left( {{\varvec{\psi}}_{0} - {\varvec{\psi}}} \right) $$

(9)

where $J_{t\psi }^{\# }$ is the pseudo inverse of the jacobian matrix ${\varvec{J}}_{{{\varvec{t}}{{\mathbf{\psi}}}}}$, and $\left( {{\varvec{I}} - {\varvec{J}}_{{{\varvec{t}}{{\mathbf{\psi}}}}}^{\# } {\varvec{J}}_{{{\varvec{t}}{{\mathbf{\psi}}}}} } \right)\user2{ }\left( {{{\mathbf{\psi}}}_{0} - {{\mathbf{\psi}}}} \right)$ is the optimization term in the null-space of Jacobian. The explicit optimization criterion provides control over robot configurations. The tendon length of actuation for the continuum segment is given by;

$$ \left[ {\begin{array}{*{20}c} {\Delta {\varvec{q}}_{1} } \\ {\Delta {\varvec{q}}_{2} } \\ {\Delta {\varvec{q}}_{3} } \\ \end{array} } \right] = {\varvec{J}}_{{{\varvec{q}},{\varvec{\psi}}}} \user2{ }\Delta {\varvec{\psi}} = \left[ {\begin{array}{*{20}c} {{\varvec{J}}_{12} } & 0 & 0 \\ {{\varvec{J}}_{21} } & {{\varvec{J}}_{22} } & 0 \\ {{\varvec{J}}_{31} } & {{\varvec{J}}_{32} } & {{\varvec{J}}_{33} } \\ \end{array} } \right]\Delta {\varvec{\psi}} $$

(10)

Tendons used for the actuation of distal segments are passed through the previous proximal segments, therefore $\Delta q_{1} ,\Delta q_{2} , \,{\text{and}}\,Lq_{3}$ are the change in length vector of the tendons and ${\varvec{J}}_{{{{\mathbf{q}}},{{\mathbf{\psi}}}}}$ is Jacobian for configuration space to joint space.

4 Position Control

Due to the complex architecture and nonlinear kinematics of multi-segment continuum robot, joint level control is quite challenging. In this section, position control of three segment continuum robot is presented. In order to avoid kinematic nonlinearity, the control input is given in configuration space, and then it is mapped into joint space variables by using Eq. (10).

The continuum robot has a redundant motion for which more solutions are available at the same end tip position. By using the optimization in null-space of Jacobian given in (12), a unique configuration has been achieved for a tip position. The presented control framework is shown in Fig. 3. Initially, desired task space trajectory (desired position and linear velocity vector) is defined by $P_{d} \left( t \right), \dot{P}_{d} \left( t \right)$ and ${\uppsi }_{s}$, $P_{s}$ represents the starting configuration and position of the robot, respectively. After introducing the position error in Eq. (9), the Equation becomes;

$$ \dot{\user2{\psi }} = {\varvec{J}}_{{\user2{t\psi }}}^{\# } .\left( {\user2{ \dot{P}}_{{\varvec{d}}} + {\varvec{K}}_{{\varvec{p}}} .{\varvec{e}}_{{\varvec{p}}} } \right) + \left( {{\varvec{I}} - \user2{ J}_{{\user2{t\psi }}}^{\# } \user2{ J}_{{\user2{t\psi }}} } \right)\left( {{\varvec{\psi}}_{0} - {\varvec{\psi}}} \right) $$

(11)

$$ {\varvec{e}}_{{\varvec{p}}} \left( {\varvec{t}} \right) = {\varvec{P}}_{{\varvec{d}}} \left( {\varvec{t}} \right) - {\varvec{P}}_{{\varvec{a}}} \left( {\varvec{t}} \right) $$

(12)

Fig. 3

Block diagram of kinematic control framework

Putting Eq. (11) in (6) will result in

$$ \dot{\user2{e}}_{{\varvec{p}}} \left( {\varvec{t}} \right) + {\varvec{K}}_{{\varvec{p}}} .{\varvec{e}}_{{\varvec{p}}} \user2{ } = 0 $$

(13)

Here, the proportional controller has been used with proportional gain $K_{p}$ and the control signal will be provided in the form of the rate of change of configuration variables. The additional term $\left( {I - J_{{t{\uppsi }}}^{\# } J_{{t{\uppsi }}} } \right)\left( {{{\mathbf{\psi}}}_{0} - {{\mathbf{\psi}}}} \right)$ in the above Equation represents the optimal null-space of Jacobian to get a unique configuration for the desired position [3]. It does not affect the robot tip position. The control input is mapped in the joint space Eq. (10) and integrated to get the actual robot tip position using forward kinematics. Motor level control will be taken care of the saturation limit of the tendon actuation. In this section, the presented control framework has been implemented for trajectory tracking.

4.1 Circular Trajectory

To verify the proposed control framework, a numerical simulation is carried out for the circular trajectory with some disturbance in the joint level as shown in Fig. 4. Here, we start the simulation from the rest position of the robot also known as the home position, that is, $\psi_{s} = \left[ {0,0,0,0,0,0} \right]$, $P_{s} = \left[ {0,0,150} \right]$ starting configuration and position of the robot, respectively. There is an initial positional error $\left( {P_{s} - P_{d} \left( 0 \right)} \right)$ has been provided to the system which has to be compensated by the proportional controller with gain $K_{p} = 30$. The desired trajectory has been formulated as;

$$ \left\{ {\begin{array}{*{20}l} {x_{d} = R.\cos \left( {\frac{2\pi }{T}t} \right)} \hfill & {} \hfill \\ {y_{d} = R.\sin \left( {\frac{2\pi }{T}t} \right)} \hfill & {t \in \left[ {0, 30} \right]s} \hfill \\ {z_{d} = 90} \hfill & {} \hfill \\ \end{array} } \right. $$

(14)

Fig. 4

Task space trajectory tracking of the circular trajectory a tracking, b position error, c tendon length variation without external disturbance, d tendon length variation with disturbance

where R = 50 mm is the radius of the circular trajectory, T is the total duration of the simulation, and set to 30 s, using fixed step time $\Delta t$ as one millisecond. During the tracking, a saturation limit is provided to the input rate of change of tendon length which depends on the motor speed to control the tendon length (by pushing and pulling). Now, the motor level actuation can be written as;

$$ r.\omega_{m} = \dot{q}\left( t \right) + \dot{\delta }_{k} \left( t \right) $$

(15)

where $\omega_{m}$ the motor speed and r is the radius of the pulley for tendon actuation. Here $\dot{\delta }_{k}$ represents the disturbance in tendon actuation for kth segment. At the motor level, we take care of the kinematic constraints by holding the motor actuation while violating the constraints. Although the motor speedn limits [0.5 − 0.5] rad/s, that is, the limit of the rate of tendon actuation $\left( {r.\omega_{m} } \right) \in$ [5, − 5] mm/s. where $r = 10$ mm. The maximum and minimum length of the tendon for each segment has been used as kinematic constraints as;

$$ \left\{ {\begin{array}{*{20}c} {\left( {l_{ij} } \right)_{\min } = S_{i} - d.\theta_{\max } } \\ {\left( {l_{ij} } \right)_{\max } = S_{i} + d.\theta_{\max } } \\ \end{array} } \right. $$

(16)

For the presented Continuum robot. $\left| \theta \right|_{\max } = \pi$, $d = 4$ mm, and the length of each segment $S_{i} = 50$ mm. Hence, the $\left( {L_{1} } \right)_{\min } = 37.434$ mm and $\left( {L_{1} } \right)_{\max } = 62.566$ mm is the minimum and the maximum length of the tendon during actuation of the first segment, similarly $\left( {L_{2} } \right)_{\min } = 2 \times 37.434$ mm, $\left( {L_{2} } \right)_{\max } = 2 \times 62.566$ mm and $\left( {L_{3} } \right)_{\min } = 3 \times 37.434$ mm, $\left( {L_{3} } \right)_{\max } = 3 \times 62.566$ mm. The robot construction and the actuation mechanism will offer disturbances in the tendon actuation due to its bucking and friction. In the present work, the disturbance in the form of $\dot{\delta }_{k} = k.\sin \left( {t.\frac{2\pi }{T}} \right)$ has been introduced at the joint level.

The trajectory tracking in the task space is shown in Fig. 4a. The position tracking errors during the simulation are shown in Fig. 4b. Variation in tendon lengths during actuation for all three segments has been shown in Fig. 4c under kinematic constraint. The position errors reduce to zero in 3.6 s, thus tracking the desired trajectory. The effect of the external disturbance in tendon length actuation in position tracking (see Fig. 4a) has also been compensated by the motor level control during trajectory tracking, for which the changes in tendon length can be seen in Fig. 4d.

4.2 Spiral Trajectory

The same control framework has been used to track the spiral curve trajectory, which also being stated from the home position with the initial positional error $\left( {P_{s} - P_{d} \left( 0 \right)} \right).$

$$ \left\{ {\begin{array}{*{20}l} {x_{d} = R.\cos \left( {\frac{2\pi }{T}t} \right)} \\ {y_{d} = R.\sin \left( {\frac{2\pi }{T}t} \right)} \\ {z_{d} = 120 - 5. \left( {\frac{4\pi }{T}t} \right)} \\ \end{array} t \in \left[ {0, 50} \right]s} \right. $$

(17)

where R = 50 mm is the radius of the trajectory, T is the total duration of the simulation, set to 50 s, using fixed time step $\Delta t$ as one millisecond. The disturbance in the form of $\delta_{k} = k.\sin \left( t \right)$ function has been introduced at a joint level as above. Figure 5a shows the tracking of the spiral trajectory, and Fig. 5b shows the position error during trajectory tracking.

Fig. 5

Task space trajectory tracking of the spiral trajectory a tracking, b position error, c tendon length variation without external disturbance, d tendon length variation with disturbance

Result and discussion: The position errors reduce to zero in 3 s (see Fig. 5b); thus, the system is successfully tracking the desired trajectory shown in Fig. 5a. Variations in the tendon lengths for all three segments are shown in Fig. 5c. The motor level control also compensates for the effect of the disturbance in tendon length actuation, due to which the changes in tendon length are shown in Fig. 5d. It is observed that when the tendon length constraints were being violated, and the motor control was instructed to hold the position ($\omega_{m} = 0$) to avoid the mechanism failure. Later, the controller compensates for the disturbance by actuating the tendons under the saturation limit.

5 Conclusion and Future Work

In this work, position control has been achieved for the three segment continuum robot using configuration space-based control architecture. The proposed control framework is simple and more efficient than the joint space control. This can be further extended to control both the position and orientation of the continuum robot for surgical application. A presented control framework can be introduced for task space mapping between the haptic device (master) and multi-segment continuum robot (slave). Development of an optimal control framework for task space trajectory (position and orientation) control with redundancy resolution and its experimental validation on the robot is our future work.