A Semi-analytical Approach for Dynamic Characteristics of Beams with the Effect of Static Load

Abstract

This work introduces a semi-analytical approach to illustrate the linearized vibration of clamped–clamped beams in the nonlinear regime due to the effect of static load. The von Karman strain and Hamilton’s principle are utilized to derive the genernal nonlinear equations of beams under static and acoustic pressure load. The nonlinear dynamic problem is analyzed in two parts: the nonlinear static problem and the linearized vibration around the nonlinear static equilibrium state. The modal equation under initial large deflection is a variable coefficient partial differential equation and is difficult to obtain an analytical solution. An approximate solution is performed by the transfer-matrix method and local homogenization. The analysis shows that the variation of pressure load affects the static deflection and the dynamic characteristics of the beam. With the gradual increase of the pressure load, the deflection of the beam has a great influence on the higher-order modal shapes of the beam. And the peak value of the modal shapes near the center of the beam is lower than the sides.

1 Introduction

During the service of a hypersonic vehicle, it has to endure a very complex dynamic environment, such as high dynamic pressure and acoustic pressure load. Clamped–clamped structures exhibit complex geometric nonlinear response characteristics under combined loads. The strain does not exceed the elastic limit, but the static equilibrium and vibration differential equations with large deflection show nonlinear characteristics.

Takabatake [1] clarify the effect of dead loads on the static characteristics of the beam. Furthermore, he considered the effect of dead loads on the dynamic characteristics of beams [2, 3] and plates [4] utilizing suitable assumptions. Zhou et al. [5] developed a load-induced stiffness matrix that considers the stiffening effect of dead loads. And the natural frequencies of beams are calculated using Finite-element methods. Saha et al. [6] studied the large amplitude free vibration of plates based on static analysis by an iterative numerical scheme. Banerjee et al. [7] utilized the nonlinear shooting and Adomain decomposition methods to analyze the large deflection of beams. Wang et al. [8] investigated the effect of static load on the vibro-acoustic characteristics of plates. Carrera et al. [9] developed a geometrical nonlinear total Lagrangian formulation to analyze the vibration modes of beams in the nonlinear regime.

In this paper, a semi-analytical approach is established to illustrate the linearized vibration of clamped–clamped beams in the nonlinear regime due to the effect of static load. By using the Rayleigh–Ritz method and transfer matrix method, the effect of static pressure load on the natural frequencies and modal shapes of beams are studied.

2 Basic Theory

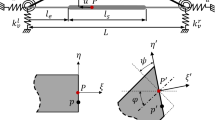
A clamped–clamped rectangular beam under pressure load, as shown in Fig. 1, is considered in this study. The L, b and h are the length, width, and thickness of the beam. The P is the pressure load. The axial displacement components in the midplane are assumed as zero. Suppose that (u, w) denotes the total displacements of a point along the (x, z) coordinates. The von Karman strain and Hamilton’s principle are utilized to derive the nonlinear static equilibrium equations and nonlinear governing equations of the beam. The basic assumptions made to derive the equation can be summarized as follows:

Fig. 1

A clamped–clamped rectangular beam under pressure load

• (1) Assuming the deformation of the beam obeying the hypothesis of the Bernoulli–Euler beam equation.

• (2) All strain components are small enough to satisfy Hooke’s law.

2.1 Semi-analytical Approach for Nonlinear Static Deflection

The Von Karman nonlinear strain–displacement relationships are

$${\varepsilon }_{0x}=-z\frac{{\partial }^{2}{w}_{0}}{\partial {x}^{2}}+\frac{1}{2}\left(\frac{\partial {w}_{0}}{\partial x}\right)^{2}$$

(1)

where ε_0x is the normal strain at an arbitrary point of the beam.

According to Hamilton’s principle, the static equilibrium equations can be derived by

$$\delta ({U}_{p}-{W}_{p})=0$$

(2)

where δ is the variational operator. U_p and W_p represent the strain energy and the potential energy, respectively, which can be written as

$${U}_{p}={\int }_{0}^{L}\frac{1}{8}EA\left(\frac{\partial {w}_{0}}{\partial x}\right)^{4}dx+{\int }_{0}^{L}\frac{1}{2}EI\left(\frac{{\partial }^{2}{w}_{0}}{\partial {x}^{2}}\right)^{2}dx$$

(3)

$${W}_{p}={\int }_{0}^{L}{P}_{0}{w}_{0}dx$$

(4)

where E, A, and I are Young’s modulus, the cross-sectional area, and the cross-sectional moment of inertia, respectively. Furthermore, P₀ is the static pressure load and w₀ is the deflection.

Analytical solutions for the deflection are obtained using Navier’s solution technique. The solution, which satisfies the clamped–clamped boundary conditions, can be assumed as follows.

$${w}_{0}=\sum_{m=1}^{n}{a}_{m}\mathrm{sin}\frac{\pi x}{L}\mathrm{sin}\frac{(2m-1)\pi x}{L}$$

(5)

Substituting Eq. (5) into the Eq. (2). According to the Rayleigh–Ritz method and the variational principle, the static equilibrium equations can be variationally calculated as

$$\frac{\partial ({U}_{p}-{W}_{p})}{\partial {a}_{m}}=0\quad m=1,2,\ldots n$$

(6)

The value of coefficients a_m can be solved by numerical methods.

2.2 Semi-analytical Approach for Modal Analysis

The governing nonlinear equations of vibration with Von Karman strain can be expressed as

$$\rho A\ddot{w}-\frac{3}{2}EA{w}^{{\prime}2}{w}^{\prime\prime}+EI{w}^{\left(4\right)}=P$$

(7)

where P is the combined load of dynamic pressure P₀ and acoustic pressure P₁. And the transverse displacement w can be divided into static deflection w₀(x) and dynamic vibration w₁(x, t). The Eq. (7) can be expressed as

$$\begin{aligned} & \rho A{\ddot{w}}_{1}-\frac{3}{2}EA{{w}^{\prime}}_{0}^{2}{w}_{0}^{{\prime\prime} }-3EA{w}_{0}^{{\prime}}{w}_{0}^{{\prime\prime} }{w}_{1}^{{\prime}}-\frac{3}{2}EA{{w}^{{\prime}}}_{1}^{2}{w}_{0}^{{\prime\prime} }-\frac{3}{2}EA{{w}^{{\prime}}}_{0}^{2}{w}_{1}^{{\prime\prime} }\\ & -3EA{w}_{0}^{{\prime}}{w}_{1}^{{\prime}}{w}_{1}^{{\prime\prime} }-\frac{3}{2}EA{{w}^{{\prime}}}_{1}^{2}{w}_{1}^{{\prime\prime} }+EI{w}_{0}^{\left(4\right)}+EI{w}_{1}^{\left(4\right)}=P \end{aligned}$$

(8)

It is assumed that dynamic pressure is much greater than acoustic pressure. The deformed state w₀(x) is defined as the reference state, and the vibration w₁(x, t) is act on this reference state. The rotations under acoustic pressure are neglected. The Eq. (8) can be rewritten as

$$\rho A{\ddot{w}}_{1}-\frac{3}{2}EA{{w}^{{\prime}}}_{0}^{2}{w}_{0}^{{\prime\prime} }-\frac{3}{2}EA{{w}^{{\prime}}}_{0}^{2}{w}_{1}^{{\prime\prime} }+EI{w}_{0}^{\left(4\right)}+EI{w}_{1}^{\left(4\right)}=P$$

(9)

Due to the dynamic pressure being much greater than acoustic pressure, it is assumed that the w₁ is much better than w₀. And the influence of w₁ on w₀ is ignored. The relationship between static deflection w₀ and dynamic pressure P₀ is expressed as

$$EI{w}_{0}^{\left(4\right)}-\frac{3}{2}EA{{w}^{{\prime}}}_{0}^{2}{w}_{0}^{{\prime\prime} }={P}_{0}(x)$$

(10)

The static deflection w₀ can be obtained by Sect. 2.1. And Eq. (9) can be rewritten as

$$\rho A{\ddot{w}}_{1}-\frac{3}{2}EA{{w}^{{\prime}}}_{0}^{2}{w}_{1}^{{\prime\prime} }+EI{w}_{1}^{\left(4\right)}={P}_{1}(x,t)$$

(11)

The governing equation of free vibration, with the effect of static load, can be simpler as

$$\rho A{\ddot{w}}_{1}-\frac{3}{2}EA{{w}^{{\prime}}}_{0}^{2}{w}_{1}^{{\prime\prime} }+EI{w}_{1}^{\left(4\right)}=0$$

(12)

Based on the separation of variables, the modal equation can be derived from Eq. (12), expressed as

$$EI{\phi }^{\left(4\right)}-\frac{3}{2}EA{{w}_{0}^{{\prime}}}^{2}{\phi }^{{\prime\prime} }-{\omega }^{2}\rho A\phi =0$$

(13)

in which ω is the natural frequency of the beam, and ϕ is the mode function. Equation (13) is a variable coefficient partial differential equation and is difficult to calculate an analytical solution. An approximate solution is performed by the transfer-matrix method based on local homogenization. The beam is divided into n segments and the modal equation of the ith beam is

$$EI{{\phi }_{i}}^{\left(4\right)}-\frac{3}{2}EA{{w}_{0}^{{\prime}}}^{2}({x}_{i}){\phi }_{i}^{{\prime\prime} }-{\omega }^{2}\rho A{\phi }_{i}=0$$

(14)

According to the homogenization theory, let

$${\delta }_{i}^{2}=\frac{1}{{x}_{i+ \text{1} }-{x}_{i}}{\int }_{{x}_{i}}^{{x}_{i+ \text{1} }}\frac{3A{{w}_{0}}^{{\prime}2}(x)}{2I}dx\qquad {\beta }^{4}=\frac{{\omega }^{2}\rho A}{EI}$$

(15)

The general solution of Eq. (14) is

$$\begin{aligned}{\phi }_{i}(x)& ={A}_{i}\sin{\beta }_{i1}(x-{x}_{i})+{B}_{i}\cos{\beta }_{i1}(x-{x}_{i})\\&\quad +\,{C}_{i}\cosh{\beta }_{i2}(x-{x}_{i})+{D}_{i}\sinh{\beta }_{i2}(x-{x}_{i})\end{aligned}$$

(16)

$${\beta }_{i1}=\sqrt{\sqrt{{\beta }^{4}+\frac{{{\delta }_{i}}^{4}}{4}}-\frac{{{\delta }_{i}}^{2}}{2}}\quad {\beta }_{i2}=\sqrt{\sqrt{{\beta }^{4}+\frac{{{\delta }_{i}}^{4}}{4}}+\frac{{{\delta }_{i}}^{2}}{2}}$$

(17)

In which, x_i ≤ x ≤ x_i+1, (i = 1, 2, 3, …, n). A_i, B_i, C_i, and D_i are constants, which are to be determined using the boundary conditions. The displacement and force are continuous between the ith segment and the i + 1th segment which can be written as

$$\begin{aligned} & {\phi }_{i}\left({x}_{i+ 1 }\right)={\phi }_{i+1}\left({x}_{i+ \text{1} }\right) \quad {\phi }_{i}^{{\prime}}\left({x}_{i+ \text{1} }\right)={\phi }_{i+1}^{{\prime}}\left({x}_{i+ \text{1} }\right)\\ & {\phi }_{i}^{{\prime\prime} }({x}_{i+ \text{1} })={\phi }_{i+1}^{{\prime\prime} }({x}_{i+ \text{1} }) \quad {\phi }_{i}^{\prime\prime\prime}({x}_{i+ \text{1} })={\phi }_{i+1}^{\prime\prime\prime}({x}_{i+ \text{1} }) \end{aligned}$$

(18)

The transfer matrix can be expressed as

$$\begin{aligned} &{\varPhi }_{i}\left({x}_{i+ \text{1} }\right){\psi }_{i}={\varPhi }_{i+ \text{1} }\left({x}_{i+ \text{1} }\right){\psi }_{i+1}\\ & {\psi }_{i+1}={\varPhi }_{i+1}^{-1}({x}_{i+ \text{1} }){\varPhi }_{i}({x}_{i+ \text{1} }){\psi }_{i}\end{aligned}$$

(19)

In which

$${\psi }_{i}={\left[\begin{array}{cccc}{A}_{i}& {B}_{i}& {C}_{i}& {D}_{i}\end{array}\right]}^{T}$$

(20)

$${\theta }_{i}(x)=\left[\begin{array}{cccc}\sin{\beta }_{i1}(x-{x}_{i})& \cos{\beta }_{i1}(x-{x}_{i})& \cosh{\beta }_{i2}(x-{x}_{i})& \sinh{\beta }_{i2}(x-{x}_{i})\end{array}\right]$$

(21)

$${\varPhi }_{i}({x}_{j})=[\begin{array}{cccc}{\theta }_{i}({x}_{j})& {\theta }_{i}^{{\prime}}({x}_{j})& {\theta }_{i}^{{\prime\prime} }({x}_{j})& {\theta }_{i}^{\prime\prime\prime}({x}_{j}){]}^{T}\end{array}$$

(22)

The relationship between the nth segment and 1st segment is

$${\psi }_{n}=\varGamma {\psi }_{1}$$

(23)

$$\varGamma =\prod_{i=1}^{i=n}{\varPhi }_{i+1}^{-1}({x}_{i+ \text{1} }){\varPhi }_{i}({x}_{i+ \text{1} })$$

(24)

In clamped boundary conditions, the natural frequencies are determined from the roots of the polynomial

$$\left[\begin{array}{c}\begin{array}{cccc}0& 1& 1& 0\end{array}\\ \begin{array}{cccc}{\beta }_{11}& 0& 0& {\beta }_{12}\end{array}\\ {\varGamma }_{1}\\ {\varGamma }_{2}\end{array}\right]=0$$

(25)

$$\left[\begin{array}{c}{\varGamma }_{1}\\ {\varGamma }_{2}\end{array}\right]=\left[\begin{array}{c}\begin{array}{cccc}\sin({\beta }_{n1}h)& \cos ({\beta }_{n1}h)& \cosh ({\beta }_{n2}h)& \sinh ({\beta }_{n2}h)\end{array}\\ \begin{array}{cccc}{\beta }_{n1}\cos({\beta }_{n1}h)& -{\beta }_{n1}\sin ({\beta }_{n1}h)& {\beta }_{n2}\sinh ({\beta }_{n2}h)& {\beta }_{n2}\cosh ({\beta }_{n2}h)\end{array}\end{array}\right]\varGamma $$

(26)

The structural modal frequency can be obtained by numerically solving Eq. (25). And then the coefficient of the general solution of each beam segment and the approximate modal shape can be obtained.

3 Numerical Results and Discussions

3.1 Verification of the Proposed Method

The following parameters are adopted for the clamped–clamped beam: E = 200 GPa, μ = 0.3, L = 350 mm, ρ = 7.93 × 10⁻⁹ t/mm³, b = 5 mm, and h = 3 mm. The static press is assumed as 0.01 MPa. The accuracy of this method is verified by ABAQUS. Through the convergence analysis, this paper takes 10 segments to solve the structural modal parameters. The Beam element B31 is adopted in ABAQUS, which includes 140 elements and 141 nodes in total. The deflection curve of the beam calculated by the two methods is shown in Fig. 2. The maximum error is 0.019 mm. The modal frequencies of the beam calculated from the proposed and ABAQUS are compared in Table 1. Results show that the modal frequencies and modal shapes obtained from the proposed method agree well with that from ABAQUS.

Fig. 2

Comparisons of the deflection

Table 1 Comparisons of modal frequencies

3.2 Results and Discussion

The effect of pressure load variation on the dynamic characteristics of the beam was investigated in this section. The reference pressure load P_r = 0.01 MPa and the pressure load P was set as P/P_r = 0, 1, 3, 5. The modal frequencies and modal shapes of the beam under varied pressure loads are shown in Figs. 3 and 4 respectively.

Fig. 3

The modal frequencies under pressure load

Fig. 4

The modal shapes under pressure load

Results show that the modal frequencies rise with the pressure load increase. The growth rate of structural deflection gradually was reduced due to geometric nonlinearity. And the increase of modal frequencies gradually slows down. With the gradual increase of the load, the shape of first and second-order modal shapes of the beam does not change significantly, which could be expressed by an approximate trigonometric function. But the third, fourth and fifth-order modal shapes change significantly, and the peak value of the modal wave near the center of the beam is lower than the sides.

4 Conclusion

The large displacement of structures may modify the modal behavior of structures significantly. This work introduces a semi-analytical approach to illustrate the nonlinear vibration of clamped–clamped beams with the effect of static, considering the correlation of moderate rotations and nonlinear vibration.

First, based on the Rayleigh–Ritz method, the static deformation analysis under pressure is carried out through the semi-analytical method. Then, based on the static deformation analysis, the governing differential equation of the beam under initial large deformation is established. The modal equation under initial large deflection is a variable coefficient partial differential equation. Finally, the equation is approximately solved by the transfer-matrix method based on the local homogenization theory.

The analysis shows that the variation of pressure load affects the static deflection and the dynamic characteristics of the beam. With the gradual increase of the load, the deflection of the beam has a great influence on the modal shape of the beam and the peak value of the modal wave near the center of the beam is lower than the sides.