State of Charge Estimation of Lithium-Ion Battery Based on EKF with Adaptive Fading Factor

Abstract

The power generation system with renewable energy supply is susceptible to the influence of external environment. Lithium battery and other energy storage devices need to be added in the new energy field to smooth the output of renewable energy generation system and improve the stability of the integrated system. Accurately estimating the state of charge (SOC) of energy storage batteries can effectively improve the use and reasonable scheduling of batteries. This paper takes ternary lithium battery pack as the research object and builds a second-order RC equivalent circuit model to estimate the SOC. According to the time-varying characteristics of battery model parameters, recursive least square method with forgetting factor was used to identify the parameters, the model parameters are modified using the current data. To solve the problem of accumulated error of extended Kalman filter (EKF) algorithm, an adaptive fading factor was introduced to correct prediction error covariance matrix and suppress the influence of historical data on the current state. Matlab simulation and dynamic stress testing experiments show that, compared with EKF algorithm, the adaptive fading EKF (AFEKF) algorithm has higher accuracy.

1 Introduction

With the continuous progress of strategic goal of ‘carbon peak and carbon neutrality’, increasing the proportion of photovoltaic and wind power generation and the other renewable energy systems in the power grid is an important measure, and the installed capacity of renewable energy continues to increase. Due to the inherent uncertainty and low inertia of distributed photovoltaic and other renewable energy sources, coupled with the off-peak output of load, it brings great challenges to the frequency stability of power system and the consumption of renewable energy sources [1, 2]. The energy storage system can be used to suppress power fluctuation and play the role of peak cutting and valley filling, which is an indispensable part of the new energy field to main source-load balance. Lithium-ion batteries are widely used in electric vehicles and energy storage systems due to their advantages of high energy density, high efficiency and long service life [3, 4]. Accurately estimating the SOC of energy storage batteries can effectively improve the battery life and the rationality of system scheduling.

At present, the SOC estimation methods of Lithium-ion battery mainly include ampere-hour integration, open circuit voltage method, internal resistance method, neural network method and Kalman filter method. As early methods, ampere-hour integration method, open-circuit voltage method and internal method have low estimation accuracy [5]. Ampere-hour integral method has a high requirement on the initial value of the charged state, and the initial error will gradually accumulate with time, and the error will gradually increase. The open-circuit voltage method requires a long period of time to achieve equilibrium within the battery and is not suitable for on-line estimation of SOC. The use of internal resistance methods has been gradually reduced because of the need for specialized equipment and the susceptibility of impedance to temperature. Neural network method requires large data and high cost [6, 7]. This method not only requires a large number of data sets and a long time of training, but also depends on the accuracy of training data to a large extent. If the data amount or conditions are insufficient, the accuracy will be reduced and it is difficult to achieve. Kalman filter algorithm is widely used in linear systems and extended Kalman algorithm extends it to nonlinear systems. It is a mainstream direction of current research to estimate SOC using Kalman algorithm based on the state equation and observation equation of battery equivalent model [8, 9]. The principle of equivalent model is clear, the calculation is simple, and it is suitable for real-time system. At present, the estimation method based on equivalent model combined with Kalman filter has attracted a lot of scholars’ research.

According with the above analysis, this paper constructed the second-order Thevenin equivalent model of lithium-ion battery. The parameters of the model were identified online by recursive least square method, and the SOC of lithium ion battery was estimated by AFEKF algorithm. The adaptive fading factor was introduced into Kalman filter algorithm to reduce the influence of historical data on filtering results. Finally, combined with the experimental results, the AFEKF algorithm is analyzed and compared to verify the superiority of the proposed algorithm.

2 Equivalent Model and Parameter Identification of Lithium-Ion Battery

2.1 Equivalent Circuit Model of Lithium-Ion Battery

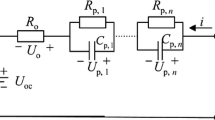
The battery model and parameter identification determine the accuracy of SOC estimation. Thevenin model is shown in Fig. 1. RC parallel network is used to characterize the polarization reaction in the battery, which reflects the nonlinear characteristics of the dynamic charge and discharge response of the battery to a certain extent. In order to simulate the battery polarization transition process and more accurately describe the polarization process and dynamic response behavior of lithium-ion battery, the second-order Thevenin equivalent circuit model was adopted in the experiment, which can improve the accuracy of the model to a certain extent [10,11,12].

Fig. 1.

Second-order Thevenin equivalent circuit model

Subsequent paragraphs, however, are indented. The equivalent model is shown in Fig. 1, where U_oc is the open-circuit voltage and U_b is the battery terminal voltage. U₁ and U₂ are polarization voltages; I_b is battery load current, R₀ is ohmic resistance; R₁ and R₂ are polarization resistors; C₁ and C₂ are polarization capacitors.

According to Kirchhoff's law, the second-order Thevenin model can be expressed as:

$$ \begin{array}{*{20}c} {\dot{U}_1 = - \frac{1}{R_1 C_1 }U_1 + \frac{1}{C_1 }I_t } \\ {\dot{U}_2 = - \frac{1}{R_2 C_2 }U_2 + \frac{1}{C_2 }I_t } \\ {U_b = U_{oc} - R_0 I_t - U_1 - U_2 } \\ \end{array} $$

(1)

SOC is defined as the ratio of the remaining battery power to the actual capacity, which can be expressed by ampere-hour integral as follows:

$$ S_t = S_0 - \frac{\eta t}{{Q_c }}\int \limits_{t_0 }^t {I_t dt} $$

(2)

where, $\eta$ is the Coulomb efficiency coefficient, Q_c is the standard capacity of the battery, and S₀ is the initial SOC of the battery pack.

Combining Eq. (1), the battery state space equation in discrete form can be obtained as follows:

$$ \left( {\begin{array}{*{20}c} {SOC_{k + 1} } \\ {U_{1,k + 1} } \\ {U_{2,k + 1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {e^{ - \frac{T}{\tau_1 }} } & 0 \\ 0 & 0 & {e^{ - \frac{T}{\tau_2 }} } \\ \end{array} } \right) \times \left( {\begin{array}{*{20}c} {SOC_k } \\ {U_{1,k} } \\ {U_{2,k} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} { - \frac{\eta T}{{Q_c }}} \\ {R_1 \left( {1 - e^{ - \frac{T}{\tau_1 }} } \right)} \\ {R_2 \left( {1 - e^{ - \frac{T}{\tau_2 }} } \right)} \\ \end{array} } \right) \times I_{t,k} + \left( {\begin{array}{*{20}c} {w_{1,k} } \\ {w_{2,k} } \\ {w_{3,k} } \\ \end{array} } \right) $$

(3)

The observation equation is as follows:

$$ U_{t,k} = U_{oc} \left( {SOC_k } \right) - U_{1,k} - U_{2,k} - R_0 I_{t,k} + v_k $$

(4)

where, T is the sampling time; w is process noise; v is measurement noise; $\tau_1$ and $\tau_2$ are the time constants of the polarization loop; The state variable is $\left[ {SOC_k ,U_{1,k} ,U_{2,k} } \right]^T$, the control variable is $I_{t,k}$, and the observation variable is $U_{t,k}$.

2.2 SOC-OCV Relationship Curve of Battery

There is a nonlinear functional relationship between the open-circuit voltage (OCV) and SOC of the power battery [9, 10]. In order to obtain the OCV-SOC relation curve of battery, the constant current intermittent charge-discharge method was used for ternary lithium battery. The specific parameters of ternary lithium battery were as follows: standard capacity is 2.5Ah, charging cut-off voltage is 4.2V, and discharge cut-off voltage is 2.75V.

On the Arbin(BT2000) battery test system, firstly, after the battery in full charge state stands for 1h, the constant current of 0.5C is used to discharge the ternary lithium battery. After 12 min of the discharge time, the battery will stand for 1h again, so that the battery will return to its equilibrium state before running the next cycle. Repeat the above steps until the battery terminal voltage is lower than 2.75V, stop discharging, record the data and perform fitting. The fitting accuracy increases with the increase of the fitting order. Therefore, the ninth order curve fitting is carried out for OCV-SOC to reduce the reduction of SOC estimation accuracy caused by the fitting curve error. The curve fitting relation is as follows:

$$ \begin{array}{*{20}c} {U_{OC} = - 14.12x^9 + 130.2x^8 - 521.3x^7 + 1095.2x^6 - 1341.7x^5 } \\ { + 1007.6x^4 - 437.4x^3 + 95.84x^2 - 8.22x + 3.92} \\ \end{array} $$

(5)

The obtained OCV-SOC relation curve is shown in Fig. 2.

Fig. 2.

OCV-SOC Relation Curve

2.3 Parameter Identification of Battery Model

Recursive least squares operation is a method developed from adaptive filtering theory for model identification and data mining [11, 12]. The recursive least square method has a small amount of computation and can identify the characteristics of the dynamic system in real time. Therefore, this method is adopted in this paper to identify the parameters of the equivalent model. The principle is as follows:

$$ y_k = \varphi_k^T \theta_k + e_k $$

(6)

where, $y_k$ is the system output; $\varphi_k$ is data vector; $\theta_k$ is the parameter vector to be measured, and $e_k$ is the equation error. The recursion formula is as follows:

$$ \left\{ {\begin{array}{*{20}l} {\hat{\theta } = \hat{\theta }_{k - 1} + K_k \left( {y_k - \varphi_k^T \hat{\theta }_{k - 1} } \right)} \hfill \\ {K_k = \frac{{P_{k - 1} \varphi_k }}{{1 + \varphi_k^T P_{k - 1} \varphi_k }}} \hfill \\ {P_k = \left( {I - K_k \varphi_k^T } \right)P_{k - 1} } \hfill \\ \end{array} } \right. $$

(7)

The recursive least square method revises the results obtained at the last moment according to the recursive formula through the newly introduced data, and obtains the new estimated value. The product of the estimated error and the system gain is taken as the estimated update value at the current time. The estimated value at the current time can be obtained by adding the estimated updated value and the estimated value at the last time. Finally, the covariance matrix at this time can be calculated according to the covariance matrix at the last time and the system gain to prepare for the next round of parameter estimation.

The transfer function of the system is as follows

$$ G(s) = \frac{U_b (S)}{{U_{oc} (S)}} = - \frac{{R_0 s^2 + \frac{R_0 R_1 C_1 + R_0 R_2 C_2 + R_2 R_1 C_1 + R_1 R_2 C_2 }{{R_1 C_1 R_2 C_2 }}s + \frac{R_0 + R_1 + R_2 }{{R_1 C_1 R_2 C_2 }}}}{{s^2 + \frac{R_1 C_1 + R_2 C_2 }{{R_1 C_1 R_2 C_2 }}s + \frac{1}{R_1 C_1 R_2 C_2 }}} $$

(8)

Z function corresponding to the S-transformed function can be written as

$$ G\left( {z^{ - 1} } \right) = \frac{{U_t \left( {z^{ - 1} } \right) - U_{oc} \left( {z^{ - 1} } \right)}}{{ - I_t \left( {z^{ - 1} } \right)}} = \frac{{\theta_3 + \theta_4 z^{ - 1} + \theta_5 z^{ - 2} }}{{1 - \theta_1 z^{ - 1} - \theta_2 z^{ - 2} }} $$

(9)

where $\theta_1$, $\theta_2$, $\theta_3$, $\theta_4$ and $\theta_5$ are the coefficients related to the model parameters, and their values are

$$ \left\{ {\begin{array}{*{20}l} {\theta_1 = \frac{8b - 2T^2 }{{4b + 2cT + T^2 }}} \hfill \\ {\theta_2 = \frac{4cT}{{4b + 2cT + T^2 }} - 1} \hfill \\ {\theta_3 = - \frac{4ab + 2eT + dT^2 }{{4b + 2cT + T^2 }}} \hfill \\ {\theta_4 = \frac{8ab - 2dT^2 }{{4b + 2cT + T^2 }}} \hfill \\ {\theta_5 = - \frac{4ab - 2eT + dT^2 }{{4b + 2cT + T^2 }}} \hfill \\ \end{array} } \right. $$

(10)

where a = R₀, b = τ₁τ₂, c = τ₁ + τ₂, d = R₀ + R₁ + R₂, e = R₀(τ₁ + τ₂) + R₁τ₂ + R₂τ₁.

The data vector and parameter vector are respectively as

$$ \left\{ {\begin{array}{*{20}l} {\theta (k) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {\theta_1 } \hfill & {\theta_2 } \hfill & {\theta_3 } \hfill & {\theta_4 } \hfill & {\theta_5 } \hfill \\ \end{array} } \\ \end{array} } \right]^T } \hfill \\ {\varphi (k) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {E(k - 1)} \hfill & {E(k - 2)} \hfill & {I(k)} \hfill & {I(k - 1)} \hfill & {I(k - 2)} \hfill \\ \end{array} } \\ \end{array} } \right]} \hfill \\ \end{array} } \right. $$

(11)

By substituting Eqs. (6) and (11) into the recursive least square method, the corresponding parameters of the battery model can be obtained.

3 Extended Kalman Filter with Adaptive Fading Factor

3.1 Traditional Extended Kalman Filter

Kalman filter algorithm is a method widely used in linear systems, and extended Kalman filter algorithm extends Kalman algorithm to nonlinear systems [5,6,7]. EKF linearizes the nonlinear model locally to obtain an approximate linearized model, and then completes the estimation of the target state.

The EKF state space expression is shown as follows:

$$ \left\{ {\begin{array}{*{20}l} {x_{k + 1} = f\left( {x_k ,u_k } \right) + w_k } \hfill \\ {y_k = h\left( {x_k ,u_k } \right) + v_k } \hfill \\ \end{array} } \right. $$

(12)

In Eq. (12), $x_k$ represents the state vector of the system at time k, $u_k$ represents the input vector of the system at time k; $f\left( {x_k ,u_k } \right)$ represents the state transition function of the system, $h\left( {x_k ,u_k } \right)$ represents the observation function in the system; $w_k$ represents the state noise in the system, $v_k$ represents the measurement noise in the system, $w \sim (0,Q)$ and $v \sim (0,R)$ satisfies the normal distribution, and represents the value of the state of the system and the covariance of the measurement equation respectively.

Using the local linear characteristics of the nonlinear system, the nonlinear model is locally linearized, and the first-order Taylor expansion is carried out on the state transition function and measurement function in Eq. (12), and the higher-order terms higher than the second-order are omitted, and Eq. (13) is obtained:

$$ \left\{ {\begin{array}{*{20}l} {x_{k + 1} \approx f\left( {\hat{x}_k ,u_k } \right) + \frac{\partial f}{{\partial \hat{x}_k }}\left( {x_k - \hat{x}_k } \right) + w_k } \hfill \\ {y_k \approx h\left( {\hat{x}_k ,u_k } \right) + \frac{\partial h}{{\partial \hat{x}_k }}\left( {x_k - \hat{x}_k } \right) + v_k } \hfill \\ \end{array} } \right. $$

(13)

The parameters of nonlinear system can be transformed into matrix form by mathematical calculation.

$$ \left\{ {\begin{array}{*{20}l} {A_k = \frac{{\partial f\left( {x_k ,u_k } \right)}}{{\partial \hat{x}_k }}} \hfill \\ {C_k = \frac{{\partial h\left( {x_k ,u_k } \right)}}{{\partial \hat{x}_k }}} \hfill \\ \end{array} } \right. $$

(14)

Substituting Eq. (14) into Eq. (13), it yields:

$$ \left\{ {\begin{array}{*{20}l} {x_{k + 1} \approx f\left( {\hat{x}_k ,u_k } \right) + A_k \left( {x_k - \hat{x}_k } \right) + w_k } \hfill \\ {y_k \approx h\left( {\hat{x}_k ,u_k } \right) + C_k \left( {x_k - \hat{x}_k } \right) + v_k } \hfill \\ \end{array} } \right. $$

(15)

Initialize the state variable.

$$ \left\{ {\begin{array}{*{20}l} {x_0 = E\left( {x_0 } \right)} \hfill \\ {P_0 = E\left( {x_0 - \hat{x}_0 } \right)\left( {x_0 - \hat{x}_0 } \right)} \hfill \\ \end{array} } \right. $$

(16)

The flow chart of EKF is shown in Fig. 3. Steps (3) and (4) are collectively called prior estimation, Steps (5) and (6) compose the posterior estimation. In Fig. 3, $\hat{x}_{k + 1}^-$ represents the prior estimated value of the system at time k + 1; $P_{k + 1}^-$ represents the prior estimated covariance of the system at time k + 1; $P_k^+$ represents the posterior estimated covariance of the system at time k; $K_{k + 1}$ is the Kalman gain at time k + 1, it is improved based on state estimation and covariance estimation. $P_{k + 1}^+$ represents the posterior estimate of the error covariance output of the system at time k + 1.

Fig. 3.

Flow Chart of EKF Algorithm

3.2 Analysis of EKF with Adaptive Fading Factor

The traditional extended Kalman filter algorithm is difficult to be used in the estimation process with complex environment, and the extended Kalman filter algorithm will diverge due to the error of mathematical model of nonlinear system, which will affect the accuracy of estimation [2,3,4]. To solve this problem, on the basis of EKF algorithm, a fading factor is introduced to weaken the proportion of old observations in the prediction process, increase the weight of new observations in the prediction correction process, and then suppress the filtering divergence. The expression is as follows:

$$ P_{k + 1}^- = \lambda_{k + 1} \left( {A_{k + 1} P_k A_{k + 1}^T + Q_{k + 1} } \right) $$

(17)

$\lambda_{k{ + }1}$ is the fading factor, and the calculation method is as follows:

The innovation dk+1 at time k is defined as the difference between the actual and predicted observations of the filter

$$ d_{k{ + }1} = y_{k{ + }1} - \hat{y}_{k{ + }1}^- $$

(18)

When the Kalman gain is the optimal gain matrix, the innovation sequences are uncorrelated, that is, the innovation sequences are all orthogonal. Thus, it yields:

$$ \begin{aligned} E\left[ {d_{k + j} d_{k + 1}^T } \right] = C_{k + j} A_{k + j} \left( {E - K_{k + j} C_{k + j - 1} } \right) & \cdots A_{k + 2} \left( {E - K_{k + 2} C_{k + 1} } \right) \\ & \cdot A_{k + 1} \left( {P_{k + 1}^ - C_{k + 1}^T - K_{k + 1} V_{k + 1} } \right) = 0 \\ \end{aligned} $$

(19)

For the optimum λk, the following equation should hold:

$$ P_{k + 1}^- C_{k + 1}^T - K_{k + 1} V_{k + 1} = 0 $$

(20)

Substituting Kalman gain into the above equation, yields:

$$ P_{k + 1}^- C_{k + 1}^T \left[ {E - \left( {C_{k + 1} P_{k + 1}^- C_{k + 1}^T + R_{k + 1} } \right)^{ - 1} V_{k + 1} } \right] = 0 $$

(21)

_Since $P_{\text{k}}^{ - }$ _{is a positive definite matrix,} $C_k^{\text{T}}$ _{is a nonsingular matrix, then yields}

$$ \left\{ \begin{gathered} E - \left( {C_{k + 1} P_{k + 1}^- C_{k + 1}^T + R_{k + 1} } \right)^{ - 1} V_{k + 1} = 0 \hfill \\ \lambda_{k + 1} C_{k + 1} \left( {A_{k + 1} P_k A_{k + 1}^T + Q_{k + 1} } \right)C_{k + 1}^T = V_{k + 1} - R_{k + 1} \hfill \\ \end{gathered} \right. $$

(22)

_{Set the minimum value of} $\lambda_k$ _{is 1, yields:}

$$ \lambda_{k + 1} = \max \left\{ {1,\frac{{tr\left( {V_{k + 1} - R_{k + 1} } \right)}}{{tr\left( {C_{k + 1} \left( {A_{k + 1} P_k A_{k + 1}^T + Q_{k + 1} } \right)C_{k + 1}^T } \right)}}} \right\} $$

(23)

Fig. 4.

Flow Chart of EKF with Adaptive Fading Factor

According to innovation covariance theory, the matrix fading factor is set to modify the prediction error covariance matrix, and then the filtering divergence caused by the continuous monotonic change of the gain matrix is contained, so as to achieve the purpose of improving the estimation accuracy and suppressing filtering divergence. The SOC estimation process of AFEKF algorithm is shown in the Fig. 4.

4 Experiment and Simulation Analysis

In order to verify the robustness and accuracy of the above algorithm, the dynamic stress testing (DST) condition was used for experimental verification. The current curve under DST condition is shown in Fig. 5.

Fig. 5.

Curve of Charging and Discharging in DST Condition

The initial SOC value of the battery is set to 100%. When the initial value is known and accurate, the SOC value of each time point is calculated by ampere integration method as the reference value, and then compared and analyzed with the estimated value of various algorithms. Figure 6 shows the comparison between the estimation results of EKF algorithm and AFEKF algorithm and the reference values. Fig. 7 shows the error curves between the estimation results of the two algorithms and the reference values.

Fig. 6.

SOC Estimation Results under DST Conditions

Fig. 7.

Estimation Error Curve under DST Conditions

As can be seen from the figure, the SOC curve estimated by AFEKF algorithm is more consistent with the real SOC curve, which indicates that the effect of AFEKF algorithm is better than that of EKF algorithm. EKF is affected by the cumulative error of historical data, resulting in a relatively large SOC estimation error. AFEKF modifies the covariance matrix of prediction error by adding an adaptive fading factor, thereby curbing the filtering divergence caused by the continuous monotonicity change of the gain matrix, and achieving the improvement of SOC estimation accuracy. The estimation errors of different algorithms is listed in Table 1.

Table 1. Estimation error of different algorithms

As can be seen from the table, the accuracy of AFEKF in estimating SOC under DST conditions can be stable within 1.5%, which is about 3.5% higher than that of EKF.

5 Conclusion

Aiming at the problem of error accumulation when using EKF algorithm to estimate SOC of lithium-ion batteries, this paper proposes a SOC estimation method based on adaptive fading extended Kalman (AFEKF). Selects the Thevenin equivalent model, using the least squares method for model parameter identification, adaptive fading factor, introduced the EKF, correct prediction error covariance matrix, which contain continuous gain matrix caused by filtering divergence of monotonous, decrease the results, the influence of old data to the filter achieve the goal of ascension estimation precision and restrain filtering divergence. The experimental results show that compared with EKF algorithm, AFEKF algorithm has smaller estimation error and smaller fluctuation range of SOC estimation error. The SOC estimation error is 1.38%, and the accuracy is increased by 3.51%, which achieves better SOC estimation accuracy.