Curve Trajectory Tracking for Autonomous Vehicles Using Linear Time-Varying MPC

Abstract

Most researches concerning the yaw stability and rollover prevention for autonomous vehicles are studied separately and decoupled the longitudinal and lateral vehicle dynamics control. However, the roll motion influences the yaw stability during high speed curve steering manoeuvres. With this in mind, a curve trajectory stable tracking controller for autonomous vehicles using linear time-varying model predictive control (LTV MPC) is proposed in this paper. The lateral dynamics control employs the LTV MPC to generate a sequence of optimal steering angles considering the constraints of control input, state output, yaw stability and roll stability together in the cost function, in which the prediction model utilizes an 8 degrees of freedom (DOF) vehicle model and the plant utilizes a 14-DOF vehicle model. The longitudinal control adopts PID control embedded in the MPC framework to update the speed at each optimization step and generate the total wheel torque for speed tracking. The trajectory tracking simulation results demonstrate that the vehicle tracks the reference trajectory and speed well with the proposed controller, which satisfies the constraints of control input, state output as well as the boundaries of yaw stability envelope, sideslip angle and roll angle, thereby reducing the risk of vehicle skid and rollover.

1 Introduction

Motion control, primarily involving longitudinal and lateral control, is one of the crucial technologies for autonomous vehicles, in which the lateral control refers to path tracking and the longitudinal control refers to speed tracking. Most researches on motion control of automated vehicles used decoupled controllers for longitudinal and lateral dynamics respectively, in which the speed is assumed constant in lateral control and the lateral coupling effects are not considered in longitudinal control [1, 2]. However, the vehicle longitudinal and lateral dynamics are strongly coupled during curve trajectory tracking. Therefore, it is essential to consider the longitudinal control and the lateral control simultaneously in autonomous trajectory tracking to improve the tracking performance in a larger operating range. A combined longitudinal and lateral control method considering the coupling effects was proposed in [3] for autonomous guidance using nonlinear MPC for the lateral control and a direct Lyapunov approach for the longitudinal control, in which the reference speed was updated to improve vehicle lateral stability. Another combined longitudinal-lateral control method was proposed in [4] to improve the yaw stability using direct yaw moment control (DYC), in which the LTV MPC was employed for the lateral control and the sliding mode control for the longitudinal control.

Aiming at addressing the problem of coupled lateral and longitudinal motion control, researchers have proposed different control methods, such as the optimal control [5, 6], the PID control [7, 8], the sliding mode variable structure control [9, 10] and the model predictive control [11], etc. However, the optimal control is influenced by external disturbances and uncertainties and usually combined with adaptive control to improve the robustness; the PID control suffers the difficulty of tuning the parameters; and the sliding mode variable structure control is confronted with the unavoidable chattering problem. The model predictive control absorbs the idea of optimal control, which accomplishes optimization problems over a finite receding horizon rather than globally. Moreover, the MPC method involving the disturbance and uncertainty naturally during feedback is convenient to consider the constraints of control input limit and state output admissible in the solution, so it is more robust than the optimal control. An adaptive model predictive trajectory tracking method was proposed in [12] to consider the influence of road curvature and the uncertainty of the time-varying tire cornering stiffness; An MPC-based trajectory tracking control was proposed in [13] to consider the influence of road curvature to the tracking stability. A dual-envelop-oriented moving horizon path tracking controller was proposed in [14] to consider shape of vehicle as inner-envelop and feasible road region as outer-envelop and employed the varied sample time and varied prediction horizon to deal with modelling error. However, the above MPC-based methods either assumed the longitudinal velocity was constant or changed very small without consideration of trajectory tracking under time-varying speed, or took the 2-DOF vehicle model as the prediction model without considering the coupling effects of longitudinal and lateral dynamics.

On the other hand, the yaw stability and roll stability during the curve trajectory tracking is essential to ensure the safety of autonomous vehicles as the longitudinal velocity increases [15]. Researchers provided different control schemes to improve the vehicle stability, such as the adaptive nonlinear control method [16], the hierarchical DYC control based on the linear quadratic regulator (LQR) method [17], the gain-scheduled linear parameter varying (LPV) $H_{\infty }$ robust control [18], the adaptive integrated control based on the Lyapunov stability theory [19], and the MPC-based yaw stability control [20], etc., in which the controllers concerning the yaw stability and roll stability were designed separately. However, the yaw stability and the rollover prevention should be demanded simultaneously during severe curve steering manoeuvres due to coupling effects. For instance, the yaw stability control alters the tire longitudinal and lateral force by applying braking which causes the change of roll dynamics; In other cases, rollover prevention control alters the tires’ vertical forces and deteriorates the yaw stability control. Hence, vehicle stability control requires yaw stability and roll stability simultaneously to achieve a safe and controlled balance. Some robust controllers based on LPV MPC were proposed to maintain the yaw and roll stability during path tracking [21], the longitudinal dynamics coupling effects on the vehicle lateral, yaw and roll motion have not been considered yet.

As summarized above, there are pros and cons in existing methods dealing with the trajectory tracking control considering the vehicle stability. In this paper, a curve trajectory tracking control for autonomous vehicles via LTV MPC is proposed to consider vehicle dynamics coupling effects and time-varying speed, in which the longitudinal velocity of the prediction model is updated through PID control while the yaw stability envelope and rollover prevention constraints are involved together in the cost function to implement the curve trajectory tracking, ensuring the vehicle yaw stability and roll stability simultaneously.

The configuration of this paper is structured as follows: the vehicle dynamics models are summarized in Sect. 2; the curve trajectory tracking controller design is specified in Sect. 3; the validation of the vehicle models and the performance of the proposed controller are detailed in Sect. 4; Sect. 5 concludes with several highlights and outlines the future work.

2 Vehicle Dynamics Models

A brief introduction of different vehicle models including a linear tire model, an 8-DOF vehicle model and a 14-DOF vehicle model is presented in this section. These models are also specified in the previous research work in [22,23,24,25,26]. Furthermore, numerical simulation results concluded that the controllers using an 8-DOF vehicle model as the prediction model exhibited better trajectory tracking performance than the one using bicycle model due to its consideration of roll motion and lateral load transfer during high-speed cornering [22].

2.1 Tire Model

Tire forces involving strong nonlinearity are the primary external factors influencing vehicle dynamic behaviour except for the gravity and aerodynamics. The longitudinal and lateral tire forces are assumed to depend on normal force, surface friction, slip angle, and slip ratio. However, if tires have small slip angle and slip ratio, a linearized tire model can be assumed to represent longitudinal and lateral tire forces. Considering the complexity of the tire modeling and the computational cost in the control algorithm, a linear tire model is employed in this paper without consideration of the influences of load transfer on tire cornering stiffness and longitudinal stiffness [22,23,24,25,26,27].

2.2 8-DOF Vehicle Model

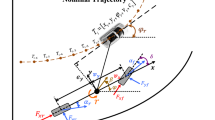
An 8-DOF vehicle model that ignores the vehicle heave and pitch motions is capable of predicting the vehicle longitudinal, lateral, yaw and roll dynamics behaviours and rotational dynamics of each wheel. The schematic of an 8-DOF vehicle model is shown in Fig. 1 [22,23,24,25,26, 28]. The equations of motion for the sprung mass are given as follows [22,23,24,25,26, 28]:

$$ m\left( {\dot{u} - \omega_{z} v} \right) = \sum {F_{xgij} + \left( {m_{uf} a - m_{ur} b} \right)\omega_{z}^{2} - 2h_{rc} m_{s} \omega_{z} \omega_{x} } $$

(1)

$$ m\left( {\dot{v} + \omega_{z} u} \right) = \sum {F_{ygij} + \left( {m_{ur} b - m_{uf } a} \right)\dot{\omega }_{z} + h_{rc} m_{s} \dot{\omega }_{x} } $$

(2)

$$ \begin{aligned} & I_{z} \dot{\omega }_{z} + I_{xz} \dot{\omega }_{x} = \left( {F_{yglf} + F_{ygrf} } \right)a - \left( {F_{yglr} + F_{ygrr} } \right)b \\ & + \frac{{\left( {F_{xgrf} - F_{xglf} } \right)c_{f} }}{2} + \frac{{\left( {F_{xgrr} - F_{xglr} } \right)c_{r} }}{2} + \left( {m_{ur} b - m_{uf} a} \right)\left( {\dot{v} + \omega_{z} u} \right) \\ \end{aligned} $$

(3)

$$ \left( {I_{x} + m_{s} h_{rc}^{2} } \right)\dot{\omega }_{x} + I_{xz} \dot{\omega }_{z} = m_{s} gh_{rc} \phi - \left( {k_{\phi f} + k_{\phi r} } \right)\phi - \left( {b_{\phi f} + b_{\phi r} } \right)\dot{\phi } + h_{rc} m_{s} \left( {\dot{v} + \omega_{z} u} \right) $$

(4)

where,

$$ h_{rc} = \frac{{h_{rcf} b + h_{rcr} a}}{a + b} $$

(5)

Fig. 1.

The 8-DOF Vehicle Model [22,23,24,25,26, 28]

The symbols used in the equations are as follows: ${ }m$ is the vehicle mass; $m_{s}$ is the sprung mass; $m_{uf}$/$m_{ur}$ is front/rear unsprung mass; a/b denotes distance from front/rear wheel center to vehicle center of mass (C.M.); $\omega_{x}$ denotes vehicle roll angular velocity; $\omega_{z}$ denotes vehicle yaw angular velocity; v represents the lateral velocity; u represents the forward vehicle speed; $F_{ygij}$ and $F_{xgij}$ denote the lateral and longitudinal forces at each tire contact patch; $h_{rc}$ is the vertical distance between the roll center and the sprung mass. $h_{rcf}$/$h_{rcr}$ denote the vertical distance of front/rear roll center below the sprung mass; $I_{x}$/$I_{z}$ denote the sprung mass roll/yaw inertial; $I_{xz}$ denotes the product of yaw and roll inertial; $c_{f}$/$c_{r}$ represent front/rear track width; $\phi$ is the roll angle; g is the acceleration of gravity; $k_{\phi f}$/$k_{\phi r}$ represent the equivalent front/rear suspension roll stiffness; $b_{\phi f}$/$b_{\phi r}$ represent the equivalent front/rear suspension roll damping coefficient; the subscripts ‘ij’ denotes left front (lf), right front (rf), left rear (lr) and right rear (rr).

2.3 14-DOF Vehicle Model

A 14-DOF vehicle model can not only consider the DOFs in 8-DOF vehicle model, but also predict the vehicle pitch and heave motions. Furthermore, it can simulate the vehicle response to vertical force inputs even after the wheel lifts off. Therefore, it is suitable to validate the rollover prevention control scheme [22,23,24,25,26, 28].

The schematic of a 14-DOF model is illustrated in Fig. 2. The coordinate frame 1, i.e., the body-fixed coordinates (xyz) is attached at the C.M. of the sprung mass. The roll, pitch and yaw angle are $\phi$, $\theta$, $\psi$, respectively. w denote the sprung mass vertical velocity. $\omega_{y}$ represents the pitch angular velocity. The coordinate frame 2 (x’y’z’) can be determined by rotating the inertial frame through yaw angel. The coordinate frame 1 and the inertial fixed coordinate frame can be determined by coordinate transformations using the cardan angles (i.e. $\phi$, $\theta$, $\psi$).

Fig. 2.

The 14-DOF Vehicle Model and the Coordinate Frames [22,23,24,25,26, 28]

In the case of a front-wheel drive vehicle, the equations of front right and rear right wheel rotational dynamics are written as [25, 26, 29]:

$$ \begin{array}{*{20}c} {I_{w} \dot{\omega }_{rf} = T_{drf} - T_{brf} - r_{rf} F_{xtrf} } \\ \end{array} $$

(6)

$$ I_{w} \dot{\omega }_{rr} = - T_{brr} - r_{rr} F_{xtrr} $$

(7)

where, $T_{drf}$ denotes the wheel driving torque and $T_{brf}$ denotes the wheel braking torque. $r_{rf}$ and $r_{rr}$ represent the front and rear effective tire rolling radius.

3 Trajectory Tracking Controller Design

In order to consider a time-varying longitudinal velocity, the PID speed tracking controller is embedded in the MPC framework to update the longitudinal velocity of the prediction model during each optimization. Based on the previous work in [24,25,26], a curve trajectory stable tracking controller considering the coupling longitudinal and lateral dynamics effects is provided in this section. The schematic of the proposed coupled controller is illustrated in Fig. 3.

Fig. 3.

Schematic of the Coupled Longitudinal and Lateral Control [24,25,26]

3.1 Lateral Dynamics Control

Taking the advantages of less computational cost and simpler calculation, the lateral control scheme employs the LTV MPC to implement the curve trajectory tracking, in which the 8-DOF vehicle model is utilized as the prediction model, thus bringing in the longitudinal and lateral coupling effects in vehicle dynamics [24,25,26].

3.1.1 Vehicle Model Linearization

The front road wheel steering angle is taken as the control input, i.e. $u = \delta$, and the state variable is set as $\chi = \left[ {\dot{x},\dot{y},\phi ,\psi ,\dot{\phi },\dot{\psi },Y,X} \right]^{T}$. The state equation at the operating point can be given as:

$$ \dot{\chi }_{o} = f\left( {\chi_{o} ,u_{o} } \right) $$

(8)

Taking the Tayler series expansion and ignoring higher order terms, the state equation at the operating point is given as [22,23,24,25,26]:

$$ \dot{\chi } = f\left( {\chi_{o} ,u_{o} } \right) + \frac{{\partial f\left( {\chi ,u} \right)}}{\partial \chi }|_{{\begin{array}{*{20}c} {\chi = \chi_{o} } \\ {u = u_{o} } \\ \end{array} }} \left( {\chi - \chi_{o} } \right) + \frac{{\partial f\left( {\chi ,u} \right)}}{\partial u}|_{{\begin{array}{*{20}c} {\chi = \chi_{o} } \\ {u = u_{o} } \\ \end{array} }} \left( {u - u_{o} } \right) $$

(9)

Subtracting Eq. (8) from Eq. (9) yields:

$$ \dot{\tilde{\chi }} = A\tilde{\chi } + B\tilde{u} $$

(10)

where, $\dot{\tilde{\chi }} = \dot{\chi } - \dot{\chi }_{o}$, $\tilde{\chi } = \chi - \chi_{o}$, $\tilde{u} = u - u_{o}$, $A = \frac{\partial f(\chi ,u)}{{\partial \chi }}|_{{\begin{array}{*{20}c} {\chi = \chi_{o} } \\ {u = u_{o} } \\ \end{array} }}$, $B = \frac{\partial f(\chi ,u)}{{\partial u}}|_{{\begin{array}{*{20}c} {\chi = \chi_{o} } \\ {u = u_{o} } \\ \end{array} }}$

In order to apply this model to the MPC-based controller design, the Eq. (10) is further described in the form of a discretized state-space expression:

$$ \chi \left( {k + 1} \right) = A_{d} \chi \left( k \right) + B_{d} u\left( k \right) + d_{k} \left( k \right) $$

(11)

where $A_{d} = I + TA$, $B_{d} = TB$, $T\, {\text{is }}\,{\text{the }}\,{\text{sampling }}\,{\text{time}},$ $d_{k} \left( k \right) = \chi_{o} (k + 1) - \left( {A_{d} \chi_{o} (k) + B_{d} u_{o} (k)} \right)$.

3.1.2 State Prediction

Defining a new state variable $\xi (k) = \left[ {\begin{array}{*{20}c} {\chi \left( k \right)} \\ {u\left( {k - 1} \right)} \\ \end{array} } \right]$, the state outputs as $\eta (k)$ and the control input increment as $\varDelta u(k) = u\left( k \right) - u\left( {k - 1} \right)$, a new form of this discrete state-space controller model can be written as [22,23,24,25,26]:

$$ \xi (k + 1) = \tilde{A}_{d} \xi (k) + \tilde{B}_{d} \varDelta u(k) + \tilde{d}_{k} (k) $$

(12)

$$ \eta (k) = \tilde{C}_{d} \xi (k) $$

(13)

where, $\tilde{A}_{d} = \left[ {\begin{array}{*{20}c} {A_{d} } & {B_{d} } \\ {0_{m \times n} } & {I_{m} } \\ \end{array} } \right]$, $\tilde{B}_{d} = \left[ {\begin{array}{*{20}c} {B_{d} } \\ {I_{m} } \\ \end{array} } \right]$, $\tilde{d}_{k} (k) = \left[ {\begin{array}{*{20}c} {d_{k} \left( k \right)} \\ {0_{m} } \\ \end{array} } \right]$, $\tilde{C}_{d} = \left[ {\begin{array}{*{20}c} {C_{d} } & {0_{p \times m} } \\ \end{array} } \right]$. m, n and p are the dimensions of control input, state variable and output, respectively.

The model state output over prediction horizon $N_{p}$ in a compact matrix form is derived as [22,23,24,25,26]:

$$ \eta_{m} \left( k \right) = \varTheta_{m} \xi \left( k \right) + \varGamma_{m} \varDelta U_{m} + \varPsi_{m} D_{k} $$

(14)

where,

3.1.3 Enforcement of Constraints

• (1) Yaw Stability Constraint

The ideal yaw rate (i.e. yaw angular velocity) and sideslip angle is challenging because the tire forces might saturate. Therefore, nominal values should be bounded at an upper limit according to the tire-road friction coefficient, i.e. $a_{y} \le \mu g$. Vehicle lateral acceleration can be written as $a_{y} = \ddot{y} + \dot{x}\dot{\psi }$, in which the first term is often small and the second one accounts for almost 85% of the total [17, 25]. Then, the upper limit for nominal yaw rate can be written as:

$$ \left| {\dot{\psi }} \right| \le 0.85\frac{\mu g}{{\dot{x}}} $$

(15)

Considering the uncertainty in the tire-road friction coefficient and nonlinearity, the nominal steady-state sideslip angle should be bounded as [17]:

$$ \left| \beta \right| \le \arctan (0.02\mu g) $$

(16)

Generally, the vehicle sideslip starts at the rear axle when the loss of yaw stability occurs. Hence, another important consideration of yaw stability is the rear tire saturation, it can be expressed as [25, 30]:

$$ \alpha_{r,sat} = \left| {\arctan \left\{ {\frac{3mg\mu }{{C_{\alpha r} }}\frac{a}{a + b}} \right\}} \right| $$

(17)

The constraint of the vehicle lateral velocity and yaw rate can be then derived from the maximum rear tire slip angle, which is given as [25, 31]:

$$ - \alpha_{r,sat} \le \frac{{\dot{y} - b\dot{\psi }}}{{\dot{x}}} \le \alpha_{r,sat} $$

(18)

The boundary for yaw rate can be derived with the maximum rear tire slip angle and lateral dynamics equations, which is given as [25, 31]:

$$ \dot{\psi }_{\max } = \frac{{C_{\alpha r} \alpha_{r,sat} \left( {1 + b/a} \right)}}{{m\dot{x}}} $$

(19)

Therefore, the boundary of yaw rate is given as:

$$ \dot{\psi }_{\lim } = \min \left\{ {\left| {\dot{\psi }_{\max } } \right|,0.85\frac{\mu g}{{\dot{x}}}} \right\} $$

(20)

Consequently, the yaw stability envelope can be written as [25]:

$$ - G_{sh} \left( k \right) \le H_{sh} \left( k \right)\xi \left( k \right) \le G_{sh} \left( k \right) $$

(21)

where, $H_{sh} = \left[ {\begin{array}{*{20}c} 0 & {1/\dot{x}} & 0 & 0 & 0 & { - b/\dot{x}} & 0 & 0 \\ 0 & {1/\dot{x}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array} } \right],G_{sh} = \left[ {\begin{array}{*{20}c} {\alpha_{r,sat} } \\ {\beta_{\lim } } \\ {\dot{\psi }_{\lim } } \\ \end{array} } \right]$.

To guarantee a feasible solution for the LTV MPC optimization problem, a slack variable $S_{sh}$ is incorporated in the yaw stability constraint to penalize the rear slip angle, vehicle sideslip angle and yaw rate, rather than enforcing the stability envelope as hard constraints. To this end, the constraints of Eq. (21) can be further written as:

$$ - G_{sh} \left( k \right) - S_{sh} \left( k \right) \le H_{sh} \left( k \right)\xi \left( k \right) \le G_{sh} \left( k \right) + S_{sh} \left( k \right) $$

(22)

where $S_{sh} \left( k \right) = \left[ {\begin{array}{*{20}c} {\alpha_{r,sh} } & {\beta_{sh} } & {\dot{\psi }_{sh} } \\ \end{array} } \right]$, $\alpha_{r,sh}$ is the slack variable for rear slip angle, $\beta_{sh}$ is the slack variable for vehicle sideslip angle and $\dot{\psi }_{sh}$ represents the slack variable for yaw rate.

• (2) Roll Stability Constraint

The rollover prevention is achieved by bounding the roll angle, in which the rollover metric is defined using lateral load transfer ratio (LTR) [32]:

$$ LTR = \frac{{F_{zR} - F_{zL} }}{mg} $$

(23)

where $F_{zR}$ and $F_{zL}$ represent the right and left wheel vertical force. The LTR value ranges from −1 to +1. When LTR = 0 means the load are equal on the left and right wheels, while LTR =  +1 or –1 means either left or right wheel vertical force reduced to zero.

As the normal forces at four wheels can be obtained from the 8-DOF vehicle model, the LTR is derived as:

$$ \begin{aligned} LTR & = 2\left( {\frac{{m_{uf} h_{uf} }}{{c_{f} }} + \frac{{m_{s} b\left( {h_{cg} - h_{rcf} } \right)}}{{c_{f} \left( {a + b} \right)}} + \frac{{m_{ur} h_{ur} }}{{c_{r} }} + \frac{{m_{s} a\left( {h_{cg} - h_{rcr} } \right)}}{{c_{r} \left( {a + b} \right)}}} \right) \cdot \frac{{\left( {\dot{v} + \omega_{z} u} \right)}}{mg} \\ & + \frac{{2\left( {k_{\phi f} \phi + b_{\phi f} \dot{\phi }} \right)}}{{c_{f} mg}} + \frac{{2\left( {k_{\phi r} \phi + b_{\phi r} \dot{\phi }} \right)}}{{c_{r} mg}} \\ \end{aligned} $$

(24)

Considering the vehicle roll dynamics model shown in Fig. 4, the equation of moment at the contact patch of outer wheel is derived as [33]:

$$ m_{s} a_{y} h_{cg} - m_{s} g\left[ {W/2 - \phi h_{rc} } \right] + F_{zL} W = 0 $$

(25)

Fig. 4.

Vehicle Roll Dynamics Model

Considering the roll angle threshold at quasi steady-state rollover, when the left wheel vertical forces become zero, i.e., $F_{zL}$ = 0, the Eq. (25) can be written as:

$$ \frac{{a_{y} }}{g} = \frac{{\left[ {W/2 - \phi h_{rc} } \right]}}{{h_{cg} }} $$

(26)

Combining equations of LTR = 1 and Eq. (26) and considering $a_{y} = \dot{v} + \omega_{z} u$, the roll angle of critical state can be calculated by the following rollover equation, which is given as:

$$ C\dot{\phi } - \left( {\frac{{Dh_{rc} g}}{{h_{cg} }} - K} \right)\phi + \frac{DWg}{{2h_{cg} }} - \frac{mg}{2} = 0 $$

(27)

where,

$$ \begin{aligned} & C = \frac{{b_{\phi f} }}{{c_{f} }} + \frac{{b_{\phi r} }}{{c_{r} }}; K = \frac{{k_{\phi f} }}{{c_{f} }} + \frac{{k_{\phi r} }}{{c_{r} }}; W = \frac{{c_{f} + c_{r} }}{2} \\ & D = \frac{{m_{uf} h_{uf} }}{{c_{f} }} + \frac{{m_{s} b\left( {h_{cg} - h_{rcf} } \right)}}{{c_{f} \left( {a + b} \right)}} + \frac{{m_{ur} h_{uf} }}{{c_{r} }} + \frac{{m_{s} a\left( {h_{cg} - h_{rcr} } \right)}}{{c_{r} \left( {a + b} \right)}} \\ \end{aligned} $$

The threshold of vehicle roll angle over each prediction horizon is then obtained:

$$ - \phi_{lim} \le \phi \le \phi_{lim} $$

(28)

Using the form of constraint matrix, equations of roll stability constraint become:

$$ - G_{roll} \left( k \right) \le H_{roll} \left( k \right)\xi \left( k \right) \le G_{roll} \left( k \right) $$

(29)

where, $H_{roll} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$, $G_{roll} = \left[ {\phi_{lim} } \right]$.

• (3) Control Input and State Output Constraints

Since the control inputs and system state outputs will be confined in practical applications, the following constraints should be considered [34]:

Control input constraint:

$$ U_{\min } \le A \varDelta U_{t} + U_{t } \le U_{\max } , $$

(30)

Control input increment constraint:

$$ \varDelta U_{\min } \le \varDelta U_{t } \le \varDelta U_{\max } , $$

(31)

State output constraint:

$$ Y_{\min } \le \varTheta_{m} \xi \left( k \right) + \varGamma_{m} \varDelta U_{m} + \varPsi_{m} D_{k} \le Y_{\max } , $$

(32)

where, $U_{\min }$ and $U_{\max }$ denote the lower and upper limits of control input, respectively; $\varDelta U_{\min }$ and $\varDelta U_{\max }$ denote the lower and upper bounds of control input increments, respectively; $Y_{\min }$ and $Y_{\max }$ denote the lower and upper bounds of vehicle state outputs, respectively.

3.1.4 Cost Function Formulation

The task of trajectory tracking considering the constraints of control inputs, vehicle state outputs, yaw stability and roll stability together can be formulated as quadratic optimal control problem over a finite prediction horizon $N_{p}$ to generate a sequence of optimal steering inputs, which incorporates a relaxation factor $\varepsilon$ to prevent infeasible solution. The cost function is given as follows [35]:

$$ \mathop {\min }\limits_{{\varDelta U_{t} ,\varepsilon }} J\left( k \right) = \sum\limits_{i = 1}^{{N_{p} }} {\left\| {\eta \left( {k + i\left| t \right.} \right) - \eta_{ref} \left( {k + i\left| t \right.} \right)} \right\|_{Q}^{2} } + \sum\limits_{i = 0}^{{N_{c} - 1}} {\left\| {\varDelta U\left( {k + i\left| t \right.} \right)} \right\|_{R}^{2} } + \rho \varepsilon^{2} $$

(33)

$$ {\text{s}}.{\text{t}}.\; U_{\min } \le A \varDelta U_{t} + U_{t } \le U_{\max } $$

(33.a)

$$ \varDelta U_{\min } \le \varDelta U_{t } \le \varDelta U_{\max } $$

(33.b)

$$ Y_{\min } \le \varTheta_{m} \xi \left( k \right) + \varGamma_{m} \varDelta U_{m} + \varPsi_{m} D_{k} \le Y_{\max } $$

(33.c)

$$ \left| {H_{sh} \left( k \right)\xi \left( k \right)} \right| \le G_{sh} \left( k \right) + S_{sh} \left( k \right) $$

(33.d)

$$ \left| {H_{roll} \left( k \right)\xi \left( k \right)} \right| \le G_{roll} \left( k \right) $$

(33.e)

where, the first term in Eq. (33) aims to minimize the vehicle position and heading angle error; the second term in Eq. (33) represents the constraints on the sequence of control input to avoid the control mutation and to ensure control input continuity; the third term in Eq. (33) penalizes the relaxation factors of the control input and sideslip constraint. The variables solved for in the cost function include the optimal steering input increment and the relaxation factors. The tuneable parameters are the weight matrices Q and R, and the weight coefficient $\rho$. The objectives can be prioritized by selecting different weight matrices.

Equations (33.a) and (33.b) confine the control inputs and control input increments within actuator physical limits; Eq. (33.c) enforces constraints on vehicle state outputs; Eq. (33.d) reflects the envelop constraints on vehicle yaw stability; Eq. (33.e) imposes constraints on vehicle roll stability.

A sequence of optimal steering control inputs can be obtained through solving the above optimization problem in which the first element is taken as the actual control input.

3.2 Longitudinal Dynamics Control

As one of the most commonly used controllers in industry and with the consideration of computational burden, the longitudinal control employs PID control to generate the total driving or braking torque and it is assumed that the torque is equally divided among the four wheels. This assumption is made to simplify the control input distribution problem and is reasonable for most front wheel drive and brake for four wheels automotive vehicle. The speed tracking errors are defined as follows:

$$ e_{u} = u_{d} - u $$

(34)

$$ e_{{\dot{u}}} = \dot{u}_{d} - \dot{u} $$

(35)

$$ e_{{s_{x} }} = \int_{{t_{1} }}^{{t_{2} }} {e_{u} dt = e_{u} T_{s} } $$

(36)

where $u_{d}$ is the reference speed, u is the plant speed, $\dot{u}_{d}$ is the reference longitudinal acceleration, $\dot{u}$ is the plant longitudinal acceleration, $T_{s}$ denotes the sampling time. In the PID speed tracking controller, simply put, when the plant speed is smaller than the reference value, a drive torque will be applied to front wheels; when the plant speed is larger than the reference value, a brake torque will be applied to the front and rear wheels; when the two values are equal, no torque is applied to the wheels.

4 Numerical Simulation and Discussion

4.1 Plant/Model Validation

CarSim® vehicle model is a high-fidelity model capable of accurately predicting the vehicle performance in reality. Hence, instead of using the real vehicle, the response of CarSim® model is often used to evaluate the proposed vehicle model. Based on the vehicle parameters listed in Appendix 1, a vehicle model in CarSim®, an 8-DOF vehicle model and a 14-DOF vehicle in MATLAB® are developed respectively. In order to validate the vehicle model accuracy, the output responses including vehicle yaw rate and roll angle between the vehicle models and the CarSim® model are compared with steering conditions.

The amplitude of the front road wheel steering input is 0.0087 rad, i.e., $0.5^{\circ}$ and the vehicle longitudinal velocity is set constant at 33.73 m/s. Herein, comparisons of vehicle state responses among 8-DOF model, 14-DOF model and CarSim® model using step steering input and sinusoidal steering input are given in Fig. 5 and Fig. 6, respectively.

Fig. 5.

Comparisons of Vehicle State Responses during Step Steering

Fig. 6.

Comparisons of Vehicle State Responses during Sinusoidal Steering

The simulation results indicate that the output responses of 8-DOF and 14-DOF vehicle model are close to the outputs of CarSim® vehicle model, which validated the accuracy of the vehicle dynamics models. As a result, these developed vehicle models can be utilized in the following control algorithm design and validation.

4.2 Reference Trajectory and Speed

In order to testify the controller performance under the curve road conditions, an 8-shaped reference trajectory with a radius of 30 m is proposed. Herein, the longitudinal velocity is set ranging from 5 m/s, 8 m/s, 10 m/s to 12 m/s during trajectory tracking to investigate various curve speeds. The longitudinal speed profile is transformed with regard to the arc length. The reference path and longitudinal velocity are given in Fig. 7.

Fig. 7.

Definitions of Reference Path and Speed: (a) Reference Path; (b) Reference Longitudinal Velocity

4.3 Trajectory Tracking Simulation Results

4.3.1 Trajectory Tracking Control

As for the tracking performance of 8-shaped curve trajectory tracking considering various curve speeds, simulation results including comparisons of the tracking trajectories and the longitudinal speeds between the plant output and the desired value, and the control inputs of the steering angle and the total wheel driving or braking torque are illustrated in Fig. 8. Since the braking torque in this case is very small, the results of total wheel braking torque are not shown independently. In the simulation, the matrices Q and R, and the weight coefficient $\rho$ for the relaxation factors used in the optimal solution are the same in order to investigate the robustness of the proposed controller. The tracking errors of the vehicle positions and the longitudinal velocity are small, indicating that the performance of the proposed trajectory tracking controller is well and robust, meanwhile, the control input of steering angle is smooth without mutation during path tracking process.

Fig. 8.

Tracking Performances and Control Inputs: (a) Comparison of Tracking Trajectories; (b) Comparison of Longitudinal Velocities; (c) Front-wheel Steering Inputs; (d) Total Wheel Driving Inputs

4.3.2 Yaw Stability and Roll Stability Performances

The phase-plane portrait of yaw rate and lateral velocity, the LTR value, the vehicle sideslip angle and the vehicle roll angle are recorded during the trajectory tracking control, which are illustrated in Fig. 9. The simulation results of vehicle yaw stability and roll stability for the 8-shaped trajectory tracking under the conditions of different reference speeds indicate that the phase-plane portrait of yaw rate and lateral velocity is enlarged with the increasement of longitudinal velocity, but still remains inside the sideslip stability envelope, which means that the vehicle maintains yaw stability. Meanwhile, the roll angle is also increased and the LTR value is approaching ±1 as the vehicle speed increases, but both of them are still confined within the steady-state rollover boundary indicating that no wheels are lifted off the ground and no risk of rollover. Therefore, the vehicle maintains both yaw stability and roll stability.

Fig. 9.

Performances of Yaw Stability and Roll Stability: (a) Phase-plane of Vehicle Yaw Stability; (b) Lateral Load Transfer Ratio; (c) Vehicle Sideslip Angle; (d) Vehicle Roll Angle

5 Conclusion and Future Work

This paper presented a curve trajectory tracking control scheme using LTV MPC to address the problem of trajectory tracking for autonomous vehicles on curved roads considering the vehicle yaw stability and roll stability simultaneously. Conclusions from the research are summarized as follows:

• (1) Compared with the output responses of the CarSim® model, the accuracy of the 8-DOF and 14-DOF vehicle model are validated under the conditions of front road wheel step steering input and sinusoidal steering input at a speed of 33.73 m/s.

• (2) Using an 8-shaped curve as the reference trajectory and considering different curve speeds (ranging from 5 m/s, 8 m/s, 10 m/s to 12 m/s) as the reference longitudinal velocities, the proposed LTV MPC-based trajectory tracking control is implemented via MATLAB® code. The trajectory tacking simulation results demonstrate that the tracking errors of both vehicle trajectory and longitudinal velocity are small, indicating good and robust tracking performance.

• (3) The vehicle stability simulation results during trajectory tracking demonstrate that the vehicle yaw stability is confined within the constraint of phase-plane envelope, the sideslip angle, the roll angle and the LTR value are also limited within the boundaries, which indicates no risk of sideslip and rollover.

In the future, in order to consider a complex situation and high-speed curve scenario, the nonlinear tire force and the optimal control allocation for the desired yaw moment will be investigated and incorporated in the controller design to further improve the performance of trajectory tracking and vehicle handling stability. Meanwhile, the real-time performance will be also considered for the physical implementation of the proposed controller.

Appendix 1. Vehicle Model Parameters

The primary vehicle modeling parameters described in Sect. 4.1 are given as follows:

• m = 1720 (kg)

• $m_{s}$ = 1400 (kg)

• $I_{x}$  = 900 (kg $\cdot$ m²)

• $I_{y}$  = 2000 (kg $\cdot$ m²)

• $I_{z}$ = 2420 (kg $\cdot$ m²)

• $I_{w}$ = 1 (kg $\cdot$ m²)

• a = 1.14 (m)

• b = 1.4 (m)

• h = 0.75 (m)

• $m_{uf}$ = 80 (kg)

• $m_{ur}$ = 80 (kg)

• $c_{f}$ = 1.5 (m)

• $c_{r}$ = 1.5 (m)

• $C_{\alpha f}$ = −44000 (N/rad)

• $C_{\alpha r}$ =  −47000 (N/rad)

• $C_{xf}$ = 5000 (N)

• $C_{xr}$ = 5000 (N)

• $r_{0}$ = 0.285 (m)

• $h_{rcf}$ = 0.65 (m)

• $h_{rcr}$ = 0.6 (m)

• $\mu$ = 0.9 (−)