Keywords

1 Introduction

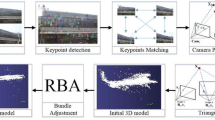
In the past decades, with the development of robots and autonomous driving, SLAM (simultaneous localization and mapping) have become increasingly important [3, 7]. In order to locate and map more accurately, people use higher quality and higher resolution images to extract more feature points. However, this caused the bundle adjustment process in SLAM to spend more time and computing resources, and some even required GPUs to speed up. Bundle adjustment is the problem that optimizes the visual reconstruction to obtain the best 3D structure and estimation of viewing angle parameters (camera calibration and pose) [22] in the SLAM. Bundle adjustment adjusts to obtain optimal camera parameters and world landmarks coordinates by utilizing the camera’s pose and the 3D coordinates of the measurement points as unknown parameters, and using the coordinate of the feature points observed on the camera at the front intersection as observation data. The optimized parameters include the coordinates of the world landmarks and the pose of the camera. Both of these determine the projection bundle during the camera projection process, so we are adjusting the bundle, which is also the origin name of the bundle adjustment.

Bundle adjustment is a non-linear optimization problem, which can be optimized through iteration using the least squares method. The Gauss-Newton and Levenberg-Marquadt methods [13] are the most popular methods in optimizing the bundle adjustment formula. The time consumed by the bundle adjustment process is related to the dimension of the optimization variable. As the dimension of the optimization variable increases, the time of the bundle adjustment will also greatly increase. In some dense and semi-dense construction maps, there are tens of thousands of optimized world coordinate points, which makes the matrix dimension of the least squares solution very large, resulting in a slow speed. Even in recent years, people have realized the sparseness of the bundle adjustment problem [6, 19], but it still takes a lot of time for large-scale reconstruction.

In order to increase the speed in bundle adjustment optimization, a related algorithm is proposed in this paper. The proposed algorithm decomposes the large Hessian matrix into two small Hessian matrices, where the dimensions of the small matrix are about half that of the large matrix, and the speed of inverting the two small matrices is much greater than that of the large matrix. The main contributions of this paper are as follows: (1) The algorithm proposes that the large matrix in the bundle adjustment process can be decomposed into two mutually constrained small matrices. The two small blocks have different world points, but their poses are the same. In this way, the ADMM [5] algorithm can be applied to constrain it for optimization. (2) The projection function is non-convex, so the convergence and termination conditions of the algorithm need to be analyzed. We analyze that projection function has local Lipschitz-continuous, and thus the augmented Lagrangian function in ADMM is convex and it can converge.

The structure of the paper is organized as follows. Section 1 reviews the time-consuming problems in large-scale bundle adjustment and proposed an improved method. In Sect. 2, we discuss the related work of incremental bundle adjustment, explain their advantages and disadvantages, and lead to our research content. Section 3 introduces the bundle adjustment and the ADMM algorithm, and discusses how to apply the ADMM algorithm in bundle adjustment. In the Sect. 4, we discussed the convergence and termination conditions of the algorithm. In Sect. 5, the experimental results using our proposed algorithm has been shown. At last, our conclusion will be showed in Sect. 6.

2 Related Work

When the robot moves in a long time and space, there are many methods using the sliding window [8] method to discard some historical data due to the many optimized variables. Or according to the practice of pose graph [17], abandon the optimization of the landmark points, and only keep the edges between poses. There are also some attempts to solve Structure-from-Motion in cities and even the earth, such as the work in [11]. However, none of these tasks has been globally optimized because the cost of global bundle adjustment optimization is very large and cannot be completed with limited time and resources.

Some approaches have been proposed for incremental bundle adjustment. The iSAM [15] transforms the graph optimization problem in bundle adjustment into a Bayesian tree establishment, update, and inference problem. The whole architecture of this method is based on probabilistic reasoning, and it uses QR matrix factorization to optimize on sparsity. But only a small part of the decomposition result has been updated in each iteration instead of the whole graph. SLAM\(++\) [20] recover estimates and variances, and update Schur complement space incrementally in bundle adjustment. However, the above algorithm is only appropriate for handling the sparse camera problem (most of the key points are only visible in few frames), which is consistent with the large-scale SfM problem. But in the SLAM problem, most of the frames in the local sliding window share a large part of the key points, so that the above incremental algorithm evolves into a conventional BA solver, and the positioning accuracy cannot be better than other latest algorithm. In visual inertial fusion of SLAM, \(ICE-BA\) [18] efficiently uses the previously optimized intermediate results to avoid new redundant calculations. This algorithm significantly improves the solution speed and can be applied to most VI-SLAM based on sliding window method, but this method only uses the repeatability of intermediate calculation results. At the same time, the good engineering in Ceres [1] and g2o [14] implements BA and is used in various SLAM systems. However, there is an obvious disadvantage in these methods: the complexity increases twice with the number of image frames. In order to achieve real-time pose estimation, SLAM systems based on these solvers can only utilize very limited measurements.

In order to deal with above problems, referring to ADMM algorithm [5], we propose an improved bundle adjustment algorithm to optimize the world points and pose. Main contributions of this paper are as follows: (1) Our algorithm proposes that the large Hessian matrix in the BA process can be decomposed into two mutually constrained small Hessian matrices. The two small blocks have different world points, but their poses are the same. In this way, the ADMM algorithm can be used to constrain it for optimization. (2) The projection function is non-convex, so the convergence and termination conditions of the algorithm need to be analyzed. We analyze that projection function has local Lipschitz-continuous, and thus the augmented Lagrangian function in ADMM is convex.

3 Proposed Method

3.1 Bundle Adjustment

Bundle adjustment is a reprojection process. With the camera parameters, the measured world landmarks are reprojected on the pixel plane and then compared with the points observed by the camera. Camera parameters include external and internal parameters. The external parameters include the camera’s translation vector and rotation matrix. The internal parameters include the distortion coefficient and focal length. At different times, the external camera parameters are not the same, but internal parameters are generally the same. Suppose we have M observed 3D points, the external parameter set of N cameras is recorded as \(\varXi =\{\xi _i \in R^C\mid i=1,...,N\}\), and the internal parameter set is recorded as \(D=\{di_i \in R^I \mid i=1,...,N\}\), record the observed 3D point set \(P=\{p_j \in R^3 \mid j=1,...,M\}\) and the observation as \(Z=\{z_{ij} \in R^2 \mid i=1,...,N;j=1,...,M\}\), \(z_{ij}\) indicates that the i-th camera observes the j-th point. The cost function can be expressed as follows

$$\begin{aligned} f(\varXi ,D,P)=\frac{1}{2}\sum _{i=1}^{N}\sum _{j=1}^{M}\Vert z_{ij}-h(\xi _i,d_i,p_j)\Vert _2^2 \end{aligned}$$
(1)

where \(h(\xi _i,d_i,p_j)\) is the reprojection equation of the j-th point on the i-th camera, is nonlinear and non-convex. The pose here includes two parameters, namely translation vector and rotation matrix. Solving this nonlinear least squares problem is equivalent to adjusting camera parameters and landmark points at the same time, and this process is called bundle adjustment.

3.2 ADMM

The proposal of ADMM algorithm [4] is to handle the following format problems:

$$\begin{aligned} \min \quad f(x)+g(z)\quad \text {subject to}\quad Ax+Bz=c \end{aligned}$$
(2)

According to the augmented Lagrangian multipliers method, we get

$$\begin{aligned} L(x,z,y)=f(x)+g(z)+y^T(Ax+Bz-c)+\frac{p}{2}\Vert Ax+Bz-c\Vert _2^2 \end{aligned}$$
(3)

The ADMM algorithm consists of iterations:

$$\begin{aligned} x^{k+1}=\mathop {argmin}\limits _{x}L_p(x,z^k,y^k) \end{aligned}$$
(4)
$$\begin{aligned} z^{k+1}=\mathop {argmin}\limits _{z}L_p(x^{k+1},z,y^k) \end{aligned}$$
(5)
$$\begin{aligned} y^{k+1}=y^k+p(Ax^{(k+1)}+Bz^{k+1}-c) \end{aligned}$$
(6)

The updates of parameters are implemented by alternating iterations.

And we want to use the ADMM algorithm to solve the general form of the consistency optimization problem:

$$\begin{aligned} \min \quad \sum _{i=1}^N f(x_i) \quad \text {subject to} \quad \hat{x_i}=\hat{z}, i=1,...,N \end{aligned}$$
(7)

Here, because the parameter space is divided into blocks, the parameter dimensions of each sub-objective function \(f_i(x_i)\) are different, which are called local variables. Local variables no longer correspond to global variables but are part of global variables. Map a part of \(x_i\) to a part of the global variable z as \(\hat{z_i}\). Using ADMM, the expressions capable of the deriving iteration are

$$\begin{aligned} x_i^{k+1}=\mathop {argmin}\limits _{x_i}(f_i(x_i)+y_i^k(\hat{x_i}-\hat{z})+\frac{p}{2}\Vert \hat{x_i}-\hat{z}\Vert _2^2) \end{aligned}$$
(8)
$$\begin{aligned} \hat{z}^{k+1}=\frac{1}{n}\sum _{i=1}^N \hat{x_i}^{k+1} \end{aligned}$$
(9)
$$\begin{aligned} y_i^{k+1}=y_i^{k}+p(\hat{x_i}^{k+1}-\hat{z}^{k+1}) \end{aligned}$$
(10)

The augmented Lagrangian constant \(p>0\), and Eq. (9) is the average of the optimization results of different nodes.

3.3 Pose Consensus

According to the algorithm given above, for a large bundle adjustment problem, we can decompose it into multiple small blocks for processing. In fact, dividing into two small blocks is the most common and can achieve better speed and accuracy [10].

In the bundle adjustment problem, a camera will observe many points at one location, and then optimize the feature points and locations together. In the optimization, the characteristics of these feature points are the same, and the constraints on the camera pose are also the same. This inspired us to divide them into two separate optimizations. When we are processing bundle adjustment, the observation set Z is divided into \(Z_1 \in Z\) and \(Z_2 \in Z\), that is \(z_{ij}\) is randomly divided into two parts. At the same time, we record the external and internal parameters of each camera as T as a whole and define \(T_1\) and \(T_2\) as the external parameters of the N cameras in the observation sets \(Z_1\) and \(Z_2\), respectively. The relationship between these blocks is shown in Fig. 1.

Fig. 1.
figure 1

Camera parameters are represented by squares, and circles represent world coordinate points. The blue line indicates that a world coordinate point is observed by a camera. Red double arrows indicate that these two poses are local poses and are constrained by the global pose. Another figure shows calculation of the first iteration of the Hessian matrix. \(A_1J_2^TJ_2\) means to take out the position-constrained part in 2-block. (Color figure online)

Full size image

Then bundle adjustment problem in the (1) can be modified as follows:

$$\begin{aligned} \min \quad \sum _{i=1}^2f(T_i,P_i)\quad \text {subject to} \quad A_iT_i=T,i=1,2 \end{aligned}$$
(11)

The top left corner of \(A_i\) is an identity matrix, and all other elements are 0. The size of the identity matrix is related to the pose that needs to be optimized.

According to the augmented Lagrangian multiplier method, the cost function obtained is as follows:

$$\begin{aligned} L_p=\sum _{i=1}^2(f(T_i,P_i)+y_i^T(T_i-T)+\frac{p}{2}\Vert T_i-T\Vert ^2) \end{aligned}$$
(12)
$$\begin{aligned} (T_1,P_1)^{k+1}=\mathop {argmin}\limits _{T_1,P_1}L_p(T_1,P_1,T_2^k,P_2^k,y_1^k,y_2^k) \end{aligned}$$
(13)
$$\begin{aligned} (T_2,P_2)^{k+1}=\mathop {argmin}\limits _{T_2,P_2}L_p(T_1^{k+1},P_1^{k+1},T_2,P_2,y_1^k,y_2^k) \end{aligned}$$
(14)
$$\begin{aligned} T=\frac{1}{2}(T_1+T_2) \end{aligned}$$
(15)
$$\begin{aligned} y_1^{k+1}=y_1^k+p(A_1*T_1-T) \end{aligned}$$
(16)
$$\begin{aligned} y_2^{k+1}=y_2^k+p(A_2*T_2-T) \end{aligned}$$
(17)

Taking the first block as an example, it can be finally derived that the first-order Jacobian matrix in the derivation of poses and landmark points is as follows.

$$\begin{aligned} \begin{aligned} \frac{\partial L_p}{\partial T_1}&=\frac{\partial f(T_1,P_1)}{\partial T_1}+y_1+p(T_1-T)\\ {}&+\, A_1(\frac{\partial f(T_2,P_2)}{\partial T_2}+y_2+p(T_2-T)), \\ \frac{\partial L_p}{\partial P_1}&=\frac{\partial f(T_1,P_1)}{\partial P_1} \end{aligned} \end{aligned}$$
(18)

From above analysis, we can also see that the constraints between the two small blocks are only poses and no landmark points. The calculation method for the first block’s Hessian matrix is shown in Fig. 1. So we calculate the Jacobian matrix independently and constrain it before iteration.

4 Convergence and Stopping Criterion

4.1 Convergence

The reprojection function f(x) in Eq. (7) should be a convex function in ADMM algorithm. But in fact, the objective function of bundle adjustment in Eq. (1) is non-convex. Some work, such as [12, 16], the proximal splitting method applied to non-convex problems has been analyzed. Work [9] proposed a convergence state and consistency of coordinate points, and [23] suggested that the camera consistency problem was convergent. Referring to the analysis above, the convergence of the improved bundle adjustment algorithm in this paper will be analyzed.

The proof of the ADMM method’s convergence on the convex function is shown in [5]. In Eq. (12), the convexity of f(x) determines the convexity of \(L_p\). If f(x) is a convex function, so is \(L_p\). But the reprojection function is not convex. With the theory in [16], f(x) should be local Lipschitz-continuous and have Lipschitz constant \(p_{min}\), which ensures that when \(p>p_{min}\), \(L_p\) is a convex function. The proximity operator should handle on all landmarks in Eq. (12), because Lipschitz-continuous is defined on all variables. Based on the requirement of Lipschitz-continuous, we discuss the objective function in bundle adjustment.

Because the internal parameter matrix does not change with changes in camera motion, we can ignore the internal parameters when analyzing convergence. Therefore, for the reprojection function of Eq. (1), we consider \(R_i^{(1:2)}\) as the first two rows of \(R_i\), and \(R_i^{(3)}\) is the third row of \(R_i\) (similarly for \(t_i^{(1:2)}\) and \(t_i^{(3)}\)). Then the projection function of the j-th point on the i-th camera can be written as follow:

$$\begin{aligned} f(P_j|R_i,t_i):= \frac{R_i^{(1:2)}P_j+t_i^{(1:2)}}{R_i^{(3)}P_j+t_i^{(3)}} \end{aligned}$$
(19)

t and R are the translation vector and rotation matrix in the external parameters, respectively. For this formula, the denominator is the only part of the f(x) gradient that may disrupt Lipschitz-continuous. To avoid infinitely small denominators, we must assume that the denominator \(R_i^{(3)}P_j+t_i^{(3)}>d_{min}>0\). This is that the depth of any point observed by any camera in bundle adjustment must be greater than \(d_min\), and this is a reasonable assumption in the SLAM problem.

Then we consider the Lipschitz-continuous of the rotation parameter of the objective function in Eq. (1). We can utilize quaternions and Euler angles to represent the rotation, and the rotation matrix R is denoted as \(r_R\). The work [25] proposed that to warrant the Lipschitz-continuous of the cost function, the Lipschitz-continuous of \(\partial R/\partial r_R\) must be guaranteed. The mapping of a quaternion to a rotation matrix is designed to normalize the quaternion, so when the quaternion is close to zero, the gradient is not limited. Although the gradient \(R^3->SO(3)\) of the exponential mapping of the angular axis to the rotation matrix also has a part of \(\Vert \theta \mathbf {v}\Vert ^{-a},a>0\), it can be proved that when \(\Vert \theta \mathbf {v}\Vert ->0\), the Jacobian tensor of the exponential mapping is a constant. Therefore, the gradient of the exponential map Lipschitz-continuous can be proved. Based on the above analysis, we can see that the augmented Lagrangian function \(L_p\) is convergent.

4.2 Stopping Criterion

For the problem in Eq. (12), when the ADMM method finally reaches the optimal solution, the following two conditions will be satisfied:

$$\begin{aligned} A_1T_1-T=0,A_2T_2-T=0 \end{aligned}$$
(20)
$$\begin{aligned} 0\in \partial f(T_1^{*})+A_1^T y_1^{*},0\in \partial f(T_2^{*})+A_2^T y_2^{*} \end{aligned}$$
(21)

We note the dual and original residuals as \(r^k=A_1T_1-T+A_2T_2-T\) and \(s^k=pA_1^TA_2(T_2^{k}-T_2^{k-1})\), respectively. According to these two formulas, it can be derived as follows:

$$\begin{aligned} \begin{aligned} 0&\in \partial f(T_1^{k+1}+A_1^T y_1^k+pA_1^T(A_1T_1-T+A_2T_2-T) \\&=\partial f(T_1^{k+1}+A_1^T(y_1^k+pr^k+pA_2(T_2^k-T_2^{k+1})) \\&=\partial f(T_1^{k+1}+A_1^Ty^{k+1}+pA_1^TA_2(T_2^k-T_2^{k+1}) \end{aligned} \end{aligned}$$
(22)

That is

$$\begin{aligned} pA_1^TA_2(T_2^{k+1}-T_2^{k})\in \partial f(T_1^{k+1}+A_1^Ty^{k+1}) \end{aligned}$$
(23)

In this algorithm, when the dual residual term approaches 0, the above conditions can be satisfied. We assume that the dual residuals and the initial residuals are reduced to a certain error range and then stop iterating. Generally set to

$$\begin{aligned} \Vert s^k\Vert _2^2< \epsilon ^{dual},\Vert r^k\Vert _2^2 < \epsilon ^{pri} \end{aligned}$$
(24)

From the above introduction and analysis of the algorithm, we can get the improved bundle adjustment algorithm process. Based on pose consensus, an improved bundle adjustment algorithm is summarized in Algorithm 1.

figure a

5 Experiments

5.1 Semi-dense Visual Odometry

In the direct method, there is no correspondence between feature points because the descriptors are not calculated and feature matching is not performed. We don’t know which point \(p_2\) on the second photo corresponds to point \(p_1\) on the first photo. Therefore, the idea of the direct method is to provide an initial value of pose, and to look for position of \(p_2\) from the current estimate. If the pose estimates given are poor, the appearance (brightness) of \(p_2\) will be significantly different from \(p_1\). To reduce this difference, we constantly adjust the camera pose to find \(p_2\), which is more similar to \(p_1\). The object of minimization is the photometric error, and the premise of the direct method is the photometric constant assumption.

Fig. 2.
figure 2

We use the rgbd\(\_\)dataset\(\_\)freiburg1\(\_\)xyz for testing to find the average time required for each frame and the iteration time changes with the number of feature points. IBA and BA represent the results of using improved and unimproved bundle adjustment, respectively.

Full size image

The semi-dense direct method is to calculate pixels with gradients in the image and then track these pixels. The advantage of the direct method is that it uses more observation information, which can be used in situations where features are missing, and to build a semi-dense map. At the same time, the shortcomings are also very clear, and the movement must be small to ensure convexity, and the photometric constant is a strong assumption.

In this paper, a semi-dense direct method of visual odometry has been implemented, which has three main characteristics. First, pick some points randomly when taking pixels, which can speed up the speed. This also utilizes the feature that the direct method does not require feature matching. Second, a four-layer image pyramid is used when estimating poses, which can improve accuracy. Third, the improved bundle adjustment algorithm proposed above is used when estimating the pose and landmark points.

TUM [21] is a large data-set, which includes ground truth data and RGB-D images, and we use it for experiments. The convergence of the proposed algorithm is tested first. According to stopping criterion, we set to stop iteration when the error is less than a certain range. Because we do not know whether the algorithm converges, we need to set the maximum number of iterations, so that even if the algorithm does not converge, it will not enter the iteration loop. If the algorithm is convergent, the time required by the algorithm will tend to stabilize with the number of iterations increases. We assume each frame takes 1000 points, and then set a different maximum iterations. Simultaneously, we analyze influence of the number of extracted feature points on algorithm time by changing the number of feature points and compare iteration time. The above experiment result is shown in the Fig. 2.

It can be obtained from the result, for a single-frame picture, when the maximum number of iterations of the bundle adjustment process is greater than 3, the time required is basically unchanged. The reason for this is that when the number of iterations has not arrived the maximum iterations, iteration process has been stopped according to the stopping criterion. This also reflects the convergence of the algorithm, because if the algorithm does not converge, the time will increase as the number of iterations increases. And it can be seen from the figure that as the number of extracted feature points increases, time required by the algorithm also increases dramatically. This is because the complexity of the matrix decomposition algorithm used in the bundle adjustment process is O(\(n_3\)), where n is the side length. It can also be seen from the curve that our improved bundle adjustment algorithm is superior to the previous one.

After getting our algorithm is convergent, we set up experiments to compare time and error. We tested four sets of data-sets, the time required for testing each set of data-sets and output estimated trajectory. Then calibrate with the real trajectory to get the RPE (relative pose error) and ATE (absolute trajectory error). At the same time, calculate average time consumed by each frame. We set 1000 points for each frame, and the results are shown in Table 1.

Table 1. Results of different data-sets under different optimization methods
Full size table

The above table is the test results of four different data-sets. Among them, BAP means that only the pose is optimized, and the landmark points are not optimized, BA and IBA are the same as the previous experiment. The four sets of experiments only optimize the pose and the speed is fast. This is because most of the time in BA is used in the calculation of matrix inversion. The matrix that only optimizes the pose is small, so the speed is fast, but the error is also large. It can be obviously obtained from the experiments in the first and second groups that the algorithm we proposed is more efficient than the previous, and the errors of the two algorithm are relatively similar. Overall, our algorithm is faster than the previous one when the error is not large, and it is more effective when it is more translation and less rotation.

Fig. 3.
figure 3

The result of applying the proposed algorithm to the BAL problem.

Full size image

5.2 BAL Problem

Bundle adjustment in the large [2] (BAL) is a geometric reconstruction problem. BAL provides a data-set that includes observation points, camera parameters, and world coordinates. We need to optimize these parameters and coordinate points according to the bundle adjustment. In our experiments, the proposed algorithm has been applied to this large-scale bundle adjustment, and some of the results obtained are shown in the following Fig. 3.

The above experiment selected a small data-set in Trafalgar Square and Dubrovnik scenes, respectively. From the reconstruction results, the reconstruction outline can be clearly seen. At the same time, the reconstruction process takes less time than the previous algorithm.

6 Conclusions and Future Work

In this paper, an improved bundle adjustment algorithm is proposed. The main contribution of this work consists of the following two parts: (1) The ADMM algorithm is introduced in the bundle adjustment process based on pose consensus, so that bundle adjustment can be processed more efficiently. (2) The convergence of proposed algorithm is analyzed in detail, and the stopping criterion is derived according to the convergence. The experiment results of semi-dense visual odometry and BAL problem show that the proposed algorithm has a faster speed when testing the data-sets. In future, the improved algorithms in global bundle adjustment in SLAM and SFM will be explored, simultaneously we will explore more efficient algorithms for different optimization problems.