Indirect Bridge Health Monitoring Employing Contact-Point Response of Instrumented Stationary Vehicle

Abstract

Indirect bridge health monitoring requires an instrumented vehicle with an accelerometer to scan bridge vibration. The indirect method is more practical than the conventional direct method due to its cost efficiency and mobility. However, the vehicle’s own response may pollute the recorded vertical acceleration signal. This paper utilizes a newly developed contact-point calculation method to show its efficiency to reflect the true vibration of bridges. A finite element model is developed for a vehicle placed in stationary state at mid-span of a bridge that is excited by a moving vehicle. Two cases considering different property of the stationary vehicle and different speed of the moving vehicle are developed. The contact-point response is extracted from the stationary vehicle response using MATLAB. The results show the discrepancy between the stationary vehicle and bridge responses. In contrast, good agreement between the contact-point and bridge responses is presented in the time and frequency domains.

1 Introduction

Structural deterioration of bridges could pose life-threatening risk to crossing pedestrians, vehicles, and trains. Therefore, health assessment and monitoring of bridges is of great interest for both authorities and stakeholders. Deterioration of bridges could occur due to flooding, earthquakes, wind, or repeated passing loads. The need to establish efficient methods to monitor bridges is increasing as aging structures have higher probabilities of damage occurrence. In Europe for example, most of bridges were constructed in the postwar era between 1945 and 1965 [1]. While in Japan, almost one third of bridges have been in service for over 50 years [2]. In the United States, there are more than 66,000 structurally deficient bridges which makes 11% of the total bridges, while most of them are more than 65 years old [3].

Bridge health monitoring refers to the identification of dynamic modal characteristics and damage detection [4, 5]. Direct vibration-based bridge monitoring is done by installing a large number of sensors directly on the bridge to record its vibration. Then, the vibration signals are processed to estimate health state of the bridge [6]. However, it is difficult to implement the direct method on a wide scale due to several reasons. First, sensory system bears high cost for equipment and installation. Second, the sensory system life expectancy is shorter than that of the bridge itself, so regular monitoring to the monitoring system is required. Third, installation could be dangerous for many types of bridges; and finally, the limitations on the locations of the sensors, as accelerometers may not be able to detect far damages.

The indirect or “drive-by” method has been proposed recently to overcome the issues of the direct method (fixed sensors). This method employs an instrumented vehicle to record the vibration signal while passing over the bridge. The recorded vibration is processed by computers in order to assess health state of the bridge as shown in Fig. 1. The indirect method is very cost effective as it requires one or few sensors installed on the vehicle. Also, it is highly mobile as the instrumented vehicle can be used for unlimited number of bridges at any desired location. Besides, the passing vehicle scans the vibration of every point of the bridge, unlike the direct method which is limited to location of the sensors.

Fig. 1.

Framework of indirect bridge health monitoring.

In 2004, Yang Y.B. and coworkers were the first to propose and prove the feasibility of extracting the fundamental frequency of a bridge from a passing vehicle [7]. Since then, the indirect method has attracted the attention of many researchers who are interested in bridge health monitoring. Despite the great efforts that was done on the indirect method, road roughness is still an obstacle in the way of implementing the indirect method [8]. One of the recent methods proposed to obtain more accurate results of the instrumented vehicle is the contact-point response calculating method developed by Yang, Zhang [9]. The accelerometer mounted on the vehicle measures the vertical vibration of the vehicle during its passage over the bridge. However, this response is contaminated with the vehicle frequency which corrupts the acceleration signal. Therefore, it is more accurate to use the contact-point response instead of the vehicle response. Yang, Zhang [9] concluded that for all the cases they studied, for vehicle varying speeds and frequencies, for smooth and rough road surfaces, with or without existing traffic, the contact-point response outperforms the vehicle response in extracting the frequencies and mode shapes of the bridge. In this study, the contact-point response of stationary vehicle is calculated and compared with the true bridge response.

The response of stationary vehicle has been utilized in methods to overcome the issue of road roughness [10]. Nevertheless, it is essential to understand the vibration of stationary vehicle for the enhancement of the indirect method [11]. This study shows the response of a stationary vehicle and compare it with the true response of the bridge using finite element (FE) simulation. It is understood that the response of the stationary vehicle will be different from the response of the bridge under the same excitation source. However, it is still not clear to what extent the contact-point response could reflect the true response of the bridge. This study will show how the contact-point response calculated from the stationary vehicle would provide accurate response of the bridge.

2 Contact-Point Response

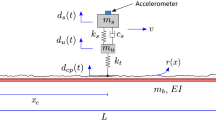
In practical applications of the indirect method, only the acceleration response extracted from the accelerometer installed on the vehicle such as $\ddot{q}_{s}$ is available. Therefore, to resemble reality, the stationary vehicle vibration ($\ddot{q}_{s}$) from the FE model is obtained and used to calculate the contact-point response ($u_{c}$), as shown in Fig. 2.

Fig. 2.

Stationary vehicle response by a moving load over a simple beam bridge.

The following equations elaborate the process of calculating the contact-point response. The equation of motion of the stationary vehicle is expressed as shown in Eq. (1):

$$ m_{s} \ddot{q}_{s} + k_{s} (q_{s} - u_{c} ) = 0 $$

(1)

where $m_{s}$ and $k_{s}$ are the mass and stiffness of the stationary vehicle, respectively. If the equation of motion of the stationary vehicle is derived twice with respect to time, the contact-point acceleration will appear as follows:

$$ k_{s} (\ddot{q}_{s} - \ddot{u}_{c} ) = m_{s} \frac{{d^{2} \ddot{q}_{s} }}{{dt^{2} }} $$

(2)

The natural frequency of the stationary vehicle can be expressed as shown in Eq. (3). Therefore, by using Eq. (3) and rearranging Eq. (2), the contact-point acceleration can be computed as shown in Eq. (4).

$$ \omega_{s} = \sqrt {\frac{{k_{s} }}{{m_{s} }}} $$

(3)

$$ \ddot{u}_{c} = \ddot{q}_{s} + \frac{{d^{2} \ddot{q}_{s} }}{{\omega_{s}^{2} dt^{2} }} $$

(4)

The term $d^{2} \ddot{q}_{s} /dt^{2}$ can be calculated by the central difference method for the discrete data of the recorded signal such as

$$ \frac{{d^{2} \ddot{q}_{s} }}{{dt^{2} }} = \frac{{\left( {\ddot{q}_{s} |_{i + 1} - 2\ddot{q}_{s} |_{i} + \ddot{q}_{s} |_{i - 1} } \right)}}{{(\Delta t)^{2} }} $$

(5)

3 FE Numerical Simulation

As mentioned earlier, in practical applications, only the acceleration of the vehicle itself is available. Therefore, a FE model representing the vibration of stationary vehicle due to moving load on a simple beam bridge is created. The acceleration response of the stationary vehicle ($\ddot{q}_{s}$) is obtained, which represent the vibration of a parked vehicle in real life. The contact-point response ($\ddot{u}_{c}$) is calculated using Eq. (4). In order to identify the accuracy of the contact-point calculation, the acceleration response from the bridge itself at midspan is used as reference. The bridge response at midspan represents a fixed sensor response mounted at the same location in real life application.

The bridge parameters adopted here for the case study are taken from Yang, Lin [7]. The bridge is a simple beam steel bridge with one span of 25 m length. The elastic modulus of the bridge is 27.5 GN/m2, moment of inertia is 0.12 m^4 and mass per unit length is 4800 kg/m. For the moving vehicle, the mass is 1200 kg, the spring stiffness is 500 kN/m, and the damping is zero. The first three bridge frequencies are 2.08 Hz, 8.33 Hz and 18.75 Hz.

The bridge, moving load and stationary vehicle are modeled by the FE element program Ls-Dyna. The stationary and moving vehicles are modeled as mass-spring system of single-degree of freedom. The bridge is modelled by Belytschko-Schwer beam elements using elastic material model (MAT_001). The interaction between bridge and the moving vehicle is modelled with RAIL_TRACK/TRAIN. The contact-point response is calculated using Eq. (4) in MATLAB. Afterwards, the calculated contact-point response is compared with the true bridge response taken from the midspan node in the FE model. In this study, two different cases are presented. The two cases are different in the stationary vehicle properties and the speed of the moving load as explained in the following section.

3.1 Case Study 1

The first case considers a stationary vehicle with vertical frequency of 1.5 Hz. The mass of the vehicle is 300 kg and the stiffness is 26621 N/m. The speed of the moving vehicle is 5 m/s. The stationary vehicle acceleration is obtained from the Ls-Dyna FE model and shown in Fig. 3. As the stationary vehicle response does not contain many fluctuations, it indicates that the signal does not contain higher modes of frequency. Nevertheless, Eq. (4) is used to calculate the contact-point response using MATLAB. The calculated contact-point response is shown in the same figure. It is clear that the contact-point acceleration carries higher modes of vibration. The contact-point response is compared with the true bridge response at midspan. The two responses agree well with each other shown in Fig. 3.

Fig. 3.

Acceleration response of (a) stationary vehicle, (b) contact-point and (c) bridge at midspan.

The responses were compared in the time-domain; however, it is important to compare the responses in the frequency domain in order to identify the ability of the signal to detect the frequencies of the bridge. Therefore, fast Fourier transform (FFT) is conducted on each signal. Figure 4 shows the acceleration spectra (FFT) of the stationary vehicle, contact-point and bridge responses. From the stationary vehicle response, the peak appears at 1.5 Hz which is the frequency of the vehicle where the bridge frequency is not visible. However, by calculating the contact-point response, the first bridge frequency is visible at 2 Hz which agrees well with the true bridge vibration. The small difference between the true frequency of the bridge (2.08 Hz) and the one obtained by the FFT (2 Hz) occurs because the exciting force doesn’t fully excite the bridge at the applied speed and selected mass of the moving vehicle.

Fig. 4.

Acceleration spectra of (a) stationary vehicle, (b) contact-point and (c) bridge responses.

3.2 Case Study 2

The second case considers a stationary vehicle with vertical frequency similar to that of the moving vehicle of 3.25 Hz. The mass of the vehicle is 1200 kg and the stiffness is 500 kN/m, same as the moving vehicle. In this case, the speed of the moving vehicle is 10 m/s. The stationary vehicle acceleration of this case is shown Fig. 5. Similar to the previous case, the stationary vehicle response does not contain higher modes of vibration. Again, Eq. (4) is used to calculate the contact-point response which is shown in the same figure. By looking at Fig. 5, the contact-point and bridge responses agree well with each other. From the FFT analysis in Fig. 6; the stationary vehicle response could detect the first mode of frequency of the bridge. However, it is clear that the stationary signal is contaminated with the vehicle frequency of 3.25 Hz. This leads to difficulties in damage identification of the bridge as the signal is polluted with the vehicle frequency. Nevertheless, when the contact-point is calculated, the stationary vehicle is almost eliminated. The contact-point response and the true bridge response show similar behavior in the frequency-domain spectra. Higher modes of the bridge are also identified such as the second and third frequencies with small margin of error.

Fig. 5.

Acceleration response of (a) stationary vehicle, (b) contact-point and (c) bridge at midspan.

Fig. 6.

Acceleration spectra of (a) stationary vehicle, (b) contact-point and (c) bridge responses.

4 Conclusion

This paper studies the response of a stationary vehicle vibration placed on a bridge traversed by a moving load. The stationary vehicle response doesn’t reflect the true vibration of the bridge as it contains the vehicle frequency. Therefore, the contact-point response was calculated to get rid of the vehicle frequency. Two cases were studied using different property of the stationary vehicle and different speed of the exciting moving load. When stationary vehicle’s frequency (1.5 Hz) is less than the bridge fundamental frequency, the first mode of vibration of the bridge was not visible in the response spectrum. However, at higher frequency of 3.25 Hz, both vehicle and bridge frequencies are detected in the stationary vehicle response spectra. Higher modes of vibration are not visible in both cases of the stationary vehicle. On the other hand, it was shown that the contact-point response could provide accurate results similar to the true bridge response in both cases. When using low speed of 5 m/s or high speed of 10 m/s, the contact-point response was in good agreement with the bridge true response. However, further work is required to investigate more cases such as more speed ranges and other properties of the stationary and moving vehicles. Also, it is important to show the analytical formulation of the contact-point response and verify it with the FE simulation.