Keywords

1 Introduction

Aircraft, missile and high-speed rail are all the complex repairable systems, which includes multi-subsystem and components, and the failures among the components are coupling. At present, commonly method for complex system reliability modeling includes the stochastic process theory, computer simulation, universal generating function (UGF) and the integrated approach among them [1,2,3, 10]. Stochastic process theory mainly includes markov equation and the renewal equation [4, 5], but it is difficult to be used to evaluate complex structure system reliability with too many components. Computer simulation method mainly includes the monte carlo simulation [6] and the discrete event scheduling [8, 9], which by using the computer software to simulate the component and system failure behavior many times to obtain reliability characteristic parameters, and can accurately reflects the topology characteristic of system structure, but there is no precise mathematical model, and the algorithm running time will increases with the increase of system components. UGF method is the Laplace transform and generating function theory in the reliability field, which is well applied in calculating reliability and availability for multi-states complex systems [11,12,13], the method can accurately reflect the topology characteristic of system structure, and improve the efficiency of operation. PENG R studied the influence of different structural forms on system reliability in the work sharing group. So far, there is no literature considered system’s failure propagation characteristics when calculating the system reliability based on UGF method. In this paper, we will fully study the system fault behavior characteristics, including components fault time distribution function and fault propagation path, system structure, then construct the 0–1 state reliability assessment model for multiple component systems based on UGF.

2 The System Reliability Assessment Model Considering Failure Propagation Based on UGF

2.1 The Introduce of UGF

UGF is a important method in the field of modern discrete mathematics, it can realize the expression of recursive relations, sequence problem such as mean and variance in a unified way. G. Levitin and A. Lisnianski have applied and developed the method in reliability theory, making it as a new tool for the reliability analysis and modeling of multi-state systems [11,12,13,14].

The basic form of the u-function f of discrete variables \( X \) is [12],

$$ u(z) = \sum\limits_{k = 1}^{K} {q_{k} z^{{x_{k} }} } $$
(1)

In the Eq. (1), \( X \) has \( K \) possible values and \( q_{k} \) is the probability for \( x_{k} \).

For a multi-component system, the \( u \)-function of the \( j \) component can be represented as

$$ u_{j} (z) = \sum\limits_{k = 1}^{K} {q_{jk} z^{{x_{jk} }} } $$
(2)

Where, the variable \( x_{jk} \) is possible values of \( j \) component, \( q_{jk} \) is the probability.

Through the composite operation of components and subsystems function, can obtain \( u \)-function of the system, but the traditional modeling method based on the system reliability of the UGF does not take into account the system fault propagation characteristics, based on this paper consider the design of the structure of the failure propagation operator.

2.2 \( u \)-Functions of Dependent Elements

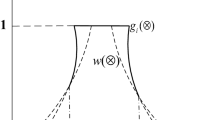
Assume that the system is composed of multiple components, and the performance between those components are dependent, which is meaning that component j performance is dependent on the component i. Let \( \text{g}_{i} \) is possible performance state for element \( i \), the set can be separated into \( M \) mutually disjoint subsets \( g_{i}^{m} (1 \le m \le M) \),

$$ \bigcup\limits_{m = 1}^{M} {g_{i}^{m} } = g_{i} \,{\text{and}}\,g_{i}^{m} \cap g_{i}^{l} = 0,\,{\text{if}}\;m \ne l $$
(3)

When element \( i \) is in the performance state \( g_{ik} \in g_{i}^{m} \), the PD of element \( j \) is defined by the ordered sets \( \text{g}_{j\left| m \right.} = \left\{ {g_{jc\left| m \right.} ,1 \le c \le C_{j\left| m \right.} } \right\} \) and \( \text{q}_{j\left| m \right.} = \left\{ {q_{jc\left| m \right.} ,1 \le c \le C_{j\left| m \right.} } \right\} \),

where

$$ q_{jc\left| m \right.} = \Pr \left\{ {G_{j} = g_{jc\left| m \right.} \left| {G_{i} = g_{ik} \in \text{g}_{i}^{m} } \right.} \right\} $$
(4)

2.3 \( u \)-Functions of Group of Dependent Elements

Assume that component \( i \) affects the impact of multiple components, such as elements \( n \) and \( j \). When component \( i \) is in state \( k \), \( g_{ik} \in \text{g}_{i}^{(k)} \); the PDs of the elements \( n \) and \( j \) are defined by the pairs of vectors \( \text{g}_{n} \): \( \text{p}_{{n\left| {u(k)} \right.}} \) and \( \text{g}_{j} \), \( \text{p}_{{j\left| {u(k)} \right.}} \), where \( \text{p}_{{n\left| {u(k)} \right.}} = \left\{ {\text{p}_{{nc\left| {u(k)} \right.}} \left| {1 \le c \le C_{n} } \right.} \right\} \). Conditional probabilities of components \( n \) and \( j \) can be obtained by comprehensively using structural operators according to system structure

$$ \sum\limits_{c = 1}^{{C_{n} }} {p_{{nc\left| {u(k)} \right.}} z^{{g_{nc} }} \mathop \otimes \limits_{\omega } } \sum\limits_{h = 1}^{{C_{j} }} {p_{{jh\left| {u(k)} \right.}} z^{{g_{jh} }} } = \sum\limits_{c = 1}^{{C_{n} }} {\sum\limits_{h = 1}^{{C_{j} }} {p_{{nc\left| {u(k)} \right.}} p_{{jh\left| {u(k)} \right.}} } z^{{\omega (g_{nc} ,g_{jh} )}} } $$
(5)

2.4 System Reliability Evaluation

System reliability can be resolved by compound operation of subsystems and components \( u \)-function. And then compute the first order partial derivative and second order partial derivatives of Eq. (6–7), mathematical expectation and variance of the reliability for the system can be obtained.

$$ E(G(t)) = \frac{\partial u}{\partial z}_{{\left| {z = 1} \right.}} $$
(6)

and

$$ \sigma^{2} (G(t)) = u^{\prime\prime} + u^{\prime} - (u^{\prime})^{2} $$
(7)

3 Illustrative Examples

Consider an power system consisting of five independent blocks. Two pump device (parts 1, 2) and three reactor (component 3, 4, 5), part 1, 2, parallel, and parts of 3, 4, 5 subsystems in series. The failure of the first pump unit (part 1) causes the component 3 to fail, and when the second pump unit (part 2) fails will cause parts 3 and 4 to fail. Therefore, there is selective failure propagation of parts 1 and 2.

According to the Fig. 1 the system’s reliability diagram can show in Fig. 1.

Fig. 1.
figure 1

The system reliability block diagram

Full size image

In Fig. 2, the dotted arrow points to the failure propagation relationship between the system components. The probability of failure of each component, based on the history statistical data of the parts in using stage, is shown in Table 1:

Fig. 2.
figure 2

Reliability function of system

Full size image
Table 1. The basic information of components
Full size table

The \( u \)-functions of the parts and systems are calculated according to Table 1, assuming the state vector of the component is

$$ x_{k} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{operation}} \hfill \\ {0,} \hfill & {\text{failure}} \hfill \\ \end{array} } \right. $$
(8)

The \( u \)-function of the part 1 is as follows

$$ \mu_{1} (z) = \sum\limits_{k = 1}^{K} {q_{1k} z^{{x_{1k} }} } = q_{0} z^{0} + q_{1} z^{1} = (0.12 + 0.08)z^{0} + (1 - 0.12 - 0.08)z^{1} = 0.2z^{0} + 0.8z^{1} $$

Also, it can easy to obtain

$$ \mu_{2} (z) = 0.2z^{0} + 0.8z^{1} $$
$$ \begin{aligned} \mu_{3} (z) & = \sum\limits_{k = 1}^{K} {q_{3k} z^{{x_{3k} }} } = q_{30} z^{0} + q_{31} z^{1} = (p_{30} + p_{{30\left| {10} \right.}} \times p_{10} + p_{{30\left| {20} \right.}} \times p_{20} )z^{0} \\ & \, +\,(1 - (p_{30} + p_{{30\left| {10} \right.}} \times p_{10} + p_{{30\left| {20} \right.}} \times p_{20} ))z^{1} = \,(0.2 + (0.12 + 0.08 + 0.12 + 0.08) \times 0.2)z^{0} \\ & \, +\, (1 - (0.2 + (0.12 + 0.08 + 0.12 + 0.08) \times 0.2))z^{1} = \,0.28z^{0} + 0.72z^{1} \\ \end{aligned} $$
$$ \begin{aligned} \mu_{4} (z) & = \sum\limits_{k = 1}^{K} {q_{4k} z^{{x_{3k} }} } = q_{40} z^{0} + q_{41} z^{1} \\ & = \,(p_{40} + p_{{40\left| {20} \right.}} \times p_{20} )z^{0} + (1 - (p_{40} + p_{{40\left| {20} \right.}} \times p_{20} ))z^{1} \\ & = \,(0.2 + (0.12 + 0.08) \times 0.2)z^{0} + (1 - (0.2 + (0.12 + 0.08) \times 0.2))z^{1} \\ & = \,0.24z^{0} + 0.76z^{1} \\ \end{aligned} $$
$$ \mu_{5} (z) = 0.1z^{0} + 0.9z^{1} $$

The \( u \)-functions of system is,

$$ u_{6} (z) = u_{1} (z)\mathop \otimes \limits_{par} u_{2} (z) = 0.04z^{0} + 0.32z^{1} + 0.64z^{2} $$
$$ u_{7} (z) = u_{3} (z)\mathop \otimes \limits_{par}^{ \Rightarrow } u_{4} (z) = 0.0672z^{0} + 0.3856z^{1} + 0.5472z^{2} $$
$$ u_{8} (z) = u_{7} (z)\mathop \otimes \limits_{par} u_{5} (z) = 0.06048z^{0} + 0.09904z^{1} + 0.40212z^{2} + 0.49428z^{3} $$
$$ u_{9} (z) = u_{6} (z)\mathop \otimes \limits_{ser}^{ \Rightarrow } u_{8} (z) = 0.1002z^{0} + 0.3813z^{1} + 0.5736z^{2} $$

Then, according to the Eq. 9, it can easy to obtain

$$ E(G(t)) = \frac{\partial u(z)}{\partial z}_{{\left| {z = 1} \right.}} = 1.5285 $$
(9)

The calculation results shows that the average reliability of the system is greater than 1, because the system structure is a redundancy structure. Add the virtual part 6 here, whose fault behavior parameters are shown in Table 1, line 7, the \( u \)-functions of part 6 is \( u_{10} = 0 \times z^{0} + 1 \times z^{1} \).

Then, \( u \) functions of system is

$$ u_{s} = u_{9} \mathop \otimes \limits_{ser} u_{10} = [(0.1002 + 0.3813 + 0.5736) \times 0 + 0.1002 \times 1]z^{0} + (0.3813 + 0.5736) \times 1z^{1} $$

According to the Eq. 9, it can easy to obtain \( E(G(t)) = \frac{\partial u(z)}{\partial z}_{{\left| {z = 1} \right.}} = 0.3813 + 0.5736 = 0.9549 \).

The results of this paper are compared with the two methods in paper [10], as shown in Table 2.

Table 2. Reliability comparisons for three methods
Full size table

The calculation results difference between the design algorithm and algorithm 1 is 0.008, and difference of algorithm 2 is 0.0059, average error is 0.00695, less than 0.7%, which indicating the correctness of the established reliability evaluation model.

Yang S. found that during division level support, failure time distribution of subsystems or components of military aircraft were subjected to exponential [14]. In this case, we assume the average failure rate of the system is the exponential distribution

$$ \lambda_{s} = 1 - E(G(t)) = 0.0451 $$
(10)

And, the system reliability is shown in Fig. 2.

4 Conclusion

In this paper, the complex system reliability were evaluated based on improved UGF method, considering failure propagation among components. A case is studied to verify the effectiveness of the proposed method, the computation result is compared with two different methods, the average error less than 0.7%, improve and expand the universal generating function theory application in the field of reliability.

In the study process, we found that the presented method can fully considering the topology of system structure and fault propagation characteristics, assessment the system average reliability, if the system is redundancy system, need to add virtual components, in order to reduce dimension of system \( u \)-function.