Keywords

1 Introduction

Event detection is one widely researched field in computer engineering [1, 2, 4, 6,7,8,9,10, 13,14,15,16,17]. Generally, event detection can be divided into complete event detection and partial event detection [15, 16]. In partial event detection, early event detection is focused on finding the target event as soon as possible. Early event detection can be applied to many applications, such as facial expression detection [8,9,10, 15, 16] and sign language detection [10, 15, 16].

Hoai and Torre [10] propose the max-margin early event detector (MMED) based on the structured output support vector machine (SOSVM) which is the generalized support vector machine (SVM) [3, 5]. Later, Huang et al. [4] design the sequential MMED (SMMED) to extend MMED to deal with multi-classes. For MMED, solving the quadratic programming problem is the major work [3]. However, if the number of constraints is very huge, it is too time consuming to be feasible. Thus, alternative solvers may be considered, for instance, Shai et al. [12] propose the primal estimated sub-gradient solver (Pegasos) in which the stochastic gradient descent method is utilized to solve the quadratic programming problem in the support vector machine instead. Furthermore, it is proven to be able to converge efficiently [12].

Thus, due to the huge number of constraints in MMED, about three thousand constraints for one simple synthetic training instance [10, 12], in this study, the stochastic gradient descent method is used to replace the quadratic programming solver in MMED. Three data sets are used in the experiments as those used in [10], and comparable experimental results are obtained to verify the feasibility of the proposed approach.

2 Proposed Approach

In order to incorporate the stochastic gradient descent mechanism, Pegasos [12], into MMED [10], the objective function of MMED [10] needs to be rewritten in the gradient-descent style [12]. In this study, for a given training sample \(S=\{{({\varvec{x}}}^{i},{{\varvec{y}}}^{i})| {{\varvec{x}}}^{i}\in X,{{\varvec{y}}}^{i}\in Y, i=1,\dots ,n\}\), where \(X\) is the input training instance set, and \(Y\) the set of early events, the proposed gradient-descent-style objective function is derived to be:

$$\mathrm{min}\frac{\lambda }{2}{\parallel {\varvec{w}}\parallel }^{2}+\frac{1}{n}\sum_{i=1}^{n}\mathrm{max}\left\{0,\mu \left(\frac{{|y}_{t}^{i}|}{\left|{{\varvec{y}}}^{{\varvec{i}}}\right|}\right)\left[f\left({{\varvec{x}}}_{{\varvec{y}}-{{\varvec{y}}}_{t}^{i}}^{i}\right)+ \varDelta \left({{\varvec{y}}}_{t}^{i},{\varvec{y}}\right)\right]\right\},$$
(1)

where \({\varvec{w}}\) is the weight vector of the linear early event detector in [10], \(\lambda \) the trade-off coefficient in [12], \({{\varvec{y}}}_{t}^{i}\) the early event observed at time t of the complete event \({{\varvec{y}}}^{{\varvec{i}}}\) in the training instance \({{\varvec{x}}}^{i}\) [10], \({\varvec{y}}\) a time segment in \({{\varvec{x}}}^{i}\) [10], \(\mu \left(\frac{{|{\varvec{y}}}_{t}^{i}|}{\left|{{\varvec{y}}}^{i}\right|}\right)\) the scaling function for soft margin [10], \(\varDelta \left({{\varvec{y}}}_{t}^{i},{\varvec{y}}\right)\) the loss function of mistaking \({\varvec{y}}\) as \({{\varvec{y}}}_{t}^{i}\) [10], and \(f\left({{\varvec{x}}}_{{\varvec{y}}-{{\varvec{y}}}_{t}^{i}}^{i}\right)=f\left({{\varvec{X}}}_{{\varvec{y}}}^{i}\right)-f\left({{\varvec{X}}}_{{{\varvec{y}}}_{t}^{i}}^{i}\right)\) the difference of the detection scores of \(f\left({{\varvec{X}}}_{{\varvec{y}}}^{i}\right)\) and \(f\left({{\varvec{X}}}_{{{\varvec{y}}}_{t}^{i}}^{i}\right)\) [10, 12]. The proposed algorithm to achieve the optimization of Eq. (1), denoted as Pegasos-based MMED (PMMED), is as follows.

figure a

For each iteration in the above algorithm, a training instance \(\left({{\varvec{x}}}^{i},{{\varvec{y}}}_{t}^{i}\right)\) is chosen randomly, the corresponding gradient is computed, and the weight vector \({{\varvec{w}}}_{i}\) is updated. Note that \({\eta }_{t}\) is the learning rate at iteration t.

As shown in Line 7 of Algorithm 1, the gradient \({\nabla }_{t}\) is

$${\nabla }_{t}={\lambda w}_{t}+1\left[{f({\varvec{X}}}_{{\varvec{y}}-{{\varvec{y}}}_{t}^{i}}^{i})+\varDelta \left({{\varvec{y}}}_{t}^{i},{\varvec{y}}\right)>0\right]\mu \left(\frac{{|{\varvec{y}}}_{t}^{i}|}{\left|{{\varvec{y}}}^{i}\right|}\right){f\mathrm{^{\prime}}({\varvec{X}}}_{{\varvec{y}}-{{\varvec{y}}}_{t}^{i}}^{i}).$$
(2)

The derivation of Eq. (2) is as follows. First, recall the objective function of MMED in [10]:

$$\mathrm{min}\frac{1}{2}{\parallel {\varvec{w}}\parallel }^{2}+\frac{C}{n}\sum_{i=1}^{n}{\xi }^{i}$$
$$\mathrm{subject\, to}\,f\left({{\varvec{X}}}_{{{\varvec{y}}}_{t}^{i}}^{i}\right)\ge f\left({{\varvec{X}}}_{{\varvec{y}}}^{i}\right)+ \varDelta \left({{\varvec{y}}}_{t}^{i},{\varvec{y}}\right)-\frac{{\xi }^{i}}{\mu \left(\frac{{|{\varvec{y}}}_{t}^{i}|}{\left|{{\varvec{y}}}^{i}\right|}\right)}$$
$$\forall i=1,\dots , n, \forall t=1,\dots , {l}^{i}, \forall {\varvec{y}}\in Y\left(t\right).$$
(3)

Since the slack variables \({\xi }^{i}\ge 0\), the violated constraint for the objective function shown in Eq. (3) can be rewritten to be the following.

$${0\le \xi }^{i}<\mu \left(\frac{{|{\varvec{y}}}_{t}^{i}|}{\left|{{\varvec{y}}}^{i}\right|}\right)\left[f\left({{\varvec{X}}}_{{\varvec{y}}}^{i}\right)-f\left({{\varvec{X}}}_{{{\varvec{y}}}_{t}^{i}}^{i}\right)+\varDelta \left({{\varvec{y}}}_{t}^{i},{\varvec{y}}\right)\right]$$
(4)

Based on the hinge loss idea [3], Eq. (4) can be expressed as:

$${\xi }^{i}=\mathrm{max}\left\{0,\mu \left(\frac{{|{\varvec{y}}}_{t}^{i}|}{\left|{{\varvec{y}}}^{i}\right|}\right)\left[f\left({{\varvec{X}}}_{{\varvec{y}}}^{i}\right)-f\left({{\varvec{X}}}_{{{\varvec{y}}}_{t}^{i}}^{i}\right)+\varDelta \left({{\varvec{y}}}_{t}^{i},{\varvec{y}}\right)\right]\right\}$$
(5)

By using Eq. (5), Eq. (3) can be rewritten to derive the following equation.

$$ \min \frac{1}{2}\parallel {\varvec{w}}\parallel^{2} + \frac{C}{n}\mathop \sum \nolimits_{i = 1}^{n} {\text{max}}\left\{ {0,\mu \left( {\frac{{|{\varvec{y}}_{t}^{i} |}}{{\left| {{\varvec{y}}^{i} } \right|}}} \right)\left[ {f\left( {{\varvec{X}}_{{{\varvec{y}} - {\varvec{y}}_{t}^{i} }}^{i} } \right) + \varDelta \left( {{\varvec{y}}_{t}^{i} ,{\varvec{y}}} \right)} \right]} \right\}. $$
(6)

Finally, change the trade-off coefficient from \(C\) in the second term to \(\lambda \) in the first term in Eq. (6), and Eq. (1) is derived. Then, the gradient \({\nabla }_{t}\) can be derived as shown in Eq. (2).

3 Experimental Results

In this study, three datasets are utilized, including synthetic data, the extended Cohn-Kanade dataset (CK+), and Australian sign language data (ASL) [10]. The ROC curve, the AMOC curve, and the F1-score curve are used to demonstrate detection precision, timeliness, and location ability of the proposed approach, respectively [10].

3.1 Synthetic Data

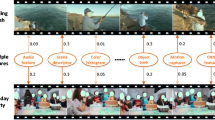
Following MMED [10], the synthetic dataset is used to check correctness of the proposed approach. One time series contains a target event, two non-target events, and four connecting segments [10]; the total length of one signal sequence is between 160 and 180 numerical values. Some examples of the synthetic data sequence can be found in Fig. 1, in which the green ones are the target events.

In the experiments, one training/testing dataset consists of 100 time series. A total of 100 pairs of training and testing datasets are generated. For each pair, the proposed PMMED and the MMED method [10] are applied, and the testing results are expressed via ROC, AMOC, and F1-score curves.

Some samples of the testing results are given in Fig. 1, in which the target event is shown in green, and the fire frames are marked as red and blue vertical lines for PMMED and MMED, respectively. It can be seen that PMMED detects the target event earlier than MMED.

Fig. 1.
figure 1

Samples of testing results of synthetic data. The horizontal axis shows the timing of the time series, and the vertical axis indicates the signal value. (Color figure online)

Full size image

In Fig. 2, the performance of PMMED and MMED are shown and compared. As shown in Fig. 2(a), all the 200 testing datasets for PMMED and MMED detect the target event with 100% accuracy with the area under ROC curve of 1. In Fig. 2(b), the AMOC curves of the set of the 100 testing datasets for PMMED and MMED are shown by thin red curves and by thin blue ones, respectively; the average AMOC curves are shown by thick ones. It can be found that, for timeliness performance, MMED is a little better than PMMED. The reason may be that the stochastic nature of PMMED selects not-so-good answers sometimes. By using the same illustration style for the F1-score curves in Fig. 2(c), it can be found that PMMED is a little better than MMED on the location ability. The reason may be that required by MMED is the optimal solution, which delays the detection of the event location. However, as shown in Fig. 2, the performance of PMMED and that of MMED are comparable for the synthetic datasets.

Fig. 2.
figure 2

Performance of synthetic data: (a) ROC curves; (b) AMOC curves; (c) F1-score curves. (Color figure online)

Full size image

3.2 Extend Cohn-Kanade Dataset

In CK+, there is a total of 327 CAPP facial image sequences from 123 subjects, including 4 kinds of negative emotions and 3 kinds of positive emotions [10]. In the experiments, 100 positive and 100 negative emotion sequences are randomly selected as a training dataset, and the remaining 127 sequences are the testing dataset. The procedure is repeated 100 times to generate 100 pairs of training and testing datasets. Then both PMMED and MMED are applied to all the pairs to get the testing results. Note that the negative emotion is the target.

In Fig. 3, the illustration style is the same as that of Fig. 2, that is, the red curves are for PMMED, the blue ones for MMED, and each thick curve for the average of 100 thin curves. As shown in Fig. 3(a) and Fig. 3(b), the areas occupied by the red curves and the blue ones are almost the same. However, it can be said that the performance of MMED is a little better than that of PMMED if the two average curves in either subfigure are carefully compared. That is, for accuracy and timeliness, the performance of PMMED and MMED are quite comparable on the CK+ dataset. However, as for the F1-score curve shown in Fig. 3(c), the performance of MMED is better than that of PMMED. The reason may be that the strategy of optimal solution finding for MMED is more suitable for event location detection when tackling more complicated events like facial expressions.

Fig. 3.
figure 3

Performance of CK+ dataset: (a) ROC curves; (b) AMOC curves; (c) F1-score curves.

Full size image

3.3 Auslan Dataset

The Auslan dataset (ASL) consists of 95 words; for each word, 27 instances can be found, and there are 22 features derived from hands are used to represent an instance [10]. In this study, based on the experimental setting in MMED [10], the target was “I love you”, and two sets of 15 randomly chosen words were added before and after the target, respectively. For each word, the first 15 instances were used for training and the remaining 12 ones for testing. The pre-processing of the training/testing data followed that designed in MMED [10].

A total of 100 sentences were generated as the training set, and a total of 200 sentences as the test set. Then PMMED and MMED were applied, and the performance was analyzed. As shown in Fig. 4, all the ROC curve, the AMOC curve, and the F1-score curve indicates that MMED works better than PMMED. Since the stochastic nature of PMMED is to find a solution based on only one instance chosen randomly, it was natural for MMED to get better results compared with PMMED. However, it is still can be claimed that PMMED and MMED are comparable in terms of accuracy according to Fig. 4(a).

Fig. 4.
figure 4

Performance of ASL dataset: (a) ROC curves; (b) AMOC curves; (c) F1-score curves.

Full size image

4 Conclusion

In this study, an approach called PMMED has been proposed to achieve early event detection. In order to tackle with huge constraints, the core work of PMMED has been designed to use the strategy of stochastic gradient descent to solve the original quadratic programming problem in MMED [10]. The performance of MMED and PMMED has been compared through the experiments based on three datasets, including synthetic data, CK+, and ASL, and based on the ROC curves, the AMOC curves, and the F1-score curves. According to the experimental results, the performance of PMMED and MMED is quite comparable in terms of accuracy and timeliness, and MMED is better than PMMED in terms of the location ability.