Design and Analysis of Modified Non-orthogonal Helical Face-Gears with a High-Order Transmission Error

Abstract

In order to improve the meshing performance of non-orthogonal helical face-gears, a designation of double-crowned tooth modification with high-order transmission error (HTE) is constructed in this paper. First, the double-crowned tooth modification is designed based on the tooth profile modification of the rack-cutter and the motion relationship between the rack-cutter and the processed pinion, and then, the designation of high-order tooth modification is verified by using tooth contact analysis (TCA). Second, a parameterized 3D grid of modified gears is generated based on MATLAB programming, and a simulation of loaded tooth contact analysis for modified non-orthogonal helical face-gears is carried out by using ABAQUS software. Third, the calculation results of the standard tooth, second-order parabolic modified tooth and high-order parabolic modified tooth are compared with and without the assembly errors. Ultimately, an example is presented and the results show that the geometric transmission error of the newly designed high-order modified non-orthogonal helical face-gears conforms to the expected design. Compared with the second-order parabolic tooth modification, the newly designed high-order tooth modification pair shows a better meshing performance with and without assembly errors. The research of this paper can provide ideas and methods for the tooth modification design of non-orthogonal helical face-gear.

1 Introduction

Face-gears has the advantages of large-stage ratio, compact structure and so on. It is of great significance to improve the technical level of power transmission of aviation equipment when it is applied to aeronautical power-split transmission. At present, the face-gears has been successfully applied to the main reducer of the helicopter. Under the working conditions of high speed and heavy load, the elastic deformation and thermal deformation of the face-gears will lead to uneven load distribution on the tooth surface, decrease of load bearing capacity, increase of vibration and noise, etc. Therefore, it is necessary to carry out the tooth modification design for face-gears in order to reduce the adverse effects of deformation and error [1,2,3,4].

Tooth modification of gears usually refers to removing a small amount of material from the tooth surface of gears. The typical tooth modification of gears is the middle-convex modification as tooth profile modification, tooth axial modification and three-dimensional modification and so on [5,6,7,8,9,10,11]. These typical methods are called the traditional tooth modification method herein. There is enough research to show that the traditional tooth modification can reduce the effect of errors. However, with the development of science and technology, the requirement of gear transmission in modern industry is higher and higher, and some disadvantages of traditional tooth modification are gradually emerging. For example, the traditional tooth modification may increase the maximum contact stresses of gears. Excessive contact stress can exacerbate the surface wear, reduce the working life and decrease the gear drive efficiency.

But it must be pointed out that the errors such as assembly, manufacturing, and so on, are inevitable in practical application. To some extent, tooth modification is necessary. Therefore, researchers have been exploring new tooth modification methods for a long time. It is hoped that the new method can not only maintain the advantages of the traditional one, but also reduce the adverse impact on gears. And high-order tooth modification is such a potential new method [12, 13].

Jiang [14] proposed a high-order transmission error (HTE) modification for cylindrical gears, and determined the coefficients of the high-order polynomial through particle swarm optimization (PSO), and the feasibility of high-order modification is proved by analyzing and comparing the loading transmission error before and after modification. Jia et al. [15] modified the tooth surface of the cylindrical gear through the pre-designed high-order transmission error to reduce the error margin of the loading transmission. Su et al. [16] proposed a seventh-order transmission error modification for helical bevel gears to prove that the bending stress of the tooth surface with the seventh-order transmission error modification is smaller than that of the parabolic tooth surface, while the contact stress is almost equal. The modification of the high-order transmission error can improve the meshing performance of the spiral bevel gear with high coincidence degree [17]. The amplitude of loaded transmission error and the gear vibration of the helical gear with high-order transmission error is reduced compared with standard gear [18]. Daqing et al. [19] derived the tooth-surface equation of the face-gears from the high-order parabolic rack based on the grinding process, and the tooth-surface equation of the pinion is worked out by means of the modification principle of the high-order parabolic curve. And the effect of new tooth-surface equation on the meshing performance of the face-gear pair is analyzed.

From above discussion, it can be found that the research of high-order tooth modification mainly focuses on the cylindrical gears and spiral bevel gears, while the research on high-order tooth modification of face-gears is rare. Therefore, to improve the meshing performance of non-orthogonal helical face-gears, a designation of double-crowned tooth modification with HTE is constructed in this paper. The double-crowned tooth modification is designed based on the tooth profile modification of the rack-cutter and the motion relationship between the rack-cutter and the processed pinion. The innovation of the new method is that the basic tooth profile of the controllable HTE is designed according to the theoretical contact path of the gear. And the design of high-order modifications is verified by tooth contact analysis (TCA) and the loaded contact analysis (LTCA).

2 Derivation of Tooth Surface Equation for Non-orthogonal Helical Face-Gears

2.1 The Principle of Face-Gear Shaping

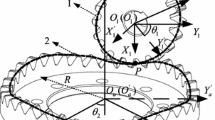
The process of face gear shaping is based on the movement of the cutter and the face gear. Its processing principle is shown in Fig. 1.

Fig. 1

Schematic diagram of face-gears shaping

2.2 Generation of Face-Gears Tooth Surface

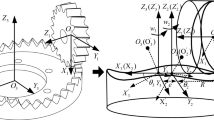
Base on the motion relationship between the cutter and the processed face-gears during the cutting process of the face-gears, establish a non-orthogonal helical face-gears machining coordinate system, $S_{2}$ and $S_{s}$ are rigidly connected to the face gear and the cutter, where $Z_{2}$ and $Z_{s}$ are the axes of the cutter and face-gears respectively. The angle $\gamma_{m}$ is the shaft angle. Convert the position vector of the cutter from the coordinate system $S_{s}$ to the coordinate system $S_{2}$ based on the movement of the cutter and the face-gears. And the face-gears tooth surface $\Sigma_{2}$ is generated by meshing equation [20] (Figs. 2 and 3).

Fig. 2

Generation of coordinate system for face-gears

Fig. 3

Profile of a rack cutter

The rack profile can be represented by Eq. (1).

$$ {\mathop{r}\limits^{\rightharpoonup}} _{as} = [\begin{array}{*{20}c} {{ - }a_{cs} u_{cs}^{2} } & {u_{cs} } & {l_{g} } & 1 \\ \end{array} ] $$

(1)

where $a_{cs}$ is modification parameter for tooth profile modification; $u_{cs}$ and $l_{g}$ are the related tooth flank parameters of the rack cutter.

The tooth surface of the face-gears can be represented by Eq. (2).

$$ {\mathop{r}\limits^{\rightharpoonup}} _{2} (u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} ))=M_{2a} {\mathop{r}\limits^{\rightharpoonup}} _{as} (u_{cs} ,l_{{\text{g}}} ,\psi_{s} ) $$

(2)

where $M_{2a}$ is a $4 \times 4$ matrix from the coordinate system $S_{a}$ to the coordinate system $S_{{2}}$ (Figs. 4 and 5).

Fig. 4

Coordinate system of face-gears

Fig. 5

Coordinate system of cutter

where $\varphi_{2}$ is rotation angle of face-gears; $\psi_{s}$ is rotation angle of cutter.

Base on the motion relationship between the cutter and the processed face-gears, the meshing equation of the cutter and face-gears can be represented by Eq. (3).

$$ f_{2} (u_{cs} ,\psi_{s} ,\varphi_{2} (\varphi_{1} )) = n_{sr}^{T} v_{g2} $$

(3)

where $n_{sr}$ is the unit normal vectors in the coordinate system $S_{s}$; $v_{{{\text{g}}2}}$ is the relative velocity of cutter and face-gears.

3 A Designation of Double-Crowned Tooth Modification of Pinion

3.1 Derivation of Parabolic Profile Equation of Helical Cylindrical Gears

According to the principle of gear meshing processing, the tooth surface of the pinion is formed by the envelopment of the tooth surface of the rack. The coordinate system $S_{c}$ is connected to the cutter and the coordinate system $S_{r1}$ is connected to the cutter pinion. Profile of rack with second order parabolic can be represented by Fig. 6.

Fig. 6

Profile of rack

The generation process of pinion can be represented by Fig. 7. The fixed coordinate system $S_{{\text{n}}}$ is connected to the pinion, The rotating coordinate system $S_{1}$ is connected to the pinion, The moving coordinate system $S_{{{\text{r}}1}}$ is connected to the rack-cutter. When the pinion rotates angle $\varphi_{1}$, the rack-cutter moves $r_{p1} \varphi_{1}$. Where $r_{p1}$ is the radii of pitch circle of pinion.

Fig. 7

Roll motion in a pinion cutting process

Position vector of rack profile can be represented by Eq. (4).

$$ {\mathop{r}\limits^{\rightharpoonup}} _{ai} = [\begin{array}{*{20}c} { - a_{ci} u_{ci}^{2} } & {u_{ci} - u_{0i} } & {l_{d} } & 1 \\ \end{array} ] $$

(4)

where $a_{ci}$ is modification parameter for tooth profile modification; $u_{ci}$ and $l_{d}$ are the related tooth flank parameters of the rack cutter, $u_{0i}$ is the distance from initial position to rack profile position.

The tooth surface of pinion can be represented by Eq. (5).

$$ {\mathop{r}\limits^{\rightharpoonup}} _{1} (u_{ci} ,l_{d} ,\varphi_{1} ) = M_{1i} {\mathop{r}\limits^{\rightharpoonup}} _{ai} (u_{ci} ,l_{d} ) $$

(5)

Base on designing modification parameter for tooth profile modification of the rack-cutter, the tooth profile of the rack-cutter can be modified to a tooth profile with second-order parabolic, so as to achieve the effect of modifying the tooth profile of the pinion (Fig. 8).

Fig. 8

Tooth profile modification of the pinion

3.2 HTE

In this paper, the tooth surface of the pinion is produced by rack-cutter. The rack-cutter performs a translational motion and the pinion rotates with the rack-cutter. The modified flank of pinion is controlled by the HTE. Based on the meshing theory of gears, Generation of a pinion tooth can be represented by Fig. 9.

Fig. 9

Generation of a pinion tooth

In Fig. 10, the TE is predesigned as a six-order parabolic function, which is controlled by five points. There are seven unknown parameters in the TE function, and a system of seven equations is provided by the five predesigned points on the TE function. The x-coordinate and y-coordinate of the five given points are the rotation angle of the pinion and the transmission error of the face-gears, respectively (Fig. 11).

Fig. 10

The high-order parabolic transmission error

Fig. 11

The traditional second-order parabolic transmission error

The TE function of Fig. 10 is written as Eq. (6).

$$ \delta \varphi_{2} = a_{0} + a_{1} \varphi_{1} + a_{2} \varphi_{1}^{2} + a_{3} \varphi_{1}^{3} + a_{4} \varphi_{1}^{4} + a_{5} \varphi_{1}^{5} + a_{6} \varphi_{1}^{6} = XY^{T} $$

(6)

where $\varphi_{1}$ and $\delta \varphi_{2}$ represent the TE angle of the pinion and face-gears, respectively, and $a_{0} - - a_{6}$ represent the coefficient of HTE function:

$$ \left\{ {\begin{array}{*{20}l} {\varphi_{1} = T_{1} ,\delta \varphi_{2} = \varepsilon_{1} } \hfill \\ {\varphi_{1} = T_{m} - \lambda_{1} T,\delta \varphi_{2} = 0} \hfill \\ {\varphi_{1} = 0.5(T_{1} + T_{2} ) = T_{m} ,\delta \varphi_{2} = \varepsilon_{2} } \hfill \\ {\varphi_{1} = T_{m} + \lambda_{2} T,\delta \varphi_{2} = \varepsilon_{3} } \hfill \\ {\varphi_{1} = T_{2} ,\delta \varphi_{2} = \varepsilon_{4} } \hfill \\ {\varphi_{1} = T_{m} + \lambda_{2} T,\frac{{\partial \delta \varphi_{2} }}{{\partial \varphi_{1} }} = 0} \hfill \\ {\varphi_{1} = T_{m} - \lambda_{1} T,\frac{{\partial \delta \varphi_{2} }}{{\partial \varphi_{1} }} = 0} \hfill \\ \end{array} } \right. $$

(7)

Solve the above formulas simultaneously to obtain the solution matrix of the high-order transmission error curve coefficients:

$$ \left\{ \begin{gathered} {\text{A}} = \left[ {\begin{array}{*{20}c} 1 & {T_{1} } & {T_{1}^{2} } & {T_{1}^{3} } & {T_{1}^{4} } & {T_{1}^{5} } & {T_{1}^{6} } \\ 1 & {(T_{m} - \lambda_{1} T)} & {(T_{m} - \lambda_{1} T)^{2} } & {(T_{m} - \lambda_{1} T)^{3} } & {(T_{m} - \lambda_{1} T)^{4} } & {(T_{m} - \lambda_{1} T)^{5} } & {(T_{m} - \lambda_{1} T)^{6} } \\ 0 & 1 & {2(T_{m} - \lambda_{1} T)} & {3(T_{m} - \lambda_{1} T)^{2} } & {4(T_{m} - \lambda_{1} T)^{3} } & {5(T_{m} - \lambda_{1} T)^{4} } & {6(T_{m} - \lambda_{1} T)^{5} } \\ 1 & {T_{m} } & {T_{m}^{2} } & {T_{m}^{3} } & {T_{m}^{4} } & {T_{m}^{5} } & {T_{m}^{6} } \\ 1 & {(T_{m} + \lambda_{2} T)} & {(T_{m} + \lambda_{2} T)^{2} } & {(T_{m} + \lambda_{2} T)^{3} } & {(T_{m} + \lambda_{2} T)^{4} } & {(T_{m} + \lambda_{2} T)^{5} } & {(T_{m} + \lambda_{2} T)^{6} } \\ 0 & 1 & {2(T_{m} - \lambda_{2} T)} & {3(T_{m} - \lambda_{2} T)^{2} } & {4(T_{m} - \lambda_{2} T)^{3} } & {5(T_{m} - \lambda_{2} T)^{4} } & {6(T_{m} - \lambda_{2} T)^{5} } \\ 1 & {T_{2} } & {T_{2}^{2} } & {T_{2}^{3} } & {T_{2}^{4} } & {T_{2}^{5} } & {T_{2}^{6} } \\ \end{array} } \right] \hfill \\ {\rm B} = \left[ {\begin{array}{*{20}c} {\varepsilon_{1} } & 0 & 0 & {\varepsilon_{2} } & {\varepsilon_{3} } & 0 & {\varepsilon_{4} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right. $$

(8)

where,

$$ \left\{ \begin{gathered} X = \left[ {\begin{array}{*{20}c} {a_{0} } & {a_{1} } & {a_{2} } & {a_{3} } & {a_{4} } & {a_{5} } & {a_{6} } \\ \end{array} } \right] \hfill \\ Y = \left[ {\begin{array}{*{20}c} 1 & {\varphi_{1} } & {\varphi_{1}^{2} } & {\varphi_{1}^{3} } & {\varphi_{1}^{4} } & {\varphi_{1}^{5} } & {\varphi_{1}^{6} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right.,\quad X = {\rm A}^{ - 1} {\rm B} $$

(9)

The higher-order transmission error can be represented by Eq. (10).

$$ \delta \varphi_{2} \left( {\varepsilon_{1} ,\varepsilon_{2} ,\varepsilon_{3} ,\varepsilon_{4} ,\lambda_{1} ,\lambda_{2} } \right) = {\rm A}^{ - 1} {\rm B}Y^{T} $$

(10)

4 Tooth Contact Analysis of Face-Gears Pair

4.1 Meshing Equation of Tooth Surface

The non-orthogonal helical face-gears pair is composed of helical cylindrical gear and non-orthogonal helical face-gears. According to the principle of tooth contact analysis, the coordinate system can be established in Fig. 12. The coordinate systems $S_{1}$ and $S_{2}$ are connected the pinion and the face-gear, respectively. In the figure, $\gamma_{f} = \gamma_{m} + \Delta \gamma$, where $\gamma_{m}$ is the shaft angle, and $\Delta \gamma$ is the shaft angle error.

Fig. 12

Face-gear pair

Transformed the position vectors ${\mathop{r}\limits^{\rightharpoonup}} _{1}$, ${\mathop{r}\limits^{\rightharpoonup}} _{2}$ and unit normal vectors ${\mathop{n}\limits^{\rightharpoonup}}_{1}$, ${\mathop{n}\limits^{\rightharpoonup}} _{2}$ into the coordinate system $S_{f}$, and then, the tooth surface of the pinion and face-gear can be represented by Eqs. (11), (12), (13) and (14).

$$ {\mathop{r}\limits^{\rightharpoonup}} _{2}^{\left( f \right)} \left( {u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} )} \right) = \left[ {M_{f2} } \right]{\mathop{r}\limits^{\rightharpoonup}} _{2} \left( {u_{cs} ,l_{g} ,\psi_{s} } \right) $$

(11)

$$ {\mathop{r}\limits^{\rightharpoonup}} _{1}^{\left( f \right)} \left( {u_{ci} ,l_{d} ,\varphi_{1} } \right) = \left[ {M_{f1} } \right]{\mathop{r}\limits^{\rightharpoonup}} _{1} \left( {u_{ci} ,l_{d} } \right) $$

(12)

$$ {\mathop{n}\limits^{\rightharpoonup}} _{2}^{\left( f \right)} \left( {u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} )} \right) = \left[ {L_{f2} } \right]{\mathop{n}\limits^{\rightharpoonup}} _{2} \left( {u_{cs} ,l_{g} ,\psi_{s} } \right) $$

(13)

$$ {\mathop{n}\limits^{\rightharpoonup}} _{1}^{\left( f \right)} \left( {u_{ci} ,l_{d} ,\varphi_{1} } \right) = \left[ {L_{f1} } \right]{\mathop{n}\limits^{\rightharpoonup}} _{1} \left( {u_{ci} ,l_{d} } \right) $$

(14)

where ${\mathop{r}\limits^{\rightharpoonup}} _{1}^{\left( f \right)}$ and ${\mathop{r}\limits^{\rightharpoonup}} _{2}^{\left( f \right)}$ are position vectors of the tooth surface of the pinion ∑₁ and face-gear ∑₂; ${\mathop{n}\limits^{\rightharpoonup}} _{1}^{\left( f \right)}$ and ${\mathop{n}\limits^{\rightharpoonup}} _{2}^{\left( f \right)}$ are unit normal vectors of the tooth surface of the pinion ∑₁ and face-gear ∑₂; $\left[ {M_{fi} } \right]\;\left( {i = 1,2} \right)$ is a $4 \times 4$ matrix; $\left[ {L_{fi} } \right]\;\left( {i = 1,2} \right)$ is a $3 \times 3$ submatrix of $\left[ {M_{fi} } \right]\;\left( {i = 1,2} \right)$.

The moving coordinate system $S_{f}$ is connected to the pinion. In $S_{f}$, surfaces ∑₁ and ∑₂ are in tangent, and their position vectors ${\mathop{r}\limits^{\rightharpoonup}} _{i}^{\left( f \right)} \;(i = 1,2)$ and unit normal vectors ${\mathop{n}\limits^{\rightharpoonup}} _{i}^{\left( f \right)} \;(i = 1,2)$ considered in $S_{f}$ must be equal, which can be represented by Eq. (15).

$$ \left\{ \begin{gathered} f(u_{cs} ,l_{g} ,\psi_{s} ) = 0 \hfill \\ {\mathop{r}\limits^{\rightharpoonup}} _{2}^{(f)} \left( {u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} )} \right) = {\mathop{r}\limits^{\rightharpoonup}} _{1}^{(f)} \left( {u_{ci} ,l_{d} ,\varphi_{1} } \right) \hfill \\ {\mathop{n}\limits^{\rightharpoonup}} _{2}^{(f)} \left( {u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} )} \right) = {\mathop{n}\limits^{\rightharpoonup}} _{1}^{(f)} \left( {u_{ci} ,l_{d} ,\varphi_{1} } \right) \hfill \\ \end{gathered} \right. $$

(15)

where $\varphi_{2}$ is the rotation angle of face-gear; $\varphi_{1}$ is the rotation angle of pinion.

By setting the value of $\varphi_{2}$ to solve the nonlinear equation system, the contact path of the face-gear tooth surface can be obtained by bringing the solved parameters into the equation.

When edge contact occurs, the edge of crest of the pinion contacts the tooth flank of the face-gear when out of meshing. At this time, in the fixed coordinate system $S_{f}$, the position vectors of the tip edge of the pinion and the tooth surface of the face-gear must be equal, and the tangent vector of the tip edge of the pinion is perpendicular to the normal vector of the tooth surface of the face-gear. Likewise, when the two gear teeth come into mesh, the edge of crest of the face-gear is in contact with the tooth flank of the pinion. In the fixed coordinate system, position vectors of the edge of crest of the face-gear and the tooth surface of the pinion must be equal, and the tangent vector of the edge of crest of the face-gear is perpendicular to the normal vector of the tooth surface of the pinion.

Both cases can be represented by Eqs. (16) and (17).

$$ \frac{{\partial {\mathop{r}\limits^{\rightharpoonup}} _{f}^{(1)} (u_{ci} ,l_{d} ,\varphi_{1} )}}{{\partial l_{d} }} \cdot {\mathop{n}\limits^{\rightharpoonup}} _{f}^{(2)} = 0 $$

(16)

$$ \frac{{\partial {\mathop{r}\limits^{\rightharpoonup}} _{f}^{(2)} (u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} ))}}{{\partial l_{g} }} \cdot {\mathop{n}\limits^{\rightharpoonup}} _{f}^{(1)} = 0 $$

(17)

where $\frac{{\partial {\mathop{r}\limits^{\rightharpoonup}} _{f}^{(1)} (u_{ci} ,l_{d} ,\varphi_{1} )}}{{\partial l_{d} }}$ is the tangent vector of the edge of crest of the pinion; $\frac{{\partial {\mathop{r}\limits^{\rightharpoonup}} _{f}^{(2)} (u_{cs} ,l_{g} ,\psi_{s} ,\varphi_{2} (\varphi_{1} ))}}{{\partial l_{g} }}$ is the tangent vector of the edge of crest of face-gear; ${\mathop{n}\limits^{\rightharpoonup}} _{f}^{(1)}$ is the normal vector of the tooth surface of pinion; ${\mathop{n}\limits^{\rightharpoonup}} _{f}^{(2)}$ is the normal vector of the tooth surface of face-gear.

By solving the above equations, the contact point of the face gear can be determined.

4.2 Calculation of Hertzian Contact Stress

According to the equations of non-orthogonal helical face-gears tooth surface and the contact path, the contact point of each meshing position can be obtained. Based on the principle of contact mechanics, at a certain meshing position, the contact point is deformed due to the action of the load, and the initial contact point expands into an elliptical contact area. The displacement at the center of the ellipse is the largest, and the contact stress is also the largest. The calculation of the elliptical contact area is related to the curvature of the two contact surfaces at the contact point, and a digital program can be written to calculate the corresponding curvature.

Based on the Hertzian elastic contact theory [21,22,23], the two gears in contact are deformed under the action of the normal load, and expand into an elliptical contact area at the initial contact point O. The contact deformation can be represented by Fig. 13.

Fig. 13

Hertzian elastic contact

$$ \frac{B}{A} = \frac{{\left( {{\text{a}}^{2} /b^{2} } \right)E\left( e \right) - K\left( e \right)}}{K\left( e \right) - E\left( e \right)} $$

(18)

$$ F_{n} = \frac{2}{3}p_{0} \pi ab $$

(19)

$$ e = \left( {1 - \frac{{b^{2} }}{{a^{2} }}} \right)^{1/2} $$

(20)

$$ \frac{1}{{E^{*} }} = \frac{{1 - v_{1}^{2} }}{{E_{1} }} + \frac{{1 - v_{2}^{2} }}{{E_{2} }} $$

(21)

$$ p_{0} = \frac{{1.5F_{n} }}{\pi ab} $$

(22)

where $F_{n}$ is the normal load of the contact point; $a$ is the semimajor axis of ellipse; $b$ is the semi-minor axis of ellipse; $K\left( e \right)$ is elliptic integral of the first kind; $E\left( e \right)$ is elliptic integral of the second kind; $e$ is the eccentricity of ellipse; $p_{0}$ is the maximum contact stress.

5 Numerical Examples and Discussions

5.1 TCA

The calculation results of the standard tooth, second-order parabolic modified tooth and high-order parabolic modified tooth without the assembly errors can be represented by Fig. 14 (Table 1).

Fig. 14

Paths of contact and transmission error on face-gear surfaces without the assembly errors

Table 1 Design parameters of face-gears

Among various assembly errors, the shaft angle error is the parameter which is most significant on the meshing performance of the face-gear pairs [24,25,26], so the shaft angle error is considered in this paper. By comparing Fig. 14a–c with Figs. 15a–c and 16a–c, it can be found that when the shaft angle error $\Delta \gamma = 1.5^{{\prime}}$, the paths of contact on face-gear surfaces moves towards the outer end of the face-gear, the contact points of the crest edge are reduced, the contact points of the tooth root edge are increased, and the transmission error is also significantly increased and when the shaft angle error $\Delta \gamma = - 1.5^{{\prime}}$, the paths of contact on face-gear surfaces moves towards the inner end of the face-gear, the contact points of the crest edge are increased, the contact points of the tooth root edge are reduced, and the transmission error is significantly increased. The meshing effect of the face-gear pair will easily be deteriorated due to the deviation of the contact point.

Fig. 15

Paths of contact and transmission error on face-gear surfaces with the assembly errors ($\Delta \gamma = 1.5^{{\prime}}$)

Fig. 16

Paths of contact and transmission error on face-gear surfaces with the assembly errors ($\Delta \gamma = - 1.5^{{\prime}}$)

5.2 Tooth Modification

The double-crowned tooth modification with HTE is designed based on the tooth profile modification of the rack-cutter and the motion relationship between the rack-cutter and the processed pinion.

Figure 17 shows the optimized tooth modification values of the pinion with different tooth modification methods. As shown in Fig. 17a, the pinion tooth is modified with the traditional second-order parabolic TE. The traditional TE is a second-order parabola; accordingly, the modification value is middle-convex. Figure 17b shows that the pinion tooth is modified with the new HTE. Unlike the tradition second-order TE, the HTE is middle-concave; then, the corresponding modification value is middle-concave. It can be seen clearly that the HTE ensures more tooth modification values in the zone of triple tooth. Meanwhile, the HTE ensures the TEs more even in the middle region on the tooth surface.

Fig. 17

Tooth modification values of the pinion

5.3 The Establishment of Parametric Mesh Model

The theoretical model of the tooth surfaces of the pinion and the face-gear are discretized to obtain the discrete data lattice of the tooth surface, and the lattice of the two tooth surfaces is rotated around their respective axes to obtain the tooth node. And a parameterized 3D grid of modified gears is generated based on MATLAB programming. Then, according to the writing order of C3D8R in ABAQUS, the nodes of the modified gears are sequentially numbered to construct an eight-node hexahedron element.

Finally, the five-tooth model of the face-gear pair is obtained by rotating the generated single-tooth mesh models of the face gear and pinion around their respective axes $\varphi_{1}$ and $\varphi_{2}$, respectively.

Due to the difference in the number of teeth participating in the meshing when the tooth surfaces are in contact and considering the deformation conditions during the meshing process of the face-gear, the single-tooth model is used to calculate the contact stress. The results of the comparison between the tooth surface contact stress calculated by ABAQUS and the theoretical Hertzian contact stress can be shown in Table 2.

Table 2 The comparison between the results of finite element method and the hertzian contact stress

According to the comparison between the results of FEM and the hertzian contact stress, the error of the tooth surface contact stress at the pitch circle is less than 10%, which verifies the correctness of the modeling method and preprocessing settings used in this paper.

5.4 FEM

The contact stress distribution of the face gear is shown in Fig. 18a. Before the tooth surface modification, at the crest and tooth root position of the face-gear, the contact area of the tooth surface is reduced, resulting in edge contact and the contact stress value increases sharply; After the modification, the load distribution of the tooth surface is optimized, and the adverse effects of stress concentration are eliminated. For the traditional second-order parabolic modification method, the modification amount of the tooth surface increases gradually from the middle area of the tooth surface to the boundary area. As mentioned earlier, the clearance between the pinion and face-gear surfaces is determined by the tooth modification. Therefore, the load on the tooth surface of the face-gear is transferred from the boundary region to the middle region, so the load in the middle region increases sharply, and the contact stress also increases accordingly. In the new modification method with HTE, the load is transferred from the boundary to the middle region, but due to the concave flank modification, the load distribution in the middle region is more uniform than the traditional second-order parabolic modification. The contact stress distribution of the modified tooth surface is shown in Fig. 18b, c. Compared with the unmodified tooth surface in Fig. 18a, The face-gear with modified tooth surface avoids the influence of edge contact. And this modification method improved tooth surface load distribution, which is very important to reduce tooth surface contact stress.

Fig. 18

Comparison of the contact stresses without assembly errors

The contact stress and bending stress distribution of the standard tooth, second-order parabolic modified tooth and high-order parabolic modified tooth of the face gear without the assembly errors are compared in Figs. 18d and 19d. As shown in Figs. 18d and 19d, before the modification, there is edge contact at the meshing of face-gear, and the contact stress of the tooth surface increases significantly. The maximum contact stress is 890.7 MPa, and the maximum bending stress is 51.1 MPa. After the traditional tooth surface modification, the edge contact at the crest and root position is avoided. The maximum contact stress is 739.7 MPa, and the maximum bending stress is 58.5 MPa. After the new high-order tooth surface modification, the concave modification in the middle meshing area makes the tooth surface load distribution more uniform, the maximum contact stress of the face-gear is only 580.4 MPa, and the maximum bending stress is only 44.6 MPa. It is clear that the traditional second-order parabolic modified gear has a much greater contact stress than that of the new high-order parabolic modified one.

Fig. 19

Comparison of the bending stresses without assembly errors

The maximum contact stress and maximum bending stress without assembly errors are shown in Table 3. There is a 34.83% decrease in maximum contact stress and a 12.72% decrease in maximum bending stress of face-gear based on the new high-order modification method; there is a 16.95% decrease in maximum contact stress, but a 14.48% increase in maximum bending stress of face-gear based on the traditional second-order parabolic tooth modification method.

Table 3 Comparison of the maximum contact stress and maximum bending stresses without assembly errors

In the face-gear transmission system, the assembly error of the shaft angle of the face- gear is inevitable. In addition, the higher the transmission ratio of the gear transmission, the greater the influence of the assembly error of the shaft angle. The gear ratio of the face gear pair is large. Therefore, it is of great significance to study the error sensitivity of the gear. Hereinafter, $\Delta \gamma$ is the assembly error of the shaft angle.

The contact stress and bending stress distribution of the standard tooth, second-order parabolic modified tooth and high-order parabolic modified tooth of the face-gear with the assembly errors ($\Delta \gamma = 1.5^{{\prime}}$) are compared in Figs. 20d and 21d. As shown in Figs. 20d and 21d, before the modification, the maximum contact stress is 858.7 MPa, and the maximum bending stress is 56.4 MPa. After the traditional tooth surface modification, the maximum contact stress is 745 MPa, and the maximum bending stress is 58.5 MPa. After the new high-order tooth surface modification, the maximum contact stress of the face-gear is only 656.2 MPa, and the maximum bending stress is only 47.7 MPa. The simulation results further verify the superiority of the method.

Fig. 20

Comparison of the contact stresses with assembly errors, $\Delta \gamma = 1.5^{{\prime}}$

Fig. 21

Comparison of the bending stresses with assembly errors, $\Delta \gamma = 1.5^{{\prime}}$

The maximum contact stress and maximum bending stress with assembly errors are shown in Table 4. There is a 23.58% decrease in maximum contact stress and a 15.42% decrease in maximum bending stress of face-gear based on the new high-order parabolic tooth modification method; there is a 13.24% decrease in maximum contact stress, but a 3.72% increase in maximum bending stress of face-gear based on the traditional second-order parabolic tooth modification method.

Table 4 Comparison of the maximum contact stress and maximum bending stresses with assembly errors, $\Delta \gamma = 1.5^{{\prime}}$

The contact stress and bending stress distribution of the standard tooth, second-order parabolic modified tooth and high-order parabolic modified tooth of the face-gear with the assembly errors ($\Delta \gamma = - 1.5^{{\prime}}$) are compared in Figs. 22d and 23d. As shown in Figs. 22d and 23d, before the modification, the maximum contact stress is 940.9 MPa, and the maximum bending stress is 63.9 MPa. After the traditional tooth surface modification, the maximum contact stress is 774 MPa, and the maximum bending stress is 80.6 MPa. After the new high-order tooth surface modification, the maximum contact stress of the face-gear is only 694 MPa, and the maximum bending stress is only 58.8 MPa. The simulation results further verify the superiority of the method.

Fig. 22

Comparison of the contact stresses with assembly errors, $\Delta \gamma = - 1.5^{{\prime}}$

Fig. 23

Comparison of the bending stresses with assembly errors, $\Delta \gamma = - 1.5^{{\prime}}$

The maximum contact stress and maximum bending stress with assembly errors are shown in Table 5. There is a 26.24% decrease in maximum contact stress and a 7.98% decrease in maximum bending stress of face-gear based on the new high-order parabolic tooth modification method; there is a 17.73% decrease in maximum contact stress, but a 26.13% increase in maximum bending stress of face-gear based on the traditional second-order parabolic tooth modification method.

Table 5 Comparison of the maximum contact stress and maximum bending stresses with assembly errors, $\Delta \gamma = - 1.5^{{\prime}}$

6 Conclusions

In order to improve the meshing performance of non-orthogonal helical face-gears, a designation of double-crowned tooth modification with new high-order transmission error is constructed in this paper. And the design of high-order modifications is verified via TCA and LTCA. From the present study, the following conclusions are drawn.

• (1) Based on the modified tooth profile of the rack cutter and the contact path in the meshing process of the face gear pair, a high-order transmission error is designed.

• (2) The introduced new modification causes significantly more stress decreases. The service life of face-gear will be further extended compared with the traditional second-order parabolic tooth modification.

• (3) By comparing the maximum contact stresses and maximum bending stresses of the tooth surfaces under the assembly error condition of the examples, the superiority of the new tooth surface high-order modification method is further verified.

• (4) The core idea of the new tooth surface high-order modification method is based on the transmission error designation and therefore it can be universal, not limited to face-gear drives, which can be extended to other types of gear drives.